A Preliminary Study on the Value of Texture Analysis in Predicting Bleeding Complications of CT-guided Percutaneous Lung Biopsy
-
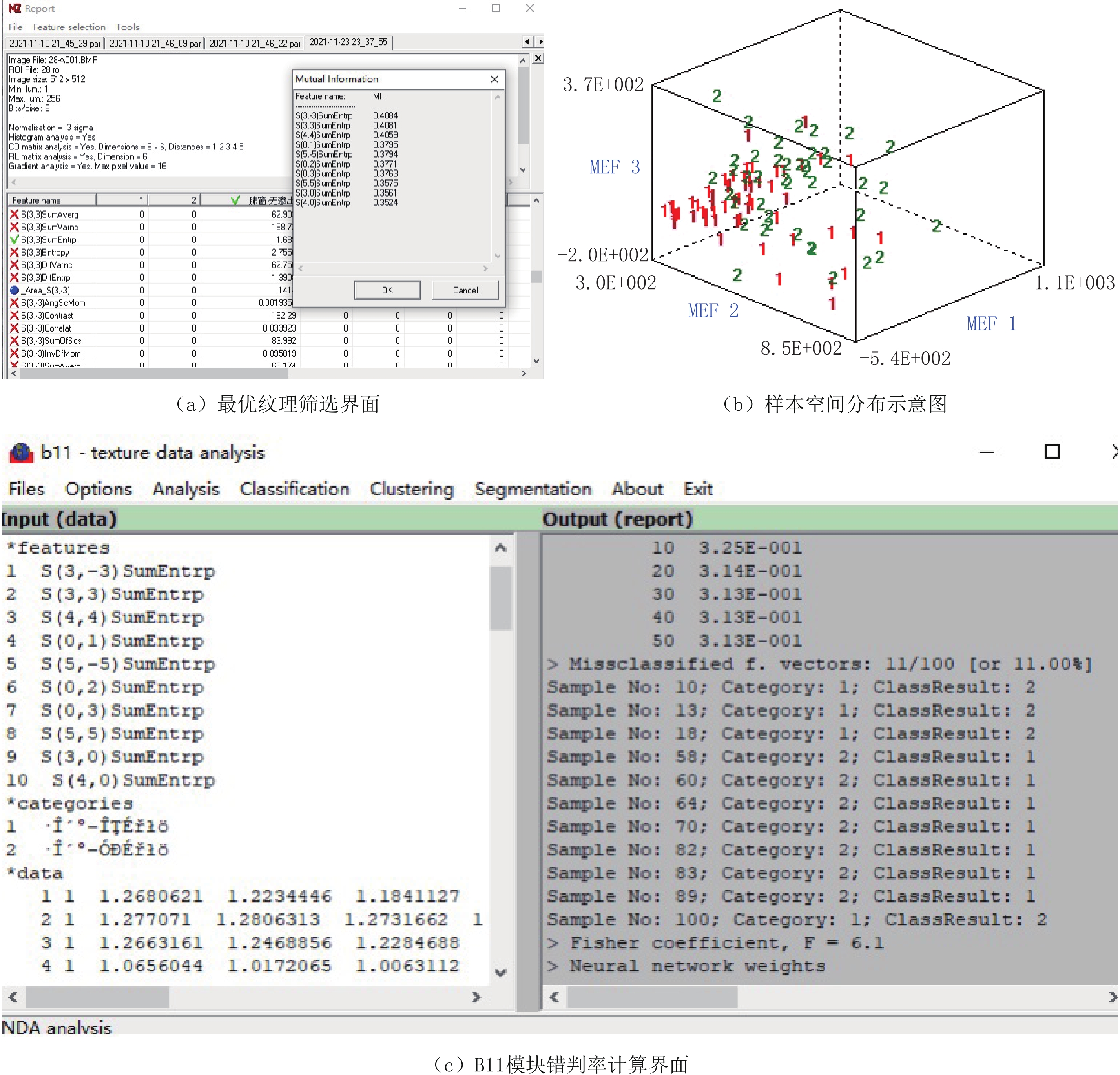
摘要: 目的：探讨基于CT图像的纹理分析对CT引导下经皮肺穿刺出血并发症的预测价值。方法：回顾性分析130例行CT引导下经皮肺穿刺活检患者的术前平扫图像，术区有大于或等于2级肺出血者为有出血组，0级或1级肺出血者为无/少量出血组。首先随机选取100例作为训练组，采用MaZda 软件，分别手动勾画出平扫肺窗图像上预穿刺路径周边的肺野作为感兴趣区（ROI），分别通过Fisher系数、分类错误概率联合平均相关系数（POE+ACC）、交互信息（MI）法筛选出区分出血组及无/少量出血组最具有价值的纹理特征，然后分别采用原始数据分析（RDA）、主要成分分析（PCA）、线性分类分析（LDA）和非线性分类分析（NDA）四种特征分类统计方法进行判断，结果以错判率形式表示；最后再根据得到的最优纹理参数及特征分类方法分别对另外30例图像加以验证。结果：以穿刺路径周边的肺野作为ROI时，最低错判率为11.00％（11/100），该结果出现在特征选择方法采用POE+ACC或MI，特征分类统计方法采用NDA时，以此结果进行验证的错判率分别为13.33％(4/30)和16.67％(5/30)，两者差异无统计学意义。结论：分析预穿刺路径周边肺野的纹理特征有助于预测CT引导下肺穿刺并发出血的风险，为选择合适的穿刺路径以减少肺出血并发症提供依据。Abstract: Objective: In this paper we intends to explore the value of texture analysis based on CT image in predicting the complications of percutaneous pulmonary puncture hemorrhage under the guidance of CT. Methods: The preoperative plain scan images of 130 patients who underwent CT-guided percutaneous lung biopsy were analyzed retrospectively. The patients with pulmonary hemorrhage greater than or equal to grade 2 in the operative area were assined into the bleeding group while the patients with grade 0 or grade 1 pulmonary hemorrhage were assined into the no / small bleeding group. 100 cases were randomly selected as the training group, and the lung field around the pre-puncture path on the plain scan lung window image was manually drawn as the region of interest (ROI) by using MaZda software. The most valuable texture features were selected by methods of Fisher coefficient, classification error probability joint average correlation coefficient (POE+ACC) and interactive information (MI) to distinguish between bleeding group and no / small amount of bleeding group. Then, the four following feature classification statistical methods; raw data analysis (RDA), principal component analysis (PCA), linear classification analysis (LDA) and nonlinear classification analysis (NDA), were used for judgement, and the results were shown by way of error rate. Finally, the other 30 cases were verified according to the optimal texture parameters and feature classification method. Results: The lowest error rate was 11.00% (11/100) when the lung field around the puncture path was used as ROI. The error rates were respectively 13.33% (4/30) and 16.67% (5/30), when the feature selection method was POE+ACC or MI, and the feature classification statistical method was NDA, there was no significant difference between the two groups. Conclusion: The analysis of the texture characteristics of the lung field around the puncture path is helpful in predicting the risk of pulmonary puncture complicated with hemorrhage under the guidance of CT, and can provide certain basis for selecting a suitable puncture path to reduce the complications of pulmonary hemorrhage.
-
由于地球介质的非完全弹性性质，地震波在实际地层中传播时往往发生显著的能量损失，引起地震子波的振幅衰减、主频降低以及频带宽度变窄[1]。吸收衰减特性是实际地球介质的固有特性，在地震勘探中一般用品质因子Q予以表征。
研究表明[2]，介质的吸收衰减特性受到多种因素的影响，介质的Q值与地层岩性、孔隙度、渗透率，以及孔隙流体类型等诸多岩石物理性质紧密相连。鉴于此，精确估计Q值，对于地层岩性精准识别、储层有效预测，乃至地震剖面分辨率的提升，都有着不可忽视的重要作用。
目前地震勘探中主要采用谱比法[3]进行Q值估算。为了避免传统频域率谱比法受时窗影响的局限性，谱比法已经发展到时频域。
Reine等[4]通过固定时窗的短时傅里叶变换、Gaber变换、变时窗的S变换和连续小波变换对比，发现变时窗的时频分析对于Q值的估计更加准确和稳定。但是时频域谱比法受噪声和频带宽度的选择影响较大，为进一步提高Q值提取的准确性和稳定性，许多学者对时频域谱比法进行了改进，其中改进Q值的计算方法和选取较高分辨率的时频分析方法是主要手段。朱耀旭等[5]依据子波Z变换的根关于单位圆移动与否构建遗传算法的编码链条，并利用全局优化算法估计了Q模型；陈文爽等[6]基于广义S变换，构建了时频域谱比斜率反演方程，通过方程组求解求取稳定的Q值；杨登锋等[7]提出了加权谱比法的Q值估计方法，降低了对频段选取的依赖性。
针对叠前数据，魏文等[8]提出小波域Q值求取方法；王小杰等[9-10]提出基于S变换Q值估计方法，后又针对不同频率的地震信号相互影响的问题，提出小波域分频Q值提取方法；李波等[11]结合Lucy-Richardson算法和广义S变换提高Q值估计的准确性；Li等[12]利用反演谱分解得到高分辨率时频谱，通过整形正则化来估计Q值；周东红等[13]基于复谱分解的高分辨率时频分析方法，通过井震联合估计Q值。
地下实际介质对振动能量的不断吸收衰减使得地震波中高频成分逐渐减少，使得地震子波具有时变特性，传统的平稳地震记录模型并不符合实际情况，于是有学者基于非平稳地震记录模型提出Q值估计方法。张繁昌等[14]通过对地震信号进行子波分解，将得到的匹配子波视为时变子波，以此来估计Q值；张瑾等[15]通过消除非本征衰减影响、结合双参考频段和频域平均化处理，提高了Q值估计精度；许李囡等[16]推导了非平稳地震记录模型在S变换域中的近似表示，并由此建立Q值和子波之间的优化函数，通过求解该优化函数估计Q值。
近年来，随着深度学习方法在地震勘探领域的发展，研究人员开展了基于深度学习的Q值估计方法研究。基于深度学习的Q值估计方法通过构建神经网络模型，直接从地震数据中学习Q值分布特征，避免了传统方法对时频变换的依赖。周晨[17]基于特征工程原则，构建了多输入单输出的深度神经网络，提高了Q值估计的精度和抗噪性；Wang等[18]提出了一种基于多任务学习的动态子波振幅谱提取方法，并将其应用于Q值估计；Li等[19]2024提出了一种基于全连接网络的VSP地震数据Q值提取方法。
实际地震数据可以看成时变子波与局部反射系数褶积后再叠加，从而使得地震记录的时频域振幅谱呈现复杂的多峰谱特性，这导致对数谱比与频率之间不再是严格的线性关系，严重影响了拟合的稳定性与Q值估计的精度。
为解决上述问题，本文基于非平稳地震道模型，通过广义S变换得到地震道时频谱，通过时频谱的对数计算，得到不同时刻地震记录的复赛谱。根据复赛谱域子波分布在低频段、反射系数位于高频段的特征，利用最小二乘法对低频段复赛谱进行平滑拟合，得到子波的复赛谱，消除了反射系数对时频振幅谱的影响，有效恢复了对数谱比与频率的线性关系。通过提取子波和理论子波的对比验证了复赛谱提取时变子波的准确性。与常规谱比法的对比表明了该方法具有更高的准确性和稳定性。
1. 方法原理
1.1 非平稳地震记录模型的广义S域表示
忽略噪声的影响，时间域的平稳地震记录模型可以表示为震源子波与反射系数的褶积。
$$ s(t) = w(t) * r(t) = \int\limits_{{{ - }}\infty }^\infty {w\left( {t - s} \right)} r(s){\mathrm{d}}s \text{，} $$ (1) 式中，
$ t $ 和$s$ 为时间变量，$s(t)$ 为平稳地震记录，$w(t)$ 为震源子波，$r(t)$ 为反射系数。平稳地震记录模型中初始子波与经过地层传播后的子波没有差别。考虑到实际地震波传播过程中的几何扩散、吸收衰减等效应，需引入衰减函数来描述子波的衰减。基于Aki常Q理论[20]的衰减函数表示为：$$ a(t,f) = {\text{exp}}\left( {\frac{{ - {\text{π}} ft}}{Q}} \right)\text{，} $$ (2) 式中
$ f $ 为频率，$Q$ 为品质因子。将平稳地震记录褶积模型转换到频率域，并引入衰减函数，推导出频率域非平稳地震记录褶积模型[21]：$$ s(f) = w(f)\int\limits_{ - \infty }^\infty {a\left( {t,f} \right)} r(t)\exp \left( { - 2{\text{π}} if} \right)t\;{\mathrm{d}}t。 $$ (3) 对地震信号
$ x(t) $ 的广义S变换[22]定义为：$$ \begin{gathered}{S_g}\left( {\tau ,f} \right) = \int\limits_{ - \infty }^\infty {x(t)} \frac{{\lambda {{\left| f \right|}^p}}}{{\sqrt {2{\text{π}} } }} \times\\ \exp \left( {\frac{{ - {\lambda ^2}{f^{2p}}{{\left( {\tau - t} \right)}^2}}}{2}} \right)\exp \left( { - i2{\text{π}} f} \right)t\;{\mathrm{d}}t \end{gathered} \text{，}$$ (4) 式中，
$ \tau $ 为滑动高斯窗函数中心点的时间；$ \lambda $ 和$ p $ 表示高斯窗函数的两个调节因子。广义S变换能够依据信号频率的动态变化，灵活地对窗函数的宽度实施精准调节。在检测信号频率的变化走向时，其表现更为出色，能够敏锐捕捉到细微的趋势变化。与传统变换方法相比[23]，广义S变换拥有多尺度的时频分辨率，这使其在不同频率段都能清晰呈现信号特征，而且还展现出了更高的时频聚焦性，意味着它能够将能量更为集中地聚焦于信号的关键时频区域，对非平稳信号频率变化的描绘更为细腻、精准，刻画能力相较于其他方法显著增强，能够有效提高非常规油气资源评价精度[24]，有效推动页岩油资源产业化发展。
将式（3）推广到广义S变换域中，推导可知非平稳地震记录所对应的广义S变换，近似等同于子波、衰减函数以及反射系数三者各自的广义 S 变换相互乘积：
$$ {S_g}\left( {\tau ,f} \right) \approx w(f)a\left( {\tau ,f} \right){R_g}\left( {\tau ,f} \right)\text{，} $$ (5) 式中，
${R_g}(\tau ,f)$ 表示反射系数的广义S变换，而$w(f)a(\tau ,f)$ 本质上是子波在经地层传播时间$\tau $ 后的傅里叶变换，将该项综合表示为时变子波：$$ {W_a}\left( {\tau ,f} \right) = w(f)a\left( {\tau ,f} \right)\text{。} $$ (6) 在广义S变换域，非平稳地震记录的时频谱近似表示为时变子波时频谱和反射系数时频谱的乘积：
$$ {S_g}\left( {\tau ,f} \right) \approx {W_a}\left( {\tau ,f} \right){R_g}\left( {\tau ,f} \right)。 $$ (7) 1.2 复赛谱域时变子波提取与Q值估计
基于反射系数谱为白谱的假设，认为反射系数影响地震记录振幅谱的细节，而子波决定地震记录振幅谱的大体形状，因此传统谱比法直接忽略反射系数的影响。但实际反射系数并不符合白谱的假设，子波与反射系数褶积后相互干涉、叠加使得地震记录振幅谱成为复杂的多峰谱。为摆脱反射系数的白谱假设，通过对地震记录的时频谱取对数将其转换至复赛谱域，从而利用复赛谱域子波分布在低频段这一特征提取时变子波的振幅谱。
式（7）给出了广义S域内非平稳地震记录在时频谱域的求取公式。仅考虑其振幅谱，将地震记录在每个时间点的振幅谱取对数后，得到时频域复赛谱，即非平稳地震记录的复赛谱：
$$ \ln \left| {{S_g}\left( {\tau ,f} \right)} \right| = \ln \big| {{W_a}\left( {\tau ,f} \right)} \big| + \ln \left| {{R_g}\left( {\tau ,f} \right)} \right| ，$$ (8) 其中，
$\ln \big| {{W_a}\left( {\tau ,f} \right)} \big|$ 表示时变子波的复赛谱，其在复赛时频域为光滑且连续的低频分量；$\ln \left| {{R_g}\left( {\tau ,f} \right)} \right|$ 则表示反射系数的复赛谱，其在复赛时频域为剧烈震荡的高频分量。在复赛谱域，根据反射系数和地震子波表现出的频率特征差异，可有效区分两者。通过对复赛谱进行平滑处理，便可提取出时变子波的振幅谱[20]。记非平稳地震记录的复赛时频谱为：
$$ {S_{\ln }}\left( {\tau ,f} \right) = \ln \left| {{S_g}\left( {\tau ,f} \right)} \right|\text{，} $$ (9) 然后通过最小二乘法拟合，平滑每个时间点的地震记录复赛谱：
$$ {S_{{\mathrm{fit}}}}\left( {\tau ,f} \right) = {\mathrm{fit}}\Big({S_{\ln }}\left( {\tau ,f} \right)\Big)\text{。} $$ (10) 在式（10）的基础上，时变子波的振幅谱可表示为：
$$ {W_a}\left( {\tau ,f} \right) = \exp \Big( {{S_{{\mathrm{fit}}}}\left( {\tau ,f} \right)} \Big)。 $$ (11) 通过上述流程，在保留时变效应的同时，可以提取到呈现平滑单峰特征的子波振幅谱。假设地震波传播到地层上下界面的旅行时为
${t_1}$ 和${t_2}$ ，取两个界面时变子波振幅谱比值的对数得到：$$ \ln \left(\frac{{{W_a}\left( {{t_2},f} \right)}}{{{W_a}\left( {{t_1},f} \right)}}\right) = - \frac{{{\text{π}} f\Delta t}}{Q} + C \text{，}$$ (12) 式中，
$\Delta t = {t_2} - {t_1}$ ，$C$ 表示与频率无关的量，式（12）中对数谱比与频率为线性关系，通过拟合得到其斜率$k = - {{\text{π}} }\Delta t/Q$ ，由此可计算Q值：$$ Q = - \frac{{{\text{π}} f\Delta t}}{k}。 $$ (13) 2. 模型测试
首先进行时频域复赛谱提取非平稳地震记录时变子波振幅谱的模型测试；然后对单道非平稳地震记录模型估计Q值，以验证复赛谱提取时变子波估计Q值的可行性与准确性；最后由含噪模型测试对比本文方法和常规方法的抗噪性。
2.1 复赛谱提取时变子波振幅谱
选取主频30 Hz的雷克子波作为震源子波，与如图1（a）所示随机反射系数序列褶积，得到平稳地震道如图1（b）所示。引入式（2）所示的衰减函数，设置其Q值为30，利用式（7）计算非平稳地震道，结果如图1（c）所示。
对比图1（b）和图1（c），明显可见在衰减函数的影响下，随着传播时间的增加，地震子波的振幅衰减，频率降低。
为了验证在复赛谱域进行非平稳地震数据子波振幅谱提取的准确性，采用广义S变化对地震数据进行时频分析，得到非平稳地震记录的时频谱如图2（a）所示。再将非平稳地震记录时频谱按式（8）取对数，得到非平稳地震记录的时频域复赛谱如图2（b）所示。图2（c）中，蓝线为某时间点的复赛谱，在复赛谱中，反射系数呈现震荡、高频特征。通过最小二乘法拟合来平滑复赛谱，其结果如图2（c）中红线所示，平滑后的结果提取出子波的复赛谱，消除了反射系数导致的剧烈波动。再对平滑结果按照式（11）计算得到该时间点子波的振幅谱。对每个时间点的复赛谱进行上述操作，得到非平稳地震道的时变子波时频振幅谱，其结果如图2（d）所示。
![]()
图 2 时频域复赛谱提取时变子波振幅谱Figure 2. Time-varying amplitude spectrum of the wavelet of cepstrum domain通过本文方法，反射系数导致的剧烈震荡现象被有效消除，可以更加清晰地展现出地震子波频谱随着传播时间的增加，振幅减小、主频降低且频带变窄的变化趋势，能够精确刻画地震子波的时变特性。
在随机反射系数序列（图1（a））中存在尖脉冲的时间点，对应如图2（a）所示的非平稳地震道时频谱的能量较为集中，选取266、553和824 ms 3个时间点，对应的非平稳地震道振幅谱、提取子波振幅谱和理论时变子波振幅谱对比结果如图3所示。图中黑线为原始的地震记录的振幅谱，因受到反射系数影响而产生很大的波动，成为复杂的多峰谱，图中红线为提取的时变子波振幅谱，蓝线为理论时变子波振幅谱，通过对比明显可见不同传播时刻的提取子波振幅谱与对应时刻的理论子波振幅谱均吻合，证明了利用复赛谱提取时变子波振幅谱方法的准确性。
2.2 无噪模型测试
为验证本文方法估计Q值的有效性，选用无噪声模型进行测试。由图4所示的随机反射系数与30 Hz雷克子波生成地震记录，品质因子Q分别设置为25、50、75和100，得到的非平稳地震道模型如图5所示。对上述模型分别用本文方法和常规时频域谱比法估计Q值，两种方法均选择0.1 s处和0.5 s处的振幅谱进行谱比，然后拟合对数谱比曲线获得斜率，两种方法拟合斜率的频率段均选取10~70 Hz，再通过式（13）计算Q值。
图6为两种方法估计Q值的结果。图7统计了不同方法估计Q值与理论Q值之间的误差。由图可知：对于不同Q值的模型，本文方法的结果比常规谱比法的结果更加接近理论值；本文方法结果的相对误差均小于常规谱比法结果的相对误差，且都小于6%。无噪声模型测试的结果表明：复赛谱提取时变子波Q值估计方法相较与常规谱比法具有更高的精确度。
![]()
图 6 本文方法与常规谱比法Q值估计结果Figure 6. Q estimation results of the proposed and the conventional spectral ratio methods![]()
图 7 本文方法与常规谱比法Q值估计结果相对误差Figure 7. Relative error between the proposed and the conventional spectral ratio methods为进一步对比本文方法和常规时频域谱比法的差异，以Q值为100的非平稳地震道模型为例，图8（a）为未经过处理的瞬时地震道振幅谱。由图可见瞬时地震道振幅谱具有剧烈的波动，其形态复杂且有多个波峰，不同时刻的振幅谱形态具有较大的差异。对地震道瞬时振幅进行处理，得到其对数谱比曲线（图9（a））。由图可见对数谱比与频率的线性关系很差，这使得拟合直线的斜率与理论值有较大的偏差，由此斜率估计的Q值误差较大。图8（b）为经过复赛谱提取的时变子波瞬时振幅谱，振幅谱为光滑的单峰形态，0.5 s的子波振幅谱与0.1 s的子波振幅谱对比，其振幅峰值降低，主频减小且频带变窄，表明提取的子波振幅谱保留了时变特征。提取子波振幅谱的对数谱比曲线如图9（b）所示，可以明显看出对数谱比与频率之间的线性关系有了显著的增强。
2.3 含噪模型测试
为对比研究本文方法与常规谱比法的抗噪性，本文进行了含噪声模型测试。选取图5中理论Q值为25的不含噪非平稳地震道模型，为其加入高斯白噪声合成含噪模型。在与无噪模型实验相同的条件下，通过本文方法和常规谱比法估计含噪模型的Q值。为分析不同强度的噪声对两种方法估计Q值的影响，设置含噪模型的信噪比为5、10和15 dB，不同信噪比的含噪模型如图10所示。用两种方法对不同信噪比的含噪模型各进行100次独立实验，每次实验所添加高斯白噪声是随机的，统计实验结果的均值和标准差。
本文方法和常规谱比法估计Q值的统计结果如表1所示，由表可知，地震数据的信噪比越高，两种方法Q值估计结果的精确度就越高；在不同强度的噪声影响下，本文方法Q值估计结果的精确度均高于常规谱比法Q值估计结果的精确度。
表 1 不同信噪比模型Q值估计统计结果Table 1. Statistical results of Q estimation for different signal-to-noise ratio models模型信噪比 5 dB 10 dB 15 dB 本文方法 均值 27.30 25.65 25.28 标准差 6.35 4.03 3.04 常规谱比法 均值 35.20 32.36 27.87 标准差 11.20 10.34 6.81 图11为本文方法对不同信噪比模型估计Q值的结果，由图可知，地震数据信噪比越高，本文方法估计Q值的结果就越接近理论Q值。由含噪模型测试结果可知，本文方法的准确性与稳定性均高于常规谱比法，具有更强的抗噪能力。
![]()
图 11 不同信噪比模型本文方法Q值估计结果Figure 11. Q estimation results of different signal-to-noise ratios using the proposed method3. 实际资料应用
将复赛谱域时变子波Q值估计方法应用于某工区的实际地震数据中。该工区整体为向斜构造，发育砂、泥岩互层沉积，主要形成砂岩上倾尖灭圈闭与砂岩透镜体圈闭。
如图12所示，选取工区内过井w1的地震剖面验证本文方法，将自然伽马测井曲线投影于该剖面（图中黑色曲线），黑圈所示位置为目的层，其岩性为砂岩。
对该地震剖面估计Q值，图13是常规时频域谱比法估计的Q值剖面，图14是利用本文方法估计的Q值剖面。由图13和图14对比可见：常规时频域谱比法估计Q值剖面的高Q值区域与低Q值区域的边界不规则，存在较多零散分布的点状低Q值区域；本文方法估计的Q值剖面，其高Q值区域与低Q值区域之间的边界清晰。在图中黑色圆圈内，本文方法估计的Q值结果与目的层处测井曲线的自然伽马值相吻合，呈现低Q值特征。对比图15（a）与图15（b）可知，本文方法获得的Q值层次切片上低Q值更好地刻画了有效储层的空间展布。
![]()
图 13 常规时频域谱比法估计Q值剖面Figure 13. Q estimation profile obtained using the conventional spectral ratio method4. 结论
本文提出一种基于时频域复赛谱时变子波提取的Q值估计方法。该方法将地震记录时频谱变换为复赛谱，进行时变子波振幅谱提取，在此基础上应用时频域谱比法估计Q值。实验结果表明：
（1）复赛谱域提取子波方法能够准确提取非平稳地震记录不同时刻的子波振幅谱，提取的子波振幅谱摆脱了反射系数的白谱假设，保留了时变特性；
（2）相对于传统的时频域谱比法，本方法提取的时变子波振幅谱有效消除了反射系数对地震子波的影响，由子波振幅谱作比得到的对数谱比与频率之间的线性关系显著增强；
（3）与传统时频域谱比法相比，本文方法具有更高的准确性与抗噪性。实际数据测试结果表明本文方法能够有效的估计Q值，具有较好的适用性。
致谢：中石化胜利油田分公司物探研究院为本文研究提供了大量资料和基础数据。
-
表 1 三种纹理特征提取法分别筛选出的的10个最优特征
Table 1 The 10 optimal features screened out respectively by the three texture feature extraction methods
方法 纹理特征 Fisher S(0,3)SumEntrp、S(4,0)SumEntrp、S(3,3)SumEntrp、S(0,2)SumEntrpS、(3,0)SumEntrp、S(0,4)SumEntrp、S(4,4)SumEntrp、S(5,0)SumEntrp、S(0,5)SumEntrp、S(2,-2)SumEntrp POE+ACC Skewness、Kurtosis、Teta3、S(5,5)SumVarnc、S(0,2)DifVarnc、Vertl_RLNonUni、WavEnLH_s-2、WavEnHH_s-4、
WavEnHL_s-4、WavEnHL_s-3MI S(3,3)SumEntrp、S(4,4)SumEntrp、S(0,2)SumEntrp、S(0,3)SumEntrp、S(3,0)SumEntrp、S(5,-5)SumEntrp、S(5,0)SumEntrp、S(4,0)SumEntrp、S(0,1)SumEntrp、S(5,5)SumEntrp 
下载: 导出CSV
表 2 纹理分析预测穿刺并发出血的错判率[％（例）]
Table 2 Misjudgment rate of puncture complicated with bleeding predicted by texture analysis [% (cases)]
纹理特征 鉴别方法 RDA PCA LDA NDA 预穿刺路径
周边的肺野Fisher 27.00
（27/100）33.00
（33/100）24.00
（24/100）12.00
（12/100）POE+AsCC 41.00
（41/100）40.00
（40/100）33.00
（33/100）11.00
（11/100）MI 30.00
（30/100）31.00
（31/100）33.00
（33/100）11.00
（11/100）注：括号内为错判数/所有例数。
下载: 导出CSV
-
[1] POULOU L S, TSAGOULI P, ZIAKAS P D, et al. Computed tomography-guided needle aspiration and biopsy of pulmomary lesions: A single-center experience in 1000 patients[J]. Acta Radiology, 2013, 54: 640−645. doi: 10.1177/0284185113481595
[2] TAVARE A N, PATEL A, SAINI A, et al. Systemic air embolism as a complication of percutaneous lung biopsy[J]. British Journal of Hospital Medicine, 2018, 79(2): 106−107. doi: 10.12968/hmed.2018.79.2.106
[3] IALONGO P, CIARPAGLINI L, TINTI M D, et al. Systemic air embolism as a complication of percutaneous computed tomography guided transthoracic lung biopsy[J]. Annals of the Royal College of Surgeons of England, 2017, 99(6): 174−176. doi: 10.1308/rcsann.2017.0091
[4] SMIT D R, KLEIJN S A, DEVOOGT W G. Coronary and cerebral air embolism: A rare complication of computed tomography-guided transthoracic lung biopsy[J]. Netherlands Heart Journal, 2013, 21(10): 464−466. doi: 10.1007/s12471-013-0411-1
[5] 董鑫哲, 邢立刚, 于金明. 肿瘤异质性的医学影像学分析及临床应用[J]. 中华肿瘤杂志, 2013,(2): 81−84. DOI: 10.3760/cma.j.issn.0253-3766.2013.02.001. DONG X Z, XING L G, YU J M. Medical imaging analysis and clinical application of tumor heterogeneity[J]. Chinese Journal of Oncology, 2013, (2): 81−84. DOI: 10.3760/cma.j.issn.0253-3766.2013.02.001. (in Chinese).
[6] GILLIES R J, KINAHAN P E, HRICAK H. Radiomics: Images are more than pictures, they are data[J]. Radiology, 2016, 278(2): 563−577. doi: 10.1148/radiol.2015151169
[7] 中国抗癌协会肿瘤介入学专业委员会, 中国抗癌协会肿瘤介入学专业委员会青委会. 胸部肿瘤经皮穿剌活检中国专家共识[J]. 中华介入放射学电子杂志, 2018,6(3): 188−194. DOI: 10.3877/cma.j.issn.2095-5782.2018.03.002. The Professional Committee of Tumor Intervention of China Anti Cancer Association, the Youth Committee of the Professional Committee of Tumor Intervention of China Anti Cancer Association. Consensus of Chinese experts on percutaneous biopsy of thoracic tumors[J]. Chinese Journal of Interventional Radiology (Electronic Edition), 2018, 6(3): 188−194. DOI: 10.3877/cma.j.issn.2095-5782.2018.03.002. (in Chinese).
[8] TAI R, DUNNE R M, TROTMAN-DICKENSON B, et al. Frequency and severity of pulmonary hemorrhage in patients undergoing percutaneous CT guided transthoracic lung biopsy: Singleinstitution experience of 1175 cases[J]. Radiology, 2016, 279(1): 287−296. doi: 10.1148/radiol.2015150381
[9] 刘丹, 耿左军, 朱青峰, 等. CT引导下经皮肺穿刺活检的临床应用[J]. 介入放射学杂志, 2018,27(6): 539−543. DOI: 10.3969/j.issn.1008-794X.2018.06.010. LIU D, GENG Z J, ZHU Q F, et al. Clinical application of CT-guided percutaneous needle biopsy of lung[J]. Journal of Interventional Radiology, 2018, 27(6): 539−543. DOI: 10.3969/j.issn.1008-794X.2018.06.010. (in Chinese).
[10] WANG Y, JIANG F M, TAN X B, et al. CT-guided percutaneous transthoracic needle biopsy for paramediastinal and nonparamediastinal lung lesions: Diagnostic yield and complications in 1484 patients[J]. Medicine, 2016, 95(31): e4460. doi: 10.1097/MD.0000000000004460
[11] 张皓, 李琳, 吕发金. 基于Fisher判别构建CT引导下肺穿刺活检并发症的预测模型[J]. 介入放射学杂志, 2020,29(1): 45−50. DOI: 10.3969/j.issn.1008-794X.2020.01.009. ZHANG H, LI L, LV F J. The establishment of a model for predicting complications of CT-guided percutaneous transthoracic needle biopsy based on Fisher discriminant[J]. Journal of Interventional Radiology, 2020, 29(1): 45−50. DOI: 10.3969/j.issn.1008-794X.2020.01.009. (in Chinese).
[12] WIENER R S, WIENER D C, GOULD M K. Risks of transthoracic needle biopsy: How high?[J]. Clinical Pulmonary Medicine, 2013, 20: 29−35. doi: 10.1097/CPM.0b013e31827a30c1
[13] 杨肖华, 黄新宇, 汪国祥. CT引导下经皮肺穿刺活检术并发症的影响因素分析[J]. 介入放射学杂志, 2013,22(8): 658−662. DOI: 10.3969/j.issn.1008-794X.2013.08.011. YANG X H, HUANG X Y, WANG G X. Complications of CT-guided percutaneous lung puncture biopsy: an analysis of influencing factors[J]. Journal of Interventional Radiology, 2013, 22(8): 658−662. DOI: 10.3969/j.issn.1008-794X.2013.08.011. (in Chinese).
[14] ZHU H, ZHANG L, WANG Y, et al. Improved image quality and diagnostic potential using ultra-high-resolution computed tomography of the lung with small scan FOV: A prospective study[J]. PLoS One, 2017, 12(2): e0172688. doi: 10.1371/journal.pone.0172688
[15] KIM G R, HUR J, LEE S M, et al. CT fluoroscopy-guided lung biopsy versus conventional CT-guided lung biopsy: A prospective controlled study to assess radiation doses and diagnostic performance[J]. European Radiology, 2011, 21(2): 232−239. doi: 10.1007/s00330-010-1936-y
[16] SHESHADRI A, RODRIGUEZ A, CHEN R, et al. Effect of reducing field of view on multi-detector quantitative computed tomography parameters of airway wall thickness in asthma[J]. Journal of Computer Assisted Tomography, 2015, 39(4): 584−590. doi: 10.1097/RCT.0000000000000238
[17] 刘玉良, 陈麦林, 朱海滨, 等. 小视野扫描方法在肺小结节CT引导下经皮穿刺活检中的应用[J]. 中国介入影像与治疗学, 2019,16(9): 517−521. DOI: 10.13929/j.1672-8475.201905002. LIU Y L, CHEN M L, ZHU H B, et al. Application of small field of view scan in CT-guided transthoracic needle lung biopsy for pulmonary small nodule[J]. Chinese Journal of Interventional Imaging and Therapy, 2019, 16(9): 517−521. DOI: 10.13929/j.1672-8475.201905002. (in Chinese).
[18] DAVNALL F, YIP C S, LJUNGQVIST G, et al. Assessment of tumour heterogeneity: An emerging imaging tool for clinical practice[J]. Insights Imaging, 2012, 3(6): 573−589.
[19] 周林丽, 冯峰. CT纹理分析对吉非替尼治疗肺腺癌疗效评估的应用[J]. CT理论与应用研究, 2020,29(4): 473−480. DOI: 10.15953/j.1004-4140.2020.29.04.10. ZHOU L L, FENG F. CT texture analysis on the response evaluation of lung adenocarcinoma treated by gifitinib[J]. CT Theory and Applications, 2020, 29(4): 473−480. DOI: 10.15953/j.1004-4140.2020.29.04.10. (in Chinese).
[20] 凡健, 高斌, 夏春华. CT平扫与动脉期图像纹理分析在鉴别膀胱乳头状瘤和膀胱癌中的应用价值[J]. CT理论与应用研究, 2020,29(6): 742−750. DOI: 10.15953/j.1004-4140.2020.29.06.13. FAN J, GAO B, XIA C H. The value of CT non-enhanced and enhanced image texture analysis in differentiating bladder papilloma from bladder cancer[J]. CT Theory and Applications, 2020, 29(6): 742−750. DOI: 10.15953/j.1004-4140.2020.29.06.13. (in Chinese).
计量
- 文章访问数: 467
- HTML全文浏览量: 134
- PDF下载量: 31
