Sparse CT Reconstruction Based on Adversarial Residual Dense Deep Neural Network
-
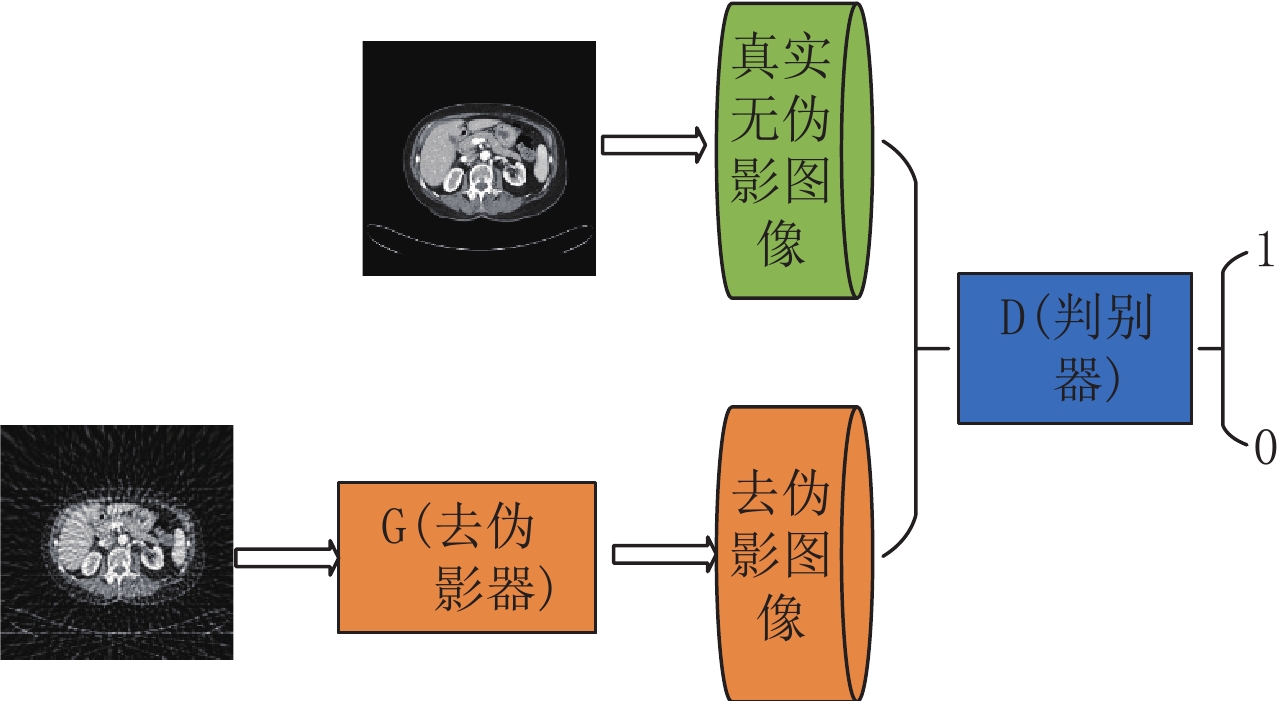
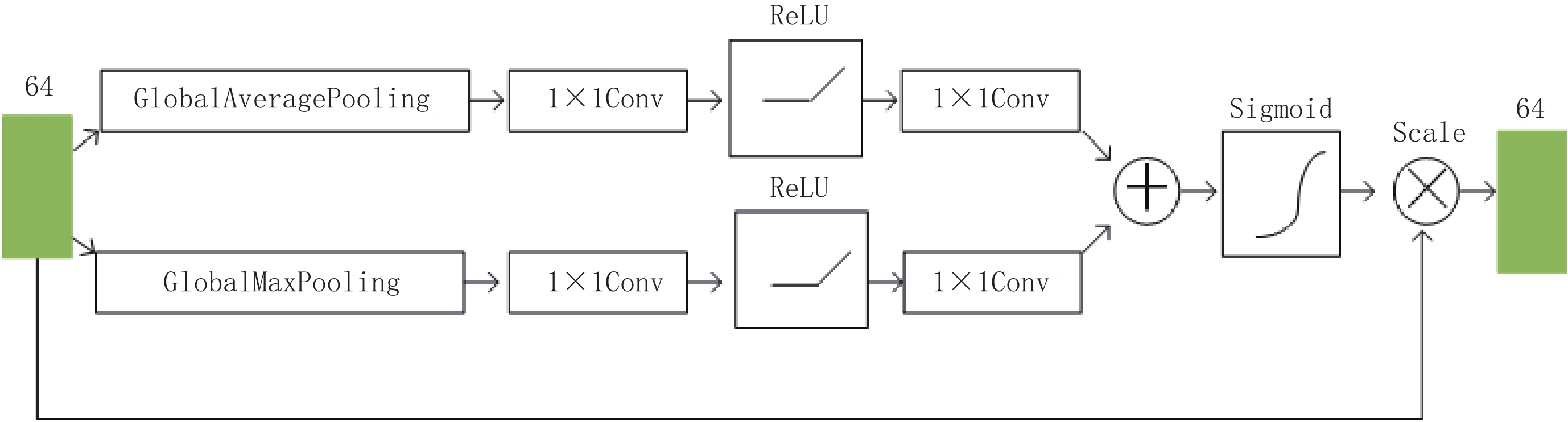
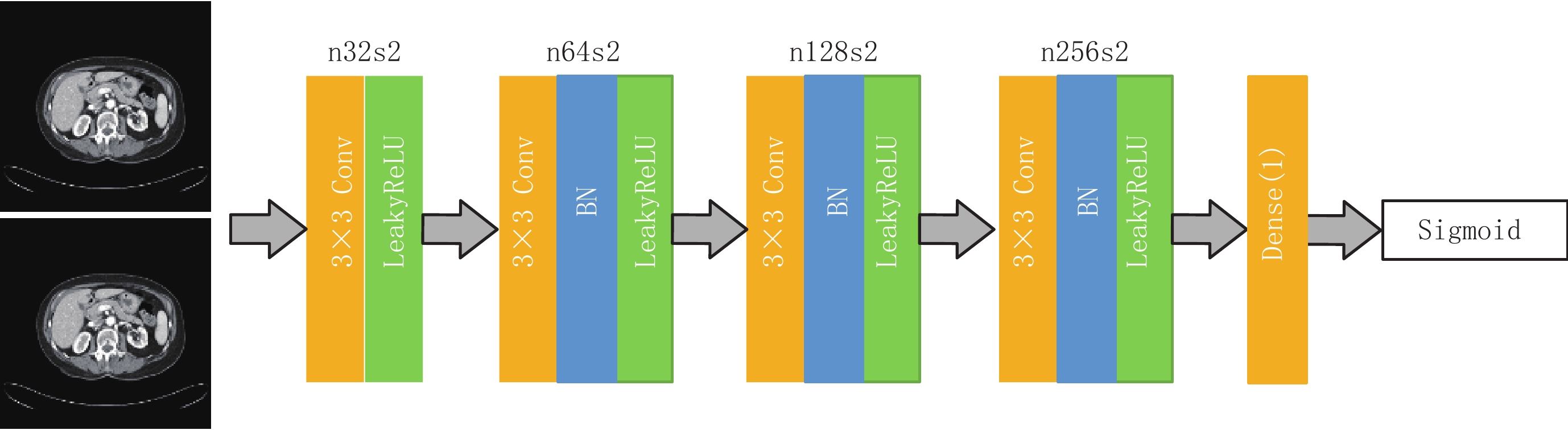
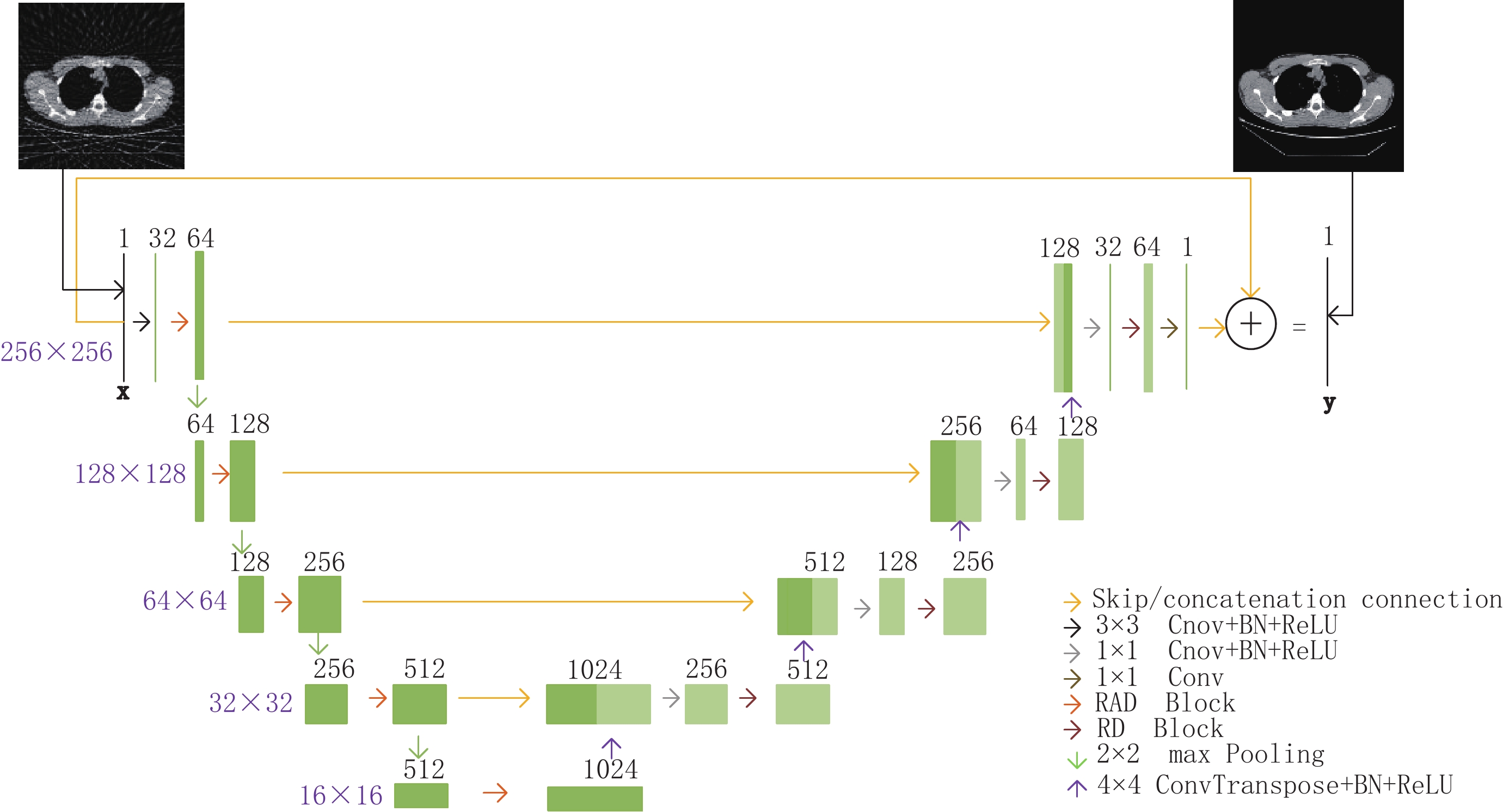
摘要: 针对计算机断层成像稀疏重建过程中产生条状伪影的问题,本文提出一种基于对抗式残差密集深度神经网络的CT图像高精度稀疏重建方法。设计一种耦合残差连接、密集连接、注意力机制和对抗机制的UNet网络,以含条状伪影图像和高精度图像作为训练样本,通过大规模训练数据,对该网络进行训练,使其具有压制条状伪影的能力。首先,利用滤波反投影算法从稀疏投影中重建出含条状伪影的CT图像;接着,将其输入深度网络,通过网络压制条状伪影;最后,得到高精度的重建图像。实验结果表明,相比于现有的若干深度学习算法,提出的新型网络重建出的图像精度更高,可以更好地压制条状伪影。Abstract: To solve the problem of severe streak artifacts in sparse-view computed tomography (CT) reconstruction, in this paper we propose a method which is based on the adversarial residual dense deep neural network to acquire high-quality sparse-view CT reconstruction. The UNet that combines residual connectioin, dense connection, adversarial mechanism and attention mechanism is designed, which is trained through large-scale training data composed of streak artifact images and high-quality images to suppress streak artifacts. First, the filtered back projection (FBP) algorithm is used to reconstruct CT images with streak artifacts from sparse projections, then these images are inputed into the deep network, which can suppress streak artifacts to output high-quality images. The experimental results show that, compared with the existing deep learning algorithms, the image reconstructed by the proposed new network possesses higher accuracy and can suppress streak artifacts better.
-
Keywords:
- sparse reconstruction /
- CT /
- UNet /
- adversarial mechanism /
- attention mechanism
-
表 1 稀疏重建结果的RMSE、SSIM和PSNR分析
Table 1 RMSE, SSIM and PSNR analysis of sparse-view reconstruction results
重建方法 FBP RED-CNN FBPConvNet FD-UNet 本文方法 PSNR 22.230 28.800 34.440 35.180 35.240 RMSE 0.077 0.036 0.019 0.017 0.017 SSIM 0.645 0.923 0.967 0.969 0.970 PSNR 19.740 27.210 35.660 35.930 36.150 RMSE 0.103 0.044 0.016 0.016 0.016 SSIM 0.593 0.941 0.981 0.979 0.981 表 2 不同稀疏度下重建图像的PSNR值、SSIM值、RMSE值
Table 2 RMSE, SSIM and PSNR analysis of reconstruction results under different sparsity
投影个数 15 30 60 90 PSNR 29.770 31.450 34.690 34.810 RMSE 0.032 0.027 0.018 0.018 SSIM 0.908 0.930 0.964 0.964 -
[1] PAN X, SIDKY E Y, VANNIER M. Why do commercial CT scanners still employ traditional, filtered back-projection for image reconstruction?[J]. Inverse Problems, 2008, 25(12): 1230009.
[2] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289−1306. doi: 10.1109/TIT.2006.871582
[3] SIDKY E Y, KAO C M, PAN X. Accurate image reconstruction from few-view limited-angle data in divergent-beam CT[J]. Journal of X-ray Science and Technology, 2006, 14(2): 119-139.
[4] SIDKY E Y, PAN X. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization[J]. Physics in Medicine & Biology, 2008, 53(17): 4777−4807. doi: 10.1088/0031-9155/53/17/021
[5] LIU Y, MA J, FAN Y, et al. Adaptive-weighted total variation minimization for sparse data toward low-dose X-ray computed tomography image reconstruction[J]. Physics in Medicine & Biology, , 2012, 57(23): 7923-7956.
[6] STRONG D, CHAN T. Edge-preserving and scale-dependent properties of total variation regularization[J]. Inverse Problems, 2003, 19(6): 165−187. doi: 10.1088/0266-5611/19/6/059
[7] XIN J, CHEN Z, XING Y. Anisotropic total variation minimization method for limited-angle CT reconstruction[C]//proceedings of the Spie Optical Engineering + Applications, F, 2012.
[8] ZHANG Y, ZHANG W H, CHEN H, et al. Few-view image reconstruction combining total variation and a high-order norm[J]. International Journal of Imaging Systems & Technology, 2013, 23(3): 249−255.
[9] ZHANG H, YAN B, WANG L, et al. Sparse-view image reconstruction with nonlocal total variation[C]//Proceedings of the 2014 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), F, 2014.
[10] SIDKY E Y, REISER I, NISHIKAWA R M, et al. Practical iterative image reconstruction in digital breast tomosynthesis by non-convex TpV optimization[J]. Proceedings of SPIE — The International Society for Optical Engineering, 2008: 6913(1): 691328-691324 .
[11] 闫慧文, 乔志伟. 基于ASD-POCS框架的高阶TpV图像重建算法[J]. CT理论与应用研究, 2021, 30(3): 279-289. DOI: 10.15953/j.1004-4140.2021.30.03.01. YAN H W, QIAO Z W. High order TpV image reconstruction algorithms based on ASD-POCS framework[J]. CT Theory and Applications, 2021, 30(3): 279-289. DOI:10.15953/j.1004-4140.2021.30.03.01. (in Chinese).
[12] LI S, CAO Q, CHEN Y, et al. Dictionary learning based sinogram inpainting for CT sparse reconstruction[J]. Optik - International Journal for Light and Electron Optics, 2014, 125(12): 2862−2867. doi: 10.1016/j.ijleo.2014.01.003
[13] ZHU J, CHEN C W. A compressive sensing image reconstruction algorithm based on low-rank and total variation regularization[J]. Journal of Jinling Institute of Technology, 2015, 31(4): 23-26.
[14] CHEN H, ZHANG Y, KALRA M K, et al. Low-dose CT with a residual encoder-decoder convolutional neural network (RED-CNN)[J]. IEEE Transactions on Medical Imaging, 2017, 36(12): 2524-2535.
[15] XU L, REN J, LIU C, et al. Deep convolutional neural network for image deconvolution[J]. Advances in neural information processing systems, 2014, 27(2): 1790−1798.
[16] HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]// Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, F, 2016.
[17] WOLTERINK J M, LEINER T, VIERGEVER M A, et al. Generative adversarial networks for noise reduction in low-dose CT[J]. IEEE Transactions on Medical Imaging, 2017, 36(12): 2536−2545. doi: 10.1109/TMI.2017.2708987
[18] GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial networks[J]. Advances in Neural Information Processing Systems, 2014, 3(11): 2672−2680.
[19] HAN Y S, YOO J, YE J C. Deep residual learning for compressed sensing CT reconstruction via persistent homology analysis[J]. 2016.
[20] RONNEBERGER O, FISCHER P, BROX T. U-Net: Convolutional networks for biomedical image segmentation[J]. Springer International Publishing, 2015, 9351: 234-241.
[21] 陈康, 狄贵东, 张佳佳, 等. 基于改进U-Net卷积神经网络的储层预测[J]. CT理论与应用研究, 2021, 30(4): 403-416. DOI:10.15953/j.1004-4140.2021.30.04.01. CHEN K, DI G D, ZHANG J J, et al. Reservoir prediction based on improved U-net convolutional neural network[J]. CT Theory and Applications, 2021, 30(4): 403-416. DOI:10.15953/j.1004-4140.2021.30.04.01. (in Chinese).
[22] JIN K H, MCCANN M T, FROUSTEY E, et al. Deep convolutional neural network for inverse problems in imaging[J]. IEEE Transactions on Image Processing, 2016, 26(9): 4509−4522.
[23] ZHANG Z, LIANG X, XU D, et al. A sparse-view CT reconstruction method based on combination of densenet and deconvolution[J]. IEEE Transactions on Medical Imaging, 2018, 37(6): 1407-1417.
[24] GAO H, ZHUANG L, MAATEN L V D, et al. Densely connected convolutional networks[J]. IEEE Computer Society, 2017: 2261-2269.
[25] HAN Y, YE J C. Framing U-Net via deep convolutional framelets: Application to sparse-view CT[J]. IEEE Transactions on Medical Imaging, 2018, 37(6): 1418−1429.
[26] STEVEN, GUAN, AMIR, et al. Fully dense UNet for 2D sparse photoacoustic tomography artifact removal[J]. IEEE Journal of Biomedical & Health Informatics, 2019, 24(2): 568-576.
[27] JIE H, LI S, GANG S, et al. Squeeze-and-excitation networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 42(8): 2011−2023.
-
期刊类型引用(4)
1. 钱金栋,孙建国. 深度学习在肿瘤智能放疗中的发展与展望. 中国医疗设备. 2025(01): 149-153 .  百度学术
百度学术
2. 晏婷,何朝良,仝骞,朱嵩涛,段晓礁. 基于双编码U-Net及离散小波变换的CBCT图像散射校正. 光学学报. 2025(09): 107-121 .  百度学术
百度学术
3. 柴世杰,黄魁东,杨富强,赵举龙. 基于多尺度生成对抗网络的锥束CT图像耦合伪影校正方法. 仪器仪表学报. 2024(09): 44-54 .  百度学术
百度学术
4. 明鑫,杨成文,孟慧鹏,翟贺争,程钰翔,杨淼龙. 基于U-Net模型从低能锥形束CT图像实现高能成像的研究. 中华放射医学与防护杂志. 2023(09): 741-746 .  百度学术
百度学术
其他类型引用(3)



 下载:
下载: