X射线成像和深度学习的交叉融合

王革

doi:10.15953/j.ctta.2021.053

X射线成像和深度学习的交叉融合

doi: 10.15953/j.ctta.2021.053

王革

1.
生物医学工程系；美国伦斯勒理工学院工学院
2.
生物医学成像中心；美国伦斯勒理工学院工学院
3.
生物技术与跨学科研究中心纽约12180. 美国
李亮译清华大学工程物理系，北京100084

详细信息

作者简介:
王革：
男，博士，美国伦斯勒理工学院生物医学成像中心主任、Clark & Crossan讲席教授。致力于医学成像和人工智能，尤其是深度学习领域的研究。1991年他发表了第一个螺旋锥束CT重建方法，并在该领域发表了许多后续论文，锥束螺旋扫描已经成为当前临床CT最主要的扫描方式。2016年，他首次提出了深度学习断层成像的线路图，并在这一领域发表了一系列的论文。多年来，他在PNAS、Nature、Nature Machine Intelli-gence、Nature Communications和其他知名期刊上发表了500多篇期刊论文。他获得多项荣誉，包括IEEE EMBS学术生涯成就奖（2021年）、IEEE Region 1杰出教学奖（2021年）、SPIE Aden and Marjorie Meinel技术成就奖（2022年），是IEEE、SPIE、AAPM、OSA、AIMBE、AAAS和NAI的Fellow，E-mail：wangg6@rpi.edu

中图分类号: O 242；TP 391.41
计量
- 文章访问数: 1700
- HTML全文浏览量: 319
- PDF下载量: 340
- 被引次数: 0
出版历程
- 收稿日期: 2021-12-01
- 录用日期: 2021-12-01
- 刊出日期: 2022-02-01

X-ray Imaging Meets Deep Learning

WANG Ge

摘要

摘要:
作为人工智能（artificial intelligence，AI）的主流，深度学习在计算机视觉、图像多尺度特征提取领域已有所进展。2016年以来，深度学习方法在计算机断层成像（从积分特性，如线积分，实现内部结构的图像重建）方面也取得了进步。总体而言，在人工智能领域，尤其是基于人工智能的成像领域，令人兴奋的前景和挑战并存，包括准确性、鲁棒性、泛化性、可解释性等一系列问题。基于2021年8月2日SPIE Optics+Photonics上的大会邀请报告，本文介绍X射线成像和深度学习的背景，低剂量CT、稀疏数据CT、深度影像组学的代表性成果，讨论对于X射线CT、其他成像模式以及多模态成像而言，数据驱动和模型驱动方法融合带来的机会，以期显著促进精准医疗的进步。
- 深度学习 /
- 机器学习 /
- 人工智能 /
- 生物医学成像 /
- X射线成像 /
- CT /
- 多模态成像

HTML全文

图 1 深度学习的基本思想。神经网络由相互连接的神经元组成，每个神经元先执行线性计算（内积），再执行非线性运算（阈值化，如ReLU）。神经元之间的权重参数被随机初始化，并通过使用训练数据迭代更新以期损失函数最小化（例如上图迭代中显示为“4”的绝对误差），最终输出正确答案（在本例中为“5”）

下载: 全尺寸图片幻灯片

图 2 人们对医学成像的关注维持不变，但对人工智能及其主流方法“深度学习”的关注出现了激增。2016年，对深度学习的关注超过了医学成像

下载: 全尺寸图片幻灯片

图 3 使用TITLE-ABS-KEY规则=（deep learning AND medical AND image AND reconstruct*）AND（X-ray OR CT OR computed tomography）在Scopus进行检索的可视化结果

下载: 全尺寸图片幻灯片

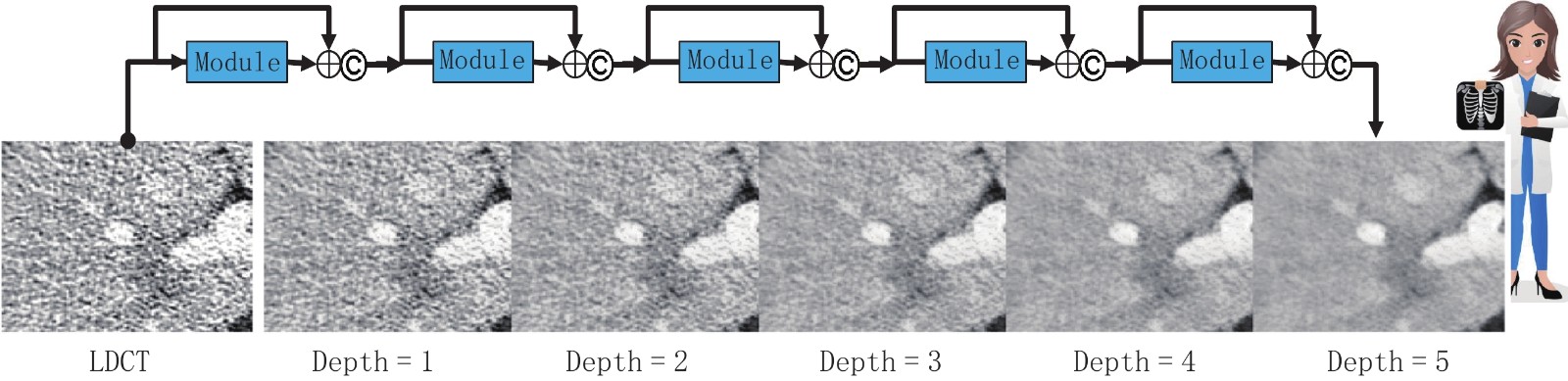
图 4 模块化的深度去噪网络是在有放射科医生参与的闭环模式下训练的^[9]。该网络生成不同程度的去噪图像，供放射科医生根据具体诊断任务决定最佳程度

下载: 全尺寸图片幻灯片

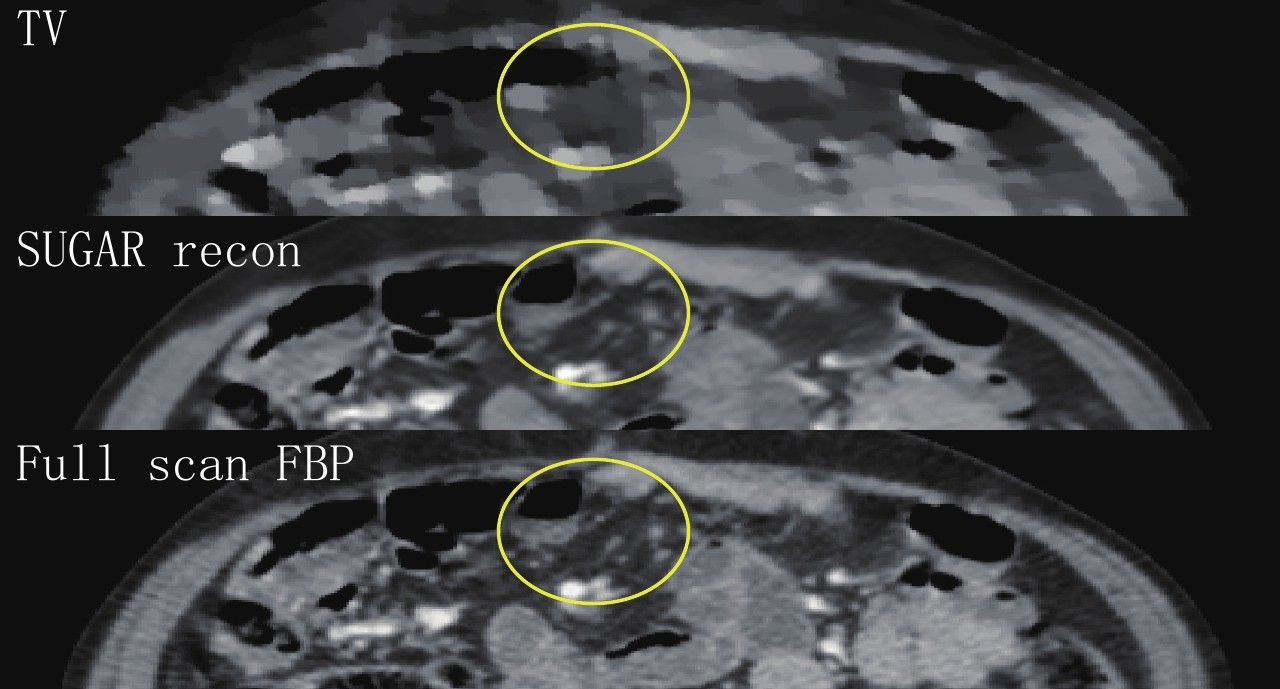
图 5 我们最近设计的SUGAR网络针对相当稀疏的数据重建出很有潜力的初步结果^[10]

下载: 全尺寸图片幻灯片

图 6 利用深度学习对如蛋白质分子的非晶体目标进行基于AlphaFold的X射线断层成像。由于超高分辨率所需的强辐射会立即摧毁目标，因此对于断层成像重建而言，只能采集到单次发射的散射波前数据，这是极具挑战性的极稀疏数据成像任务

下载: 全尺寸图片幻灯片

图 7 对抗性攻击使训练好的深度网络处于高度危险之中。虽然原始数字图像（左）被深度分类器正确分类，但是我们能设计一个微小的对抗噪声（中）并添加到原始图像中，形成视觉上差不多的图像（右），让该图像被同一分类器错误分类

下载: 全尺寸图片幻灯片

图 8 解析、压缩、深度迭代（ACID）网络的总体思想示意图，用于整合解析重建、稀疏性提升、迭代优化和深度学习的优势

下载: 全尺寸图片幻灯片

图 9 结合数据驱动和基于规则的方法，运用知识图谱技术进行深度模糊逻辑解释和知识提取

下载: 全尺寸图片幻灯片

图 10 构建性价比高的便携移动式混合成像仪器是可行的,方便现场医护

下载: 全尺寸图片幻灯片

图 11 在深度学习框架下更紧密更经济地融合成像模式和开发合成仪器

下载: 全尺寸图片幻灯片

图 12 使用Scopus TITLE-ABS-KEY规则=（"deep learning" AND medical AND image AND reconstruct*）AND（X-ray OR CT OR "computed tomography"）获得的，关于X射线成像和深度学习的交叉研究的全球景观

下载: 全尺寸图片幻灯片

参考文献(33)

[1]	KERMELIOTIS T. X-ray voted top modern discovery[EB/OL]. Cable News Network, (2009-01-01). https://www.cnn.com/2009/WORLD/europe/11/04/xray.machine.science.museum/index.html.
[2]	WANG G, YE J C, DE MAN B. Deep learning for tomographic image reconstruction[J]. Nature Machine Intelligence, 2020, 2(12): 737-748.
[3]	LELL M M, KACHELEß M. Recent and upcoming technological developments in computed tomography: High speed, low dose, deep learning, multienergy[J]. Investigative Radiology, 2020, 55(1): 8−19. doi: 10.1097/RLI.0000000000000601
[4]	MAIER A, SYBEN C, LASSER T, et al. A gentle introduction to deep learning in medical image processing[J]. Journal of Medical Physics, 2018, 29(2): 86−101.
[5]	SAHINER B, PEZESHK A, HADJIISKI L M, et al. Deep learning in medical imaging and radiation therapy[J]. Medical Physics, 2019, 46(1): e1−e36. DOI: 10.1002/mp.13264.
[6]	WANG G. A perspective on deep imaging[J]. IEEE Access 4, 2016: 8914−8924.
[7]	WANG G, CONG W X, YANG Q S. Tomographic image reconstruction via machine learning: US 10, 970, 887 B2[P]. (2016-06-24)[2021-04-06]. https://patents.google.com/patent/US10970887B2/en?oq=10970887.
[8]	WANG G, ZHANG Y, YE X J, et al. Machine learning for tomographic imaging[J]. IOP Publishing Ltd, 2019.
[9]	SHAN H, PADOLE A, HOMAYOUNIEH F, et al. Competitive performance of a modularized deep neural network compared to commercial algorithms for low-dose CT image reconstruction[J]. Nature Machine Intelligence, 2019, 1(6): 269−276. doi: 10.1038/s42256-019-0057-9
[10]	WU W W, NIU C, EBRAHIMIAN S, et al. AI-enabled ultra-low-dose CT reconstruction[J/OL].(2021-01-01). https://arxiv.org/abs/2106.09834.
[11]	CHAO H, SHAN H, HOMAYOUNIEH F, et al. Deep learning predicts cardiovascular disease risks from lung cancer screening low dose computed tomography[J]. Nature Communications, 2021, 12(1): 2963. doi: 10.1038/s41467-021-23235-4
[12]	RAINES K S, SALHA S, SANDBERG R L, et al. Three-dimensional structure determination from a single view[J]. Nature, 2010, 463(7278): 214-217.
[13]	WEI H. Fundamental limits of ‘ankylography’ due to dimensional deficiency[J]. Nature, 2011, 480(7375): E1.
[14]	WANG G, YU H, CONG W X, et al. Non-uniqueness and instability of ‘ankylography’[J]. Nature, 2011, 480(7375): E2-3.
[15]	SENIOR A W, EVANS R, JUMPER J, et al. Improved protein structure prediction using potentials from deep learning[J]. Nature, 2020, 577(7792): 706-710.
[16]	AKHTAR N, MIAN A. Threat of adversarial attacks on deep learning in computer vision: A survey[J]. IEEE Access 6, 2018, 14410-14430.
[17]	ANTUN V, RENNA F, POON C, et al. On instabilities of deep learning in image reconstruction and the potential costs of AI[J]. Proceedings of the National Academy of Sciences, 2020, 117(48): 201907377.
[18]	WU W W, HU D L, CONG W X, et al. Stabilizing deep tomographic reconstruction networks[J/OL]. https://arxiv.org/abs/2008.01846 (v1, v2, and v3, 2020, v4, 2021).
[19]	WU E, WU K, DANESHJOU R, et al. How medical AI devices are evaluated: Limitations and recommendations from an analysis of FDA approvals[J]. Nature Medicine, 2021, 27(4): 582-584.
[20]	CHAN K H R, YU Y D, YOU C, et al. ReduNet: A white-box deep network from the principle of maximizing rate reduction[J]. 2021.
[21]	FAN F L, XIONG J J, LI M Z, et al. ReduNet: A white-box deep network from the principle of maximizing rate reduction[J]. IEEE Trans Radiat Plasma Med Sci, 10.1109/TRPMS.2021.3066428 (2021).
[22]	SHAMSHIRBAND S, FATHI M, DEHZANGI A, et al. A review on deep learning approaches in healthcare systems: Taxonomies, challenges, and open issues[J]. Journal of Biomedical Informatics, 2021, 113: 103627.
[23]	MONTAVON G, SAMEK W, MÜLLER K R. Methods for interpreting and understanding deep neural networks[J]. Digital Signal Processing, 2018, 73: 1-15.
[24]	FAN F L, WANG G. Fuzzy logic interpretation of quadratic networks[J]. Neurocomputing, 2020, 374: 10-21.
[25]	FAN F F, XIONG J J, WANG G. Universal approximation with quadratic deep networks[J]. Neural Networks, 2020, 124, 383-392.
[26]	SABOUR S, FROSST N, HINTON G E. Dynamic routing between capsules[J]. Adv Neural Inf Process Syst, 2017-Decem, 3857-3867.
[27]	FAN F L, LAI R J, WANG G. Quasi-equivalence of width and depth of neural networks[EB/OL]. (2020-01-01). https://arxiv.org/abs/2002.02515.
[28]	NICKEL M, MURPHY K, TRESP V, et al. A review of relational machine learning for knowledge graphs[J]. Proceeding of the IEEE, 2015, 104(1): 11-33.
[29]	WANG Q, MAO Z, WANG B, et al. Knowledge graph embedding: A survey of approaches and applications[J]. IEEE Trans Knowl Data Eng, 2017, 29(12): 2724-2743.
[30]	LIU J, ZHU X X, LIU F, et al. OPT: Omni-perception pre-trainer for cross-modal understanding and generation[EB/OL]. (2021-01-01). https://arxiv.org/abs/2107.00249.
[31]	WANG G, ZHANG J, GAO H, et al. Towards omni-tomography: Grand fusion of multiple modalities for simultaneous interior tomography[J]. PLoS One, 2012, 7(6).
[32]	WANG G, KALRA M, MURUGAN V, et al. Vision 20/20: Simultaneous CT-MRI-Next chapter of multimodality imaging[J]. Medical Physics, 2015, 42(10): 5879-5889.
[33]	DINELEY J. Tackling the silent crisis in cancer care[EB/OL]. (2018-01-01). https://www.lindau-nobel.org/blog-tackling-the-silent-crisis-in-cancer-care-with-innovation/.