基于U型生成对抗网络的编码孔径CT成像方法

王志腾; 冒添逸; 张昕; 朱书进; 朱建建; 戴修斌

doi:10.15953/j.ctta.2021.070

基于U型生成对抗网络的编码孔径CT成像方法

王志腾^1a,,
冒添逸^1b,
张昕^1a,
朱书进^1b,
朱建建²,
戴修斌^{1a, b, ,}

1.
通信与信息工程学院；南京邮电大学
2.
地理与生物信息学院，南京210003 南京邮电大学
2.
如皋市人民医院神经内科, 江苏如皋226500

基金项目: 国家自然科学基金（基于编码孔径的非扫描四维CT成像方法（62005128））；江苏省自然科学基金（基于多尺度细粒度网络和二值自编码模型的病理图像快速检索研究（BK20200745））；江苏省高等学校自然科学研究（基于动态变尺度栈式二值自编码的病理图像实时检索研究（20KJB510022））。

详细信息

作者简介:
王志腾: 男，南京邮电大学电子信息专业硕士研究生，主要从事CT理论与应用研究，E-mail：1220013724@njupt.edu.cn

戴修斌: 男，南京邮电大学地理与生物信息学院副教授、硕士生导师，主要从事CT理论与应用研究，E-mail：daixb@njupt.edu.cn

中图分类号: TP 391.41；TP 183
计量
- 文章访问数: 674
- HTML全文浏览量: 158
- PDF下载量: 92
出版历程
- 收稿日期: 2021-12-19
- 录用日期: 2022-02-24
- 网络出版日期: 2022-03-09
- 发布日期: 2022-05-22

Coded Aperture Computed Tomography Via Generative Adversarial U-net

1.
Nanjing University of Posts and Telecommunications, Nanjing 210003, China School of Communications and Information engineering
2.
Nanjing University of Posts and Telecommunications, Nanjing 210003, China School of Geographic and Biologic Information
2.
Department of Neurosurgery, Rugao People’s Hospital, Rugao 226500, China

摘要

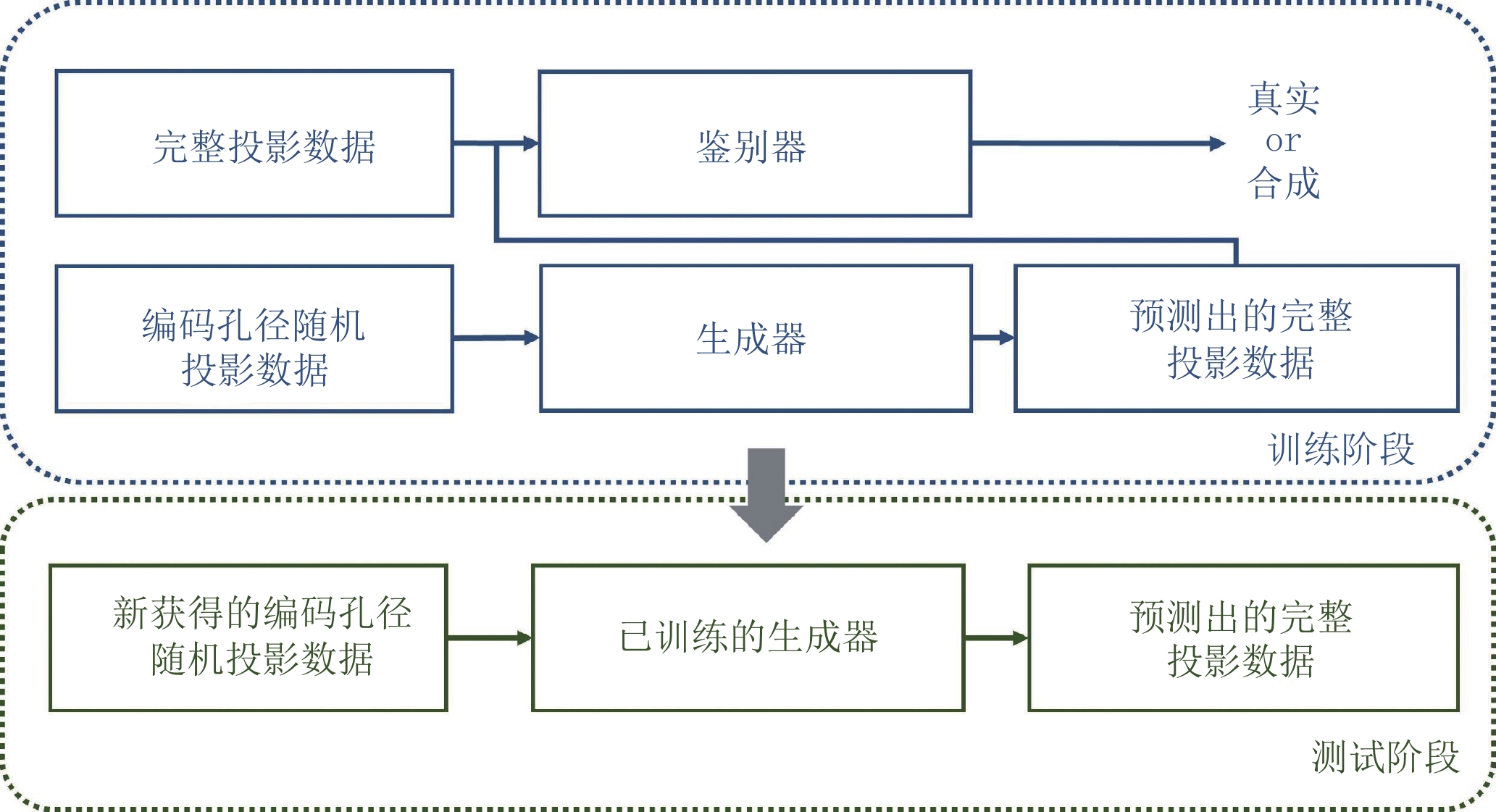
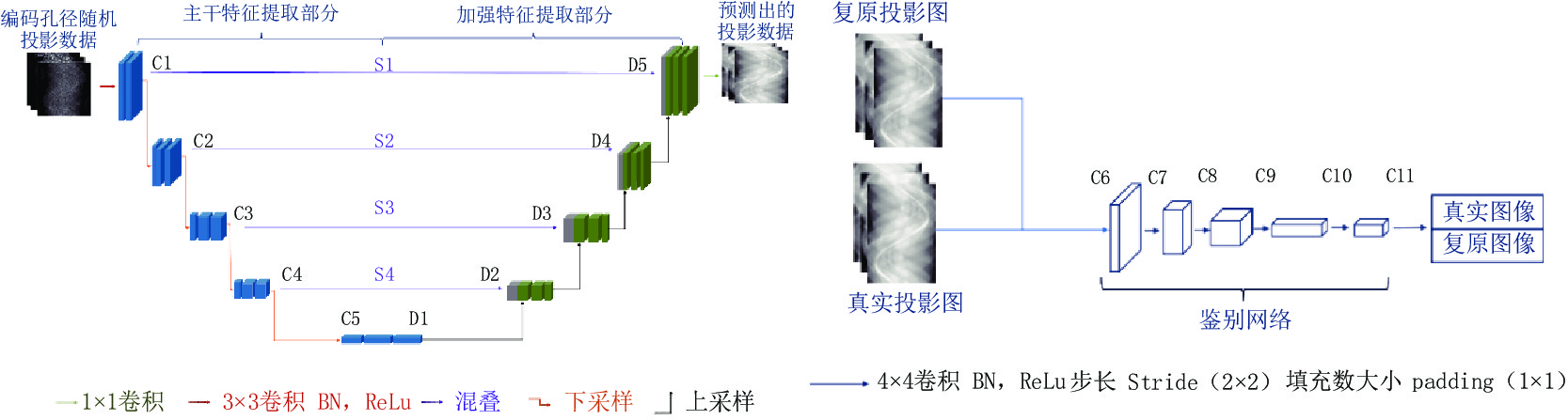
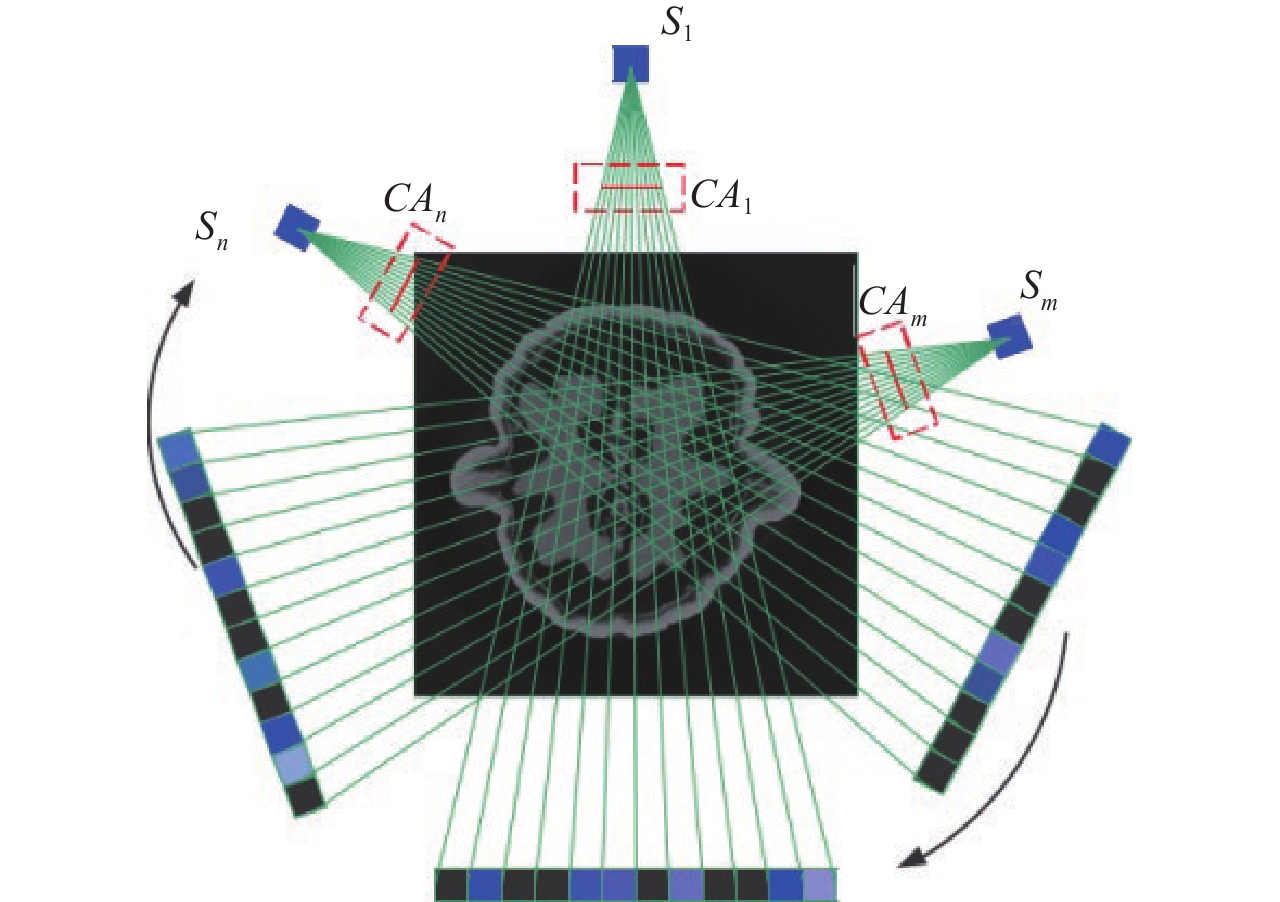
摘要: 针对编码孔径CT成像非连续稀疏采样只能通过代数类迭代重建算法的缺点，本文提出一种基于U型生成对抗网络的编码孔径CT成像方法。通过构建基于U型生成对抗网络的非连续稀疏投影的动态博弈模型，结合联合损失函数，预测正弦图的结构性缺失，实现编码孔径CT成像分析类（非迭代）快速重建。实验结果表明，在辐射剂量降低95％的条件下，基于U型生成对抗网络的编码孔径CT成像方法实现了峰值信噪比大于30 dB @ 256×256的高质量重建。相比于目前最先进的编码孔径CT成像方法，其重建时间降低了约两个数量级。
- CT成像 /
- 编码孔径 /
- 生成对抗网络
Abstract: Generative adversarial U-net for coded aperture computed tomography (CT) is proposed in this paper to alleviate the tradeoff between the non-continuous sparse projections and the ill-posedness iterative reconstruction problem. A non-continuous sparse projection model is presented based on generative adversarial U-net and the corresponding joint penalty function is formulated. Simulations using real datasets show that CT images with 256×256 pixels can be reconstructed with peak signal-to-noise ration more than 30 dB at only 5% transmittance. Furthermore, the computational time in the reconstructions is reduced by two orders of magnitude when compared with the state-of-the-art iterative algorithms in coded aperture computed tomography.
- computed tomography /
- coded aperture /
- generative adversarial net

HTML全文

图 1 编码孔径CT成像光学几何结构示意图

Figure 1. The setup of coded aperture computed tomography

下载: 全尺寸图片幻灯片

图 2 正弦图

Figure 2. Sinogram

下载: 全尺寸图片幻灯片

图 3 本文提出的非连续性投影数据训练和测试框架

Figure 3. The framework of training and testing for discrete projection data

下载: 全尺寸图片幻灯片

图 4 U型生成对抗网络结构图

Figure 4. Generative Adversarial U-Net for coded aperture computed tomography

下载: 全尺寸图片幻灯片

图 5 编码掩膜板透过率为20％，训练次数为115个epoch的结果图

Figure 5. The results for coded apertures at 20％ transmittance

下载: 全尺寸图片幻灯片

图 6 编码掩膜板透过率为25％时基于U型生成对抗网络的编码孔径CT成像结果

Figure 6. The reconstructed images for coded apertures computed tomography at 25％ transmittance

下载: 全尺寸图片幻灯片

图 7 编码掩膜板透过率为5％、15％和25％时基于U型生成对抗网络的编码孔径CT成像结果

Figure 7. The reconstructed images for coded apertures computed tomography at 5％, 15％ and 25％ transmittance, respectively

下载: 全尺寸图片幻灯片

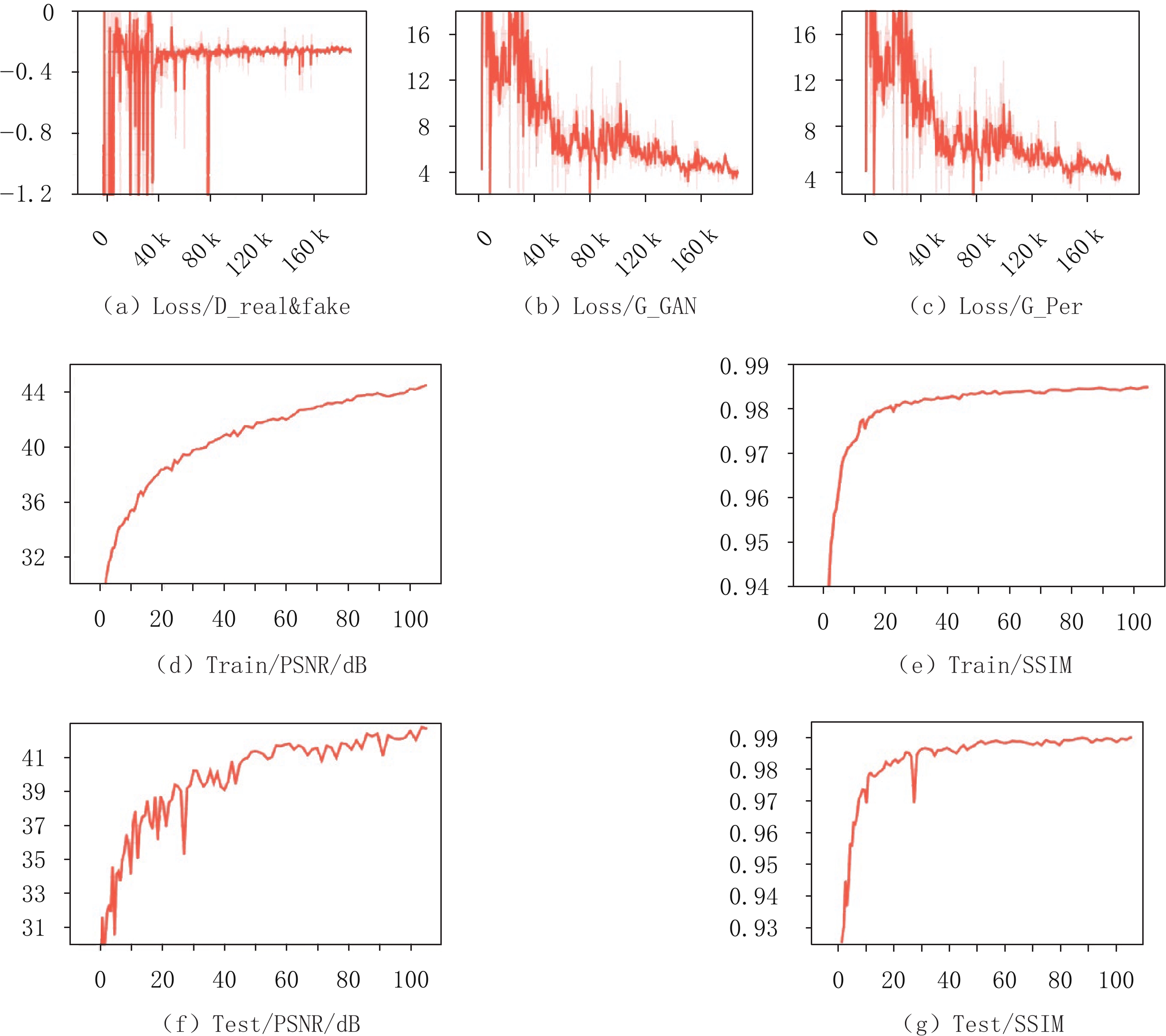
表 1 不同编码掩膜板透过率下，测试集中预测的正弦图和CT重建图像的平均值

Table 1 The average results of sonograms and CT reconstructions at different transmission rates

测试数据集	图像质量评价指标	编码掩膜板透过率
测试数据集	图像质量评价指标	5％	10％	15％	20％	25％
预测的正弦图	PSNR/dB	39.1	41.6	40.9	42.6	43.8
预测的正弦图	SSIM	0.98	0.97	0.98	0.99	0.98
CT重建图像	PSNR/dB	33.7	32.0	33.5	35.3	33.6
CT重建图像	SSIM	0.88	0.88	0.89	0.91	0.90

下载: 导出CSV

参考文献(24)

[1]	KALENDER W A. Computed tomography: Fundamentals, system technology, image quality, applications[M]. John Wiley & Sons, 2011.
[2]	KALENDER W A. X-ray computed tomography[J]. Physics in Medicine & Biology, 2006, 51(13): R29.
[3]	WILLEMINK M J, PERSSON M, POURMORTEZA A, et al. Photon-counting CT: Technical principles and clinical prospects[J]. Radiology, 2018, 289(2): 293−312. doi: 10.1148/radiol.2018172656
[4]	FUCHS T, KACHELRIE M, KALENDER W A. Technical advances in multi-slice spiral CT[J]. European Journal of Radiology, 2000, 36(2): 69−73. doi: 10.1016/S0720-048X(00)00269-2
[5]	ZHU Z, WAHID K, BABYN P, et al. Improved compressed sensing-based algorithm for sparse-view CT image reconstruction[J]. Computational and Mathematical Methods in Medicine, 2013: 185750:1−185750:15.
[6]	MCCOLLOUGH C H, LENG S, YU L, et al. CT dose index and patient dose: They are not the same thing[J]. Radiology, 2011, 259(2): 311−316. doi: 10.1148/radiol.11101800
[7]	CHOI K, BRADY D J. Coded aperture computed tomography[C]//International Society for Optics and Photonics. Adaptive Coded Aperture Imaging, Non-Imaging, and Unconventional Imaging Sensor Systems. 2009, 7468: 74680B.
[8]	JEREZ A, MARQUEZ M, ARGUELLO H. Adaptive coded aperture design for compressive computed tomography[J]. Journal of Computational and Applied Mathematics, 2021, 384: 113174. doi: 10.1016/j.cam.2020.113174
[9]	ZHANG T, ZHAO S, MA X, et al. Nonlinear reconstruction of coded spectral X-ray CT based on material decomposition[J]. Optics Express, 2021, 29(13): 19319−19339. doi: 10.1364/OE.426732
[10]	YAN K, LI D, HOLMGREN A, et al. Compressed sampling strategies for tomography[J]. Journal of the Optical Society of America A, 2014, 31(7): 1369−1394. doi: 10.1364/JOSAA.31.001369
[11]	ZHAO Q, MA X, CUADROS A, et al. Single-snapshot X-ray imaging for nonlinear compressive tomosynthesis[J]. Optics Express, 2020, 28(20): 29390−29407. doi: 10.1364/OE.392054
[12]	TZOUMAS S, VERNEKOHL D, XING L. Coded-aperture compressed sensing X-ray luminescence tomography[J]. IEEE Transactions on Biomedical Engineering, 2017, 65(8): 1892−1895.
[13]	MOJICA E, PERTUZ S, ARGUELLO H. High-resolution coded-aperture design for compressive X-ray tomography using low resolution detectors[J]. Optics Communications, 2017, 404: 103−109. doi: 10.1016/j.optcom.2017.06.053
[14]	CUADROS A, MA X, ARCE G R. Compressive spectral X-ray tomography based on spatial and spectral coded illumination[J]. Optics Express, 2019, 27(8): 10745−10764. doi: 10.1364/OE.27.010745
[15]	CUADROS A P, MA X, RESTREPO C M, et al. Static code CT: Single coded aperture tensorial X-ray CT[J]. Optics Express, 2021, 29(13): 20558−20576. doi: 10.1364/OE.427382
[16]	CUADROS A P, LIU X, PARSONS P E, et al. Experimental demonstration and optimization of X-ray static code CT[J]. Applied Optics, 2021, 60(30): 9543−9552. doi: 10.1364/AO.438727
[17]	MA X, YUAN X, FU C, et al. LED-based compressive spectral-temporal imaging[J]. Optics Express 2021, 29(7): 10698-10715.
[18]	CUADROS A P, ARCE G R. Coded aperture optimization in compressive X-ray tomography: A gradient descent approach[J]. Optics Express, 2017, 25(20): 23833−23849. doi: 10.1364/OE.25.023833
[19]	CUADROS A P, PEITSCH C, ARGUELLO H, et al. Coded aperture optimization for compressive X-ray tomosynthesis[J]. Optics Express, 2015, 23(25): 32788−32802. doi: 10.1364/OE.23.032788
[20]	MEJIA Y, ARGUELLO H. Binary codification design for compressive imaging by uniform sensing[J]. IEEE Transactions on Image Processing, 2018, 27(12): 5775−5786. doi: 10.1109/TIP.2018.2857445
[21]	MAO T, CUADROS A P, MA X, et al. Fast optimization of coded apertures in X-ray computed tomography[J]. Optics Express, 2018, 26(19): 24461−24478. doi: 10.1364/OE.26.024461
[22]	SWINEHART D F. The beer-lambert law[J]. Journal of Chemical Education, 1962, 39(7): 333. doi: 10.1021/ed039p333
[23]	MAO T, CUADROS A P, MA X, et al. Coded aperture optimization in X-ray tomography via sparse principal component analysis[J]. IEEE Transactions on Computational Imaging, 2019, 6: 73−86.
[24]	YI X, WALIA E, BABYN P. Generative adversarial network in medical imaging: A review[J]. Medical Image Analysis, 2019, 58: 101552. doi: 10.1016/j.media.2019.101552