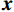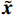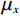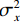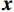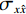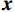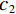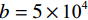Low-dose CT Reconstruction Based on Deep Energy Models
-
摘要: 降低计算机断层扫描(CT)的剂量对于降低临床应用中的辐射风险至关重要,深度学习的快速发展和广泛应用为低剂量CT成像算法的发展带来了新的方向。与大多数受益于手动设计的先验函数或有监督学习方案的现有先验驱动算法不同,本文使用基于深度能量模型来学习正常剂量CT的先验知识,然后在迭代重建阶段,将数据一致性作为条件项集成到低剂量CT的迭代生成模型中,通过郎之万动力学迭代更新训练的先验,实现低剂量CT重建。实验比较,证明所提方法的降噪和细节保留能力优良。Abstract: Reducing the dose of computed tomography (CT) is essential for reducing the radiation risk in clinical applications. With the rapid development and wide application of deep learning, it has brought new directions for the development of low-dose CT imaging algorithms. Unlike most existing prior-driven algorithms that benefit from manually designed prior functions or supervised learning schemes, in this paper, we use an energy-based deep model to learn the prior knowledge of normal-dose CT, and then in the iterative reconstruction phase, we integrate data consistency as a conditional item into the iterative generation model of low-dose CT, and realize the low-dose CT reconstruction through the prior experience of iterative updating training of Langevin dynamics. The experimental results show that the proposed method hold excellent noise reduction and detail retention capabilities.
-
Keywords:
- low-dose CT /
- deep learning /
- Langevin dynamics /
- deep energy based model
-
计算机断层扫描(computed tomography,CT)是一种准确、非侵入式的体内异常检测技术,可应用于生物学、医学和其他领域。CT检查的广泛使用引起了人们对X射线辐射致癌和遗传损伤潜在风险的担忧[1],于是,减少CT扫描次数降低CT的辐射剂量成为科研人员关注的焦点。针对如何在尽可能低的扫描剂量条件下获取与常规剂量CT质量相近的CT图像,即低剂量CT(low-dose CT,LDCT)可以对许多临床适应症进行成像,以最大限度地减少与辐射相关的风险,而不会显著影响筛查或诊断的性能。然而,降低辐射剂量会增加数据噪声并将伪影引入重建图像,如果不解决这些问题,则会对其诊断性能产生不利影响[2]。
为了解决这个问题,许多研究工作致力于设计算法来提高低剂量CT的图像质量。传统的重建算法一般可以分为解析法和迭代法[3]。其中解析法具备算法简单、计算速度快等优点,常用的解析算法有滤波反投影算法(filtered back projection,FBP);但是,解析法需要较完整的投影数据,且对噪声敏感,容易产生伪影和噪声污染。迭代算法将重建图像当作未知变量,以此建立目标函数进行迭代求解,比如全变分模型(total variation,TV)[4]和噪声统计模型[5-6];虽然这些迭代算法确实提高了图像质量,但是算法复杂度大,运行时占用内存等问题也限制了其应用。
随着深度学习的快速发展,卷积神经网络(convolutional neural networks,CNN)在图像去噪领域取得了很好进展[7-9]。最近,几种基于深度学习的算法已被应用于CT重建。这些方法主要分为两种,一种是使用端到端的有监督深度学习技术作为后处理方法[10-11],例如Würfl等[12]采用神经网络来进行CT图像重建;Cheng等[13]使用基于深度学习的跨越策略模拟了迭代重建过程;Han等[14]提出了一种基于深度残差学习网络的稀疏投影CT重建方法,结果表明,仅由条纹伪影组成的残差图像比原始CT图像简单得多;Jin等[15]结合FBP和U-net[16]的深度卷积网络,并充分利用了多分辨率CNN和残差学习[17]。
另一种是将深度学习驱动的先验知识集成到迭代方案,该类方法可以将神经网络学习的先验用来处理各种任务,而无需重新训练或者修改网络。具体来说,Baguer等[18]使用深度图像先验进行CT重建,在低维数据时取得优异的结果。同时,基于生成模型的特征学习,从网络结构和目标函数的角度提出了许多图像重建方法。最新的进展主要有两种方法:变分自编码器(variational auto-encoder,VAE)[19-20]和生成对抗网络[21](generative adversarial networks,GAN),前者使用对数似然函数作为训练目标,而后者使用对抗性训练来最小化模型和数据分布之间的f 散度[22]或积分概率度量[23]。蔡宁等[24]通过构建和分析普通CNN与GAN两者的性能差异,提出了一种创新的扫描方式,可有效获取低噪声的微米级计算机断层扫描(Micro-CT)数据,并取得了很好的重建效果;Niu等[25]提出的基于相似性的无监督深度去噪方法,能够以非局部和非线性的方式抑制图像中噪声,结果证明该方式从低剂量CT图像中恢复原有的特征效果;Wu等[26]采用K-稀疏自动编码器用于无监督的特征学习任务,并在重建过程中最小化重建图像和流形表示之间的距离以及数据保真度来提高图像重建质量;Zhang等[27]提出的REDAEP算法在去噪自编码先验模型的基础上,采用变量增强技术和
$ {L^p} $ 正则化约束以挖掘图像更高维的先验信息。遗憾的是,尽管生成模型在处理自然图像方面取得了成功,但在医学成像领域的研究却不是很多,尤其是在低剂量CT方面。最近,基于深度能量的模型[29](energy-based model,EBM)在生成建模方面取得了可喜的成果。EBM通过将标量能量(兼容性的度量)与变量相关联来捕获相关性,做出预测或决策的推理包括设置观察变量的值并找到使能量最小化的剩余变量的值。EBM在于找到一个能量函数,该函数将低能量与剩余变量的正确值相关联,将较高能量与不正确的值相关联。因此,本文提出一种基于深度能量模型的新型CT重建方法,对本方法和现有技术之间的实验比较,证明本方法的降噪和细节保留能力优良。
1. 基于深度能量低剂量CT成像
1.1 深度能量模型
2019年,Du等[29]的工作已经证明,EBM作为生成模型应用于自然图像恢复表现出了优秀的性能,具备显著的优势。首先,它提供明确的非标准化的密度信息,具备组合性和灵活性;此外,与自回归模型和基于流的模型不同的是,EBM不需要特殊的模型架构。最近,在Nijkamp等[30]和Du等[29]的工作中可见,EBM能够成功地进行最大似然训练,并用于后续图像重建任务中。
基于能量的模型在机器学习中有着悠久的历史,将无监督生成模型与EBM相结合是一种新颖的深度学习方法。它由玻尔兹曼分布显式地定义概率,通常对密度函数建模,旨在学习一个函数E,该函数将低能量值分配给数据分布中的输入,并将高能量值分配给其他输入。它们允许使用样本来生成目标中间过程,其中通过马尔科夫链蒙特卡洛采样方法从
$ {\boldsymbol{x}} \sim\exp \Big( { - E( {\boldsymbol{x}} )} \Big) $ 中采样样本$ {\boldsymbol{x}} $ 。与使用隐式函数生成样本的GAN和求对数似然函数下界的VAE等方法相比,显式采样与基于深度能量的模型相结合进行生成建模具有简单、稳定和灵活等优势。本文将能量函数用一个神经网络
$ E( {\boldsymbol{x}} ) $ 表示,${\boldsymbol{x}}$ 是输入数据,${\boldsymbol{ \theta}} $ 为神经网络权重,则概率分布为${p_\theta }({\boldsymbol{x}}) = {{\exp \Big( { - {E_{\boldsymbol{\theta}} }({\boldsymbol{x}})} \Big)} /Z}({\boldsymbol{\theta}} )$ ,其中$ Z({\boldsymbol{\theta}} ) = \int {\exp \Big( { - {E_{\boldsymbol{\theta}} }({\boldsymbol{x}})} \Big){\rm{d}}{\boldsymbol{x}}} $ 。从这种分布中对样本采样是很困难的,以前的工作依赖于随机游走或吉布斯采样等方法。这些方法混合时间长,特别是对于图像等高维复杂数据就难以处理。1.2 郎之万动力学采样
郎之万动力学[31]可以通过计算概率密度
$ p({\boldsymbol{x}}) $ 的对数的梯度${\nabla _x}\Big( {\log p({\boldsymbol{x}})} \Big)$ 从而生成样本。给定一个固定的步长$ \varepsilon > 0 $ ,一个初始值${\tilde {\boldsymbol{x}}^0}\sim\pi ({\boldsymbol{x}})$ ,其中$\pi$ 是一个先验分布,郎之万动力学方法递归地通过公式(1)计算:$$ {\tilde {\boldsymbol{x}}^t} = {\tilde {\boldsymbol{x}}^{t - 1}} + \frac{{\,\varepsilon \,}}{2}{\nabla _x}\bigg( {\log p\left( {{{\tilde {\boldsymbol{x}}}^{t - 1}}} \right)} \bigg) + \sqrt \varepsilon {{\boldsymbol{z}}^{{t}}} , $$ (1) 其中
${ {\boldsymbol{z}} ^t}\sim N(0,{\boldsymbol{I}})$ ,当$ \varepsilon \to 0 $ 和$t \to \infty$ 时,${\tilde {\boldsymbol{x}}^t}$ 的分布等于$p({\boldsymbol{x}})$ 。在这种情况下,${\tilde {\boldsymbol{x}}^t}$ 在某些条件下成为来自$p({\boldsymbol{x}})$ 的精确样本。当$ \varepsilon > 0 $ 和$t < \infty$ 时,需要一个马尔可夫链蒙特卡罗方法来更新纠正公式(1),但在实践中这经常被忽略。本文假设在步长$ \varepsilon $ 足够小且$t$ 足够大时,真实和采样数据间误差可忽略不计。将以郎之万动力学为基础的公式(1)与深度能量模型概率分布相结合,可得:
$$ \begin{gathered} {{\tilde {\boldsymbol{x}}}^t} = {{\tilde {\boldsymbol{x}}}^{t - 1}} + \frac{{{\kern 1pt} \varepsilon {\kern 1pt} }}{2}{\nabla _x}\log \Bigg( {{{\exp \bigg( { - {E_{\boldsymbol{\theta}} }\left( {{{\tilde {\boldsymbol{x}}}^{t - 1}}} \right)} \bigg)} \bigg/Z}({\boldsymbol{\theta}} )} \Bigg) + \sqrt \varepsilon {{\boldsymbol{z}}^t} \\ ={\text{ }}{{\tilde {\boldsymbol{x}}}^{t - 1}} - \frac{{{\kern 1pt} \varepsilon {\kern 1pt} }}{2}{\nabla _x}E{}_{\boldsymbol{\theta}} \left( {{{\tilde {\boldsymbol{x}}}^{t - 1}}} \right) + \sqrt \varepsilon {{\boldsymbol{z}}^t} \qquad \qquad \qquad\;\\ \end{gathered} 。 $$ (2) 公式(2)中定义概率分布为
${q_{\boldsymbol{\theta}} }$ ,使得${\tilde x_K}\sim{q_{\boldsymbol{\theta}} }$ 。正如上述所说,当$ \varepsilon \to 0 $ 和$t \to \infty$ 时,${q_{\boldsymbol{\theta}} } \to {p_{\boldsymbol{\theta}} }$ 。此过程通过郎之万动力学公式从能量函数定义的概率分布中生成样本。因此,样本由能量函数$ {E_{\boldsymbol{\theta}} }({\boldsymbol{x}}) $ 采样生成,而不是仅由前馈网络生成。1.3 基于深度能量模型的训练
希望由能量函数
$ E $ 定义的分布对数据分布$ {p_D} $ 进行建模,通过最小化负对数似然${L_{ML}}(\theta ) = {{{\mathbb{E}}}_{x\sim{p_D}}}\Big( { - \log {p_{\boldsymbol{\theta}} }({\boldsymbol{x}})} \Big)$ 来实现,其中$- \log {p_{\boldsymbol{\theta}} }({\boldsymbol{x}}) = {E_{\boldsymbol{\theta}} }({\boldsymbol{x}}) - \log Z({\boldsymbol{\theta}} )$ 。该目标函数的梯度为:$$ {\nabla _{\boldsymbol{\theta}} }{L_{ML}}({\boldsymbol{\theta}} ) = {{{\mathbb{E}}}_{{ {\boldsymbol{x}} ^ + }\sim{p_D}}}\Big( {{\nabla _{\boldsymbol{\theta}} }{E_{\boldsymbol{\theta}} }({{\boldsymbol{x}}^ + })} \Big) - {{{\mathbb{E}}}_{{ {\boldsymbol{x}} ^ - }\sim{p_{\boldsymbol{\theta}} }}}\Big( {{\nabla _{\boldsymbol{\theta}} }{E_{\boldsymbol{\theta}} }({{\boldsymbol{x}}^ - })} \Big) \text{。} $$ (3) 公式(3)直观地表明这个梯度减小了正样本
$ {x^ + } $ 的能量,同时增加了来自模型$ {p_{\boldsymbol{\theta}} } $ 的能量,通过公式(2)来生成$ {q_{\boldsymbol{\theta}} } $ 作为$ {p_{\boldsymbol{\theta}} } $ 的近似值。则公式(3)可近似为:$$ {\nabla _{\boldsymbol{\theta}} }{L_{{ML} }}({\boldsymbol{\theta}} ) \approx {{{\mathbb{E}}}_{{ {\boldsymbol{x}} ^ + }\sim{p_D}}}\Big( {{\nabla _{\boldsymbol{\theta}} }{E_{\boldsymbol{\theta}} }({{\boldsymbol{x}}^ + })} \Big) - {{{\mathbb{E}}}_{{ {\boldsymbol{x}} ^ - }\sim{q_{\boldsymbol{\theta}} }}}\Big( {{\nabla _{\boldsymbol{\theta}} }{E_{\boldsymbol{\theta}} }({{\boldsymbol{x}}^ - })} \Big) \text{。} $$ (4) 1.4 低剂量CT深度能量成像模型
本文用以下成像模型来表示低剂量CT图像的成像过程:
$$ \hat {\boldsymbol{x}} = \arg \mathop {\max }\limits_x \bigg( {\log \Big( {p({\boldsymbol{x}})} \Big)} \bigg){\text{ }}\quad{\rm{s}}.{\text{ }}{\rm{t}}.{\text{ }}\quad {\boldsymbol{y }}= {\boldsymbol{Ax}} + {\boldsymbol{\mu}} , $$ (5) 其中
${\boldsymbol{ \mu }}$ 是随机噪声。低剂量CT观测数据$ {\boldsymbol{y}} $ 不是直接由$ p({\boldsymbol{x}}) $ 采样而来,而是由后验数据分布$ p({\boldsymbol{x}}|{\boldsymbol{y}}) $ 采样而来。基于贝叶斯法则得$p({\boldsymbol{x}}|{\boldsymbol{y}}) = {{p({\boldsymbol{y}}|{\boldsymbol{x}})p({\boldsymbol{x}})} / {p({\boldsymbol{y}})}}$ ,结合公式(1)得到公式(6):$$ \begin{gathered} {{\tilde {\boldsymbol{x}}}^t} = {{\tilde {\boldsymbol{x}}}^{t - 1}} - \frac{{\,\varepsilon \,}}{2}{\nabla _{\boldsymbol{x}}}\bigg( {\log p\left( {{{\tilde {\boldsymbol{x}}}^{t - 1}}} \right) + \log p\left( {{\boldsymbol{y}}|{{\tilde {\boldsymbol{x}}}^{t - 1}}} \right)} \bigg) + \sqrt \varepsilon {{\boldsymbol{z}}^t} \\ \qquad\qquad\;\;\;\ ={\text{ }}{{\tilde {\boldsymbol{x}}}^{t - 1}} - \frac{{\,\varepsilon \,}}{2}{\nabla _x}\bigg( {\log p\left( {{{\tilde {\boldsymbol{x}}}^{t - 1}}} \right)} \bigg) - \frac{{{\kern 1pt} \varepsilon \lambda {\kern 1pt} }}{2}{\nabla _x}\bigg( {{{\left\| {{\boldsymbol{y}} - {\boldsymbol{A}}{{\tilde {\boldsymbol{x}}}^{t - 1}}} \right\|}^2}} \bigg) + \sqrt \varepsilon {{\boldsymbol{z}}^t} \\ \end{gathered}\text{,} $$ (6) 其中
$p\left( {{\boldsymbol{y}}|{{\tilde {\boldsymbol{x}}}^t}} \right)$ 由数据模型给出,并由事先已知的有关真实模型参数的信息的先验模型给出,超参数$ \lambda $ 平衡了先验和数据保真度之间的权衡。结合能量函数定义${p_{\boldsymbol{\theta}} }({\boldsymbol{x}}) = {{\exp \Big( { - {E_{\boldsymbol{\theta}} }({\boldsymbol{x}})} \Big)}/Z}({\boldsymbol{\theta}} )$ 和公式(6),得出基于深度能量模型的低剂量CT成像模型公式:$$ {\tilde {\boldsymbol{x}}^t} = {\tilde {\boldsymbol{x}}^{t - 1}} - \frac{{\,\varepsilon \,}}{2}{\nabla _x}{E_{\boldsymbol{\theta}} }\left( {{{\tilde {\boldsymbol{x}}}^{t - 1}}} \right) - \frac{{{\kern 1pt} \varepsilon \lambda {\kern 1pt} }}{2}{\nabla _x}\left( {{{\left\| {{\rm{y}} - {\boldsymbol{A}}{{\tilde {\boldsymbol{x}}}^{t - 1}}} \right\|}^2}} \right) + \sqrt \varepsilon {{\boldsymbol{z}}^t} 。 $$ (7) 其次,采用轮换更新方法来求公式(7)。将公式(7)分为两个子迭代步骤:
$$ {\tilde {\boldsymbol{u}}^t} = {\tilde {\boldsymbol{x}}^{t - 1}} - \frac{{\,\varepsilon \,}}{2}{\nabla _x}E{}_{\boldsymbol{\theta}} \left( {{{\tilde {\boldsymbol{x}}}^{t - 1}}} \right) + \sqrt \varepsilon {{\boldsymbol{z}}^t}, $$ (8) $$ {\tilde {\boldsymbol{x}}^t} = \arg \mathop {\min }\limits_x \bigg( {{{\left\| {{\boldsymbol{y}} - {\boldsymbol{A}}{{\tilde {\boldsymbol{x}}}^{t - 1}}} \right\|}^2} + \beta {{\left\| {{\boldsymbol{x}} - {{\tilde {\boldsymbol{u}}}^t}} \right\|}^2}} \bigg), $$ (9) 其中第2项为解决不适定逆问题而引入的正则化项,
$ \beta = \beta (\lambda ) $ 是正则化参数,与$ \lambda $ 相关。值得注意的是,公式(9)的第1项${\left\| {{\boldsymbol{y}} - {\boldsymbol{Ax}}} \right\|^2}$ 很难直接最小化,采用可分离二次迭代(SQS)算法[32]从凸问题中获得CT重建数据:$$ {\boldsymbol{x}}_j^k = {\boldsymbol{x}}_j^{k - 1} - \frac{{\displaystyle\sum\limits_{i = 1}^M {\bigg( {{{\boldsymbol{A}}^{\rm{T}}}\left( {{\boldsymbol{Ax}}_i^{k - 1} - {{\boldsymbol{y}}_i}} \right)} \bigg)} + \beta \left( {{\boldsymbol{x}}_j^{t - 1} - {\boldsymbol{u}}_j^k} \right)}}{{{{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{A}}{\boldsymbol{1}} + \beta {\boldsymbol{1}}}}, $$ (10) 其中
${{\boldsymbol{A}}^{\rm{T}}}$ 是${\boldsymbol{A}}$ 转置即反投影,1是一个全1向量。式中的除法指的是逐分量运算符,它使得算法迭代快速。首先初始化
${{\boldsymbol{z}}^1}$ 为标准高斯噪声向量,然后对${\tilde{\boldsymbol{ u}}^t}$ 和${\tilde {\boldsymbol{x}}^t}$ 分别进行轮换更新,假设其中一项已知来求解另外一项。此外,为了加速交替更新过程,应用了先前下降方向的Nesterov动量[33]。动量项可以是${{\boldsymbol{w}}^{t + 1}} = {\tilde {\boldsymbol{x}}^{t + 1}} + \gamma \left( {{{\tilde {\boldsymbol{x}}}^{t + 1}} - {{\tilde {\boldsymbol{x}}}^t}} \right)$ ,其中$\gamma $ 是介于0和1之间的松弛因子。综上所述,表1给出的算法1展示了EBM-LDCT算法的重建流程,具体来说,通过对
${\tilde {\boldsymbol{u}}^t}$ 、${\tilde{\boldsymbol{ x}}^t}$ 和${{\boldsymbol{w}}^t}$ 进行迭代更新来完成。首先,将随机产生的标准高斯噪声输入网络以获得能量标量,之后采用郎之万动力学和SQS轮换迭代更新以获得重建结果。表 1 EBM-LDCT算法的重建过程Table 1. The reconstruction process of the EBM-LDCT algorithm算法1 初始化:输入数据${\tilde x^0}\sim N(0,{\boldsymbol{I}})$,动量项${{\boldsymbol{w}}^0}$,参数$ \beta $,松弛因子$ \gamma $,迭代次数$ T $
开始循环:$t = 1,{\text{ }}2,{\text{ }} \cdots ,{\text{ }}T$
设定$ { {\boldsymbol{z} }^t}\sim N(0,{\boldsymbol{I} }) $
根据公式(10)更新:$ {\tilde {\boldsymbol{u} }^t} = {\tilde {\boldsymbol{x} }^{t - 1} } - \displaystyle\dfrac{ {\,\varepsilon \,} }{2}{\nabla _x}E{}_\theta \left( { { {\tilde {\boldsymbol{x} } }^{t - 1} } } \right) + \sqrt \varepsilon { {\boldsymbol{z} }^t} $
根据公式(8)更新:$ {\tilde {\boldsymbol{x} }^t} = { {\boldsymbol{w} }^{t - 1} } - \displaystyle\dfrac{ { {\kern 1 pt} { {\boldsymbol{A} }^{\rm{T} } }\left( { {\boldsymbol{A} }{ {\tilde {\boldsymbol{x} } }^{t - 1} } - {\boldsymbol{y} } } \right) + \beta \left( { { {\tilde {\boldsymbol{x} } }^{t - 1} } - { {\tilde {\boldsymbol{u} } }^t} } \right){\kern 1 pt} } }{ { { {\boldsymbol{A} }^{\rm{T} } }{\boldsymbol{A} }{\boldsymbol{1} } + \beta {\boldsymbol{1} } } } $
最后更新:${{\boldsymbol{w}}^t} = {\tilde {\boldsymbol{x}}^t} + \gamma \left( { { {\tilde {\boldsymbol{x}}}^t} - { {\tilde {\boldsymbol{x}}}^{t - 1} } } \right)$
${\tilde {\boldsymbol{x}}^t} \leftarrow {{\boldsymbol{w}}^t}$
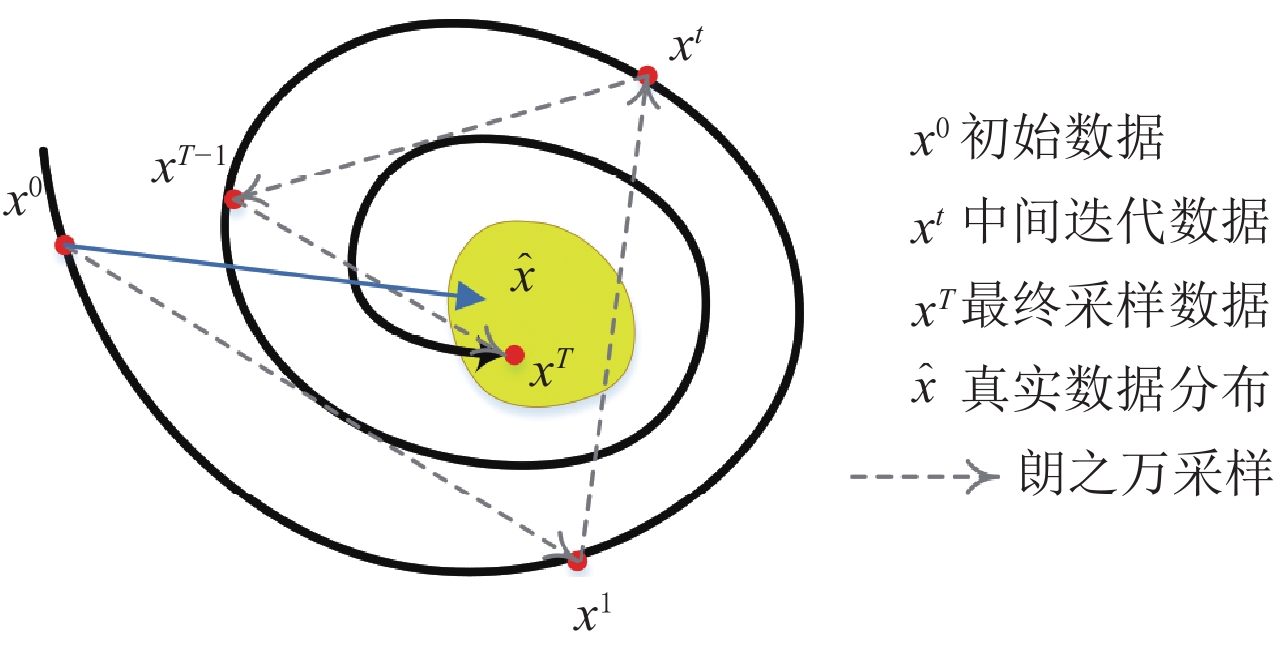
结束结合数据测量拟合项约束下的郎之万动力学采样过程如图1所示。
1.5 卷积神经网络结构
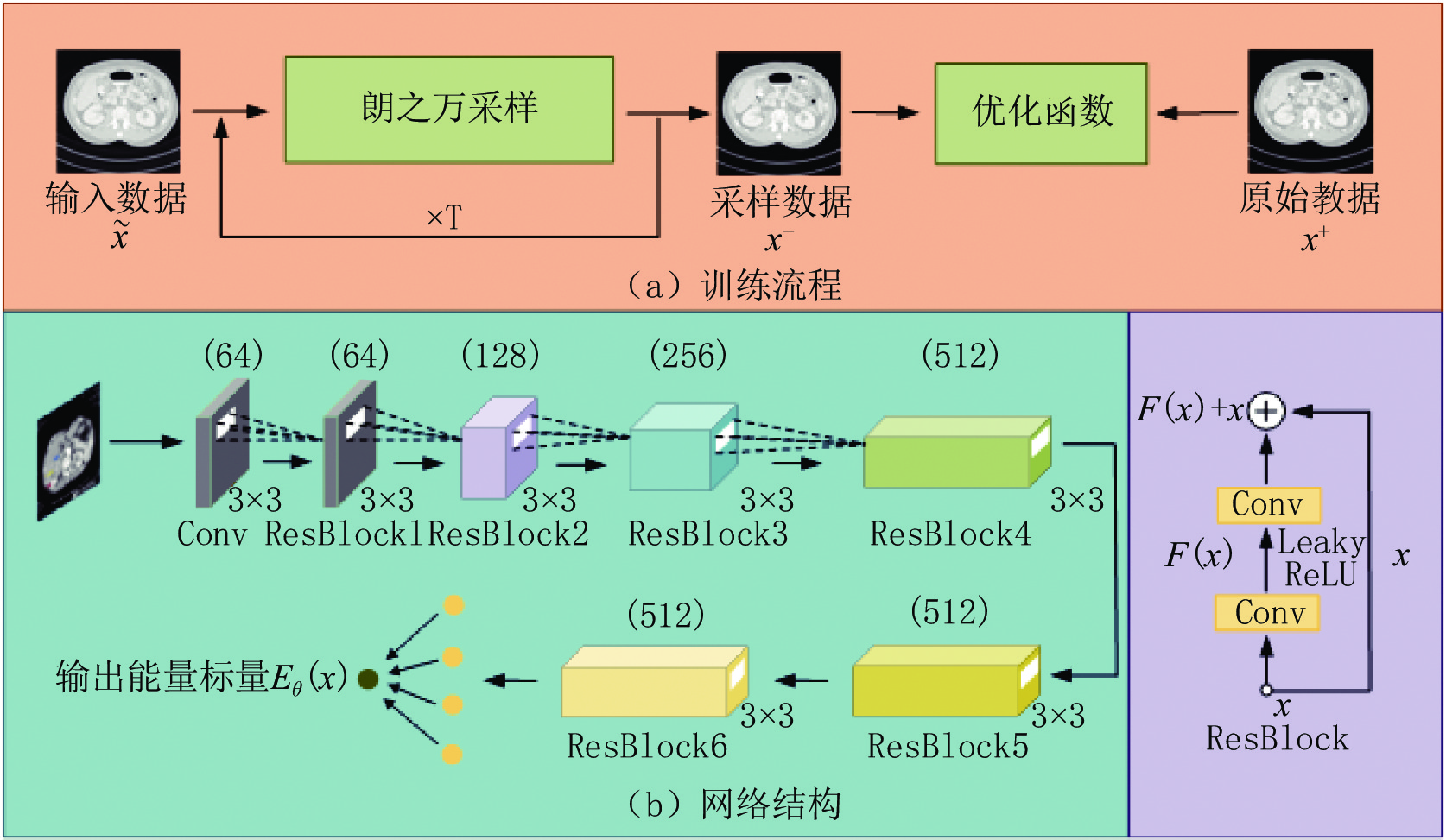
He等[17]在2016年首次提出了ResNet结构,该结构的使用能够有效缓解梯度消失问题从而训练更深的网络结构。本研究采用ResNet结构作为标准的特征提取器,提出的低剂量CT深度能量模型的训练流程和网络结构如图2所示。
在网络中首先对输入数据进行3×3的卷积以达到升维目的,并采用6个Resblock对数据逐步提取深度语义信息,其卷积核大小均为3×3,前4个Resblock会进行步长为2的下采样运算,第6个Resblock后的全连接层能够对提取的特征进行线性求和,最终得到网络输出的能量标量。
1.6 评价指标
为了评估重建图像的质量,选择平均绝对误差(mean absolute error,MAE)、峰值信噪比(peak signal to noise ratio,PSNR)和结构相似性指数(structural similarity,SSIM)3个指标进行定量评估。在统计学中,MAE是对表达相同现象的成对观察之间的误差的度量,它的定义为:
$$ {\text{MAE}} = \sum\limits_{i = 1}^N \left({\frac{{\left| {{{\boldsymbol{x}}_i} - {{\hat {\boldsymbol{x}}}_i}} \right|} }{ N}}\right) \text{,}$$ (11) 其中N是重建图像像素的个数,MAE的值越趋近于0说明重建的图像越接近原图。
PSNR度量描述了信号的最大功率与噪声功率之间的关系。更高的PSNR意味着更好的图像质量。
${\boldsymbol{x}}$ 和$\tilde{\boldsymbol{ x}}$ 对应重建图像和真实图像,PSNR表示为:$$ {\text{PSNR}}\left( {{\boldsymbol{x}},\hat {\boldsymbol{x}}} \right) = 20\lg \left({\frac{{{\text{Max}}(\hat {\boldsymbol{x}})}} {{{{\left\| {{\boldsymbol{x}} - \hat {\boldsymbol{x}}} \right\|}_2}}}}\right) \text{。} $$ (12) SSIM用于衡量原始图像和重建图像之间的相似性,它从3个方面进行评估:亮度、对比度和结构相关性。SSIM值在0和1之间,1表示两个图像相等的情况,越高的SSIM值表示更好的结构相似性。SSIM的定义为:
$$ {\text{SSIM}}({\boldsymbol{x}},\hat {\boldsymbol{x}}) = \frac{{\Big(2{\mu _x}{\mu _{\hat x}} + {c_1}\Big)\Big(2{\sigma _{x\hat x}} + {c_2}\Big)}}{{\Big(\mu _x^2 + \mu _{\hat x}^2 + {c_1}\Big)\Big(\sigma _x^2 + \sigma _{\hat x}^2 + {c_2}\Big)}}, $$ (13) 其中
$ {\mu _x} $ 和$ \sigma _x^2 $ 分别是是${{{\boldsymbol{x}}}}$ 的均值和方差,$ {\sigma _{x\hat x}} $ 是${\boldsymbol{x}}$ 和$\hat {\boldsymbol{x}}$ 协方差。$ {c_1} $ 和$ {c_2} $ 是用于维持平衡的常数。为了保证本文所提模型和算法的重复可实现性,我们已经将代码上传至Github网站:https://github.com/yqx7150/EBM-LDCT。2. 实验结果与分析
2.1 CIRS仿真数据集
本文使用了两个训练数据集来测试所提出的模型,首先采用的是CIRS数据集。它是从GE Discovery HD750 CT系统中获得的一套拟人CIRS体模的高质量CT体积((512×512×100) mm3)体素信息,体素尺寸((0.78×0.78×0.625) mm3),其中管电流值设置600 mAs以保证150 mAs以下低剂量模拟良好的图像质量。在重建阶段中,通过将噪声等级为
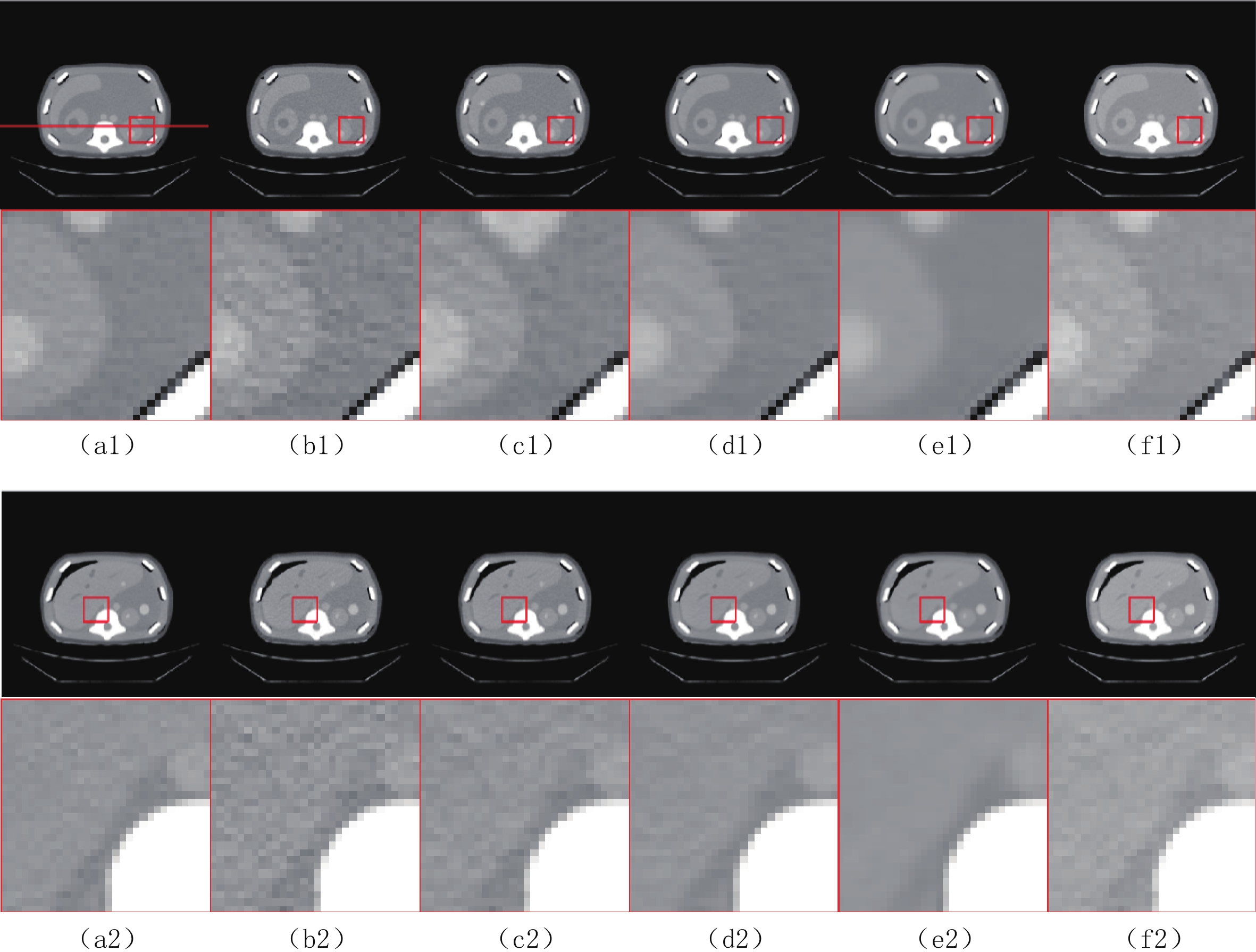
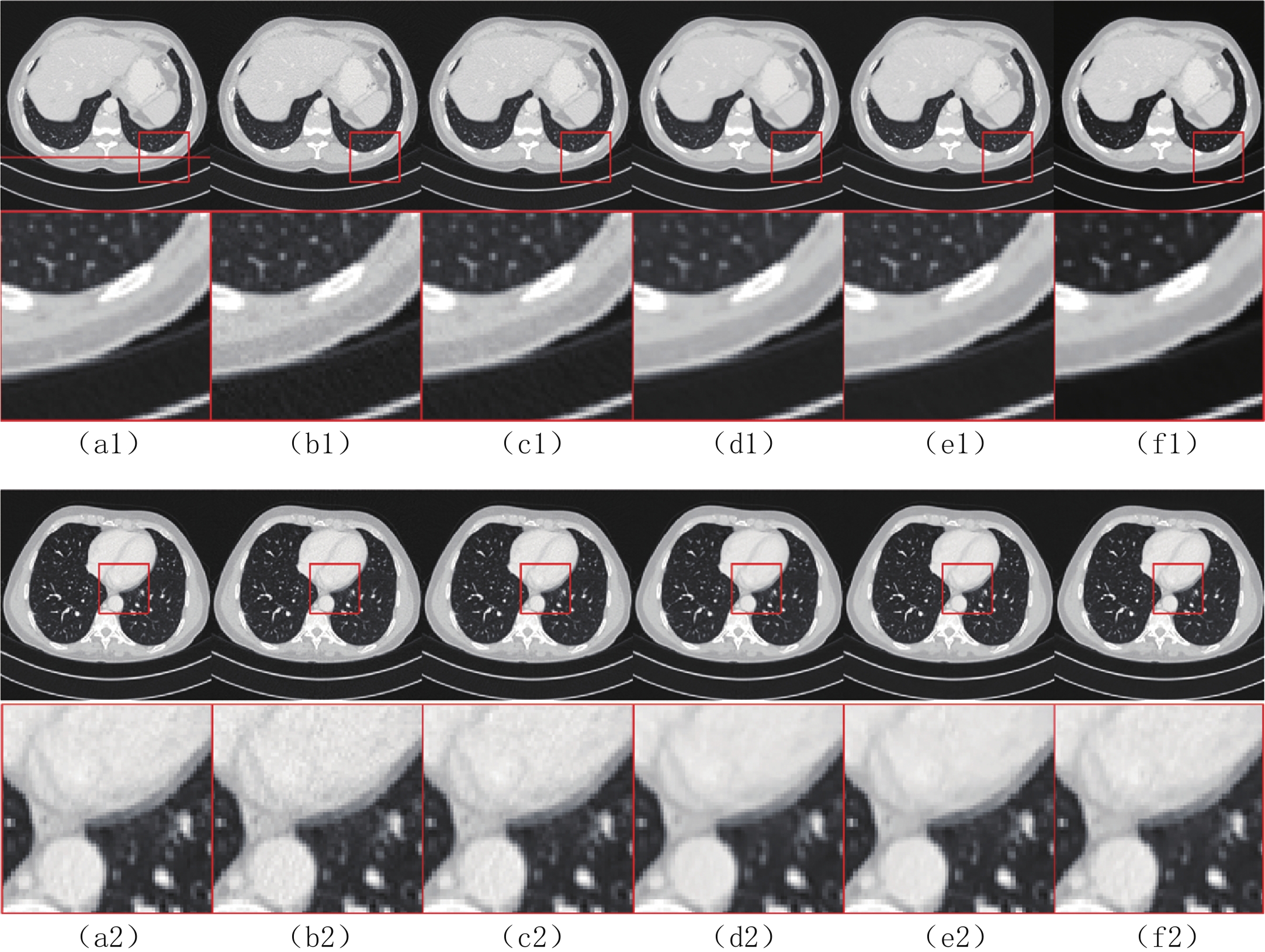
$ b = 5 \times {\text{1}}{{\text{0}}^{\text{4}}} $ 的泊松噪声加入到正弦投影数据中,可以模拟相应的低剂量CT图像。实验给出的重建结果及误差图从左至右分别说明如下,(a1)和(a2)是参考图像,(b1)和(b2)是FBP方法重建结果,(c1)和(c2)是TV方法重建结果,(d1)和(d2)是K-SVD方法重建结果,(e1)和(e2)是RED-CNN方法重建结果,(f1)和(f2)是EBM-LDCT方法重建结果。从表2的实验结果可以看出,在本研究进行的对比实验中,EBM用于CT任务得到的重建图像质量是最好的,并产生较高的MAE和SSIM。可见与端到端的成像方法相比,无监督生成方法重建的低剂量CT图像具有更好的细节与结构相似性。
表 2 使用CIRS数据集的多种低剂量CT重建方法定量结果比较Table 2. Comparison of quantitative results of multiple LDCT reconstruction methods using CIRS dataset方法 MAE PSNR/dB SSIM/10-2 FBP(Ramp-filter) 9.48±0.64 40.67±0.59 94.36±0.87 TV 7.64±0.41 42.12±0.35 96.58±0.51 K-SVD 7.01±0.19 42.86±0.34 97.01±0.36 RED-CNN 6.74±0.07 41.76±0.12 97.47±0.16 EBM-LDCT 6.29±0.23 42.73±0.20 97.81±0.27 为了直观地说明重建性能,图3描绘了由红色矩形标记的放大感兴趣区域(region of interest,ROI)。观察图3的(b1)和(b2)中的FBP重建结果,我们可以看到FBP重建导致低剂量CT图像严重退化,噪声和伪影明显放大。作为传统方法,图3中(c1)和(c2)表现了K-SVD能够生成具有视觉上更平滑外观的重建图像。但是一些微小结构可能会被平滑从而导致组织对比度降低。此外,还可以看出深度学习方法有效地降低了噪声,它们提高了降噪效果并抑制了大多数伪影。然而,它们对细节和纹理信息的保存不完整。
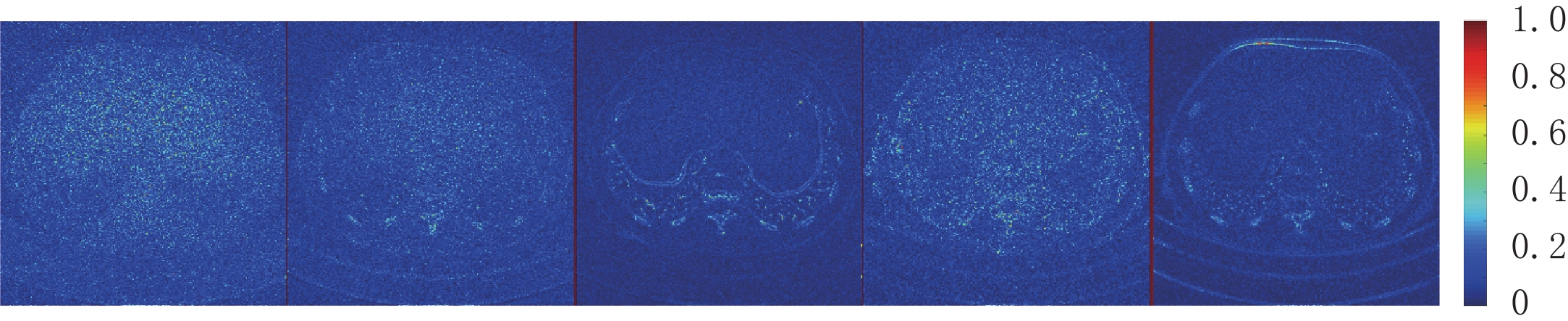
比较图3中(f1)和(f2)的结果,可见所提EBM-LDCT方法在噪声伪影抑制和组织特征保留方面实现了最佳性能。相应的残差图像如图4所示,EBM-LDCT在边缘与细节方面可以实现比其他算法更好的重建精度。
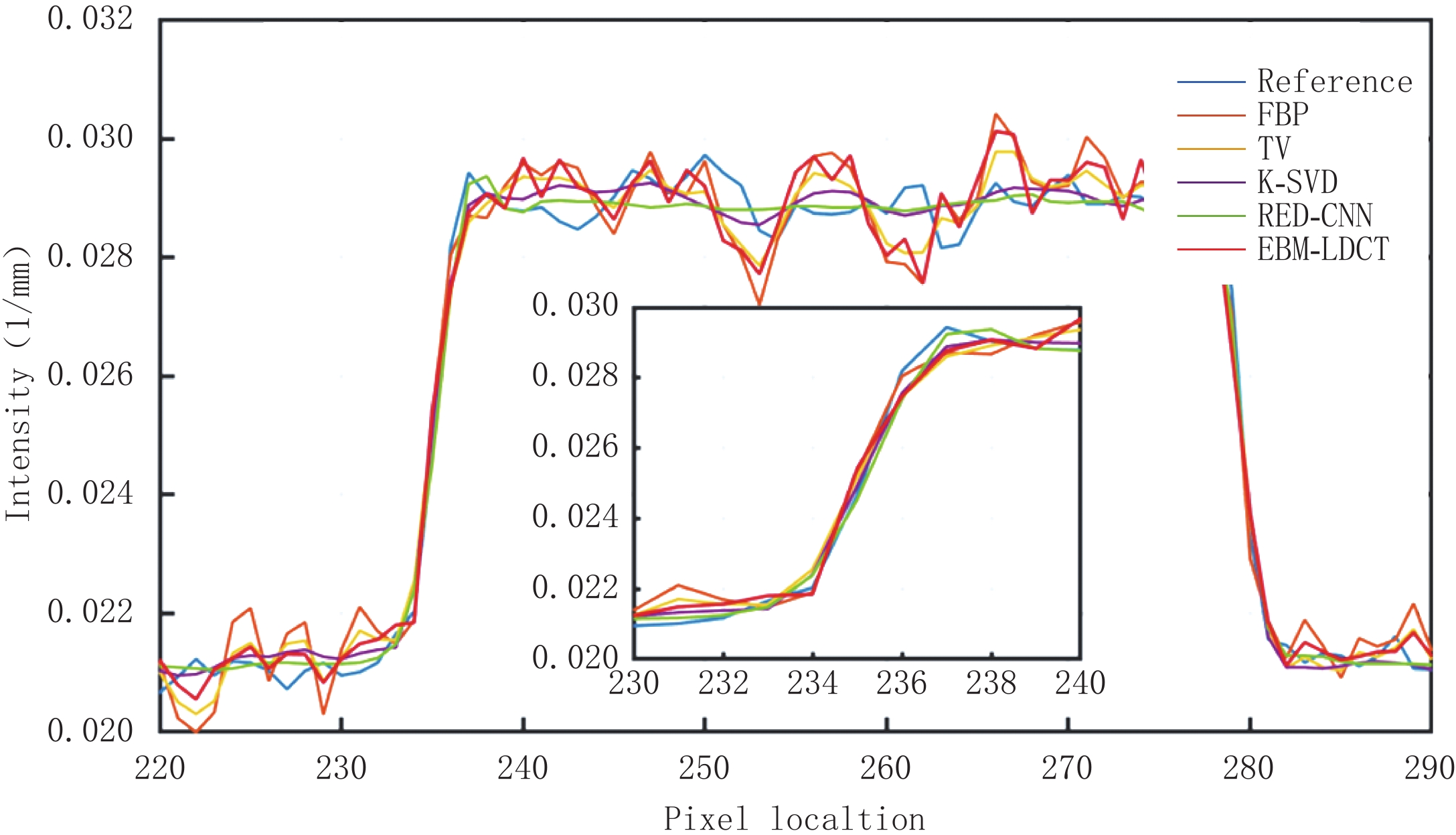
为了更好地说明EBM-LDCT去除噪声的有效性,图5绘制了通过图3中(a1)的红线的一维线强度分布图,它比较来自不同方法重建的CT图像的相同线强度分布。通过观察发现,所提方法中的线强度分布与正常剂量CT图像中的线强度分布最相似,比较证明了所提出的重建方法在边缘保留方面优于其他重建算法。
2.2 AAPM挑战数据集
本研究使用的第2个数据集是Mayo Clinic提供的AAPM低剂量CT挑战赛的人体CT扫描重建模拟数据[34]。数据包括来自10位患者在高剂量CT下的扫描数据,其中9位患者数据用于训练,另外1位患者数据用于评估。本研究使用单切片厚度进行重建,每张图像的大小为512×512像素。CT成像数据采集系统带有1000个采集角度,放射源到中心轴的距离为500 mm,探测器到中心轴的距离为500 mm,成像扫描方式为二维扇形光束。
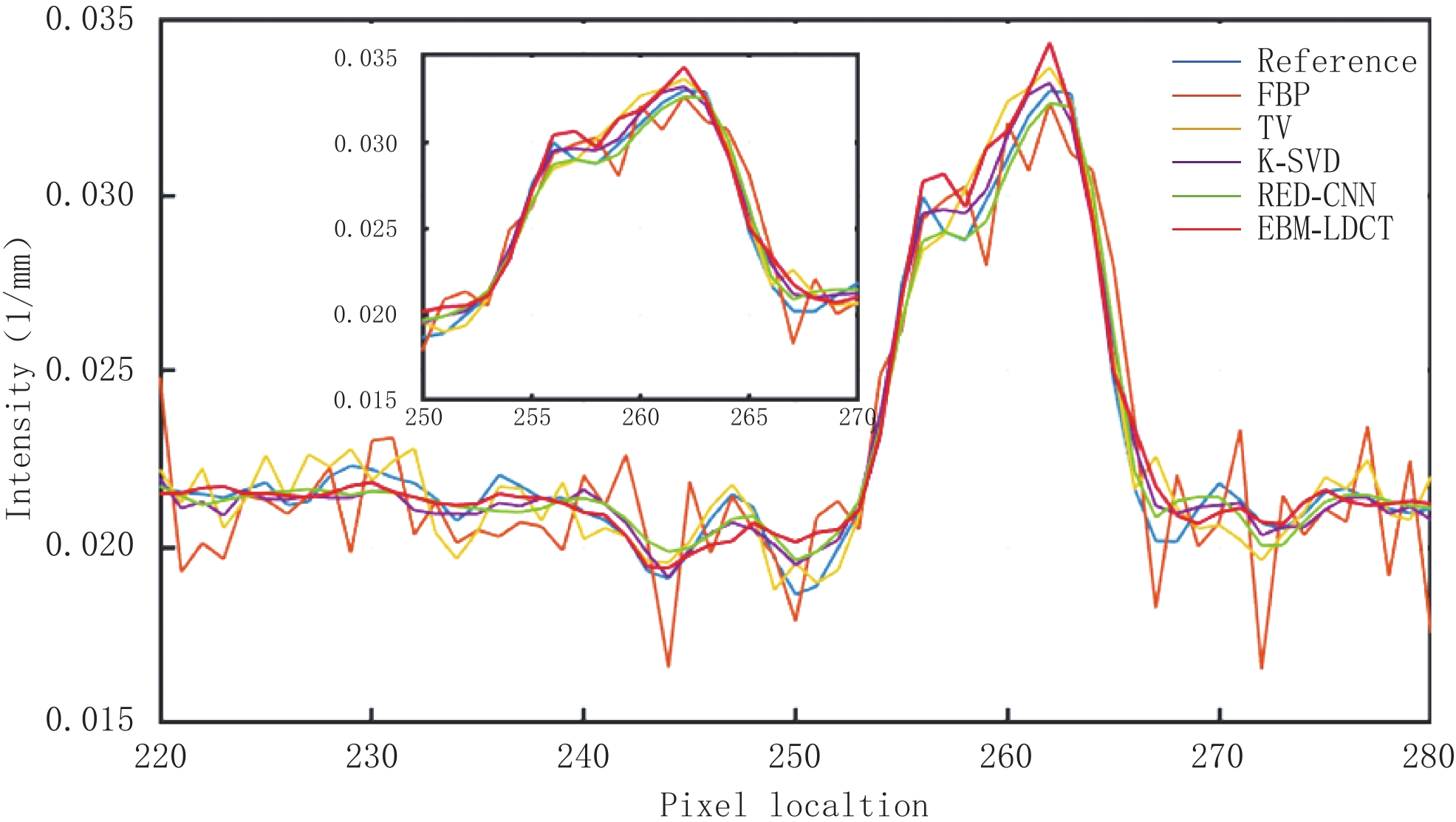
因为AAPM数据集比CIRS数据集更为复杂,相对来说数据的噪声更大。从表3可知,EBM-LDCT取得了最高的PSNR值39.56 dB。观察图6可以看出,得益于RED-CNN方法优秀的去噪能力,在噪声较大的时候,RED-CNN能有效地抑制大噪声,但是却将一些图像细节平滑化了。观察残差图7可知,K-SVD算法性能优秀,RED-CNN能较好地去除边缘突出处的噪声,EBM-LDCT则更注重区域块的整体去噪。根据图8可知,通过观察实验重建结果的一维强度图,EBM-LDCT依旧表现出了良好的去噪效果。
表 3 使用AAPM数据集的多种LDCT重建方法定量结果比较Table 3. Comparison of quantitative results of multiple LDCT reconstruction methods using AAPM dataset方法 MAE PSNR/dB SSIM/10-2 FBP(Ramp-filter) 67.69±13.16 28.68±2.03 44.43±7.18 TV 29.65±4.60 34.98±1.32 86.10±3.48 K-SVD 21.00±1.04 35.68±2.26 81.98±2.41 RED-CNN 16.97±1.02 39.37±1.87 94.78±0.56 EBM-LDCT 18.75±1.31 39.56±0.54 94.16±0.68 3. 结束语
本文提出了一种基于深度能量模型的低剂量CT重建方法,该方法通过将深度能量模型、郎之万动力学和低剂量CT成像模型结合,通过深度能量模型对低剂量CT概率密度函数建模,并用郎之万动力学采样公式,对复杂的概率密度函数采样,并且有效地训练神经网络,生成了高质量的重建图像,体现了该方法的优越性。但是,郎之万动力学采样的时间往往比端对端的模型需要更多的时间,更有效的对数据概率密度采样将是我们以后提升的方向。
-
表 1 EBM-LDCT算法的重建过程
Table 1 The reconstruction process of the EBM-LDCT algorithm
算法1 初始化:输入数据${\tilde x^0}\sim N(0,{\boldsymbol{I}})$,动量项${{\boldsymbol{w}}^0}$,参数$ \beta $,松弛因子$ \gamma $,迭代次数$ T $
开始循环:$t = 1,{\text{ }}2,{\text{ }} \cdots ,{\text{ }}T$
设定$ { {\boldsymbol{z} }^t}\sim N(0,{\boldsymbol{I} }) $
根据公式(10)更新:$ {\tilde {\boldsymbol{u} }^t} = {\tilde {\boldsymbol{x} }^{t - 1} } - \displaystyle\dfrac{ {\,\varepsilon \,} }{2}{\nabla _x}E{}_\theta \left( { { {\tilde {\boldsymbol{x} } }^{t - 1} } } \right) + \sqrt \varepsilon { {\boldsymbol{z} }^t} $
根据公式(8)更新:$ {\tilde {\boldsymbol{x} }^t} = { {\boldsymbol{w} }^{t - 1} } - \displaystyle\dfrac{ { {\kern 1 pt} { {\boldsymbol{A} }^{\rm{T} } }\left( { {\boldsymbol{A} }{ {\tilde {\boldsymbol{x} } }^{t - 1} } - {\boldsymbol{y} } } \right) + \beta \left( { { {\tilde {\boldsymbol{x} } }^{t - 1} } - { {\tilde {\boldsymbol{u} } }^t} } \right){\kern 1 pt} } }{ { { {\boldsymbol{A} }^{\rm{T} } }{\boldsymbol{A} }{\boldsymbol{1} } + \beta {\boldsymbol{1} } } } $
最后更新:${{\boldsymbol{w}}^t} = {\tilde {\boldsymbol{x}}^t} + \gamma \left( { { {\tilde {\boldsymbol{x}}}^t} - { {\tilde {\boldsymbol{x}}}^{t - 1} } } \right)$
${\tilde {\boldsymbol{x}}^t} \leftarrow {{\boldsymbol{w}}^t}$
结束表 2 使用CIRS数据集的多种低剂量CT重建方法定量结果比较
Table 2 Comparison of quantitative results of multiple LDCT reconstruction methods using CIRS dataset
方法 MAE PSNR/dB SSIM/10-2 FBP(Ramp-filter) 9.48±0.64 40.67±0.59 94.36±0.87 TV 7.64±0.41 42.12±0.35 96.58±0.51 K-SVD 7.01±0.19 42.86±0.34 97.01±0.36 RED-CNN 6.74±0.07 41.76±0.12 97.47±0.16 EBM-LDCT 6.29±0.23 42.73±0.20 97.81±0.27 表 3 使用AAPM数据集的多种LDCT重建方法定量结果比较
Table 3 Comparison of quantitative results of multiple LDCT reconstruction methods using AAPM dataset
方法 MAE PSNR/dB SSIM/10-2 FBP(Ramp-filter) 67.69±13.16 28.68±2.03 44.43±7.18 TV 29.65±4.60 34.98±1.32 86.10±3.48 K-SVD 21.00±1.04 35.68±2.26 81.98±2.41 RED-CNN 16.97±1.02 39.37±1.87 94.78±0.56 EBM-LDCT 18.75±1.31 39.56±0.54 94.16±0.68 -
[1] BRENNER D J, HALL E J. Computed tomography: An increasing source of radiation exposure[J]. New England Journal of Medicine, 2007, 357(22): 2277−2284. doi: 10.1056/NEJMra072149
[2] KALRA M K, MAHER M M, TOTH T L, et al. Strategies for CT radiation dose optimization[J]. Radiology, 2004, 230(3): 619−628. doi: 10.1148/radiol.2303021726
[3] 韩泽芳, 上官宏, 张雄, 等. 基于深度学习的低剂量CT成像算法研究进展[J]. CT理论与应用研究, 2022, 31(1): 118-136. DOI: 10.15953/j.1004-4140.2022.31.01.14. HAN Z F, SHANGGUAN H, ZHANG X, et al. Research progress of low-dose CT imaging algorithm based on deep learning[J]. CT Theory and Applications, 2022, 31(1): 118-136. DOI: 10.15953/j.1004-4140.2022.31.01.14. (in Chinese).
[4] TIAN Z, JIA X, YUAN K, et al. Low-dose CT reconstruction via edge-preserving total variation regularization[J]. Physics in Medicine & Biology, 2011, 56(18): 5949.
[5] MA J, LIANG Z, FAN Y, et al. A study on CT sinogram statistical distribution by information divergence theory[C]//2011 IEEE Nuclear Science Symposium Conference Record. IEEE, 2011: 3191-3196.
[6] ELBAKRI I A, FESSLER J A. Statistical image reconstruction for polyenergetic X-ray computed tomography[J]. IEEE Transactions on Medical Imaging, 2002, 21(2): 89−99. doi: 10.1109/42.993128
[7] ZHANG K, ZUO W, CHEN Y, et al. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising[J]. IEEE Transactions on Image Processing, 2017, 26(7): 3142−3155. doi: 10.1109/TIP.2017.2662206
[8] LEFKIMMIATIS S. Universal denoising networks: A novel CNN architecture for image denoising[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018: 3204-3213.
[9] ZHANG K, ZUO W, ZHANG L. FFDNet: Toward a fast and flexible solution for CNN-based image denoising[J]. IEEE Transactions on Image Processing, 2018, 27(9): 4608−4622. doi: 10.1109/TIP.2018.2839891
[10] CHEN H, ZHANG Y, ZHANG W, et al. Low-dose CT via convolutional neural network[J]. Biomedical Optics Express, 2017, 8(2): 679−694. doi: 10.1364/BOE.8.000679
[11] CHEN H, ZHANG Y, KALRA M K, et al. Low-dose CT with a residual encoder-decoder convolutional neural network[J]. IEEE Transactions on Medical Imaging, 2017, 36(12): 2524−2535. doi: 10.1109/TMI.2017.2715284
[12] WÜRFL T, GHESU F C, CHRISTLEIN V, et al. Deep learning computed tomography[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, Cham, 2016: 432-440.
[13] CHENG L, AHN S, ROSS S G, et al. Accelerated iterative image reconstruction using a deep learning based leapfrogging strategy[C]//International Conference on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine, 2017: 715-720.
[14] HAN Y S, YOO J, YE J C. Deep residual learning for compressed sensing CT reconstruction via persistent homology analysis[J]. arXiv preprint arXiv: 1611.06391, 2016.
[15] JIN K H, MCCANN M T, FROUSTEY E, et al. Deep convolutional neural network for inverse problems in imaging[J]. IEEE Transactions on Image Processing, 2017, 26(9): 4509−4522. doi: 10.1109/TIP.2017.2713099
[16] RONNEBERGER O, FISCHER P, BROX T. U-net: Convolutional networks for biomedical image segmentation[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, Cham, 2015: 234-241.
[17] HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016: 770-778.
[18] BAGUER D O, LEUSCHNER J, SCHMIDT M. Computed tomography reconstruction using deep image prior and learned reconstruction methods[J]. Inverse Problems, 2020, 36(9): 094004. doi: 10.1088/1361-6420/aba415
[19] KINGMA D P, WELLING M. Auto-encoding variational bayes[J]. arXiv preprint arXiv: 1312.6114, 2013.
[20] DINH L, KRUEGER D, BENGIO Y. Nice: Non-linear independent components estimation[J]. arXiv preprint arXiv: 1410.8516, 2014.
[21] GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[J]. Advances in Neural Information Processing Systems, 2014: 27.
[22] NOWOZIN S, CSEKE B, TOMIOKA R. F-GAN: Training generative neural samplers using variational divergence minimization[C]//Proceedings of the 30 th International Conference on Neural Information Processing Systems, 2016: 271-279.
[23] ARJOVSKY M, CHINTALA S, BOTTOU L. Wasserstein generative adversarial networks[C]// International Conference on Machine Learning. PMLR, 2017: 214-223.
[24] 蔡宁, 王世杰, 陈璐杰, 等. 基于渐进式网络处理的低剂量Micro-CT成像方法[J]. CT理论与应用研究, 2020,29(4): 435−446. DOI: 10.15953/j.1004-4140.2020.29.04.06. CAI N, WANG S J, CHEN L J. Low-dose Micro-CT imaging method based on progressive network processing[J]. CT Theory and Applications, 2020, 29(4): 435−446. DOI: 10.15953/j.1004-4140.2020.29.04.06. (in Chinese).
[25] NIU C, LI M Z, FAN F L, et al. Suppression of correlated noises with similarity-based unsupervised deep learning[J]. arXiv: 2011.03384.
[26] WU D, KIM K, E L FAKHRI G, et al. Iterative low-dose CT reconstruction with priors trained by artificial neural network[J]. IEEE Transactions on Medical Imaging, 2017, 36(12): 2479−2486. doi: 10.1109/TMI.2017.2753138
[27] ZHANG F Q, ZHANG M H, QIN B J, et al. REDAEP: Robust and enhanced denoising autoencoding prior for sparse-view CT reconstruction[J]. IEEE Transactions on Radiation and Plasma Medical Sciences, 2021, 5(1): 108−119. doi: 10.1109/TRPMS.2020.2989634
[28] LECUN Y, CHOPRA S, HADSELL R, et al. A tutorial on energy-based learning[M]. Predicting Structured Data, 2006: 191-241.
[29] DU Y, MORDATCH I. Implicit generation and modeling with energy based models[J]. Advances in Neural Information Processing Systems, 2019: 32.
[30] NIJKAMP E, HILL M, ZHU S C, et al. Learning non-convergent non-persistent short-run MCMC toward energy-based model[J]. arXiv preprint arXiv: 1904.09770, 2019.
[31] WELLING M, TEH Y W, Bayesian learning via stochastic gradient Langevin dynamics[C]// International Conference on International Conference on Machine Learning. Omnipress, 2011.
[32] ERDOGAN H, FESSLER J A. Monotonic algorithms for transmission tomography[C]//5th IEEE EMBS International Summer School on Biomedical Imaging, 2002.
[33] DEVOLDER O, GLINEUR F, NESTEROV Y. First-order methods of smooth convex optimization with inexact oracle[J]. Mathematical Programming, 2014, 146(1): 37−75.
[34] YIN X, ZHAO Q, LIU J, et al. Domain progressive 3D residual convolution network to improve low-dose CT imaging[J]. IEEE transactions on medical imaging, 2019, 38(12): 2903−2913. doi: 10.1109/TMI.2019.2917258
-
期刊类型引用(1)
1. 吴凡,刘进,张意,陈阳,陆志凯. 面向CT成像的深度重建算法研究进展. 中国体视学与图像分析. 2022(04): 387-404 .  百度学术
百度学术
其他类型引用(0)
-
其他相关附件
-
DOCX格式
2021.077-资源附件文件 10KB
-





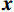
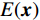
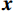

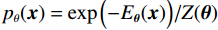
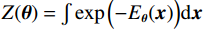
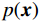
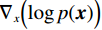
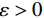
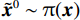

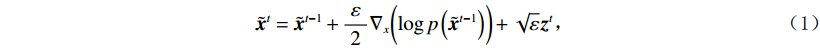
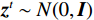
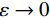
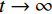
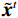
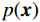
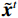
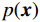
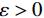
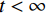
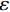


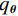
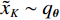
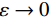
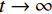
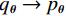
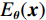

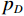
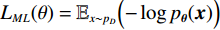
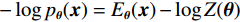

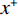
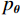
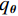
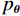


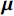
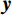
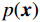
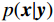
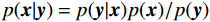

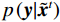
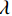
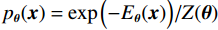

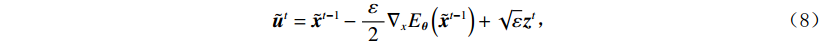

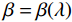
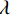
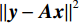

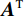
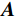
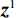
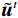
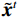
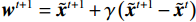
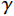
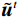
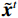
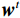
 下载:
下载: