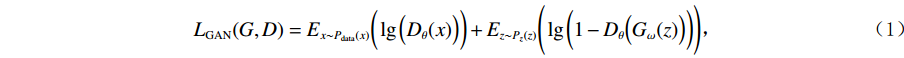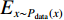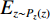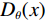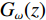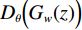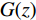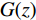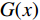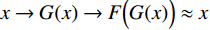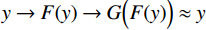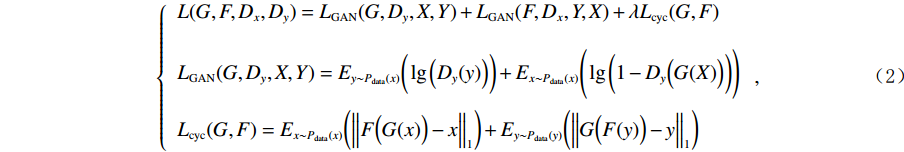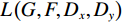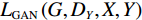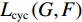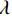Shallow Profile Data Denoising Method Based on Improved Cycle-consistent Generative Adversarial Network
-
摘要: 为解决浅地层剖面数据噪声多、分辨率低问题,本文将环形生成对抗网络的方法应用于浅地层剖面资料的去噪,实现智能去噪。首先,选择具有特殊对称生成对抗网络循环机制以及“循环一致性”损失的环形生成对抗性网络,并对其进行结构改进,提升网络学习和训练的性能。然后,基于优化的浅地层剖面样本集训练网络,实现对于浅地层剖面数据随机噪声的去除,提升数据的信噪比。通过对实验和实际资料的试算,以及与传统带通滤波方法的对比,验证本文方法对浅地层剖面数据去噪的有效性和适应性。Abstract: This study applied the cycle-consistent generative adversarial network method to the denoising of shallow profile data to realize intelligent denoising. This could help resolve the problem of noise and low resolution of shallow profile data. To do this, the cycle generative adversarial network with special symmetric generation countermeasure network cycle mechanism and "cycle consistency loss" was selected. We improved the performance of the network learning and training by optimizing the network structure. Next, based on the optimized shallow profile sample set training network, random noise was removed from the shallow profile data and the signal-to-noise ratio of the data was improved. The effectiveness and adaptability of this method for denoising shallow profile data were verified by trial calculations of experimental and actual data and by comparison with the traditional band-pass filtering method.
-
Keywords:
- artificial intelligence /
- shallow profile data /
- random noise /
- data denoising
-
浅地层剖面探测技术因其低耗、高效、直观的工作特点[1],被广泛应用于探查浅层海底结构[2]、了解海底断裂构造分布[3]、识别浅层气[4]等方面,对海洋工程项目的建立具有重要的意义[5]。
由于海洋环境的复杂性和多样性,容易受到海底底质、船只摆动等因素的影响,导致浅剖地震资料受噪声干扰严重,主要有有源噪声和环境噪声两大类[6],其中有源噪声是由震源或次生震源形成的干扰背景,包括直达波、多次波、气泡效应等;环境噪声主要是洋流波浪、机械振动以及船动力干扰等引起的,随机产生、分布较不均匀,在时间剖面上呈不规则形态,构成地震记录的主要背景,容易对海底底质分层产生较大影响[7]。
针对随机噪声的不可预测性,相关学者提出不同方法去除随机噪声,提高浅剖资料的质量。传统的地震资料随机噪声去除方法包括中值滤波法[8]和小波变换[9]等,这些方法主要用于陆地资料的处理。针对海洋随机噪声的去除方法主要有f-x(频率-偏移距)域预测去噪技术[10]、表面多次波压制技术(surface related multiple elimination,SRME)[11]等。目前常用的方法是f-x域预测去噪技术[12],该方法可以有效消除同相轴抖动,增强有效数据的占比,取得了较好的应用效果,但该方法适用于较为平缓的反射层,对于起伏较大的反射层容易削减有效能量导致地质构造出现误差。因此,对于复杂的反射层,传统的去噪方法仍然存在一些不足,探究新的去噪算法具有重要的研究意义。
近年来,由于人工智能表现出的显著优势,很多学者也开始利用人工智能解决地球物理问题,包括应用于地球物理反演[13]、断层识别[14]、孔隙度预测[15]和速度自动拾取[16]等。人工智能处理地震勘探数据去噪问题已经成为当前研究的热点之一,如应用卷积神经网络处理不同类型噪声、海上数据去噪等。
在数据去噪方面,传统的基于模型驱动的方法,如基于传统滤波器的去噪方法,针对数据本身和噪声的特点进行分析,设计包括针对中值滤波器[17]、高效率自适应中值滤波器[18]等实现噪音的压制;而基于特征学习的去噪方法,是通过学习含噪声数据与去噪数据之间的映射关系进行去噪。Jain等[19]首次将卷积神经网络应用于自然图像去噪,验证了卷积神经网络在盲去噪环境的可行性,但是该方法的去噪效果严重依赖提取深度,导致去噪性能不稳定;针对该方法的缺点,Zhang等[20]提出前馈卷积神经网络(denoising convolutional neural network,DnCNN),首次将残差思想应用于去噪方面,该网络模型显著改善了去噪效果,但在细节和直观效果方面还有待提高。生成对抗网络(generative adversarial networks,GAN)是Goodfellow等[21]提出的一种新的无监督学习算法,具有较强的自主学习和样本生成能力,能够在一定程度上解决卷积神经网络在细节方面的问题;2020年Wang等[22]将GAN用于沙漠地震数据去噪;Dong等[23]将GAN与CNN结合运用于光纤地震数据去噪,说明GAN可以有效抑制不同地区、不同特性的地震资料的噪声。
在前人的研究基础上,本文使用生成对抗网络延伸出的环形生成对抗网络[24](cycle generative adversarial network,CycleGAN)对浅地层剖面数据进行随机噪声去噪。CycleGAN在GAN的基础上引入循环一致性损失,不需要一一对应的数据集,可以减少获取浅剖数据的成本,同时可以弥补GAN损失无效化的不足。本文根据浅剖数据的特点,训练针对浅剖数据去噪的CycleGAN网络模型,并将其应用于实际数据,取得良好的去噪效果,与传统去噪方法对比,本文方法在不损失有效信息的基础上,可以有效去除浅地层剖面数据中的随机噪声。
1. 方法原理
1.1 浅地层剖面原理
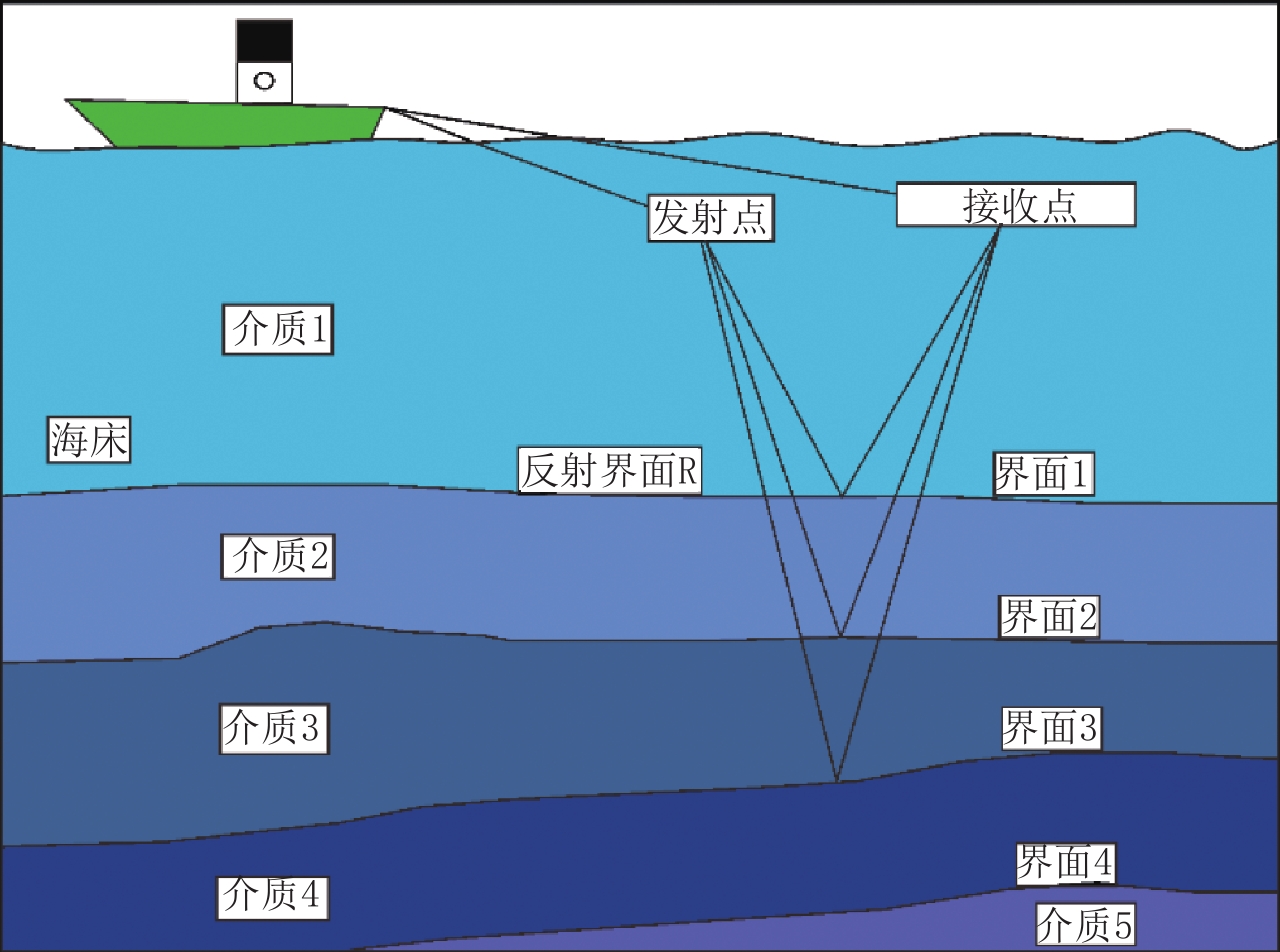
浅地层剖面是一种基于水声学原理的海底浅层地质构造探测技术,原理如图1所示。浅地层剖面探测系统的换能器按一定时间间隔向海底发射大功率声波,抵达海底时,部分声波直接反射回换能器,完成海水深度的测量;另一部分声波则继续向地层深层传播,由于地层结构复杂,在不同界面上又会有部分声波被反射回来。由于这些反射界面的特性和深度不同,在船上接收到回波信号的时间和强度也不同,通过对回波信号的滤波放大处理后,并在显示器上显现为由不同灰度点组成的线条,可以清晰地描绘出地层的剖面结构。
1.2 CycleGAN基本原理及方法改进
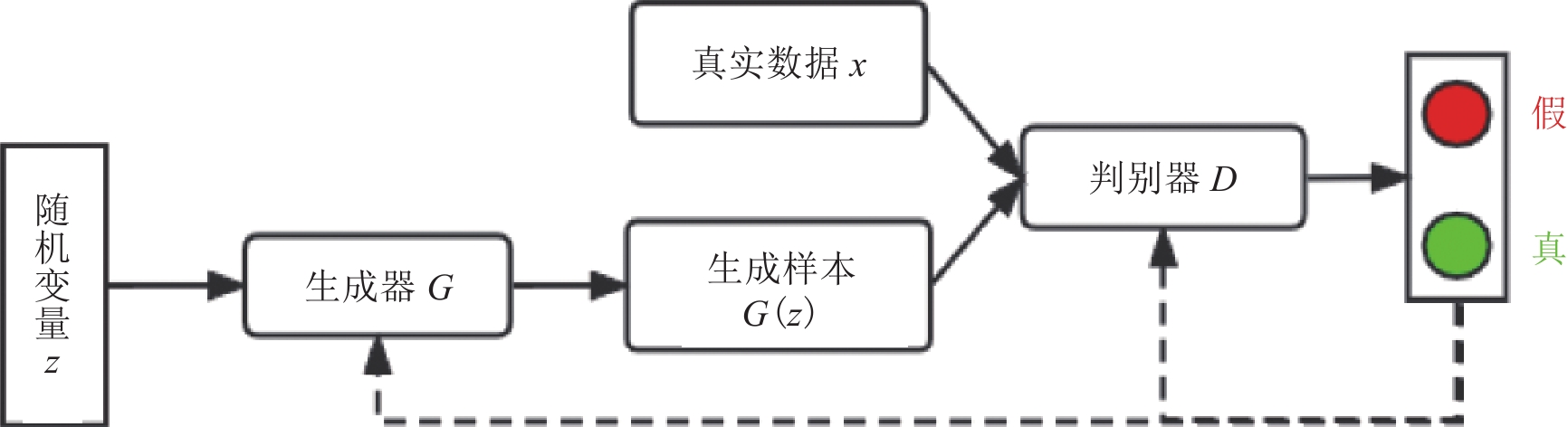
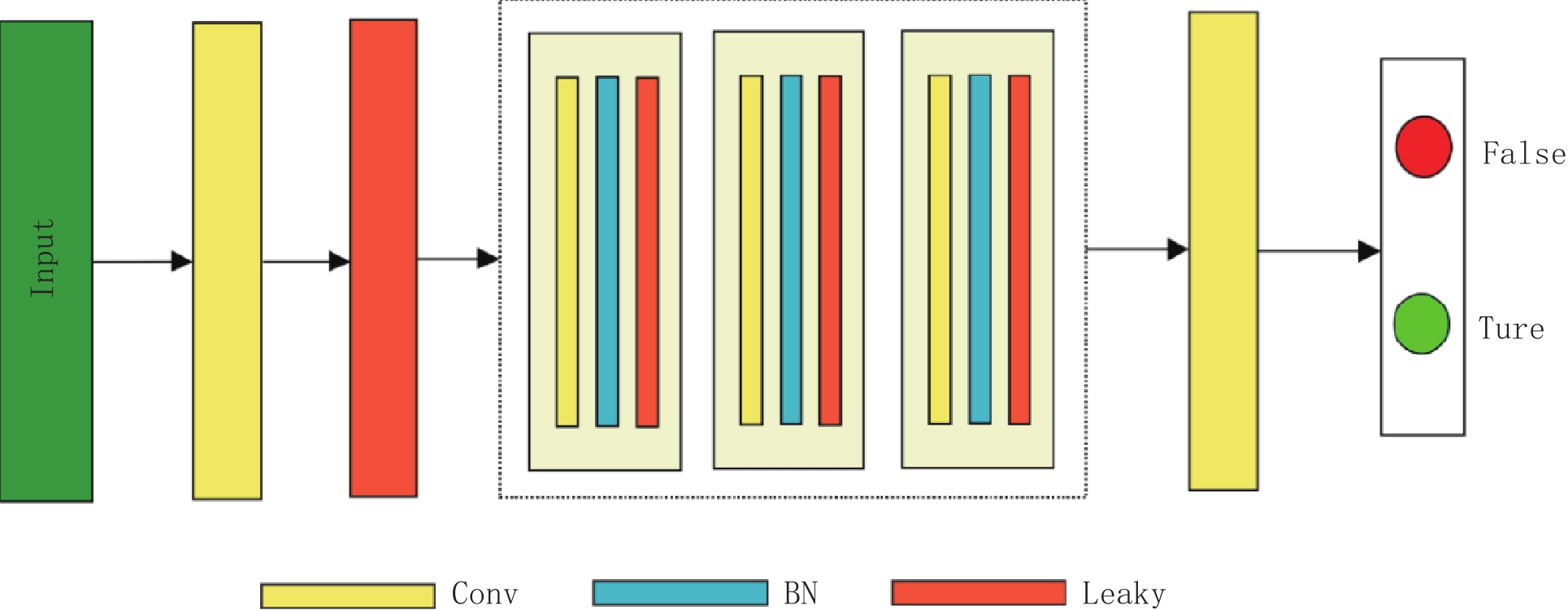
本文采用的CycleGAN是GAN的改进网络。GAN同时训练生成网络G(generative network)和判别网络D(discriminative network),通过对抗来学习产生一个类似训练集分布图像的模型[25]。训练过程通过相互对抗来交替优化生成网络和判别网络。训练生成网络G生成样本来欺骗判别网络D,训练判别网络D来判别图片的真实性[26]。GAN结构如图2所示。
GAN的目标函数被定义为:
$$ {L_{{\rm{GAN}}}}(G,D) = {E_{x\sim{P_{{\rm{data}}}}(x)}}\bigg(\lg \Big({D_\theta }(x)\Big)\bigg) + {E_{z\sim{P_z}(z)}}\Bigg(\lg \bigg(1 - {D_\theta }\Big({G_\omega }(z)\Big)\bigg)\Bigg) ,$$ (1) 式中,z为随机噪声,x为真实数据输入,θ和w分别代表D和G的参数,
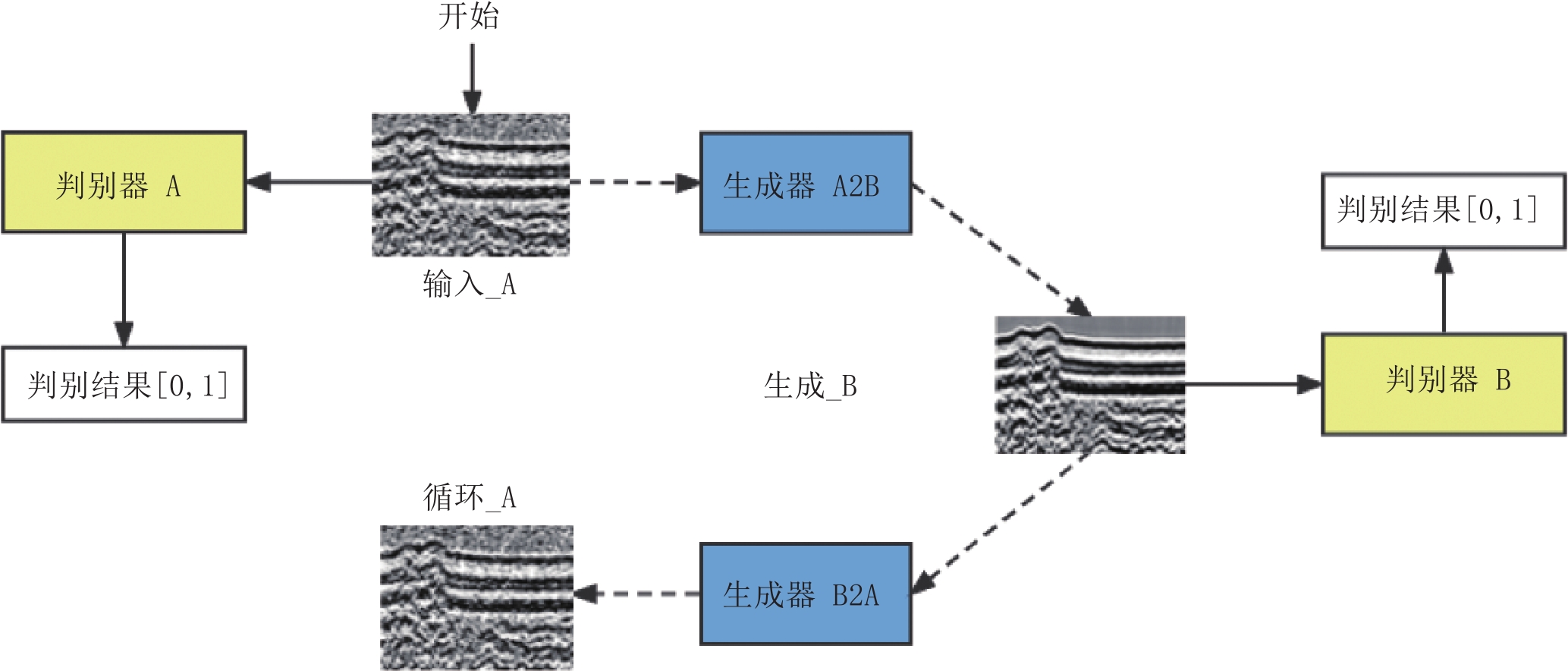
${E_{x\sim{P_{{\rm{data}}}}(x)}}$ 、${E_{z\sim{P_z}(z)}}$ 分别表示x、z满足的分布律,$ D_{\theta}(x) $ 表示真实图像被识别为真实的概率,$ G_{\omega}(z) $ 为生成网络生成的图像,$ D_{\theta}\Big(G_{w}(z)\Big) $ 表示生成网络生成的图像被识别为真实图像的概率。随机变量z作为生成器G的输入,经过G的非线性映射,输出信号$ G(z) $ 取决于G的结构和计算复杂性,从z到$ G(z) $ 一般经过高度复杂的非线性变换,使得随机变量$ G(z) $ 具备拟合高度复杂分布的能力。从上述GAN网络结构可以看出,原始的GAN网络是一个完全无监督的神经网络。为了对其实施监督,出现了针对于图像处理的传统生成对抗网络pix2pix[27]。然而pix2pix的训练常常需要成对并严格对齐的训练样本,而在实际应用中提供符合要求的训练样本常常很难且成本昂贵。为了解决成对样本的问题,研究者们提出了环形生成对抗网络CycleGAN。CycleGAN本质上是两个对称的GAN,构成了一个环形网络。如图3所示,CycleGAN的两个GAN共享2个生成器,并各自有1个判别器,即共有两个判别器和两个生成器。1个单向GAN两个loss,2个即共4个loss。
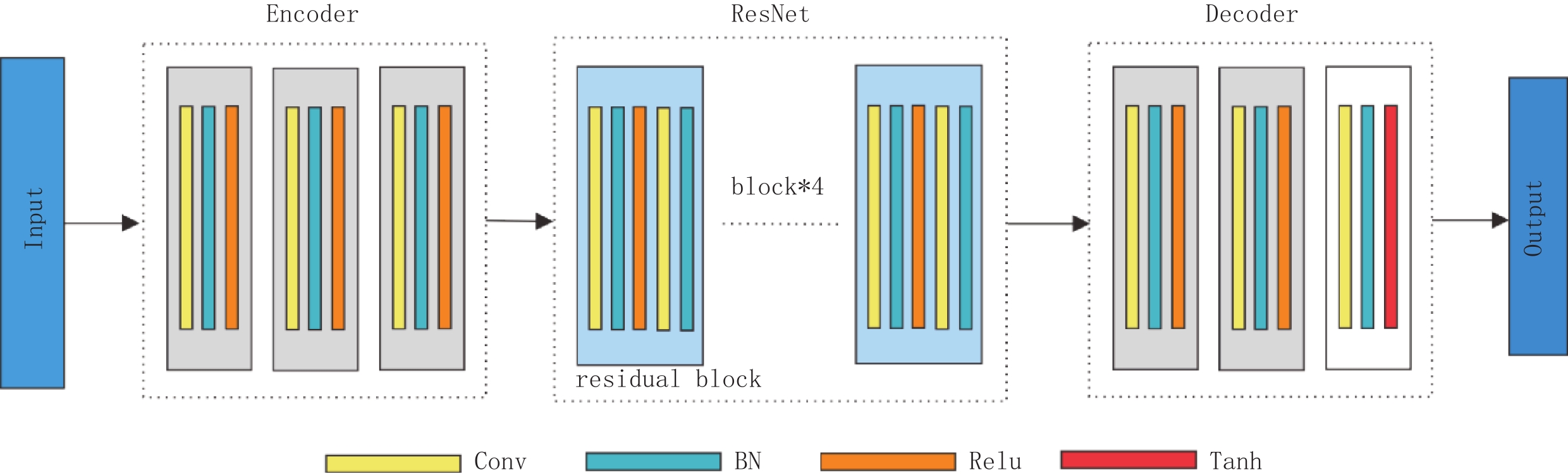
生成器G用于模拟数据的分布,生成模拟样本,本文的CycleGAN的生成网络具体结构如图4所示。样本A输入到生成器A2B中,首先经过一个编码器(Encoder);然后中间由6个残差块(residual block)组成,其中残差块包括卷积层、归一化层和激活层;最终再经过一个解码器(Decoder),输出生成样本。
残差网络补充了预测值与观测值之间的差值[28],构造一种类似天然的恒等映射。为防止在训练过程中出现梯度消失,导致网络退化的问题,将残差网络ResNet引入环形生成对抗网络的生成网络中,实现以跳层连接的形式,使得网络更加快速地收敛,解决了网络退化的问题。残差网络由一系列的残差块(residual block)组成,残差块分为直接映射和残差两个部分,每个残差块的网络由两个卷积层、两个归一化层和一个激活层组成。本文所使用的生成器网络结构在残差块中加入双层卷积,强化了残差块的结构,可以获得更加精准的数据特征。
判别器D的目的是根据输入的图像对判断两幅图像的配准程度,本文的CycleGAN的判别网络具体结构如图5所示。使用了Leaky Relu函数[29]代替Relu激活函数[30],即便输入小于零的值,同样可以计算梯度值,避免了反向传播过程中的梯度方向锯齿问题。样本A2B对生成样本和真实样本数据进行判别。判别器由卷积层、归一化层和激活层构成。
CycleGAN的实际目标就是学习从X到Y的映射,对抗性训练本身既可以学习正向映射G,也可以学习反向映射F,网络将同一组输入数据映射到目标域中的任意数据随机排列,其中任何学习到的映射都可以产生与目标分布相匹配的输出分布,并且会产生大量的无效映射,并且增大映射函数空间,即映射过程中可以将所有x都映射为Y空间中的同一元素y,使损失无效化,并且占据大量的存储空间。对于浅地层剖面数据来讲,重要的是得到清晰的海底浅层地质构造,一旦出现损失无效会影响最终的去噪效果。因此,为保持转换前后的一致性,本文利用了CycleGAN的“循环一致性损失”(cycle-consistency loss)来保证数据循环的有效性。
循环一致性损失的原理如图6所示,域X中的每个图像x的循环周期将生成的
$ G(x) $ 转换为原始图像x,即$x \rightarrow G(x) \rightarrow F\Big(G(x)\Big) \approx x$ ;同理,对于来自Y域的每幅图像y,其也应满足反向循环一致性,即$y \rightarrow F(y) \rightarrow G\Big(F(y)\Big) \approx y$ 。本文的CycleGAN损失函数共有3部分组成,分为两个对抗性损失,用于生成模型的分布和目标域中的数据相匹配,以及循环一致性损失,用于防止学习的正向映射G和反向映射F相互矛盾。公式如(2)所示:$$ \left\{ {\begin{array}{*{20}{l}} {L(G,F,{D_x},{D_y}) = {L_{{\rm{GAN}}}}(G,{D_y},X,Y) + {L_{{\rm{GAN}}}}(F,{D_x},Y,X) + \lambda {L_{{\rm{cyc}}}}(G,F)}\\ {{L_{{\rm{GAN}}}}(G,{D_y},X,Y) = {E_{y\sim{P_{{\rm{data}}}}(x)}}\bigg(\lg \Big({D_y}(y)\Big)\bigg) + {E_{x\sim{P_{{\rm{data}}}}(x)}}\Bigg(\lg \bigg(1 - {D_y}\Big(G(X)\Big)\bigg)\Bigg)}\\ {{L_{{\rm{cyc}}}}(G,F) = {E_{x\sim{P_{{\rm{data}}}}(x)}}\bigg({{\Big\| {F\Big(G(x)\Big) - x} \Big\|}_1}\bigg) + {E_{y\sim{P_{{\rm{data}}}}(y)}}\bigg({{\Big\| {G\Big(F(y)\Big) - y} \Big\|}_1}\bigg)} \end{array}} \right. ,$$ (2) 其中,
$L\left(G,F,{D}_{x},{D}_{y}\right) $ 表示CycleGAN损失函数,${L}_{\mathrm{G}\mathrm{A}\mathrm{N}}\left(G,{D}_{Y},X,Y\right) $ 表示对抗性损失函数;${L}_{\mathrm{c}\mathrm{y}\mathrm{c}}\left(G,F\right) $ 表示循环一致性损失函数:$\lambda $ 为循环一致性损失系数,其作用是控制损失函数所占比例[31],即控制两种损失的在训练中的相对重要性。2. 基于改进的CycleGAN网络去噪技术
在准备网络的过程中,为了增加网络的特征学习能力,生成器的残差块增加了两层卷积层;同时,简化了编码和解码结构,以此增强了训练的效率。基于改进后的CycleGAN对浅剖数据进行智能去噪处理,首先向无噪的数据中加入高斯噪声,为增加样本数量将原始数据和加噪数据分别进行切割,分成数小块;然后将加噪数据和原始数据分别放入CycleGAN的数据集中进行训练;通过分析去噪效果不断优化网络参数,最终获得理想的去噪CycleGAN网络,将其应用到实际资料的去噪中,测试网络的有效性和适应性。本文将无噪的浅剖数据资料和有噪声数据同时输入网络模型进行特征转换训练,以此达到对噪声数据去噪的目的。去噪流程如图7,具体步骤包括建立数据集、数据集预处理、网络训练、模型预测、模型评价。
首先要建立用于训练环形生成网络的样本集,环形生成网络作为对称结构的生成对抗网络,需要两个对照的样本集。在本文的训练中,需要一个无噪声的浅剖数据样本集和一个加入高斯噪声的噪声数据样本集。无噪声数据集需要选取地层清晰可见,质量较高的浅剖数据,保证网络的学习质量。给无噪声数据集加入随机的高斯噪声形成噪声数据集。为了增加样本的数量和多样性,将较大的数据分割成128×128的小块数据,从而降低网络的学习难度。
数据集建立后进而对样本中的数据进行预处理,数据预处理是对浅地层剖面数据在训练之前进行归一化、标准化等预处理。数据的差值过大会影响训练效果,为了保证网络的有效收敛,需要对数据进行规范处理。本文基于原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化:
$$ {x^*} = \frac{{x - \mu }}{\sigma } ,$$ (3) $\mu $ 表示所有样本数据的均值,σ表示所有样本数据的标准差。经过处理的数据符合标准正态分布,即均值为0,标准差为1,既保证了数据的可收敛性也不会过度减少数据的多样性。处理好训练数据集后续用于网络模型的训练。训练过程中选择每40个step输出一次训练结果和训练时间,每1000个step保存相应的去噪网络模型。由于环形生成对抗网络的对称性,只需保存去噪方向的网络模型。网络模型在训练过程中根据误差函数的loss值不断调整训练方向,使得训练结果能够更加优化,最终得到符合要求的网络模型。将准备的测试噪声样本输入到相应的模型中进行测试,如果测试效果不佳还需要调整网络参数重新训练,若是网络模型保存的不够精准还需调节保存步长。但训练集和测试集原本是同一区域浅剖数据集,相似度较高,为确保网络的普遍有效性,还需得选择不同区域的浅地层剖面数据输入网络进行迁移学习训练。
网络模型训练的成功与否需要有一定的数据支持,除了直观对比去噪效果外,还需要通过一些指标参数对训练结果进行分析,使得最终结果更加客观。通过对比预测值与实际值,及相关评价指标(本文选择峰值信噪比)对模型的性能评价,从而验证了本文智能去噪方法的正确性和适应性。
3. 实验与实际结果试算
本文采用基于改进环形生成对抗网络的去噪方法,利用经过处理的浅地层剖面实验数据训练CycleGAN网络的去噪功能,基于训练好的网络模型,对于实际数据进行智能去噪,并和常规的滤波去噪方法进行对比,验证本文方法的有效性。
3.1 实验数据训练
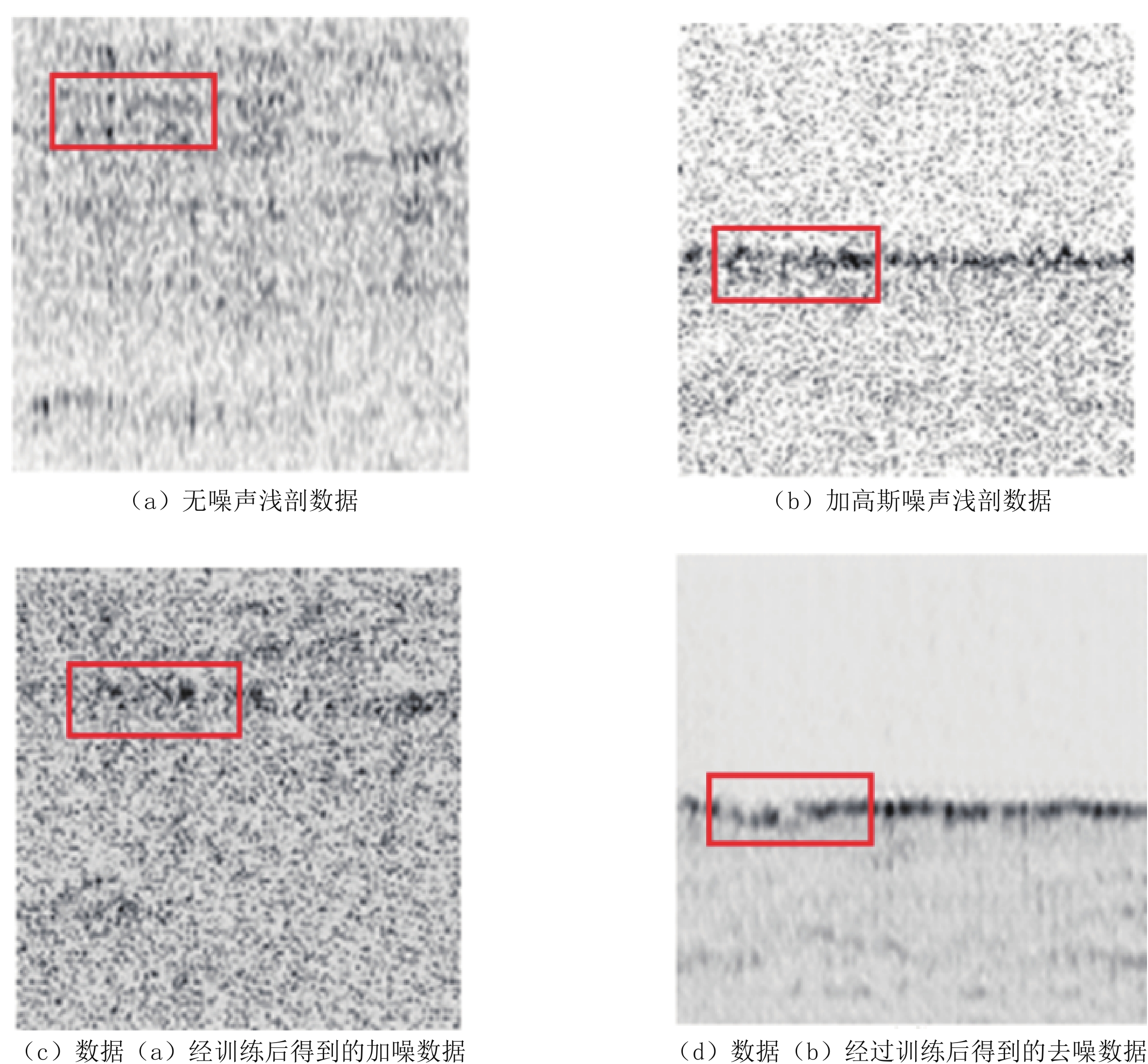
将挑选过的符合要求的浅地层剖面数据进行预处理后得到1645张128×128×1的无噪声浅剖数据,并给数据加高斯噪声,形成对照样本集。然后将准备好的浅剖数据样本输入到CycleGAN中进行网络训练,每次设置20000~30000个step,训练时长约2 h,训练结果如图8和图9所示。
图8和图9展示了两个不同的数据域经过CycleGAN的转化从而获得对方数据特征的结果。图8(a)和图8(c)为同一数据加噪前后的效果,可以从图中看到原本层位较为清晰的数据在获得了图8(b)数据中的噪声特性后,变为了同相轴不清晰的含噪数据图8(c)。同理,图8(b)和图8(d)为带有高斯噪声数据去噪前后的效果,图8(d)学习图8(a)中的数据特征,相较于图8(b)去掉了大量的高斯噪声并使浅剖数据的层位更加清晰,并且未发生有效信息的损失。图9为网络训练的直接结果,通过左右对比显示两个样本数据集的差异特征,通过上下对比可以明显看出数据重建后的效果。
由图所示,CycleGAN对浅地层剖面数据的样本集进行双向加噪和去噪的训练结果都较为成功,从图像的对比来看,无噪数据在原有的基础上加入了定量的高斯噪声,而噪声数据也得到有效的噪声去除。说明网络对于样本集的特征学习方向正确,层位未发生明显偏移并且效果良好,证明CycleGAN在浅地层剖面数据去噪方面的可行性。
3.2 实际浅地层剖面数据预测与分析
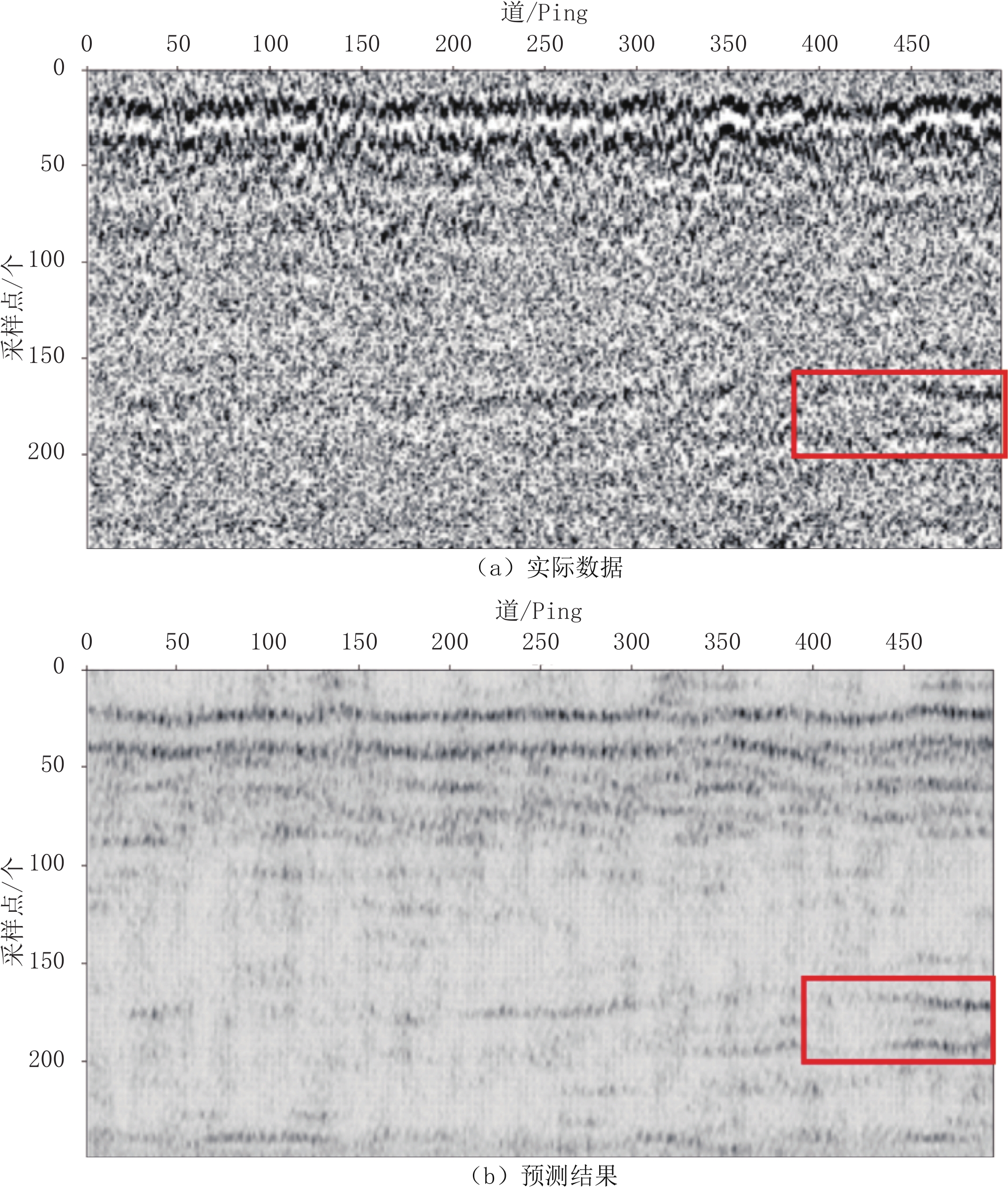
运用环形生成对抗网络对未训练过的另一区域的浅地层剖面实际数据进行去噪处理。从测线中截取500×250大小的数据直接输入训练好的网络模型中进行去噪,结果如图10所示。从结果中可以看出,该网络模型能够较好地去除浅地层剖面数据的随机噪声。由图10(a)和图10(b)中的对比中可以看出,环形生成对抗网络CycleGAN能够在去除随机噪声的同时保留层位有效信息,基本不会造成有效信号的损失或层位信息的偏移。
本文选取传统的带通滤波方法对浅地层剖面实际数据进行去噪处理与基于环形生成对抗网络的去噪方法进行对比。带通滤波方法结果如图11所示。
从图10(b)和图11的对比可以看到,基于改进环形生成对抗网络的去噪方法可以有效去除浅地层剖面数据中大部分的随机噪声数据,并且保证有效信息的完整性。而传统带通滤波根据数据的频率进行去噪操作,只能去除一定频率范围内的噪声。滤波范围设置过大容易误伤具有同样频率的有效信息,范围设置过小则去噪能力有限难以得到良好的去噪结果。而改进后的环形生成对抗网络通过特征学习将噪声从浅地层剖面数据中剔除,去噪效果更好且保护了原始数据的基本特征。预测结果与原数据相比能够清晰分辨出海底以及海底以下浅层反射位置(如图中红框所示)。
3.3 信噪比
衡量去噪效果的方法有许多种,其中信噪比是常见的衡量标准。本文选用了峰值信噪比(peak signal to noise ratio,PSNR)对CycleGAN去噪和带通滤波去噪效果进行了对比,峰值信噪比公式如公式(4)所示。
$$ {{\rm{PSNR}}} = 10\lg \Bigg(\frac{{{{\rm{MA}}}{{{\rm{X}}}^2}}}{{{{\rm{MSE}}}}} \Bigg) = 20\lg \Bigg( \frac{{{\rm{{MAX}}}}}{{\sqrt {{{\rm{MSE}}}} }}\Bigg) ,$$ (4) 式中:MAX为地震数据中最大值,MSE代表数据的均方误差。两种去噪方法的峰值信噪比对比结果如表1所示,可以看出CycleGAN用于地震数据去噪的峰值信噪比大于带通滤波方法的峰值信噪比,证明了该网络去噪能力的有效性与优越性。
表 1 两种去噪方法PSNR对比Table 1. PSNR comparison of two denoising methods去噪方法 PSNR/dB 带通滤波去噪 18.729 CycleGAN去噪 25.247 4. 结论
本文提出了基于改进环形生成对抗网络的智能去噪方法,实现了对浅地层剖面数据的随机噪声去除,并利用实验数据和实际数据的试算对该方法进行验证,得到了如下结论:
(1)基于循环一致性的环形生成对抗网络CycleGAN同时训练有噪声和无噪声的数据,能够得到对浅地层剖面数据有效去噪的网络模型和训练数据。在增强了生成器的卷积效果后,网络的学习效果良好,在训练过程中可以细致还原数据特征。即便是样本层位信息不是非常清晰的数据仍然可以获得良好的训练结果。
(2)与传统的带通滤波方法进行对比,基于改进环形生成对抗网络CycleGAN的去噪方法能够智能学习到更多随机噪声的特征并将其去除,峰值信噪比得到了一定的提升,在不损失有效信号的前提下,可以更好的去除随机噪声。
虽然实验数据和实际数据均取得了不错的去噪效果,但由于不同地区海底构造的差异性,仍然需要更多不同区域的浅地层剖面数据来保证本文方法的普适性。因此,后期还需要获取不同区域大量的浅地层剖面数据进行训练以及测试,提高本文方法的迁移学习效果。
-
表 1 两种去噪方法PSNR对比
Table 1 PSNR comparison of two denoising methods
去噪方法 PSNR/dB 带通滤波去噪 18.729 CycleGAN去噪 25.247 -
[1] 李一保, 张玉芬, 刘玉兰, 等. 浅地层剖面仪在海洋工程中的应用[J]. 工程地球物理学报, 2007,(1): 4−8. LI Y B, ZHANG Y F, LIU Y L, et al. Application of subbottom profiler to ocean engineering[J]. Chinese Journal of Engineering Geophysics, 2007, (1): 4−8. (in Chinese).
[2] 刘玉萍, 丁龙翔, 杨志成, 等. 利用浅剖资料进行海底底质分析[J]. 物探与化探, 2016,40(1): 66−72. LIU Y P, DING L X, YANG Z C, et al. Seabed sediment analysis using sub-bottom profile data[J]. Geophysical and Geochemical Exploration, 2016, 40(1): 66−72. (in Chinese).
[3] 李平, 杜军. 浅地层剖面探测综述[J]. 海洋通报, 2011,30(3): 344−350. LI P, DU J. Review on the probing of sub-bottom profiler[J]. Marine Science Bulletin, 2011, 30(3): 344−350. (in Chinese).
[4] 顾兆峰, 张志珣, 刘怀山. 南黄海西部地区浅层气地震特征[J]. 海洋地质与第四纪地质, 2006,(3): 65−74. GU Z F, ZHANG Z X, LIU H S. Seismic features of shallow gas in the western area of the Yellow Sea[J]. Marine Geology & Quaternary Geology, 2006, (3): 65−74. (in Chinese).
[5] 颜中辉, 栾锡武, 潘军, 等. 海上浅地层剖面处理的关键去噪技术[J]. 海洋地质前沿, 2016,32(9): 64−70. YAN Z H, LUAN X W, PAN J, et al. Key denoising techniques in marine sub-bottom shallow profiling[J]. Marine Geological Frontiers, 2016, 32(9): 64−70. (in Chinese).
[6] 施凤. 浅地层剖面数据精处理关键技术研究[D]. 武汉: 武汉大学, 2017. [7] 冯强强, 温明明, 吴衡, 等. 海洋浅地层剖面资料的数据处理方法[J]. 海洋地质前沿, 2013,29(11): 49−53, 66. FENG Q Q, WEN M M, WU H, et al. Data processing methods for marine sub-bottom profiles[J]. Marine Geological Frontiers, 2013, 29(11): 49−53, 66. (in Chinese).
[8] JEONG B J, LEE Y H. Design of weighted order statistic filters using the perceptron algorithm[J]. IEEE Transactions on Signal Processing, 1994, 42(11): 3264−3269. doi: 10.1109/78.330393
[9] GONZALEZ R C, WOODS R E. 数字图像处理[M]. 阮秋琦, 阮宇智, 译. 北京: 电子工业出版社, 2003. [10] MA Y Y, LI G F, WANG Y J, et al. Random noise attenuation by f-x spatial projection-based complex empirical mode decomposition predictive filtering[J]. Applied Geophysics, 2015, 12(1): 47−54. doi: 10.1007/s11770-015-0467-3
[11] 潘军, 栾锡武, 孙运宝, 等. SRME技术在海洋浅水高分辨率地震勘探中的应用[J]. 地球物理学进展, 2015,30(1): 429−434. PAN J, LUAN X W, SUN Y B, et al. Application of SRME technology in marine shallow water high resolution seismic exploration[J]. Progress in Geophysics, 2015, 30(1): 429−434. (in Chinese).
[12] 王兆湖, 王建民, 高振山, 等. 叠前自适应f-x域相干噪音衰减技术及应用[J]. 地球物理学进展, 2013,28(5): 2605−2610. WANG Z H, WANG J M, GAO Z S, et al. Pre-stack self-adaptive f-x domain coherent noise attenuation technology and application[J]. Progress in Geophysics, 2013, 28(5): 2605−2610. (in Chinese).
[13] YANG J, LIN N, ZHANG K, et al. Reservoir characterization using multi-component seismic data in a novel hybrid model based on clustering and deep neural network[J]. Natural Resources Research, 2021: 1−26.
[14] 杨晶, 丁仁伟, 林年添, 等. 基于深度学习的地震断层智能识别研究进展[J]. 地球物理学进展, 2022,37(1): 298−311. YANG J, DING R W, LIN N T, et al. Research progress of intelligent identification of seismic fault based on deep learning[J]. Progress in Geophysics, 2022, 37(1): 298−311. (in Chinese).
[15] 刘俊, 曹俊兴, 丁蔚楠, 等. 基于双向长短期记忆神经网络的储层孔隙度预测方法研究[J/OL]. 地球物理学进展: 1-9. (2021-07-23)[2021-12-18]. http://kns.cnki.net/kcms/detail/11.2982.P.20210723.1308.045.html. LIU J, CAO J X, DING W N, et al. Research on reservoir porosity prediction method based on bidirectional long-term and short-term memory neural network[J/OL]. Progress in Geophysics: 1-9. (2021-07-23)[2021-12-18]. http://kns.cnki.net/kcms/detail/11.2982.P.20210723.1308.045.html. (in Chinese).
[16] TUKEY J W. Exploratory data analysis[J]. Journal of the American Statistical Association, 1977, 28(1): 163−182.
[17] SUMAN S. Image denoising using new adaptive based median filter[J]. Signal & Image Processing an International Journal, 2014, 5(4): 1−13.
[18] QUAN H D, ZHANG H C, JIA H T. An improved adaptive median filtering algorithm[C]//International Symposium on Test Automation and Instrumentation, 2006: 269-272. [19] JAIN V, SEUNG H S. Natural image denoising with convolutional networks[C]//International Conference on Neural Information Processing Systems. Piscataway: IEEE Press, 2008: 769-776.
[20] ZHANG K, ZUO W, CHEN Y, et al. Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing, 2016, 26(7): 3142−3155.
[21] GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[C]// Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, 2014. Cambridge: MIT Press, 2014: 2672-2680.
[22] WANG H, LI Y, DONG X. Generative adversarial network for desert seismic data denoising[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020. DOI:10.1109/ TGRS.2020.3030692.
[23] DONG X T, LI Y. Denoising the optical fiber seismic data by using convolutional adversarial network based on loss balance[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020. DOI: 10.1109/TGRS.2020.3036065.
[24] ZHU J Y, PAKR T, ISOLA P, et al. Unpaired image-to-image translation using cycle-consistent adversarial networks[C]//Proceedings of the 2017 IEEE International Conference on Computer Vision, Venice, 2017. Washington: IEEE Computer Society, 2017: 2242-2251.
[25] 梁俊杰, 韦舰晶, 蒋正锋. 生成对抗网络GAN综述[J]. 计算机科学与探索, 2020,14(1): 1−17. LIANG J J, WEI J J, JIANG Z F. Generative adversarial networks GAN overview[J]. Journal of Frontiers of Computer Science & Technology, 2020, 14(1): 1−17. (in Chinese).
[26] 梁雪灿. 基于生成对抗网络的声学图像超分辨率研究[D]. 哈尔滨: 哈尔滨工程大学, 2019. [27] ISOLA P, ZHU J Y, ZHOU T H, et al. Image-to-image translation with conditional adversarial networks[C]//Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, 2017. Washington: IEEE Computer Society, 2017: 5967-5976.
[28] 王照, 陈恩庆. 基于深度残差生成对抗网络的本征图像分解算法[J]. 计算机应用与软件, 2022,39(3): 201−206. WANG Z, CHEN E Q. Eigen image decomposition algorithm for generating countermeasure network based on depth residual[J]. Computer Applications and Software, 2022, 39(3): 201−206. (in Chinese).
[29] NAYEF B H, ABDULLAH S N H S, SULAIMAN R, et al. Optimized leaky ReLU for handwritten Arabic character recognition using convolution neural networks[J]. Multimedia Tools and Applications, 2021, 81(2): 2065−2094.
[30] 杨久强, 林年添, 张凯, 等. 深度神经网络模型超参数选取及评价研究: 以含油气性多波地震响应特征提取为例[J]. 石油物探, 2022,61(2): 236−244. YANG J Q, LIN N T, ZHANG K, et al. Hyperparametric selection and evaluation of deep neural network models: A case study of feature extraction of multi-wave seismic response in an oil-gas reservoir[J]. Geophysical Prospecting for Petroleum, 2022, 61(2): 236−244. (in Chinese).
[31] 王议迎, 丁仁伟, 李建平, 等. 联合改进STA/LTA与MLoG算子的微震P波到时自动拾取方法[J]. 山东科技大学学报(自然科学版), 2021,40(6): 1−10. WANG Y Y, DING R W, LI J P, et al. Automatic pickup of microseismic P-wave arrival based on improved STA/LTA and MloG operators[J]. Journal of Shandong University of Science and Technology (Natural Science), 2021, 40(6): 1−10. (in Chinese).



 下载:
下载: