Research on Image Analysis Method of Spectral CT Based on Principal Component Analysis
-
摘要: 基于光子计数探测器的能谱CT，可以同时采集多个能谱通道的投影数据，并获得相应能量范围内物质的吸收特征，可以有效应用于物质识别与材料分解。主成分分析是一种很好的多元数据分析技术，可以用于处理多能谱CT数据。本文分别在投影域和图像域对能谱CT数据进行主成分分析，并对分析结果做出系统比较。为了减少噪声的影响，提高能谱CT图像的彩色表征性能，提出双域滤波与像素值平方相结合的方法，用于含噪声的主成分图像去噪，然后将所选取的主成分图像映射到RGB颜色通道。实验结果表明，无论是在投影域还是图像域进行主成分分析，都可以获取清晰的CT图像，识别出物质的不同成分。相较于在图像域的主成分分析方法，在投影域进行主成分分析能够保留物质的更多细节，获取更清晰的彩色CT图像。Abstract: Spectral computed tomography (CT) based on photon counting detector can simultaneously collect projection data of multiple spectral channels and obtain absorption characteristics of material within corresponding energy ranges, so it can be effectively applied to material identification and material decomposition. Principal component analysis is an excellent multivariate analysis technique, which can be applied to process multi-energy spectral CT data. In this paper, principal component analysis was performed on spectral CT data in projection domain and image domain respectively, and the analysis results were compared systematically. Meanwhile, in order to reduce the influence of noise and improve the color characterization performance of spectral CT images, the method of combining double domain filtering with pixel value square was proposed to denoise the noisy principal component images, and then the selected principal component images were mapped to RGB color channels. The experimental results demonstrate that the principal component analysis can obtain clear CT images and identify the different components of the substance, whether in the projection domain or the image domain. However, compared with the principal component analysis method in the image domain, principal component analysis in the projection domain can retain more details of the substance and acquire clearer color CT images.
-
据全球癌症数据统计显示，2020年估计有1930万新发癌症病例和近1000万癌症死亡病例，其中，肺癌是癌症死亡的主要原因，据估计死亡人数约180万[1]。肺癌气道播散（spread through air space，STAS）是指肿瘤细胞以微乳头状细胞团、实性细胞巢或单个细胞等形式存在于主瘤体之外的气道中[2]，这一概念是1980年Kodama等[3]在对1例在主病灶外的气道中发现同源癌细胞的肺癌病例的报道中首次提出。目前关于STAS的中文表述有气道播散[4]、气腔播散[5]、肺泡间转移[6]、肺泡间隙转移[7]等，目前尚未有统一的中文术语。
随着近年来对肺癌研究的不断深入，研究者们发现STAS对肺癌预后有着不可忽视的影响，2015年世界卫生组织将其确定为肺腺癌的一种新的侵袭方式。本文就STAS的病理学、相关临床意义及影像学方面的研究进展予以综述。
1. STAS相关病理研究
STAS是否与取材过程中导致的肿瘤细胞移位有关。Metovic等[8]对51例肺癌手术标本进行取材，每次取材均包括肿瘤前后组织，为避免刀片的影响，每切一次均更换洁净刀片，结果发现肿瘤前后组织的STAS发生率无明显差别。Lu等[9]发现，即使在手术过程中刀片没有经过瘤体而仅进行了肺的楔形切除，在瘤体周围的肺组织中也发现STAS的存在，说明STAS是客观存在的。但也有研究报道93％ 的瘤体外肺泡腔内的组织碎片是由于手术或者病理标本处理过程引起的机械性位移所致[10]，Villalba等[11]也发现人为导致的肿瘤细胞的移位现象。总的来说，STAS是客观存在的，人为的因素可能会夸大STAS发生率，因此需要严格规范标本取材的过程。
术中冰冻切片诊断STAS的可行性。Walts等[12]发现冰冻切片检测STAS的特异性高（100％），但灵敏度（50％）和阴性预测值（8％）都很低，与石蜡包埋切片相比，冰冻切片诊断STAS的总体准确率为74％[13]。因此用冰冻切片诊断STAS是不可靠的，这可能与大部分冰冻切片中没有足够的癌周组织而影响STAS的诊断有关[11]。
术前支气管肺泡灌洗液诊断STAS的可行性。有研究[14]显示术前支气管肺泡灌洗液诊断STAS的敏感性、特异性、阳性预测值和阴性预测值分别为45％、71％、86％ 和26％，利用术前支气管肺泡灌洗液诊断STAS的可靠性尚需要进一步研究。但另有学者[15]发现肺腺癌标本的灌洗液诊断STAS的敏感性、特异性和阳性预测值分别为80％、100％ 和100％，且灌洗液和石蜡切片中STAS细胞的形态极其相似，提示术后标本支气管肺泡灌洗液可用于诊断STAS。
STAS与肺癌组织类型之间的关系。STAS更常见于微乳头状、乳头状和实体瘤等更具侵袭性的肺癌类型中[16-20]，STAS阳性在中低分化肺癌中比例高于高分化肺癌[21]，浸润性腺癌中比例高于原位癌[22]。
STAS会导致更广泛的淋巴结转移、更多的胸膜及神经血管侵犯[4,18,23-24]，纵隔淋巴结肿大被认为是STAS阳性的独立预测因子[25]。
2. STAS的临床相关研究
关于STAS与肺癌患者的年龄、性别及吸烟情况等的关系，目前不同的研究，结果并不一致。有研究认为年龄是最佳预测因子之一，且STAS阳性肺癌患者更年轻[26-27]；男性肺癌患者出现STAS的概率更高[24,27]；吸烟是STAS的相关因素[27-28]。但另一些研究却认为STAS的存在与患者年龄、性别及是否吸烟无关[4,16-17,22-23,28]。
STAS与肺癌外科术式的相关研究。原发性肺腺癌患者接受亚肺叶切除术后，STAS阳性者的无复发生存期及总生存期显著低于STAS阴性者[29]，但在肺叶切除组中复发率没有明显差异[30]。但另一项关于直径≤2 cm的非小细胞肺癌患者的研究结果显示，虽然STAS阳性患者的累积复发率比阴性患者高，但采用肺叶切除和亚肺叶切除并不影响STAS阳性患者的总体生存率[31]。目前更倾向于将肺叶切除术作为合并STAS的早期肺腺癌（直径≤3 cm）患者的标准术式[32]。
STAS是肺癌复发的重要因素。临床分期为T1N0M0的肺腺癌患者中，STAS阳性者更易复发，且STAS阳性是T1b和T1c期肺腺癌复发的危险因素[5]。
3. STAS的影像学特征
3.1 常规CT特征的价值
STAS与瘤体实变比例（consolidation tumor ratio，CTR）的相关性研究。CTR是STAS的独立危险因素[17,27,33]。在≤3 cm的肺腺癌中，CTR能较好的对STAS进行预测，但是特异性较差[32]。与使用结节长径的模型相比，使用CTR的模型对STAS具有更好的预测性能[16]。纯实性结节、部分实性结节及实性成分占比＞50％ 是STAS的重要预测因子[34]，实性结节出现STAS的概率是部分实性结节的3倍[19]。虽然纯磨玻璃结节中也能发现STAS，但发生率较低，有文献报道纯磨玻璃结节中STAS出现的概率为2.42％[32]。
STAS与肿瘤直径及结节实变部分直径的关系。Zhuo等[25]和Zhang等[32]的结果显示结节最大直径、实性成分最大直径与STAS显著相关。实性成分最大直径预测STAS的敏感性和特异性分别为73.9％ 和69.1％，临界值为1.18 cm[18]。也有部分研究报道STAS阳性与阴性组间肿瘤最大直径不存在差异[17,19]。总的来说，可认为瘤体直径及实变部分直径越大，STAS出现的概率越高，但是其对STAS的诊断能力仍不如CTR。
其他常规CT征象与STAS的关系，一些研究认为STAS与分叶征[4,6,21,25,33]及毛刺征[6,18,21,25]、肿瘤周围卫星灶、瘤体边界模糊[4,17]相关，分叶与毛刺说明了肿瘤的膨胀性及浸润性生长，瘤体边缘模糊与卫星灶可能与肿瘤肺内播散及堵塞小支气管相关。另外，支气管充气征[7,19,32,35]、胸膜牵拉[4,7,35]、血管集束征[32]、肺气肿[6]等CT征象也被认为与STAS相关。有研究[4]还认为STAS阳性者瘤体多位于中下叶（51.16％）、阴性者瘤体多位于上叶（67.07％），而左右侧肺STAS发生率无明显差异。
3.2 能谱CT的价值
尹柯等[36]基于双能量CT回顾性分析了52例实性肺腺癌结节定量参数在STAS阳性与阴性组间的差异，发现动脉期碘浓度、动脉期标准化碘浓度及静脉期碘浓度间的差异存在统计学意义。其预测STAS的曲线下面积（area under the curve，AUC）分别为0.82、0.83及0.73，其中动脉期碘浓度和动脉期标准化碘浓度均为实性肺腺癌STAS的独立预测因子，两者联合诊断的AUC为0.89，作者认为双能量CT能有效帮助预测实性肺腺癌STAS的发生。
目前这方面的研究刚刚起步，需要更多的研究对上述结果进行验证。
3.3 影像组学的价值
Chen等[20]基于机器学习建立的模型在内部验证和外部验证的AUC分别为0.63和0.69。Liu等[37]的模型对STAS的误判率仅为7.69％。有研究[38]利用5个不同制造商、11个不同机构和22个不同型号CT的图像建立了STAS的预测模型，并进行了前瞻性的外部验证设计，最后该模型内外部验证的精度分别为0.66和0.78。上述结果说明影像组学在临床上诊断STAS具有一定的可行性。
研究发现基于瘤周组学特征的模型相比于基于瘤体组学特征的模型可对STAS进行更加精准的预测，将瘤体及瘤周组学特征结合后能得到更高的诊断性能。Zhuo等[25]基于瘤体影像组学特征建立的列线图及提取结节周围 0.5、1.0和1.5 cm内的影像组学特征建立的诺莫图对STAS都有着良好的预测性能。另有研究[39]发现，相对于瘤体本身的影像组学特征，瘤周1.5 cm的组学特征对STAS具有更好的预测性能，且将瘤体特征与瘤周特征结合后预测效果更佳。Qi等[17]对瘤周 0.2、0.4、0.6、0.8、1.0和2.0 cm的组学特征进行提取分析，也认为将肿瘤内部和周围的组学特征进行结合后才能更好地预测STAS（其建立的模型在训练和验证集中的AUC和诊断准确度分别为0.907、0.897、0.909和0.849），且瘤体周围特征对STAS的预测至关重要（占总的有效特征的75％）。
总的来说，人工智能的应用将进一步帮助影像学在临床实践中更好地预测STAS。
3.4 PET/CT的价值
研究提示STAS与肿瘤的高代谢相关。研究发现肿瘤代谢体积（metabolic tumor volume，MTV）与肿瘤CT体积（CT volume，CTV）的比值＞1能用于预测STAS的发生[40]。STAS阳性的瘤体标准化摄取值（standardized uptake value，SUV）明显高于阴性者[24]，用最大SUV值预测STAS的AUC为0.74，当诊断界值取2.48时，其敏感性为89.5％，特异性为52.8％[41]。
当肿瘤与肝脏的SUV比值（SUV T/L）小于0.65时，排除STAS的敏感性和特异性分别为84.1％、55.9％；将CT上磨玻璃成分体积百分比≥75％、SUV T/L比值≤0.65和贴壁生长型肺癌结合后建立的分层流程图预测STAS阳性的敏感性、特异性分别为79.3％ 和68.5％[42]。
4. 小结
综上所述，STAS在诊治和预后中有重要的价值，利用影像学方法预测STAS成为近年来的研究热点。常规CT的一些特征（如CTR、分叶及毛刺征）可用于STAS的预测；相比于常规CT特征，影像组学显示了更好地预测STAS的能力，但其临床实用性有待提高；PET/CT及能谱CT在预测STAS中也表现出很高的价值。
目前研究证实了影像学预测STAS的可行性，但由于目前研究数量相对较少，研究样本也较小，研究的结果尚存在差异性，因此需要进一步深入研究来发现更加可靠和准确的影像学预测方法。
-
![]()
图 4 小鼠胸腔投影域的主成分分析图像
Figure 4. PCA images of projection domain of mouse thoracic cavity
![]()
图 5 小鼠胸腔投影域主成分分析重建图像
Figure 5. Reconstructed images of projection domain of mouse thoracic cavity by PCA
![]()
图 6 小鼠胸腔图像域的主成分分析图像
Figure 6. PCA images of the image domain of the mouse thoracic cavity
![]()
图 7 小鼠胸腔的像素值平方去噪的主成分分析图像
Figure 7. PCA image of pixel value square denoising of mouse thoracic cavity
![]()
图 8 小鼠胸腔的双域滤波与像素值平方相结合去噪的主成分分析图像
Figure 8. PCA image denoising combining dual-domain filtering with pixel value square of mouse thoracic cavity
![]()
图 13 临床前小鼠投影域的主成分分析重建图像
Figure 13. Reconstructed images of projection domain preclinical mice by PCA
![]()
图 14 临床前小鼠图像域的主成分分析图像
Figure 14. PCA images of the image domain of the preclinical mice
![]()
图 15 临床前小鼠投影域第2主成分重建图像的去噪图像
Figure 15. Denoised images of the PCA-2 recon-structed images in the projection domain of preclinical mice
![]()
图 16 临床前小鼠图像域第2主成分的去噪图像
Figure 16. Denoised images of PCA-2 in the image domain of preclinical mice
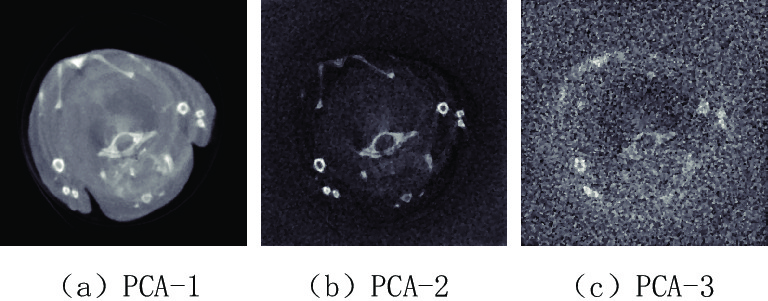
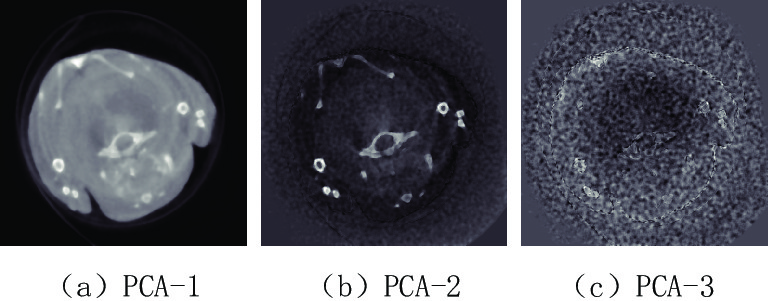
表 1 小鼠胸腔投影域与图像域进行主成分分析的各个主成分的贡献率
Table 1 The contribution rate of each principal component of the projection domain and image domain of the mouse thoracic cavity for PCA
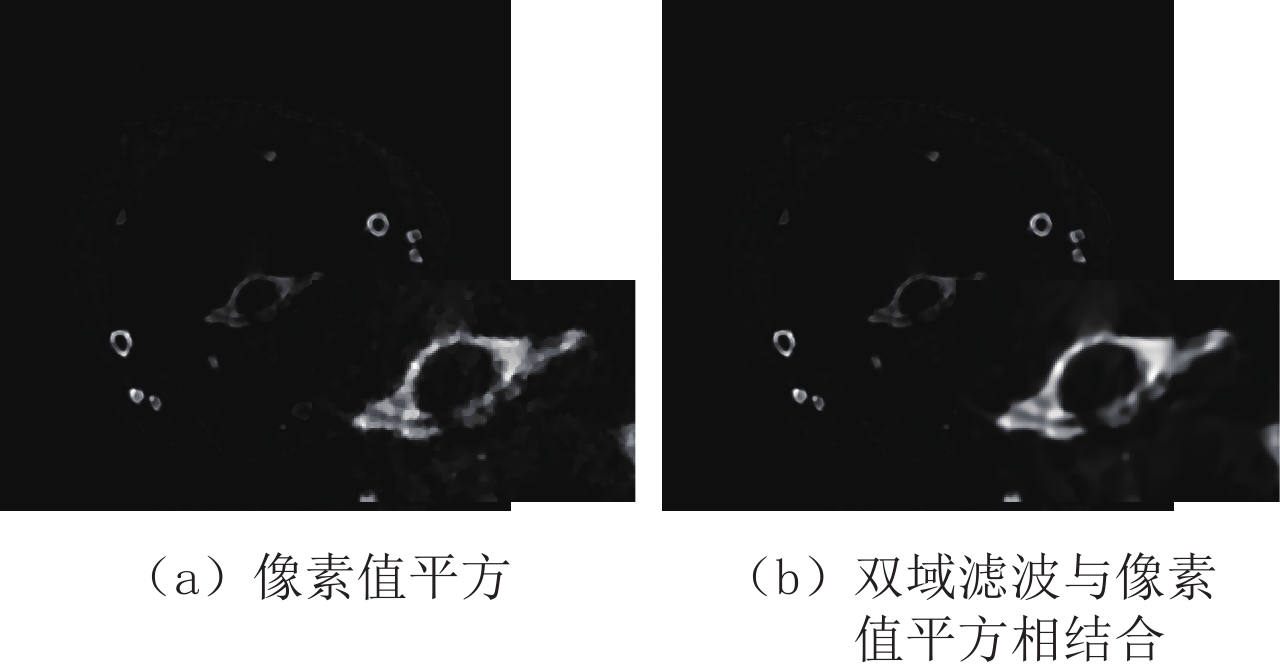
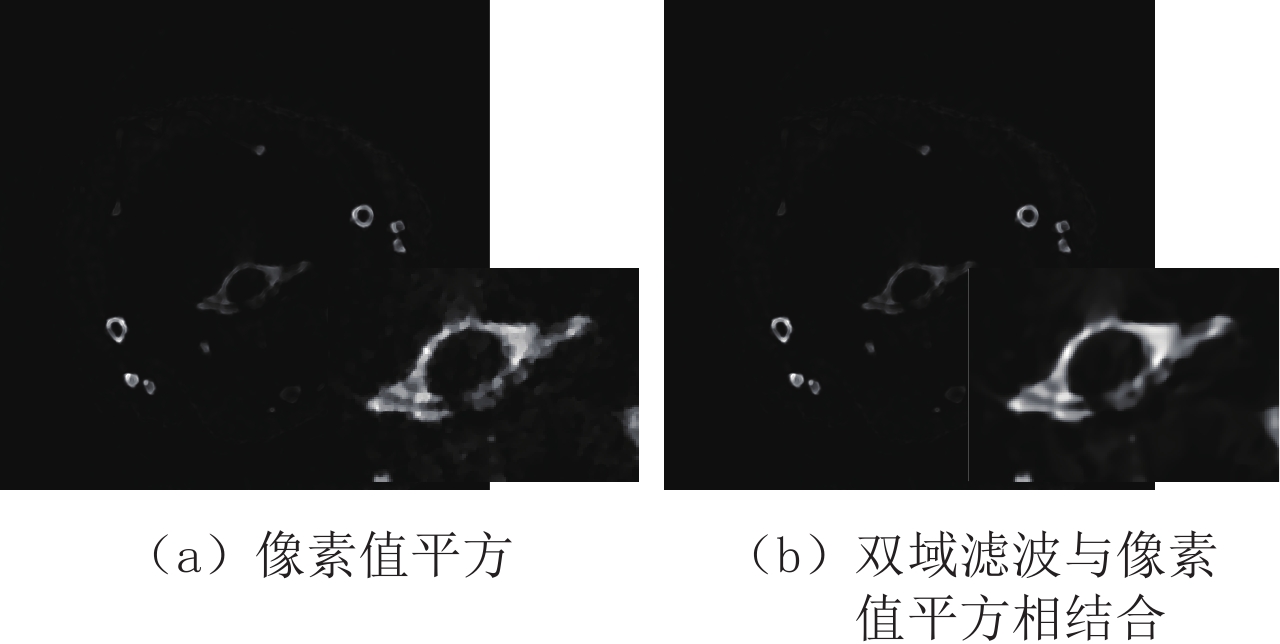
区域 各个主成分的贡献率/％ PCA-1 PCA-2 PCA-3 PCA-4 PCA-5 PCA-6 PCA-7 PCA-8 投影域 99.758 0.146 0.071 0.007 0.005 0.005 0.004 0.004 图像域 98.094 1.234 0.591 0.026 0.020 0.014 0.012 0.009 
下载: 导出CSV
表 2 两种去噪算法在小鼠胸腔投影域与图像域主成分图像上的峰值信噪比
Table 2 Peak signal to noise ratio of the two denoising algorithms for principal component images of mouse thoracic cavity in the projection domain and image domain
方法 投影域 图像域 PCA-2 PCA-3 PCA-2 PCA-3 像素值平方 64.209 49.139 51.590 61.749 双域滤波与像素值平方相结合 64.257 49.139 51.589 61.865
下载: 导出CSV
表 3 临床前小鼠在投影域与图像域进行主成分分析的各个主成分的贡献率
Table 3 The contribution rate of each principal component of the projection domain and image domain of the preclinical mice for PCA
区域 PCA-1 PCA-2 PCA-3 PCA-4 PCA-5 PCA-6 PCA-7 投影域PCA贡献率/％ 99.727 0.060 0.024 0.020 0.020 0.019 0.019 图像域PCA贡献率/％ 99.544 0.222 0.032 0.022 0.021 0.021 0.021 区域 PCA-8 PCA-9 PCA-10 PCA-11 PCA-12 PCA-13 投影域PCA贡献率/％ 0.019 0.019 0.019 0.018 0.018 0.018 图像域PCA贡献率/％ 0.020 0.020 0.020 0.020 0.019 0.018
下载: 导出CSV
-
[1] WU X C, HE P, ZHANG Y, et al. The small animal material discrimination study based on equivalent monochromatic energy projection decomposition method with dual-energy CT system[J]. Journal of X-ray Science and Technology, 2018, 26(6): 919−929. doi: 10.3233/XST-180418
[2] AARON S, SAVVAS N. Spectral computed tomography: Fundamental principles and recent developments[J]. Korean Journal of Radiology, 2021, 22(1): 86−96. doi: 10.3348/kjr.2020.0144
[3] FRÉDÉRIC J, CLARISSE F, MICHEL G, et al. An alternating projection-image domains algorithm for spectral CT[C]//Proceedings. IEEE International Symposium on Biomedical Imaging, United states, 2020: 187-190.
[4] GENG M F, TIAN Z F, JIANG Z, et al. PMS-GAN: Parallel multi-stream generative adversarial network for multi-material decomposition in spectral computed tomography[J]. IEEE Transactions on Medical Imaging, 2021, 40(2): 571−584. doi: 10.1109/TMI.2020.3031617
[5] LIU J L, DING H J, MOLLOI S, et al. TICMR: Total image constrained material reconstruction via nonlocal total variation regularization for spectral CT[J]. IEEE Transactions on Medical Imaging, 2016, 35(12): 2578−2586. doi: 10.1109/TMI.2016.2587661
[6] FENG J, YU H J, WANG S Y, et al. Image-domain based material decomposition by multi-constraint optimization for spectral CT[J]. IEEE Access, 2020, 8: 155450−155458. doi: 10.1109/ACCESS.2020.3016675
[7] WU W W, YU H J, CHEN P J, et al. Dictionary learning based image-domain material decomposition for spectral CT[J]. Physics in Medicine and Biology, 2020, 65(24): 245006. doi: 10.1088/1361-6560/aba7ce
[8] ABASCAL J F P J, DUCROS N, PEYRIN F. Nonlinear material decomposition using a regularized iterative scheme based on the bregman distance[J]. Inverse Problems, 2018, 34(12): 124003. doi: 10.1088/1361-6420/aae1e7
[9] 乔志伟. 总变差约束的数据分离最小图像重建模型及其Chambolle-Pock求解算法[J]. 物理学报, 2018,67(19): 383−396. doi: 10.7498/aps.67.20180839 QIAO Z W. The total variation constrained data divergence minimization model for image reconstruction and its Chambolle-Pock solving algorithm[J]. Acta Physica Sinica, 2018, 67(19): 383−396. (in Chinese). doi: 10.7498/aps.67.20180839
[10] KONG H H, LIU R, YU H Y. Ordered-subset split-bregman algorithm for interior tomography[J]. Journal of X-ray Science and Technology, 2016, 24(2): 221−240. doi: 10.3233/XST-160547
[11] BHAYANA R, PARAKH A, KAMBADAKONE A, et al. Material decomposition with dual- and multi-energy computed tomography[J]. MRS Communications, 2020, 10(4): 558−565. doi: 10.1557/mrc.2020.86
[12] ANTHONY B, JOCHEN B, NANETTE S, et al. Processing of spectral X-ray data with principal components analysis[J]. Nuclear Instruments and Methods in Physics Research, Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2011, 633(S1): S140−S142.
[13] ANDERSON N G, BUTLER A P, SCOTT N J A, et al. Spectroscopic (multi-energy) CT distinguishes iodine and barium contrast material in MICE[J]. European Radiology, 2010, 20(9): 2126−2134. doi: 10.1007/s00330-010-1768-9
[14] HE P, YU H Y, THAYER P, et al. Preliminary experimental results from a MARS micro-CT system[J]. Journal of X-ray Science and Technology, 2012, 20(2): 199−211. doi: 10.3233/XST-2012-0329
[15] KONG H H, LIU R, PAN J X, et al. Evaluation of an analytic reconstruction method as a platform for spectral cone-beam CT[J]. IEEE Access, 2018, 6: 21314−21323. doi: 10.1109/ACCESS.2018.2820500
[16] XIE H Q, REN Y, LONG W T, et al. Principal component analysis in projection and image domains: Another form of spectral imaging in photon-counting CT[J]. IEEE Transactions on Biomedical Engineering, 2021, 68(3): 1074−1083. doi: 10.1109/TBME.2020.3013491
[17] 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016. ZHOU Z H. Machine Learning[M]. Beijing: Tsinghua University Press, 2016.
[18] KNAUS C, ZWICKER M. Dual-domain image denoising[C]//2013 IEEE International Conference on Image Processing, ICIP 2013: Proceedings, Australia, 2013: 440-444.
[19] 孔慧华, 连祥媛, 陈平, 等. 基于能谱CT的材料组分彩色表征研究[J]. 光谱学与光谱分析, 2021,41(11): 3612−3617. KONG H H, LIAN X Y, CHEN P, et al. Research on color characterization of material components based on spectral CT[J]. Spectroscopy and Spectral Analysis, 2021, 41(11): 3612−3617. (in Chinese).
计量
- 文章访问数: 701
- HTML全文浏览量: 226
- PDF下载量: 248
