Evaluation of the Invasion of Pulmonary Subsolid Nodules by the Artificial Intelligence Volumetric Density Method
-
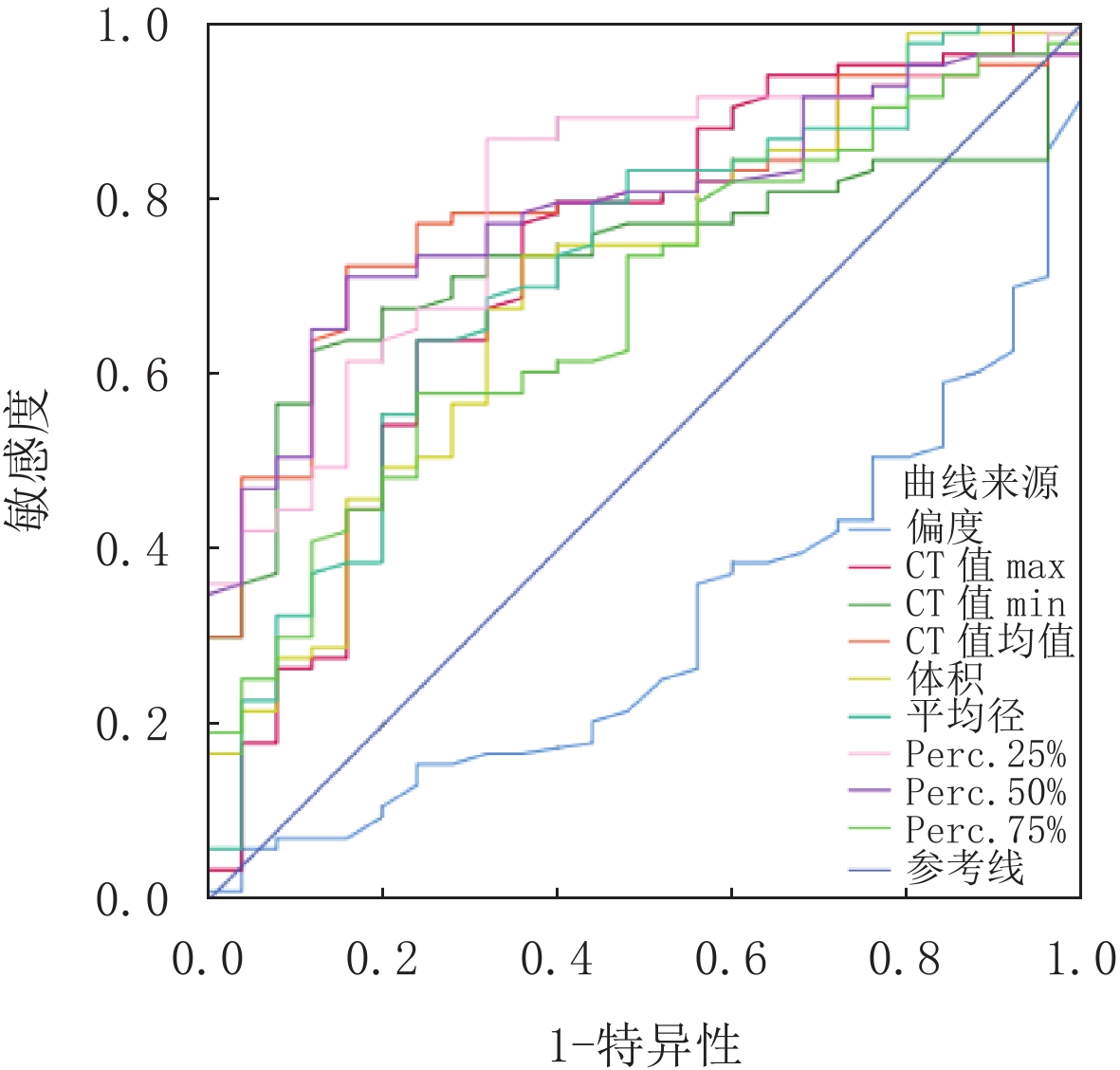
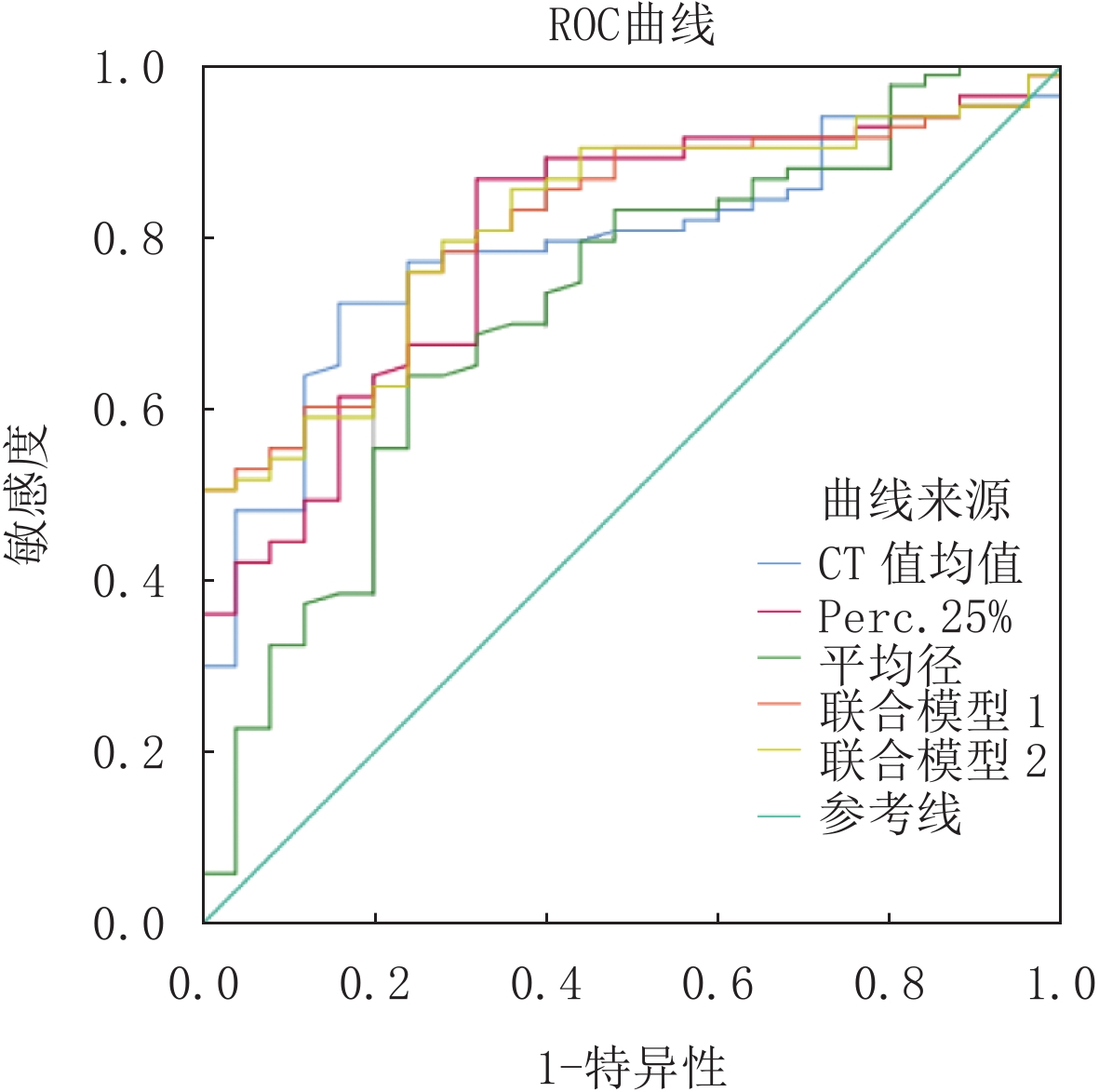
摘要: 目的：探讨人工智能（AI）体积密度法判断肺亚实性结节（SSNs）浸润性的价值。方法：回顾性分析106例患者的108枚SSNs的CT和病理结果，将结节分为腺体前驱病变组和腺癌组。通过肺结节AI软件测量并比较两组的最大CT值、最小CT值、平均CT值、峰度、偏度、Perc.25％、Perc.50％、Perc.75％、Perc.95％、结节体积、结节平均径等CT定量参数。使用Medcalc软件得出受试者工作特征曲线（ROC），评价诊断SSNs浸润性的敏感度、特异度、阳性预测值及阴性预测值，用逻辑回归分析评估他们的诊断性能。结果：SSNs的多数CT定量参数差异存在统计学意义，其中，诊断效能最高的是Perc.25％，AUC达0.797；其次为Perc.50％ 和平均CT值，AUC均为0.787。Logistic回归分析显示，将诊断效能最高的Perc.25％ 分别与Perc.50％ 和平均CT值两两建立联合诊断模型1，其中Perc.25％ 与平均CT值的模型诊断效能最高，且联合诊断模型诊断效能高于Perc.25％ 与平均CT值单独的诊断效能。Medcalc软件分析显示，Perc.25％≥-578 HU和平均CT值≥-468 HU的SSNs病理表现为腺癌的可能性大。将Perc.25％ 与结节平均径结合，可获得对判断SSNs浸润性非常有价值的联合诊断模型2。结论：AI体积密度法对SSNs的浸润性有较高的诊断价值，联合使用Perc.25％ 与平均CT值比单独使用更能准确地判断浸润性。Abstract: Objective: To explore the value of the artificial intelligence (AI) volumetric density method in determining the invasion of pulmonary hyposolid nodules (SSNs). Methods: A total of 108 SSNs and the pathological results of 106 patients were reviewed, and these were divided into a glandular prodromal lesions group and an adenocarcinoma group. Pulmonary nodule AI software was used to measure and compare the CT quantitative parameters of the two groups, including the maximum CT value, minimum CT value, average CT value, kurtosis, skewness, Perc.25%, Perc.50%, Perc.75%, Perc.90%, nodule volume, and mean nodule diameter. Moreover, a receiver operating characteristic curve (ROC) was obtained by MedCalc software to evaluate the sensitivity, specificity, positive predictive value, and negative predictive value for the diagnosis of SSN infiltration, and their diagnostic performance was evaluated by logistic regression analysis. Results: There were significant differences in most CT quantitative parameters of SSNs. The highest diagnostic efficiency was Perc.25% and the AUC was 0.797, while the AUC was 0.787 for Perc.50% and the mean CT value. Logistic regression analysis showed that Perc.25% with the highest diagnostic efficiency was combined with Perc.50% and the mean CT value. The model with Perc.25% and the mean CT value had the highest diagnostic efficiency, and the combined diagnostic model had a higher diagnostic efficiency than Perc.25% and the mean CT value alone. According to MedCalc software, SSNs with Perc.25% ≥−578 HU and mean CT values ≥ −468 HU were more likely to be in the adenocarcinoma group. In this study, Perc.25% was combined with the mean diameter of nodules, and a very valuable combined diagnostic model II was obtained to judge the infiltration of SSNs. Conclusion: The AI volume density method has a high diagnostic value for SSN invasion. Moreover , the combination of Perc.25% and mean CT value can accurately judge the invasion than the use of average CT value alone, providing a quantitative basis for the clinical management of SSNs.
-
Keywords:
- CT /
- artificial intelligence /
- volume density method /
- pulmonary subsolid nodules
-
由于采集成本、坏道、噪声、地形等诸多因素的影响，实际的地震数据往往会出现缺失道和野值道[1-2]，这些不规则或稀疏的地震数据，给地震数据的处理与解释工作造成了一定的困扰[3-4]，因此不完整、不规则数据的数据重构对于地震数据处理具有重要意义[5-6]。常用的地震数据重构方法有基于信号变换重构法[7-8]、基于预测滤波重构法[9-10]、基于波动方程重构法[11-12]等。其中基于信号变换重构方法是将地震数据从时间域转换到变换域，再根据变换域内信号的特征进行重构，计算结果比较稳健，得到了广泛的应用[13-15]。
基于压缩感知理论，在地震数据大量缺失的情况下恢复出地震数据[16-17]，可以转化为一个稀疏优化问题，相继出现了基于该理论的多种迭代阈值方法[18-19]。而凸集投影法（project onto convex sets，POCS）由Bregman提出，可以很好地与各种变换域相结合，被应用于地震数据的重构及数据规则化领域[20-23]。Gao等[24-25]基于傅里叶变换及POCS法对不规则缺失地震道进行重构，对线性或拟线性同相轴比较好，但是对弯曲同相轴则需分窗口处理；刘国昌等[26]将POCS法与曲波变换相结合，可以更好地对弯曲同相轴进行恢复；Yang等[27]和Wang等[28]从收缩阈值（iterative shrinking threshold，IST）算法的角度推导出POCS公式，进而比较了两种方法的重构效果的异同，并得出了POCS硬阈值重构效果较好的结论；王本锋等[29]和张华等[30]提出了基于Jitter采样理论的曲波域实现地震数据重构，有效地提高了计算效率；冯飞等[31]、张良等[32]、闫海洋等[33]将Shearlet变换与POCS算法结合起来，在动校正预处理后对地震数据进行重构，增强了地震数据在Shearlet域的稀疏性，有效地解决了假频问题。另一方面阈值函数的选取对于地震数据重构效果产生较大影响，王本锋等[29]、余江奇[34]等、张入化等[35]都对阈值函数进行对比分析，其中指数阈值函数比线性阈值参数效果好。Curvelet域对于曲线同相轴具有较好的重构效果，但是对于线性直达波的恢复方面能力较弱，并且相对其它地震波场（反射波、多次散射波等）直达波的能量较强，使其在迭代重构地震数据的过程中产生较强的干扰噪音。
本文在前人研究的基础上，将直达波及上部空白区域作为约束，对迭代算法进行改进，实现基于先验信息约束的Curvelet域地震数据POCS插值方法（prior project onto convex sets，PPOCS）。该算法可以有效地保留直达波等信息，且可以有效地压制其在迭代后期产生的噪音，保持重构地震波场高信噪比与高精度的特征。最后，通过对简单及复杂速度模型正演地震炮记录的稀疏数据重构测试与实际地震采集炮记录的野值去噪测试，讨论基于先验信息约束的Curvelet域PPOCS方法的优势。
1. 理论方法
1.1 压缩感知理论
压缩感知（compressive sensing，CS）是一种寻找欠定线性系统的稀疏解的技术。对于完整的数据
${\boldsymbol{ D}} $ 可以在$ {\boldsymbol{\varPhi }}$ 域表示：$$ {\boldsymbol{D}}_{{}}^{} = {\boldsymbol{\varPhi}} {\boldsymbol{x}} \text{，} $$ (1) 其中
$ {\boldsymbol{\varPhi}} \in {R^N} $ 为变换域的基函数向量，$ {\boldsymbol{x}} $ 为变换域系数向量，向量$ {\boldsymbol{x}} $ 中非零元素的个数可以表示为$ {\left\| x \right\|_{\text{0}}} = M $ ，若$ M < < N $ ，则数据${\boldsymbol{ D}} $ 可以在${\boldsymbol{ \varPhi }}$ 域稀疏表示。由于采集条件的限制以及后续地震处理中废炮、废道的剔除，致使地震数据不规则或稀疏：
$$ {\boldsymbol{D}}_{{{\text{obs}}}}^{} = {{\boldsymbol{P}}_{}}{\boldsymbol{D}} \text{，} $$ (2) 其中
$ {{\boldsymbol{D}}_{{\text{obs}}}} $ 为观测的不规则或稀疏数据，$ {\boldsymbol{D}} $ 为要恢复的完整数据，$ {{\boldsymbol{P}}_{}} $ 为采样矩阵。将式（2）代入式（1），可以写为：
$$ {\boldsymbol{D}}_{{{\text{obs}}}}^{} = {\boldsymbol{P}}{\boldsymbol{\varPhi}} {\boldsymbol{x}} = {\boldsymbol{Kx}} \text{，} $$ (3) 其中，
$ {\boldsymbol{K}} $ 为$ M \times N $ 的矩阵，称为测量矩阵。地震数据重构就是由不完整数据$ {\boldsymbol{D}}_{{{\text{obs}}}}^{} $ 和采样矩阵$ {\boldsymbol{K }}$ 恢复、重构出完整$ {\boldsymbol{x}} $ 的过程。如果$ {\boldsymbol{x}} $ 可以重构出来，则可以得到完整的地震数据${\boldsymbol{ D}} $ 。由于式（3）的求解是不适定的，考虑到
$ {\boldsymbol{D}} $ 在$ {\boldsymbol{\varPhi }}$ 域的稀疏性，采用稀疏促进策略，构建如下目标泛函：$$ \min \Big(J(x)_{{{\text{obs}}}}^{}\Big) = \frac{1}{2}\big\| {{{\boldsymbol{D}}_{{\text{obs}}}} - {\boldsymbol{Kx}}} \big\|_2^2 + \tau {\big\| {\boldsymbol{x}} \big\|_0} \text{，} $$ (4) 其中
$ \tau $ 为域系数向量的阈值。对于式（4）发展了一系列的迭代求解算法，其中基于阈值收缩法（IST）的凸集投影（POCS）方法在解决地震数据重构的方法中具有较好的效果[27]。1.2 凸集投影
利用阈值收缩求解方程（4）的地震数据重构的公式为：
$$ {\boldsymbol{x}}_{}^{k + 1} = {S_{{\tau _k}}}\bigg( {{x^k} + {{\boldsymbol{K}}^{\mathrm{T}}}\left( {{{\boldsymbol{D}}_{{\text{obs}}}} -{\boldsymbol{ K}}{{\boldsymbol{x}}^k}} \right)} \bigg),\;\;\;\;k = 1,2,\cdots,{{n}} \text{，} $$ (5) 其中，
$ {\boldsymbol{x}}_{}^{k + 1} $ 为${\boldsymbol{k}}+1 $ 次迭代所得到变换域系数向量，$ {{\boldsymbol{K}}^{\mathrm{T}}} $ 为测量矩阵的逆变换，$ {{n}} $ 为迭代的总次数。阈值函数
$ S $ 一般分为硬阈值函数和软阈值函数，Yang等[27]比较了两种阈值函数，认为硬阈值重构效果较好，因此本文采用硬阈值函数：$$ {S_{{\tau _k}}}({x_i}) = \left\{ {\begin{array}{*{20}{c}} {{x_i}{\text{ }}\;\;\left| {{x_i}} \right| \geq {\tau _k}} \\ {0{\text{ }}\;\;\left| {{x_i}} \right| < {\tau _k}} \end{array}} \right. \text{，} $$ (6) 其中，
$ {\tau _k} $ 为第k次的门槛阈值，其随着迭代次数不同而变化。利用式（1）、式（5）可以改写为：$$ \begin{aligned} \;&\quad\qquad{\boldsymbol{{\boldsymbol{D}}}}_{}^{k + 1} = {\boldsymbol{\varPhi}} {{\boldsymbol{x}}^{k + 1}} {\text{ }} = {\boldsymbol{\varPhi}} {S_{{\tau _k}}}\left( {{{\boldsymbol{\varPhi}} ^{\mathrm{T}}}{{\boldsymbol{D}}^k} + {{\Big({\boldsymbol{P}}{\boldsymbol{\varPhi}} \Big)}^{\mathrm{T}}}\Big({{\boldsymbol{D}}_{{\text{obs}}}} - {\boldsymbol{P}}{{\boldsymbol{D}}^k}\Big)} \right)=\\ & {\boldsymbol{\varPhi}} {S_{{\tau _k}}}\bigg( {{{\boldsymbol{\varPhi}} ^{\mathrm{T}}}{{\boldsymbol{D}}^k} + {{\boldsymbol{\varPhi}} ^{\mathrm{T}}}\Big({{\boldsymbol{P}}^{\mathrm{T}}}{{\boldsymbol{D}}_{{\text{obs}}}} - {{\boldsymbol{P}}^{\mathrm{T}}}{\boldsymbol{P}}{{\boldsymbol{D}}^k}\Big)} \bigg) ={\boldsymbol{\varPhi}} {S_{{\tau _k}}}\Bigg( {{{\boldsymbol{\varPhi}} ^{\mathrm{T}}}\bigg( {{{\boldsymbol{D}}^k} + \left( {{{\boldsymbol{D}}_{{\text{obs}}}} - {\boldsymbol{P}}{{\boldsymbol{D}}^k}} \right)} \bigg)} \Bigg){\text{ }} \end{aligned} 。 $$ (7) 通过公式（7）可以得到POCS的迭代公式：
$$ {\boldsymbol{D}}_{}^{k + 1} = {{\boldsymbol{D}}_{{\text{obs}}}} + \left( {{\boldsymbol{I}} - {\boldsymbol{P}}} \right){\boldsymbol{\varPhi}} {S_{{\tau _k}}}\left( {{{\boldsymbol{\varPhi}} ^{{{\mathrm{T}}}}}{{\boldsymbol{D}}^k}} \right) \text{，} $$ (8) 其中，
${\boldsymbol{I }}$ 是单位对角阵。由于式（8）在迭代中考虑了观测炮集的信息，因此其在重构地震数据的过程中，在收敛速度和重构精度方面POCS方法都要高于IST的迭代方法。曲波域对于曲线具有较好的重构效果，但是对于线性直达波的恢复方面能力较弱，并且相对于其它地震波场（反射波、多次散射波等）直达波的能量较强，使其在迭代重构地震数据的过程中产生较强的干扰噪音，影响重构效果。在重构过程中将直达波进行切除处理，再进行数据恢复，然而有些直达波与反射波等波场耦合在一起，并且直达波及早至波在后期处理中，尤其在速度反演中具有重要作用。本文利用先将炮记录直达波区域基本拉平，利用式（8）先进行重构直达波等部分迭代重构地震数据，将变换域的炮记录反变换得到重构的直达波炮集；将其作为约束进行重构，可以有效地压制其在迭代后期产生的噪音，进而保持重构地震波场高信噪比与高精度的特征。本文在式（8）的基础上，通过加入待重构炮集的信息作为约束项，处理得到第k+1次迭代的地震数据公式：
$$ {\boldsymbol{D}}_{{\text{new}}}^{k + 1} = \left( {1 - {\boldsymbol{L}}{m_{k + 1}}} \right)*{{\boldsymbol{D}}^{k + 1}} +{\boldsymbol{ L}}{m_{k + 1}}*{\boldsymbol{D}}_{{\text{pre}}}^{} \text{，} $$ (9) 其中
$ {\boldsymbol{D}}_{{\text{new}}}^{k + 1} $ 为第k+1次迭代的重构地震数据，$ {\boldsymbol{D}}_{{\text{pre}}}^{} $ 为要重构的地震数据中已知的先验信息，例如炮记录上部的空白区域，线性插值得到的直达波信息等，$ {\boldsymbol{L}}{m_{k + 1}} $ 为加权矩阵因子，其值取决于对先验信息的准确性，如果一个区域对先验信息越准确则对应的矩阵元素值越接近于1，${\boldsymbol{ L}}{m_{k + 1}} $ 可以取固定值，也可以随着迭代的次数k改变。由于式（9）加上了对重构数据的先验信息约束，因此可以较好的压制由能量剧烈变化区域（如地震信号的直达波与上部空白区域）随着迭代次数增加而产生的噪音。1.3 曲波变换
由于曲线是稀疏表示地震波场的理想字典，依据反射系数在曲波域更为稀疏的特点，因此可以利用曲波变换实现POCS方法。考虑二维情况下的曲波变换，
$$ {c_m} = \Big\langle {{\boldsymbol{D}},{\phi _m}} \Big\rangle = \sum\limits_{{t_1},{t_2}} {{\boldsymbol{D}}[{t_1},{t_2}]} \overline {{\phi _m}[{t_1},{t_2}]} \text{，} $$ (10) 式中
$ {\phi _m} $ 表示Curvelet基函数，$ m = (j,{k_d},l) $ ，其中$ j，{k_d}，l $ 分别为尺度、方向、位置参数，${{\boldsymbol{c}}_m}$ 为曲波域内的系数，$ {t_1}，{t_2} $ 为数据D的时间窗，则地震数据可以用曲波系数和基函数表示为：$$ {\boldsymbol{D}} = \sum\limits_m {\Big\langle {{\boldsymbol{D}}{\boldsymbol{}},{\phi _m}} \Big\rangle {\phi _m}} = \sum\limits_m {{{\boldsymbol{c}}_m}{\phi _m}} 。 $$ (11) 将式（1）的
$ \varPhi $ 域选取为Curvelet域，则式（11）与式（1）相对应。即可以推导出Curvelet域地震的数据POCS插值方法的公式，则第k次迭代的地震数据在曲波域的硬阈值约束为：$$ {{\boldsymbol{D}}_k} = \sum\limits_{n \in \left\{ {m:|\left\langle {{\boldsymbol{D}},{\phi _m}} \right\rangle > {\tau _k}} \right\}} {\left\langle {{\boldsymbol{D}},{\phi _n}} \right\rangle {\phi _n}} = \sum\limits_m {{S_{{\tau _k}}}({{\boldsymbol{c}}_m}){\phi _m}} \text{，} $$ (12) 其中，
${S_{{\tau _k}}}({{\boldsymbol{c}}_m})$ 表示对曲波域系数进行硬阈值约束，取大于$ {\tau _k} $ 的部分。本文采用指数衰减的形式阈值函数：
$$ {\tau _k} = {\tau _0} * \exp\left(\frac{1-k}{M}\right)，\;\;\;\;k = 1,2,\cdots,{{n}} \text{，} $$ (13) 其中M为控制衰减快慢的系数。给定初始的最大阈值
$ {\tau _0} $ ，系数衰减项M和迭代次数k即可确定对应的阈值。1.4 流程图
本文采用的地震数据重构流程如图1所示：①输入初始的观测地震数据
${\boldsymbol{D}}$ ，并且拾取初至gc；②对炮记录利用坐标映射进行变换得到新的炮集${\boldsymbol{D}}_2 $ ；③对数据${\boldsymbol{D}}_2 $ 做曲波变换得到曲波域内的系数${{\boldsymbol{c}}_m}$ ；④对曲波域的系数利用阈值函数$ {\tau _k} $ 进行滤波；⑤利用 POCS方法进行迭代重构的到新的炮集${\boldsymbol{P}}_2' $ ；⑥反变换得到的炮集$ {\boldsymbol{D}}_{{\text{pre}}}^{} $ ；⑦对$ {{\boldsymbol{D}}^{k + 1}} $ 加上先验约束信息的得到新的重构地震数据$ D_{{\text{new}}}^{k + 1} $ ；⑧满足迭代次数或者信噪比要求，输出最终的重构结果。![]()
图 1 基于先验信息约束的Curvelet域地震数据POCS插值方法实现流程Figure 1. Flow diagram of seismic data reconstruction based on the POCS method in the curvelet domain with prior information2. 模型试算
在编程实现方法的基础上，为了测试改进POCS算法的优越性，本节对由4个平层界面构建的速度模型，其中速度从1 500 m/s到3 500 m/s等间隔变化，层的厚度分别为第1层为250 m其余层厚150 m，采用有限差分正演模拟得到的地震炮记录数据，以及Marmousi模型的正演模拟产生的含有复杂波场的地震炮记录数据分别进行抽稀与重构，并对比分析改进方法相对于常规方法的有效性及优点。
2.1 模型 一：简单层状速度模型的炮记录测试
为验证先验信息约束的曲波域POCS方法的有效性及优点，分别对简单层状模型的炮记录（图2（a））进行了随机缺失50％ 与70％ 的抽稀（图2（b）和图2（c）），并用常规POCS方法与先验信息约束的POCS方法进行重构测试。
重构测试的结果如图3所示，测试中都采用80次迭代，其中图3（a）和图3（b）分别为随机缺失50％ 炮记录常规POCS方法、先验信息约束POCS方法重构结果，图3（c）和图3（d）分别为随机缺失70％ 的常规POCS方法、先验信息约束POCS方法重构结果。
![]()
图 3 重构炮记录剖面（a）随机缺失50％曲波域常规POCS方法重构剖面，（b）随机缺失50％先验信息约束曲波域POCS方法重构剖面，（c）随机缺失70％曲波域常规POCS方法重构剖面，（d）随机缺失70％先验信息约束曲波域POCS方法重构剖面。Figure 3. Interpolated results using different methods由图4可知：①当炮记录随机缺失 50％ 地震道时，常规POCS与先验信息的POCS方法的重构结果都可以较好的重构反射轴，但是常规POCS方法对于直达波区域存在明显的迭代噪音，而应用先验信息约束后，重构剖面中的直达波区域的噪音得到压制，且剖面重构剖面信噪比更高；②当炮记录随机缺失70％地震道时，常规POCS方法可以较好的恢复深层同相轴，但是由于受到直达波强能量的影响，重构结果中噪音比较强，尤其在靠近直达波的区域，并且由于缺失数据过多，在两侧的边界位置，同相轴恢复出现较强的噪音；③应用先验信息约束的 POCS方法，重构的炮记录剖面的信噪比明显改善，直达波区域可以较好的恢复，并且对反射层可以有一些较好的改善，但是由于缺失数据较多，在中深部没有先验信息，所以重构中边界处依旧存在噪音的影响。
![]()
图 4 重构测试的信噪比SNR曲线对比Figure 4. Convergence curves of different seismic data reconstruction using different methods为了对比本文算法与常规POCS的收敛性，图4（a）和图4（b）分别展示整个剖面和直达波以下区域的重建测试信噪比SNR曲线。由图4（a）可以看出：不论是否应用先验信息的约束，迭代重构过程都是稳定的，信噪比都可以提高，但是PPOCS方法的信噪比更高，这是由于直达波的能量较强，PPOCS可以更好的约束直达波的区域，因此信噪比更高，并且两种方法地震数据缺失越少重构的效果更好，信噪比更高。为了比较约束区域以外的信噪比，本文将直达波以下的波场信噪比单独输出，可以看出，曲波域POCS方法对曲线地震同相轴具有较好的重构，信噪比都可以得到很大的提高，但PPOCS也可以对地下的反射波场等具有改善，并且在高精度恢复中（缺失50％）效果更明显。并且当地震缺失70％的时候，POCS方法的重构具有较大误差。
2.2 Marmous模型的炮记录测试
为验证本文方法在复杂波场的适用性，本节对Marmousi模型（图5）进行有限差分正演，得到炮记录如图6（a）所示，对炮记录进行随机抽稀50％ 得到抽稀的炮记录如图6（b）所示，并用常规POCS方法与先验信息约束的POCS方法进行重构测试。
![]()
图 6 重构炮记录剖面（a）原始的炮记录剖面，（b）随机缺失50％，（c）坐标变换域随机缺失50％，（d）坐标变换域的重构炮集，（e）反坐标变换域的重构炮集，（f）随机缺失50％ PPOCS方法重构剖面，（g）随机缺失50％常规POCS方法重构剖面。Figure 6. Interpolated results of shot profiles采用常规POCS方法与PPOCS方法进行重构测试，结果如图6所示，测试中都采用80次迭代，其中图6（e）～图6（g）分别为随机缺失50％ 炮记录直接坐标变换的重构、先验信息约束POCS方法、常规POCS方法重构结果。由图6可知：当炮记录随机缺失50％ 地震道时，常规POCS与先验信息的POCS方法的重构结果都可以较好的重构地震反射轴，但是常规POCS方法对于直达波区域存在明显的迭代噪音，而应用先验信息约束后，重构剖面中的直达波区域的噪音得到压制，且剖面重构剖面信噪比更高；而坐标变换域重构方法，直达波区域的噪音得到压制，但是在反射波地震波存在一定的问题，尤其炮点下方存在一定的异常。
为对比本文算法与常规POCS的总信噪比以及对直达波以外恢复的信噪比和恢复效果，图7展示重构测试的信噪比SNR曲线。由图7可以看出，不论是否应用先验信息的约束，迭代重构过程中总的信噪比都随着迭代次数而提高，但是PPOCS方法的信噪比收敛更快并且收敛到更高值，这是由于直达波的能量较强，PPOCS可以更好的约束直达波的区域，信噪比更高。
![]()
图 7 重构测试的信噪比SNR曲线对比Figure 7. SNR curves of different seismic data reconstruction methods为了比较约束区域以外的信噪比，本文将直达波以下的波场信噪比单独输出，可以看出，曲波域POCS方法对曲线地震同相轴具有较好的重构，信噪比都可以得到很大的提高，但PPOCS也可以对地下的反射波场等收敛到更高的信噪比值，说明在复杂波场的情况下约束信息对于非约束区域同样具有改善效果。
2.3 实际炮记录测试
本文在模型炮记录试验的基础上对某陆上二维高密度实际地震数据也做了重构测试，该地震资料的接收道距为10 m，479道接收，采样率4 ms，炮记录中含有明显的野值道。对野值道进行抽稀如图8（b），在分别利用常规方法与PPOCS方法进行重构，进行噪音压制，重构结果如图8（c）和图8（d）所示。
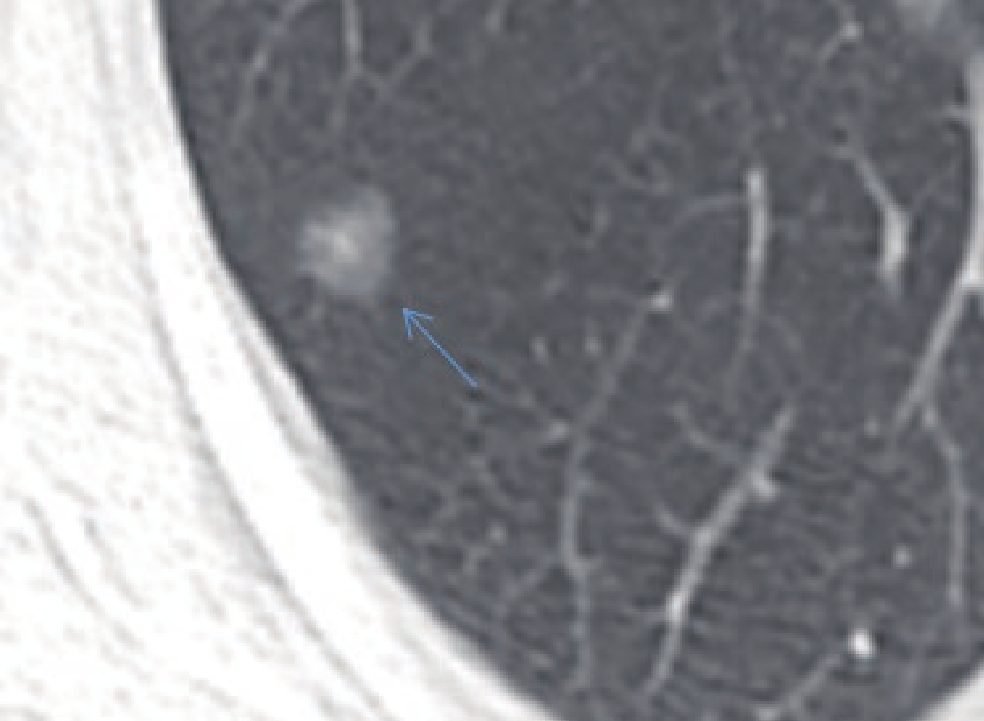
通过图8可以看出，原始炮记录中野值道通过两种方法都可以较好的压制，同相轴变的更加连续。但是PPOCS方法可以更好的进行恢复重构炮记录，尤其在近地表区域，为显示比较两种方法重构炮记录的效果，本文对横向1到88道，纵向上1.08 s到1.98 s的区域进行放大（图9）。通过图9还可以看出原始炮记录中野值道比较明显（图9红色箭头的位置），POCS方法可以较好的压制野值道的噪音，实现炮记录同相轴的连续性，相比于常规方法，PPOCS可以更好的重构地震数据，其同相轴连续性可以较好的改善，且重构噪音可以得到更好的压制。
3. 结论与讨论
本文在POCS重构稀疏地震数据的算法基础上通过引入先验信息约束项进行迭代重构稀疏地震数据，发展一种基于先验模型约束的Curvelet域地震数据POCS插值方法。在实现算法的基础上，通过合成地震炮记录与实际炮集进行测试对比，得到了如下认识：
（1）基于先验模型约束的POCS插值方法减弱了常规POCS插值方法对直达波以及上部空白区域对地震数据在迭代重构过程中的噪音干扰，在提高地震数据构建的精度的同时，可以改善剖面的信噪比，并且能保持地震波场同相轴的连续性。
（2）基于先验模型约束的POCS插值方法相对于常规POCS插值方法，对复杂速度模型的地震波场具有更好的适应性。
（3）在理论模型数据重构测试中，基于先验模型约束的POCS插值方法比常规POCS插值方法更快地收敛（SNR），且信噪比最终会收敛到一个较高值。
本文提出的基于先验模型约束的POCS插值方法能够提高重构地震波场的精度，改善常规POCS重构方法的信噪比和对直达波场的适应性。
-
![]()
图 1 女，48岁，CT显示右肺上叶后段SSN（蓝色箭头）。结节平均经约9.6 mm，术后病理诊断为AIS
Figure 1. A 48-year-old woman with SSN (blue arrow) of the posterior upper lobe of the right lung. The average length of the nodules was approximately 9.6 mm on CT, and the postoperative pathological diagnosis was AIS
![]()
图 2 腺体前驱病变组与腺癌组的灰度直方图参数ROC图，其中Perc.25％ 诊断效能最佳
Figure 2. The gray histogram parameters of the adenocar- cinoma group and the glandular precursor lesion group were ROC plots, in which Perc.25％ had the best diagnostic efficiency
![]()
图 3 腺体前驱病变组与腺癌组的Perc.25％、平均CT值及结节平均直径联合模型的ROC比较
Figure 3. Perc.25％, mean CT value and ROC comparison between the glandular precursors and adenocarcinoma groups
表 1 腺体前驱病变组与腺癌组临床资料比较
Table 1 Comparison of clinical data between the glandular prodromal disease group and adenocarcinoma group
临床资料 组别 统计检验 腺体前驱病变组（25例） 腺癌组（83例） t/χ2 P 年龄/岁 60.93±8.72 60.78±9.68 0.088 0.930 性别 男 7 32 0.928 0.335 女 18 51 结节分布 右上 13 34 4.263 0.370 右中 1 5 右下 5 14 左上 3 19 左下 3 11 结节类型 pGGNs 5 13 0.260 0.760 mGGNs 20 70 
下载: 导出CSV
表 2 腺体前驱病变组、腺癌组的CT值分布直方图纹理参数及结节体积、结节平均径比较
Table 2 Comparison of the CT value distribution histogram texture parameters, nodule volume and mean nodule diameter between the glandular precursor lesion group and adenocarcinoma group
参数 组别 P 腺体前驱病变组（n＝25） 腺癌组（n＝83） 偏度/HU 0.45（0.25～0.70） 0.215（0.06～0.45） 0.001 峰度/HU -0.64（-1.03～-0.02） -0.95（-1.10～-0.53） 0.260 CT最大值/HU 22.00（-122.00～126.00） 167.00（41.00～338.00） <0.001 CT最小值/HU -757.00（-782.00～-711.00） -653.00（-752.25～-597.00） <0.001 平均CT值/HU -536.67±99.18 -390.16±165.59 <0.001 Perc.25％/HU -605.00（-659.00～-496.00） -416.00（-532.25～-233.50） <0.001 Perc.50％/HU -580.00（-650.00～-522.00） -418.50（-545.00～-296.00） <0.001 Perc.75％/HU -508.00（-673.00～-433.00） -449.00（-610.00～-208.75） 0.003 Perc.95％/HU -329.00（-722.00～-107.00） -528.50（-685.00～-5.25） 0.819 结节体积/mm3 646.86（278.79～1647.36） 1467.00（534.50～3270.94） <0.001 结节平均直径/mm 9.90（8.40～13.50） 15.65（11.12～19.65） <0.001
下载: 导出CSV
表 3 ROC分析结果
Table 3 ROC analysis results
参数 AUC 最佳临界值 敏感度/％ 特异性/％ 阳性预测
值/％阴性预测
值/％95％ CI 下限 上限 偏度 0.689 0.24 56.63 76.00 88.7 34.5 0.593 0.775 CT最大值/HU 0.725 39.00 77.11 64.00 87.7 45.7 0.631 0.807 CT最小值/HU 0.731 -692.00 62.65 88.00 94.5 41.5 0.737 0.812 平均CT值/HU 0.787 -468.00 72.29 84.00 97.9 47.7 0.697 0.860 Perc.25％/HU 0.797 -578.00 86.75 68.00 90.0 60.7 0.709 0.869 Perc.50％/HU 0.787 -500.00 71.08 84.00 93.7 46.7 0.698 0.860 Perc.75％/HU 0.678 -474.00 57.83 76.00 88.9 35.2 0.581 0.765 体积/mm3 0.701 777.38 73.49 64.00 87.1 42.1 0.606 0.785 平均径/mm 0.718 13.50 63.86 76.00 89.9 38.8 0.623 0.800 联合模型1 0.814 － 75.90 76.00 91.3 48.7 0.728 0.883 联合模型2 0.816 － 75.90 76.00 91.7 48.3 0.730 0.884
下载: 导出CSV
-
[1] SUNG H, FERLAY J, SIEGEL R L, et al. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries[J]. CA: A Cancer Journal for Clinicians, 2021, 71(3): 209−249. DOI: 10.3322/caac.21660.
[2] ZHANG Y, FU F, CHEN H, et al. Management of ground-glass opacities in the lung cancer spectrum[J]. The Annals of Thoracic Surgery, 2020, 110(6): 1796−1804. DOI: 10.1016/j.athoracsur.2020.04.094.
[3] QIU T, RU X, YIN K, at al. Two nomograms based on CT features to predict tumor invasiveness of pulmonary adenocarcinoma and growth in pure GGN: A retrospective analysis[J]. Japanese Journal of Radiology, 2020, 38(8): 761−770. DOI: 10.1007/s11604-020-00957-x.
[4] SUN Y, LI C, JIN L, et al. Radiomics for lung adenocarcinoma manifesting as pure ground-glass nodules: Invasive prediction[J]. European Radiology, 2020, 30(7): 3650-3659. DOI: 10.1007/s00330-020-06776-y.
[5] ZHU N, ZHANG D, WANG W, et al. A novel coronavirus from patients with pneumonia in China, 2019[J]. The New England Journal of Medicine, 2020, 382(8): 727−733. DOI: 10.1056/NEJMoa2001017.
[6] LI X, ZHANG W, YU Y, et al. CT features and quantitative analysis of subsolid nodule lung adenocarcinoma for pathological classification prediction[J]. British Medical Council Cancer, 2020, 20(1): 60. DOI: 10.1186/s12885-020-6556-6.
[7] 李艳伶. 病灶直径和CT值联合评估浸润性肺腺癌的诊断价值[J]. 医学信息, 2021, 34(17): 172-174. LI Y L. Diagnosis value of invasive lung adenocarcinoma combined with tumor diameter and CT value[J]. Medical Informatics, 2021, 34(17): 172-174. (in Chinese).
[8] 虞梁, 王俊, 李洪, 等. 肺磨玻璃结节CT影像征象鉴别诊断肺浸润性腺癌与微浸润腺癌[J]. 南京医科大学学报(自然科学版), 2020,40(2): 248−251. YU L, WANG J, LI H, et al. Differential diagnosis of pulmonary infiltrating adenocarcinoma and microinfiltrating adenocarcinoma with CT features of ground glass nodules[J]. Journal of Nanjing Medical University (Natural Science), 2020, 40(2): 248−251. (in Chinese).
[9] 刘娜, 赵正凯, 邹佳瑜, 等. 基于人工智能的胸部CT肺结节检出及良恶性诊断效能评估[J]. CT理论与应用研究, 2021,30(6): 709−715. DOI: 10.15953/j.1004-4140.2021.30.06.06. LIU N, ZHAO Z K, ZOU J Y, et al. Detection of pulmonary nodules and evaluation of benign and malignant diagnosis in chest CT based on artificial intelligence[J]. CT Theory and Applications, 2021, 30(6): 709−715. DOI: 10.15953/j.1004-4140.2021.30.06.06. (in Chinese).
[10] 温德英, 潘雪琳, 姚辉, 等. 探讨CT扫描剂量对人工智能检测肺结节效能的影[J]. CT理论与应用研究, 2021,30(4): 455−465. DOI: 10.15953/j.1004-4140.2021.30.04.06. WEN D Y, PAN X L, YAO H, et al. Effects of CT scanning dose on the performance of artificial intelligence in detecting pulmonary nodules[J]. CT Theory and Applications, 2021, 30(4): 455−465. DOI: 10.15953/j.1004-4140.2021.30.04.06. (in Chinese).
[11] CHEN X, WEI X, ZHANG Z, et al. Differentiation of true-progression from pseudoprogression in glioblastoma treated with radiation therapy and concomitant temozolomide by GLCM texture analysis of conventional MRI[J]. Clinical Imaging, 2015, 39(5): 775-80.
[12] 蔡雅倩, 周小君, 张正华, 等. CT直方图分析鉴别肺良恶性纯磨玻璃结节的价值[J]. 放射学实践, 2020,35(8): 949−952. DOI: 10.13609/j.cnki.1000-0313.2020.08.001. CAI Y Q, ZHOU X J, ZHANG Z H, et al. Value of CT histogram analysis in differentiating lung benign and malignant pure ground glass nodules[J]. Practice Radiology, 2020, 35(8): 949−952. DOI: 10.13609/j.cnki.1000-0313.2020.08.001. (in Chinese).
[13] 毛海霞, 徐蒙莱, 冯银波, 等. CT图像纹理分析对小于10 mm纯磨玻璃结节侵袭性的诊断价值[J]. 中华临床医师杂志(电子版), 2019,13(5): 367−370. MAO H X, XU M L, FENG Y B, et al. Diagnostic value of CT image texture analysis for nodular invasivity in pure ground glass smaller than 10 mm[J]. Chinese Journal of Clinical Physicians (Electronic edition), 2019, 13(5): 367−370. (in Chinese).
[14] YAGI T, YAMAZAKI M, OHASHI R, et al. HRCT texture analysis for pure or part-solid ground-glass nodules: Distinguishability of adenocarcinoma in situ or minimally invasive adenocarcinoma from invasive adenocarcinoma[J]. Japanese Journal of Radiology, 2018, 36(2): 113-121. DOI: 10.1007/s11604-017-0711-2.
[15] 张宏, 丁必彪, 魏恒乐, 等. 高分辨率CT对肺纯磨玻璃结节侵袭性的预测价值[J]. 临床放射学杂志, 2019,38(3): 436−440. DOI: 10.13437/j.cnki.jcr.2019.03.017. ZHANG H, DING B B, WEI H L, et al. High resolution computed tomography (CT) for lung pure glass grinding nodules of invasive predictive value[J]. Journal of Clinical Radiology, 2019, 38(3): 436−440. DOI: 10.13437/j.cnki.jcr.2019.03.017. (in Chinese).
[16] 徐小东, 李君权, 吴向飞, 等. CT密度直方图对肺内纯磨玻璃样结节病理分级的预测价值[J]. 医学影像学杂志, 2021,31(1): 37−39, 42. XU X D, LI J Q, WU X F, et al. The prognostic value of CT density histogram in the pathological grading of pure ground glass nodules in lung[J]. Journal of Medical Imaging, 2021, 31(1): 37−39, 42. (in Chinese).
[17] KITAMI A, SANO F, HAYASHI S, et al. Correlation between histological invasiveness and the computed tomography value in pure ground-glass nodules[J]. Surgery Today, 2016, 46(5): 593−598. DOI: 10.1007/s00595-015-1208-1.
[18] IKEDA K, AWAI K, MORI T, et al. Differential diagnosis of ground-glass opacity nodules: CT number analysis by three-dimensional computerized quantification[J]. Chest, 2007, 132(3): 984−990. DOI: 10.1378/chest.07-0793.
[19] HAMMER M M, PALAZZO L L, KONG C Y, et al. Cancer risk in subsolid nodules in the national lung screening trial[J]. Radiology, 2019, 293(2): 441−448. DOI: 10.1148/radiol.
[20] WANG H, WENG Q, HUI J, et al. Value of TSCT features for differentiating preinvasive and minimally invasive adenocarcinoma from invasive adenocarcinoma presenting as subsolid nodules smaller than 3 cm[J]. Academic Radiology, 2020, 27(3): 395−403. DOI: 10.1016/j.acra.10.1016/j.acra.2019.05.005.
[21] 步玉兰, 李云, 戚元刚, 等. 纯磨玻璃密度结节高分辨率CT征象与病理组织学相关性研究[J]. 临床放射学杂志, 2018,5(2): 247−250. DOI: 10.13437/j.cnki.jcr.2018.02.016. BU Y L, LI Y, QI Y G, et al. Study on the relationship between density nodules and histopathology in high resolution CT of pure ground glass[J]. Journal of Clinical Radiology, 2018, 5(2): 247−250. DOI: 10.13437/j.cnki.jcr.2018.02.016. (in Chinese).
[22] LIU L H, LIU M, WEI R, at al. CT findings of persistent pure ground glass opacity: Can we predict the invasiveness?[J] Asian Pacific Journal of Cancer Prevention, 2015: 16(5): 1925-1928. DOI: 10.7314/apjcp.
-
期刊类型引用(1)
1. 许鹏君，许晨思，孙钢，张翼，赵苏莉，冯亚斌，刘锴. 膝骨性关节炎关节状态与西安大略和麦克马斯特大学骨关节炎指数评分水平的定量CT研究. 创伤与急危重病医学. 2025(02): 145-147+160 . 
百度学术
其他类型引用(0)
计量
- 文章访问数: 349
- HTML全文浏览量: 168
- PDF下载量: 33
- 被引次数: 1
