基于非局部广义总变分正则化的稀疏角度CT重建算法

蒋敏; 陶红伟; 程凯

doi:10.15953/j.ctta.2023.170

基于非局部广义总变分正则化的稀疏角度CT重建算法

蒋敏^1,,
陶红伟^1, ,,
程凯²

1.
郑州轻工业大学计算机与通信工程学院，郑州 450000
2.
之江实验室，杭州 311121

基金项目: 河南省科技攻关项目（222102210032）；河南省科技攻关项目（232102210014）。

详细信息

作者简介:
蒋敏，女，讲师，主要从事CT图像重建与CT应用研究，E-mail：jm_zqu@163.com

通讯作者:
陶红伟✉，男，副教授、硕士生导师，主要从事计算机网络安全理论与应用研究，E-mail：tthhww_811@163.com。

中图分类号: P 631.3；O 242；TP 391.41
计量
- 文章访问数: 207
- HTML全文浏览量: 84
- PDF下载量: 59
出版历程
- 收稿日期: 2023-08-29
- 修回日期: 2023-12-10
- 录用日期: 2023-12-12
- 网络出版日期: 2024-06-03
- 刊出日期: 2025-01-04

Sparse View CT Reconstruction Algorithm Based on Non-Local Generalized Total Variation Regularization

1.
College of Computer and Communication Engineer, Zhengzhou University of Light Industry, Zhengzhou 450000, China
2.
Zhejiang Lab, Hangzhou 311121, China

摘要

摘要:
基于广义总变分（TGV）正则化的CT图像重建算法可以有效克服总变分（TV）正则化的阶梯效应，从而能保护重建图像过渡区域的结构特征。尽管TGV重建方法优于TV重建方法，但它仍然忽略了非局部自相似先验信息在恢复CT图像细节方面的显著作用。为了克服TGV重建方法的上述局限性，本文引入一种非局部广义总变分（NLTGV）正则项，并提出基于NLTGV正则化的稀疏角度CT重建算法。该方法不仅可以利用不同阶的非局部变分信息来保护图像结构特征，而且还可以利用非局部自相似性来恢复重建图像的细节。由于重建模型包含双非光滑项，难以直接求解，因此提出基于凸集投影的优化算法，将其分解为几个简单子问题实现有效求解。仿真和实验结果表明，与其他变分正则化重建方法相比，本文重建方法可以有效提高CT图像重建质量。
- X射线CT /
- 稀疏角度采样 /
- 非局部广义全变分 /
- 凸集投影算法 /
- 分裂Bregman算法
Abstract:
CT image reconstruction algorithm based on generalized total variation (TGV) can overcome the staircase effect of total variation (TV) regularization, thereby protecting the structural features of the reconstructed image transition region. Although the TGV reconstruction method is superior to the TV reconstruction method, it still ignores the role of non-local self-similar prior information in restoring CT image details. To overcome the aforementioned limitations of TGV reconstruction method, we introduce a non-local TGV (NLTGV) regularization term and propose a sparse view CT reconstruction algorithm based on NLTGV regularization. The proposed method can not only utilize non-local variational information of different orders to protect image structural features but can also utilize non-local self-similarity to restore the details of the reconstructed image. Owing to the inclusion of dual non-smooth terms in the reconstruction model, solving it directly is difficult. Therefore, we proposed an optimization algorithm based on convex set projection, which decomposes the problem into several sub-problems to be solved. The simulation and experimental results show that the proposed NLTGV regularization reconstruction method can effectively improve the quality of reconstructed images compared with other variational reconstruction methods.
- X-ray CT /
- sparse view sampling /
- non-local generalized total variation /
- projection on convex set /
- split Bregman algorithm

HTML全文

图 1 搜索非局部相似图像块原理

Figure 1. Schematic illustrating the searching of non-local similarity patches

下载: 全尺寸图片幻灯片

图 2 仿真数据重建结果

Figure 2. Reconstruction results for simulated data

下载: 全尺寸图片幻灯片

图 3 仿真数据重建图像ROI放大图

Figure 3. Zoom-in display of ROI of the images reconstructed from the simulated data

下载: 全尺寸图片幻灯片

图 4 仿真数据重建图像的RMSE随迭代次数变化曲线

Figure 4. RMSE of the image reconstructed from simulated data versus iterations

下载: 全尺寸图片幻灯片

图 5 实际投影数据重建结果

Figure 5. Reconstruction results for real projection data

下载: 全尺寸图片幻灯片

图 6 实际数据重建图像ROI放大图

Figure 6. Zoom-in display of ROI of the images reconstructed from the real data

下载: 全尺寸图片幻灯片

图 7 实际数据重建图像的RMSE随迭代次数变化曲线

Figure 7. RMSE of the image reconstructed from real data versus iterations

下载: 全尺寸图片幻灯片

表 1 不同变分正则项特性的比较

Table 1 Comparison of characteristics with different variation regularization

算法	TV	TGV	NLTV	NLTGV
邻域	局部	局部	非局部	非局部
变分阶次	一阶	高阶	一阶	高阶

下载: 导出CSV

表 2 基于NLTGV正则化的稀疏角度CT图像重建算法步骤

Table 2 Procedures of a sparse-view CT image reconstruction algorithm based on NLTGV regularization

算法1 基于NLTGV的稀疏角度CT重建算法
（1）初始化: 给定初值$ {{{\boldsymbol u}}^0}， $$ {t_{\max }} ，$令初始化: 给定初值　　$ {{{\boldsymbol u}}^0} ，$设置$ {t_{\max }} $,$ {q_{\max }} $,$ {k_{\max }} $,令$ k = 1 $
（2） while （不满足停止准则） do
（3）令$ {{{\boldsymbol f}}^0} = {{{\boldsymbol u}}^{k - 1}} $，t=1
（4） while（t$ \leq $t_max） do
（5） for j=1,2,···,N
（6） $ f_j^t = f_j^{t - 1} + \displaystyle\frac{\lambda }{{{A_{ + ,j}}}}\sum\limits_{i = 1}^M {\frac{{{a_{i,j}}}}{{{A_{i, + }}}}} （{p_i} - {\bar p_i}） $
（7） $ {A_{i, + }} = \displaystyle\sum\limits_{j = 1}^N {{a_{i,j}}} ,\ i = 1,2,\cdots,M $
（8） $ {A_{ + ,j}} = \displaystyle\sum\limits_{i = 1}^M {{a_{i,j}}} ,\ j = 1,2,\cdots,N $
（9）$ {\bar p_i} = {A_i}{f^{t - 1}} $
（10）$ t = t + 1 $
（11） end for loop
（12） end while loop
（13）非负约束，得到$ {{{\boldsymbol u}}^{{\text{pos}}}} $
（14）令$ q = 1, $ b=0, d=0
（15） while（$ q \le {q^{\max }} $） do
（16）共轭梯度法求解u, g
（17）根据公式（18）与（19）求解s与r子问题
（18）根据公式（16）与（17）更新变量b与d
（19） $ q = q + 1 $
（20） end while loop
（21） $ {{{\boldsymbol u}}^k} = {{{\boldsymbol u}}^{{q_{\max }}}} $
（22） $ k = k + 1 $
（23） end while loop
（24）输出: 重建图像$ {{{\boldsymbol u}}^*} $

下载: 导出CSV

表 3 仿真数据重建图像的PSNR和SSIM结果

Table 3 PSNR and SSIM for reconstructing images from simulated data

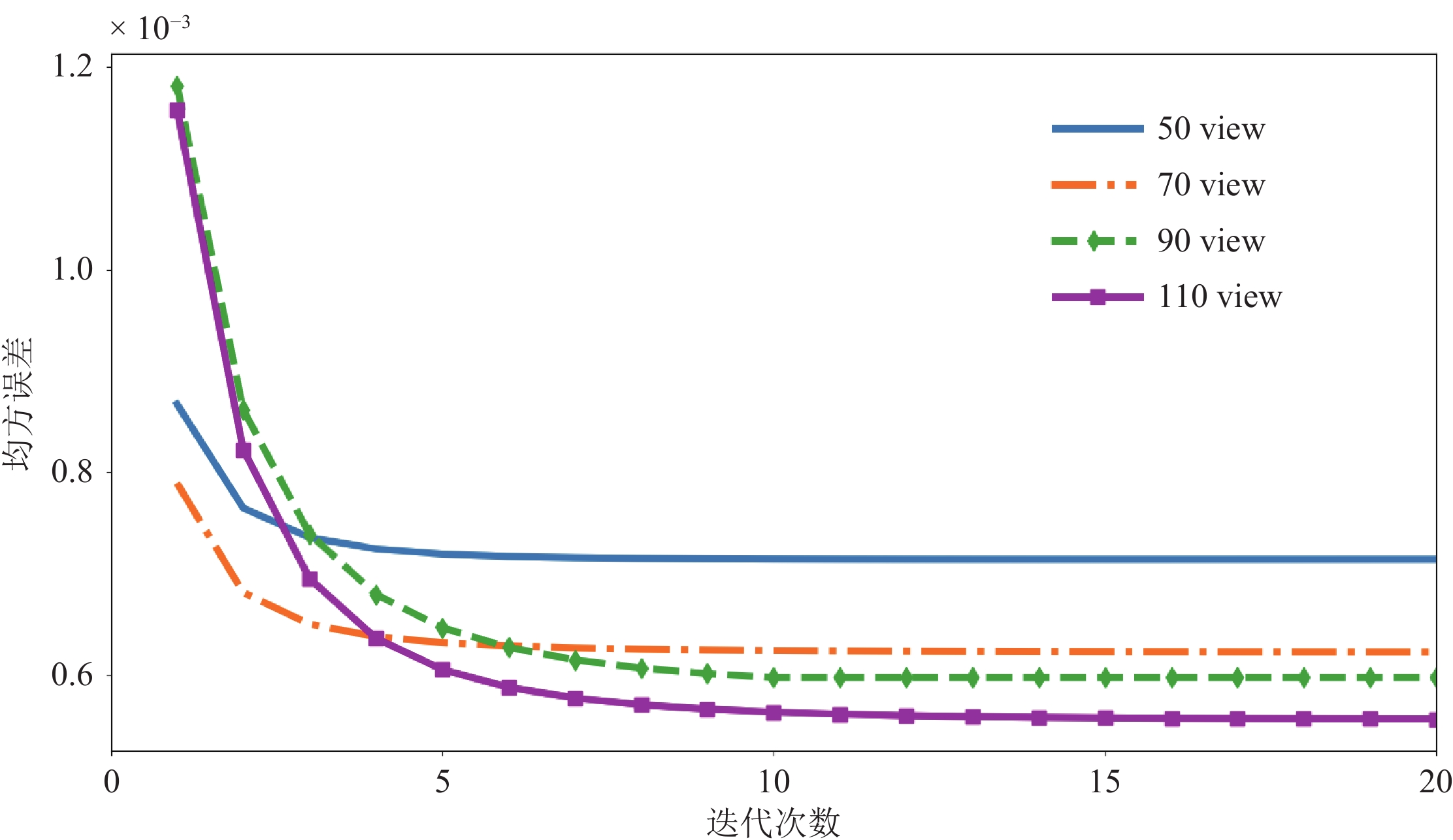
采样角度数目	指标	算法
		TV		TGV		NLTV		NLTGV
		ROI1	ROI2	ROI1	ROI2	ROI1	ROI2	ROI1	ROI2
50	PSNR	26.16	25.98	26.19	26.12	26.15	26.18	26.59	26.83
50	SSIM×10^-2	80.02	79.97	80.37	80.52	78.73	79.71	80.48	81.78
70	PSNR	26.80	26.10	26.90	25.84	27.38	26.98	28.28	27.82
70	SSIM×10^-2	81.96	80.90	79.78	80.16	83.05	83.53	85.10	84.93
90	PSNR	27.07	26.20	27.19	26.10	27.63	26.51	28.51	28.56
90	SSIM×10^-2	81.64	82.95	82.37	81.80	82.62	83.34	85.11	87.29
110	PSNR	27.07	27.11	27.77	27.00	27.86	27.59	28.71	28.78
110	SSIM×10^-2	84.24	84.74	82.71	84.03	83.20	84.72	85.47	87.36

下载: 导出CSV

表 4 真实数据重建图像的PSNR和SSIM结果

Table 4 PSNR and SSIM for reconstructing images from real data

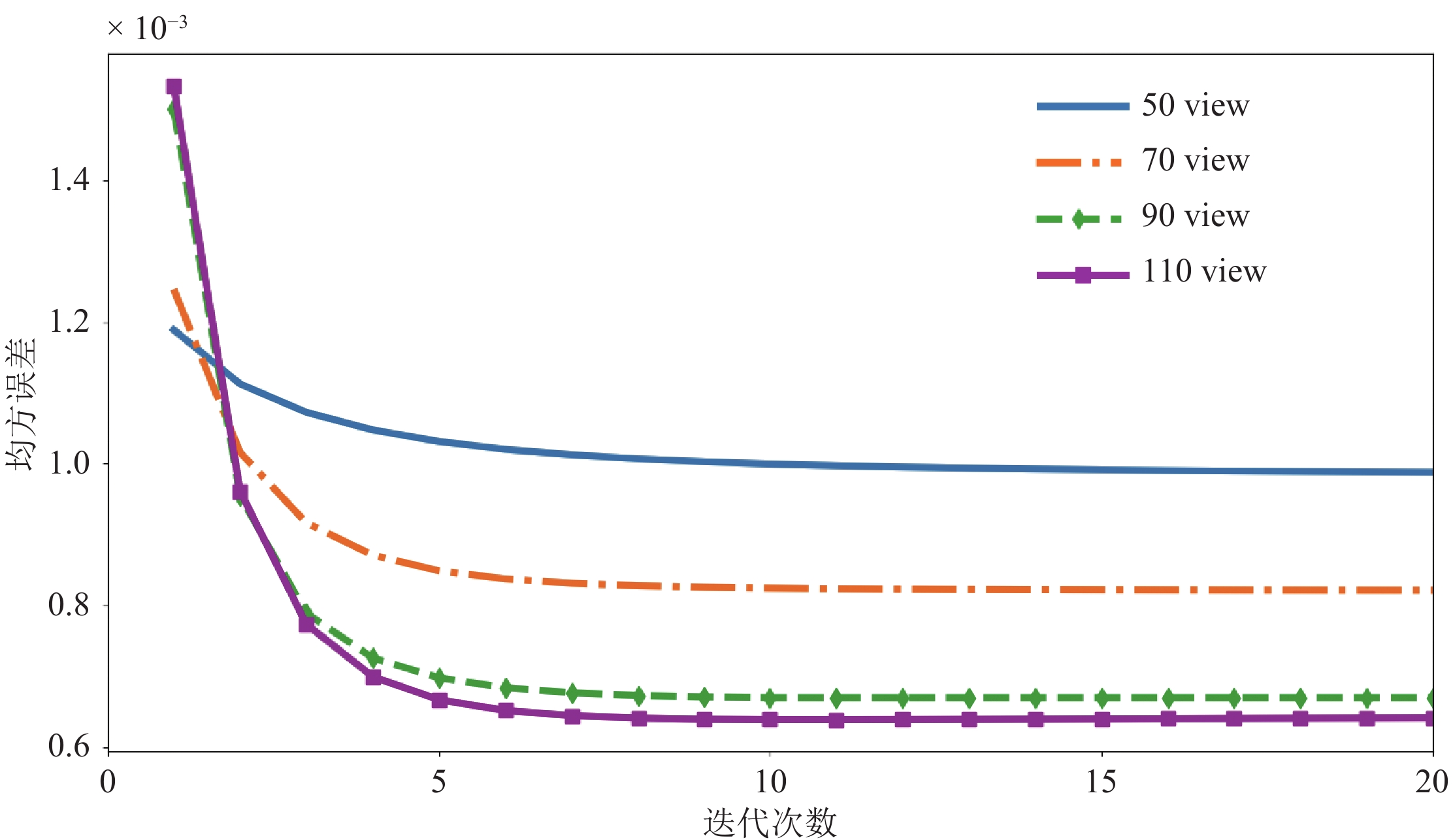
采样角度数目	指标	算法
		TV		TGV		NLTV		NLTGV
		ROI1	ROI2	ROI1	ROI2	ROI1	ROI2	ROI1	ROI2
50	PSNR	25.38	26.17	25.85	26.45	26.18	26.77	26.83	26.98
50	SSIM×10^-2	79.97	79.98	79.52	81.12	79.71	82.74	81.78	82.70
70	PSNR	26.10	27.02	26.34	27.02	26.98	27.39	27.82	28.94
70	SSIM×10^-2	80.90	80.00	80.16	83.67	83.53	86.91	84.93	88.18
90	PSNR	26.20	27.16	26.30	27.32	26.51	27.82	28.36	29.21
90	SSIM×10^-2	81.95	84.68	82.80	84.27	83.34	84.21	87.29	89.04
110	PSNR	27.11	27.51	27.00	27.54	27.19	28.64	28.78	29.67
110	SSIM×10^-2	83.74	84.42	84.03	84.67	84.72	86.22	87.36	89.56

下载: 导出CSV

参考文献(24)

[1]	PARCERO E, FLORES L, SÁNCHEZ M G, et al. Impact of view reduction in CT on radiation dose for patients[J]. Radiation Physics and Chemistry, 2017, 137(8): 173-175.
[2]	CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. DOI: 10.1109/TIT.2005.862083.
[3]	SIDKY E Y, KAO C M, PAN X. Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT[J]. Journal of X Ray Science & Technology, 2009, 14(2): 119-139.
[4]	SIDKY E Y, PAN X. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization[J]. Physics in Medicine & Biology, 2008, 53(17): 4777-4807.
[5]	RUDIN L I, OSHER S, FATEMI E. Nonlinear total variation based noise removal algorithms[J]. Physica D: Nonlinear Phenomena, 1992, 60(1/4): 259-268.
[6]	GORDON R, BENDER R, HERMAN G T. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and X-ray photography[J]. Journal of Theoretical Biology, 1970, 29(3): 471-481. DOI: 10.1016/0022-5193(70)90109-8.
[7]	LANGE K, CARSON R E. EM reconstruction algorithms for emission and transmission tomography[J]. Journal of Computer Assisted Tomography, 1984, 8(2): 306-316.
[8]	BREDIES, K, KUNISCH, K, POCK, T. Total genera-lized variation[J]. SIAM Journal on Imaging Sciences, 2010, 3(3): 492-526. DOI: 10.1137/090769521.
[9]	NIU S, GAO Y, BIAN Z, et al. Sparse-view X-ray CT reconstruction via total generalized variation regularization[J]. Physics in Medicine & Biology, 2014, 59(12): 2997-3017.
[10]	SUN T, SUN N, WANG J, et al. Iterative CBCT reconstruction using Hessian penalty[J]. Physics in Medicine and Biology, 2015, 60(5): 1965-1987. DOI: 10.1088/0031-9155/60/5/1965.
[11]	ZHANG H M, WANG L Y, YAN B, et al. Constrained total generalized p-variation minimization for few-view X-ray computed tomography image reconstruction[J]. Plos One, 2016, 11(2): e0149899.
[12]	XI Y R, QIAO Z R, WANG W J, et al. Study of CT image reconstruction algorithm based on high order total variation[J]. Optik, 2020, 204: 163814. DOI: 10.1016/j.ijleo.2019.163814.
[13]	闫慧文, 乔志伟. 基于 ASD-POCS 框架的高阶 TpV 图像重建算法[J]. CT 理论与应用研究, 2021, 30(3): 279-289. DOI: 10.15953/j.1004-4140.2021.30.03.01. YAN H W, QIAO Z W. High order TpV image reconstruction algorithms based on ASD-POCS framework[J]. CT Theory and Applications, 2021, 30(3): 279-289. DOI:10.15953/j.1004-4140.2021.30.03.01. (in Chinese).
[14]	XI Y, ZHOU P, YU H, et al. Adaptive-weighted high order TV algorithm for sparse-view CT reconstruction[J]. Medical Physics, 2023, 50: 5568-5584. DOI: 10.1002/mp.16371.
[15]	HUANG J, MA J, LIU N, et al. Sparse angular CT reconstruction using non-local means based iterative-correction POCS[J]. Computers in Biology and Medicine, 2011, 41(4): 195-205. DOI: 10.1016/j.compbiomed.2011.01.009.
[16]	KIM H, CHEN J, WANG A, et al. Non-local total-variation (NLTV) minimization combined with reweighted L1-norm for compressed sensing CT reconstruction[J]. Physics in Medicine & Biology, 2016, 61(18): 6878.
[17]	KIM K, EL F G, LI Q. Low-dose CT reconstruction using spatially encoded nonlocal penalty[J]. Physics in Medicine & Biology, 2018, 63(3): 035045.
[18]	GILBOA G, OSHER S. Nonlocal operators with applications to image processing[J]. Multiscale Modeling & Simulation, 2009, 7(3): 1005-1028.
[19]	RANFTL R, BREDIES K, POCK T. Non-local total generalized variation for optical flow estimation[C]//ECCV, 2014, (6): 439-454.
[20]	TOMASI C, MANDUCHI R. Bilateral filtering for gray and color images[C]//ICCV, 1998: 839-846.
[21]	JIANG M, WANG G. Convergence of the simultaneous algebraic reconstruction technique (SART)[J]. IEEE Transactions on Image Processing, 2003, 12(8): 957-961. DOI: 10.1109/TIP.2003.815295.
[22]	GOLDSTEIN T, OSHER S. The split Bregman method for L1-regularized problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 323-343. DOI: 10.1137/080725891.
[23]	WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment: From error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. DOI: 10.1109/TIP.2003.819861.
[24]	WANG J, LI T, XING L. Iterative image reconstruction for CBCT using edge-preserving prior[J]. Medical Physics, 2009, 36(1): 252-260. DOI: 10.1118/1.3036112.