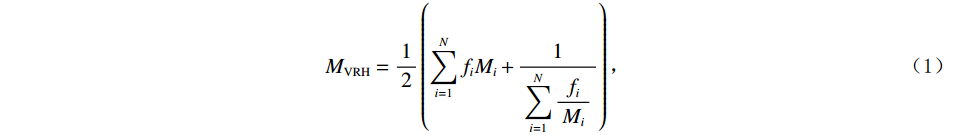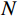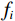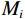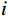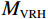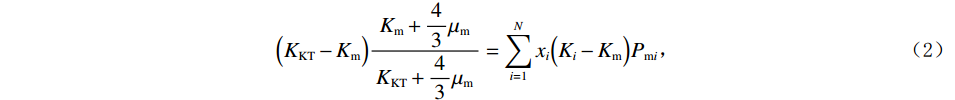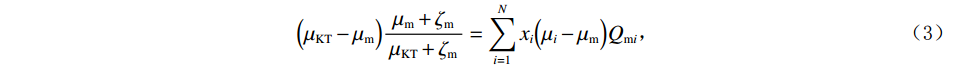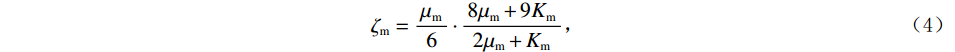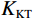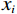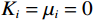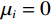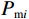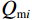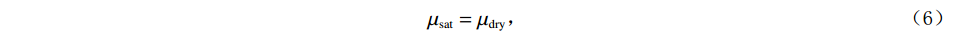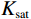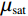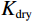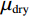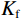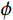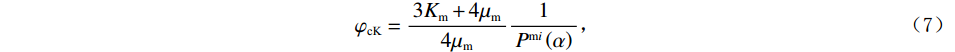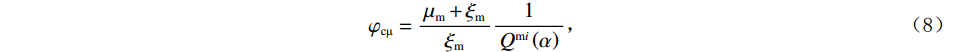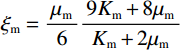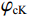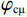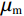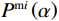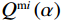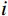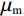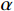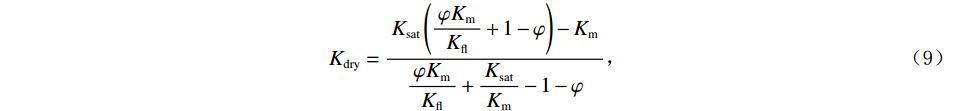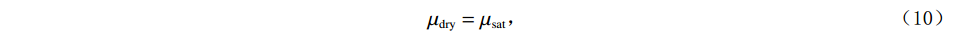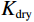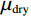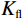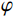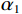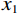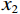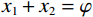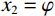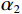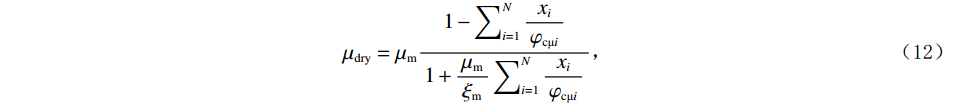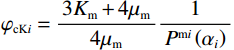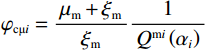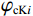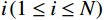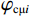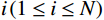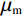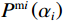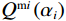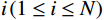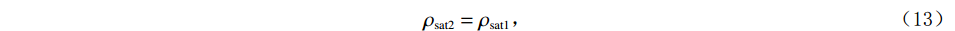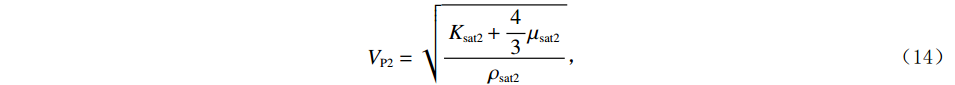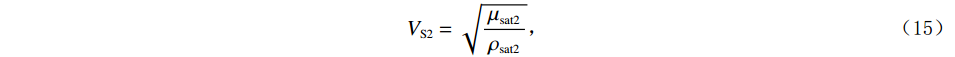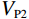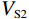Carbonate Rock Physical Property Parameter Substitution Method Based on Rock Physics Models
-
摘要:
碳酸盐岩的物性参数在油气勘探和开发的过程中起着重要的作用，且碳酸盐岩为具有多重孔隙类型的岩石，复杂的孔隙类型使得孔隙度与弹性参数之间的关系非常离散。本文基于岩石物理模型，提出一种碳酸盐岩物性参数替换的方法，首先对碳酸盐岩储层进行岩石物理建模，对模型中的等效孔隙纵横比进行反演，在进行替换时，保持其他参数不变，只改变孔隙度、方解石含量、含水饱和度和孔隙形状的体积分数中的一项。再结合AVO理论，进行正演模拟，正演模拟揭示孔隙度与孔隙形状的变化对地震响应的影响更为强烈，远远大于方解石含量、含水饱和度变化的影响，方解石含量和含水饱和度的变化对于地震响应的影响较微弱。实际资料应用表明，文章提出的碳酸盐岩物性参数的替换方法可以有效地分析物性参数及孔隙形状变化的影响，表征岩石的物理性质并判断岩石的孔隙类型。
Abstract:The physical properties of carbonate rocks play a crucial role in the exploration and development of oil and gas. Carbonate rocks are characterized by multiple types of porosity, and the complex porosity types result in a highly discrete relationship between porosity and elastic parameters. In this paper, a method based on rock physics models for substituting the physical property parameters of carbonate rocks is proposed. Initially, rock physics modeling is conducted on carbonate rock reservoirs, and inversion of the equivalent pore aspect ratio in the model is performed. During the substitution, all other parameters are kept constant, and only one of the porosity, calcite content, water saturation, or volumetric fraction of pore shapes is changed. In combination with amplitude versus offset (AVO) theory, forward modeling simulations are performed. The simulations reveal that the impacts of changes in porosity and pore shapes on seismic response are more significant, far exceeding the influences of variations in calcite content and water saturation, which have a weaker effect on seismic response. Application of actual data demonstrates that the method for substituting the physical property parameters of carbonate rocks proposed in this article can effectively analyze the impact of changes in physical property parameters and pore shapes, characterize the physical properties of rocks, and determine the types of rock porosity.
-
物性参数的预测和估计在地震定量预测中具有重要的地位[1-2]，物性参数的替换则在这项工作中起到了奠定基础的作用，可为后续的研究提供理论依据。而物性参数的替换是建立在岩石物理模型及岩石物理反演[3]基础上的，岩石物理模型[4]构建的内容包括岩石基质、岩石骨架、饱和岩石等，在此过程中，可分为以下几种模型。在岩石基质的混合过程中，主要包括Voigt-Reuss-Hill平均模型[5]、Hashin-Shtrikman边界模型[6]等；在构建岩石骨架的步骤中，主要有基于弹性波的散射理论的Kuster-Toksöz模型[7]、将材料的各组分按照微小的梯度完全混合，再使用循环迭代的方法计算介质的弹性模量的微分等效模型（differential effective medium，DEM）[8]等；对构建完成的岩石骨架进行流体填充，包括Gassmann方程[9]，Gassmann方程主要应用在低频条件下，Brown等[10]将Gassmann方程推广到各向异性，通过关系式的推导实现了对各向异性的岩石的流体填充。
碳酸盐岩在全球范围内占沉积岩面积总和的20％，其中蕴含的油气藏在世界油气总储量中占很大的比重，具有重要的开采和研究价值。碳酸盐岩内部的孔隙结构相较于碎屑岩较为特殊，碳酸盐岩具有更强的非均质性，次生改造作用对碳酸盐岩产生了较大的影响，使其储集空间多样，内部不仅发育了如粒间孔这类的原生孔隙，同时还发育较多的次生孔隙，如铸模孔、溶蚀孔、粒内孔和裂缝[11-12]等。在相同的孔隙度下含有近球形的铸模孔的碳酸盐岩会出现速度超过2500 m/s的差异[13]。复杂的孔隙结构造就了碳酸盐岩储层的速度与孔隙度之间非常离散的关系[14]。即使在矿物基质与孔隙内流体完全相同的情况下，孔隙类型的变化对碳酸盐岩产生的影响有时会超过孔隙度对岩石的影响[15]。碳酸盐岩中的横波速度与纵波速度之间的线性关系较差[12]，而其他种类的岩石如碎屑岩，碎屑岩的纵波速度与横波速度则具有较好的线性关系。因此在对碳酸盐岩进行岩石物理模型的构建的时候，需要选取合适的岩石物理模型，以此来提高岩石物理建模及岩石物理反演的准确度。孔隙结构对碳酸盐岩储层弹性参数变化的影响起主导作用[13-14]，李宏兵等[16]研究发现在碳酸盐岩物性参数反演的进程中，孔隙结构处在至关重要的地位。一般情况下使用岩石物理中的包裹体等效介质模型和孔隙弹性理论模型来求取包含复杂孔隙结构的岩石的弹性模量，常见的包裹体模型有Mori-Tanaka平均场模型[17]、Kuster-Toksöz模型[7]和微分等效介质理论（DEM）[18]，这些理论模型将孔隙及裂缝的形状同孔隙度一起考虑在岩石骨架弹性模量的影响因素中。Baechle等[13]和Sayers[14]分别证明了碳酸盐岩的弹性性质可以用Mori-Tanaka平均场模型和微分等效介质理论进行模拟。相比于其他两种模型，DEM理论可以对复合材料的等效弹性特性进行更为准确和有效的模拟，这种准确性和有效性在包裹体的体积分数很大时依然有效[18-19]。
利用岩石物理模型从地震数据中预测碳酸盐岩储层的孔隙结构的方法已经被多次研究[12,20-23]，目前主要使用两种方法描述碳酸盐岩内部的孔隙类型，分为以下两类。
一类是假设在岩石中只含有一种孔隙类型，通过岩石物理建模及反演计算其等效孔隙纵横比，再通过计算得到的结果来判断储层内部的的孔隙类型是偏向孔隙，还是偏向裂缝，亦或是偏向溶洞类型的。另一类是基于Xu-Payne模型预先假设岩石中含有孔、洞、缝3种类型的孔隙，通过估计这3种类型孔隙的孔隙度来描述储层中孔、洞、缝的发育程度。李宏兵等[20]应用微分等效介质理论和 Gassmann方程通过纵波速度反演计算等效孔隙纵横比，并由此实现了横波速度的预测；Xu等[12]使用Xu-Payne模型，使用测井资料预测得到碳酸盐岩储层中的3种类型孔隙各自对应的孔隙度；Zhang等[24]推导了岩石临界孔隙度与孔隙纵横比之间的关系，构建了多孔可变临界孔隙度模型，可以用来描述包含多种孔隙类型的碳酸盐岩储层。
本文所使用的正演模型是基于AVO技术构建的，AVO技术以Zoeppritz方程[25]为研究基础，但是Zoeppritz方程的完整形式比较复杂且实用性较低，很多学者在基于各种假设的情况下对Zoeppritz方程进行了简化和近似，如Aki等[26]于1980年提出的Aki-Richard近似式，Shuey[27]在1985年提出的Shuey近似式，以及许多其他的简化形式，通过对储层的AVO特征进行分析，得到物性参数的变化对于振幅及AVO特性的影响。
本文在对目标的碳酸盐岩储层进行岩石物理建模后，通过对测井资料中的孔隙度、方解石含量、含水饱和度以及孔隙类型进行替换，观察物性参数和岩石中的孔隙形状改变后，碳酸盐岩中的纵波速度与横波速度受到的影响，以及各自的地震响应分产生的变化，建立储层物性参数与弹性参数之间的关系，分析储层物性参数变化与地震弹性性质变化的规律；其次基于AVO理论和正演模拟分析，分析反射振幅随孔隙度、方解石含量、含水饱和度以及孔隙形状变化的特征，根据理论模型分析得到孔隙形状和物性参数变化对地震响应的影响，为后续的研究提供理论基础。
1. 岩石物理建模
根据碳酸盐岩储层的地质特点及相关背景，构建以碳酸盐岩为主要矿物的岩石物理模型（图1），具体包括以下过程。
![]()
图 1 碳酸盐岩岩石物理模型构建示意图Figure 1. Schematic diagram of carbonate rock petrophysical model construction地震岩石物理模型通过使用合理的假设将实际岩石看作一种理想的介质，基于物理学原理将储层岩石的物性参数与弹性参数结合起来，得到两者的量化关系。岩石物理建模的步骤大致分为岩石基质、岩石骨架和饱和岩石。
1.1 岩石基质
基质的构建使用Voigt-Reuss-Hill平均模型将方解石、石英和粘土等背景矿物按照各自的体积分数进行混合，在VRH模型中，假设不同类型的矿物成分具有相同的应变和应力，可以根据Voigt模型和Reuss模型分别求取混合矿物的上边界和下边界，Hill平均则通过求取Voigt上界和Reuss下界的算术平均值来表征岩石基质的等效模量。
$$ {M_{{\mathrm{VRH}}}} = \frac{1}{2}\left( { \sum\limits_{i = 1}^N {f_i}{M_i} + \frac{1}{{\displaystyle\sum\limits_{i = 1}^N \frac{{{f_i}}}{{{M_i}}}}}} \right) \text{，} $$ (1) 式中：
$ N $ 为矿物的种类数量；$ {f_i} $ 、$ {M_i} $ 分别表示第$ i $ 种矿物的体积分数和弹性模量；$ {M_{{\mathrm{VRH}}}} $ 为二者的算术平均值，用来表示混合后整体的矿物基质的等效弹性模量。1.2 岩石骨架
基于碳酸盐岩的物理性质，使用Kuster-Toksöz模型进行岩石中孔隙的填充，Kuster-Toksöz模型以一阶散射理论为基础，进而得到在矿物基质包含不同形状孔隙时的岩石骨架的等效模量，具体的表达式为：
$$ \Big( {{K_{{\mathrm{KT}}}} - {K_{\mathrm{m}}}} \Big)\frac{{{K_{\mathrm{m}}} + \displaystyle\frac{4}{3}{\mu _{\mathrm{m}}}}}{{{K_{{\mathrm{KT}}}} + \displaystyle\frac{4}{3}{\mu _{\mathrm{m}}}}} = \sum\limits_{i = 1}^N {{x_i}\Big( {{K_i} - {K_{\mathrm{m}}}} \Big){P_{{\mathrm{m}}i}}} \text{，} $$ (2) $$ \Big( {{\mu _{{\mathrm{KT}}}} - {\mu _{\mathrm{m}}}} \Big)\frac{{{\mu _{\mathrm{m}}} + {\zeta _{\mathrm{m}}}}}{{{\mu _{{\mathrm{KT}}}} + {\zeta _{\mathrm{m}}}}} = \sum\limits_{i = 1}^N {{x_i}\Big( {{\mu _i} - {\mu _{\mathrm{m}}}} \Big){Q_{{\mathrm{m}}i}}} \text{，} $$ (3) $$ {\zeta }_{{\mathrm{m}}}=\frac{{\mu }_{{\mathrm{m}}}}{6}\cdot\frac{8{\mu }_{{\mathrm{m}}}+9{K}_{{\mathrm{m}}}}{2{\mu }_{{\mathrm{m}}}+{K}_{{\mathrm{m}}}} \text{，} $$ (4) 式中：
$ {K_{{\mathrm{KT}}}} $ 、$ {\mu _{{\mathrm{KT}}}} $ 为在加入各种孔隙后的岩石骨架的等效体积模量和剪切模量；$ {x_i} $ 为不同类型孔隙的体积分数，如果添加的孔隙为干燥孔隙，那么此时$ {K_i} = {\mu _i} = 0 $ ，如果为流体填充的饱和孔隙，此时$ {\mu _i} = 0 $ ；$ {P_{{\mathrm{m}}i}} $ 、$ {Q_{{\mathrm{m}}i}} $ 为与孔隙包含物类型相关的系数，可以用来表征不同类型孔隙的包含物对岩石等效模量的影响。1.3 流体填充
Gassmann方程是目前最为常用的流体替换模型，该模型是假设在低频的条件下饱和流体岩石的等效弹性模量的计算公式，该方程建立了岩石的等效模量与孔隙流体的类型、背景矿物混合的基质、岩石骨架之间的关系。表达式为：
$$ {K_{{\mathrm{sat}}}} = {K_{{\mathrm{dry}}}} + \frac{{{{\Big( {1 - {{{K_{{\mathrm{dry}}}}}/ {{K_{\mathrm{m}}}}}} \Big)}^2}}}{{\displaystyle\frac{\phi }{{{K_{\mathrm{f}}}}} + \displaystyle\frac{{1 - \phi }}{{{K_{\mathrm{m}}}}} - \displaystyle\frac{{{K_{{\mathrm{dry}}}}}}{{K_{\mathrm{m}}^2}}}} \text{，} $$ (5) $$ {\mu _{{\mathrm{sat}}}} = {\mu _{{\mathrm{dry}}}} \text{，} $$ (6) 式中：
$ {K_{{\mathrm{sat}}}} $ 、$ {\mu _{{\mathrm{sat}}}} $ 分别为饱和流体岩石的体积模量和剪切模量；$ {K_{{\mathrm{dry}}}} $ 、$ {\mu _{{\mathrm{dry}}}} $ 分别为干燥岩石骨架的体积模量和剪切模量；$ {K_{\mathrm{f}}} $ 为孔隙填充的流体的体积模量；$ {K_{\mathrm{m}}} $ 为岩石基质的体积模量；$ \phi $ 为孔隙度。1.4 孔隙形状的替换
这里假设在碳酸盐岩储层中包含两种形状的孔隙，分别为孔隙纵横比为0.5～1的孔洞及孔隙纵横比为0.01的裂缝。由于在改变孔隙形状并不会改变孔隙度的大小，所以在对岩石孔隙中流体的密度及弹性模量进行计算时，岩石的密度和弹性模量与单一孔隙计算得到的数值相同。
对于碳酸盐岩储层孔隙形状不单一的特性，Zhang等[24]在2020年基于Kuster-Toksöz模型[7]和临界孔隙度模型，推导得到岩石的临界孔隙度与孔隙形状及岩石基质的弹性模量之间的关系：
$$ {\varphi _{{\text{cK}}}} = \frac{{3{K_{\mathrm{m}}} + 4{\mu _{\mathrm{m}}}}}{{4{\mu _{\mathrm{m}}}}}\frac{1}{{{P^{{\mathrm{m}}i}}\left( \alpha \right)}} \text{，} $$ (7) $$ \varphi_{\text{c}\text{μ}}=\frac{\mu_{\mathrm{m}}+\xi_{\mathrm{m}}}{\xi_{\mathrm{m}}}\frac{1}{Q^{\mathrm{m}i}\left(\alpha\right)}\text{，} $$ (8) 其中
$ {\xi _{\mathrm{m}}} = \displaystyle\frac{{{\mu _{\mathrm{m}}}}}{6}\frac{{9{K_{\mathrm{m}}} + 8{\mu _{\mathrm{m}}}}}{{{K_{\mathrm{m}}} + 2{\mu _{\mathrm{m}}}}} $ 。式中，$ {\varphi _{{\text{cK}}}} $ 为岩石体积模量的临界孔隙度数值，$ \varphi_{\text{c}\text{μ}} $ 为岩石剪切模量的临界孔隙度数值；$ {K_{\mathrm{m}}} $ 为岩石基质的体积模量；$ {\mu _{\mathrm{m}}} $ 为岩石基质的剪切模量；$ {P^{{\mathrm{m}}i}}\left( \alpha \right) $ 和$ {Q^{{\mathrm{m}}i}}\left( \alpha \right) $ 分别为极化因子，用来表示在岩石基质中加入第$ i $ 类形状的孔隙之后的效果，是$ {K_{\mathrm{m}}} $ 、$ {\mu _{\mathrm{m}}} $ 和孔隙纵横比$ \alpha $ 的函数。此时应用Smith在2003年根据Gassmann方程推导得到的计算含有单一孔隙形状的岩石骨架的体积模量和剪切模量：
$$ {K_{{\mathrm{dry}}}} = \frac{{{K_{{\mathrm{sat}}}}\left( {\displaystyle\frac{{\varphi {K_{\mathrm{m}}}}}{{{K_{{\mathrm{fl}}}}}} + 1 - \varphi } \right) - {K_{\mathrm{m}}}}}{{\displaystyle\frac{{\varphi {K_{\mathrm{m}}}}}{{{K_{{\mathrm{fl}}}}}} + \frac{{{K_{{\mathrm{sat}}}}}}{{{K_{\mathrm{m}}}}} - 1 - \varphi }} \text{，} $$ (9) $$ {\mu _{{\mathrm{dry}}}} = {\mu _{{\mathrm{sat}}}} \text{，} $$ (10) 式中，
$ {K_{{\mathrm{dry}}}} $ 为含有一种孔隙形状的岩石的体积模量；$ {\mu _{{\mathrm{dry}}}} $ 为含有一种孔隙形状的岩石的剪切模量；$ {K_{\mathrm{m}}} $ 和$ {K_{{\mathrm{fl}}}} $ 分别为岩石基质的体积模量和孔隙内填充的流体的体积模量；$ \varphi $ 为演示的孔隙度。假设岩石内只包含一种类型孔隙时（假定为孔隙形状1），孔隙的等效纵横比为
$ {\alpha _1} $ ，然后对岩石进行孔隙形状的替换，将岩石中的孔隙形状2按照一定的比例增加，对岩石中的孔隙形状1进行部分替换。在这里，将孔隙形状1的体积含量定义为$ {x_1} $ ，将孔隙形状2的体积含量定义为$ {x_2} $ ，并且$ {x_1} + {x_2} = \varphi $ ，当孔隙形状1被完全替换为孔隙形状2时，则有$ {x_2} = \varphi $ ，孔隙形状2的等效孔隙纵横比为$ {\alpha _2} $ 。基于公式（7）和公式（8），Zhang等[24]在 2020年对上述公式进一步推导，得到了包含多种孔隙形状的多孔可变临界孔隙度模型：
$$ K_{\mathrm{dry}}=K_{\mathrm{m}}\frac{1-\displaystyle\sum\nolimits_{i=1}^N\frac{x_i}{\varphi_{\mathrm{cK}i}}}{1+\displaystyle\frac{3K_{\mathrm{m}}}{4\mu\mathrm{_m}}\sum\nolimits_{i=1}^N\frac{x_i}{\varphi_{\mathrm{cK}i}}}\text{，} $$ (11) $$ \mu_{\mathrm{dry}}=\mu_{\mathrm{m}}\frac{1-\displaystyle\sum\nolimits_{i=1}^N\frac{x_i}{\varphi_{\mathrm{c}\text{μ}i}}}{1+\displaystyle\frac{\mu_{\mathrm{m}}}{\xi_{\mathrm{m}}}\sum\nolimits_{i=1}^N\frac{x_i}{\varphi_{\mathrm{c}\text{μ}i}}}\text{，} $$ (12) 其中，
$ \varphi_{\text{cK}i}=\displaystyle\frac{3K_{\mathrm{m}}+4\mu_{\mathrm{m}}}{4\mu_{\mathrm{m}}}\frac{1}{P^{\mathrm{m}i}\left(\alpha_i\right)} $ ，$ \varphi_{\text{c}\text{μ}i}=\displaystyle\frac{\mu_{\mathrm{m}}+\xi\mathrm{_m}}{\xi_{\mathrm{m}}}\frac{1}{Q^{\mathrm{m}i}\left(\alpha_i\right)} $ 。式中，$ \varphi_{\text{cK}i} $ 为第$ i\left( {1 \leq i \leq N} \right) $ 类形状孔隙的体积模量的临界孔隙度数值；$ {\varphi _{{\text{c}}\text{μ}i}} $ 为第$ i\left( {1 \leq i \leq N} \right) $ 类形状孔隙的剪切模量的临界孔隙度数值；$ K_{\mathrm{m}} $ 为岩石基质的体积模量；$ \mu_{\mathrm{m}} $ 为岩石基质的剪切模量；$ P^{\mathrm{m}i}\left(\alpha_i\right) $ 和$ Q^{\mathrm{m}i}\left(\alpha_i\right) $ 分别为第$ i\left( {1 \leq i \leq N} \right) $ 类形状孔隙对应的极化因子，用来表示在岩石基质中加入第$ i $ 类形状的孔隙之后的效果，是$ K_{\mathrm{m}} $ 、$ \mu_{\mathrm{m}} $ 和孔隙纵横比$ {\alpha _i} $ 的函数。因为在孔隙形状替换的过程中，矿物基质、孔隙度和孔隙填充的流体均未改变，因此在孔隙形状替换的过程中，替换后的岩石的密度与替换前的密度相同，即：
$$ {\rho _{{\mathrm{sat}}2}} = {\rho _{{\mathrm{sat}}1}} \text{，} $$ (13) 式中，
$ {\rho _{{\mathrm{sat}}2}} $ 为同时包含孔隙形状1和孔隙形状2的饱和岩石的密度。1.5 速度计算
对于碳酸盐岩储层，基于之前构建的岩石物理模型，其中纵波速度、横波速度与体积模量、剪切模量之间的关系为：
$$ {V_{{\mathrm{P}}2}} = \sqrt {\frac{{{K_{{\mathrm{sat}}2}} + \displaystyle\frac{4}{3}{\mu _{{\mathrm{sat}}2}}}}{{{\rho _{{\mathrm{sat}}2}}}}} \text{，} $$ (14) $$ {V_{{\mathrm{S}}2}} = \sqrt {\frac{{{\mu _{{\mathrm{sat}}2}}}}{{{\rho _{{\mathrm{sat}}2}}}}} \text{，} $$ (15) 式中的
$ {V_{{\mathrm{P}}2}} $ 和$ {V_{{\mathrm{S}}2}} $ 分别孔隙形状替换之后，同时包含1类和2类两种孔隙形状的岩石的纵波速度与横波速度。2. 正演及响应特征分析
本文使用的正演模型是基于AVO理论[28]建立的，AVO理论的基础就是Zoeppritz方程，这里使用的是Zoeppritz方程的Aki-Richards近似式。
2.1 正演模型设计
本次建立正演模型所使用的子波类型为Richer子波，所使用的主频为60 Hz。采样间隔与井数据的采样间隔相同，不加入噪声，旨在研究不同比例的孔隙度、方解石含量以及含水饱和度对于井曲线以及地震响应的影响，为后续的反演解释工作提供基础。
首先根据测井资料对目标层段的碳酸盐岩储层进行岩石物理模型的构建，并在建立岩石物理模型的过程中对模型中一些参数进行反演，使岩石物理模型的准确性达到可接受的标准范围内。对实际的测井数据进行孔隙度、方解石含量及孔隙形状的替换，该井段为巴西某含油的碳酸盐岩储层，以方解石、石英和泥质为主要矿物，流体的成分为水和石油，其中6303～6 475 m为主要的含油层（图2）。
![]()
图 2 原始井曲线和岩石物理模型的计算结果Figure 2. Calculation results of the original well curve and the petrophysical model首先对测井资料中的原始弹性参数（纵波速度、横波速度、密度）进行正演（表1），得到原始井曲线的地震响应。这里的叠后合成地震记录为10道相同角度（0°）的地震记录，叠前合成地震记录为角度由3°～30° 的不同角度的地震记录。
表 1 井资料中的主要矿物成分的弹性参数和物性参数Table 1. Elastic parameters and physical property parameters of main mineral components in well data岩性 纵波速度/（m/s） 横波速度/（m/s） 密度/（g/cm3） 体积模量/GPa 剪切模量/GPa 方解石 6640 3440 2.71 77 32 石英 6050 4090 2.65 37 44 泥质 3810 1880 2.55 25 9 由图3可以得出结论，当角度发生改变的时，地震记录的每一道均会发生变化，是由入射角的差异，使合成地震记录的振幅的大小发生改变。
![]()
图 3 原始井曲线的叠前和叠后的合成地震记录Figure 3. Pre- and post-stack synthetic seismograms of the original well curve2.2 孔隙度的替换
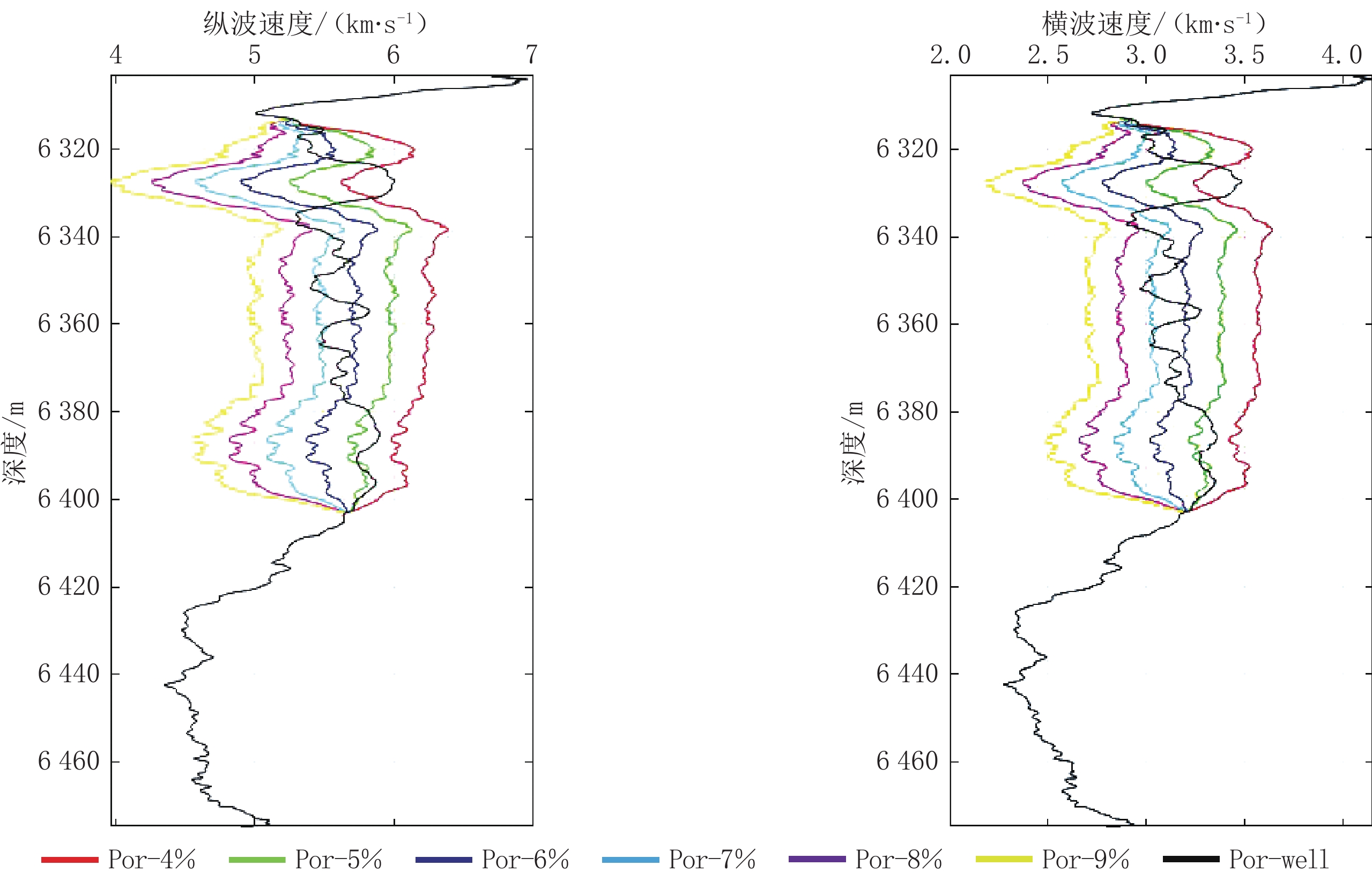
这里首先对测井数据中的孔隙度进行替换，将井中的随深度不断变化的孔隙度分别替换为4％、5％、6％、7％、8％ 和9％ 的孔隙度，并将对应的孔隙度代入到岩石物理模型中，经过计算得到不同孔隙度对应的纵波速度与横波速度。井的深度范围：6303～6 475 m（图4）。
![]()
图 4 孔隙度的变换对纵波速度和横波速度的影响Figure 4. Influence of porosity transformation on P-wave velocity and S-wave velocity从图中可以看出，随着孔隙度的提高（4％～9％）纵波速度和横波速度会随之降低，图中的黑色曲线为测井资料中提供的井曲线。在区间6316.25～6 400 m内，依靠已有的岩石物理模型对测井资料中的孔隙度进行替换，将井中的孔隙度替换成为4％～9％ 的固定数值的孔隙度。
通过观察可以发现，井资料中的纵波速度与横波速度的数值在替换的孔隙度（4％～9％）的速度区间内，可以说明，在这一区间内的孔隙度在4％～9％ 之间。同时可以得知孔隙度的变化对于该区间的影响较为明显，每当孔隙度变化1％，经过岩石物理模型计算得到的纵波速度与横波速度均会发生较明显的变化。
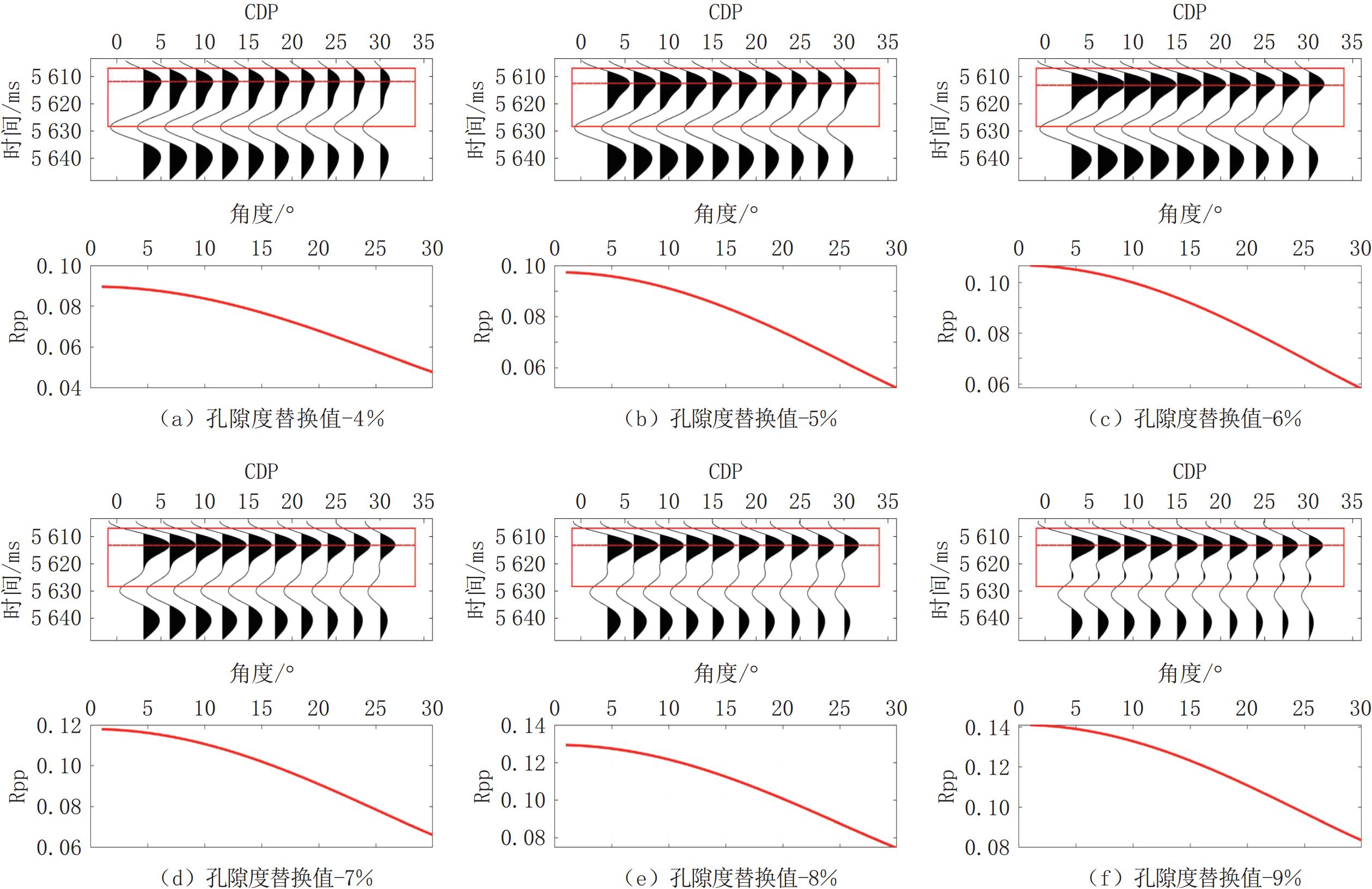
图5为不同孔隙度对应的叠前地震记录以及对应的反射系数的变化，这里使用的是Aki-Richards公式进行AVO正演模拟。图5（a）～图5（f）分别为孔隙度替换数值分别为4％、5％、6％、7％、8％ 和9％，角度由3°～30°（每隔3° 取一道，总计取十道）的地震记录，可以从不同孔隙度对应的合成地震记录中，在5604.2～5 648.4 ms这个区间内。随着角度的增加，地震记录每一道的振幅存在明显的变化。图中截取的片段是5607.65～5 627.68 ms，即孔隙度替换的区间，图中所展示的反射系数的变化为此区间内的反射系数的变化。
![]()
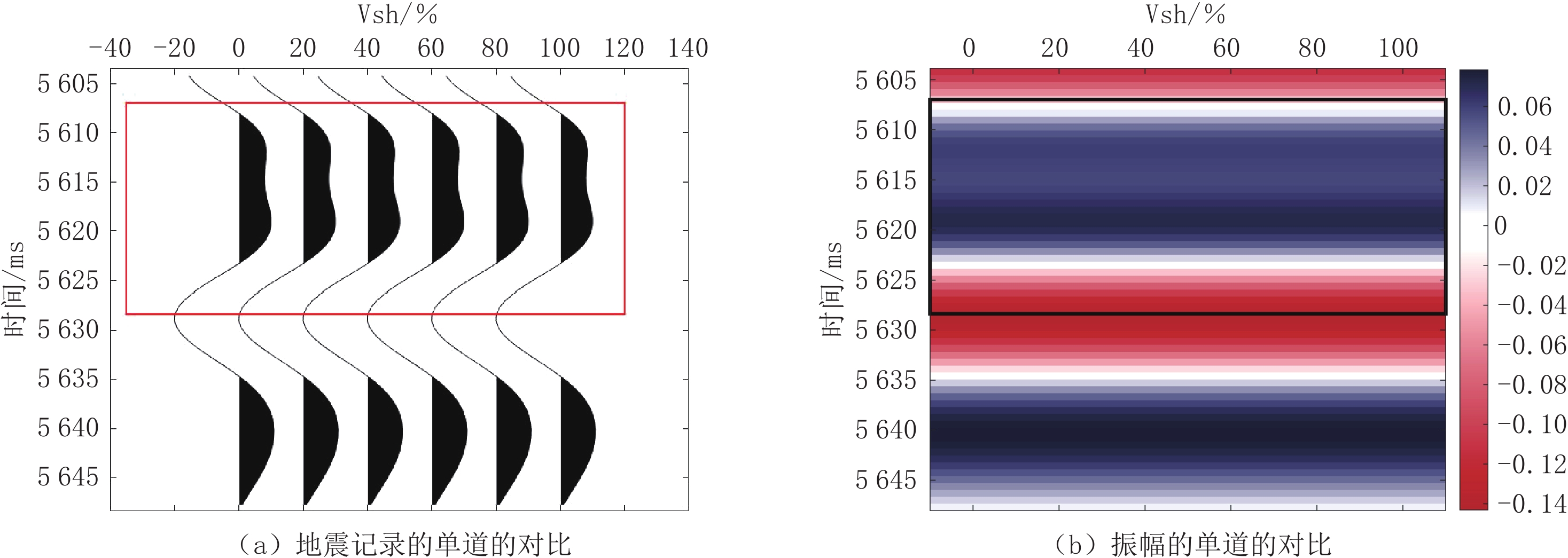
图 5 不同孔隙度对应的合成地震记录Figure 5. Synthetic seismograms corresponding to different porosity values图6（a）是不同孔隙度对应的地震记录，通过将不同孔隙度的合成地震记录的第一道（0°）提取出来，对比每一道的合成地震记录的区别，可以看到不同的孔隙度对于对应的碳酸盐岩储层的影响。随着孔隙度的增大，地震响应也会发生变化，有一组波峰逐渐变化为两组波峰，再次说明孔隙度的变化对地震记录的影响效果较为显著。图6（b）是将不同的孔洞的占比的地震记录的振幅表示出来，可以看到当孔隙度逐渐增大（4％～9％）时，第一道（0°）地震记录的振幅的变化。
2.3 方解石含量的替换
这里首先对测井数据中的方解石含量进行替换，将井中的随深度不断变化的方解石含量分别替换为0％、20％、40％、60％、80％ 和100％ 的百分含量，并将对应的方解石含量数值代入到岩石物理模型中，经过计算得到不同方解石含量对应的纵波速度与横波速度。井的深度范围：6303～6 475 m（图7）。
![]()
图 7 方解石含量的变换对纵波速度和横波速度的影响Figure 7. Influence of calcite volume fraction transformation on P-wave velocity and S-wave velocity从图中可以看出，随着方解石的体积分数的提高（0％～100％）纵波速度和横波速度会随之变大，图中的黑色曲线为测井资料中提供的井曲线。方解石的体积分数的深度的替换范围为6310～6 400 m，可以看出方解石的体积分数的改变对于纵波速度的影响更为明显。由于碳酸盐岩的背景矿物为方解石、石英和泥质，方解石的体积模量和剪切模量均大于石英和泥质，因此矿物基质混合后基质的模量会呈现增大的趋势，而且模量的增大的幅度大于密度增大的幅度，所以就造成了方解石含量增大，纵波速度与横波速度均增大的现象。合成地震记录的观察区间采样在6303～6 475 m之间。
图8（a）～图8（f）为不同体积分数的方解石对应的叠前地震记录，目的层段为6303～6 475 m，对应的时间范围为5604.2～5 648.4 ms，可以从不同体积分数的方解石对应的合成地震记录中，在5604.2～5 648.4 ms这个区间内。随着角度的增加，地震记录的振幅存在明显的变化，随着角度的增加，反射系数也随之变化。反射系数的变化会进一步影响到地震记录中振幅的大小，可以看到地震记录中的振幅逐渐变小。方解石的体积分数的时间的替换区间为5607.65～5 627.68 ms，如图中的红色方框所示。振幅的变化为图中红色虚线所指示的点。
![]()
图 8 不同方解石含量对应的合成地震记录Figure 8. Synthetic seismograms corresponding to different calcite volume fractions图9（a）是不同体积分数的方解石对应的地震记录，通过将不同体积分数的方解石的合成地震记录的第一道（0°）提取出来，对比每一道的合成地震记录的区别，可以看到不同体积分数的方解石对于对应的碳酸盐岩储层的影响，将替换后的地震记录与测井资料中的数据计算得到的地震记录相对比发现当方解石的体积分数为60％～80％ 时与原始地震记录较接近，可以大致推断出井中方解石的体积分数在60％～80％，之后随着方解石的体积分数的变化，地震记录与井中的原始地震记录产生偏差。
![]()
图 9 不同体积分数的方解石所引起的差异Figure 9. Differences caused by different volume fractions of calcite图9（b）是将不同的比例体积分数的方解石的地震记录的振幅表示出来，可以看到当方解石的体积分数逐渐增大（0％～100％）时，第一道（0°）地震记录的振幅的变化。
2.4 含水饱和度的替换
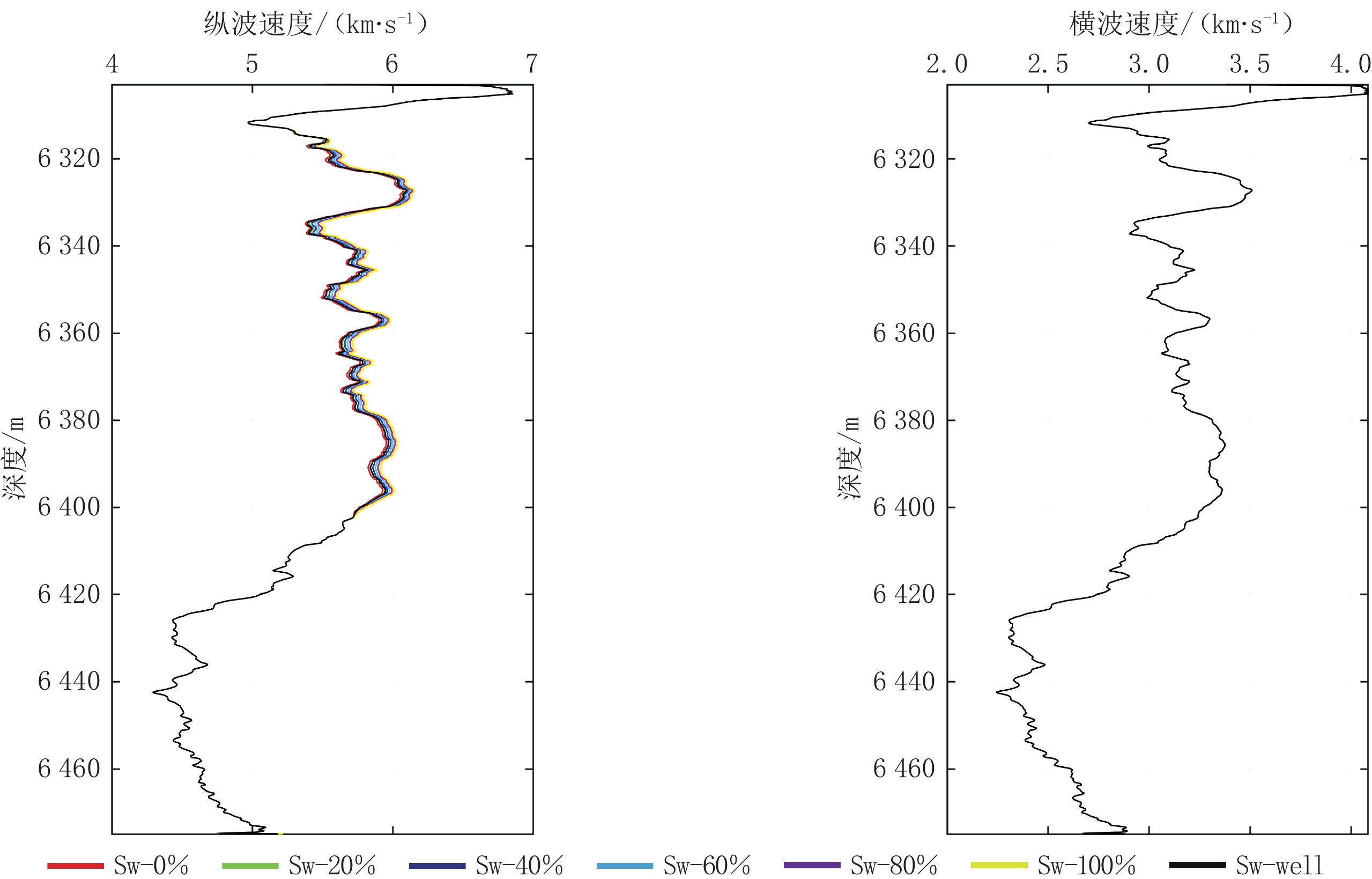
这里首先对测井数据中的含水饱和度进行替换，将井中的随深度不断变化的含水饱和度分别替换为0％、20％、40％、60％、80％ 和100％ 并将对应的含水饱和度代入到岩石物理模型中，经过计算得到不同含水饱和度对应的纵波速度与横波速度。井的深度范围：6303～6 475 m（图10）。
![]()
图 10 含水饱和度的变换对纵波速度和横波速度的影响Figure 10. Influence of water saturation transformation on P-wave velocity and S-wave velocity从图中可以看出，随着含水饱和度的提高（0％～100％）纵波速度和横波速度变化很小，图中的黑色曲线为测井资料中提供的井曲线。含水饱和度的深度的替换范围为6316.25～6 400 m，由于此区间内碳酸盐岩的孔隙度较低，使得孔隙中流体的作用降低，因此当含水饱和度变化时，弹性模量受到的影响较小。合成地震记录的观察区间采样在6303～6 475 m之间。
图11（a）～图11（f）为不同的含水饱和度对应的叠前地震记录，目的层段为6303～6 475 m，对应的时间范围为5604.2～5 648.4 ms，可以从不同含水饱和度对应的合成地震记录中，在5604.2～5 648.4 ms这个区间内，随着角度的增加，地震记录的振幅存在明显的变化，随着角度的增加，反射系数也随之变化。反射系数的变化会进一步影响到地震记录中振幅的大小，可以看到地震记录中的振幅逐渐变小。含水饱和度的时间的替换区间为5607.65～5 627.68 ms，如图中的红色方框所示。
![]()
图 11 不同含水饱和度对应的合成地震记录Figure 11. Synthetic seismograms corresponding to different water saturations图12（a）是不同含水饱和度对应的地震记录，通过将不同含水饱和度的合成地震记录的第一道（0°）提取出来，对比每一道的合成地震记录的区别，可以看到不同的含水饱和度对于对应的碳酸盐岩储层的影响，将替换后的地震记录与测井资料中的数据计算得到的地震记录相对比发现当含水饱和度为20％～40％ 时与原始地震记录较接近，可以大致推断出井中的含水饱和度大致为20％～40％，之后随着含水饱和度的变化，地震记录与井中的原始地震记录产生偏差。
图12（b）是将不同的比例的含水饱和度的地震记录的振幅表示出来，可以看到当含水饱和度逐渐增大（0％～100％）时，0° 地震记录的振幅的变化。
2.5 孔隙形状的替换
这里对测井数据中的孔洞的体积分数进行替换，由于该储层的特点，该储层的孔洞的体积分数高于70％，所以在孔洞的体积分数替换的研究过程中，将井中的孔洞的体积分数分别替换为70％、76％、82％、88％、94％ 和100％，并将对应的孔洞的体积分数代入到岩石物理模型中，经过计算得到不同体积分数的孔洞对应的纵波速度与横波速度。井的深度范围：6303～6 475 m（图13）。
![]()
图 13 孔隙形状的变化对纵波速度和横波速度的影响Figure 13. Influence of pore shape on P-wave velocity and S-wave velocity井中的替换深度为6316.25～6 400 m，从图中可以看出，随着孔洞的体积分数的提高（70％～100％）纵波速度和横波速度会随之增大，图中的黑色曲线为测井资料中提供的井曲线。但由工区的储层特性使得孔洞的体积分数要高于70％，所以在研究过程中将孔洞的体积分数的起始值设置为70％，可以看出在该井中孔洞的体积分数大部分在94％ 以上，只有小部分的深度区间在94％以下。
图14为使用Aki-Richards公式进行的AVO正演模拟。图14（a）～图14（f）分别为孔隙形状替换后的合成地震角度道集，目的层段为6303～6 475 m，对应的时间范围为5604.2～5 648.4 ms,图中截取的片段为5607.65～5 627.68 ms，如图中的红色方框所示。图14（a）～图14（f）所显示的为红色方框中的反射系数的变化趋势，可以看到不同的孔洞体积分数的地震记录随着入射角度的变化产生的变化。
![]()
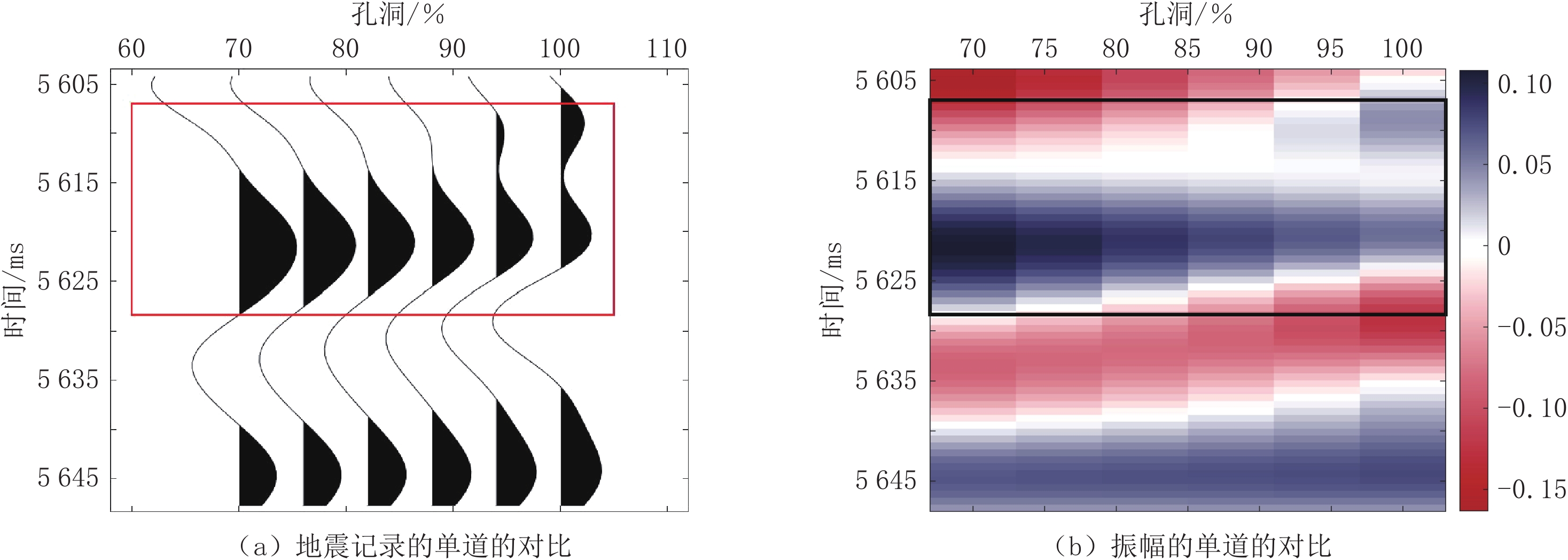
图 14 不同比例的孔洞含量对应的合成地震记录Figure 14. Synthetic seismograms corresponding to different proportions of cavity content图15（a）是不同的孔洞的体积分数对应的地震记录，通过将不同孔洞体积分数的合成地震记录的第1道（0°）提取出来，对比每一道的合成地震记录的区别，可以看到孔洞的体积分数的变化对于对应的碳酸盐岩储层的影响，从正演模拟结果中可以清晰地看到。随着孔洞含量的逐渐提高，地震记录的振幅逐渐变小，在孔洞占比达到94％ 时，此时的0° 的地震记录与测井数据计算得到的地震记录最为接近，因此可以对孔隙的形状的占比进行大致的预测，可以判断得到孔洞（α=0.6）的占比约为94％，裂缝（α=0.01）的占比约为4％。
![]()
图 15 不同孔洞的体积分数所引起的差异Figure 15. Difference caused by the volume fraction of different pores图15（b）是将不同的孔洞的占比的地震记录的振幅表示出来，可以看到当孔洞的体积分数逐渐增大（70％～100％）时，第1道（0°）地震记录的振幅的变化。
3. 结论
本文提出了一种基于岩石物理模型的碳酸盐岩物性参数替换方法，对于碳酸盐岩储层的孔隙结构和物性参数的研究有着较好的实用性。将碳酸盐岩的物性参数、多孔岩石物理模型、Gassmann方程、AVO理论与反演算法相结合，首先对碳酸盐岩储层完成岩石物理模型的构建，建立孔隙度、方解石含量、含水饱和度和孔隙形状与纵波速度和横波速度之间的定量关系。实现了复杂的孔隙结构的孔隙纵横比的反演，对不同的孔隙度、方解石含量、含水饱和度以及孔隙形状进行替换，并进行相应的地震正演模拟。
将模型应用在测井数据中，首先反演出岩石中的等效孔隙纵横比，再将不同的孔隙度、方解石含量、含水饱和度和孔隙形状带入到模型中进行计算，然后与原始井数据进行对比。通过观察发现：在进行替换的区间内，对于纵波速度与横波速度来说，孔隙度的替换对井曲线的影响较大，方解石含量的替换对于纵波速度的影响较大，对于横波速度的影响较小，含水饱和度的替换对纵波速度和横波速度的影响均较小，孔隙形状替换对速度曲线的影响较大，对井中的纵波速度与横波速度的作用较强。
使用替换后的数据根据AVO理论进行反射系数的计算，褶积后得到地震记录，其中受纵波速度与横波速度的影响，由于在进行孔隙度替换时，纵波速度与横波速度受影响较大，不同的孔隙度对应的地震记录存在较大差异，变化较大，证明孔隙度的变化对于地震响应的影响强烈。方解石含量进行替换时，纵波速度变化较大，但横波速度变化较小，因此不同的方解石含量对应的地震记录存在差异，但相比于孔隙度的变化，方解石含量变化的效果产生的作用较弱。含水饱和度进行替换时，纵波速度与横波速度变化均较小，因此不同的含水饱和度对应的地震记录差异较小，含水饱和度变化的效果产生的作用微弱。孔隙形状进行替换时，纵波速度与横波速度受影响较大，不同的孔洞含量对应的地震记录差异显著，孔隙形状的变化对于地震响应的影响强烈。
通过理论模型与实际数据应用表明，孔隙度和孔隙形状对于碳酸盐岩储层的影响较大，可以用来表征储层的物理性质及孔隙结构，而方解石含量与含水饱和度对该储层的影响较小，影响效果微弱，对于储层的物理性质无法很好的描述。
本文所选择的物性参数的替换模型对于所选定的碳酸盐岩储层有着较好的实用性，但对于其他区块的碳酸盐岩储层可能需要更换模型以及调整参数，以及在孔隙形状替换时是否存在更好的参数对孔隙结构进行描述，可以在后续的研究中进行探索。
-
![]()
图 1 碳酸盐岩岩石物理模型构建示意图
Figure 1. Schematic diagram of carbonate rock petrophysical model construction
![]()
图 2 原始井曲线和岩石物理模型的计算结果
Figure 2. Calculation results of the original well curve and the petrophysical model
![]()
图 3 原始井曲线的叠前和叠后的合成地震记录
Figure 3. Pre- and post-stack synthetic seismograms of the original well curve
![]()
图 4 孔隙度的变换对纵波速度和横波速度的影响
Figure 4. Influence of porosity transformation on P-wave velocity and S-wave velocity
![]()
图 5 不同孔隙度对应的合成地震记录
Figure 5. Synthetic seismograms corresponding to different porosity values
![]()
图 7 方解石含量的变换对纵波速度和横波速度的影响
Figure 7. Influence of calcite volume fraction transformation on P-wave velocity and S-wave velocity
![]()
图 8 不同方解石含量对应的合成地震记录
Figure 8. Synthetic seismograms corresponding to different calcite volume fractions
![]()
图 9 不同体积分数的方解石所引起的差异
Figure 9. Differences caused by different volume fractions of calcite
![]()
图 10 含水饱和度的变换对纵波速度和横波速度的影响
Figure 10. Influence of water saturation transformation on P-wave velocity and S-wave velocity
![]()
图 11 不同含水饱和度对应的合成地震记录
Figure 11. Synthetic seismograms corresponding to different water saturations
![]()
图 13 孔隙形状的变化对纵波速度和横波速度的影响
Figure 13. Influence of pore shape on P-wave velocity and S-wave velocity
![]()
图 14 不同比例的孔洞含量对应的合成地震记录
Figure 14. Synthetic seismograms corresponding to different proportions of cavity content
![]()
图 15 不同孔洞的体积分数所引起的差异
Figure 15. Difference caused by the volume fraction of different pores
表 1 井资料中的主要矿物成分的弹性参数和物性参数
Table 1 Elastic parameters and physical property parameters of main mineral components in well data
岩性 纵波速度/（m/s） 横波速度/（m/s） 密度/（g/cm3） 体积模量/GPa 剪切模量/GPa 方解石 6640 3440 2.71 77 32 石英 6050 4090 2.65 37 44 泥质 3810 1880 2.55 25 9 
下载: 导出CSV
-
[1] AVSETH P, MUKERJI T, MAVKO G. Quantitative seismic interpretation: Applying rock physics tools to reduce interpretation risk[M]. Cambridge: Cambridge University Press, 2005.
[2] 印兴耀, 宗兆云, 吴国忱. 岩石物理驱动下地震流体识别研究[J]. 中国科学: 地球科学, 2015, 45: 8−21. DOI: 10.1007/s11430-014-4992-3. YI Y Y, ZONG Z Y, WU G, et al. Research on seismic fluid identification driven by rock physics[J]. Scientia Sinica (Terrae)2015, 45: 8−21. DOI: 10.1007/s11430-014-4992-3. (in Chinese).
[3] MUKERJI T, JØRSTAD A, AVSETH P, et al. Mapping lithofacies and pore-fluid probabilities in a North Sea reservoir: Seismic inversions and statistical rock physics[J]. Geophysics, 2001, 66: 988−1001. DOI: 10.1190/1.1487078.
[4] 马淑芳, 韩大匡, 甘利灯, 等. 地震岩石物理模型综述[J]. 地球物理学进展, 2010, 25(2): 460−471. DOI: 10.3969/j.issn.1004-2903.2010.02.012. MA S F, HAN D K, GAN L D, et al. A review of seismic rock physics models[J]. Progress in Geophysics, 2010, 25(2): 460-471. DOI: 10.3969/j.issn.1004-2903.2010.02.012. (in Chinese).
[5] HILL R. The elastic behaviour of a crystalline aggregate[J]. Proceedings of the Physical Society, 1952, 65(5): 349−354. DOI: 10.1088/0370-1298/65/5/307.
[6] HASHIN Z, SHTRIKMAN S. A variational approach to the theory of the elastic behavior of multiphase materials[J]. Journal of the Mechanics and Physics of Solids, 1963, 11(2): 127−140. DOI: 10.1016/0022-5096(63)90060-7.
[7] KUSTER G T, TOKSÖZ M N. Velocity and attenuation of seismic waves in two-phase media[J]. Geophysics, 1974, 39: 587−618. DOI: 10.1190/1.1440450.
[8] BERRYMAN J G. Long-wavelength propagation in composite elastic media I: Spherical inclusions[J]. Journal of the Acoustical Society of America, 1980, 68(6): 1801−1819. DOI: 10.1121/1.385170.
[9] GASSMANN F. Uber die elastizitat poroser medien[J]. Vier. der Natur. Gesellschaft Zurich, 1951, 96: 1−23.
[10] BROWN R, KORRINGA J. On the dependence of the elastic properties of a porous rock on the compressibility of the pore fluid[J]. Geophysics, 1975, 40: 608−616. DOI: 10.1190/1.1440551.
[11] ANSELMETTI F S, EBERLI G P. Controls on sonic velocity in carbonates[J]. Pure & Applied Geophysics, 1993, 141: 287−323. DOI: 10.1007/BF00998333.
[12] XU S, PAYNE M A. Modeling elastic properties in carbonate rocks[J]. Leading Edge, 2009, 28: 66−74. DOI: 10.1190/1.3064148.
[13] BAECHLE G, COLPAERT A, EBERLI G, et al. Effects of microporosity on sonic velocity in carbonate rocks[J]. The Leading Edge, 2008, 27(8): 1012−1018. DOI: 10.1190/1.2967554.
[14] SAYERS C M. The elastic properties of carbonates[J]. Leading Edge, 2008, 27: 1020−1024. DOI: 10.1190/1.2967555.
[15] DOU Q, SUN Y, SULLIVAN C. Rock-physics-based carbonate pore type characterization and reservoir permeability heterogeneity evaluation, Upper San Andres reservoir, Permian Basin, west Texas[J]. Journal of Applied Geophysics, 2011, 74: 8−18. DOI: 10.1016/j.jappgeo.2011.02.010.
[16] 李宏兵, 张佳佳, 蔡生娟, 等. 复杂孔隙储层三维岩石物理模版[J]. 地球物理学报, 2019, 62(7): 2711−2723. DOI: 10.6038/cjg2019K0672. LI H B, ZHANG J J, CAI S J, et al. 3D rock physics template for reservoirs with complex pore structure[J]. Chinese Journal of Geophysics, 2019, 62(7): 2711−2723. DOI: 10.6038/cjg2019K0672. (in Chinese).
[17] MORI T, TANAKA K. Average stress in matrix and average elastic energy of materials with misfitting inclusions[J]. Acta Metall, 1973, 21: 571-574.
[18] NORRIS A N. A differential scheme for the effective moduli of composites[J]. Mech Mater, 1985, 4: 1−16. DOI: 10.1016/0167-6636(85)90002-X.
[19] 李宏兵, 张佳佳. 多重孔岩石微分等效介质模型及其干燥情形下的解析近似式[J]. 地球物理学报, 2014, 57(10): 3422−3430. DOI: 10.6038/cjg20141028. LI H B, ZHANG J J. A differential effective medium model of multiple-porosity rock and its analytical approximations for dry rock[J]. Chinese Journal of Geophysics, 2014, 57(10): 3422−3430. DOI: 10.6038/cjg20141028. (in Chinese).
[20] 李宏兵, 张佳佳, 姚逢昌. 岩石的等效孔隙纵横比反演及其应用[J]. 地球物理学报, 2013, 56(2): 608−615. DOI: 10.6038/cjg20130224. LI H B, ZHANG J J, YAO F C. Inversion of effective pore aspect ratios for porous rocks and its applications[J]. Chinese Journal of Geophysics, 2013, 56(2): 608−615. DOI: 10.6038/cjg20130224. (in Chinese).
[21] ZHAO L, NASSER M, HAN D. Quantitative geophysical pore-type characterization and its geological implication in carbonate reservoirs[J]. Geophys Prospect, 2013, 61: 827−841. DOI: 10.1111/1365-2478.12043.
[22] ZHANG T T, ZHANG R F, TIAN J Z, et al. Two-parameter prestack seismic inversion of porosity and pore-structure parameter of fractured carbonate reservoirs: Part 2: Applications[J]. Interpretation, 2018, 6: 1−36.
[23] LI H B, ZHANG J J, CAI S J, et al. A two-step method to apply Xu–Payne multi-porosity model to estimate pore type from seismic data for carbonate reservoirs[J]. Petroleum Science, 2020, 17: 615−627. DOI: 10.1007/s12182-020-00440-2.
[24] ZHANG J J, YIN X Y, ZHANG G Z. Rock physics modelling of porous rocks with multiple pore types: A multiple-porosity variable critical porosity model[J]. Geophysical Prospecting, 2020, 68: 955−967. DOI: 10.1111/1365-2478.12898.
[25] ZOEPPRITZ K. Erdbebenwellen VIII B, uber reflexion and durchgang seismischer wellen durch unstetigkeitsflachen[J]. Goettinger Nachrichten, 1919, 1: 66−84.
[26] AKI K, RICHARDS P G. Quantitative seismology, theory and methods[M]. San Francisco: WH. Freeman and Company. 1980: v1−v2.
[27] SHUEY R T. A simplification of the Zoeppritz equations[J]. Geophysics, 1985, 50: 609−614. DOI:10.1190/ 1.1441936.
[28] FRED J. Seismic amplitude interpretation[M]. Houston: Society of Exploration Geophysicists and the European Association of Geoscientists and Engineers, 2001. https://doi.org/10.1190/1.9781560801993.
-
期刊类型引用(1)
1. 杨蓉蓉. 碳酸盐岩储层二次孔隙发育机理与增产技术研究. 化学工程与装备. 2024(08): 83-85+132 . 
百度学术
其他类型引用(0)
计量
- 文章访问数: 191
- HTML全文浏览量: 63
- PDF下载量: 36
- 被引次数: 1
