The Value of Multi-slice Computed Tomography Based on Intestinal Distribution Combined with Mesenteric Vascular Travel for Accurate Localization of Gastrointestinal Bleeding
-
摘要:
目的:评价MSCT依据肠管分布联合肠系膜血管走行对消化道出血(GIB)精准定位的能力。方法:搜集2021年1月至2023年9月于我院临床诊断GIB并行腹部CT增强扫描且经手术或内窥镜确诊GIB病例的临床及影像资料,由两名观察者(副主任医师及以上)采用双盲法回顾性分析所有病例MSCT薄层轴位图像,记录有无GIB;出血病例采用两种观察方法确定出血部位,A组:依据肠管分布判断出血部位,B组:依据肠管分布联合肠系膜血管走行判断出血部位。比较两种方法的对GIB精准定位的能力。结果:经手术或内窥镜确诊GIB的病例130例,MSCT检出GIB 109例,准确率83.85%;A组(依据肠管分布)定位出血部位71例,定位准确率为65.14%;B组(依据肠管分布联合肠系膜血管走行)定位出血部位85例,定位准确率为77.98%,两组差异有统计学意义。结论:MSCT依据肠管分布联合肠系膜血管走行定位GIB部位的准确性优于单纯依据肠管分布。
Abstract:Objective: This study aimed to evaluate the accuracy of multi-slice computed tomography (MSCT) to locate gastrointestinal bleeding (GIB) based on intestinal distribution combined with mesenteric vascular travel. Methods: The clinical and imaging data of GIB cases diagnosed in our hospital between January 2021 and September 2023 were collected and confirmed by surgery or endoscopy by abdominal CT-enhanced scanning, Two associate chief physicians retrospectively analyzed the thin-slice axial images of MSCT in all cases using the double-blind method, and recorded the presence or absence of GIB. Two observation methods were used to determine the bleeding site; the bleeding site was judged according to the intestinal distribution (group A), and intestinal distribution combined with mesenteric vascular travel (group B). The accuracy of both methods to locate the GIB was compared. Results: There were 130 cases of GIB diagnosed by surgery or endoscopy, and 109 cases were detected by MSCT, with an accuracy rate of 83.85%. There were 71 cases in group A and 85 cases in group B, and the accuracy to locate the bleeding site was 77.98%, with a statistically significant difference. Conclusion: The accuracy of MSCT in locating GIB sites based on intestinal distribution combined with mesenteric vascular travel is better than that based on intestinal distribution alone.
-
Keywords:
- GIB /
- MSCT /
- positioning /
- intestinal distribution /
- mesenteric vascular travel
-
消化道出血(gastrointestinal bleeding,GIB)是临床常见急腹症,其中急性上GIB是急诊常见危急重症之一,病死率高达2%~15%[1],快速诊断有无GIB并进行精准定位是临床关注的焦点。
近年来MSCT飞速发展,作为一种非侵袭性、快速的检查方法,被广泛应用于GIB的诊断[2]。大量的研究表明MSCT对于GIB的诊断存在优势,其诊断效能优于消化道内镜检查[3-5],但关于MSCT如何对GIB精准定位的方法研究报道较少。
本文将接受CT增强扫描的GIB患者130例列为样本进行研究,分别通过依据肠管分布、依据肠管分布联合肠系膜血管走行两种阅片方式定位出血部位,通过评价MSCT依据肠管分布联合肠系膜血管走行对GIB精准定位的能力,旨在为消化道出血的定位诊断提供一种新的诊断思路,以期为临床后续治疗提供更多的影像学证据。
1. 资料与方法
1.1 一般资料
搜集2021年1月至2023年9月于华北理工大学附属医院临床诊断GIB行腹部CT增强扫描,并经手术或内窥镜确诊GIB病例的临床及影像资料。
所有患者均符合GIB的相关诊断标准,临床症状包括呕血、黑便、鲜血便、腹痛腹胀、全血细胞减少等,并详细询问病史排除非胃肠道出血因素,如咯血与吐血、口鼻腔及咽喉部出血、食物及药物引起的黑便等。
按照纳入及排除标准共收集130例,其中经MSCT诊断GIB 109例,平均年龄(63.29±12.42)岁,包括男性68例,女性41例。
1.2 检查方法
扫描设备:GE Revolution CT。扫描方法:患者采用仰卧位、从头侧到足侧扫描。扫描范围:从横膈至耻骨下支。扫描序列:行平扫及双增强扫描。
扫描参数。管电流260 mA,管电压120 kV,螺距1.0;扫描层厚及层间距:均为5 mm,重建图像层厚及层间距均为1.25 mm。
对比剂碘海醇(300 mgI/mL),注射剂量1.5 mL/kg;采用高压注射器经肘静脉,注射流率3.5 mL/s;采用对比剂智能跟踪(smart prep)技术确定扫描时间;感兴趣区(region of interest,ROI)内CT值达到120 HU时,自动触发动脉期增强扫描,再延迟35 s进行静脉期扫描。
1.3 观察指标
由两名观察者分别独立采用双盲法回顾性分析所有病例的MSCT薄层轴位图像,记录有无GIB,意见不一致时协商解决。
MSCT诊断GIB的直接征象是增强扫描与平扫比较胃肠腔内出现高密度的对比剂外溢,CT值>90 HU。
间接征象包括胃肠腔内高密度凝血块、肠管局限性扩张、局灶性肠壁增厚及异常强化、肠周脂肪水肿、肠壁肿物及憩室等[6]。
MSCT检出GIB的病例分别采用两种观察方法确定出血部位。A组(依据肠管分布):采用曲面重组(curved planar reformation,CPR)、多平面重组(multi planar reformation,MPR)后处理及技术观察平扫及增强图像。B组(依据肠管分布联合肠系膜血管走行),在A组观察方法的基础上,运用动脉期薄层图像进行最大密度投影(maximum intensity projection,MIP)重组,观察显示肠系膜动脉血管,包括肠系膜上动脉、胰十二指肠上动脉、空肠动脉和回肠动脉、中结肠动脉、右结肠动脉、回结肠动脉、肠系膜下动脉、左结肠动脉、乙状结肠动脉和直肠上动脉等,通过观察供血的肠系膜血管有无病变,进而追踪到相应病变肠管,结合肠管分布综合判断出血部位。
1.4 统计学分析
采用SPSS 19.0进行分析,计数资料用n/%表示,用卡方检验。以P<0.05为差异有统计学意义。
2. 结果
共搜集临床诊断GIB并行腹部CT增强扫描且经手术或内窥镜确诊GIB病例的临床及影像资料130例(包括经手术确诊GIB 43例,内窥镜确诊GIB 87例),MSCT诊断GIB 109例,准确率83.85%,其中102例由两名观察者分别独立诊断且诊断结果一致,有7例由于MSCT诊断GIB的间接征象存疑,经协商后达成一致诊断。
GIB的定性诊断。包括炎症(急慢性炎症、糜烂、溃疡等)35例;机械因素(憩室继发感染出血、胃肠道黏膜脱落)4例;血管因素(食管或胃底静脉曲张破裂出血、血管畸形、血管栓塞)19例;肿瘤(消化道的良恶性肿瘤)49例;其他病因2例(表1)。
表 1 GIB病因分布情况(n/%)Table 1. Etiological distribution of GIB (n/%)N 炎症 机械因素 血管因素 肿瘤 其他 109 35(32.11) 4(3.67) 19(17.43) 49(44.95) 2(1.83) GIB的定位诊断。A组和B组个别病例观察到多部位出血,遂分别记录了出血部位及出血点。A组(依据肠管分布):定位出血部位71例(出血点72个),定位准确率为65.14%;B组(依据肠管分布联合肠系膜血管走行):定位出血部位85例(出血点88个),定位准确率为77.98%。两种方法的定位准确率存在统计学差异,依据肠管分布联合肠系膜血管走行对GIB的定位准确率高于单纯依据肠管分布(表2)。
表 2 A组、B组对GIB精准定位的能力比较(n/%)Table 2. Comparison of the accuracy of groups A and B to locate GIB (n/%)组别 N 食管或胃底 胃腔 十二指肠 空肠 回肠 回盲部 结直肠 精准定位 A组 109 11 21 1 1 0 1 37 71(65.14) B组 109 11 22 5 4 3 3 40 85(77.98) $\chi^2 $ − − − − − − − − 4.418 P − − − − − − − − 0.036 注:P<0.05差异有统计学意义。 3. 讨论
GIB是指从食管到肛门的消化管道出血,包括食管、胃、十二指肠、空肠、回肠、盲肠、结肠及直肠的某个或多个部位的出血[7]。轻症可无明显症状,重症可表现为血容量下降、休克等,严重威胁患者生命安全,早期精准的定位及定性诊断是目前临床关注的重点。
3.1 GIB的诊断方法
GIB较为常见的检查方法有:内镜检查、胶囊内镜、数字减影血管造影(digital subtraction angiography,DSA)、放射性核素检查以及MSCT[8]。
内镜检查前需要进行肠道准备,不适合活动性出血患者的检查,且出血较多时会影响内镜的观察,同时由于小肠冗长,对下消化道出血患者的检查存在一定的局限性。胶囊内镜弥补了内镜检查在小肠检查方面的不足,但其价格昂贵,临床难推广,且容易发生嵌顿[9]。放射性核素检查不适合急诊检查且定位不准确。DSA被认为是胃肠道出血放射学诊断的金标准,但其属于有创检查,急诊应用具有局限性。
相较于造影和内镜检查只能观察黏膜及腔内情况、DSA只能观察血管,MSCT能够全面的观察肠腔内外情况以及毗邻血管,对GIB诊断的优势更加显著,且MSCT属于无创检查,患者的耐受程度更高,适用范围更广,近年来越来越受到临床医生的关注。
3.2 MSCT诊断GIB的研究进展
MSCT利用多排螺旋CT血管成像技术进行多期扫描,具有简单、无创、扫描范围大、快速、明显降低运动和呼吸伪影、敏感度的特点[10]。梁韬等[3]通过研究发现:CT诊断出血部位的准确率为88.5%,出血原因的准确率为88.5%,高于内镜检查的73.1%和73.1%,DSA检查的80.7%和76.9%,提示CT检查能够较准确掌握患者GIB的原因和出血部位,这与潘亚菊[4]的研究结果基本一致。MSCT是诊断GIB快捷、简便、无创及有效的影像学方法,可较准确诊断出血的部位和出血的原因,可作为内镜、DSA及外科干预手术前的一种综合术前筛选检查手段,为治疗方案的制订提供重要的参考信息,具有重要的实际临床指导意义。
能谱成像作为CT的一项新技术实现了混合成像向单能量成像的转变,拥有更高的图像质量、信噪比及对比噪声比[11]。刘文冬等[12]、胡伟杰等[13]实验表明,利用能谱CT可以提高微量活动性出血的诊断阳性率,另外在出血定量方面,能谱CT基物质碘(水)基图具有一定的可行性。能谱CT在诊断GIB方面较传统MSCT具有一定优越性,但目前临床应用较少,大多用于实验室研究,因此,本研究主要讨论常规MSCT。
3.3 MSCT对GIB定位的诊断价值
有些研究认为,GIB的处理需要影像科室与相关临床科室积极配合,必须及时知道出血部位和原因,从而达到针对性的处理。GIB作为消化道急症,疾病发展迅速,若不能快速定位并控制出血灶,随之而来的血容量下降和休克会严重危及患者生命,甚至导致患者死亡。
在急诊处理中,临床医生最关心最迫切的信息就是GIB的定位问题,特别是小肠的病变,通过影像检查获取定位并进行及时有效地处理达到止血的目的从而快速稳定患者的生命体征无疑是对GIB患者的最优解,下一步的诊疗过程才是明确出血原因及性质,在此基础上开展更具针对性的治疗,保证患者预后。
小肠起自胃幽门,最后进入盲肠的回盲部,包括十二指肠、空肠及回肠,在影像上一般通过肠管解剖分布及粘膜皱襞来定位肠管。
十二指肠位置较为固定,状如C形包绕胰头,容易区分。空肠起自十二指肠空肠曲,一般将空回肠全长的近端五分之二称为空肠,余下部位称为回肠,两者之间无明显分界。空肠一般位于左上腹和右上腹,回肠在右下腹、左下腹及盆腔,但由于小肠相互重叠、活动度大、疾病种类多(例如肿瘤性病变会推挤肠管移位,炎症性病变可能出现肠管粘连,血管性病变会导致肠管坏死等),根据肠管解剖分布往往不能获得准确定位。空肠管径较粗,一般约4 cm,管壁较厚,粘膜皱襞密且多,呈弹簧状或鱼肋状,皱襞间多保持平衡距离贯穿肠壁;回肠管径细,一般约3.5 cm,管壁较空肠薄,粘膜皱襞浅且稀疏,扩张状态下可呈光滑的空管状。
但GIB属于急腹症,往往患者在接受CT检查时是没有时间做好肠道准备的,导致肠管充盈欠佳,粘膜皱襞显示欠清,因此通过管径、肠壁厚度及粘膜皱襞也不能很好的区分空回肠。综上,单纯依据肠管分布不能很好定位。
以MSCT薄层轴位图像为基础,结合VR、MIP等重建技术对肠系膜血管进行观察可以得到更多肠外影像征象。
MIP图像类似于传统血管造影,对比度很高,能够较真实反应组织的密度差异,显示血管壁上的钙化和对比剂充盈的血管腔,观察血管狭窄、扩张及充盈缺损等,借此可以显示细小的肠系膜分支血管以及病变小血管的位置。从腹腔干、肠系膜上、下动脉三大主支开始向下逐级追踪肠系膜血管走行,观察肠系膜血管是否显影、有无迂曲扩张、有无走行异常及共干,观察管腔内有无充盈缺损以及血管壁有无斑块、钙化[14],通过观察供血的肠系膜血管有无病变,进而追踪相应的供血肠管有无异常[15]。
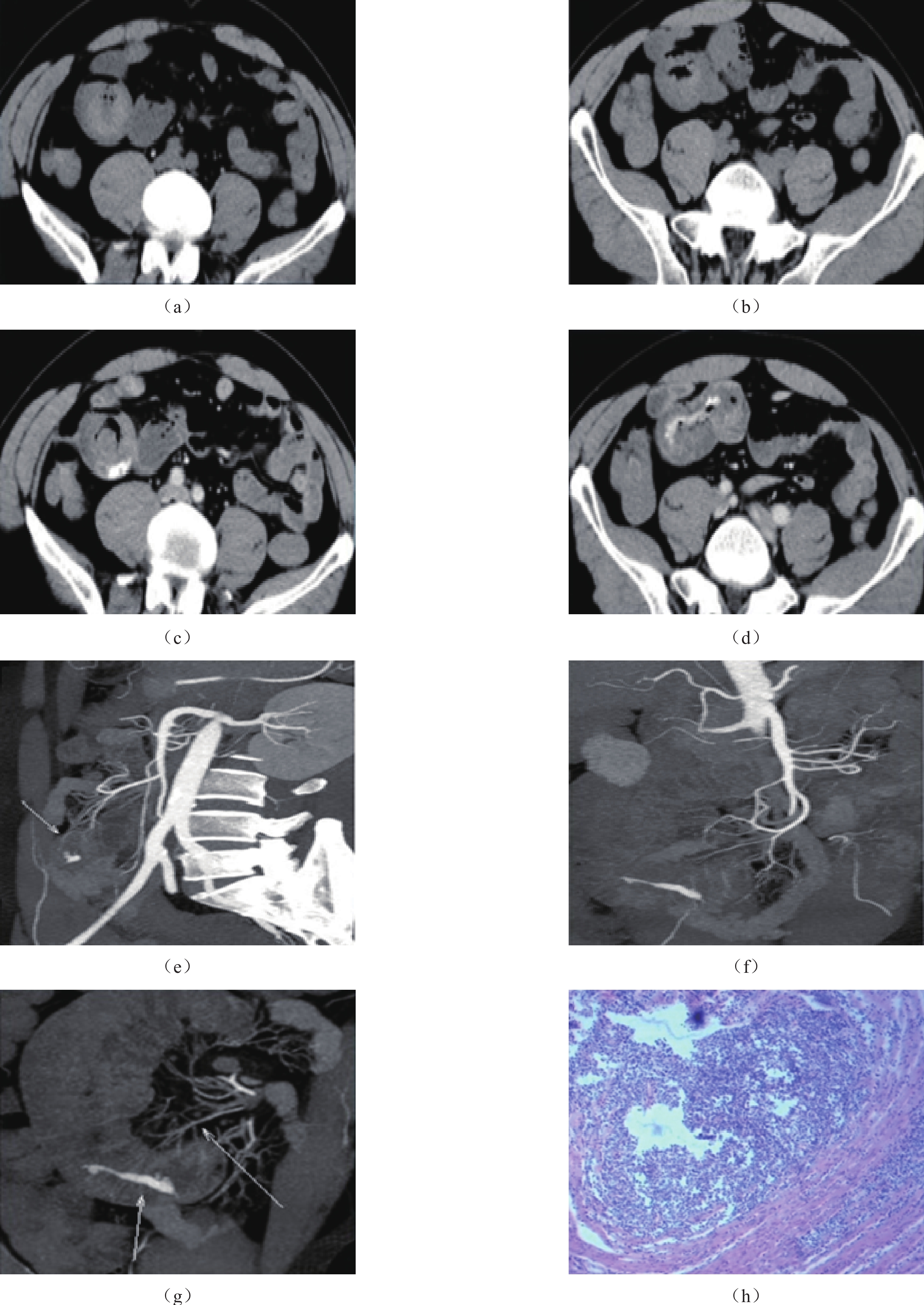
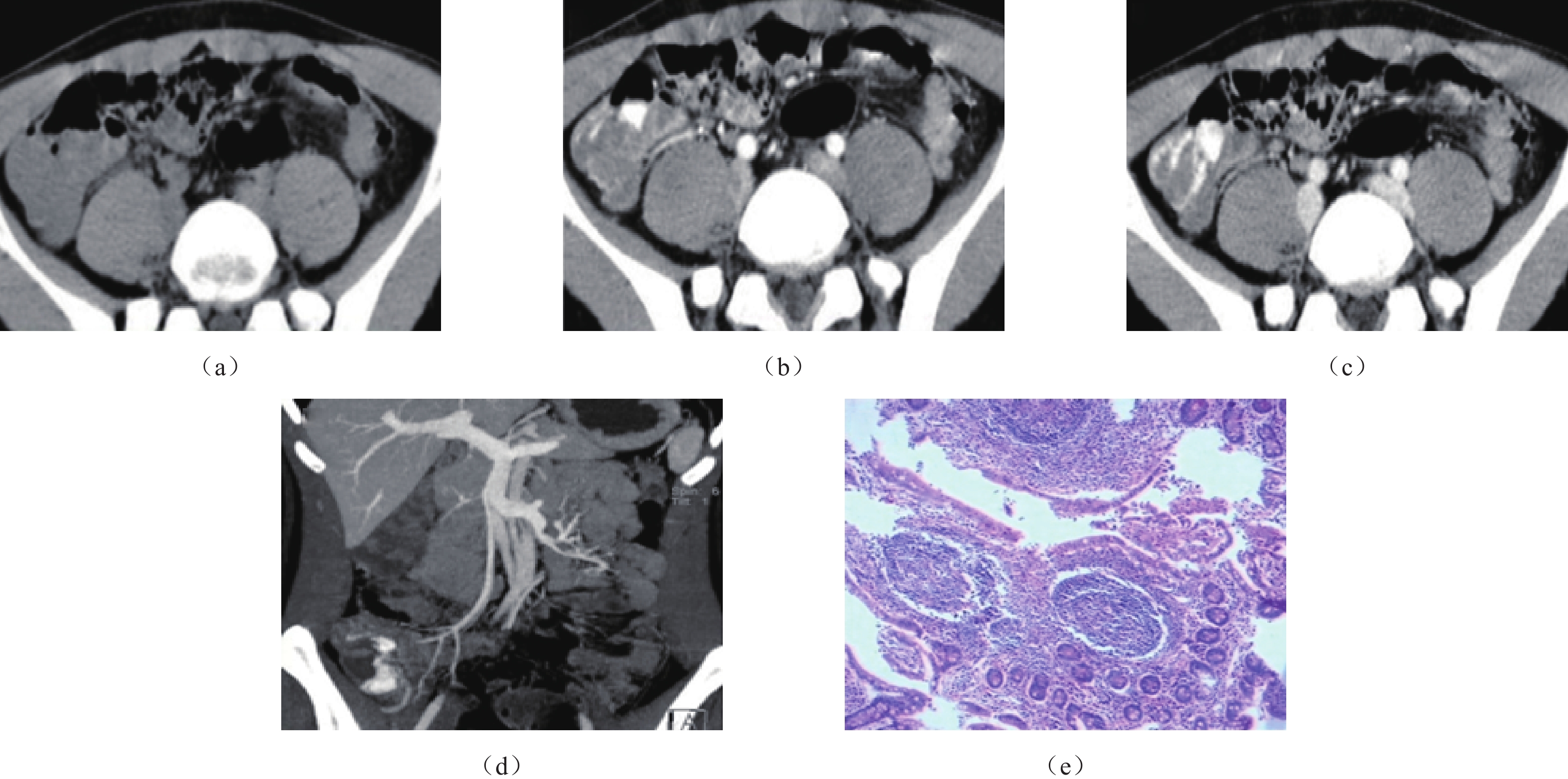
肠系膜上动脉约平第1腰椎的高度起自腹主动脉前壁,此动脉向右发出胰十二指肠下动脉、中结肠动脉、右结肠动脉和回结肠动脉,供应了右半结肠及大部横结肠;向左发出约12~18条空、回肠动脉,供应所有小肠,由于小肠长且扭曲,活动度大的解剖特点,小肠部位的疾病通常起病隐匿且病变部位深而不固定,诊断较困难,内镜、钡餐等诊断价值有限[16],通过重建显示肠系膜血管走行,可以更好的显示血管解剖及病变,再依据血管解剖来推断出肠管具体部位,可以更好的显示肠管相互套叠的小肠病变(图1和图2),为后续介入或外科手术治疗提供影像学支持[17]。
从病因学分析,小肠出血的病因和年龄有关,就全年龄段而言,小肠出血病因以血管畸形最为常见,这也支持了利用MSCT进行小肠出血的定位诊断时,依据肠管分布联合肠系膜血管走行可以获取更多影像学信息,帮助消化道出血定位诊断。
有一部分肠管病变导致的GIB由于病变部位相对表浅,如病变位于浆膜层,病理结构改变细微,即使开腹也难以发现病变位置,易被漏诊或误诊,剖腹探查的失败率很高。依据肠管分布联合肠系膜血管走行的方法在术前进行准确定位,对于传统外科手术治疗,可以明确切口位置,从而缩短开腹之后寻找病变肠管的时间,对于介入治疗,可以缩短介入时间,减少辐射剂量。
大量研究[3-4]表明MSCT对消化道出血的诊断存在优势,其诊断效能优于传统消化道内镜检查,临床上消化道病变进行MSCT检查时往往需要肠道适度扩张,消化道出血作为急腹症通常没有时间进行肠道准备,影像医师往往依据肠管分布对消化道出血进行定位,但是没做肠道准备的肠管绝大部分是空虚状态,尤其是小肠。此外,血管源性消化道出血由于出血量大、难以定位,一旦发病进展迅速且预后不良,这些因素无疑增加了消化道出血检出和定位诊断的难度。
本次研究结果显示单纯依据肠管分布定位GIB的准确率为65.14%,依据肠管分布联合肠系膜血管走行定位GIB的准确率为77.98%,通过重建MIP等能够提供更多详细的肠系膜血管系统的三维图像,从而可以更加直观地观察血管解剖和病变,帮助影像医师快速检出及定位出血。
本研究的不足之处在于采用回顾性研究且纳入研究的病例过少。在以后的研究中,扩大样本量并结合前瞻性研究会更具有临床应用价值。关于本次研究扫描期相的选择,常规选用平扫及双期增强扫描,部分学者认为延迟期对GIB的诊断亦有很高的价值,未将延迟期纳入研究是为不足。
综上,MSCT依据肠管分布联合肠系膜血管走行对GIB定位的准确性优于依据肠管分布,可以作为探寻GIB部位的一种思路,对后续临床治疗具有重要现实意义。
-
表 1 GIB病因分布情况(n/%)
Table 1 Etiological distribution of GIB (n/%)
N 炎症 机械因素 血管因素 肿瘤 其他 109 35(32.11) 4(3.67) 19(17.43) 49(44.95) 2(1.83) 表 2 A组、B组对GIB精准定位的能力比较(n/%)
Table 2 Comparison of the accuracy of groups A and B to locate GIB (n/%)
组别 N 食管或胃底 胃腔 十二指肠 空肠 回肠 回盲部 结直肠 精准定位 A组 109 11 21 1 1 0 1 37 71(65.14) B组 109 11 22 5 4 3 3 40 85(77.98) $\chi^2 $ − − − − − − − − 4.418 P − − − − − − − − 0.036 注:P<0.05差异有统计学意义。 -
[1] 徐军, 戴佳原, 尹路. 急性上消化道出血急诊诊治流程专家共识[J]. 中国急救医学, 2021, 41(1): 1-10. DOI: 10.3969/j.issn.1002-1949.2021.01.001. XU J, DAI J Y, YIN L. Expert consensus on emergency diagnosis and treatment of acute upper gastrointestinal bleeding[J]. Chinese Journal of Emergency Medicine, 2021, 41(1): 1-10. DOI: 10.3969/j.issn.1002-1949.2021.01.001. (in Chinese).
[2] MOHAMMADINEJAD P, KWAPISZ L, FIDLER J L, et al. The utility of a dual-phase, dual-energy CT protocol in patients presenting with overt gastrointestinal bleeding[J]. Acta Radiologica Open, 2021, 10(7): 1114514914-1217658238.
[3] 梁韬, 曾苗雨, 王毓佳, 等. 64层螺旋CT在上消化道出血诊断中的临床应用价值[J]. 中华临床医师杂志(电子版), 2016, 10(10): 1432-1436. LIANG T, ZENG M Y, WANG Y J, et al. Clinical value of 64-slice spiral CT in the diagnosis of upper gastrointestinal bleeding[J]. Chinese Journal of Clinical Physicians (Electronic Edition), 2016, 10(10): 1432-1436. (in Chinese).
[4] 潘亚菊. 多层螺旋CT在消化道出血诊断中的价值[J]. 基层医学论坛, 2014, 18(34): 4695-4696. PAN Y J. Value of multi-slice spiral CT in the diagnosis of gastrointestinal bleeding[J]. Primary Medicine Forum, 2014, 18(34): 4695-4696. (in Chinese).
[5] 李宜亮, 张春霞, 李勇, 等. 多层螺旋CT增强扫描在胃肠道血管畸形诊断中的应用价值[J]. 中国当代医药, 2020, 27(9): 111-114. DOI: 10.3969/j.issn.1674-4721.2020.09.033. LI Y L, ZHANG C X, LI Y, et al. Application value of multi-slice spiral CT enhanced scanning in the diagnosis of gastrointestinal vascular malformations[J]. Chinese Journal of Contemporary Medicine, 2020, 27(9): 111-114. DOI: 10.3969/j.issn.1674-4721.2020.09.033. (in Chinese).
[6] 丁玲, 张玉忠, 鄂林宁. 多期增强CT诊断急性活动性胃肠道出血临床案例分析[J]. CT理论与应用研究, 2023, 32(6): 807-814. DOI: 10.15953/j.ctta.2023.065. DING L, ZHANG Y Z, E L N. Clinical case study of multi-stage contrast-enhanced CT in the diagnosis of acute active gastrointestinal bleeding[J]. CT Theory and Applications, 2023, 32(6): 807-814. DOI: 10.15953/j.ctta.2023.065. (in Chinese).
[7] BOND A, SMITH P J. British Society of Gastroenterology: Diagnosis and management of acute lower gastrointestinal bleeding[J]. Frontline Gastroenterology, 2019, 10(4): 417-420. DOI: 10.1136/flgastro-2019-101220.
[8] FEINGOLD D L, PAPPOU E P, LEE-KONG S A. Diagnostic modalities in gastrointestinal bleeding[J]. Clinics in Colon and Rectal Surgery, 2020, 33(1): 5-9. DOI: 10.1055/s-0039-1693440.
[9] 廖小丽. 胶囊内镜联合多排螺旋CT对不明原因消化道出血的诊断价值[J]. 影像研究与医学应用, 2020, 4(18): 187-188. DOI: 10.3969/j.issn.2096-3807.2020.18.100. LIAO X L. Value of capsule endoscopy combined with multidetector spiral CT in the diagnosis of unexplained gastrointestinal bleeding[J]. Imaging Research and Medical Application, 2020, 4(18): 187-188. DOI: 10.3969/j.issn.2096-3807.2020.18.100. (in Chinese).
[10] 陈茹萱, 孙昊, 李晓光, 等. 多排螺旋CT血管成像诊断急性消化道出血的价值及相关进展[J]. 协和医学杂志, 2014, 5(4): 460-463. DOI: 10.3969/j.issn.1674-9081.2014.04.022. CHEN R X, SUN H, LI X G, et al. The value of multidetector spiral CT angiography in the diagnosis of acute gastrointestinal bleeding and related advances[J]. Medical Journal of Peking Union Medical College Hospital, 2014, 5(4): 460-463. DOI: 10.3969/j.issn.1674-9081.2014.04.022. (in Chinese).
[11] SO A, NICOLAOU S. Spectral computed tomography: Fundamental principles and recent developments[J]. Korean Journal of Radiology, 2021, 22(1): 86-96. DOI: 10.3348/kjr.2020.0144.
[12] 刘文冬, 吴兴旺, 刘斌, 等. 碘基图在能谱CT探测肠道活动性出血中的价值——模型研究[J]. 中国医学影像技术, 2014, 30(1): 122-125. LIU W D, WU X W, LIU B, et al. The value of iodine-based diagram in the detection of active intestinal bleeding by spectroscopic CT spectroscopy: A model study[J]. Chinese Journal of Medical Imaging Technology, 2014, 30(1): 122-125. (in Chinese).
[13] 胡伟杰, 刘文冬, 刘斌, 等. 能谱CT碘基图定量诊断小肠活动性出血的模型研究[J]. 中国医学影像技术, 2016, 32(2): 163-166. HU W J, LIU W D, LIU B, et al. Model study on the quantitative diagnosis of active bleeding in the small intestine by energy spectroscopic CT iodine-based diagram[J]. Chinese Journal of Medical Imaging Technology, 2016, 32(2): 163-166. (in Chinese).
[14] 尹昕茹, 文良志, 王斌, 等. 肠系膜血管源性消化道出血的临床诊治[J]. 胃肠病学, 2018, 23(7): 391-394. YIN X R, WEN L Z, WANG B, et al. Clinical diagnosis and treatment of mesenteric vascular gastrointestinal bleeding[J]. Gastroenterology, 2018, 23(7): 391-394. (in Chinese).
[15] 刘卉, 肖潇, 颜綦先, 等. 37例肠系膜血管病变致消化道出血的回顾性分析[J]. 胃肠病学和肝病学杂志, 2018, 27(1): 66-69. DOI: 10.3969/j.issn.1006-5709.2018.01.015. LIU H, XIAO X, YAN Q X, et al. Retrospective analysis of gastrointestinal bleeding caused by mesenteric vascular lesions in 37 cases[J]. Journal of Gastroenterology and Hepatology, 2018, 27(1): 66-69. DOI: 10.3969/j.issn.1006-5709.2018.01.015. (in Chinese).
[16] 张靖, 杨艳敏, 陆建环, 等. 胶囊内镜及小肠CT成像对不明原因消化道出血的诊断价值[J]. 中国临床医学影像杂志, 2016, 27(3): 183-186. ZHANG J, YANG Y M, LU J H, et al. Value of capsule endoscopy and small bowel CT imaging in the diagnosis of unexplained gastrointestinal bleeding[J]. Chinese Journal of Clinical Medical Imaging, 2016, 27(3): 183-186. (in Chinese).
[17] 张悦, 刘潇, 刘铁. 肠系膜动脉CTA在老年性消化道出血诊断中的应用价值[J]. 医学影像学杂志, 2020, 30(6): 1037-1040. ZHANG Y, LIU X, LIU T. Application value of mesenteric artery CTA in the diagnosis of senile gastrointestinal bleeding[J]. Journal of Medical Imaging, 2020, 30(6): 1037-1040. (in Chinese).



 下载:
下载: