Research on the Identification of Sandstone Vanishing Points Based on Synchronous Compression Matching Pursuit Method
-
摘要:
砂体尖灭的刻画是构造岩性复合圈闭有效性评价的关键，而受地震资料带限影响难以准确识别砂体的尖灭位置。为了有效解决地震剖面上尖灭识别不准的问题，本文创新引入同步压缩匹配追踪时频分辨率和能量聚焦性双重优势开展砂体尖灭识别研究。首先利用时频域褶积算子与初始模型约束构建匹配追踪的冗余字典，在时频域内筛选出所有可能的匹配原子构成备选原子库；将初始模型约束与时频域联合反演方法引入反演框架，可获得更精确的反演结果；再利用同步压缩匹配追踪变换，通过逐道分析提取优势频率，筛选时频瞬时谱，得到具有最优频率的单频谱剖面。对所提方法进行的二维模型及实际资料的测试，结果表明，基于同步压缩匹配追踪的高分辨率地震谱分解砂体尖灭点识别方法能够获得更丰富的时频域信息，得到最优频率的单频谱剖面，进而精确识别地下地质体尖灭位置。该方法对超覆型及削蚀型岩性圈闭尖灭线的刻画具有重要的借鉴意义。
Abstract:The portrayal of sand cusp extinction is the key to evaluating the effectiveness of tectonic-lithological composite confinement, and it is difficult to accurately identify the location of sand cusp extinction due to the influence of seismic data band limitations. In order to effectively solve the problem of inaccurate identification of cusp extinction on seismic sections, this paper innovatively introduces the dual advantages of time-frequency resolution and energy focusing of synchronous compression match tracing to carry out the sand-cusp extinction identification research. Firstly, the time-frequency domain pleated-product operator is used to construct the redundancy dictionary of match tracing with the constraints of the initial model, and all the possible matching atoms are screened out to form the alternative atom bank in the time-frequency domain. The initial model constraints and the time-frequency domain joint inversion method are introduced into the inversion framework, which can obtain more accurate inversion results. Then, the dominant frequencies are extracted by channel-by-channel analysis using the simultaneous compressive match-tracking transform, and the time-frequency transient spectra are screened to obtain the single-frequency spectral profile with the optimal frequencies. The two-dimensional model and actual data testing of the proposed method show that the high-resolution seismic spectral decomposition sand-cusp identification method based on synchronous compression and matching tracking can obtain richer time-frequency domain information and get the single-frequency spectral profile with the optimal frequency, thus accurately identifying the location of cusps of subsurface geological bodies, which is of great significance for the depiction of cusps of overburden-type and erosion-type lithological confinement.
-
随着勘探开发逐步深入，勘探目标逐步由简单构造油气藏向构造岩性复合油气藏的延伸，尤其对于复杂河流相储层，砂体横向变化快，砂体尖灭位置的识别是岩性油气藏评价的关键。而常规地震在砂体尖灭附近砂体较薄地震能量反射较弱，且存在复杂的干涉现象，地震反射信号存在严重干扰，导致常规地震剖面上尖灭点识别存在多解性，进而影响油气藏井位部署和油藏精细评价。
常用岩性尖灭位置的识别技术主要包括薄层调谐原理应用以及瞬时谱分析技术。在薄层调谐应用方面，Widess提出调谐厚度概念[1]，即为地震记录在纵向上所能识别的最小厚度，薄层调谐成为尖灭点识别的重要依据。在时频分析方面，通过时频域高分辨率进行尖灭识别，王军等[2]利用S变换瞬时谱分析方法，建立薄层调谐的瞬时谱特征模板，利用薄层调谐原理识别出不同厚度三角洲砂体的尖灭位置；王志杰[3]将频率成像技术与相位分析技术结合识别砂体尖灭线，利用频谱成像刻画砂体尖灭边界，结合相位属性提高砂体横向分辨精度；张军华等[4]结合谱分解技术，提取分频数据体的下波谷幅值属性，识别出主力油层的尖灭线；张繁昌等[5]通过分析楔状尖灭的时间域和频率域响应特征，利用优势调谐频带内瞬时谱分量进行砂体尖灭线的识别和刻画；汪瑞良等[6]借助快速动态匹配追踪算法，有效利用时频谱分量来指示砂体实际尖灭位置。但随着勘探精度的不断提高，高精度的时频分析方法决定着砂体尖灭位置的可靠度和精准度。
目前针对地震时频分析主要包含短时傅里叶变换[7]、小波变换[8]、Wigner-Ville分布[9]、经验模态分解[10]等，其中短时傅里叶变换和小波变换的时频分辨率取决于时窗和基函数的选择，由于时窗和基函数在分析中固定不变，因此对多分量时变信号分辨效果不佳；Wigner-Ville分布对噪声的鲁棒性不足且对多分量时变信号存在交叉干扰项，经验模态分解存在端点效应和模态混叠等问题。
传统时频分析方法普遍存在瞬时频率曲线幅值不集中、时频谱会出现模糊分辨率不高的现象，为了实现理想的时频表示，在原始时频谱的基础上进行能量重排是当前研究的热点。基于同步压缩变换的时频分析方法通过频率方向的匹配追踪结果进行压缩重构，能够对复杂多分量信号实现高分辨率表达，有效提高时频谱的分辨率能力和能量聚焦性。
本文借助同步压缩匹配追踪时频分辨率和能量聚焦性双重优势，将其应用于砂体尖灭位置的识别。首先利用时频域褶积算子与初始模型约束构建匹配追踪的冗余字典，在时频域内筛选出所有可能的匹配原子构成备选原子库；将初始模型约束与时频域联合反演方法引入反演框架，可获得更精确的反演结果；再利用同步压缩匹配追踪变换，通过逐道分析提取优势频率，筛选时频瞬时谱，得到具有最优频率的单频谱剖面，进而精确识别地下地质体尖灭位置。
模型及实际资料测试结果表明，同步压缩匹配追踪的单频谱相对传统的时频分析方法识别尖灭点的精度更高。本文方法相较于利用地震剖面进行尖灭点识别与直接利用反演所获得的识别结果能量更加集中，尖灭位置更加清晰和准确。
1. 理论与方法
1.1 时间域反演方法
地震记录是地震子波矩阵与反射系数的褶积，其近似公式可表示为[11]：
$$ {\boldsymbol{d}}={\boldsymbol{Gm}}+{\boldsymbol{n}}， $$ (1) 式中，
$ {\boldsymbol{d}} $ 为地震记录；$ {\boldsymbol{G}} $ 为子波时移后地震子波矩阵；$ \boldsymbol{m}=\left(r_1\ \ r_2\ \ \cdots\ \ r_N\right)^{\mathrm{T}} $ 为反射系数序列；n为随机噪声，通常假设其满足高斯分布。反射系数能够反映地下地层的界面位置及岩性变换等，稀疏反演的目标则是得到稀疏的反射系数，通常情况下采用最小二乘法来求解目标函数，即：
$$ {\boldsymbol{F}}\left( r \right) = \arg \min \big\| {{\boldsymbol{d}} - {\boldsymbol{Gm}}} \big\|_2^2 。$$ (2) 考虑到地震数据频宽局限性和反演不稳定性，为防止反演结果陷入局部的
$ {\boldsymbol{d}} $ 最小值，国内外的专家和学者们提出了很多解决策略[12-13]，其中比较有效的策略是将低频模型对反演目标函数加以约束，以增强模型参数反演可靠性。式（2）可进步转变为：$$ {\boldsymbol{F}}\left( r \right) = \arg \min \left\{ {\big\| {{\boldsymbol{d}} -{\boldsymbol{ Gm}}} \big\|_2^2 + \lambda {J_{{\mathrm{prior}}}}\left( {\boldsymbol{m}} \right)} \right\}， $$ (3) 式中，
$ {J_{{\mathrm{prior}}}}\left( {\boldsymbol{m}} \right) $ 为包含先验低频模型信息的约束项；$ \lambda $ 为先验信息的约束系数，用于衡量先验信息参与地震反演的比重。稀疏性作为衡量信号品质非常重要的性质，在时间域地震反演中，
$ {L_0} $ 、$ {L_1} $ 、$ {L}_{1,2} $ 范数被用于约束反演过程，即：$$ \min\left( {\boldsymbol{m}} \right) = \big\| {{\boldsymbol{d}} - {\boldsymbol{Gm}}} \big\|_2^2 + \lambda {L_p}\left( {\boldsymbol{m}} \right)， $$ (4) 式中，
$ {L_p}\left( {\boldsymbol{m}} \right) $ 表示范数。当$ p{\text{ = }}0 $ 时，求解算法为匹配追踪算法，即利用不断进行迭代的方式，从原子库中找到最佳匹配的子波来不断地逼近原始信号，属于贪婪的算法；$ p{\text{ = 1}} $ 时，求解反演过程的算法为基追踪算法，通过奇偶分解算法得到奇偶反射系数对，最终得到的反演结果趋于块化；$ p\text{=1},\text{2} $ 为利用混合范数对反演过程进行约束，反演求解过程稳定性更强。1.2 频率域反演方法
$$ {\boldsymbol{S}}(\omega ) = {\boldsymbol{W}}(\omega ){\boldsymbol{R}}(\omega ) + {\boldsymbol{N}}(\omega )， $$ (5) 式中，
$ {\boldsymbol{W}}(\omega ) $ 为频率域子波，$ {\boldsymbol{R}}(\omega ) $ 为时间域反射系数，$ {\boldsymbol{N}}(\omega ) $ 为随机噪声频谱，$ \omega $ 为角频率。为了将上述过程表达更加清楚更加直观，将式（5）中的
$ {{{R}}}(\omega) $ 展开，得到：$$ \boldsymbol{S}\left(\omega\right)=\boldsymbol{W}\left(\omega\right)\left(\int_0^{+\infty}\boldsymbol{r}\left(z\right)\exp\left(-i\omega\tau\left(z\right)\right)\mathrm{d}z\right)， $$ (6) 式中，
$ {\boldsymbol{r}}(z) $ 为介质反射系数序列，${\boldsymbol{ \tau}} (z) $ 为对应反射系数的时间深度，$ \exp \left( \cdot \right) $ 为自然指数函数运算。将上式用矩阵的形式来表达，如下式所示：
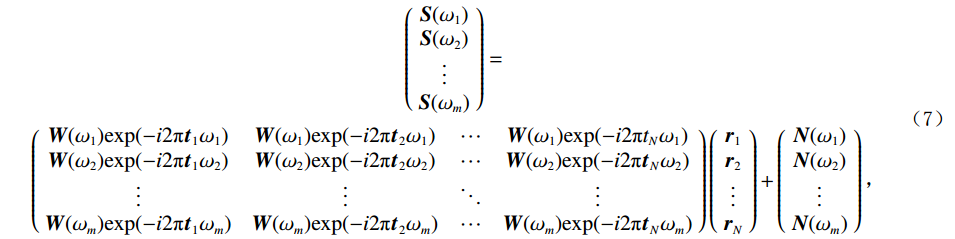
$$ \begin{aligned} &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\left( {\begin{array}{*{20}{c}} {{\boldsymbol{S}}({\omega _1})} \\ {{\boldsymbol{S}}({\omega _2})} \\ \vdots \\ {{\boldsymbol{S}}({\omega _m})} \end{array}} \right) =\\ &\left( {\begin{array}{*{20}{c}} {{\boldsymbol{W}}({\omega _1}){\exp({ - i2{\text{π}} {{\boldsymbol{t}}_1}{\omega _1}})}}&{{\boldsymbol{W}}({\omega _1}){\exp({ - i2{\text{π}} {{\boldsymbol{t}}_2}{\omega _1}})}}&\cdots&{{\boldsymbol{W}}({\omega _1}){\exp({ - i2{\text{π}} {t_{{N}}}{\omega _1}})}} \\ {{\boldsymbol{W}}({\omega _2}){\exp({ - i2{\text{π}} {{\boldsymbol{t}}_1}{\omega _2}})}}&{{\boldsymbol{W}}({\omega _2}){\exp({ - i2{\text{π}} {{\boldsymbol{t}}_2}{\omega _2}})}}&\cdots&{{\boldsymbol{W}}({\omega _2}){\exp({ - i2{\text{π}} {{\boldsymbol{t}}_{{N}}}{\omega _2}})}} \\ \vdots & \vdots & \ddots & \vdots \\ {{\boldsymbol{W}}({\omega _{{m}}}){\exp({ - i2{\text{π}} {{\boldsymbol{t}}_1}{\omega _{{m}}}})}}&{{\boldsymbol{W}}({\omega _{{m}}}){\exp({ - i2{\text{π}} {{\boldsymbol{t}}_2}{\omega _{{m}}}})}}&\cdots&{{\boldsymbol{W}}({\omega _{{m}}}){\exp({ - i2{\text{π}} {{\boldsymbol{t}}_{{N}}}{\omega _m}})}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{\boldsymbol{r}}_1}} \\ {{{\boldsymbol{r}}_2}} \\ \vdots \\ {{{\boldsymbol{r}}_{{N}}}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{\boldsymbol{N}}({\omega _1})} \\ {{\boldsymbol{N}}({\omega _2})} \\ \vdots \\ {{\boldsymbol{N}}({\omega _{{m}}})} \end{array}} \right)，\end{aligned} $$ (7) 式中，
$ r_{\mathrm{\mathit{k}}}\left(k=1,\ 2,\ \cdots,\ N\right) $ 为界面$ {{N}} $ 个反射系数，$ \omega_{\mathrm{i}}\left(i=1,\ 2,\ \cdots,\ m\right) $ 为参与反演$m $ 个频率成分。将式（7）简写为：
$$ {\boldsymbol{S }}= {\boldsymbol{Gm}} + {\boldsymbol{N}}， $$ (8) 式中，
$ {\boldsymbol{S}}={\Big( {{\boldsymbol{S}}({\omega _1})}\;\;{{\boldsymbol{S}}({\omega _2})}\;\;\cdots\;\;{{\boldsymbol{S}}({\omega _{\mathrm{m}}})} \Big)^{\mathrm{T}}} $ ，$ \boldsymbol{m}=\left(r_1\ r_2\ \cdots\ r_n\right)^{\mathrm{T}} $ 为待反演参数列向量，$ {\boldsymbol{G}} $ 为频率域正演算子。在频率域反演过程中需要分析各频率分量信噪比，选取高信噪比频率分量[16]。考虑到复数域反演过程复杂，将上式改写为如下表达形式：
$$ \left( {\begin{array}{*{20}{c}} {{{\mathrm{Re}}} \left( {\boldsymbol{S}} \right)} \\ {{{\mathrm{Im}}} \left( {\boldsymbol{S}} \right)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{\mathrm{Re}}} \left( {\boldsymbol{G}} \right)} \\ {{{\mathrm{Im}}} \left( {\boldsymbol{G}} \right)} \end{array}} \right){\boldsymbol{m}} + {\boldsymbol{N}} ，$$ (9) 式中，
$ {\boldsymbol{S}}={\Big( {{\boldsymbol{S}}({\omega _1})}\;\;{{\boldsymbol{S}}({\omega _2})}\;\;\cdots\;\;{{\boldsymbol{S}}({\omega _{{m}}})} \Big)^{\mathrm{T}}} $ ，$ {\boldsymbol{m}}={( {{{\boldsymbol{r}}_1}}\;\;{{{\boldsymbol{r}}_2}}\;\;\cdots\;\;{{{\boldsymbol{r}}_{{n}}}} )^{\mathrm{T}}} $ 为待反演模型参数组成的列向量，$ \mathrm{Re}\left(\cdot\right) $ 为实部运算符，$ \mathrm{Im}\left(\cdot\right) $ 为虚部运算符。令向量
$ {\boldsymbol{S}}'={\Big( {{{\mathrm{Re}}} \left( {\boldsymbol{S}} \right)}\;\;{{{\mathrm{Im}}} \left({\boldsymbol{ S}} \right)} \Big)^{\mathrm{T}}} $ ，$ {\boldsymbol{G}}' = {\Big( {{{\mathrm{Re}}} \left( {\boldsymbol{G}} \right)}\;\;{{{\mathrm{Im}}} \left( {\boldsymbol{G}} \right)} \Big)^{\mathrm{T}}} $ 为频率域反演的核矩阵，式（9）可以改写为：$$ {\boldsymbol{S}}'={\boldsymbol{G}}'{\boldsymbol{m}} + {\boldsymbol{N}} 。$$ (10) 基于褶积模型的频率域地震反演通常不包含先验信息的，直接利用频率域地震信号进行求解方程式，最终得到地下地层反射系数序列，这样的求解方式通常是不适定的。因此，在实际中进行频率域反演时，通常引入低频模型约为约束条件，进而得到不适定问题的正则化解。
1.3 基于匹配追踪的时频域反演
Margrave等[17]于1998推导得到地震信号在时间域、频率域和混合域的平稳褶积模型表达式，为了得到更高分辨率的反演结果，将提取的波阻抗模型作为约束参与到地震反演中，首先介绍时频域地震正演方程构建过程，其中
$ {\boldsymbol{G}} $ 表示时间域地震子波矩阵，$ {\boldsymbol{G}}' $ 表示频率域地震子波矩阵，$ {\boldsymbol{C}} $ 为一个下三角矩阵，因此构建匹配追踪反演矩阵$ {{\boldsymbol{G}}_{{\mathrm{new}}}} $ （子波字典），具体可以表示为：$$ {{\boldsymbol{G}}_{{\mathrm{new}}}} = \left( {\begin{array}{*{20}{c}} {\boldsymbol{G}} \\ {{{\boldsymbol{G}}'}} \\ {\boldsymbol{C}} \end{array}} \right),\;\;C = \left( {\begin{array}{*{20}{c}} 1&{}&{}&{} \\ 1&1&{}&{} \\ 1 & 1 &1&{} \\ 1&1&1&1 \end{array}} \right) 。$$ (11) 相应地，如果把时频域的地震信号与模型波阻抗
$ {\boldsymbol{P}} $ 联合起来，其中${\boldsymbol{ S}} $ 为时间域地震信号，$ {\boldsymbol{S}}' $ 为频率域地震信号，可以得到新的已知向量$ {{\boldsymbol{S}}_{{\mathrm{new}}}} $ ，可表述为：$$ {{\boldsymbol{S}}_{{\mathrm{new}}}} = \left( {\begin{array}{*{20}{c}} {\boldsymbol{ S}} \\ {{{\boldsymbol{S}}'}} \\ {\boldsymbol{S}} \end{array}} \right) ，$$ (12) 构建的时频域正演方程为：
$$ {{\boldsymbol{S}}_{{\mathrm{new}}}}={{\boldsymbol{G}}_{{\mathrm{new}}}}{\boldsymbol{m}}+{\boldsymbol{N}}。 $$ (13) 基于
$L_2 $ 范数的最小二乘反演方法，构建目标函数如下：$$ {\boldsymbol{F}}\left({\boldsymbol{ m}} \right) = \min \left( {\big\| {{\boldsymbol{S }}- {\boldsymbol{Gm}}} \big\|_2^2 + \big\| {{\boldsymbol{S}}' - {\boldsymbol{G}}'{\boldsymbol{m}}} \big\|_2^2 + \big\| {{\boldsymbol{P}} - {\boldsymbol{Cm}}} \big\|_2^2} \right)， $$ (14) 简写为：
$$ {\boldsymbol{F}}\left( {\boldsymbol{m}} \right) = \min \left( {\big\| {{{\boldsymbol{S}}_{{\mathrm{new}}}} - {{\boldsymbol{G}}_{{\mathrm{new}}}}{\boldsymbol{m}}} \big\|_2^2} \right) 。$$ (15) 匹配追踪反演方法通过不断迭代分解的方式以达到反演结果稀疏表示目的[18]，反演问题的目标泛函为
$ {\boldsymbol{F}}\left( {\boldsymbol{m}} \right) $ 为：$$ \left\{ {\begin{aligned} & {{\boldsymbol{F}}\left( {\boldsymbol{m}} \right) = \min \left( {{\lambda _1}\big\| {{\boldsymbol{S}} - {\boldsymbol{Gm}}} \big\|_2^2 + {\lambda _2}\big\| {{\boldsymbol{S}}' - {\boldsymbol{G}}'{\boldsymbol{m}}} \big\|_2^2 + {\lambda _3}\big\| {{\boldsymbol{P}} - {\boldsymbol{Cm}}} \big\|_2^2} \right)} \\ &{{{\big\| {\boldsymbol{m}} \big\|}_0} < K,\qquad\displaystyle\frac{{\big\| {{{\boldsymbol{S}}_{{\mathrm{new}}}} - {{\boldsymbol{G}}_{{\mathrm{new}}}}{\boldsymbol{m}}} \big\|_2^2}}{{{{\boldsymbol{S}}_{{\mathrm{new}}}}}} < \xi } \end{aligned}} \right. ，$$ (16) 式中，
$ {\lambda _1} $ 控制时间域地震信号${\boldsymbol{ S}} $ 参与反演的权重，$ {\lambda _2} $ 控制频率域地震信号$ {\boldsymbol{S}}' $ 参与反演的权重，$ {\lambda _3} $ 控制模型参数参与反演的权重，$ K $ 为设定的总迭代次数，$ \xi $ 为残差阈值，当迭代次数大于或等于$ K $ 或残差值小于或等于$ \xi $ ，则反演终止。利用匹配追踪算法求解得到叠后反射系数结果，然后通过积分的方式得到纵波阻抗，表示为：
$$ {\boldsymbol{Z}}(t) = {\boldsymbol{Z}}({t_0})\exp\left( {\int\limits_{{t_0}}^t {2 \cdot{\boldsymbol{ m}}(\tau ){\mathrm{d}}\tau } } \right)。 $$ (17) 1.4 基于同步压缩匹配追踪的地震谱分解方法
匹配追踪算法能够将信号
$ {\boldsymbol{Z}}(t) $ 分解为多个最佳匹配原子的和的形式，对每个时频原子求取其Wigner-Ville分布，再叠加起来就得到原信号的时频谱，对信号$ {\boldsymbol{Z}}(t) $ 的时频表征可以表示为：$$ WZ\left(t,z\right)=\sum\limits_{n=1}^Ma_n^2Wg_{\gamma_n}\left(t,z\right)+\sum\limits_{n=1}^M\sum\limits_{m=1,m\ne n}^Ma_n\cdot\overline{a}_mW\left(\boldsymbol{g}_{\gamma_n},\boldsymbol{g}_{\gamma_m}\right)\left(t,z\right)， $$ (18) 式中，
$ W{g_{{\gamma _{{n}}}}}\left( {t,z} \right) $ 代表最佳匹配子波$ {{\boldsymbol{g}}_{{\gamma _{{n}}}}} $ 的Wigner-Ville分布，式（18）中项为Wigner-Ville分布的交叉干扰项。考虑到时频原子的振幅能量有限支撑的特征，所以通过把时间域的时频原子沿着频率轴走向，然后按照振幅谱的大小展开，就可得出下式中所示的时频能量表达式：
$$ {r_\gamma }\left( {t,f} \right) = \left| {{{\mathop {\boldsymbol{g}}\limits^ \sim }_\gamma }\left( f \right)} \right| \cdot {{\boldsymbol{g}}_\gamma }\left( t \right) \text{，} $$ (19) 式中，
$ {\mathop {\boldsymbol{g}}\limits^ \sim }_\gamma\left( f \right) $ 为的$ {{\boldsymbol{g}}_\gamma }\left( t \right) $ Fourier 变换。考虑到Ricker子波的波形与实际地震子波更为接近，选择构建Ricker子波库对信号进行分解，已知Ricker子波的时域表达式为：$$ {w _\gamma }\left( t \right) = \left( {1 - 2{{\left( {{\text{π}} \xi t} \right)}^2}} \right){\exp\Big({ - {{\left( {{\text{π}} \xi t} \right)}^2}}}\Big)， $$ (20) 其相应的频率域表达式为：
$$ {\mathop{w} \limits^ \sim} _\gamma \left( f \right) = \frac{{2{f^2}}}{{\sqrt {\text{π}} {\xi ^3}}}\exp\Biggr({ - {{\left( {\frac {f}{\xi }} \right)}^2}}\Biggr)。 $$ (21) 将式（20）和式（21）代入式（19）中，即可得Ricker子波的时频表达式为：
$$ {r_\gamma }\left( {t,f} \right) = \big| {{ {\mathop{\boldsymbol{w}} \limits^ \sim}_\gamma }\left( f \right)} \big| \cdot {{\mathop{\boldsymbol{w}} \limits^ \sim}_\gamma }\left( t \right) = \frac{{2{f^2}}}{{\sqrt {\text{π}} {\xi ^3}}}\left( {1 - 2{{\left( {{\text{π}} \xi t} \right)}^2}} \right){\exp\Biggr({ - \left( {\frac {{{f^2}}}{{{\xi ^2}}} + {{\left( {{\text{π}} \xi t} \right)}^2}} \right)}\Biggr)} 。$$ (22) 利用匹配追踪算法对地震信号进行迭代处理，可以得到一系列的最优匹配子波
$ {{\boldsymbol{g}}_{{\gamma _{{n}}}}}\left( t \right)( {{n}} = 1,2, \cdots ,{{M}} ) $ ，然后根据（21）式对每个最优子波进行时频变换求取时频分布，最后将所有的时频分布进行叠加求和，就可以得到原始地震信号新的匹配追踪时频表征结果：$$ r\left(t,f\right)=\sum\limits_{\mathrm{n}=1}^M\boldsymbol{A}_nr_{\gamma_n}\left(t,f\right)=\sum\limits_{n=1}^M\boldsymbol{A}_n\cdot\left|\tilde{\boldsymbol{g}}_{\gamma}\left(f\right)\right|\cdot\boldsymbol{g}_{\gamma}\left(t\right)， $$ (23) 式中，
$ {{\boldsymbol{A}}_{{n}}} $ 为时频原子$ {{\boldsymbol{g}}_{{\gamma _{{n}}}}}\left( t \right) $ 的复数幅度。假定某次迭代搜索得到的最佳Ricker子波的时间和频率参数分别用
$ u $ 和$ \xi $ 表示，则相应构建的二维高斯函数可表示为：$$ {\boldsymbol{G}}\left( {t,f} \right) = \exp \Biggr( { - \left( {\frac{{{{\left( {t - u} \right)}^2}}}{{2\Delta {t^2}}} + \frac{{{{\left( {f - \xi } \right)}^2}}}{{2\Delta {f^2}}}} \right)} \Biggr)， $$ (24) 式中，
$ \Delta t $ 和$ \Delta f $ 分别为时间和频率间隔。通过压缩后时频原子的时频表征可以表示为：$$ {\mathrm{SSTF}}\Big({r_\gamma }\left( {t,f} \right) \Big)= {r_\gamma }\left( {t,f} \right) \cdot {\boldsymbol{G}}\left( {t,f} \right) = \frac{{2{f^2}}}{{\sqrt {\text{π}} {\xi ^3}}}\left( {1 - 2{{\left( {{\text{π}} \xi t} \right)}^2}} \right){\exp\Biggr({ - \left( { \frac{{{f^2}}}{{{\xi ^2}}} + {{\left( {{\text{π}} \xi t} \right)}^2} + \frac{{{{\left( {t - u} \right)}^2}}}{{2\Delta {t^2}}} + \frac{{{{\left( {f - \xi } \right)}^2}}}{{2\Delta {f^2}}}} \right)}\Biggr)}。 $$ (25) 最后将整个地震剖面逐道进行时频表征，并择优抽取固定频率信号，并进行逐道复原，以得到不同频率的单频地震剖面。用
$ {{\boldsymbol{X}}_f} $ 表征基于同步压缩匹配追踪获取的单个频率的信号，那么，某一道地震信号可以表示为：$$ \boldsymbol{X}_{\mathrm{m}}=\int_{f=1}^n\boldsymbol{X}_f\mathrm{d}f， $$ (26) 则整个地震剖面可以表示为：
$$ \boldsymbol{S}_{\mathrm{profile}(t)}=\left(\boldsymbol{X}_1^{\mathrm{T}},\boldsymbol{\ X}_2^{\mathrm{T}},\ \cdots,\boldsymbol{\ X}_m^{\mathrm{T}}\right)\text{，} $$ (27) 其中
$ {{\boldsymbol{S}}_{{\mathrm{profile}}(t)}} $ 为时间域地震剖面，$ {{\boldsymbol{X}}_i} $ 为不同地震道，我们对每一道地震信号进行同步压缩匹配追踪时频展开，并抽取优势频率信号，也即$ {{\boldsymbol{X}}_{f = fi}} $ ，$ {f_i} $ 为优势频率，此时，单频地震剖面则可以表示为：$$ \boldsymbol{S}_{\mathrm{profile}(fi)}=\left(\boldsymbol{X}_{1fi}^{\mathrm{T}},\boldsymbol{\ X}_{2fi}^{\mathrm{T}},\ \cdots,\boldsymbol{\ X}_{m_{fi}}^{\mathrm{T}}\right)。 $$ (28) 2. 二维模型试算
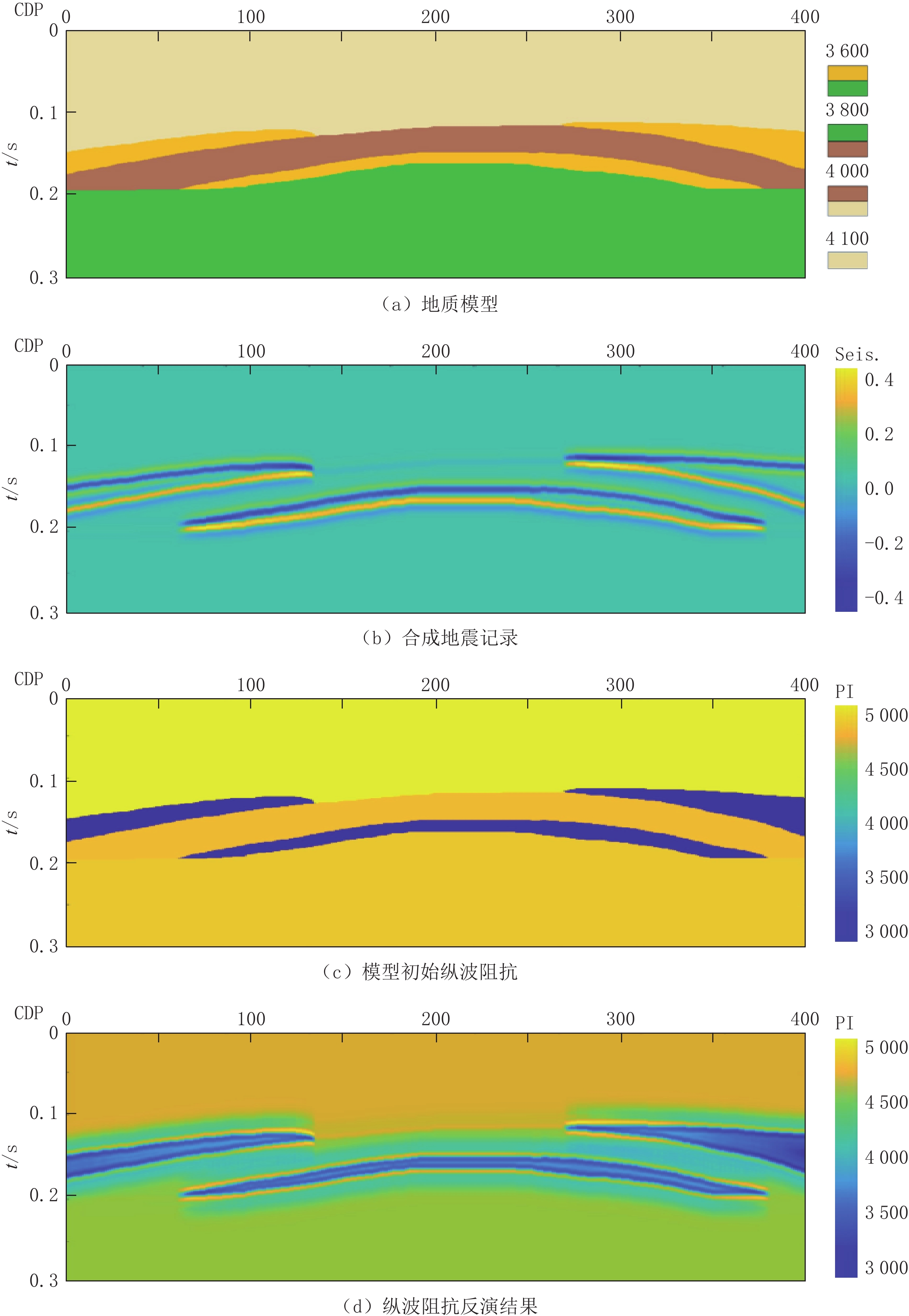
为了验证方法有效性，本文建立二维地质模型进行测试（图1），其中图1（a）为设计的地质模型，图1（b）为合成地震记录，图1（c）为模型原始纵波阻抗，图1（d）为模型反演结果。对比可知，利用匹配追踪时频域反演方法得到的纵波阻抗反演结果具有更好的层位边界保真度，反演结果与地质模型保持高度一致。
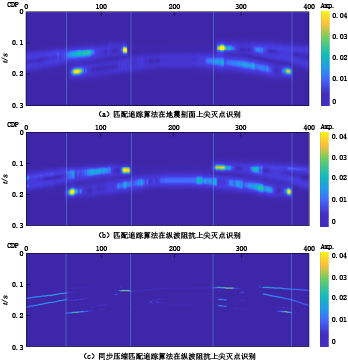
图2为不同匹配追踪算法尖灭点识别效果对比，其中图2（a）为利用匹配追踪算法在地震剖面上进行尖灭点识别结果，图2（b）为利用匹配追踪算法在纵波阻抗反演剖面上进行尖灭点识别结果，图2（c）为利用同步压缩匹配追踪算法在纵波阻抗反演剖面上进行尖灭点识别结果。对比图2（a）和图2（b）可知，由于反演阻抗尖灭点识别结果更加贴近真实尖灭点位置（实线）。相较于利用地震剖面进行尖灭点识别，通过反演结果进行尖灭点识别，其能量更加集中，尖灭位置更加清晰。
![]()
图 2 不同匹配追踪算法尖灭点识别方法对比Figure 2. Comparison of different matching tracking algorithm cusp extinction point图2（b）和图2（c）展示在纵波阻抗剖面上利用匹配追踪算法和同步压缩匹配追踪算法结果对比，分析可知，利用同步压缩匹配追踪算法进行尖灭点识别不仅提高了横向分辨率，也提高了纵向分辨率。
3. 实际资料应用
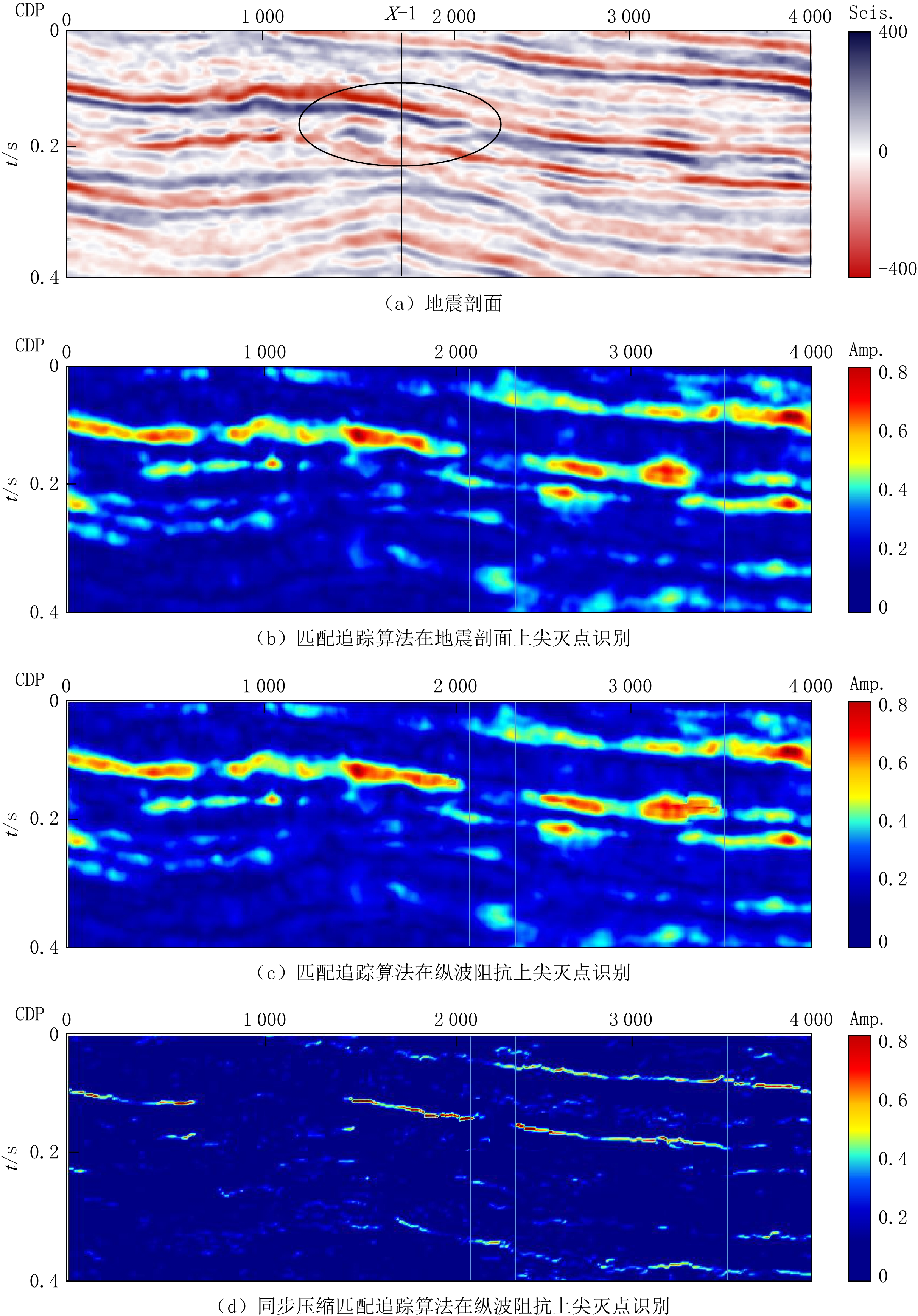
在模型测试基础上，利用实际资料对本文方法的实用性进一步测试。图3（a）所示为实际地震剖面，横坐标代表地震道数，纵坐标代表时间。X-1已钻井揭示椭圆圈处为砂岩储层。图3（b）为匹配追踪算法在地震剖面上尖灭点识别结果，图3（c）为匹配追踪算法在纵波阻抗上尖灭点识别结果，图3（d）为同步压缩匹配追踪算法在纵波阻抗上尖灭点识别结果。
![]()
图 3 不同尖灭点识别方法在实际地震数据测试Figure 3. Different cusp extinction point identification methods tested on real seismic data通过对比发现，本文提出的基于匹配追踪的时频联合域反演方法得到的纵波阻抗，相较于常规反演结果分辨率更高，且相较于常规的谱分解方法，引入的同步压缩匹配追踪算法提高了时频分辨率和能量聚焦性。对比传统岩性尖灭识别方法，该方法得到的尖灭点识别结果能量更加集中，尖灭位置更加清晰。
4. 结论
借助同步压缩匹配追踪时频分辨率和能量聚焦性双重优势开展砂体尖灭识别研究，主要获得以下几方面认识。
（1）相较于传统时频分析方法，同步压缩匹配追踪具有更高的时频聚焦性，在单频剖面提取上更具优势，纵向、横向双重提高时频谱的分辨能力。
（2）通过模型和实际资料对比验证，相较于常规地震剖面信息，纵波阻抗反演结果在尖灭点识别上，横向连续性及边界保真度均相对提高，同步压缩匹配追踪求取的单频亮点进步提高尖灭点识别精准度。
-
![]()
图 2 不同匹配追踪算法尖灭点识别方法对比
Figure 2. Comparison of different matching tracking algorithm cusp extinction point
-
[1] WIDESS M B. Quantifying resolving power of seismic systems[J]. Geophysics, 1982, 47(8): 1160−1173. DOI: 10.1190/1.1441379.
[2] 王军, 张中巧, 滕玉波, 等. 基于地震瞬时谱分析的三角洲砂体尖灭线识别技术[J]. 断块油气田, 2011, 18(5): 585−588. WANG J, ZHANG Z Q, TENG Y B, et al. Pinch-out boundary recognition technology of delta sand body based on seismic instantaneous spectral analysis[J]. Fault-Block Oil & Gas Field, 2011, 18(5): 585−588. (in Chinese).
[3] 王志杰. 东营凹陷小营油田沙二段砂体尖灭线地震描述技术[J]. 石油地球物理勘探, 2012, 47(2): 305−308. WANG Z J. Seismic description on reservoirs pinchout line of the second members of Shahejie formation in Xiaoying, Dongying Depression[J]. Oil Geophysical Prospecting, 2012, 47(2): 305−308. (in Chinese).
[4] 张军华, 范腾腾, 杨勇, 等. 永进油田西山窑组砂岩储层尖灭线的地震识别技术[J]. 石油物探, 2016, 55(2): 261−270. ZHANG J H, FAN T T, YANG Y, et al. Seismic recognition techniques for sandstone reservoir pinch-out line in Xishanyao formation in Yongjin Oil field[J]. Geophysical Prospecting for Petroleum, 2016, 55(2): 261−270. (in Chinese).
[5] 张繁昌, 李传辉, 印兴耀. 三角洲砂岩尖灭线的地震匹配追踪瞬时谱识别方法[J]. 石油地球物理勘探, 2012, 47(1): 82−88. ZHANG F C, LI C H, YIN X Y. Delta fringe line recognition based on seismic matching pursuit instantaneous spectral characteristics[J]. Oil Geophysical Prospecting, 2012, 47(1): 82−88. (in Chinese).
[6] 汪瑞良, 张文珠, 刘徐敏, 等. 基于匹配追踪时频谱计算的砂体尖灭线检测方法[J]. 物探化探计算技术, 2017, 39(6): 799−807. WANG R L, ZHANG W Z, LIU X M, et al. The method of thin sand pinch-out boundary detection via T-F spectrum based on matching pursuit[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2017, 39(6): 799−807. (in Chinese).
[7] 李振春, 刁瑞, 韩文功, 等. 线性时频分析方法综述[J]. 勘探地球物理进展, 2010, 33(4): 239−246. LI Z C, DIAO R, HAN W G, et al. Review on linear time frequency analysis methods[J]. Progress in Exploration Geophysics, 2010, 33(4): 239−246. (in Chinese).
[8] 高静怀, 汪文秉, 朱光明. 小波变换与信号瞬时特征分析[J]. 地球物理学报, 1997, 40(6): 821−832. GAO J H, WANG W B, ZHU G M. Wavelet transform and instantaneous attributes analysis[J]. Chinese Journal of Geophysics, 1997, 40(6): 821−832. (in Chinese).
[9] 吴小羊, 刘天佑. 基于时频重排的地震信号Wigner-Ville分布时频分析[J]. 石油地球物理勘探, 2009, 44(2): 201−205. WU X Y, LIU T Y. Time-frequency analysis on Wigner-Ville distribution of seismic signal based on time-frequency rearrangement[J]. Oil Geophysical Prospecting, 2009, 44(2): 201−205. (in Chinese).
[10] 陈林, 宋海斌. 基于经验模态分解的地震瞬时属性提取[J]. 地球物理学进展, 2008, 23(4): 1179−1185. CHEN L, SONG H B. Seismic instantaneous attribute extraction based on empirical mode decomposition[J]. Progress in Geophysics, 2008, 23(4): 1179−1185. (in Chinese).
[11] ROBINSON E A. Predictive decomposition of time series with applications to seismic exploration[D]. Massachusetts: Massachusetts Institute of Technology (MIT), 1954.
[12] LEVY S, FULLAGAR P K. Reconstruction of a sparse spike train from a portion of its spectrum and application to high-resolution deconvolution[J]. Geophysics, 2012, 46(9): 1235−1243.
[13] SACCHI M D, VELIS D R, COMÍNGUEZ A H. Minimum entropy deconvolution with frequency-domain constraints[J]. Geophysics, 1994, 59(6): 938−945. DOI: 10.1190/1.1443653.
[14] PORTNIAGUINE O, CASTAGNA J. Spectral inversion: Lessons from modeling and Boonesville case study[C]//Seg Technical Program Expanded Abstracts, 2005.
[15] CHOPRA S, CASTAGNA J, PORTNIAGUINE O. Thin-bed reflectivity inversion[J]. Seg Technical Program Expanded Abstracts, 2006, 25(1): 3541.
[16] 印兴耀, 李坤, 宗兆云, 等. 时频联合域贝叶斯地震反演方法[J]. 石油物探, 2017, 56(2): 250−260. YIN X Y, LI K, ZONG Z Y, et al. Seismic inversion in joint time-frequency domain based on Bayesian scheme[J]. Geophysical Prospecting for Petroleum, 2017, 56(2): 250−260. (in Chinese).
[17] MARGRAVE G F. Theory of nonstationary linear filtering in the Fouier domain with application to time variant filtering[J]. Geophysics, 1998, 63:244-259.
[18] 李坤, 印兴耀, 宗兆云, 等. 基于快速匹配追踪的混合域地震稀疏反演方法[J]. 中国石油大学学报(自然科学版), 2018, 42(1): 50−59. LI K, YIN X Y, ZONG Z Y, et al. Seismic sparse inversion in mixed-domain utilizing fast matching pursuit algorithm[J]. Journal of China University of Petroleum (Edition of Natural Science), 2018, 42(1): 50−59. (in Chinese).
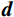
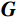
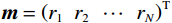
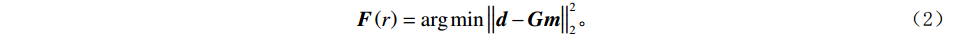
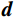
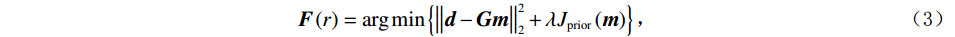
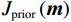
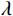
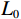
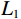
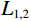
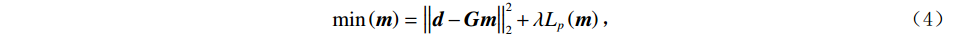
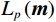
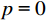
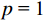
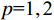
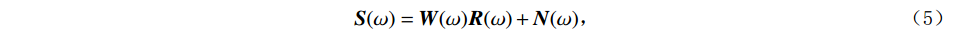
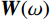
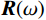
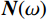
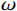
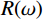
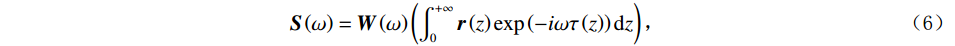
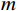
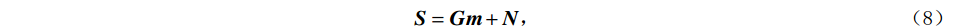
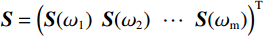
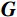
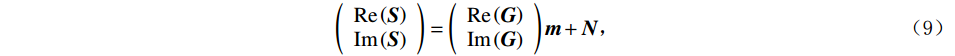
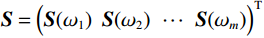
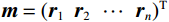
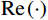
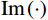
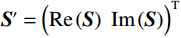
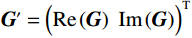
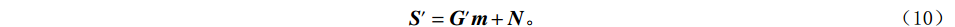
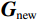
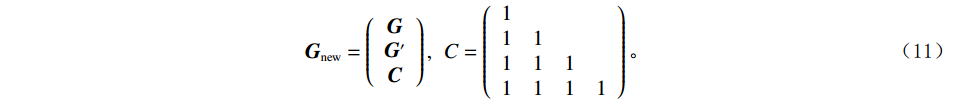
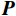
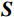
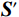
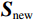
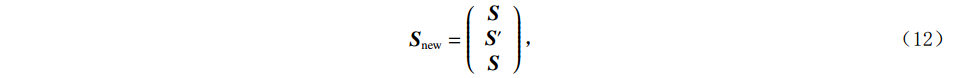
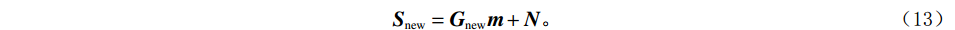
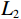
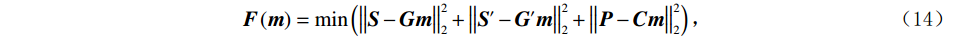
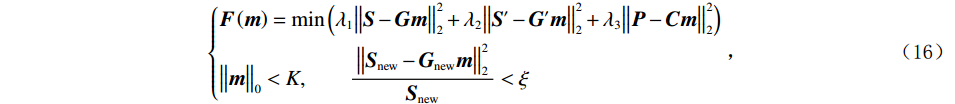
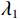
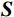
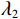
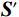
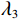
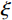
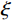
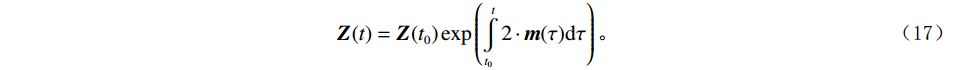
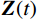
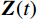
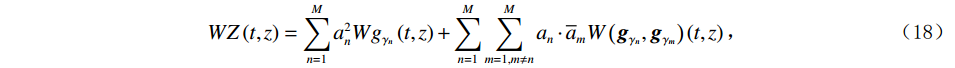
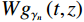
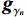
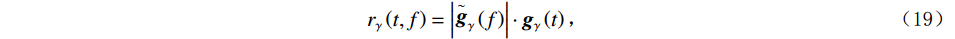
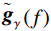
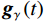
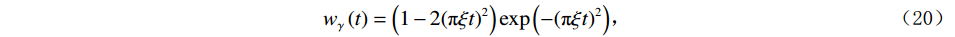
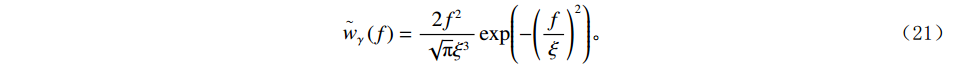
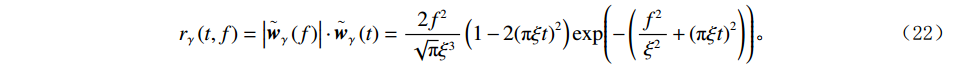
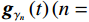
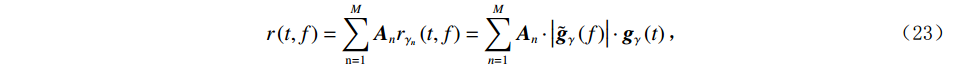
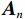
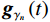
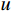
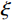
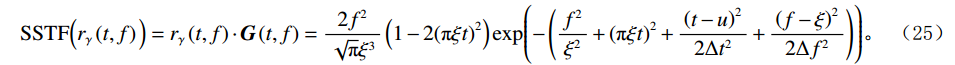
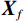
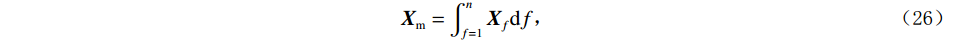
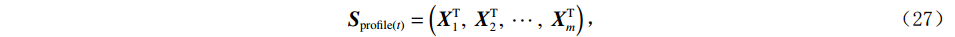
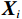
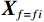
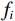
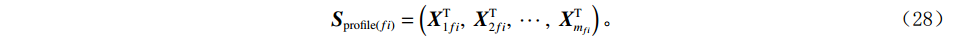
下载:
计量
- 文章访问数: 140
- HTML全文浏览量: 40
- PDF下载量: 28
