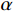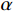Application of Multi-scale Curvature in Fault Interpretation of K Oilfield in Bohai Sea
-
摘要:
复杂断裂系统是影响K油田开发的关键问题，常规属性（如相干属性、纹理属性等）在解释断层方面存在局限，特别是微小断层的识别和多尺度复杂断裂系统的成像效果较差，并且容易受噪音干扰。为了解决这些问题，本文采用保边平滑滤波（EPS）技术对地震资料进行预处理，既能有效压制随机噪音，提高信噪比，又保持地震数据的边缘结构信息。在此基础上，利用时频波数域多尺度算子实现多尺度曲率分析。这种组合创新方法在渤海K油田的断裂识别和解释中表现良好，为开发井位的顺利实施提供有力指导，帮助规避风险断层，提高了开发效率和成功率。
Abstract:Ascertaining the curvature attributes of fault systems depends on the partial derivative, which is easily disturbed by noise. Therefore, an edge-preserving de-noising filter is used to preprocess seismic data, effectively improving the signal-to-noise ratio and maintaining information on the edge structure. On this basis, multi-scale curvature analysis is realized by using multi-scale operators in a time–frequency–wavenumber domain. This attribute fully considers the complexity of geological structure and fault distribution characteristics. Small-scale curvature attributes can better represent subtle changes in geological structure, which is conducive to avoiding risk faults in the oilfield development phase. Large-scale curvature attributes are conducive to the macro analysis of fault distribution characteristics, which plays an important role in regional exploration. The multi-scale curvature method has been well applied to fault interpretation in the Bohai K Oilfield and has proven beneficial to the drilling of oilfield development wells.
-
海洋石油资源储量丰富，具备很大的勘探和开发潜力，但海洋石油勘探开发与陆地有所不同。由于受到天气及海水等自然条件限制，海上油田的勘探比陆地油田要更加复杂、难以预测，这对海底地层的储层勘探开发技术也有着更高的要求[1]。
渤海K油田位于沙垒田凸起的低幅断裂背斜区域，由于地处多个构造单元的交汇处，受到郯庐走滑断裂、张蓬走滑断裂的双重影响，油田区域内断裂系统十分发育，直接影响油田的储层特征和流体特征。
由于常规属性断裂系统的解释存在不确定性，使得油田的勘探和开发变得更为困难，一方面油气的分布和流动规律因断层的不确定性变得难以准确预测和把握，导致油田开发过程中需要更多的勘探井和测试井，增加开发成本和风险；另一方面在复杂断裂区域进行钻井作业时，受到断层解释不确定性的影响，将面临更多的风险和挑战。因此，为更好地分析油田区域内的断裂特征，为油气勘探开发工作服务，本文尝试多尺度曲率分析技术。
曲率属性能够有效描述地层的弯曲程度，与地震反射体的弯曲程度相对应，对于断层、裂缝、弯曲河道以及地层之间的褶皱信息有较好的刻画作用，该属性在断裂预测以及地质异常体刻画方面得到了广泛应用。
Lisle[2]探讨了地质露头中，高斯曲率与张开裂缝之间的关系。Ericsson[3]分析了曲率与油气生产动态的联系，并提出曲率成像有利于常规构造和地质异常体解释。Roberts[4]首次把曲率属性用于地震资料的构造解释，对曲率属性进行了全面分类，并提出了二维层面曲率的详细计算方法。Al-Dossary等[5]为了充分利用地震资料的空间几何特征，在沿层二维曲率计算的基础上，提出了三维体曲率计算方法，并把分波数傅里叶变换应用于曲率属性的多尺度计算，使检测结果体现了一定的尺度特征，该方法很快便得到了较好的推广应用。Chen[6]把小波变换用于多尺度曲率的求取，并把不同尺度的曲率结果进行有效融合，实现了对宏观构造信息以及局部构造细节的清晰展示。然而，这些研究忽视了曲率属性对噪音的敏感性以及对地震数据处理方法的依赖性。
针对这些问题，杨威等[7-8]将结构方位滤波用于地震数据的预处理，在有效压制地震数据噪音的同时，较好地保持了地震资料的边缘信息，提高了对地质构造细节的刻画精度。郑静静[9]将曲波变换理论应用于曲率属性的提取，提出了裂缝发育方位预测方法并在实际应用中取得了较好效果，有效预测了裂缝分布范围。高京华[10]在2015年利用中值滤波对视倾角数据体进行预处理，对原始构造细节进行了有效保护。张文等[11]提出使用递归滤波器和构造导向滤波器提高相干和曲率属性的计算效率、改善计算结果。胡建波等[12]在2023年从影响沿层曲率刻画断裂层位的敏感源进行分析，明确了曲率属性精细解释构造中适用的断裂类型、断裂方位角和断裂带频段，以进一步提升曲率属性对微小断裂的刻画效果。
这些研究主要依赖于构造导向滤波类方法来进行预处理，但也存在着一定的局限性：①在一定程度上减少噪音，但效果依赖于局部构造的平滑性和方向性，在噪音水平较高的情况下，可能无法充分抑制噪音；②在处理复杂地质构造的边缘时，可能会出现边缘效应，导致边界区域数据处理不准确，边缘细节丢失；③适用于地震反射特征相对平滑且具有明确方向性的区域，对于高度复杂或非线性的地质构造，适应性较差；④主要在单一尺度上进行处理，对于多尺度复杂断裂系统的成像效果有限。
为此本文尝试将保边平滑技术与多尺度分析相结合，该技术能够更好地保留地震数据的边缘信息，适应性更强，能够适用复杂地质构造，尤其是复杂断裂。
1. 理论与方法
多尺度曲率分析是一种从不同尺度上对构造地质体进行分析的方法，可以有效地揭示地震数据中蕴含的断裂走向及展布信息。与传统的相干属性相比多尺度曲率分析具有以下几方面的优势：
（1）多尺度性质。多尺度曲率分析可以在不同的尺度下对地质体进行分析，从而更全面地识别小断裂。相比之下，传统的相干属性通常只在固定的频率范围内进行分析，可能会错过一些尺度上的小断裂信息。
（2）准确性。多尺度曲率分析采用了傅里叶正变换和逆变换等数学工具，可以更准确地计算曲率，提高小断裂识别的准确性。而传统的相干属性在处理复杂地质结构时可能存在一定的误差，特别是对于具有多尺度特征的地质体。
（3）灵活性。多尺度曲率分析通过调整不同的尺度和步长参数，可以灵活地适应不同地质环境的需求，实现对小断裂特征的精细识别。相比之下，传统的相干属性可能受到频率范围的限制，灵活性较差。
（4）前塑性变形的揭示。多尺度曲率分析可以揭示断裂前的塑性变形程度，这为判断断裂类型提供重要的参考依据。相比之下，传统的相干属性通常难以提供关于地质体前塑性变形的信息。
1.1 多尺度曲率分析
多尺度曲率分析是一种在地形地貌分析中非常有用的方法，它可以从不同尺度上对地质构造进行深入分析。通过使用高精度的地震勘探数据，我们可以更准确地了解地质体内部的结构特征。通过应用多尺度曲率计算方法可以在不同的尺度上分析地震数据，从而更好地识别和判断断裂的位置和性质。在进行多尺度曲率分析时，我们通常采用两种主要的导数求取方法：网格差分法和分波数傅里叶变换法。
网格差分法是一种基于网格的导数计算方法，通过计算相邻网格点之间的微分来估计曲率的值。这种方法在计算曲率时具有简单、直观的优点，并且可以很容易地应用于不规则的网格数据。然而，网格差分法可能会受到网格大小和形状的影响，因此在处理复杂的地震数据时需要谨慎选择合适的网格大小和形状。
分波数傅里叶变换法是一种基于频率域的导数计算方法，通过将地震数据转换到频率域并计算不同波长的傅里叶系数来估计曲率。这种方法在处理复杂地形数据时表现卓越，能够更精确地估算曲率值，从而提供对地质构造更细致、更准确的认知。然而，分波数傅里叶变换法需要更多的计算资源和更复杂的算法，因此在处理大规模的地震数据时可能会受到限制。
总体来说，多尺度曲率分析作为一种高效的地质构造分析手段，为我们提供了深入了解地质体内部构造和断裂特性的有力工具。借助高精度的地震勘探数据以及精确的导数计算技术，能够更加准确地识别和判断断裂的位置与性质，为油气田的勘探与开发提供坚实的技术支撑。
1.1.1 网格差分法
三维空间中某点的曲率是由该点及其相邻点的空间曲面方程得到，利用最小二乘法逼近拟合N次曲面方程的表达式为：
$$ z(x,y) = \sum\limits_{i = N}^0 {\left( {\sum\limits_{j = i}^0 {{C_{i.j - 1}}{x^i}{y^{j - i}}} } \right)} 。 $$ (1) 当N=2时，二次曲面拟合方程为：
$$ z(x,y) = a{x^2} + b{y^2} + cxy + dx + ey + f \text{，} $$ (2) 其中
$ {z_{i,j}} $ 为网格结点上的值，$ \Delta x $ 、$ \Delta y $ 为道间距。在实际应用中最常使用的是最大正曲率$ {K_{{\mathrm{pos}}}} $ 以及最小负曲率$ {K_{{\mathrm{neg}}}} $ ，最大正曲率和最小负曲率有利于描述断层、裂缝和褶皱[13-15]。$$ K_{\mathrm{pos}}=\left(a+b\right)+\left(\left(a-b\right)^2+c^2\right)^{\tfrac{1}{2}}， $$ (3) $$ {K_{{\mathrm{neg}}}} = \left( {a + b} \right) - \left( {{{\left( {a - b} \right)}^2} + {c^2}}\right) ^{\tfrac{1}{2}}。 $$ (4) 1.1.2 分波数傅里叶变换法
分波数傅里叶变换的目的是在不同波数尺度上进行分析和处理信号或者函数，特别是进行微分操作和曲率分析时，通过在频率域中处理，可以更方便实现这些操作。利用傅里叶变换的微分性质，可以得到信号在频率域表达式为[16-17]：
$$ \frac{{{\mathrm{d}}u}}{{{\mathrm{d}}x}} = {F^{ - 1}}\bigg( {i{k_x}\,F\Big( {u(x)} \Big)} \bigg)， $$ (5) $ F $ 与$ {F^{ - 1}} $ 分别为傅里叶变换与傅里叶逆变换，$ {k_x} $ 为波数。在此基础上对公式（5）引入分波数导数：$$ {F_\alpha}\left( {\frac{{\partial u}}{{\partial x}}} \right) = i{({k_x})^\alpha}\,F\Big( {u({{x}})} \Big)\,T\left( {{k_x}} \right) \text{，} $$ (6) 其中
$ \alpha $ 为分波数系数，$ T({k_x}) $ 为升余弦函数。根据傅里叶逆变换定义可知：$$ \frac{{{\partial ^\alpha}u}}{{\partial {x^\alpha}}} = \frac{1}{{2{\text π} }}\int\limits_{ - \infty }^\infty {i{{\left( {{k_x}} \right)}^\alpha}} \,\hat u\left( {{k_x}} \right)\,T\left( {{k_x}} \right)\,{\exp({i{k_x}x}}){\mathrm{d}}{k_x} \text{，} $$ (7) 其中
$ \hat u({k_x}) $ 为$u(x) $ 的傅里叶变换。此时，取升余弦函数$ T({k_x}) $ 为$ \cos \left( {\displaystyle\frac{{{\text π} {k_x}}}{{2 k}}} \right) $ 则得到：$$ \frac{{{\partial ^\alpha}u}}{{\partial {x^\alpha}}} = \frac{1}{{2{\text π} }}\int\limits_{ - \infty }^\infty {i{{\left( {{k_x}} \right)}^\alpha}}\, \hat u\left( {{k_x}} \right)\,\cos \left( {\frac{{{\text π} {k_x}}}{{2k}}} \right)\,{\exp({i{k_x}x}}){\mathrm{d}}{k_x} 。 $$ (8) 当取二阶导时，即
$\alpha $ =2时，方程可写为：$$ \frac{{{\partial ^2}u}}{{\partial {x^2}}} = \frac{1}{{2{\text π} }}\int\limits_{ - \infty }^\infty { - {{\left( {{k_x}} \right)}^2}} \,\hat u\left( {{k_x}} \right)\,\cos \left( {\frac{{{\text π} {k_x}}}{{2K}}} \right)\,{\exp({i{k_x}x}}){\mathrm{d}}{k_x} 。 $$ (9) 最大正负曲率对应公式（9）二阶导数极值，通过公式（9）参数的调整，即可得到不同尺度的曲率属性。
1.2 保边平滑滤波
Luo[18]首次提出了保边平滑（EPS）算法，并把该方法用于地震数据的边缘检测；Liu等[19]在此基础上提出了基于最小二乘法的EPS算法，拓展了该方法在地震资料处理中的应用范围；Albinhassan等[20]设计了能够应用于三维地震数据的保边滤波器，使得该滤波方法得到了有效推广；张莹芳等[21]提出一种用于稀疏图像重建的双约束迭代 CT重建算法，对重建图像进行稀疏正则化，达到保边平滑的效果；周俊捷等[22]提出了基于分块字典学习理论的地震数据去噪方法。与传统去噪方法采用固定形状（如正方形或立方体）的滤波器不同，EPS滤波能够根据地震同相轴的具体产状动态调整滤波器的形状。这种灵活性使得EPS滤波在消除随机噪音的同时，能够更好地保持地质构造的边缘细节，从而提供更准确的地质解释[23-24]，该方法目的是找到一个平滑图像u，使其在某种意义上与原始图像I相似，并且u在局部区域内是平滑的。
设加权最小二乘滤波的目标函数为：
$$ E(u) = {\sum\limits_i {\left( {{u_i} - {I_i}} \right)} ^2} + \lambda \sum\limits_{i,j} {{w_{ij}}} {\left( {{u_i} - {u_j}} \right)^2} \text{，} $$ (10) 其中，目标函数包含两个部分：数据保真项
$ {\displaystyle\sum\nolimits_i {\left( {{u_i} - {I_i}} \right)} ^2} $ ；平滑项$ \lambda \displaystyle\sum\nolimits_{i,j} {{w_{ij}}} {\left( {{u_i} - {u_j}} \right)^2} $ ；$ {u_i} $ 是滤波后图像在像素i处的值；$ {I_i} $ 是原始图像在像素i处的值；$ {w_{ij}} $ 是权重，通常依赖于像素i和j的相似度；$ \lambda $ 是正则化参数，控制数据保真项和平滑项之间的平衡。为得到最小目标函数，对
$ {u_i} $ 求导并设导数为零：$$ \frac{{\partial E(u)}}{{\partial {u_i}}} = 2\left( {{u_i} - {I_i}} \right) + 2\lambda \sum\limits_j {{w_{ij}}} {\left( {{u_i} - {u_j}} \right)^2} = 0 。 $$ (11) 通过求解这个线性系统，我们可以得到滤波后的图像u，在实际应用中，加权最小二乘滤波常用于图像去噪和细节增强。
渤海K油田断裂构造广泛发育，但工区现有地震资料信噪比低，有效信号常被噪音所淹没。油田区域内的大断层相对容易识别，但小断层的成像却较为模糊，地层之间的接触关系难以准确判断（图1（a））。然而，通过EPS滤波技术对地震数据进行预处理后，不仅显著提高地震资料的信噪比，还极大地改善小断层的成像品质，使得地层展布特征更加清晰可辨（图1（b））。
为了凸显EPS滤波方法在处理地震数据中的优势，我们对该区域的地震数据进行曲率属性提取，并以最大正曲率作为具体的分析示例。图2（a）显示，虽然利用原始地震数据求取的最大正曲率可以识别主断裂的展布特征，但是由于曲率属性对噪音比较敏感，小断层以及裂缝等有效地质信息与噪音混杂在一起，严重影响该区断裂展布特征的有效识别。而EPS滤波以后的最大正曲率则较好地压制噪音干扰，清晰刻画小断层的展布特征。但是由于该方法计算的曲率细节过于丰富，在实际应用中需要去伪存真判别断裂的可靠性，并不是每一个尺度的断裂都需要精细解释出来，细节太丰富反而不利于地震资料的解释。
![]()
图 2 EPS滤波前后最大正曲率属性对比图Figure 2. Comparison of maximum positive curvature attributes pre- and post-EPS filtering因此在实际应用中，随着油田勘探开发的稳步推进，需要分析不同尺度的曲率属性，并选择合适尺度的曲率属性对断裂展布特征进行精细研究，从而达到较好的构造识别效果。
2. 应用实例
渤海矿区K油田主要构造特征是披覆于潜山之上的被断层复杂化的披覆背斜构造，该构造自南向北逐渐抬升，形成西北高、东南低的构造格局，内部被次生断层划分为多个断块。区域内发育3类断层，第1类为长期活动断层，主要呈北东东走向和近东西走向，控制构造格架和圈闭发育规模，平面延伸较长；第2类为走滑断层，走向以近南北为主，活动时间长、平面延伸长，起到分区分带作用；第3类为晚期层间活动断层，断层晚期活动，规模小，难于识别。依据断层类型进行统计、分类，区域内64％ 的断层为第3类断层，断层横向变化快，展布范围小，对地层连续性有较大影响。
文中所述多尺度曲率分析方法在目标油田区域内断层预测上具有较大的优势，基于该区域断裂特点将该方法应用于渤海K油田，取得较好的断层预测和识别效果。
随着勘探开发的不断深入，尤其是在油田区域，由于断裂展布特征的复杂性增加，常规属性（如相干属性、纹理属性等）已经难以满足对断裂精确识别的需求；特别是在开发阶段，小尺度的地质构造对注采关系产生直接且重要的影响。因此，我们必须转向更为精细的尺度来研究曲率属性，以便更准确地刻画断裂展布；这要求我们不仅要分析不同尺度下的曲率属性，还要从中找到最适合描述当前地质条件的尺度，进而为断裂展布的精细研究提供更为准确和可靠的基础。
以最大正曲率为例，当
$ \alpha = 1 $ 时，此时短波长曲率属性能够展现出丰富的细节，清晰地刻画出局部小断层以及较小尺度构造的延伸方向和分布范围；然而随着分波数系数$ \alpha $ 值逐渐减小，虽然南北向的大尺度地质构造得到了较好的识别、刻画，但是局部小断层已经较难刻画。在勘探阶段，工作重点更偏向于储量的评估，此时断层的研究尺度相对较大。在这种背景之下ODP开发方案中的井位被部署在A处（图3（c））。但在ODP方案实施过程中，为确保开发井之间的注采连通关系并有效规避潜在风险断层，我们对工区内的地震资料进行了多尺度曲率分析。利用
$ \alpha $ 值较大，断裂尺度较小的曲率属性对断裂展布特征进行了深入分析，得到如图3（a）和图3（b）所示的平面曲率属性。对比两图所示的地震曲率平面属性，可以明显观察到在曲率尺度减小的情况下，原始地震曲率属性平面上的A点附近地震方差数据出现了明显差异。具体来说，A点附近曲率属性展现出不光滑、差异性增强的特征，而B点附近地震曲率属性则呈现出平整的一致性特性。这些因局部小尺度断层发育而引起的曲率属性变化特征，已经在工区内的实钻井中得到了验证。因此，依据以上认识，推断A点附件50 m以内存在两条小尺度断层，遂将开发井从A点处平移到B点处（图3（a）），最终B处开发井顺利实施，并喜获高产。![]()
图 3 不同尺度情况下对应的最大正曲率属性Figure 3. Maximum positive curvature attribute corresponding to different scales3. 结论
本文通过对该方法的研究，得到结论如下：
（1）曲率的计算依赖于微分的求取，对噪音非常敏感，因此需要选择合适的方法对地震资料进行预处理，进而有效提高曲率计算精度，增加微小断裂识别能力；
（2）EPS滤波去噪根据地震同相轴产状，在有效消除噪音的同时，最大限度实现对边缘信息的保真，利用该方法可以有效提高断层分辨能力；
（3）多尺度体曲率属性尤其是小尺度曲率属性可以更好地识别地质构造的细微变化，有利于开发阶段规避风险断层。
渤海K油田工区内受郯庐走滑断裂和张蓬走滑断裂的影响，地质构造复杂。这种复杂性导致地震数据中地层结构的解释困难，尤其容易出现地震轴反射杂乱的情况。因此，有效识别断裂体系成为该区域研究的重点，清晰的断裂系统方案可以为储层研究提供有力依据。
应用多尺度曲率算法处理后的地震资料，对断裂系统的识别具有显著优势，该算法的有效性经实际地震资料验证，能够高精度地识别断裂。这项工作在实际应用中指导了32口开发井的部署，对指导油田有效开发具有重要意义。
-
![]()
图 2 EPS滤波前后最大正曲率属性对比图
Figure 2. Comparison of maximum positive curvature attributes pre- and post-EPS filtering
-
[1] 魏天罡, 李福强, 李久, 等. 基于匹配追踪的反射系数反演在渤海PL油田的应用[J]. 海洋技术学报, 2022, 41: 69−75. DOI: 10.3969/j.issn.1003-2029.2022.02.009. WEI T G, LI F Q, LI J, et al. The application of reflection coefficient inversion based on matching pursuit in Bohai PL Oilfield[J]. Journal of Ocean Technology, 2022, 41: 69−75. DOI: 10.3969/j.issn.1003-2029.2022.02.009. (in Chinese).
[2] LISLE R J. Detection of zones of abnormal strains in structures using gaussian curvature analysis[J]. AAPG Bulletin, 1994, 78: 1811−1819.
[3] ERICSSON J B. Facies and curvature controlled 3D fracture models in a cretaceous carbonate reservoir, Arabian Gulf[J]. Geological Society, London, Special Publications, 1998, 147: 299−312. DOI: 10.1144/GSL.SP.1998.147.01.20.
[4] ROBERTS A. Curvature attributes and their application to 3D interpreted horizons[J]. First Break, 2001, 19(2): 85−100. DOI: 10.1046/j.0263-5046.2001.00142.x.
[5] AL-DOSSARY S, MARFURT K J. 3D volumetric multispectral estimates of reflector curvature and rotation[J]. Geophysics, 2006, 71(5): 41−51. DOI: 10.1190/1.2242449.
[6] CHEN X H. The algorithm of 3D multi-scale volumetric curvature and its application[J]. Applied Geophysics, 2012, 9(1): 65−72. DOI: 10.1007/s11770-012-0315-7.
[7] 杨威, 贺振华, 陈学华. 三维体曲率属性在断层识别中的应用[J]. 地球物理学进展, 2011, 26(1): 110−115. DOI: 10.3969/j.issn.1004-2903.2011.01.011. YANG W, HE Z H, CHEN X H. Application of three-dimensional volumetric curvature attributes to fault identification[J]. Progress in Geophysics, 2011, 26(1): 110−115. DOI: 10.3969/j.issn.1004-2903.2011.01.011. (in Chinese).
[8] 杨威. 曲率属性分析及应用[D]. 成都: 成都理工大学, 2011. [9] 郑静静. 基于曲波变换和贝叶斯理论的储层预测方法研究[D]. 东营: 中国石油大学(华东), 2011. [10] 高京华. 基于离心窗扫描的地震几何属性提取方法研究[D]. 东营: 中国石油大学(华东), 2015. [11] 张文, 伍新明, 漆杰. 地震几何属性的快速算法实现[J]. 地球物理学报, 2023, 66(8): 3374−3390. DOI: 10.6038/cjg2022Q0367. ZHANG W, WU X M, QI J. Fast computation of seismic geometric attributes[J]. Chinese Journal of Geophysics, 2023, 66(8): 3374−3390. DOI: 10.6038/cjg2022Q0367. (in Chinese).
[12] 胡建波, 刘之的, 段玉顺, 等. 小尺度断裂沿层曲率敏感性研究[J]. 地质与勘探, 2023, 59(4): 0891−0900. DOI: 10.12134/j.dzykt.2023.04.015. HU J B, LIU Z D, DUAN Y S, et al. Sensitivity of small-scale faults curvature along the layer[J]. Geology and Exploration, 2023, 59(4): 0891−0900. DOI: 10.12134/j.dzykt.2023.04.015. (in Chinese).
[13] CHOPRA S, MARFURT K J. Curvature attribute applications to 3D surface seismic data[J]. The Leading Edge, 2007, 26(4): 404−414. DOI: 10.1190/1.2723201.
[14] CHOPRA S, MARFURT K J. Volumetric curvature attributes add value to 3D seismic data interpretation[J]. The Leading Edge, 2007, 26(7): 856−867. DOI: 10.1190/1.2756864.
[15] CHOPRA S, MARFURT K J. Emerging and future trends in seismic attributes[J]. The Leading Edge, 2008, 27(3): 298−318. DOI: 10.1190/1.2896620.
[16] 王伟. 地震几何属性识别断层技术研究及应用[D]. 东营: 中国石油大学(华东), 2009. [17] 张军华, 王伟, 谭明友, 等. 曲率属性及其在构造解释中的应用[J]. 油气地球物理, 2009, 7(2): 1−7. ZHANG J H, WANG W, TAN M Y, et al. Curvature attributes and their application in structural interpretation[J]. Petroleum Geophysics, 2009, 7(2): 1−7. (in Chinese).
[18] LUO Y. Edge preserving smoothing and its applications in seismic edge detection[J]. The Leading Edge, 2002, 21: 136−141. DOI: 10.1190/1.1452603.
[19] LIU Y, LUO Y. Edge preserving smoothing for oblique images[J]. Geophysical Research Letters, 2003, 30(13).
[20] ALBINHASSAN N M, LUO Y, MOHAMMED N. 3D edge preserving smoothing and applications[J]. Geophysics, 2006, 71(4): 5−11.
[21] 张莹芳, 陈平, 潘晋孝. 基于全变分与交替保边扩散平滑的稀疏角度CT重建算法[J]. 中国体视学与图像分析, 2022, 27(2): 113−121. [22] 周俊捷, 吴相伶, 李文杰, 等. 基于分块字典学习理论的地震数据去噪[J]. CT理论与应用研究, 2022, 31(5): 557−566. DOI: 10.15953/j.1004-4140.2022.31.05.03. ZHOU J J, WU X L, LI W J, et al. Denoising of seismic data based on block dictionary learning theory[J]. CT Theory and Applications, 2022, 31(5): 557−566.10.15953/j.1004-4140.2022.31.05.03. (in Chinese).
[23] 赵岩, 贺振华, 黄德济. 基于保边去噪的高精度相干体分析应用研究[J]. 长江大学学报(自然科学版), 2009, 6(4): 169−171. ZHAO Y, HE Z H, HUANG D J. High-accuracy coherence analysis based on edge-preserving smoothing[J]. Journal of Yangtze University (Natural Science Edition), 2009, 6(4): 169−171. (in Chinese).
[24] 范桃园, 杨长春. 自适应三维地震保边界去噪方法及应用[J]. 石油地球物理勘探, 2009, 44(5): 558−563. DOI: 10.3321/j.issn:1000-7210.2009.05.007. FAN T Q, YANG C C. 3D adaptive seismic edge-preserving smoothing and its application[J]. Oil Geophysical Prospecting, 2009, 44(5): 558−563. DOI: 10.3321/j.issn:1000-7210.2009.05.007. (in Chinese).
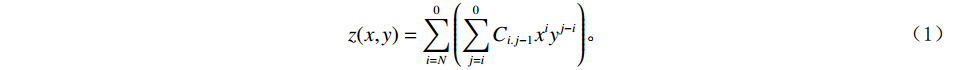
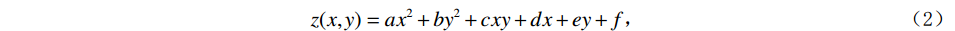
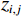
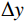
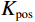
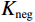
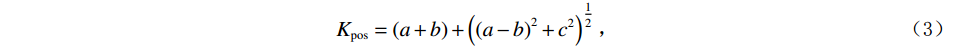
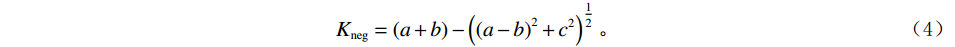
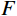
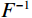
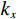
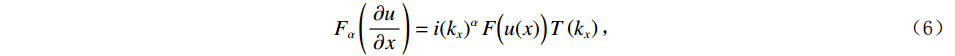
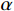
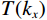
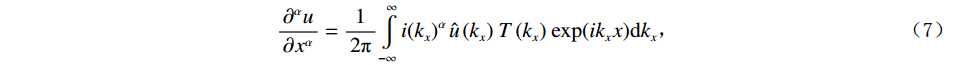
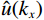
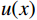
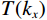
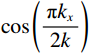
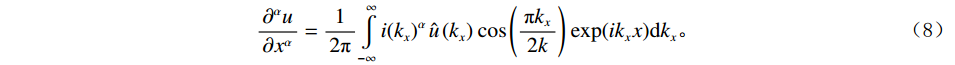
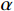
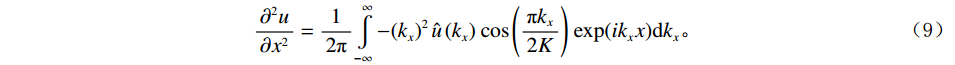
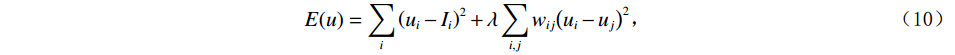
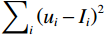
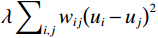
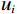
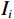
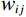
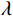
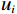
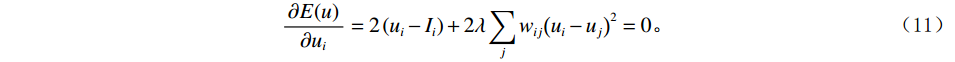
下载:
计量
- 文章访问数: 116
- HTML全文浏览量: 22
- PDF下载量: 22
