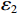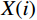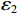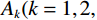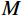Quantitative strata calibration method based on the reflection coefficient proportions
-
摘要:
层位标定是层位解释和储层分析的基础,目前常用的标定方法将地层界面与波峰、波谷等进行比对,注重地层界面的时深关系,将地层界面与特定的波峰、波谷或者过零点相关联,不能反映地层横向变化,误差大,无法满足精细解释的需求。本文提出了一种反射系数占比计算方法,在合成地震记录标定的基础上,根据测井声波时差曲线和密度曲线,计算出地层界面反射系数序列,进而根据地震子波计算各反射系数对指定的波峰或波谷的振幅贡献占比,建立地震波形与反射系数组成和振幅占比的定量关系。通过对该定量关系的分析,建立地层界面与井旁地震道波峰、波谷之间的对应关系,将地震数据的目标层位同相轴与其贡献占比最大的反射界面进行对应,从而确定地层分界面对应的敏感相位,选择敏感相位能够更加准确地对目标层位进行横向追踪和岩性对比分析。将该方法应用于胜利油田胜坨探区沙三下1砂组的追踪,提高了砂体解释的精度,将钻井吻合率由75%提高到92%,表明该方法在开发地震解释中具有广泛的应用前途。
Abstract:Strata calibration is the foundation of stratigraphic interpretation and reservoir analysis. Current used calibration methods qualitatively compare geological interfaces with wave peaks, troughs, and other features, thus emphasizing the depth-time relationship of geological interfaces. These methods associate geological interfaces with specific wave peaks, troughs, or zero-crossing points but fail to reflect lateral changes in stratigraphy. This results in significant errors and insufficient interpretation. The present study proposes a method for calculating the contribution ratio of the reflection coefficients. Based on the calibration of the synthetic seismic records, the reflection coefficient sequence of the geological interfaces was computed using sonic travel time and density curves from well logging. Subsequently, the contribution ratio of each reflection coefficient to the specified wave peaks or troughs was calculated based on the seismic waveforms. This established a quantitative relationship between the seismic waveforms and the composition of the reflection coefficients and their amplitude contributions. Through the analysis of this quantitative relationship, a correspondence between geological interfaces and wave peaks or troughs with well seismic traces was established. The target stratigraphic level in the seismic data was then correlated with the reflection interface that had the maximum contribution ratio to determine the sensitive phase corresponding to the stratigraphic boundary interface. By selecting the sensitive phase, it was possible to track and analyze the lateral variations in the target stratigraphic level and lithology more accurately. The application of this method to the Shasan Lower Sandstone of the Shengtuo exploration area in the Shengli Oilfield improved the accuracy of sandbody interpretation, increasing the drilling matching rates from 75% to 92%. This indicates the broad potential applicability of the proposed method for the seismic interpretation of reservoir development.
-
0. 引言
近年来,随着油气勘探开发技术的不断发展,油气勘探工作越来越向隐蔽性油气藏发展,目标尺度越来越小,油气勘探目标逐步转向低幅度构造和薄层。以东营凹陷北部陡坡带为例,发育了多种沉积类型的砂砾岩扇体,具有“小、碎、深、薄”的特点,成为目前勘探开发的重点和难点。胜坨探区位于东营凹陷北部陡坡带中段,北邻陈家庄凸起,勘探程度较高,其中沙三砂体是关注的主要目标,如何找到其在地震剖上的响应,并据此勾画砂体平面分布成为油气勘探开发的关键。
砂体解释中地震层位标定是最为基础和重要的一项工作,是沟通测井、地质体和地震之间的桥梁[1],是地震资料构造解释的基础[2−3]。常用的层位标定方法包括两类:一类是人工合成地震记录法标定;另外一类是利用VSP测井数据进行标定[4−5]。其中人工合成地震记录法标定是目前最常用的层位标定方法。高精度合成记录的制作是人工合成记录标定的前提,张雪建等[6]将合成地震记录从时间域推导到了深度域,陈裕明等[7]使用变频子波进行非均匀采样求取反射系数来增加合成地震记录质量。李希元[8]等通过确定各界面反射子波作用延续时间,利用插值及连续子波叠加的方法合成地震记录。这些方法均不同程度提高了合成记录的精度。但由于地震速度和测井速度之间存在差异,这类方法的人为干预较强,进行精细的储层标定时精度较低。垂直地震剖面(简称VSP)通过地表激发地震波,井下不同深度接收信号的方式,导致在接收信号时同时具有时间域和深度域的信息,可以用于层位标定。单独利用VSP资料叠加剖面进行标定极性精度较低,VSP资料处理结果对标定结果影响较大[9−10]。王轶等[11]对合成地震记录层位标定和VSP层位标定进行总结,指出两者在单一标定过程中的局限性,并提出利用VSP资料合成地震记录再进行标定的方法提高层位标定质量。李本才等[12]将VSP层位标定方法利用到薄层砂体识别上,取得了较好效果。LUO等[13]分析了井深误差与地震资料误差的分布特征, 提出了一种基于动态深度翘曲(DDW)算法的井间地震标定方法,实现对地震深度的误差校正。
随着油气勘探目标尺度越来越小,油气勘探环境也日益复杂,地震解释人员通过地震剖面中的同相轴认识地下构造层的难度也随之增加。充分利用经过精细保幅地震处理与高精度成像的地震处理资料,解决同相轴与构造层的错误匹配、提高砂体刻画精度,标定起到至关重要的的作用。传统标定方法将合成地震记录与井旁地震道对比,建立时深关系,将反射界面映射到特定的同相轴。然而地震剖面上的同相轴与地层界面之间不是一一对应关系,或者说同相轴并不只对应单一界面反射波,特别是当油气勘探目标为薄层时,相邻地层界面的反射子波叠加在一起形成特定的反射同相轴。从地层界面反射系数的角度来说,同一个同相轴接收到相邻多个地层分界面反射系数引起的子波响应。因此简单地将波峰或者波谷标定为时深关系所确定的某一特定地层分界面,存在误差。为了解决上述问题,本文提出了一种定量计算反射系数占比方法,该方法在传统合成地震记录标定的基础上,进一步计算目标范围内各反射系数对目标同相轴的贡献占比,标定出对波峰或波谷反射贡献最大的主要反射界面位置以及相邻干扰地层界面位置,实现复杂储层地震响应特征的定量分析。将该方法应用于东营凹陷北带胜坨地区的勘探中,精准地标定了沙三下1砂组反射所在的同相轴,提高了砂体横向追踪对比精度,取得了较好的地质效果。
1. 反射系数占比估算方法原理
1.1 合成记录制作方法
反射系数占比估算方法是在常规合成记录标定法的基础上,对地震记录的波峰与波谷进行定量标定,常规合成记录标定方法如下:
通过声波时差测井曲线和密度测井曲线计算波阻抗曲线
${Z_i}$ ,利用计算出的波阻抗曲线${Z_i}$ 通过波阻抗曲线计算时间域反射系数${R_i}$ ,使用褶积模型计算合成地震记录$s(t)$ :$$ {Z}_{i}={\rho }_{i}\times {v}_{i}, \text{ }i=1,2,\cdots, n\text{,} $$ (1) $$ {R}_{i}=({Z}_{i+1}-{Z}_{i})/({Z}_{i+1}+{Z}_{i})\text{,} $$ (2) $$ s(t)={\displaystyle \sum _{i=1}^{N}{R}_{i}w(t-{t}_{0i})}。 $$ (3) 式中
${t_{0 i}}$ 表示分界面的双程旅行时。根据公式(3)可知某一时刻$t$ 的地震波场是各地层分界面反射系数与地震子波相乘后$t$ 时刻数值的总和。将合成地震记录与井旁地震道进行对比标定,一般要求两者的吻合率达到80%以上。合成记录制作过程中,由于地震子波一般为有限延续长度的脉冲波,因而某一时刻的波场值与有限范围内的地层分界面的反射系数相关。因而对于特定的波峰或者波谷,可以计算其附近范围内各地层分界面的反射子波对其贡献。
1.2 反射系数占比计算
在地震数据中,当地层存在薄层时,根据常规合成记录制作方法,某一时刻的波场值与有限范围内的地层分界面的反射系数相关。通过计算各地层分界面的发射系数占比可以更好的标定目标层位的深度及范围。
可以设某一波峰或者波谷的极值点对应的振幅值和时间分别为
$A$ 和$t$ ,附近范围(大概为实际地震资料的一个主周期)内存在$K$ 个地层分界面,对应的反射系数和双程旅行时分别为${R_i}$ 和${t_{0 i}}$ 则反射系数占比定义为:$$ \phi (i)=\frac{{R}_{i}\omega (t-{t}_{i})}{A},i=1,2,\cdots,K。 $$ (4) 根据公式(4)计算得到波峰或者波谷的反射系数占比,可知其主要反映的地层分界面,将该地层分界面标定到相应的同相轴上。利用这种方法进行砂体标定并开展砂体横向对比追踪,得到的砂体分布范围更加合理。
在实际生产中,采用图1所示的流程图进行反射系数占比的计算。由于测井曲线采样率非常小,每个采样点均能得到一个反射系数,一般这些反射系数幅值都很小,主要反映地层内部的非均质性。只有在两个地层的分界面处反射系数数值才比较大,代表波阻抗的突变。因此对根据测井资料计算的反射系数序列,设置阈值
${\varepsilon _1}$ ,拾取大于${\varepsilon _1}$ 的${R_i}$ 得到主要反射系数${R_k}(k = 1,2,3,\cdots,m)$ ,这相当于对测井曲线进行方波化处理,排除极小的反射系数对结果影响。地震记录中存在幅值非常小的波不便于对比追踪。因此设置阈值
${\varepsilon _2}$ ,只拾取合成地震记录$X(i)$ 中幅值大于${\varepsilon _2}$ 的波峰或波谷,记为${A_k}(k = 1,2, 3,\cdots,M)$ ,其中$M$ 为波峰和波谷的总数。在传统标定的基础上,选择目标层位标定附近的波峰或波谷,根据公式(4)计算反射系占比。通过这些反射系数占比找到目标层位反射系数影响最大的波峰或者波谷,作为层位对比追踪的同相轴,该同相轴对目标层位最敏感,其变化也主要反映目标层位的变化。因此采用这样定量标定方法更有利于砂体横向追踪对比。
2. 数值模拟分析
通过一组含薄砂体的理论模型来展示反射系数占比的计算,验证反射系数占比的必要性和有效性。如图2所示,建立一个泥页岩背景下的薄砂体模型,设定上层泥岩速度为
2500 m/s,下层泥岩速度为3000 m/s,砂砾岩体速度为3500 m/s。砂砾岩体为目标地层,上下泥岩之间的分界面为砂砾岩体的干扰界面。选取主频为26 Hz的雷克子波进行正演模拟,地震剖面如图2下部所示。对比正演模拟的地震剖面与介质模型可以看出,当目标地层与干扰界面距离较小时,两者的波峰波谷会叠加在一起:当目标地层与干扰界面距离为0 m时,地震数据的波峰可以与砂砾岩体形成很好的对应;当目标层位与干扰界面距离为10 m时,干扰层与砂砾岩体的波峰近乎叠加在一起,尽管波峰与砂砾岩体的顶界面完全对应,但是该波峰也是干扰界面的反射,其横向变化受到两重因素的影响,与砂砾岩体的关系存在不确定性;当目标地层与干扰界面距离为20 m时,目标层位与干扰界面的反射波叠加在一起形成了复杂的复波,且复波的波峰位置与目标地层并不一致;当目标地层与干扰界面距离为40 m时,目标地层的波形与干扰界面的波形可以较为清楚的分开,且地层的对应关系明显。由此可见,在强背景干扰层下,砂体发育的位置不同,地震调谐响应特征存在差异。所以常规的地震层位标定方法在面对砂体发育位置靠近干扰层情况时,不能进行准确的标定。
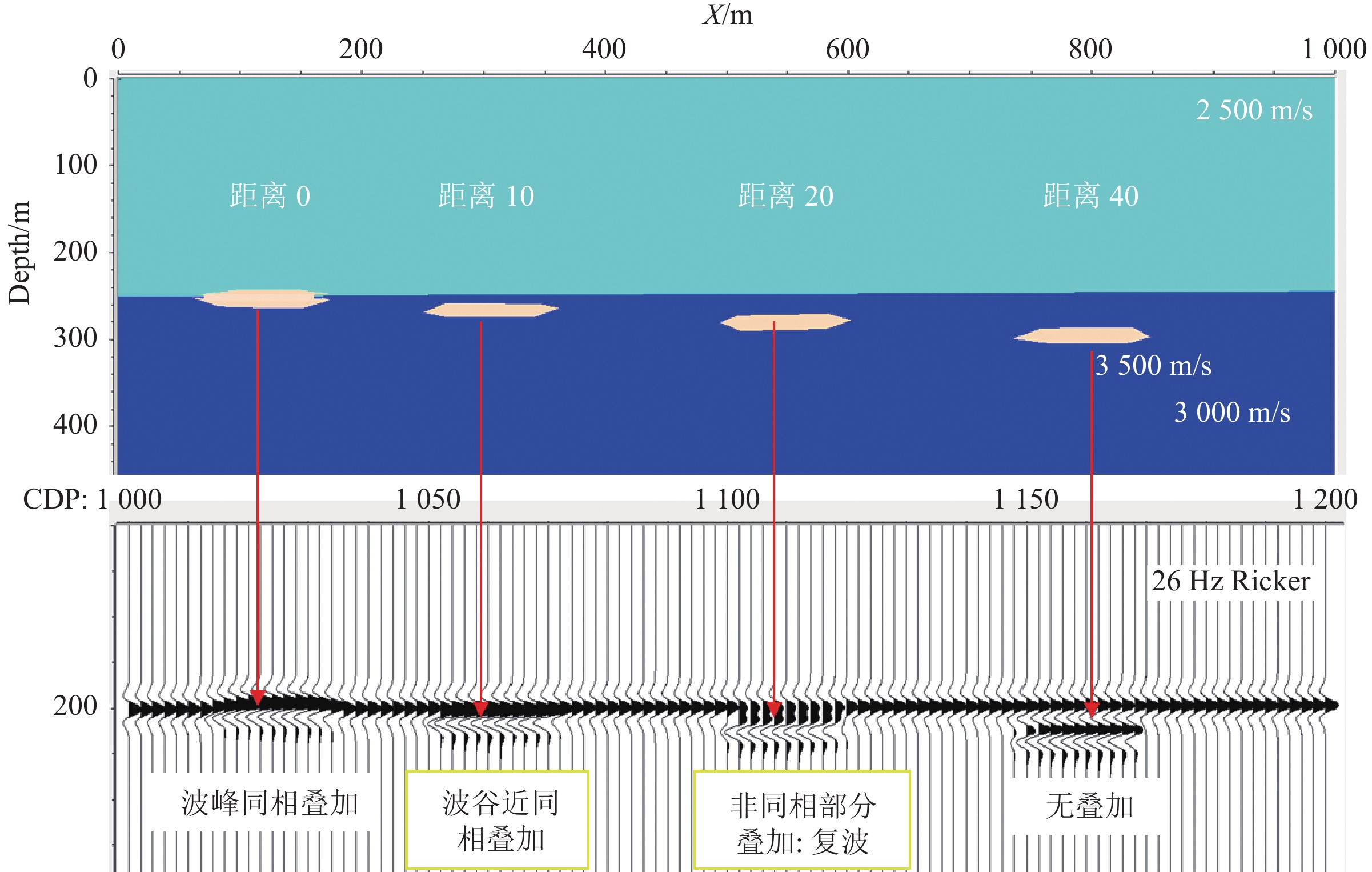
图3(a)为构建的一维岩性模型,其中浅层泥岩(黑色)速度为
2500 m/s,深层泥岩速度为3000 m/s,砂岩(黄色条带)速度为3500 m/s。使用25 Hz的Ricker子波合成地震记录,计算结果如图3(b)(绿线)所示。传统标定将砂体顶界标定为波峰,实际上波峰介于泥岩段界面和砂岩顶界面之间。波谷主要是砂岩反射的能量,更能直接反映砂体的阻抗。因此对该模型来说在砂体横向追踪中解释波谷意义更加明确。为了定量表述波峰、波谷与相邻地层分界面反射系数的关系,需要计算反射系数占比。假设地下有7个地层界面反射系数,如图4b中蓝点所示,从下到上七个反射系数的数值分别为−0.3、−0.3、0.3、0.1、−0.1、0.0和0.4。采用主频为30 Hz的雷克子波进行褶积,得到图4c所示的合成地震记录。
图4c中从下到上可以识别处5个波谷或者波峰,不妨编号为波谷1、波峰1、波谷2、波峰2和波谷3。利用公式(4)计算7个反射系数对波峰或者波谷的占比,结果如表1所示。根据表中反射系数占比可知,波谷1受到了下方四个反射系数的共同影响,且反射系数2对其振幅贡献最大,为
0.4647 ,因此波谷1更加直接地反映了反射系数2对应的地层分界面。在波谷2处,同一深度,反射系数5与其直接对应,但从反射系数占比看,反射系数5对波谷2的占比为0.2854 ,而射系数7的占比最大,为0.4672 。这一结果也表面,当地层中存在薄层时,反射波的同向轴与反射系数在深度上并不是一一对应的,因此传统合成地震记录标定主要确定了时深关系,而本文的反射系数占比分析则进一步确定具体反射界面对波峰或者波谷的贡献,从而确定适合于目标地层追踪的最有利波峰或者波谷。表 1 反射系数占比计算结果Table 1. Calculation results of reflection coefficient proportions−0.3 −0.3 0.3 0.1 −0.1 0 0.4 波谷1 0.1959 0.4647 0.3257 0.0138 0 0 波峰1 0.0904 0.2610 0.6474 − 0.0474 0.0486 0 0 波谷2 0 − 0.0013 0.0844 0.1642 0.2854 0 0.4672 波峰2 0 0 0 − 0.0012 0.0419 0 0.9593 3. 胜坨探区沙三下1砂组定量标定
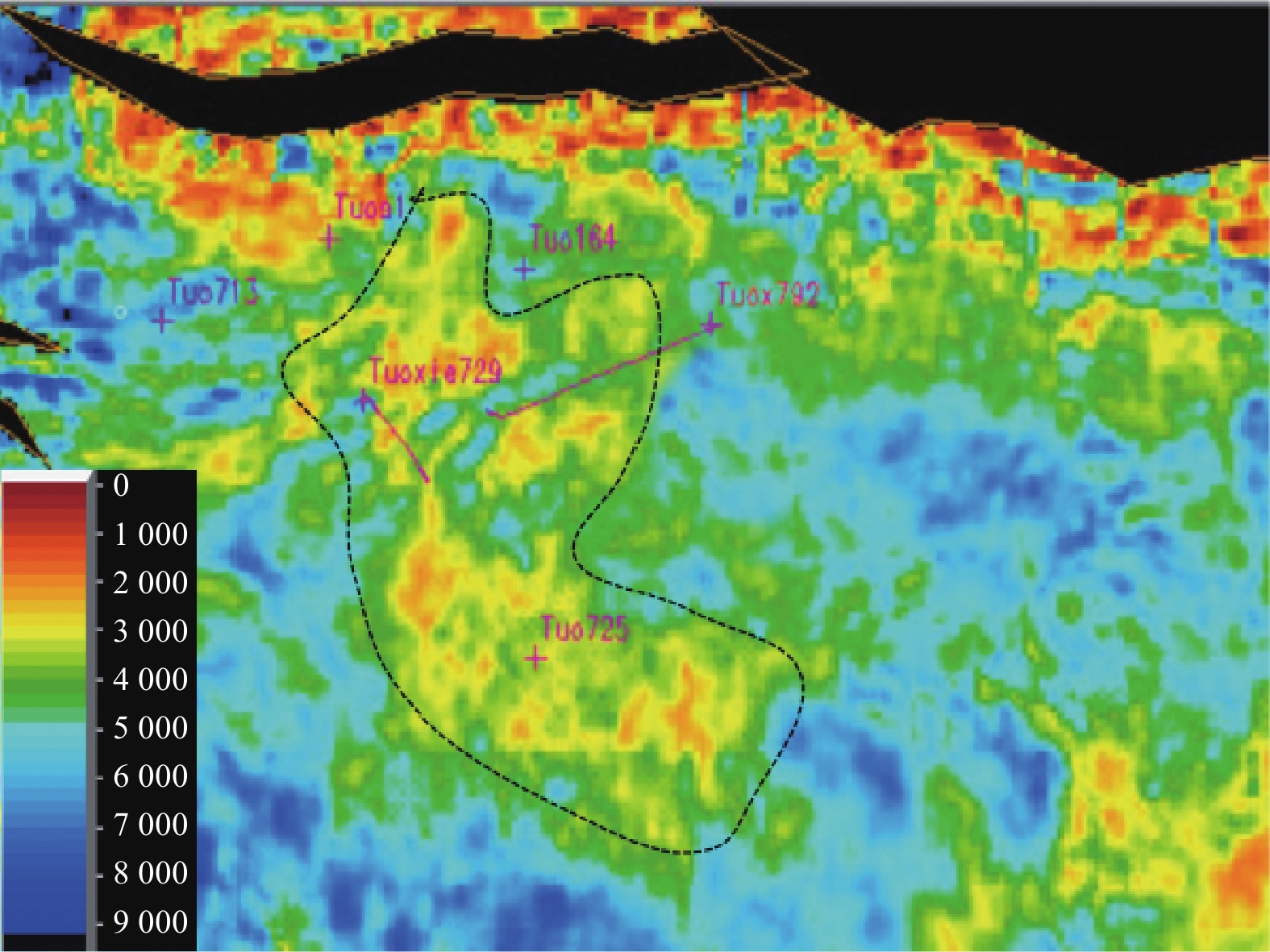
胜坨探区沙河街组储层较薄,砂体主要位于沙三下1砂组顶部,发育一冲积扇(图5中黄色区域)。
研究区部署T725成功后,通过常规标定认为在
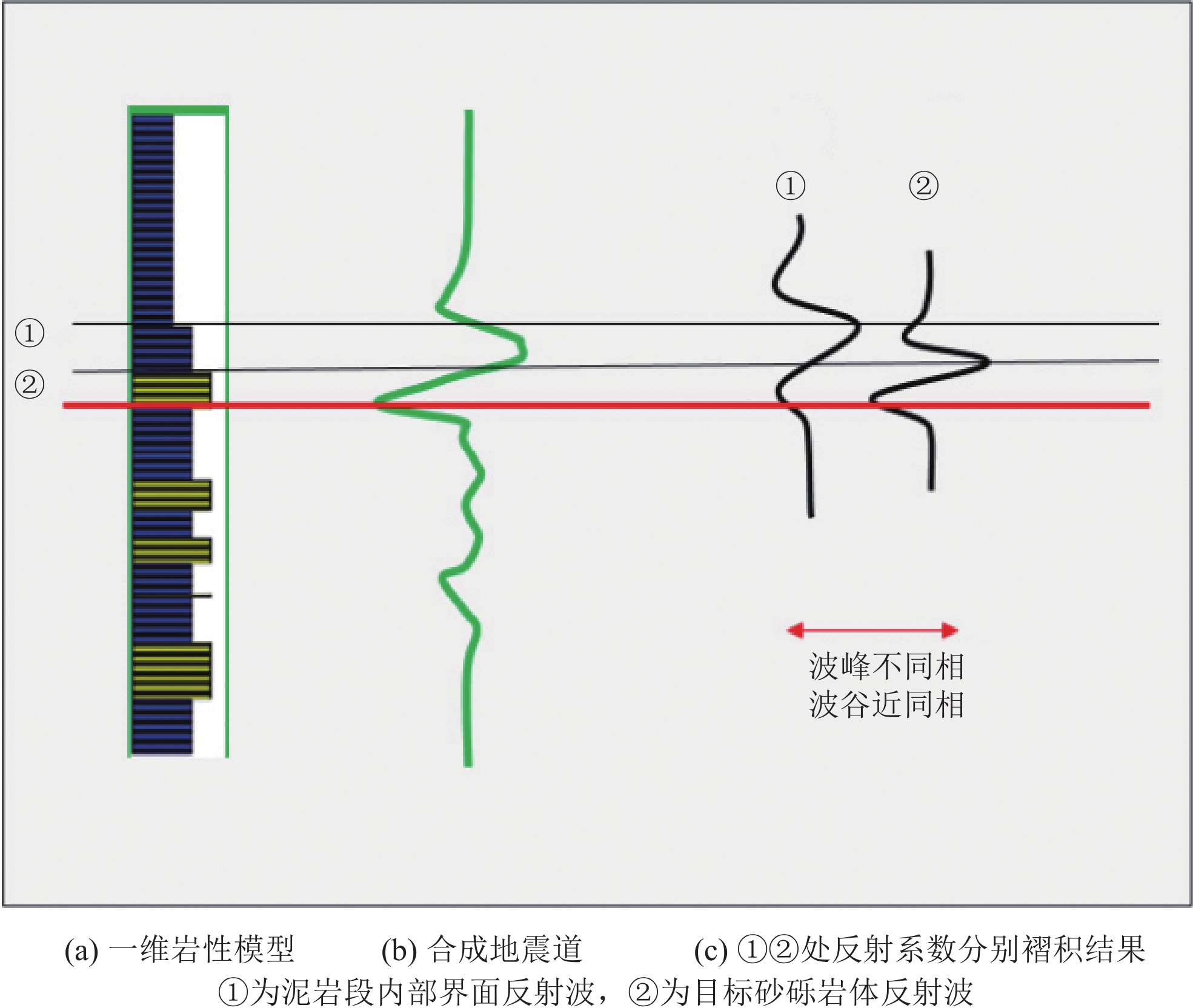
2950 Ms处为储层反射,针对该反射同相轴提取了均方根振幅属性(图7),并进行了砂体追踪解释,后续部署了Tx729、Tx792井、T164井,钻探结果,Tx729获得成功,而Tx792井和T164井未钻遇砂体而失利。为了精细落实储层,明确失利的原因,在研究区开展反射系数占比法分析。通过传统合成地震记录标定,采用28 Hz,长度60 ms、正极性、0.001 ms采样率的雷克子波,与反射系数进行褶积得到合成地震记录,并得到测井主要地层反射界面对应的反射波的位置(图6),图6在左向右为3口井的结果。
在坨725砂体反射界面(图6中标注为21)之上,存在一强的反射界面(图6中标注为20),形成强反射振幅,而储层反射掩盖在该强反射振幅之下,形成相对较弱的复波。坨斜725井,储层反射特征与此一致,砂体反射(图6中标注为16)之上存在一更强的反射界面,在合成记录上,储层为强反射(图6中标注为15)之下的中弱复波反射。坨斜792,未钻遇砂体,基本没有复波特征。
以上分析表明,该区泥岩地层中存在一中等强度反射,(图5中的黄色解释虚线),储层反射为该反射之下的复波。尽管在时深关系上储层的地震响应对应该中强度反射,实际上则是其下的较弱的波谷能更加准确反演砂体展布。
根据反射系数占比分析,砂体反射对该反射下20 ms的波谷贡献率最大,为此避开强反射波峰,提取波谷振幅特征(图8),得到了新的属性图,在新属性图上,对砂体进行追踪解释,解释结果与井位部署结果更加相符,储层分布表现的更加合理。对研究区5口井沙河街沙层组全部层位进行基于反射系数占比的敏感相位分析,进而提取敏感相位的瞬时振幅属性,用于砂体圈定,经过小层统计分析发现,钻井吻合率由原来的75%提高到了92%,大幅度提高了砂体预测精度。
4. 结论
传统合成地震记录标定主要关注的是时深关系,在层位解释和构造图绘制中具有重要的用途。然而在地层岩性解释中更关注的是哪个波峰或者波谷更能反映砂体的分布,因此本文提出的反射系数占比可以用来定量标定砂体反射的敏感相位,进而提高地震属性分析等对砂体的刻画能力。
在砂体比较厚或者地震分辨率比较高时,传统标定方法能够满足砂体解释的需求;在地层厚度小于地震分辨率时,则需要采用本文方法。本文方法主要适用于多种岩性组成的薄互层、存在强背景干扰层、弱反射层等地区的地震勘探。
5. 致谢
中石化胜利油田勘探开发研究院为研究提供了实际资料,对实际资料综合分析、反射系数占比定量分析方法提出了许多建设性意见,在此表示衷心感谢。
-
表 1 反射系数占比计算结果
Table 1 Calculation results of reflection coefficient proportions
−0.3 −0.3 0.3 0.1 −0.1 0 0.4 波谷1 0.1959 0.4647 0.3257 0.0138 0 0 波峰1 0.0904 0.2610 0.6474 − 0.0474 0.0486 0 0 波谷2 0 − 0.0013 0.0844 0.1642 0.2854 0 0.4672 波峰2 0 0 0 − 0.0012 0.0419 0 0.9593 -
[1] 吴奎, 周东红, 吴俊刚, 等. 合成地震记录制作在油气勘探中的应用[J]. 海洋石油, 2012, 32(1): 28-32. DOI: 10.3969/j.issn.1008-2336.2012.01.028. WU K, ZHOU D H, WU J G, et al. Application of synthetic seismogram on oil and gas exploration[J]. Offshore Oil, 2012, 32(1): 28-32. DOI: 10.3969/j.issn.1008-2336.2012.01.028. (in Chinese).
[2] 王立歆, 孙振涛, 董月昌. 合成地震记录制作中存在的问题及对策[J]. 勘探地球物理进展, 2007, 0(4): 292-296. WANG L X, SUN Z T, DONG Y C. Problems and so-lutions in construction of synthetic seismogram[J]. Progress In Exploration Geophysics, 2007, 0(4): 292-296. (in Chinese).
[3] 张永华, 陈萍, 赵雨晴, 等. 基于合成记录的综合层位标定技术[J]. 石油地球物理勘探, 2004(01): 92-96, 126-13 ZHANG Y H, CHEN P, ZHAO Y Q. Integrative layer-labeling technique based on synthetic seismogram[J]. Oil Geo-physical Prospecting, 2004, 39(1): 92-96, 126-131. (in Chinese).
[4] 浦世照, 李世宏, 牟中海. 地震地质综合层位标定方法及其应用[J]. 石油地质与工程, 2007(04): 27-29,10. DOI: 10.3969/j.issn.1673-8217.2007.04.008. PU S Z, LI S H, MOU Z H. Seismic and geological comprehensive horizon calibration method and it’s a-pplication[J]. Petroleum Geology And Engineering, 2007(04): 27-29,10. DOI: 10.3969/j.issn.1673-8217.2007.04.008. (in Chinese).
[5] 崔汝国, 曹国滨, 王彦春, 等. 影响VSP层位标定的问题及对策[J]. 石油地球物理勘探, 2006(S1): 96-99,142. CUI R G, CAO G B, WANG Y C. Problems affecting VSP horizon calibration and countermeasures[J]. Oil Geophysical Prospecting, 2006(S1): 96-99,142. (in Chinese).
[6] 张雪建, 梁锋, 王桂玲. 深度域合成地震记录的制作方法研究[J]. 石油地球物理勘探, 2000, 35(3): 377-380,385 DOI: 10.3321/j.issn:1000-7210.2000.03.015. ZHANG X J, LIANG F, WANG G L. A method for synthesizing seismogram in depth domain[J]. Oil Geophysical Prospecting, 2000, 35(3): 377-380,385. DOI: 10.3321/j.issn:1000-7210.2000.03.015. (in Chinese).
[7] 陈裕明, 李晶, 周亚同. 合成地震记录的改进方法讨论[J]. 石油地球物理勘探, 2001, 36(4): 495-498,507. DOI: 10.3321/j.issn:1000-7210.2001.04.016. CHEN Y M, LI J, ZHOU Y T. A discussion on method for improving synthetic seismogram[J]. Oil Geophysical Prospec-ting, 2001, 36(4): 495-498,507. DOI: 10.3321/j.issn:1000-7210.2001.04.016. (in Chinese).
[8] 李希元, 胡望水, 张楠, 等. 连续子波反射叠加合成地震记录方法[J]. 大庆石油地质与开发, 2020, 39(02 LI X Y, HU Wang S, ZHANG N. Synthetic seismic recording method by the continuous wavelet-reflection superposition[J]. Petroleum Geology&Oilfield Development in Daqing, 2020, 39(02). (in Chinese).
[9] D. C. Ganley. A method for calculating synthetic seismograms which include the effects of absorption and dispersion, GEOPHYSICS[J]. 1981, 46: 1100-1107.
[10] 杨国权, 王永刚, 朱兆林, 等. 井间地震资料层位标定方法研究[J]. 石油物探, 2005, 44(4): 217-219+4-5. DOI: 10.3969/j.issn.1000-1441.2005.03.006. YANG G Q, WANG Y G, ZHU Z L. Stratigraphic calibration method for seismic crosshole data[J]. Geophysical Prospecting for Petroleum, 2005, 44(4): 217-219. DOI: 10.3969/j.issn.1000-1441.2005.03.006. (in Chinese).
[11] 王轶. 地震层位标定方法综述及应用[J]. 重庆科技学院学报(自然科学版), 2011, 13(01): 40-42 WANG Y. Summarize and Practice of Seismic Horizon C-alibration Method[J]. Southwest Petroleum University, 2011, 13(01): 40-42. (in Chinese).
[12] 李本才, 曹卿荣, 李珮, 等. 垂直地震测井(VSP)技术在薄层砂体识别中的应用[J]. 岩性油气藏, 2010, 22(01): 109-113. LI B C, CAO Q R, LI P. Application of VSP to t-he identification of thin sand[J]. Lithologic Reservoirs, 2010, 22(01): 109-113. (in Chinese).
[13] LUO H, XING Y, WANG C, et al. A well-to-seismic calibration method for seismic data in depth domain[C]//SEG International Exposition and Annual Meeting. SEG, 2019: D043S132R004.



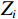
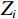
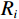
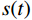
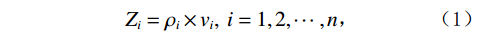
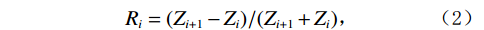
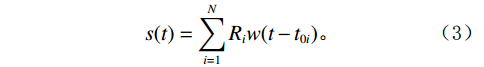
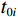
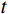
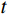
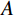
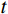

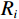
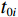
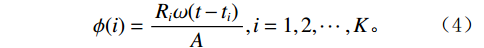
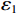
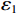
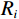
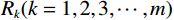

 下载:
下载: