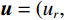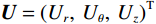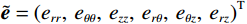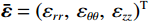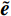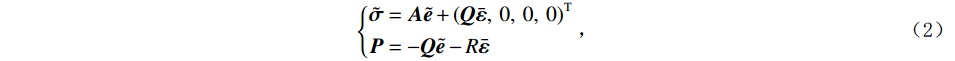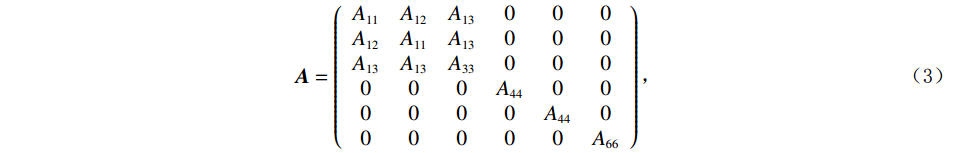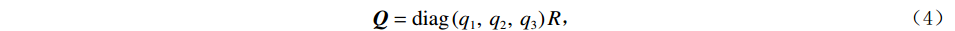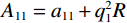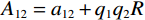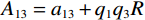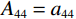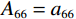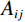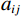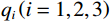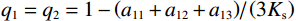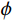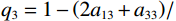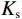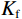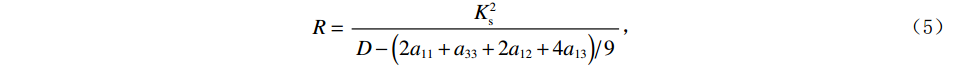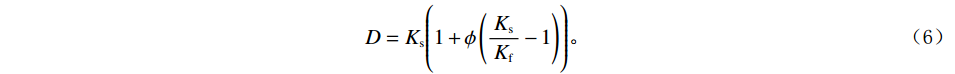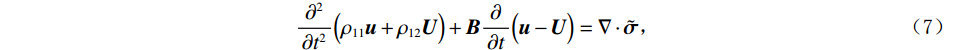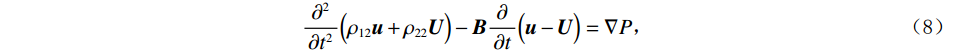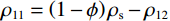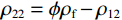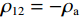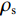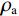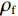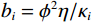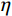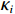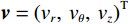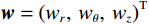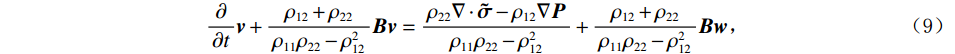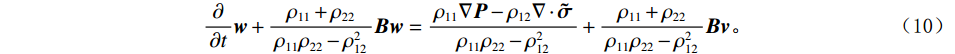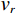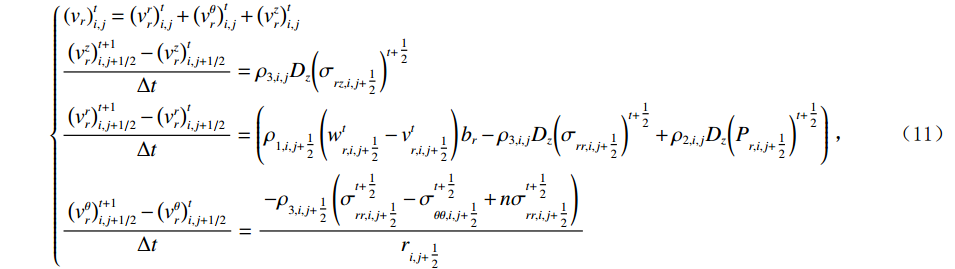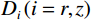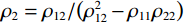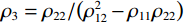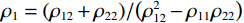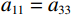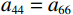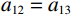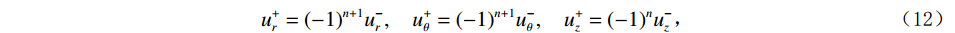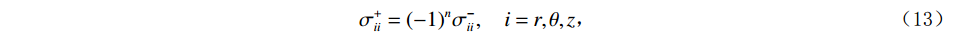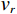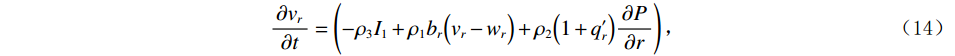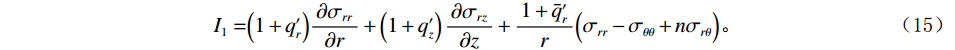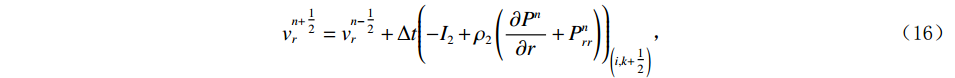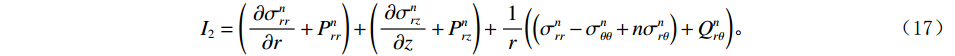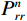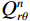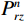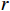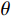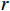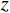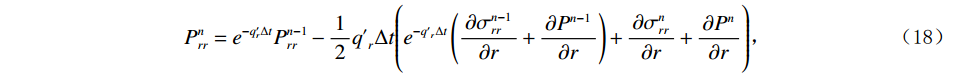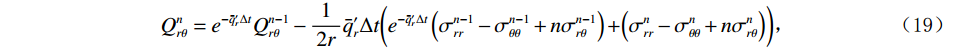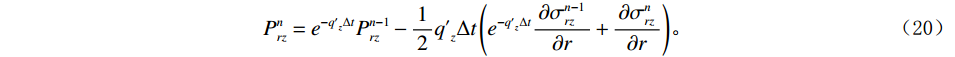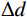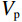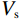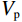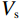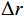Study on the Numerical Simulation of Array Sonic Logging Responses and Their Velocity Dispersion Characteristics in Fractured Formation
-
摘要:
为分析裂缝性储层中裂缝发育带对阵列声波测井响应的影响，本文采用交错网格有限差分算法实现孔弹介质阵列声波测井波列响应的数值模拟。通过对模拟波形速度频散信息的提取，总结裂缝发育带与扩径井段不同模式波的吸收衰减与速度频散响应特征的差异性。首先基于Biot孔弹介质模型导出柱坐标下弹性波的速度-应力方程；其次，用交错网格有限差分方法对孔弹波动方程进行离散化，为提高模拟算法效率与精度，使用高阶差分格式与NPML；最后，基于含倾斜裂缝带模型与井壁坍塌地层模型的响应模拟，用前后向振幅相位估计法分析阵列声波的波形幅度相位响应特征与速度频散的差异性。结果表明，低速裂缝带纵横波波场时差会增大，且衰减幅度随裂缝带倾角变化；井壁塌陷在径向与轴向上扩大时，会增强斯通利波与伪瑞利波衰减。声波纵横波时差、速度频散与幅度衰减均可反映一定的裂缝带特征，这些影响对评价和开发裂缝性储层具有重要意义。
Abstract:To understand the effects of fractured formation on the responses of array sonic logging, the wave propagation of array acoustic logging was simulated based on the staggered grid finite difference method and poroelastic theory. Methods of velocity dispersion analysis and attenuation estimation were carried out on simulated sonic waveforms, and the differences of velocity dispersion and wave amplitude attenuation among these wave modes were summarized. First, the velocity-stress equation in cylindrical coordinates was deduced for the Biot poroelastic model. Next, the velocity-stress wave equation was discretized by using the staggered grid finite difference method. Furthermore, the higher order finite difference format and nearly perfect match layer (NPML) were adopted to improve the efficiency and accuracy of the finite difference method. Finally, simulated sonic waveforms in formation models with a tilted fracture zone and collapsed interval were applied to the velocity dispersion analysis by using forward and back amplitudes and the phase estimation method. The results show that the time difference of the P and S wave field in the low-velocity fracture zone increases and that the attenuation amplitude changes with the dip angle of the fracture zone. The attenuation of Stoneley waves and pseudo-Rayleigh waves is enhanced when the shaft collapse expands in the radial and axial directions. The time difference of acoustic waves, velocity dispersion, and amplitude attenuation can reflect the characteristics of the fracture zone, which is of great significance to the evaluation and development of fractured reservoirs.
-
裂缝性储层是一类以次生孔隙为主的油气储层，该类储层的储集空间以裂缝为主，且具有强非均质性，至今，该类储层的孔隙空间的定量评价与有效性分析存在诸多难题[1-3]。现有综合测井方法的径向探测范围大多局限于井周0.05～2.5 m范围内，几乎没有方位探测能力，而基于阵列声波测井发展起来的声波测井成像技术可以探测径向数米至数十米的范围，能有效地探测井旁的缝洞发育带，对于尺度较大的洞穴或局部井段的扩径也有较好的识别与评价能力。然而，由于阵列声波测井接收器采集的波场数据包含有多种模式波，进行波场分离与信息提取时需要深入了解各类模式波的响应特征与到时分布规律。因此，开展阵列声波测井响应数值模拟及应用研究对于储层缝洞发育带的识别与有效性评价具有重要意义[4]。
阵列声波测井采用多个发射器和接收器组成的阵列接收来自井旁目标地层的散射、折射与反射波场数据，通过信号处理的手段，提取不同模式波的速度、幅度与相位变化等信息，进而确定目标地层的孔渗等岩石物理，阵列声波远探测成像技术进一步将接收到的反射波聚焦成像，可以得到井旁地质构造的成像[4-5]。对于复杂地质体的阵列声波测井响应的规律分析，需要首先通过数学或物理模拟手段，对阵列声波波场进行模拟，掌握不同模式波的时频分布特征与不同地层模型的响应规律[6]。
近年来，国内外学者在碳酸盐岩缝洞型储层的阵列声波测井评价方法方面开展了大量的研究与应用实践，成功地将声波远探测技术应用于裂缝、断层、溶蚀孔洞、洞穴等构造的识别与解释[7]。楚泽涵等[8]、乔文孝等[9]、陶果等[10]分别开展了单极子源激发和多接收器采集的全波列提取反射波分量用于缝洞成像的解释，指出了单极子声波成像的不足。针对单极子声波成像的局限性，Tang等[11-12]于2004年首次提出了偶极声波的远探测成像方法，2009年又与Patterson用四分量偶极数据实现了井旁构造的成像，并用实测数据验证了成像效果。针对缝洞碳酸盐岩储层的弹性波波场模拟，文中选用了Biot的孔隙弹性介质理论用于近似模拟缝洞介质的弹性波波场响应特征。
为了考察阵列声波测井波列对慢度频散与吸收衰减特征的响应关系，Nolte等[13-14]基于傅里叶变换理论提出了处理阵列谱相干函数的加权频谱相干法（weighted spectral semblance，WSS），采用多点加权策略提高了算法精度及抗噪性，但该方法不适用于处理单一频率下多个模式波共存的波形数据。Li等[15]提出了一种自适应有限脉冲滤波器算法，也称为振幅相位估计法（amplitude phase estimation，APES），该方法可以准确地估计不同模式波慢度频散的响应。王瑞甲等[16]将矩阵束算法与WSS相结合，给出了一种多道波形信号的频散分析方案，压制了WSS处理中出现的周期性伪解。刘航等[17]通过纵波的频散分析提出纵波频散谱处理方法，Zhang等[18]通过纵波的频散反演给出了更为连续与准确的频散谱处理结果，Chen等[19]用高分辨率反演方法实现了全波列的频散谱计算，得到了良好的实用效果。
本研究首先简单回顾Biot理论与阵列声波测井数据的波场模式；其次，应用Biot理论的弹性波动方程的柱坐标形式得到各向同性介质中弹性波的速度-应力方程；再次，采用交错网格时域有限差分方法对波动方程进行离散与稳定求解，并用均匀无限介质模型、轴向分层介质模型、含井中流体介质模型对模拟算法的有效性进行了验证；最后，基于含倾斜裂缝带模型与井壁坍塌地层模型，分析阵列声波测井的特征响应，并与实测储层的缝洞发育特征进行对比分析，得到对缝洞型储层定量评价有意义的认识。
1. 孔隙弹性介质波动方程及交错网格有限差分离散格式
1.1 孔弹介质中的波动方程
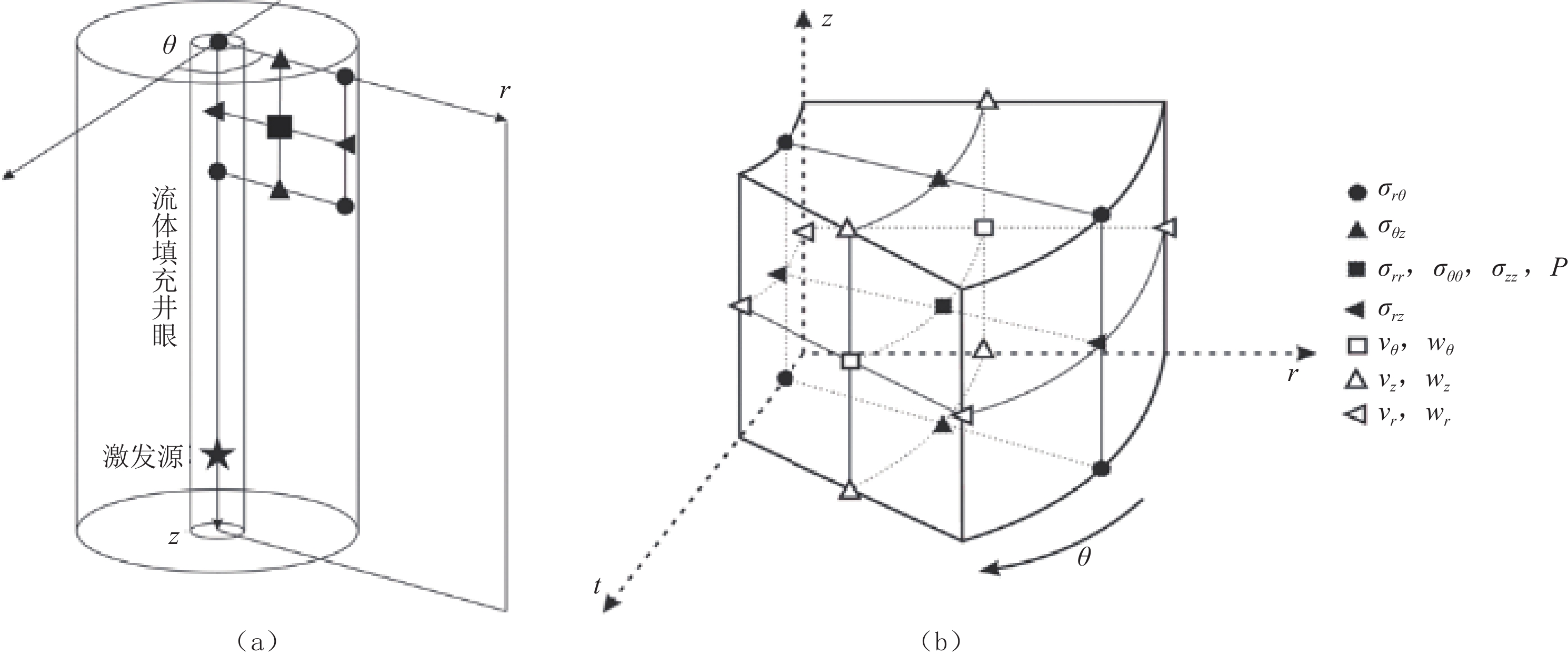
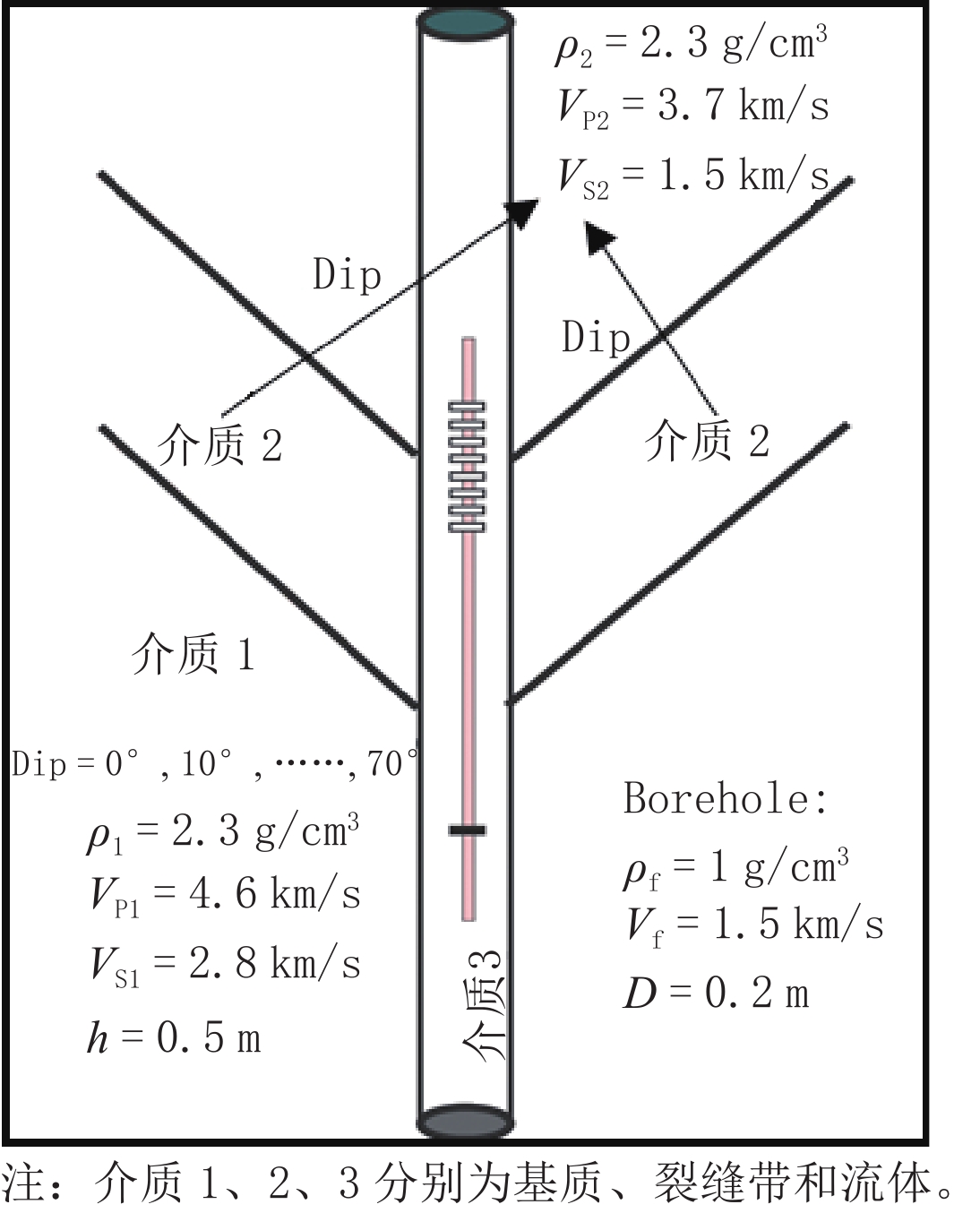
Biot孔隙弹性介质中，地震波传播考虑了孔隙流体和固体基质之间的相对运动引起的能量耗散，部分揭示了孔弹介质中波传播的速度频散与能量衰减的规律。该理论将多孔介质的变形分解为固体基质的弹性变形和饱和孔隙流体流动引起的变形，同时考虑了固相和液相之间的耦合及流体压缩性和流体饱和度变化的影响。图1给出了Biot孔弹介质模型的示意图。
在阵列声波测井数值模拟中，若激发源置于井轴，设Biot固液双相中固相位移矢量
$ {\boldsymbol{u}} = ( {u_r}, {u_\theta },\;{u_z} )^{{\mathrm{T}}} $ ，液相位移矢量${\boldsymbol{U}} = {\left( {{U_r},\;{U_\theta },\;{U_z}} \right)^{{\mathrm{T}}}}$ ，固相体应变与切应变${{\tilde {\boldsymbol{e}}}} = {\left( {{e_{rr}},\;{e_{\theta \theta }},\;{e_{zz}},\;{e_{r\theta }},\;{e_{\theta z}},\;{e_{rz}}} \right)^{{\mathrm{T}}}}$ ，液相体应变${{\bar {\boldsymbol{\varepsilon}} }} = {({\varepsilon _{rr}},\;{\varepsilon _{\theta \theta }},\;{\varepsilon _{zz}})^{{\mathrm{T}}}}$ ，与位移分量有如下关系：$$ \left\{ \begin{aligned} &{e_{rr}} = \frac{{\partial {u_r}}}{{\partial r}},\quad {e_{\theta \theta }} = \frac{{{u_r}}}{r} + \frac{1}{r}\frac{{\partial {u_\theta }}}{{\partial \theta }},\quad {e_{zz}} = \frac{{\partial {u_z}}}{{\partial z}} \\ &{e_{r\theta }} = \frac{{\partial {u_\theta }}}{{\partial r}} + \frac{1}{r}\frac{{\partial {u_r}}}{{\partial \theta }} - \frac{{{u_\theta }}}{r},\quad {e_{rz}} = \frac{{\partial {u_r}}}{{\partial z}} + \frac{{\partial {u_z}}}{{\partial r}},\quad {e_{\theta z}} = \frac{1}{r}\frac{{\partial {u_z}}}{{\partial \theta }} + \frac{{\partial {u_\theta }}}{{\partial z}} \\ & {\varepsilon _{rr}} = \frac{{\partial {U_r}}}{{\partial r}},\quad {\varepsilon _{\theta \theta }} = \frac{{{U_r}}}{r} + \frac{1}{r}\frac{{\partial {U_\theta }}}{{\partial \theta }},\quad {\varepsilon _{zz}} = \frac{{\partial {U_z}}}{{\partial z}} \end{aligned} \right.。 $$ (1) 考虑平行于波传播方向的流体流动的情况，根据Biot理论，固-液双相横向各向同性孔隙弹性介质中应力
${{\tilde {\boldsymbol{\sigma}} }} = {\left( {{\sigma _{rr}},\;{\sigma _{\theta \theta }},\;{\sigma _{zz}},\;{\sigma _{r\theta }},\;{\sigma _{\theta z}},\;{\sigma _{rz}}} \right)^{{\mathrm{T}}}}$ 及应变${{\tilde {\boldsymbol{e}}}}$ 与${{\bar {\boldsymbol{\varepsilon}} }}$ 和孔隙压力关系如下[20]：$$ \left\{ \begin{aligned} & {{\tilde {\boldsymbol{\sigma}} }} = {{{\boldsymbol{A}}\tilde {\boldsymbol{e}}}} + {\left( {{{{\boldsymbol{Q}}\bar {\boldsymbol{\varepsilon}} }},\;0,\;0,\;0} \right)^{\rm T}} \\ & {\boldsymbol{P}} = - {{{\boldsymbol{Q}}\tilde {\boldsymbol{e}}}} - R{{\bar {\boldsymbol{\varepsilon}} }} \end{aligned} \right. \text{，} $$ (2) $$ {\boldsymbol{A}} = \left( {\begin{array}{*{20}{c}} {{A_{11}}}&{{A_{12}}}&{{A_{13}}}&0&0&0 \\ {{A_{12}}}&{{A_{11}}}&{{A_{13}}}&0&0&0 \\ {{A_{13}}}&{{A_{13}}}&{{A_{33}}}&0&0&0 \\ 0&0&0&{{A_{44}}}&0&0 \\ 0&0&0&0&{{A_{44}}}&0 \\ 0&0&0&0&0&{{A_{66}}} \end{array}} \right)\text{，} $$ (3) $$ {\boldsymbol{Q}} = {{\mathrm{diag}}}\left( {{q_1},\;{q_2},\;{q_3}} \right)R\text{，} $$ (4) 其中，P为流体相对岩石骨架产生的压力，
${A_{11}} = {a_{11}} + q_1^2 R$ ，${A_{12}} = {a_{12}} + {q_1}{q_2}R$ ，${A_{13}} = {a_{13}} + {q_1}{q_3}R$ ，${A_{33}} = {a_{33}} + q_3^2 R$ ，${A_{44}} = {a_{44}}$ ，${A_{66}} = {a_{66}}$ ；${A_{ij}}$ 是干岩石状态下的弹性常数；${a_{ij}}$ 是含流体状态下的弹性常数；${q_i}\left( {i = 1,2,3} \right)$ 为Biot有效系数[20]，${q_1} = {q_2} = 1 - {{\left( {{a_{11}} + {a_{12}} + {a_{13}}} \right)} \mathord{\left/ {\vphantom {{\left( {{a_{11}} + {a_{12}} + {a_{13}}} \right)} {\left( {3{K_{\text{s}}}} \right)}}} \right. } {\left( {3{K_{\text{s}}}} \right)}}$ ，$\phi $ 为孔隙度，${q_3} = 1 - {\left( {2{a_{13}} + {a_{33}}} \right)} / {\left( {3{K_{\text{s}}}} \right)}$ ，${K_{\rm s}}$ 为固相的体积模量，${K_{\rm f}}$ 为流体的体积模量，R为孔隙流体的弹性参数，由如下关系计算：$$ R = \frac{{K_{{\mathrm{s}}}^{2}}}{{D - {{\Big( {2{a_{11}} + {a_{33}} + 2{a_{12}} + 4{a_{13}}} \Big)} \mathord{\left/ {\vphantom {{\left( {2{a_{11}} + {a_{33}} + 2{a_{12}} + 4{a_{13}}} \right)} 9}} \right. } 9}}} \text{，} $$ (5) $$ D = {K_{{\mathrm{s}}}}\Biggr({1 + \phi \left( {\frac{{{K_{{\mathrm{s}}}}}}{{{K_{{\mathrm{f}}}}}} - 1} \right)}\Biggr)。 $$ (6) 相应地，Biot方程在流体饱和孔隙弹性介质中波传播的运动方程为[12]：
$$ \frac{{{\partial ^2}}}{{\partial {t^2}}}\Big( {{\rho _{11}}{\boldsymbol{u}} + {\rho _{12}}{\boldsymbol{U}}} \Big) + {\boldsymbol{B}}\frac{\partial }{{\partial t}}\Big( {{\boldsymbol{u}} - {\boldsymbol{U}}} \Big) = \nabla \cdot {{\tilde {\boldsymbol{\sigma}} }} \text{，} $$ (7) $$ \frac{{{\partial ^2}}}{{\partial {t^2}}}\Big( {{\rho _{12}}{\boldsymbol{u}} + {\rho _{22}}{\boldsymbol{U}}} \Big) - {\boldsymbol{B}}\frac{\partial }{{\partial t}}\Big( {{\boldsymbol{u}} - {\boldsymbol{U}}} \Big) = \nabla P \text{，} $$ (8) 其中，
${\rho _{11}} = \left( {1 - \phi } \right){\rho _{\text{s}}} - {\rho _{12}}$ ，${\rho _{22}} = \phi {\rho _{\text{f}}} - {\rho _{12}}$ ，${\rho _{12}} = - {\rho _{\text{a}}}$ ，${\rho _{\text{s}}}$ 为介质骨架密度，${\rho _{\rm a}}$ 为固相与液相之间的耦合密度，${\rho _{\rm f}}$ 为孔隙流体密度，B为阻尼系数矩阵，在各个方向上的阻尼系数${b_i} = {\phi ^2}\eta /{\kappa _i}$ ，$\eta $ 为流体粘度，${\kappa _i}$ 由达西定律给出。设固相速度∂u/∂t为
$ {\boldsymbol{v}} = {\left( {{v_r},\;{v_\theta },\;{v_z}} \right)^{{\mathrm{T}}}} $ ，液相速度∂U/∂t为$ {\boldsymbol{w}} = {\left( {{w_r},\;{w_\theta },\;{w_z}} \right)^{{\mathrm{T}}}} $ ，代入式（7）和式（8）的运动方程整理得到固相速度及液相速度与应力的关系[15,21]：$$ \frac{\partial }{{\partial t}}{\boldsymbol{v}} + \frac{{{\rho _{12}} + {\rho _{22}}}}{{{\rho _{11}}{\rho _{22}} - \rho _{12}^2}}{\boldsymbol{Bv}} = \frac{{{\rho _{22}}\nabla \cdot {\boldsymbol{\tilde \sigma }} - {\rho _{12}}\nabla {\boldsymbol{P}}}}{{{\rho _{11}}{\rho _{22}} - \rho _{12}^2}} + \frac{{{\rho _{12}} + {\rho _{22}}}}{{{\rho _{11}}{\rho _{22}} - \rho _{12}^2}}{\boldsymbol{Bw}}\text{，} $$ (9) $$ \frac{\partial }{{\partial t}}{\boldsymbol{w}} + \frac{{{\rho _{11}} + {\rho _{22}}}}{{{\rho _{11}}{\rho _{22}} - \rho _{12}^2}}{\boldsymbol{Bw}} = \frac{{{\rho _{11}}\nabla {\boldsymbol{P}} - {\rho _{12}}\nabla \cdot {\boldsymbol{\tilde \sigma }}}}{{{\rho _{11}}{\rho _{22}} - \rho _{12}^2}} + \frac{{{\rho _{11}} + {\rho _{22}}}}{{{\rho _{11}}{\rho _{22}} - \rho _{12}^2}}{\boldsymbol{Bv}}。 $$ (10) 1.2 波动方程的有限差分离散
在极坐标下的钻井地层中，具有轴向对称性（沿井轴）的配置如图2（a）所示，用于空间域和时间域离散化的交错网格剖分如图2（b）所示。
![]()
图 2 轴向对称性地层的配置（a）与非轴对称空间域离散化的交错网格剖分示意图（b）Figure 2. Scheme of formation with (a) axial symmetric and (b) asymmetric staggered grids in a three-dimensional discretized space domain在同一时间点下分别将速度与应力项在
$ \left(r,\theta ,z\right) $ 方向上展开，以${v_r}$ 为例，依据图2所示的网格剖分方法，可以将流体饱和孔隙弹性介质中的波动方程（9）和方程（10）中的各项，按如下形式进行离散：$$ \left\{ \begin{aligned} & \left( {{v_r}} \right)_{i,j}^t = \left( {v_r^r} \right)_{i,j}^t + \left( {v_r^\theta } \right)_{i,j}^t + \left( {v_r^z} \right)_{i,j}^t \\ &\frac{{\left( {v_r^z} \right)_{i,j + 1/2}^{t + 1} - \left( {v_r^z} \right)_{i,j + 1/2}^t}}{{\Delta t}} = {\rho _{3,i,j}}{D_z}{\left( {{\sigma _{rz,i,j + \tfrac{1}{2}}}} \right)^{t + \tfrac{1}{2}}} \\ &\frac{{\left( {v_r^r} \right)_{i,j + 1/2}^{t + 1} - \left( {v_r^r} \right)_{i,j + 1/2}^t}}{{\Delta t}} = \left( {{\rho _{1,i,j + \tfrac{1}{2}}}\left( {w_{r,i,j + \tfrac{1}{2}}^t - v_{r,i,j + \tfrac{1}{2}}^t} \right){b_r} - {\rho _{3,i,j}}{D_z}{{\left( {{\sigma _{rr,i,j + \tfrac{1}{2}}}} \right)}^{t + \tfrac{1}{2}}} + {\rho _{2,i,j}}{D_z}{{\left( {{P_{r,i,j + \tfrac{1}{2}}}} \right)}^{t + \tfrac{1}{2}}}} \right) \\ &\frac{{\left( {v_r^\theta } \right)_{i,j + 1/2}^{t + 1} - \left( {v_r^\theta } \right)_{i,j + 1/2}^t}}{{\Delta t}} = \frac{{ - {\rho _{3,i,j + \tfrac{1}{2}}}\left( {\sigma _{rr,i,j + \tfrac{1}{2}}^{t + \tfrac{1}{2}} - \sigma _{\theta \theta ,i,j + \tfrac{1}{2}}^{t + \tfrac{1}{2}} + n\sigma _{rr,i,j + \tfrac{1}{2}}^{t + \tfrac{1}{2}}} \right)}}{{{r_{i,j + \tfrac{1}{2}}}}} \end{aligned} \right. ， $$ (11) 式中
$ {D}_{i}\left(i=r,z\right) $ 为对r方向与z方向上的差分符号，${\rho _2} = {{{\rho _{12}}} / {\left( {\rho _{12}^2 - {\rho _{11}}{\rho _{22}}} \right)}}$ ，${\rho _3} = {{{\rho _{22}}} / {\left( {\rho _{12}^2 - {\rho _{11}}{\rho _{22}}} \right)}}$ ，${\rho _1} = {{\left( {{\rho _{12}} + {\rho _{22}}} \right)}/ {\left( {\rho _{12}^2 - {\rho _{11}}{\rho _{22}}} \right)}}$ 。文中将有垂直对称轴的横向各向同性介质VTI（transversal isotropy with vertical symmetric axis）或倾斜对称轴的横向各向同性介质TTI（transversal isotropy with tilt symmetric axis）中用等效各向同性介质近似，取
${q_1} = {q_3}$ ，${b_r} = {b_z}$ ，${a_{11}} = {a_{33}}$ ，${a_{44}} = {a_{66}}$ ，${a_{12}} = {a_{13}}$ ，和单极源n=0的情况。2. 高效数值模拟的实现策略
2.1 井轴对称边界条件
由于文中差分方法在极坐标下实现，因此需要考虑在井轴处的对称性边界条件。设网格的左边界总是与井轴重合，那么在此边界处需用对称条件，即所有剪切分量为0，且位移和主应力满足如下条件[22]：
$$ u_r^ + = {( - 1)^{n + 1}}u_r^ - ,\quad u_\theta ^ + = {( - 1)^{n + 1}}u_\theta ^ - ,\quad u_z^ + = {( - 1)^n}u_z^ - \text{，} $$ (12) $$ \sigma _{ii}^ + = {( - 1)^n}\sigma _{ii}^ - ,\quad i = r,\theta ,z\text{，} $$ (13) 式中，n为激发源的极数，单极子源时n=0，偶极子源时n=1，四极子源时n=2；角标“+”和“-”分别表示井轴左侧和右侧的网格节点。
2.2 边界区域二阶与四阶融合处理策略
对于四阶精度有限差分格式，图3中当i=2的网格点与i=n-1的网格点进行差分计算时，需要用i=0处与i=n+1处的值，然而i=0点与i=n+1点均不在剖分网格范围内，文中据此提出两种在网格边界临界点处的差分方法。
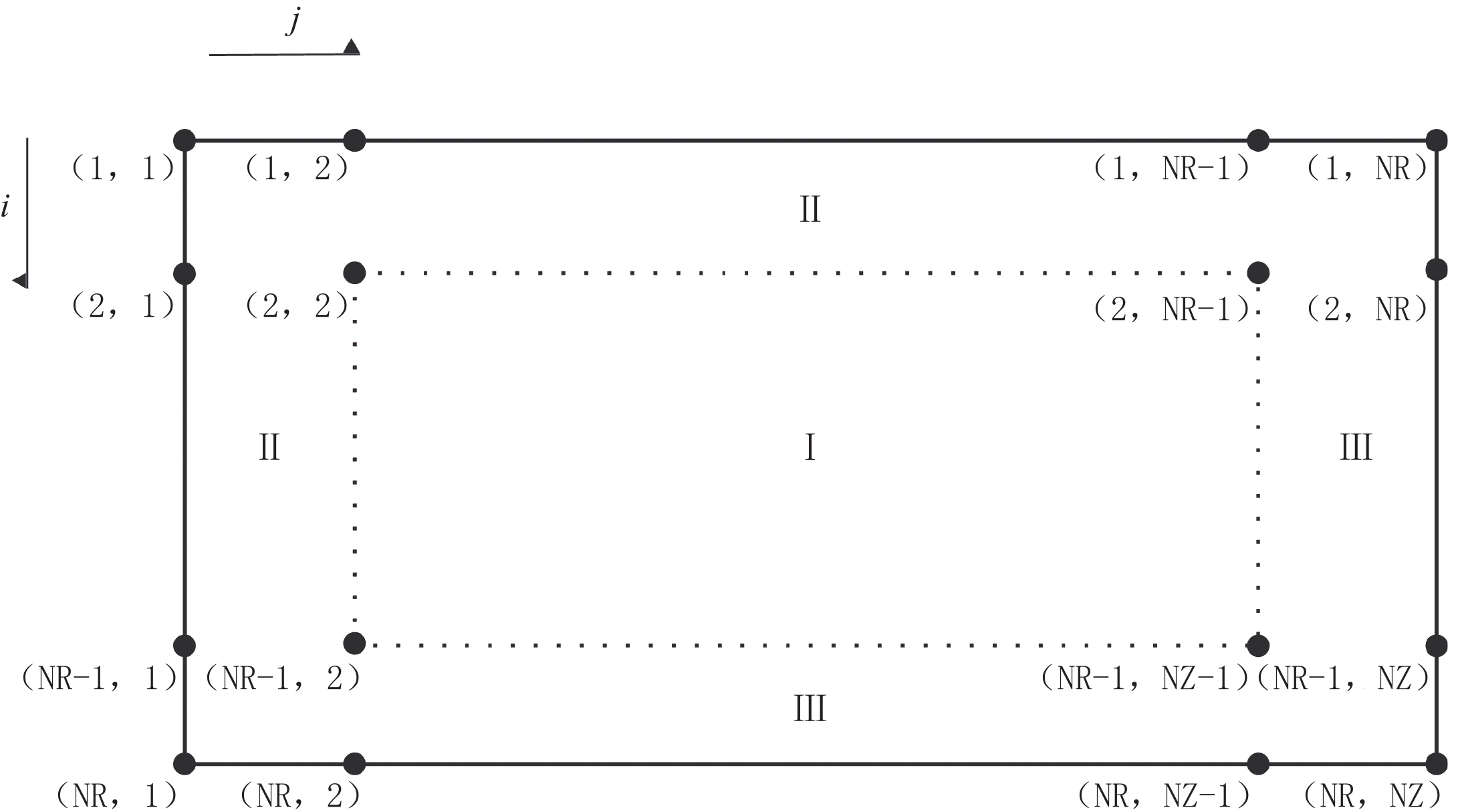
如图4所示，在区域Ⅰ内用四阶有限差分格式进行计算，在区域Ⅱ与 Ⅲ内，用二阶有限差分格式计算，此时可以保证所有参与计算点均在剖分网格范围内。该处理方法的局限性是随着阶数提高，采用的低阶处理的网格数也随之增加，难以保证所有网格点精度的一致性。
2.3 非分裂式完全匹配层吸收边界条件
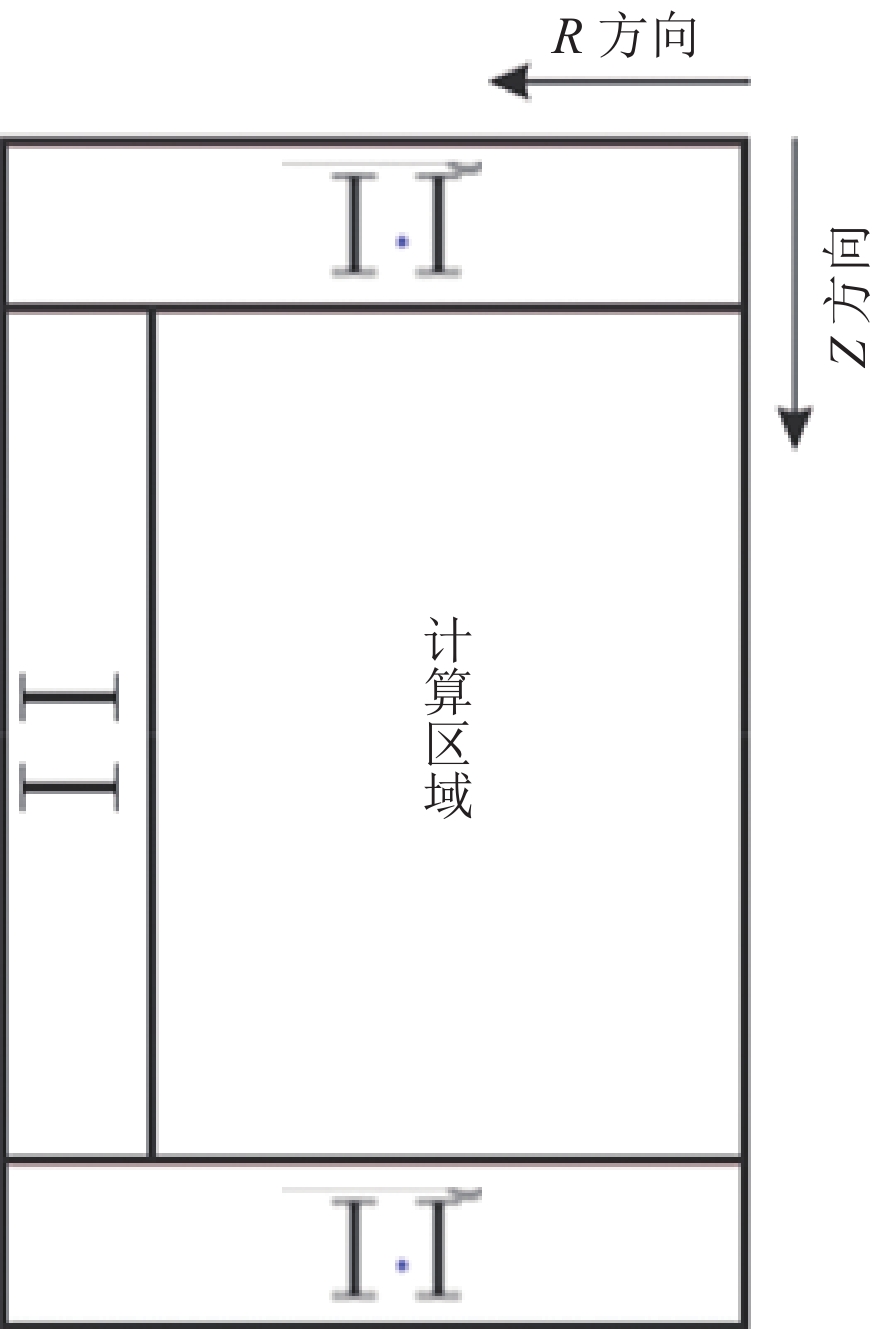
在波场数值模拟时，当弹性波传播到离散网格截断边界，最外层波场幅度突降为0，会在边界处发生反射。为减弱边界反射对计算域波场的干扰，文中采用了非分裂式完全匹配层（nearly perfect match layer，NPML）吸收边界条件[23-24]，使用的边界区域如图5所示。
非分列式完全匹配层吸收边界条件，无需对波场分量进行几个方向的分离。以
${v_r}$ 为例，在应力项添加衰减项：$$ \frac{{\partial {v_r}}}{{\partial t}} = \left( { - {\rho _3}{{{I}}_1} + {\rho _1}{b_r}\Bigr( {{v_r} - {w_r}} \Bigr) + {\rho _2}\Bigr( {1 + {q'_r}} \Bigr)\frac{{\partial P}}{{\partial r}}} \right) \text{，} $$ (14) 其中，
$$ {{{I}}_1} = \Bigr( {1 + {q'_r}} \Bigr)\frac{{\partial {\sigma _{rr}}}}{{\partial r}} + \left( {1 + {q'_z}} \right)\frac{{\partial {\sigma _{rz}}}}{{\partial z}} + \frac{{1 + {\bar q'_r}}}{r}\Bigr( {{\sigma _{rr}} - {\sigma _{\theta \theta }} + n{\sigma _{r\theta }}} \Bigr) 。 $$ (15) 对式（15）进行中心差分得到离散关系：
$$ v_r^{n + \tfrac{1}{2}} = v_r^{n - \tfrac{1}{2}} + \Delta t{\Biggr( { - {I_2} + {\rho _2}\left( {\frac{{\partial {P^n}}}{{\partial r}} + P_{rr}^n} \right)} \Biggr)_{\left( {i,k + \tfrac{1}{2}} \right)}}\text{，} $$ (16) 其中，
$$ {{{I}}_2} = \left( {\frac{{\partial \sigma _{rr}^n}}{{\partial r}} + P_{rr}^n} \right) + \left( {\frac{{\partial \sigma _{rz}^n}}{{\partial z}} + P_{rz}^n} \right) + \frac{1}{r}\bigg( {\Bigr( {\sigma _{rr}^n - \sigma _{\theta \theta }^n + n\sigma _{r\theta }^n} \Bigr) + Q_{r\theta }^n} \bigg)。 $$ (17) $P_{rr}^n$ 、$Q_{r\theta }^n$ 、$P_{rz}^n$ 分别为$r$ 方向、$\theta $ 映射到$r$ 方向与$z$ 方向上的NPML衰减系数，且有：$$ {P_{rr}^n = {e^{ - q_r'{{\Delta }}t}}P_{rr}^{n - 1} - \frac{1}{2}{{q'}_r}\Delta t\Biggr( {{e^{ - {{q'}_r}{{\Delta }}t}}\left( {\frac{{\partial \sigma _{rr}^{n - 1}}}{{\partial r}} + \frac{{\partial {P^{n - 1}}}}{{\partial r}}} \right) + \frac{{\partial \sigma _{rr}^n}}{{\partial r}} + \frac{{\partial {P^n}}}{{\partial r}}} \Biggr)} \text{，} $$ (18) $$ Q_{r\theta }^n = {e^{ - \bar q_r'{{\Delta }}t}}Q_{r\theta }^{n - 1} - \frac{1}{{2r}}\bar q_r'\Delta t\bigg( {{e^{ - \bar q_r'{{\Delta }}t}}\left( {\sigma _{rr}^{n - 1} - \sigma _{\theta \theta }^{n - 1} + n\sigma _{r\theta }^{n - 1}} \right) + \Bigr( {\sigma _{rr}^n - \sigma _{\theta \theta }^n + n\sigma _{r\theta }^n} \Bigr)} \bigg)\text{，} $$ (19) $$ {P_{rz}^n = {e^{ - {{q'}_z}{{\Delta }}t}}P_{rz}^{n - 1} - \frac{1}{2}{{q'}_z}\Delta t\left( {{e^{ - {{q'}_z}{{\Delta }}t}}\frac{{\partial \sigma _{rz}^{n - 1}}}{{\partial r}} + \frac{{\partial \sigma _{rz}^n}}{{\partial r}}} \right)} 。 $$ (20) 3. 数值模拟算法的精度分析
3.1 均匀TI介质模型的计算结果对比
本文使用基于阿特拉斯公司生产的某型多极阵列测井仪器来设置模拟的阵列声波测井仪器参数，并在图6中展示其基本配置与参数[25]。该模拟阵列声波测井仪器由一个远端单极子源与8个阵列接收器组成，接收器极板间距为0.15 m，从源至首个接收器的距离为2.59 m。
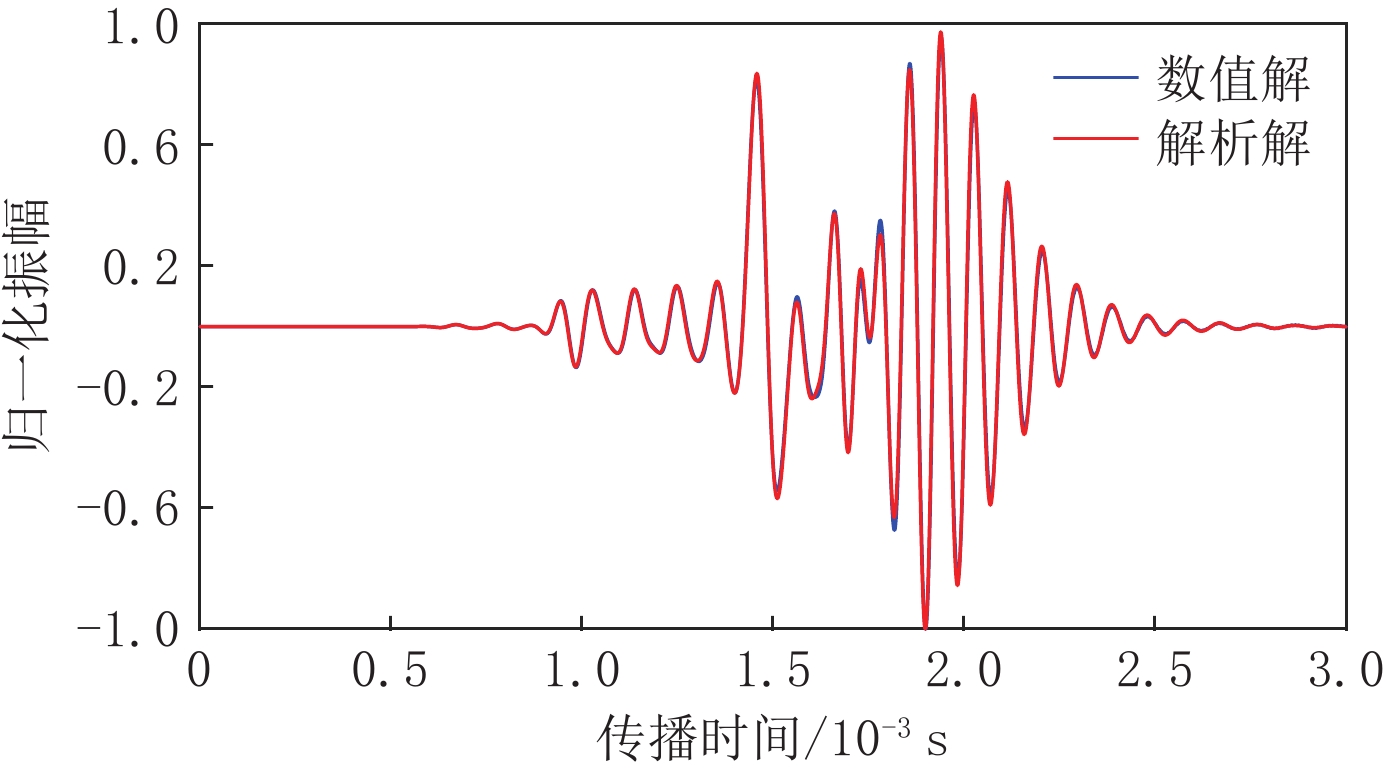
图7为弹性介质数值模拟与经典实轴积分第一个接收器的对比结果，模型参数参照Carlos等的介质模型[20]，接收器位于主频为8 kHz的点源下方，网格为400×800，空间步长为1×10-3 m，时间步长为5×10-7 s。其中蓝色波形为本研究的差分数值模拟结果，红色波形为经典解析解的离散波数法的数值结果，两个波形吻合较好，初步验证模拟算法的正确性。
![]()
图 7 有限差分数值解与经典波数积分解结果对比Figure 7. Comparisons between FD numerical simulation results and those of a classic wave number integral4. 裂缝性地层阵列声波测井响应及速度频散特征分析
为考察裂缝性地层和扩径层段的阵列声波测井响应，根据实际生产中出现的裂缝情况，设计相应的模型，计算阵列声波测井的波列响应，以分析裂缝的影响与可能的识别与校正思路。
4.1 含不同倾角等效裂缝带地层模型的波场响应
为了便于分析及降低计算资源的需求，文中用各向同性的等效介质理论将裂缝带等效成低密度的慢速地层，进而用分析裂缝带倾角变化对波场响应的影响。文中设置了4套物性参数相同但裂缝带倾角不同的Biot双相介质模型，模型的基质参数见表1所示。在每个模型中，裂缝与井筒交点深度z=-0.67 m处，裂缝带倾角增量为20°，角Dip从30° 至70°，宽度
$\Delta d$ =0.5 m，裂缝带等效参数如表1所示。图8为简化的含倾斜裂缝带地层模型。表 1 含倾斜慢速地层模型物性参数Table 1. Simulated parameters of inclined slow formation分区介质 分层位置 固相参数 流相参数 耦合参数 耗散参数 A11 A13 A44 $ \rho_{_{11}} $ R $ \rho_{_{22}} $ Q $ \rho_{_{12}} $ b 井中流体 0.1 R/m 2.25 2.25 0 1.00 0 1.00 0 0 0 基质地层 3.0 R/m 43.39 13.62 14.89 2.27 0.30 0.16 1 -0.06 1 慢速地层 -6.7 Z/m 8.00 2.24 2.88 2.08 0.30 0.16 1 -0.06 1 以阵列声波测井形式分别对4个地层模型计算模场响应，采用井眼居中激发与接收方式，仪器模拟参数表2所示。
表 2 阵列声波测井模拟参数Table 2. Simulated schematic for array sonic logging参数 取值 起始深度/m -11 结束深度/m -6 深度间隔/m 0.2 源类型 单极子源 子波类型 Ricker子波 采样点数 12000 采样间隔/μs 0.47 首接收器与源的距离/m 2.59 接收器间隔/m 0.152 接收器数量 8 图9为3种含有不同倾角慢速地层模型进行阵列声波测井在各个深度下首个接收器采集到的模拟响应对比，图9（a）为不含裂缝带时的波场，图9（b）～图9（d）分别为30°、50° 和70° 倾斜裂缝带地层模型的模拟响应。
![]()
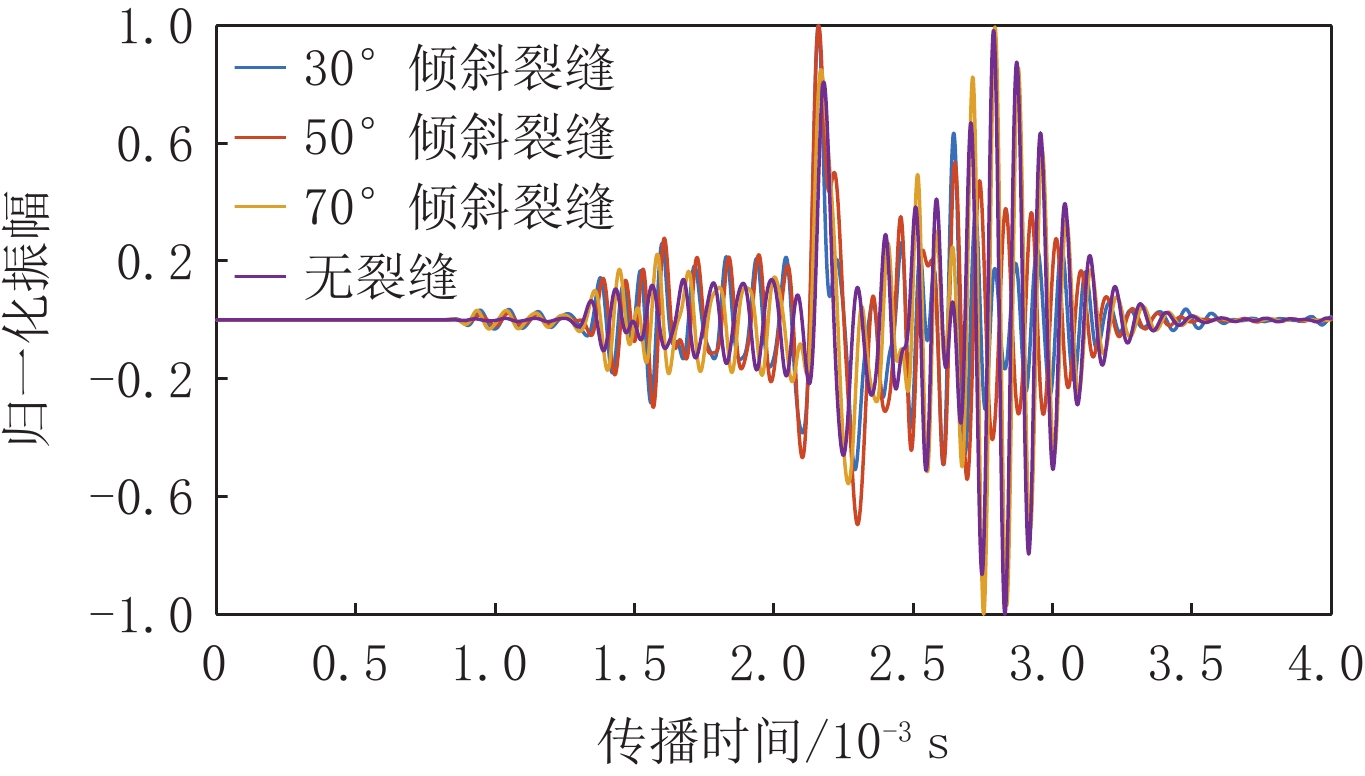
图 9 （a）基质地层，（b）30°，（c）50°，（d）70°倾斜裂缝带地层模型的波场模拟结果Figure 9. (a) No slow formation, (b) inclined slow formation (dip = 30), (c) inclined slow formation (dip = 50), (d) inclined slow formation (dip = 70)图10是源处于5 m处时7.59 m处的第1个接收器在4个模型中的全波波形，图中看到，与无裂缝时相比，不同角度的倾斜裂缝带，造成全波列波形的幅度与相位的变化，这也是阵列声波波形分析识别与评价裂缝的基础。图11和图12均是基于图10位置得到的8个波列的波形分析结果。
![]()
图 10 源处于5 m处时7.59 m处第1个接收器在4个模型中的全波波形Figure 10. Waveforms of the first receiver when the source is at 5.0 and the receiver is at 7.59 m in four models![]()
图 11 含50°倾角裂缝带与基质地层在7.59 m处的频率-慢度图Figure 11. Dispersion plot velocity slowness at 7.59 m, (a) formation with an inclined fracture zone （dip=50） and （b） matrix formation![]()
图 12 8个不同倾角裂缝带地层模型的模拟波形用STC方法提取横波速度谷值点随倾角与深度的变化注：（a）速度随裂缝带倾角与深度的变化，（b）速度谷值点随裂缝带倾角与深度的变化。Figure 12. STC analysis of simulated scenarios with different inclined sediments从图11（a）～图11（b）的波场模拟结果可以清楚识别P波、S波、直达斯通利波与伪瑞雷波p-R波，并可以观察到由裂缝与基质地层的上下交界面产生的上行与下行斯通利波，可用于地层渗透率反演[26-28]。
当裂缝带倾角分别为30°、50° 与70° 时，在深度7.59 m由首个接收器采集的波列如图12所示，在裂缝带分布的纵向深度范围内，纵波首波初至时间变化较小，横波有明显滞后，斯通利波与伪瑞雷波p-R波衰减明显。
当源处于5 m，第1个接收器在深度为7.59 m时，裂缝带和基质地层模型模拟的全波列数据用FBAPES（forward and backward amplitude phase estimation）算法[25]分析得到频散特征分别示于图11（a）和图11（b）。图中看到，在存在倾斜的地层模型中，深度为7.59 m处横波慢度增大明显，一阶伪瑞利波与斯通利波幅度衰减也较明显，但难以识别出二阶伪瑞利波。
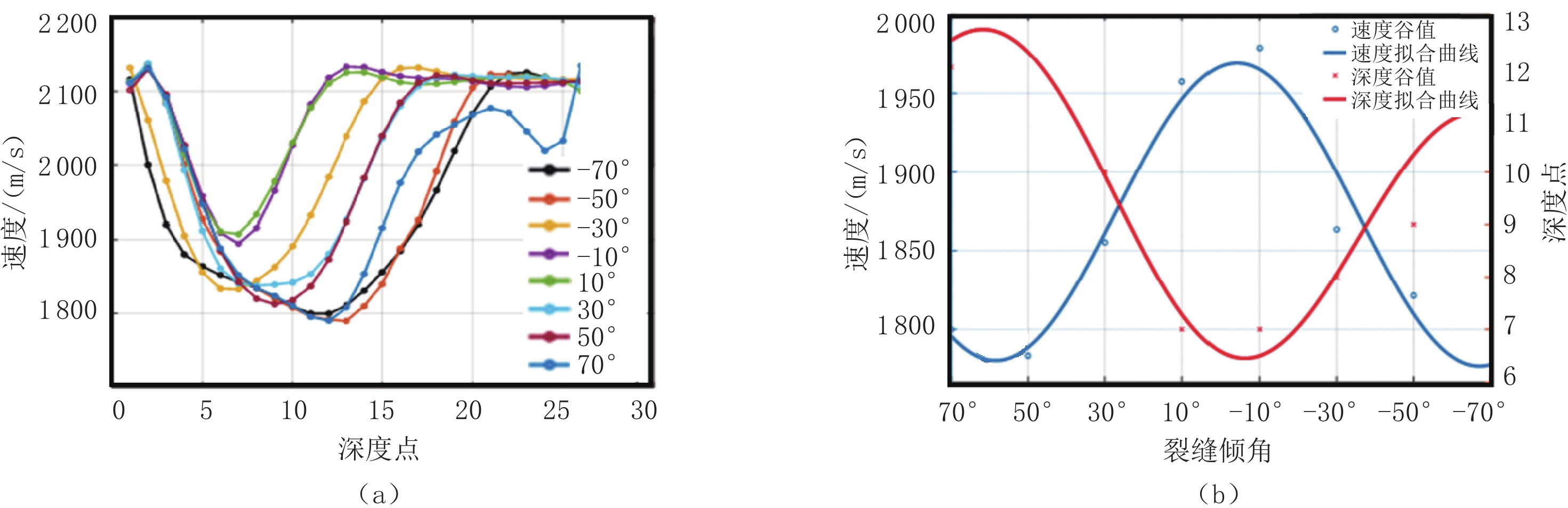
对8个不同倾角的裂缝带模型的数值模拟波形数据用慢度相关分析（slowness time correlation，STC）方法分别提取横波与纵波速度，（图12和图13）。由图12（a）可以看到，
$ {V}_{\rm s} $ 随着裂缝带倾角增大而减小，而且速度谷值逐渐增大。另外，图12（b）给出的速度曲线谷值对应的深度点也会随着裂缝带的倾角减小向慢速地层与井眼的交会深度点方向靠近。图13（a）看到，$ {V}_{\rm p} $ 的变化趋势与$ {V}_{\rm s}$ 的变化趋势相反，随着裂缝带倾角的减小速度也逐渐减小，图13（b）的速度曲线谷值对应的深度点也会随着裂缝带倾角的减小偏向远离裂缝带与井眼交会的深度点。![]()
图 13 8个不同倾角裂缝带地层模型的模拟波形用STC方法提取纵波速度谷值点随倾角与深度的变化注：（a）速度随裂缝带倾角与深度的变化，（b）速度谷值点随裂缝带倾角与深度的变化。Figure 13. STC analysis of simulated scenarios with different inclined sediments总体上，裂缝带倾角对
$ {V}_{\rm p} $ 变化的影响远远小于$ {V}_{\rm s} $ 这也表明阵列声波测井中偶极横波测量对于裂缝识别与定量评价的必要性。4.2 井壁坍塌扩径层段的波场响应
在钻井过程中，由于地层的卸压、应力释放和泥浆浸泡，井壁地层发生变形、破碎或坍塌，造成部分井段井径扩大，引起声波波场在扩径井段额外散射和衰减，造成扩径井段采集的波场信号与未扩径井段存在较大差异，表现出声波时差、速度频散与波场幅度的明显变化。下文对出现不同扩径深度范围与扩径幅度大小对声波波场影响进行模拟。对于两种扩径情况，采取相同的地层物性参数，在扩径处井中流体填充。
图14（a）为扩径发生的深度范围相同，径向扩径大小以
$\Delta r$ =0.1 m为间隔依次增大的地层模型和参数，图14（b）为径向扩径深度相同，纵向扩径深度从z1=7.59 m开始以dz=0.5 m为间隔依次增大的地层模型和参数。以阵列声波测井形式分别对5个地层模型进行模拟，采用井眼居中激发与测量的方式，参数与表3相同。图15（a）～图15（d）分别为不扩径和0.2、0.4和0.6 m径向扩径地层模型的全波列响应。图17（a）看到无扩径时波形的相位和幅度均一致。图15（b）～图15（d）表现出不同扩径深度时，波场响应存在微弱的差异，随着径向扩张深度$\Delta r$ 的增加，伪瑞利波急剧衰减。图15（c）看到，当$\Delta r$ =0.4 m时，几乎已经无法观测到直达斯通利波，但上下行斯通利波随着扩径界面的加深反射增强。在深度为8.59 m时分别对0.2 m扩径与0.6 m扩径模型采集到的模拟数据进行FBAPES分析，得到结果如图16（a）和图16（b），斯通利波与一阶伪瑞利波明显衰减。![]()
图 14 含径向（a）和纵向（b）扩径模拟地层配置示意图Figure 14. Scheme of simulated formation configurations with radial borehole enlargement (a) and vertical borehole enlargement (b)表 3 阵列声波测井模拟参数Table 3. Simulated parameters of inclined slow formation分区介质 分层位置 固相参数 流相参数 耦合参数 耗散参数 A11 A13 A44 $ \rho_{_{11}} $ R $ \rho_{_{22}} $ Q $ \rho_{_{12}} $ b 井中流体 0.1 R/m 2.25 2.25 0 1.00 0 1.00 0 0 0 快速地层 3.0 R/m 43.39 13.62 14.89 2.27 0.30 0.16 1 -0.06 1 坍塌填充 -7.0 Z/m 2.25 2.25 0 1.00 0 1.00 0 0 0 ![]()
图 15 （a）无扩径，（b）0.2 m扩径，（c）0.4 m扩径，（d）0.6 m扩径全波列数据Figure 15. Full waveform data of (a) no enlargement, and with enlargement of (b) 0.2 m, (c) 0.4 m and (d) 0.6 m![]()
图 17 （a）无扩径，（b）扩径范围0.4 m，（c）扩径范围0.8 m，（d）扩径范围1.2 m全波列数据Figure 17. Full waveform data with (a) no enlargement and enlargement of (b) 0.4 m, (c) 0.8 m and (d) 1.2 m![]()
图 16 （a）0.2 m扩径，（b）0.6 m扩径在8.59 m处的FBAPES结果Figure 16. FBAPES results at 8.59 m of (a) 0.2 m and (b) 0.6 m以阵列声波测井形式分别对5套地层进行模拟，采用井眼居中激发与测量的方式，其模拟参数与表3相同。由于扩径深度范围较大，可以从图17中看到有两道平行的一次反射斯通利波，它们是由图14（b）中z1和z2两个扩径突变点处上下界面产生的上下行斯通利波。比较图17（a）到图17（d）可知，不规则井眼的均匀地层深度范围中存在直达波和反射斯通利波。即均匀地层只要发生井径变化就能产生反射斯通利波，这一结论与徐冰等[29]的认识一致。
5. 结论
文中采用各向同性孔隙弹性介质模型与交错网格有限差分算法实现裂缝发育带与扩径井段的阵列声波测井波列响应的数值模拟，总结裂缝发育带与扩径井段的不同模式波的速度频散响应特征。基于含倾斜裂缝带模型与井壁坍塌地层模型的响应模拟，用前后向振幅相位估计法（FBAPES）分析阵列声波的波形幅度相位响应特征与速度频散的差异性，与实测储层的裂缝发育层段阵列声波测井响应的对比分析，得到了如下认识：
（1）针对高阶精度下对网格边界区域进行有限差分计算时边界区域精度降低的问题，应用洛必达极限近似解决极坐标系下离散波动方程在井轴处的奇异性，提出差分网格边界区域使用高阶插值的高精度计算方法，取得了良好应用效果。
（2）低速裂缝带对纵横波波场具有较大影响，不仅时差增大，波形幅度也有一定程度衰减，且衰减幅度随裂缝带倾角而变化。裂缝带倾角在30°～70° 之间时对纵波幅度衰减较大，对横波的幅度衰减相对较小，裂缝带倾角在0°～30° 与70°～90° 之间时，对纵波幅度衰减相对较小，而对横波幅度衰减较大，这是阵列声波波场对研究不同角度裂缝分布的物质基础。
（3）在井壁塌陷的扩径井段，随着径向与轴向上塌陷范围的变化，采集到的波列中斯通利波与伪瑞利波衰减逐渐增强，根据快纵波分析得到了衰减规律曲线。
尽管文中推导的2.5维各向异性波动方程，适用于裂缝各向异性的弹性波场模拟，限于计算效率文中采用了等效各向同性介质对裂缝带进行了近似，带来一定的误差。若需要更精细刻画裂缝的波场响应特征，任意各向异性裂缝的建模和用斯通利波进行地层物性参数分析是进一步研究的方向。
致谢：感谢中石油大港油田研究院丁娱娇提供应用实例中部分测试数据。
-
![]()
图 2 轴向对称性地层的配置（a）与非轴对称空间域离散化的交错网格剖分示意图（b）
Figure 2. Scheme of formation with (a) axial symmetric and (b) asymmetric staggered grids in a three-dimensional discretized space domain
![]()
图 7 有限差分数值解与经典波数积分解结果对比
Figure 7. Comparisons between FD numerical simulation results and those of a classic wave number integral
![]()
图 9 （a）基质地层，（b）30°，（c）50°，（d）70°倾斜裂缝带地层模型的波场模拟结果
Figure 9. (a) No slow formation, (b) inclined slow formation (dip = 30), (c) inclined slow formation (dip = 50), (d) inclined slow formation (dip = 70)
![]()
图 10 源处于5 m处时7.59 m处第1个接收器在4个模型中的全波波形
Figure 10. Waveforms of the first receiver when the source is at 5.0 and the receiver is at 7.59 m in four models
![]()
图 11 含50°倾角裂缝带与基质地层在7.59 m处的频率-慢度图
Figure 11. Dispersion plot velocity slowness at 7.59 m, (a) formation with an inclined fracture zone （dip=50） and （b） matrix formation
![]()
图 12 8个不同倾角裂缝带地层模型的模拟波形用STC方法提取横波速度谷值点随倾角与深度的变化
注：（a）速度随裂缝带倾角与深度的变化，（b）速度谷值点随裂缝带倾角与深度的变化。
Figure 12. STC analysis of simulated scenarios with different inclined sediments
![]()
图 13 8个不同倾角裂缝带地层模型的模拟波形用STC方法提取纵波速度谷值点随倾角与深度的变化
注：（a）速度随裂缝带倾角与深度的变化，（b）速度谷值点随裂缝带倾角与深度的变化。
Figure 13. STC analysis of simulated scenarios with different inclined sediments
![]()
图 14 含径向（a）和纵向（b）扩径模拟地层配置示意图
Figure 14. Scheme of simulated formation configurations with radial borehole enlargement (a) and vertical borehole enlargement (b)
![]()
图 15 （a）无扩径，（b）0.2 m扩径，（c）0.4 m扩径，（d）0.6 m扩径全波列数据
Figure 15. Full waveform data of (a) no enlargement, and with enlargement of (b) 0.2 m, (c) 0.4 m and (d) 0.6 m
![]()
图 17 （a）无扩径，（b）扩径范围0.4 m，（c）扩径范围0.8 m，（d）扩径范围1.2 m全波列数据
Figure 17. Full waveform data with (a) no enlargement and enlargement of (b) 0.4 m, (c) 0.8 m and (d) 1.2 m
![]()
图 16 （a）0.2 m扩径，（b）0.6 m扩径在8.59 m处的FBAPES结果
Figure 16. FBAPES results at 8.59 m of (a) 0.2 m and (b) 0.6 m
表 1 含倾斜慢速地层模型物性参数
Table 1 Simulated parameters of inclined slow formation
分区介质 分层位置 固相参数 流相参数 耦合参数 耗散参数 A11 A13 A44 $ \rho_{_{11}} $ R $ \rho_{_{22}} $ Q $ \rho_{_{12}} $ b 井中流体 0.1 R/m 2.25 2.25 0 1.00 0 1.00 0 0 0 基质地层 3.0 R/m 43.39 13.62 14.89 2.27 0.30 0.16 1 -0.06 1 慢速地层 -6.7 Z/m 8.00 2.24 2.88 2.08 0.30 0.16 1 -0.06 1 
下载: 导出CSV
表 2 阵列声波测井模拟参数
Table 2 Simulated schematic for array sonic logging
参数 取值 起始深度/m -11 结束深度/m -6 深度间隔/m 0.2 源类型 单极子源 子波类型 Ricker子波 采样点数 12000 采样间隔/μs 0.47 首接收器与源的距离/m 2.59 接收器间隔/m 0.152 接收器数量 8
下载: 导出CSV
表 3 阵列声波测井模拟参数
Table 3 Simulated parameters of inclined slow formation
分区介质 分层位置 固相参数 流相参数 耦合参数 耗散参数 A11 A13 A44 $ \rho_{_{11}} $ R $ \rho_{_{22}} $ Q $ \rho_{_{12}} $ b 井中流体 0.1 R/m 2.25 2.25 0 1.00 0 1.00 0 0 0 快速地层 3.0 R/m 43.39 13.62 14.89 2.27 0.30 0.16 1 -0.06 1 坍塌填充 -7.0 Z/m 2.25 2.25 0 1.00 0 1.00 0 0 0
下载: 导出CSV
-
[1] 漆立新. 塔里木盆地顺托果勒隆起奥陶系碳酸盐岩超深层油气突破及其意义[J]. 中国石油勘探, 2016, 21(3): 38-51. QI L X. Oil and gas break through in ultra-deep ordovician carbonate formations in Shuntuoguole, Uplift Tarim Basin[J]. China Petroleum Exploration, 2016, 21(3): 38-50. (in Chinese).
[2] 焦方正. 塔里木盆地顺北特深碳酸盐岩断溶体油气藏发现意义与前景[J]. 石油与天然气地质, 2018, 39(2): 207-216. JIAO F Z. Significance and prospect of ultra-deep carbonate fault karst reservoirs in Shunbei area, Tarim Basin[J]. Oil & Gas Geology, 2016, 39(2): 207-216. (in Chinese).
[3] 苏可嘉, 秦臻, 邓呈祥, 等. 致密砂岩裂缝填充识别及其测井响应特征——以鄂尔多斯盆地镇泾油田延长组为例[J]. 科学技术与工程, 2022, 22(21): 9095−9104. DOI: 10.3969/j.issn.1671-1815.2022.21.011. SU K J, QIN Z, DENG C X, et al. Fracture filling identification and logging response characteristics of tight sandstone: A case study of Yanchang Formation in Zhenjing oilfield, Ordos Basin[J]. Science Technology and Engineering, 2022, 22(21): 9095−9104. DOI: 10.3969/j.issn.1671-1815.2022.21.011. (in Chinese).
[4] 唐晓明, 魏周拓. 利用井中偶极声源远场辐射特性的远探测测井[J]. 地球物理学报, 2012, 55(8): 2798-2807. TANG X M, WEI Z T. Single-well acoustic reflection imaging using far-field radiation characteristics of a borehole dipole source[J]. Chinese Journal of Geophysics, 2012, 55(8): 2798-2807. (in Chinese).
[5] 陆云龙, 崔云江, 关叶钦, 等. 基于阵列声波测井的裂缝有效性定量评价方法[J]. 测井技术, 2022, 46(1): 64−70. LU Y L, CUI Y J, GUAN Y Q, et al. Quantitative evaluation method of fracture effectiveness based on array acoustic logging[J]. Well Logging Technology, 2022, 46(1): 64−70. (in Chinese).
[6] 张波, 李超, 张晋言, 等. 三维声波测井探测特性分析与处理技术应用[J]. 应用声学, 2021, 40(5): 774−784. ZHANG B, LI C, ZHANG J Y, et al. Analysis of detecting characteristics and application of data processing technology for 3D array acoustic logging[J]. Journal of Applied Acoustics, 2021, 40(5): 774−784. (in Chinese).
[7] 本建林, 车小花, 乔文孝, 等. 方位反射声波成像测井技术在井旁地质体评价中的应用[J]. 测井技术, 2021, 45(1): 23−29. BEN J L, CHE X H, QIAO W X, et al. Application of near borehole geologic reflector evaluation using azimuthal acoustic reflection imaging logging[J]. Well Logging Technology, 2021, 45(1): 23−29. (in Chinese).
[8] 楚泽涵, 徐凌堂, 尹庆文, 等. 远探测反射波声波测井方法实验研究进展[J]. 测井技术, 2005, 29(2): 98−101. DOI: 10.3969/j.issn.1004-1338.2005.02.003. CHU Z H, XU L T, YIN Q W, et al. Progress of lab study on remote exploration acoustic reflection logging methods[J]. Well Logging Technology, 2005, 29(2): 98−101. DOI: 10.3969/j.issn.1004-1338.2005.02.003. (in Chinese).
[9] 乔文孝, 车小花, 李刚, 等. 反射声波成像测井的物理模拟[J]. 石油物探, 2004, (3): 294-297. QIAO W X, CHE X H, LI G, et al. The physical modeling of acoustic reflection image logging[J]. Geophysical Prospecting for Petroleum, 2004, 43(3): 294-297. (in Chinese).
[10] 陶果, 何峰江, 王兵, 等. 声反射成像测井在地层中的三维波场模拟方法研究[J]. 中国科学(D辑: 地球科学), 2008, 38(S1): 166−173. TAO G, HE J F, WANG B. Study on numerical modeling of three-dimension wave field of acoustic reflection image logging in formation[J]. Science in China: Esrarth Science, 2008, 38(S1): 166−173. (in Chinese).
[11] TANG X M. Imaging near-borehole structure using directional acoustic-wave measurement[J]. Geophysics, 2004, 69(6): 1378−1386. DOI: 10.1190/1.1836812.
[12] TANG X M, PATTERSON D J. Single-well S-wave imaging using multicomponent dipole acoustic-log data[J]. Geophysics, 2009, 74(6): WCA211−WCA223. DOI: 10.1190/1.3227150.
[13] NOLTE B, CHENG A. Estimation of nonorthogonal shear wave polarizations and shear wave velocities from four-component dipole logs[R]. USA: The Annual Technology Report of The Earth Resources Laboratory (ERL), MIT, 1996.
[14] NOLTE B, RAO R, HUANG X J. Dispersion analysis of split flexural waves[R]. USA: The Annual Technology Report of the Earth Resources Laboratory (ERL), MIT, 1997.
[15] LI W, TAO G, MATUSZYK J P, et al. Forward and backward amplitude and phase estimation method for dispersion analysis of borehole sonic measurements[J]. Geophysics, 2015, 80(3): D295−D308. DOI: 10.1190/geo2014-0298.1.
[16] 王瑞甲, 乔文孝, 鞠晓东. 一种多通道声波测井信号频散分析方法[J]. 测井技术, 2012, 36(2): 135−140. DOI: 10.3969/j.issn.1004-1338.2012.02.006. WANG R J, QIAO W X, JU X D. A multi-channel acoustic logging signal dispersion analysis method[J]. Well Logging Technology, 2012, 36(2): 135−140. DOI: 10.3969/j.issn.1004-1338.2012.02.006. (in Chinese).
[17] 刘航, 陈彦竹, 姚梦麟, 等. 基于纵波频散谱的缝洞碳酸盐岩储层有效性评价[J]. 测井技术, 2021, 45(3): 330−335. LIU H, CHEN Y Z, YAO M L, et al. Effectiveness evaluation of fractured vuggy carbonate reservoir based on P-wave dispersion spectrum[J]. Well Logging Technology, 2021, 45(3): 330−335. (in Chinese).
[18] ZHANG C, CHEN D, HU H S, et al. A method for transforming aliased modes to true modes based on density clustering and Riemann sheets selection in acoustic logging dispersion inversion[J]. Geophysics, 2024, 89(1): D15−D29. DOI: 10.1190/geo2022-0706.1.
[19] CHEN D, GUAN W, ZHANG C, et al. High-resolution inversion for dispersion characteristics of acoustic logging waveforms[J]. Journal of Geophysics and Engineering, 2020, 17(3): 439−450. DOI: 10.1093/jge/gxaa003.
[20] GUAN W, HU H S, HE X. Finite-difference modeling of the monopole acoustic logs in a horizontally stratified porous formation[J]. Journal of the Acoustical Society of America, 2009, 125(4): 1942−1950. DOI: 10.1121/1.3081518.
[21] LI X F. PML absorbing boundary condition for seismic numerical modeling by convolutional differentiator in fluid-saturated porous media[J]. Journal of Earth Science, 2011, (22): 377−385.
[22] GUAN W, HU H S. The parameter averaging technique in finite-difference modeling of elastic waves in combined structures with solid, fluid and porous subregions[J]. Communications in Computational Physics, 2011, 10(3): 695-715.
[23] COLLINO F, TSOGKA C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 2001, 66(1): 294−307. DOI: 10.1190/1.1444908.
[24] PAN C D, ABUBAKAR A, HABASHY T M. An effective perfectly matched layer design for acoustic fourth-order frequency-domain finite-difference scheme[J]. Geophysical Journal International, 2012, 188(1): 211−222. DOI: 10.1111/j.1365-246X.2011.05244.x.
[25] WANG H, TAO G, SHANG X F, et al. Stability of finite difference numerical simulations of acoustic logging-while-drilling with different perfectly matched layer schemes[J]. Applied Geophysics, 2013, 10: 384−396. DOI: 10.1007/s11770-013-0400-6.
[26] 李宁, 王克文, 刘鹏, 等. 不同裂缝条件下斯通利波幅度衰减实验[J]. 石油勘探与开发, 2021, 48(2): 258−265. DOI: 10.11698/PED.2021.02.03. LI N, WANG K W, LIU P, et al. Experimental study on attenuation of Stoneley wave under different fracture factors[J]. Petroleum Exploration and Development, 2021, 48(2): 258−265. DOI: 10.11698/PED.2021.02.03. (in Chinese).
[27] 聂南方,郭智奇,刘财. 改进的地震AVAZ裂缝弱度反演方法及其在致密砂岩储层中的应用[J]. 地球与行星物理论评(中英文), 2024, 55(3): 358−368. DOI: 10.19975/j.dqyxx.2023-02. DOI: 10.19975/j.dqyxx.2023-025. Nie N F, Guo Z Q, Liu C. Application of the improved seismic AVAZ inversion method for fracture characterization of a tight sandstone gas reservoir in the Ordos Basin[J]. Reviews of Geophysics and Planetary Physics, 2024, 55(3): 358-368. DOI: 10.19975/j.dqyxx.2023-025. (in Chinese).
[28] 王晨光, 蔺学旻, 周显华, 等. 基于地震多属性融合的断层识别与评价——以塔里木盆地SHB地区碳酸盐岩缝洞型储层为例[J]. CT理论与应用研究, 2021, 30(1): 35−48. DOI: 10.15953/j.1004-4140.2021.30.01.04. WANG C G, LIN X M, ZHOU X H, et al. Fault detection and evaluation based on fusion of multiple seismic attributes——An example of fractured and vuggy carbonate formation in SHB area,tarimu basin[J]. CT Theory and Applications, 2021, 30(1): 35-48. DOI: 10.15953/j.1004-4140.2021.30.01.04. (in Chinese).
[29] 徐冰, 李文博, 王易安, 等. 不规则井眼的斯通利波反射数值模拟[J]. 科学技术与工程, 2012, 20(9): 2029-2032. XU B, LI W B, WANG Y, et al. Numerical simulation of stonely wave reflection in irregular borehole[J]. Science Technology and Engineering, 2012, 12(9): 2029-2032. (in Chinese).
-
期刊类型引用(1)
1. 李振宇，何碧竹，贠晓瑞，蔡志慧，张盛生，刘若涵，马绪宣，陈希节. 共和盆地东北部花岗岩型干热岩井下裂缝系统及其构造成因. 岩石学报. 2024(12): 3964-3983 . 
百度学术
其他类型引用(0)
计量
- 文章访问数: 230
- HTML全文浏览量: 40
- PDF下载量: 24
- 被引次数: 1
