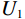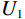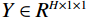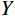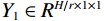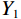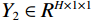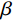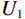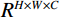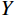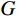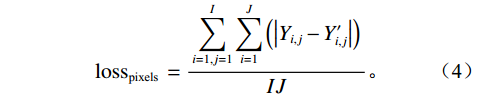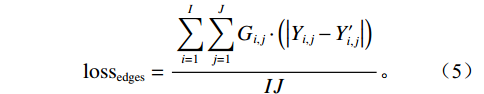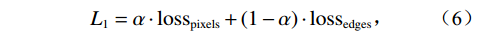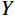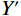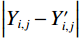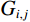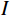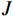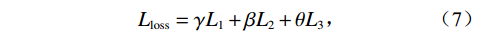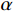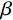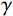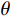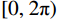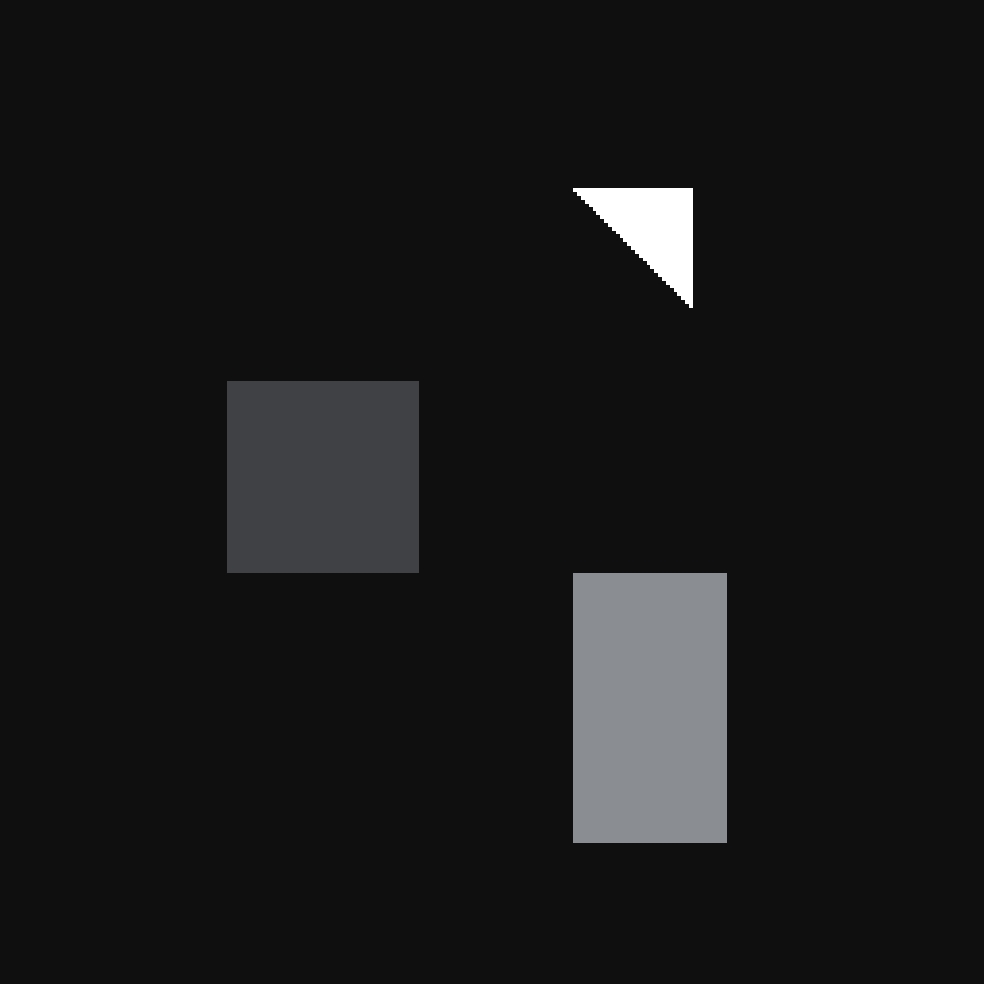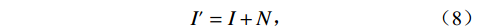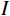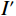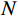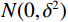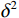Dense Sandstone Material Decomposition Based on Improved Convolutional Neural Network
-
摘要:
能谱CT能够提供扫描对象的定量信息，实现材料分解。基于神经网络的材料分解方法有效克服了传统迭代算法在分解效果上的局限性，但是在细节特征恢复方面仍存在不足。为了提高材料分解精度并保留图像的细节信息，我们提出一种基于残差挤压激励网络（RS-Net）的材料分解方法。本方法利用U-Net网络的结构，采用Resnet-152作为主干网络提取多尺度特征；利用并行非对称卷积来完成大核卷积，减少网络的参数数量和计算量；在解码器部分引入HD-SE注意力机制帮助网络恢复图像特征；采用混合损失监督网络学习，提高网络的分解精度。在仿真岩石数据集和人造砂岩数据集上验证该方法的可行性，仿真和实际实验结果表明，RS-Net结合混合损失保留更多图像内部细节信息，分解后的图像边缘更为清晰，图像质量更高。
Abstract:Energy spectrum computed tomography can provide quantitative information of scanned objects and realize material decomposition. At present, the material decomposition method based on neural networks overcomes the limited decomposition effect of traditional iterative algorithms. However, the performance of traditional neural networks in feature detail recovery is still not satisfactory. To improve the material decomposition accuracy, a material decomposition method based on a Resnet and Squeeze excitation network (RS-Net) is proposed. The proposed method uses the structure of the U-Net network and Resnet-152 as the backbone network to extract multi-scale features. Parallel asymmetric convolution is used to complete the large kernel convolution, which reduces the number of parameters and computation of the network. The HD-SE attention mechanism is introduced in the decoder part to help the network recover the image features. Hybrid loss supervised network learning is used to improve the decomposition accuracy of the network. The feasibility of this method is verified on simulated rock and artificial sandstone datasets. The simulation and experimental results show that RS-Net combined with mixing loss can retain more internal details of the image, the decomposed image edge is clearer, and the image quality is higher.
-
与传统CT相比，能谱CT可以通过材料分解来识别物质成分。材料分解算法是由阿尔瓦雷斯和马科夫斯基在1976年基于双能CT（dual-energy computed tomography, DECT）率先提出的[1]。随着能谱CT探测器的发展，更高精度的多材料分解算法应用而生[2-5]。
多材料分解（material decomposition, MD）算法已被开发用于双能和多能CT[6-7]。传统的多材料分解算法主要分为一步法和两步法，一步法即直接迭代的材料分解方法，该方法将多能材料分解与图像重建两个过程合并，降低了计算速度。两步法包括基于投影域和基于图像域的材料分解方法[8-9]。基于投影域的材料分解方法能够有效消除伪影，提高分解效果[10]，但是不同能量区间下投影数据失配会严重影响该方法的分解精度。基于图像域的材料分解方法的分解性能与重建算法密切相关[11]，图像域分解可以直接应用于商用多能 CT 扫描系统获取的图像。因此，本文主要研究基于图像域的材料分解方法。
近年来，神经网络在图像去噪、分割、检测、识别等各种成像应用中受到了广泛关注[12-14]。许多研究表明，神经网络通过特征学习和特征提取来解决识别问题，可有效地提高材料分解的效率和准确性。研究者们通过串联的深度神经网络以及改进的全卷积神经网络实现了双能CT的组分分解问题。Incept-Net提高了DECT材料的分解鲁棒性，克服了对剂量变化的敏感性，表现出良好的泛化能力[13]。基于改进的全卷积神经网络（FCDense-Net）的方法在多材料分解中表现出良好的性能，图像对比度和去噪在MD中得到了进一步的发展[14]。SeNAS-Net将Ne2 Ne引入多能CT材料分解中，在抑制能谱CT材料分解中的噪声和伪影方面具有良好的性能。已经开发的前馈神经网络投影分解技术，在仿真数据上成功实现了对多种材料的投影分解[15]。在此基础上，部分学者将传统的模型驱动的分解方法与数据驱动的神经网络相结合，构建联合模型驱动的深度学习方法，验证了神经网络方法具有更好的投影分解效果[16]。利用联合模型驱动的卷积神经网络进行能谱CT图像处理，可以避免传统重建方法的局限性，同时降低图像的噪声和伪影，从而提高了分解的准确性和效率[17-18]。
注意力机制在图像处理中已经成为一种流行方法，其独特的能力和优势主要体现在突出关键细节、抑制多余信息，进而增强表征能力。挤压激励（squeeze-and-excitation, SE）注意通过全局平均池化来学习特征关系，以获取通道维度上的上下文信息[19]。ECA-Net采用了一种局部跨通道交互策略，保持了通道特征的维度，有效避免了降维对通道特征的影响[20]。除了单通道注意机制外，卷积注意模块（convolutional block attention module, CBAM）结合通道注意力模块和空间注意力模块，充分利用它们之间的互补性，以获取重要信息并抑制无用信息[21]。
为了改进多能CT图像域材料分解方法，获得高质量的分解材料图像，本文提出一种基于卷积神经网络的RS-Net材料分解方法。RS-Net采用并行非对称卷积代替大核卷积提取多尺度特征图中的全局特征信息，并在多层特征图的融合过程中嵌入注意机制，利用HD-SE模块从图像中提取重要的特征，避免计算资源的浪费，引入混合损失监督网络学习，提高网络的效率。
1. 方法论述
1.1 图像域的材料分解模型
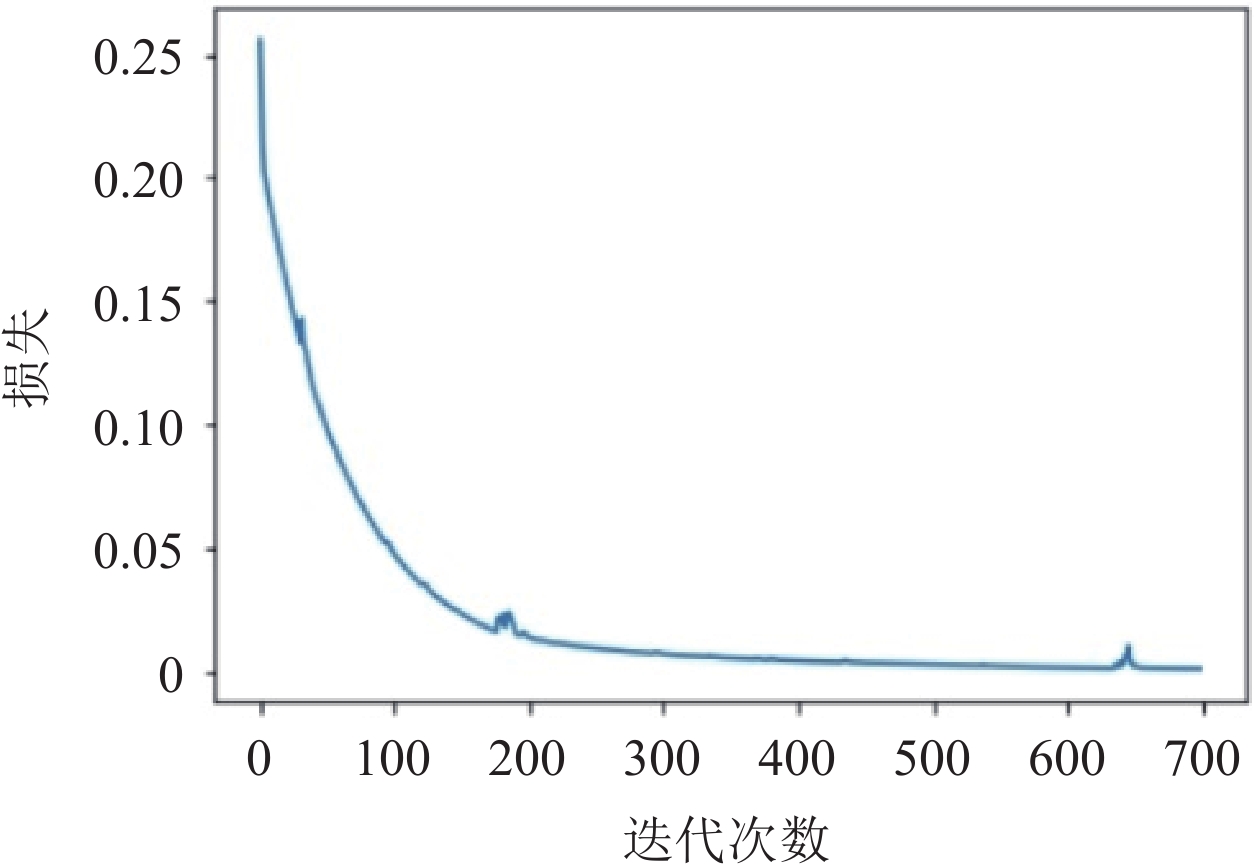
材料分解是通过分析X射线光子能量的吸收进而可以识别其成分。对于能量为E的单能量X射线，在位置
$\vec r$ 的线性衰减系数$ \mu (E,\stackrel{\rightharpoonup }{r}) $ ，可以分解为$k$ 个基本材料线性组合：$$ \mu (E,\stackrel{\rightharpoonup }{r})=\sum _{k=1}^{K}{a}_{k}(\stackrel{\rightharpoonup }{r})\;{\mu }_{k}(E)， $$ (1) 式中
${a_k}(\vec r)$ 为第$k$ 种材料在$\vec r$ 位置的体积分数。对于能谱CT图像，式（1）可表示为一个矩阵：$$ \left( \begin{gathered} \mu \left( {{E_1},\stackrel{\rightharpoonup } r } \right) \\ \quad\;\;\; \vdots \\ \mu \left( {{E_M},\stackrel{\rightharpoonup }r } \right) \\ \end{gathered} \right) = \left( {\begin{array}{*{20}{c}} {{\mu _1}({{\mathop E\limits^{} }_1})}& \cdots &{{\mu _K}({{\mathop E\limits^{} }_1})} \\ \vdots & \ddots & \vdots \\ {{\mu _1}({{\mathop E\limits^{} }_M})}& \cdots &{{\mu _K}({{\mathop E\limits^{} }_M})} \end{array}} \right) \left( {\begin{array}{*{20}{c}} {{a_1}\left( {\stackrel{\rightharpoonup } r } \right)} \\ \vdots \\ {{a_K}\left( {\stackrel{\rightharpoonup } r } \right)} \end{array}} \right)， $$ (2) 其中，
$m(1,\;2,\; \cdots,\; M)$ 表示能量通道。通过对基材料的衰减系数矩阵进行反求，可以很容易地得到材料分解映射矩阵。但是，矩阵（2）通常是病态的，轻微扰动会导致分解精度急剧下降。因此，引入可逆算子$ \mathcal{M} $ ，建立映射关系：$$ {\mathcal{M}^{ - 1}}:{\boldsymbol{\mu}} \mapsto {\boldsymbol{a}}， $$ (3) 这里
${\mathcal{M}^{ - 1}}$ 是图像域中混合算子的反演。在RS-Net网络中，以多通道重建图像作为输入，以单物质重建图像作为输出。因此，材料分解可以看作是一个成像逆问题。算子${\mathcal{M}^{ - 1}}$ 是解决问题的关键。1.2 基于RS-Net的材料分解模型
不同能量通道之间的能谱CT图像存在相似的结构特征，但它们所包含的衰减信息不同。因此，可以根据能谱CT图像的衰减差异和结构相关性构建足够大的数据集，并通过深度学习技术提高能谱CT图像中物质分解的精度。深度学习能够有效地进行特征信息的提取与学习，从而挖掘数据集中的内在规律和深层次特征。U-Net是专为语义分割而设计的，其结构包括收缩路径和扩张路径，为深度学习框架开辟了一条新的途径。
1.2.1 RS-Net网络结构
我们在U-Net算法的基础上，设计用于能谱CT图像材料分解的残差挤压激励网络（rsenet and squeeze excitation network, RS-Net）。RS-Net网络的结构如图1所示。网络将能谱CT图像输入，生成相应的物质分解预测图，同时通过引入边缘损失函数优化网络参数，使得图像边缘更加清晰。
RS-Net网络为U型网络。本研究采用Resnet-152作为RS-Net的骨干网，骨干网详细信息如表1所示。首先，输入图像经过卷积最大池化块（Convolutional and maxpool block, CMB）初步提取图像特征，之后从骨干网络的不同阶段提取输入的多尺度特征图。随后，采用全局卷积块（global convolutional block, GCB）提取特征图的全局信息，采用边界细化块（boundary refinement block, BRB）帮助模型学习特征图的边界信息。GCB采用大卷积核实现全局卷积，使每一层的特征信息与像素类别紧密相关。然而，较大卷积核的卷积运算在学习过程中会带来过多的计算和存储需求。因此，GCB采用并行非对称卷积来完成大核卷积，有效地减少了网络的参数数量和计算量。
表 1 骨干网络结构Table 1. Backbone network structure项目 Conv 2D（kerne_size,out_channels） CMB 3$ \times $3 Conv BN ReLU Maxpool, strid 2 Resnet152-layer0 $\left( \begin{gathered} 1 \times 1,\,64 \\ 3 \times 3,\,64 \\ 1 \times 1,\,256 \\ \end{gathered} \right) \times 3$ Resnet152-layer1 $\left( \begin{gathered} 1 \times 1,\,128 \\ 3 \times 3,\,128 \\ 1 \times 1,\,512 \\ \end{gathered} \right) \times 8$ Resnet152-layer2 $\left( \begin{gathered} 1 \times 1,\,256 \\ 3 \times 3,\,256 \\ 1 \times 1,\,1024 \\ \end{gathered} \right) \times 36$ Resnet152-layer3 $\left( \begin{gathered} 1 \times 1,\,512 \\ 3 \times 3,\,512 \\ 1 \times 1,\,2048 \\ \end{gathered} \right) \times 3$ 然后利用CTB（Conv 2D transpose block）反卷积上采样块对特征图进行上采样，并与特征图合并生成新的特征图。最后一个CB（convolutional block）生成最终的预测图，用于输出RS-Net的分解结果。GCB、BRB、CTB和CB的组成见表2。
表 2 GCB、BRB、CMB结构Table 2. GCB, BRB, and CMB structureGCB BRB CTB CB 1$ \times $16 Conv，16$ \times $1 Conv 3$ \times $3 Conv 3$ \times $3 Conv 3$ \times $3 Conv 3$ \times $3 Conv 16$ \times $1 Conv，1$ \times $16 Conv BN 3$ \times $3 Conv2 DTranspose 3$ \times $3 Conv ReLU 1.2.2 HD-SE模块结构
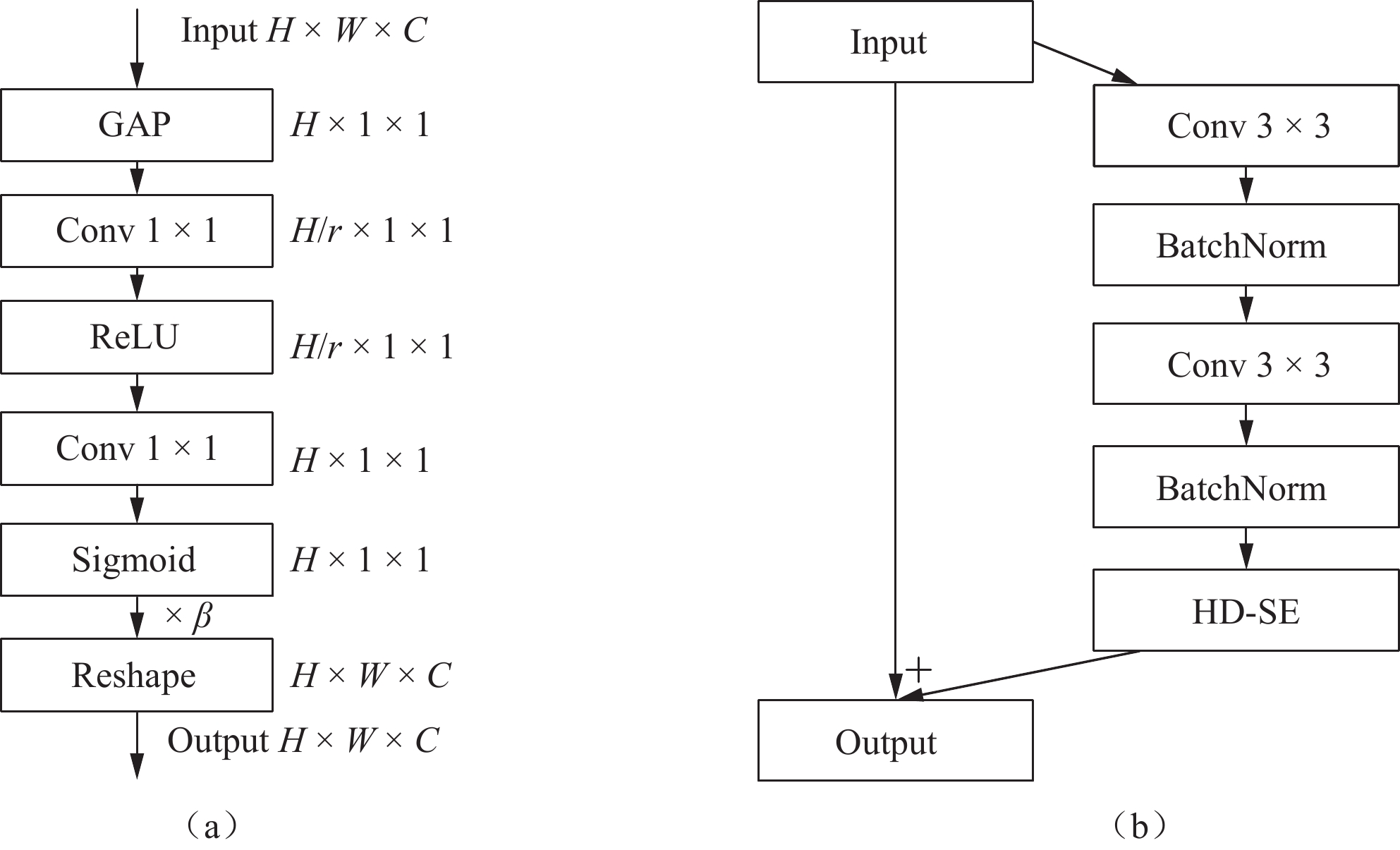
注意力机制能够赋予特征图不同的权重，从而有助于网络学习关键信息，使其在学习过程中作出更精确的决策。最近，注意机制已经成为执行深度学习任务的强大工具。我们引入HD-SE（height dimensional SE）模块，并将它们整合到网络中[22]。图2显示了HD-SE的结构及应用于RS-Net的结构。在RS-Net残差结构中，将 HD-SE嵌入于解码器块的第二个卷积操作之后，用来捕获更多的特征图隐藏的信息。
![]()
图 2 （a）HD-SE网络结构，（b）Resnet+HD-SE结构图Figure 2. (a) HD-SE network structure, (b) Resnet+HD-SE structure diagramHD-SE 模块将挤压激励操作应用于特征图的高度维度，进而捕获更多有用的信息，增强特征图张量的高度维度信息。在应用HD-SE模块之前，首先特征图
${U_1}$ 按照高度×宽度×通道输入，之后对${U_1}$ 使用全局平均池化进行挤压操作，得到$Y \in {R^{H \times 1 \times 1}}$ 特征向量；接着对$Y$ 降维得到${Y_1} \in {R^{H/r \times 1 \times 1}}$ ，最后采用升维卷积模块对${Y_1}$ 进行升维得到${Y_2} \in {R^{H \times 1 \times 1}}$ ；最后，将惩罚系数$\beta $ 运用到挤压激励后的${U_1}$ 中，恢复到原来的${R^{H \times W \times C}}$ 维度得到输出的特征图。1.2.3 损失函数
为了增强网络的材料分解性能，除考虑预测图像与标签图像在像素值上的对应外，还需要考虑基材料图像的边缘信息和纹理细节。鉴于此，提出使用混合损失函数监督网络学习。
边缘损失函数优化了重建图像的边缘像素，可以产生更清晰的图像。边缘损失函数分为基于像素的损失函数与基于结构的损失函数[23]。为了形成边缘损失分量，我们首先将Canny边缘检测器（使用Python默认参数）应用于原始训练图像
$Y$ 以获得边缘图$G$ 。Python默认Canny边缘检测器使用两个阈值来判断边缘像素是否是真正的边缘。如果边缘像素的梯度值超过高阈值，则被认为是强边缘；如果位于高低阈值之间，则被认为是弱边缘；如果低于低阈值，则被丢弃。基于像素的损失函数提高了重建图像的整体准确性，即像素值与原始图像的像素值直接相似。这确保了图像的颜色、明暗和整体对比度没有重大变化。函数如下：$$ \operatorname{loss}_{\text {pixels }}=\frac{\displaystyle\sum_{i=1, j=1}^{I} \displaystyle\sum_{i=1}^{J}\left(\left|Y_{i, j}-Y_{i, j}^{\prime}\right|\right)}{I J} 。$$ (4) 结构损失函数确保生成的图像具有清晰的、易于识别的边缘和结构。结构如下：
$$ {{{\mathrm{loss}}_{{\mathrm{edges}}}}}=\frac{\displaystyle\sum_{i=1}^I\displaystyle\sum_{j=1}^JG_{i,j}\cdot\left(\left|Y_{i,j}-Y_{i,j}'\right|\right)}{IJ}。 $$ (5) 总体损失为：
$$ {L_1} = \alpha \cdot {\mathrm{los}}{{\mathrm{s}}_{{\mathrm{pixels}}}} + (1 - \alpha ) \cdot {\mathrm{los}}{{\mathrm{s}}_{{\mathrm{edges}}}} ，$$ (6) 其中
$Y$ 和$Y'$ 分别是网络输出的图像和真实的图像，$\Big|{Y_{i,j}} - {Y'_{i,j}}\Big|$ 表示了输出图像与真实图像的对应像素点的绝对误差$ {G_{i,j}} $ 为提取的边缘图像，$I$ 和$J$ 分别为图像的宽度和高度此外，引入MSE和交叉熵损失函数共同监督网络学习。定义混合损失函数为：
$$ {L_{{\mathrm{loss}}}} = \gamma {L_1} + \beta {L_2} + \theta {L_3} ，$$ (7) 其中，
$\alpha $ 、$\beta $ 、$\gamma $ 和$\theta $ 表示权重。2. 实验设置与结果分析
我们提出的RS-Net是使用Keras和TensorFlow框架在GPU（NVIDIA RTX A6000）的计算机平台上实现的，该模型的学习率最初设置为1×10−5，在本研究中，使用Adam来优化损失函数。
为了评价所提出来的材料分解方法的性能，采用结构相似性指数（SSIM），峰值信噪比（PSNR）作为评估指标，判断预测结果和真实标签之间的相似性。
2.1 仿真模体实验
多能 X 射线由Spekpyv 2.0能谱仿真软件生成，仿真的X射线源为点源。X射线源距离旋转中心100 mm，探测器长度为20 mm，探测器共有256个单元，每次扫描在
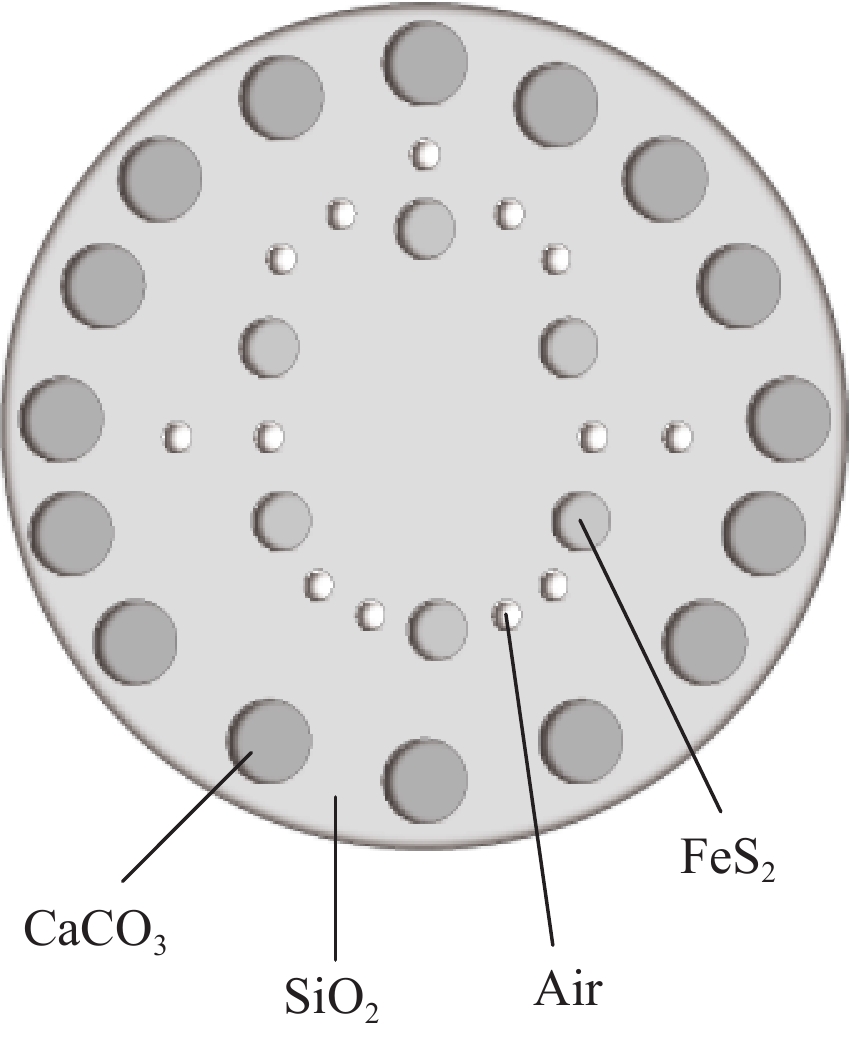
$[0,\,2\text{π})$ 范围内均匀采集256个角度的投影。图3为该实验设计的仿真模体结构，该模体包含空气（Air）、石英和钠长石（SiO2）、方解石（CaCO3）和黄铁矿（FeS2），图像大小为256×256。模体仿真实验在3个能量通道中进行，分别为：[20, 30）、[30, 40）和[40, 50）keV，共生成800组数据，其中700组用作数据集，100组用作测试集。
2.1.1 基本算法比较实验
收集测试数据集中的分解结果，比较传统U-Net，改进Inecpt-Net[13]和RS-Net的分解精度。为验证网络的性能，我们采用相同的数据集和训练次数。图4显示了3种网络的分解结果
![]()
图 4 不同方法图像域的分解结果，从上到下分别为SiO2、FeS2、CaCO3Figure 4. Decomposition results of image domains using different methods. From top to bottom: SiO2, FeS2, and CaCO3第一列图像为输入图像，第二列为真实值，第三~六列图像是每种方法对SiO2、FeS2和CaCO3的分解结果。从分解结果来看，U-Net方法和Incept_Net网络都不能得到理想的分解效果；提出的RS-Net方法在结合交叉熵损失时分解效果较U-Net方法和Incept_Net网络有显著提升，但是边缘效果不好，在SiO2的分解效果中可以很明显的看出；RS-Net方法结合边缘损失可以更好的恢复边缘信息并提高分解精度。表3为定量分析的结果。
表 3 不同方法下图像域多材料分解的定量测量结果Table 3. Quantitative measurement results of projection domain multi-material decomposition using different methods材料 方法 U-Net Incept-Net RS-Net交叉熵损失 RS-Net混合损失 SiO2 SSIM 0.6066 0.4616 0.4823 0.9550 PSNR 28.0910 27.9885 29.2897 29.8026 FeS2 SSIM 0.6924 0.6033 0.7823 0.9703 PSNR 37.1515 32.9031 36.0319 37.7823 CaCO3 SSIM 0.3748 0.5835 0.6381 0.9656 PSNR 28.1097 30.8245 32.1277 33.8001 定量分析结果显示，改进后的RS-Net算法具有更高的SSIM值和PSNR值，在3种成分的结构相似度分别达到了较高的
0.9550 、0.9703 和0.9656 。尤其FeS2的PSNR值达到了37.7823 。改进RS-Net在SiO2上的分解效果次于FeS2和CaCO3这可能是因为SiO2内部结构复杂导致的。定性和定量的评估表明，所提出的RS-Net具有优越的性能。这意味着该算法在分解含有SiO2、FeS2、CaCO3的岩石方面表现更佳。2.1.2 衰减系数相似实验
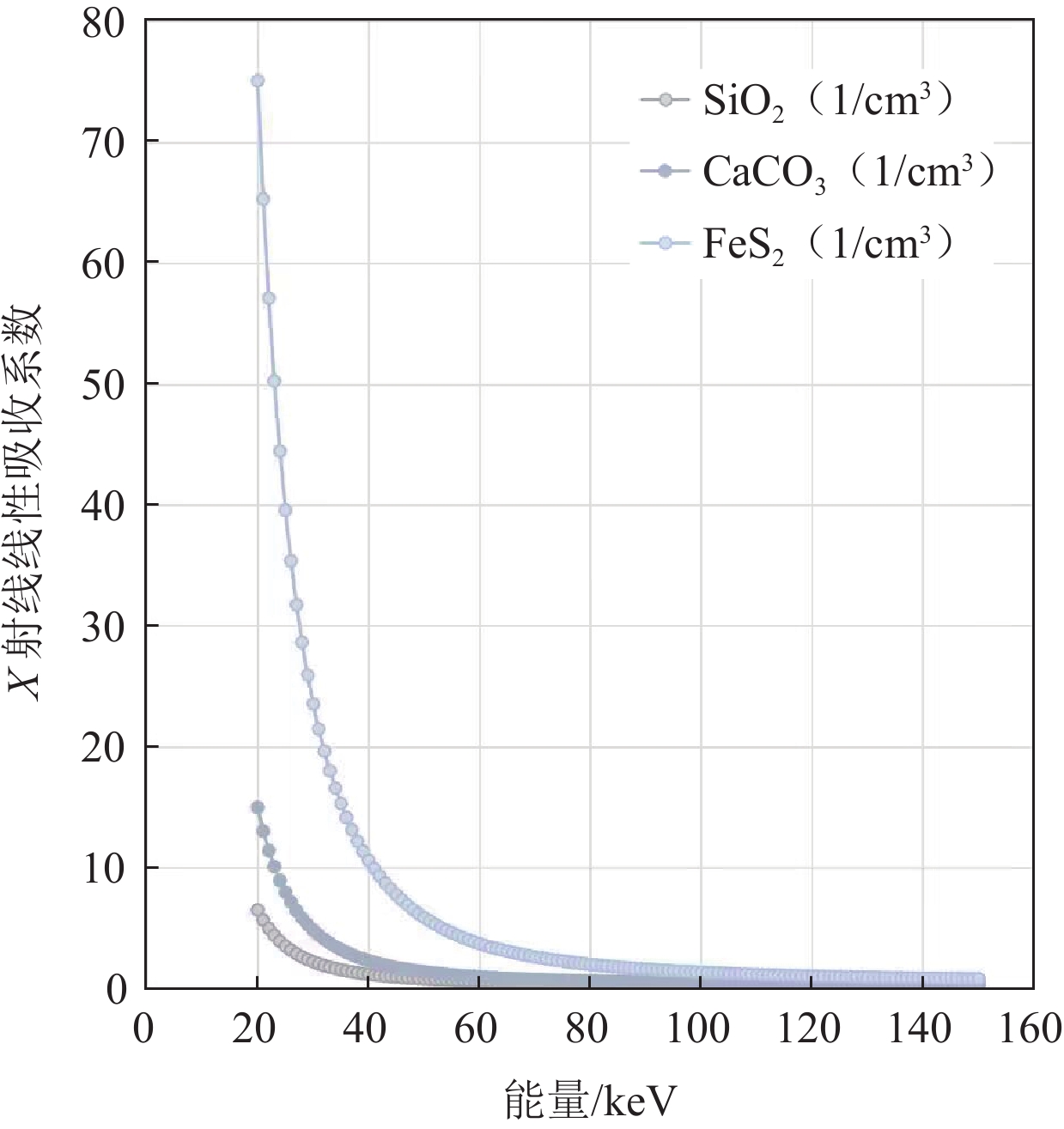
为了验证提出方法对衰减系数相近的材料的分解效果，将模体仿真实验在3个能量通道中进行，分别为：[60, 80）、[80, 100）和[100, 120）keV中进行。在这3个能量段下，石英和钠长石（SiO2）、方解石（CaCO3）和黄铁矿（FeS2）这3种物质的衰减系数相近（图5）。
如图6为在[60, 80）、[80, 100）和[100, 120）keV 3个能量段下的训练集样例。
为验证网络的泛化性能，采用的测试集的数据在训练集中完全没有出现过，即测试集中的数据是完全独立于训练集数据的。实验结果如图7所示。
从分解结果来看，当测试集与训练集存在较大差异时，U-Net方法和Incept_Net网络的分解效果较差，尤其是在SiO2的分解上尤为明显。提出的RS-Net方法在结合交叉熵损失后，相较于U-Net和Incept_Net方法，分解效果有了显著提升。然而，RS-Net方法在边缘效果方面仍有不足，特别是在SiO2右侧的圆形区域和FeS2上侧的椭圆形区域都可以观察到这一点。通过结合边缘损失，RS-Net方法能够更好地恢复边缘信息，提高分解精度。定量分析结果见表4。
表 4 测试集分解定量结果Table 4. Quantitative results of test set decomposition材料 方法 U-Net Incept-Net RS-Net交叉熵损失 RS-Net混合损失 SiO2 SSIM 0.8875 0.9034 0.9946 0.9989 PSNR 37.6035 40.3960 48.7807 49.8026 FeS2 SSIM 0.9684 0.9553 0.9959 0.9986 PSNR 45.3823 44.9185 48.1235 49.6732 CaCO3 SSIM 0.9879 0.9795 0.9779 0.9970 PSNR 47.8170 45.0905 44.7654 49.3658 根据表中的数据分析，RS-Net结合混合损失在所有测试材料中的表现均优于其他方法。在SiO2的分解中，RS-Net结合混合损失显示出最佳的分解效果，明显超越了U-Net和Incept-Net。类似地，在FeS2的分解中，RS-Net结合混合损失也表现出最优的结果，表明在恢复结构信息方面具有显著优势。总体来说，RS-Net结合混合损失在各种材料的分解精度上都表现最佳，优于U-Net和Incept-Net，尤其在细节恢复和结构准确性方面具有显著优势。
为了更客观地评估模型的性能，实验中，新建模体如图8所示，其中正方形为SiO2，长方形为CaCO3，三角形FeS2。为值得注意的是，该模体只在测试阶段被使用，并没有被包含在用来训练模型的数据集中，即测试集中的数据是完全独立于训练集数据的。实验结果如图9所示。
从分解结果来看，当测试集与训练集之间存在显著差异时，U-Net 方法和 Incept_Net 网络的分解效果表现较差。具体来说，U-Net 方法无法有效分解 FeS2，而对于 SiO2，虽然整体框架有所呈现，但效果仍不理想。Incept_Net 网络虽然能整体分解目标，但仍存在一定的分解错误，且边缘效果不佳。相对而言，提出的 RS-Net 方法在结合交叉熵损失函数后，相比 U-Net 和 Incept_Net，显著减少分解错误，提升分解效果。然而，RS-Net 方法在边缘效果方面仍有不足，尤其是在FeS2和CaCO3的直线区域表现较差。结合边缘损失函数后，RS-Net在恢复边缘信息和提高分解精度方面取得了进展，在直线区域效果较好，但由于训练数据集中只有圆形数据，对测试集中数据的顶点部分效果恢复不佳，例如 SiO2 的四个角信息恢复效果不理想。表5显示了定量分析的结果。
表 5 新增测试集分解定量结果Table 5. Added quantitative results of test set decomposition材料 方法 U-Net Incept-Net RS-Net交叉熵损失 RS-Net混合损失 SiO2 SSIM 0.9353 0.9769 0.9867 0.9987 PSNR 52.9134 51.7182 55.9413 67.0735 FeS2 SSIM 0.8928 0.9340 0.9281 0.9597 PSNR 51.3739 51.4266 54.9261 57.7916 CaCO3 SSIM 0.9304 0.9364 0.9285 0.9806 PSNR 52.7683 52.9481 53.9886 56.4517 定量分析结果显示，虽然Incept-Net的整体表现略优于U-Net，但差距并不明显。两者在所有材料的SSIM与PSNR值都低于RS-Net。RS-Net在所有材料的分解效果上均表现最佳，尤其在结合混合损失后，进一步提高网络的分解精度。其中，SiO2的分解效果明显优于FeS2和CaCO3在，这表明不同材料的特性对分解效果有直接影响。但是该实验的效果没有圆形仿真实验的效果好，这可能是因为训练集中没有方形数据造成的，之后的研究要更进一步提高网络的泛化性能。
2.1.3 加噪实验
为了进一步研究所提出的RS-Net对噪声是否敏感，将高斯噪声引入到图像中。
$$ {I'} = I + N ，$$ (8) 其中
$I$ 表示加噪前的图像；${I'}$ 表示加噪后的图像；$N$ 服从$N(0,{\delta ^2})$ 的高斯分布，0表示噪声平均值为0，不偏离原图像亮度，${\delta ^2}$ 表示噪声强度，文中取值为0.6。加噪后的图像域图像如图10所示。加噪后的图像域分解结果如图11所示。
![]()
图 10 加噪后的3个能量段下的图像域的图像Figure 10. Images in the image domain under three energy levels after adding noise![]()
图 11 加噪后的3个能量段下的图像域分解的图像Figure 11. Decomposed images in the image domain under three energy levels after adding noise从实验结果来看，本文提出的RS-Net在噪声抑制方面有很好的效果，从分解结果来看，在SiO2上效果更好。该网络能有效抑制噪声和伪影。
2.1.4 消融实验
为了判断HD-SE模块对网络的影响，引入消融实验，由于HD-SE关注模块具有良好的兼容性和稳定性，可以很好地提取图像的全局信息，并在各个方向上提高网络性能。在消融实验中，我们引入HD-SE注意机制来修正网络。根据HD-SE模块的不同位置，本文提出了3种方案：一是在编码器和解码器的对称位置添加HD-SE模块；二是在编码器中添加HD-SE模块；三是在解码器块中添加HD-SE模块。结果如图12所示。
实验结果表明，在编码器和解码器的对称位置添加HD-SE模块，由于对称位置HD-SE模块会产生对消效应，这种方案效果并不理想。在编码器中添加HD-SE模块，虽然该方案避免了模块间的抵消效应，但HD-SE模块在下采样过程中图像特征缩小而加速了特征信息的丢失。在解码器中添加HD-SE模块，该解决方案可以发挥出关注模块的优势，有效提高基材料分解的准确性和质量。
图13展示了RS-Net经过700次迭代后的损失变化情况。
从图中可以观察到，在大约进行了175次迭代后，损失值开始趋于稳定。尽管在训练过程中，损失值存在轻微波动，但总体上呈现出持续下降的趋势。此外，随着训练的进行，模型参数的更新幅度逐渐减小，表明模型的学习过程逐渐收敛。这种现象使得模型能够更快地收敛到最优解，同时避免了由于学习率过大而引起的权重更新误差。
2.2 人造砂岩样品实验
为评估所提出的RS-Net在图像域的分解效果，实验采用人造砂岩样品，样品由碳酸钙和石英制作而成，CT实验所用设备为天津三英精密仪器股份有限公司的NanoVoxel-
3000 HX射线三维高分辨成像系统，70 kVp的管电压，在两个能量通道中进行，分别为：[25, 35）keV，[45, 55）keV。射线源到物体的距离为14.6 mm，射线源到探测器的距离为648.9 mm。模型假设孔隙、碳酸钙和二氧化硅3种组分在人造砂岩样品的CT体元中以不同体积分数存在，并且人造砂岩中每一体元对X射线的吸收与该体元中孔隙、碳酸钙和二氧化硅对X射线吸收之和相等[24]。选取第200~349层共150张CT切片训练网络，选取第400~419层共20张CT切片测试网络。图14展示了不同能量段下训练数据样本示例。图15展示了不同方法的分解结果。
![]()
图 14 不同能量段下训练数据样本示例Figure 14. Examples of training data samples under different energy segments![]()
图 15 人造砂岩样品实验结果。从上到下分别为CaCO3、SiO2、融合后的图像Figure 15. Experimental results of artificial sandstone samples. From top to bottom: CaCO3, SiO2, and pores实验中，只分解CaCO3和SiO2，空白部分作为孔隙。比较传统U-Net，改进Inecpt-Net和RS-Net的分解精度不同方法的分解结果彩色表示如图15所示。
图15第1列为实际的CaCO3、SiO2，第2列和第3列分别为传统U-Net方法和Incept-Net方法分解结果，实验表明在CaCO3、SiO2上分解结果都不准确，在Incept-Net方法融合图像中可以很明显看到有重合部分。第4列为采用提出的RS-Net网络结合交叉熵损失函数的分解结果，在边缘部分分解精度不高。第5列为采用提出的RS-Net网络结合混合损失函数的分解结果分解精度，从整体上看，效果更好，边缘和内部信息更加清晰完整，整体更接近真实值，提供了更多重要的细节信息和更好的视觉效果。定量分析结果如表6所示。
表 6 不同方法分解效果的定量分析结果Table 6. Quantitative analysis results of decomposition effect of different methods材料 方法 U-Net Incept-Net RS-Net交叉熵损失 RS-Net混合损失 CaCO3 SSIM 0.4979 0.5859 0.8216 0.9590 PSNR 30.8033 32.2043 33.4598 33.9354 SiO2 SSIM 0.9073 0.8653 0.9638 0.9790 PSNR 31.9615 31.1594 32.7502 33.2538 表6展示了使用不同方法进行图像分解后的定量分析结果，比较U-Net网络、Incept-Net网络、RS-Net网络结合交叉熵损失函数和RS-Net网络结合混合损失函数的性能，结果显示，U-Net网络和Incept-Net网络在分解内部结构较复杂的人造砂岩时，SSIM和PSNR值都偏低，RS-Net结合交叉熵损失函数分解精度在一定程度上有提高，但是整体效果没有RS-Net结合混合损失的效果好，在分解结构较复杂的人造砂岩时，SiO2的SSIM值也可达0.979。
3. 结论
本文提出了一种基于卷积神经网络的深度学习策略（RS-Net），用于解决在材料分解算法中，材料分解精度不高问题。该方法采用全局卷积块和边界细化块来实现全局卷积。在解码器部分增加HD-SE模块，对每个高度维度的同一位置赋予不同的权重，提取不同高度维度的特征信息。对比了U-Net、Incept-Net网络、RS-Net网络结合交叉熵损失函数和RS-Net网络结合混合损失函数的物质分解效果，结果表明，本文提出的RS-Net算法在SSIM值和PSNR值上均表现出更好的性能，能有效抑制噪声。但是，对于内部结构较为复杂的材料，分解精度还有待提升，本文后续会针对该问题做进一步研究。
综上所述，RS-Net算法在提高材料分解精度方面具有很大的潜力，可为相关研究和应用提供有力支持。
-
![]()
图 2 （a）HD-SE网络结构，（b）Resnet+HD-SE结构图
Figure 2. (a) HD-SE network structure, (b) Resnet+HD-SE structure diagram
![]()
图 4 不同方法图像域的分解结果，从上到下分别为SiO2、FeS2、CaCO3
Figure 4. Decomposition results of image domains using different methods. From top to bottom: SiO2, FeS2, and CaCO3
![]()
图 10 加噪后的3个能量段下的图像域的图像
Figure 10. Images in the image domain under three energy levels after adding noise
![]()
图 11 加噪后的3个能量段下的图像域分解的图像
Figure 11. Decomposed images in the image domain under three energy levels after adding noise
![]()
图 14 不同能量段下训练数据样本示例
Figure 14. Examples of training data samples under different energy segments
![]()
图 15 人造砂岩样品实验结果。从上到下分别为CaCO3、SiO2、融合后的图像
Figure 15. Experimental results of artificial sandstone samples. From top to bottom: CaCO3, SiO2, and pores
表 1 骨干网络结构
Table 1 Backbone network structure
项目 Conv 2D（kerne_size,out_channels） CMB 3$ \times $3 Conv BN ReLU Maxpool, strid 2 Resnet152-layer0 $\left( \begin{gathered} 1 \times 1,\,64 \\ 3 \times 3,\,64 \\ 1 \times 1,\,256 \\ \end{gathered} \right) \times 3$ Resnet152-layer1 $\left( \begin{gathered} 1 \times 1,\,128 \\ 3 \times 3,\,128 \\ 1 \times 1,\,512 \\ \end{gathered} \right) \times 8$ Resnet152-layer2 $\left( \begin{gathered} 1 \times 1,\,256 \\ 3 \times 3,\,256 \\ 1 \times 1,\,1024 \\ \end{gathered} \right) \times 36$ Resnet152-layer3 $\left( \begin{gathered} 1 \times 1,\,512 \\ 3 \times 3,\,512 \\ 1 \times 1,\,2048 \\ \end{gathered} \right) \times 3$ 
下载: 导出CSV
表 2 GCB、BRB、CMB结构
Table 2 GCB, BRB, and CMB structure
GCB BRB CTB CB 1$ \times $16 Conv，16$ \times $1 Conv 3$ \times $3 Conv 3$ \times $3 Conv 3$ \times $3 Conv 3$ \times $3 Conv 16$ \times $1 Conv，1$ \times $16 Conv BN 3$ \times $3 Conv2 DTranspose 3$ \times $3 Conv ReLU
下载: 导出CSV
表 3 不同方法下图像域多材料分解的定量测量结果
Table 3 Quantitative measurement results of projection domain multi-material decomposition using different methods
材料 方法 U-Net Incept-Net RS-Net交叉熵损失 RS-Net混合损失 SiO2 SSIM 0.6066 0.4616 0.4823 0.9550 PSNR 28.0910 27.9885 29.2897 29.8026 FeS2 SSIM 0.6924 0.6033 0.7823 0.9703 PSNR 37.1515 32.9031 36.0319 37.7823 CaCO3 SSIM 0.3748 0.5835 0.6381 0.9656 PSNR 28.1097 30.8245 32.1277 33.8001
下载: 导出CSV
表 4 测试集分解定量结果
Table 4 Quantitative results of test set decomposition
材料 方法 U-Net Incept-Net RS-Net交叉熵损失 RS-Net混合损失 SiO2 SSIM 0.8875 0.9034 0.9946 0.9989 PSNR 37.6035 40.3960 48.7807 49.8026 FeS2 SSIM 0.9684 0.9553 0.9959 0.9986 PSNR 45.3823 44.9185 48.1235 49.6732 CaCO3 SSIM 0.9879 0.9795 0.9779 0.9970 PSNR 47.8170 45.0905 44.7654 49.3658
下载: 导出CSV
表 5 新增测试集分解定量结果
Table 5 Added quantitative results of test set decomposition
材料 方法 U-Net Incept-Net RS-Net交叉熵损失 RS-Net混合损失 SiO2 SSIM 0.9353 0.9769 0.9867 0.9987 PSNR 52.9134 51.7182 55.9413 67.0735 FeS2 SSIM 0.8928 0.9340 0.9281 0.9597 PSNR 51.3739 51.4266 54.9261 57.7916 CaCO3 SSIM 0.9304 0.9364 0.9285 0.9806 PSNR 52.7683 52.9481 53.9886 56.4517
下载: 导出CSV
表 6 不同方法分解效果的定量分析结果
Table 6 Quantitative analysis results of decomposition effect of different methods
材料 方法 U-Net Incept-Net RS-Net交叉熵损失 RS-Net混合损失 CaCO3 SSIM 0.4979 0.5859 0.8216 0.9590 PSNR 30.8033 32.2043 33.4598 33.9354 SiO2 SSIM 0.9073 0.8653 0.9638 0.9790 PSNR 31.9615 31.1594 32.7502 33.2538
下载: 导出CSV
-
[1] ALVAREZ R E, MACOVSKI A. Energy-selective reconstructions in X-ray computerised tomography[J]. Physics in Medicine and Biology, 1976, 21(5): 733-744. DOI: 10.1088/0031-9155/21/5/002.
[2] GENG M, TIAN Z, JIANG Z, et al. PMS-GAN: Parallel multi-stream generative adversarial network for multi-material decomposition in spectral computed tomography[J]. IEEE Transactions on Medical Imaging, 2021, 40(2): 571-584. DOI: 10.1109/TMI.2020.3031617.
[3] FANG W, WU D, KIM K, et al. Iterative material decomposition for spectral CT using self-supervised Noise2Noise prior[J]. Physics in Medicine and Biology, 2021, 66(15): 155013. DOI: 10.1088/1361-6560/ac0afd.
[4] YAO Y, LI L, CHEN Z. Dynamic-dual-energy spectral CT for improving multi-material decomposition in image-domain[J]. Physics in Medicine and Biology, 2019, 64(13): 135006. DOI: 10.1088/1361-6560/ab196d.
[5] BARBER R F, SIDKY E Y, SCHMIDT T G, et al. An algorithm for constrained one-step inversion of spectral CT data[J]. Physics in Medicine and Biology, 2016, 61(10): 3784-3818. DOI: 10.1088/0031-9155/61/10/3784.
[6] LEHMANN L A, ALVAREZ R E, MACOVSKI A, et al. Generalized image combinations in dual kVP digital radiography[J]. Medical Physics, 1981, 8(5): 659-667. DOI: 10.1118/1.595025.
[7] LI Z, LENG S, YU L, et al. Image-based material decomposition with a general volume constraint for photon-counting CT[A]. Proceedings of SPIE the International Society for Optical Engineering, 2015, 94120T.
[8] SUKOVIC P, CLINTHORNE N H. Penalized weighted least-squares image reconstruction for dual energy X-ray transmission tomography[J]. IEEE Transactions on Medical Imaging, 2000, 19(11): 1075-1081. DOI: 10.1109/42.896783.
[9] HEISMANN B J, LEPPERT J, STIERSTORFER K. Density and atomic number measurements with spectral X-ray attenuation method[J]. Journal of Applied Physics, 2003, 94(3): 2073-2079. DOI: 10.1063/1.1586963.
[10] SCHLOMKA J P, ROESSL E, DORSCHEID R, et al. Experimental feasibility of multi-energy photon-counting K-edge imaging in pre-clinical computed tomography[J]. Physics in Medicine and Biology, 2008, 53(15): 4031-4047. DOI: 10.1088/0031-9155/53/15/002.
[11] CARMI R, NAVEH G, ALTMAN A. Material separation with dual-layer CT[A]. IEEE Nuclear Science Symposium Conference Record, 2005, 1876-1878. DOI: 10.1109/NSSMIC.2005.1596697.
[12] WANG G. A perspective on deep imaging[J]. IEEE Access, 2016, 4: 8914-8924. DOI: 10.1109/ACCESS.2016.2624938.
[13] GONG H, TAO S, RAJENDRAN K, et al. Deep-learning-based direct inversion for material decomposition[J]. Medical Physics, 2020, 47(12): 6294-6309. DOI: 10.1002/mp.14523.
[14] WU X, HE P, LONG Z, et al. Multi-material decomposition of spectral CT images via Fully Convolutional DenseNets[J]. Journal of X-ray Science and Technology, 2019, 27(3): 461-471. DOI: 10.3233/XST-190500.
[15] JI X, LU Y, ZHANG Y, et al. SeNAS-Net: Self-supervised noise and artifact suppression network for material decomposition in spectral CT[J]. IEEE Transactions on Computational Imaging, Computational Imaging, IEEE Transactions on, IEEE Trans Comput Imaging, 2024, 10: 677-689. DOI: 10.1109/TCI.2024.3394772.
[16] 王冲旭, 陈平, 潘晋孝, 等. 基于迭代残差网络的双能CT图像材料分解研究[J]. CT理论与应用研究, 2022, 31(1): 47-54. DOI: 10.15953/j.1004-4140.2022.31.01.05. WANG C X, CHEN P, PAN J X, et al. Research on material decomposition of dual-energy CT images based on iterative residual network[J]. CT Theory and Applications, 2022, 31(1): 47-54. DOI: 10.15953/j.1004-4140.2022.31.01.05. (in Chinese).
[17] ZIMMERMAN K C, SCHMIDT T G. Experimental comparison of empirical material decomposition methods for spectral CT[J]. Physics in Medicine and Biology, 2015, 60(8): 3175-3191. DOI: 10.1088/0031-9155/60/8/3175.
[18] NADKARNI R, ALLPHIN A, CLARK D P, et al. Material decomposition from photon-counting CT using a convolutional neural network and energy-integrating CT training labels[J]. Physics in Medicine and Biology, 2022, 67(15): 155003. DOI: 10.1088/1361-6560/ac7d34.
[19] HU J, SHEN L, SAMUEL A, et al. Squeeze-and-excitation networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(8): 2011-2023.
[20] WANG Q L, WU B G, ZHU P F, et al. ECA-Net: Efficient channel attention for deep convolutional neural networks[C]// 2020 IEEE Transaction on Pattern Analysis and Machine Intelligence. 2020: 11531–11539. DOI: 10.1109/TPAMI.2019.2913372.
[21] WOO S, PARK J, LEE J Y, et al. CBAM: Convolutional block attention module[C]//Lecture Notes in Computer Science, 2018: 3-19. DOI: 10.1007/978-3-030-01234-2_1.
[22] 吕振虎, 许新征, 张芳艳. 基于挤压激励的轻量化注意力机制模块[J]. 计算机应用, 2022, 42(8): 2353-2360. DOI: 10.11772/j.issn.1001-9081.2021061037. LV Z H, XU X Z, ZHANG F Y. Lightweight attention mechanism module based on squeeze incentive[J]. Computer Applications, 2022, 42(8): 2353-2360. DOI: 10.11772/j.issn.1001-9081.2021061037. (in Chinese).
[23] SEIF G, ANDROUTSOS D. Edge-based loss function for single image super-resolution[A]. 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). 2018: 1468-1472. DOI: 10.1109/ICASSP.2018.8461664.
[24] 王晋庥, 王海鹏, 刘锐, 等. 人造砂岩样品多尺度微观结构表征和流体流动模拟[J]. 山西大学学报(自然科学版), 2023, 46(6): 1378-1385. DOI: 10.13451/j.sxu.ns.2023030. WANG J X, WANG H P, LIU R, et al. Multi-scale microstructure characterization and fluid flow simulation of artificial sandstone samples[J]. Journal of Shanxi University (Natural Science Edition), 2023, 46(6): 1378-1385. DOI: 10.13451/j.sxu.ns.2023030. (in Chinese).
计量
- 文章访问数: 123
- HTML全文浏览量: 37
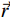
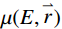
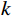
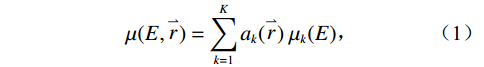
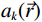
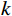
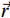
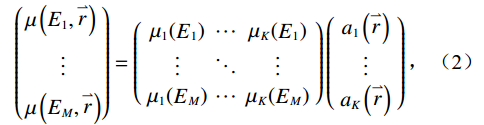
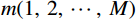
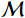
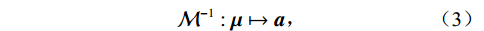
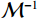
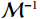
- PDF下载量: 16
