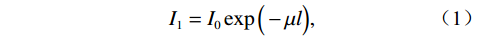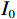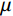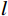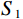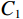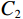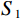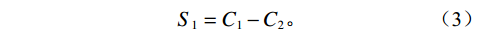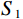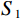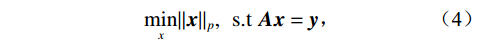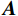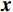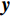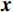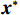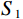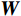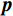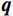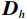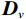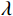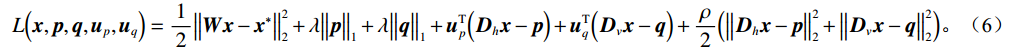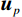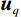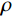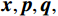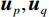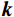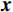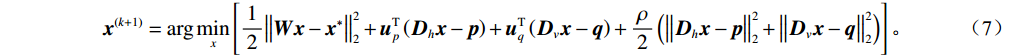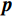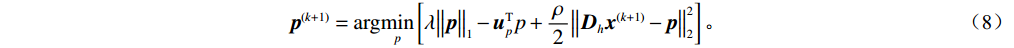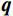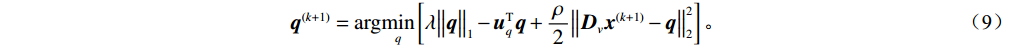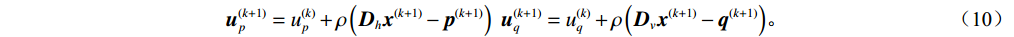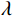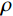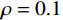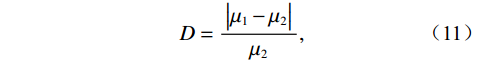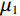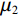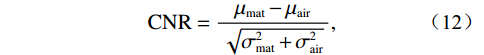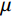CT Scatter Correction Based on Beam-hole Array and ADMM Algorithm
-
摘要:
在锥束计算机断层扫描(CBCT)系统中,散射信号的存在会导致图像产生伪影,影响图像质量,降低图像的对比度和信噪比。为了精确估计散射信号以抑制散射伪影,提出一种基于散射校正板和交替方向乘子法(ADMM)的锥束CT散射校正方法。基于射束孔阵列(BHA)散射校正板的校正原理,在待测工件和探测器之间添加散射校正板对工件进行扫描,获取投影数据并计算射束孔中心处散射信号。同时,结合压缩感知理论,建立L1范数约束模型,采用交替方向乘子法获取完整散射场分布,并通过扫描角度插值算法,减少全角度散射场重构所需时间。去除散射后进行重建即可得散射校正后的CT图像。通过数据分析对重建切片的图像质量进行评估,分析结果表明,基于BHA散射校正板的散射校正方法有效提升图像对比度,减少散射伪影,改进的散射信号重构方法进一步提高散射信号的准确性,散射抑制效果更为明显。同时,使用扫描角度插值算法提高散射场重构效率;采用BHA与ADMM相结合的方法能够更好的去除散射,图像质量得到进一步改善。
Abstract:In cone-beam computed tomography (CT) systems, scatter signals can result in artifacts in images, thus adversely affecting image quality by reducing the contrast and signal-to-noise ratio. To accurately estimate and suppress scatter artifacts, a new scatter-correction method for cone-beam CT based on a beam-hole array (BHA) scatter-correction plate and the alternating direction method of multipliers (ADMM) are proposed. Based on the correction principle of the BHA scatter-correction plate, the plate is placed between the object under test and the detector during scanning. This setup captures projection data and computes scatter signals at the centers of the beam holes. Simultaneously, by incorporating the theory of compressed sensing, an L1-norm constrained model is established, and the ADMM is utilized to obtain a complete scatter-field distribution. Using an interpolation algorithm to scan angles reduces the time required for a full-angle reconstruction of the scatter field. Post-scatter removal and reconstruction yield scatter-corrected CT images. Data analysis of the reconstructed slices reveals the image quality, which indicates that the scatter-correction method based on the BHA plate effectively enhances the image contrast and reduces scatter artifacts. The improved scatter-signal reconstruction method further increases the accuracy of scatter-signal estimation, thus rendering scatter suppression more pronounced. Furthermore, using scanning-angle interpolation algorithms improves the efficiency of scatter-field reconstruction. The combined use of BHA and ADMM provides better scatter removal and further improvement in image quality.
-
X射线成像技术作为经典的无损检测技术,在医学检测、航天航空、零件制造等领域有重要应用[1]。在工业无损检测中,对工件如航空发动机涡轮叶片使用CT检测,涡轮叶片因其高密度和复杂的几何形状,在扫描中容易引发噪声问题,导致重建图像出现伪影。大部分伪影由康普顿散射引起,导致探测器接收到的光子包含了初始光子和散射光子[2],产生散射伪影[3],使得测量结果与实际强度测量结果存在偏差,降低图像的对比度,影响图像质量、边界及内部结构信息模糊。因此,为提高图像质量,获取更清晰的图像细节,需要对CT图像进行散射校正。
对于散射校正,国内外开展了许多研究工作,主要分为硬件校正、软件校正和软硬件结合校正的方法[4]。
硬件校正,即在X射线成像系统的各个部件上添加校正工具以减少到达探测器的散射信号,如准直器法、空气隙法、过滤器法等[5-7]。硬件校正的核心在于通过降低探测器所接收到的散射信号来实现校正,但这一过程会对初始射线的能量分布产生影响,并且受限于成像系统的形状、探测器的大小等原因,硬件方法有较大限制。
软件校正,主要通过数字图像处理,分析采集图像和估计被扫描物体性质,得到散射分布,利用软件完成校正过程,主要包括卷积法、反卷积法、模型估计法和蒙特卡罗模拟等[8-11]。
软硬件结合的方法,有射束阻止阵列法(beam stop array,BSA)[12]、射束孔阵列法(beam hole array,BHA)[13]和射束阻止网格法(beam stop grid,BSG)[14]等。以BHA方法为例,BHA散射校正板是对一块质地均匀的铅板加工,对铅板每隔特定距离穿透形成孔洞,射线通过孔洞来对被测工件进行扫描,其余信号被铅板吸收。由于散射校正板的遮挡,探测器接收到的数据较少,只选取孔洞中心处信号进行插值获得完整图像,会导致拟合出的散射信号准确率降低[15]。孔洞中心的信号可能无法全面代表整个孔洞区域接收到的信号强度,这样的选择忽略了孔洞边缘及其他区域的信号,会降低采集图像的利用率和拟合图像的准确度。
面对这一挑战,需要探索一种新的数据处理方法。随着压缩感知(compressed sensing,CS)理论的不断发展,为我们提供了一种从欠采样数据[16]中精确恢复CT图像的新思路。CS理论的核心在于,即使数据不完整,也能通过特定的算法和模型从有限的信息中恢复出原始信号。
这种方法为我们解决不完整投影数据的重建问题提供了理论支持,并且有效提高散射信号拟合的准确性。因此,我们可以将压缩感知理论应用于当前的问题中,通过其高效的数据处理能力,来弥补因校正板遮挡而缺失的数据,从而减少插值拟合过程中的误差,尤其是在铅块边缘处。这样,我们不仅能够提高散射信号的拟合准确率,还能够更有效地处理和利用探测器接收到的有限数据。当投影数据不完备时,其在成像过程中可能会产生严重的伪影。
与传统解析算法相比,基于总变差(total variation,TV)的CS方法在欠采样或缺失数据方面有着明显改善[17],利用CS理论中的大跨度信息感知,可以提高对离散欠采样数据的利用率,进而更加精确地重建图像[18]。Wahlberg等[19]提出了交替方向乘子法(alternating direction method of multipliers,ADMM),ADMM算法是整合了对偶上升和多乘子法的最优化迭代算法。该算法以其分裂特性和卓越的收敛性,可以有效的简化模型,处理稀疏问题。
本文基于BHA散射校正方法,结合CS理论,通过校正板所采集到的离散区域,设计合适的采样矩阵,对建立的L1范数约束模型采用ADMM算法进行求解,得到完整的散射信号,最后使用扫描角度插值算法提高采集效率,建立CS理论下的基于BHA散射校正板和ADMM算法的散射信号重构技术流程,提高对添加校正板采集的投影图像离散区域的数据利用率,实现散射校正。
1. 方法论述
1.1 BHA散射校正方法
首先进行投影图像数据采集,选用BHA散射校正板对工件进行散射校正。BHA散射校正板是一块含有均匀排布孔洞的铅板,射线通过孔洞来对被测工件进行扫描,其余信号被铅板吸收。BHA散射校正流程如图1所示。
校正过程需要对工件进行两次全面的扫描,以及对校正板进行单独的扫描。为确保数据的准确性,两次扫描过程中必须保证工件位置保持不变,并且所有扫描参数均需一致。在第1次扫描中,工件被放置在载物台上,通过探测器获取的投影图像集,记为Scan I。这些图像包含了散射信号和工件的真实信号。随后进行第2次扫描,在待测工件与探测器之间加入BHA散射校正板,获取第2组投影图像集,记为Scan II。最后移除工件,对校正板进行单幅投影图像的采集。
完成数据采集之后,进行数据处理。首先对采集到的单幅散射校正板投影中的孔洞位置进行轮廓提取,以确定投影中孔洞区域的分布。第1组扫描用于采集含有散射射线和真实射线的图像,如图2(a)所示。根据朗伯比尔定律有:
$$ {I_1} = {I_0}\exp\Big( - \mu l\Big), $$ (1) 式中,X射线初始强度为
${I_0}$ ,穿过工件后,强度变为${I_1}$ ,$\mu $ 代表工件的衰减系数,$l$ 为射线穿过的工件厚度。在探测器位置上,由于散射射线$ {S_1} $ 的存在,接收到的实际射线${C_1}$ 为:$$ {C_1} = {I_1} + {S_1} 。 $$ (2) 第2组扫描用于采集离散的真实射线图像,如图2(b)所示。进入孔洞的散射射线会被铅板吸收,因此探测器上孔洞位置的实际射线
${C_2}$ 视作真实射线的离散分布,即$ {C_2} = {I_1} $ 。两组扫描采集到的射线强度对应角度相减,可以得到对应的离散散射$ {S_1} $ :$$ {S_1} = {C_1} - {C_2} 。 $$ (3) 将数据集Scan Ⅰ与Scan Ⅱ的每幅投影对应角度相减,提取校正板孔洞区域的散射数据,即式(3)中的离散散射
$ {S_1} $ 。离散散射信号位于校正板孔洞区域,成像视野内非孔洞区域散射信号缺失,需要对其进行估计以重构完整散射场。通过离散散射$ {S_1} $ 重构得到完整散射场后,即可从投影图像集Scan I中减去散射,实现散射校正。为了从这些离散数据中重构出完整的散射场,本文建立一个基于L1范数的约束模型,采用ADMM算法来求解这一优化问题,通过ADMM算法的应用,从离散的散射数据中重构得到完整散射场。
1.2 改进的L1范数约束模型
随着稀疏性理论的研究和发展,有研究者提出了通过求解优化模型获得稀疏解的稀疏优化理论[20]:
$$ \underset{x}{\mathrm{min}}\Vert {\boldsymbol{x}}{\Vert }_{p},\;\;{\mathrm{s.t}}\;{\boldsymbol{Ax}}={\boldsymbol{y}} \text{,} $$ (4) 其中
${\boldsymbol{A}}$ 为测量矩阵,${\boldsymbol{x}}$ 为待重构图像,${\boldsymbol{y}}$ 为探测器接收到的投影数据。通常情况下,待重建的图像大多不具有稀疏性,可通过某种变换基使得待重建的图像在该变换域下具有更稀疏的表示,以有效地应用压缩感知理论进行图像重建。考虑到压缩感知能够在少量观测数据的情况下利用先验信息重建完整信号[21],本文利用散射图像的低频光滑特性,通过引入稀疏约束的L1范数正则化来提高对欠采样数据的利用率并精确重建图像。具体地,构建以下优化模型:
$$ \underset{x}{\rm min}\Bigg(\frac{1}{2}{\big{\Vert}} {\boldsymbol{Wx}}-{{\boldsymbol{x}}}^{*}{\big{\Vert}}_{2}^{2}+\lambda {\big{\Vert}} {\boldsymbol{p}}{\big{\Vert}}_{1}+\lambda {\big{\Vert}} {\boldsymbol{q}}{\big{\Vert}}_{1}\Bigg) \;\;\;\; {\mathrm{s.t}}\;\;{{\boldsymbol{D}}}_{h}{\boldsymbol{x}}-{\boldsymbol{p}}=0,\;\;{{\boldsymbol{D}}}_{v}{\boldsymbol{x}}-{\boldsymbol{q}}=0\text{,} $$ (5) 其中,向量
${\boldsymbol{x}}$ 表示待重构的散射信号,${{\boldsymbol{x}}^ * }$ 为对应的在校正板孔洞位置处的已知散射分布,即式(3)中的离散散射$ {S_1} $ ,矩阵${\boldsymbol{W}}$ 是一个对角线加权矩阵,用于表示散射校正板的位置信息。在孔洞区域,该矩阵元素设为1,其他元素设为0,以反映位置上的采样特征。变量$ {\boldsymbol{p}} $ 和变量$ {\boldsymbol{q}} $ 分别代表散射信号在水平和垂直方向上的差分,本文选用的散射校正板在水平和竖直方向上均匀排列着孔洞,基于这一构造,设立水平和垂直差分矩阵$ {{\boldsymbol{D}}_h} $ 和${{\boldsymbol{D}}_v}$ ,以提供图像的梯度信息。由于散射图像是低频光滑的,相邻位置的灰度值差异通常较小,从而导致离散梯度变换后图像绝大部分区域接近于零,可采用稀疏约束的L1范数正则化函数来对差分信号进行惩罚。正则化参数$ \lambda $ 用于控制L1范数的稀疏性约束,进而促进模型在保持数据一致性的同时实现稀疏重构。此优化模型不仅利用CS理论中的大跨度信息感知能力,而且通过L1范数增强模型的稀疏性,使得在有限的采样条件下能有效的重构散射信号。为了高效处理式(5)中引入的L1范数约束问题,本研究采用交替方向乘子法(ADMM)进行求解。在应用ADMM算法的过程中,引入增广拉格朗日函数来形式化目标函数,具体形式如下:
$$ L\Big({\boldsymbol{x}},{\boldsymbol{p}},{\boldsymbol{q}},{{\boldsymbol{u}}}_{p},{{\boldsymbol{u}}}_{q}\Big)=\frac{1}{2}{\big{\Vert}} {\boldsymbol{Wx}}-{{\boldsymbol{x}}}^{\ast }{{\big{\Vert}} }_{2}^{2}+\lambda {\big{\Vert}} {\boldsymbol{p}}{{\big{\Vert}} }_{1}+ \lambda {\big{\Vert}} {\boldsymbol{q}}{{\big{\Vert}} }_{1}+{{\boldsymbol{u}}}_{p}^{{\mathrm{T}}}\Big({{\boldsymbol{D}}}_{h}{\boldsymbol{x}}-{\boldsymbol{p}}\Big)+{{\boldsymbol{u}}}_{q}^{{\mathrm{T}}}\Big({{\boldsymbol{D}}}_{v}{\boldsymbol{x}}-{\boldsymbol{q}}\Big)+ \frac{\rho }{2}\Big({\big{\Vert}} {{\boldsymbol{D}}}_{h}{\boldsymbol{x}}-{\boldsymbol{p}}{{\big{\Vert}} }_{2}^{2}+{\big{\Vert}} {{\boldsymbol{D}}}_{v}{\boldsymbol{x}}-{\boldsymbol{q}}{{\big{\Vert}} }_{2}^{2}\Big)。 $$ (6) 在此式中,
$ {{\boldsymbol{u}}_p} $ 和${{\boldsymbol{u}}_q}$ 是对应水平和垂直约束的对偶变量,$\rho $ 是调节参数,通过调节对偶更新步骤的步长大小,从而影响算法的收敛速度和稳定性。ADMM算法通过迭代优化${\boldsymbol{x}},{\boldsymbol{p}},{\boldsymbol{q}},$ $ {{\boldsymbol{u}}_p},{{\boldsymbol{u}}_q} $ 来逐步接近最优解。在第${\boldsymbol{k}}$ 次迭代时,更新步骤如下:$\boldsymbol x$ 更新:$$ {{\boldsymbol{x}}^{(k + 1)}} = \arg \mathop {\min }\limits_x \left[ \frac{1}{2}\big\| {{\boldsymbol{Wx}} - {{\boldsymbol{x}}^*}} \big\|_2^2 + {\boldsymbol{u}}_p^{\mathrm{T}}\left( {{{\boldsymbol{D}}_h}{\boldsymbol{x}} - {\boldsymbol{p}}} \right) + {\boldsymbol{u}}_q^{\mathrm{T}}\left( {{{\boldsymbol{D}}_v}{\boldsymbol{x}} - {\boldsymbol{q}}} \right) + \frac{\rho }{2}\left( {\big\| {{{\boldsymbol{D}}_h}{\boldsymbol{x}} - {\boldsymbol{p}}} \big\|_2^2 + \big\| {{{\boldsymbol{D}}_v}{\boldsymbol{x}} - {\boldsymbol{q}}} \big\|_2^2} \right) \right] \text{。} $$ (7) $\boldsymbol p$ 更新:$$ {{\boldsymbol{p}}}^{(k+1)}=\mathrm{arg}\underset{p}{\mathrm{min}}\left[\lambda {\big{\Vert}} {\boldsymbol{p}}{{\big{\Vert}} }_{1}-{{\boldsymbol{u}}}_{p}^{{\mathrm{T}}}p+\frac{\rho }{2}{{\big{\Vert}} {{\boldsymbol{D}}}_{h}{{\boldsymbol{x}}}^{(k+1)}-{\boldsymbol{p}}{\big{\Vert}} }_{2}^{2}\right] \text{。} $$ (8) $\boldsymbol q$ 更新:$$ {{\boldsymbol{q}}}^{(k+1)}=\mathrm{arg}\underset{q}{\mathrm{min}}\left[\lambda {\big{\Vert}} {\boldsymbol{q}}{{\big{\Vert}} }_{1}-{{\boldsymbol{u}}}_{q}^{{\mathrm{T}}}{\boldsymbol{q}}+\frac{\rho }{2}{{\big{\Vert}} {{\boldsymbol{D}}}_{v}{{\boldsymbol{x}}}^{(k+1)}-{\boldsymbol{q}}{\big{\Vert}} }_{2}^{2}\right] \text{。} $$ (9) 乘子更新:
$$ \begin{aligned} {{\boldsymbol{u}}_p^{(k + 1)} = u_p^{(k)} + \rho \left( {{{\boldsymbol{D}}_h}{{\boldsymbol{x}}^{(k + 1)}} - {{\boldsymbol{p}}^{(k + 1)}}} \right)} \;\; {{\boldsymbol{u}}_q^{(k + 1)} = u_q^{(k)} + \rho \left( {{{\boldsymbol{D}}_v}{{\boldsymbol{x}}^{(k + 1)}} - {{\boldsymbol{q}}^{(k + 1)}}} \right)} \end{aligned} 。 $$ (10) 通过上述步骤,ADMM算法能有效重构完整的散射信号分布。重构后的散射信号可用于原图像集中的散射校正。计算出散射信号后,对数据集Scan I中的原始投影扣除散射,实现散射校正。参数
$\lambda $ 、$\rho $ 根据经验选取为$\lambda = 2$ ,$\rho = 0.1$ 。这种方法不仅确保约束的满足,而且通过交替更新策略有效地分离原始变量和增广变量,提高算法的收敛速度和稳定性。1.3 扫描角度插值
在锥束CT扫描过程中,工件在旋转1周的过程中等间距采集投影图像,通常的采集数量范围从几百幅到上千幅不等。因此,相邻投影图像之间的差异通常非常小。而散射场的大小主要受到工件内部结构密度的影响,其特点是模糊且不包含具体的结构细节,导致相邻投影图像中散射场的差异会更小。鉴于采集方式的特性以及散射场自身的性质,可以采用扫描角度插值算法来减少所需的重构散射场数量,从而缩短全部散射场的重构时间。
本文中选择使用3次样条插值算法进行角度插值处理。具体地,在原始的
1700 张投影图像中,等间距地选取了100张投影图像用以重构其对应角度的散射场图像,后进行角度插值处理,生成全部角度下的散射场图像。这种方法有效减少全角度散射场重构所需的时间,同时保持散射场图像的连续性和整体质量。1.4 采集系统参数
本文采用的实验设备为v|tome|x C 450 CT系统,设备配备450 kV X射线源,使用平板探测器。系统可实现对直径达500 mm×长度
1000 mm的大尺寸样品进行扫描。采集图像灰度范围为0~65535 ,扫描参数如表1所示。其中FDD为射线源中心到探测器的距离,FOD为射线源中心到物体的距离。探测器大小为2 016×2 016,像素尺寸为0.2 mm。实验使用的BHA校正板材料为纯铅,厚度为20 mm,经过测量确认,20 mm厚的铅能够吸收绝大部分实验的初始射线。对铅板进行穿孔操作,孔洞需要笔直穿透铅板,根据经验,孔洞直径长度选择在探测器像素的5到10倍,探测器像素大小为0.2 mm,故孔洞大小选择设为2 mm,垂直孔间距为6 mm,水平孔间距为10.5 mm。校正板大小应完全覆盖工件,本文选用的校正板大小和探测器大小相同。数据采集时,校正板紧贴探测器放置。BHA校正板详细参数如表2所示。表 1 CT扫描参数Table 1. CT scanning parameters扫描电压/kV 扫描电流/μA FDD/mm FOD/mm 像素尺寸/mm 图像尺寸/(pixel×pixel) 430 1600 1158 500 0.2 1300 ×1300 表 2 BHA校正板参数Table 2. Beam-hole array parameters校正板高度/mm 校正板宽度/mm 校正板厚度/mm 孔洞直径/mm 垂直孔间距/mm 水平孔间距/mm 400 400 20 2 6 10.5 扫描角度为360°,扫描一周采集
1700 幅DR投影图像,基于MATLAB平台编写校正程序,散射校正后使用VGStudio Max3.0软件进行重建,重建算法为FDK(feldkamp-davis-kress)算法,重建大小为512×512×512(0.11 mm/pixel)。2. 实验结果与分析
2.1 实验结果
对插值法和CS法重构散射场的校正效果取同一角度进行对比分析,图3为CT投影散射场重构图像。图3(a)为添加BHA校正板采集的投影原图,图3(b)为使用插值法重构得到的散射场图像,图3(c)为使用CS方法重构的散射场图像,图3(d)为散射校正后的投影图像。从图中可以看出,插值法重构的散射场仍有部分的黑色点状结构,这对应了散射校正板的孔洞结构,说明插值法对散射场的重构效果不够理想。图3(c)说明CS方法较好重构了散射场图像,散射更为均匀平滑。
为了更加直观有效的比较散射校正效果,选取FDK算法重建结果的切片图像进行数据分析。图4到图6分别展示了CT重建图像第216层、256层、296层的切片图像,包括散射校正前后的不同处理结果。图4(a)、图5(a)和图6(a)为未散射校正的原始切片图像,该图像明显受到散射的污染,导致图像轮廓不清晰和对比度降低。图4(b)、图5(b)、图6(b)和图4(c)、图5(c)、图6(c)分别展示了使用插值和CS方法进行散射校正后的切片图像。
经过这两种校正方法处理后,可以明显看到散射被有效抑制,图像的对比度显著提高,结构和细节更加清晰,特别是CS方法的校正效果更为显著。此外,图4(d)、图5(d)和图6(d)展示了使用扫描角度插值算法处理后的切片图像,算法使用原始投影集1/17的数据量进行散射场的重构。由于散射场受角度变化的影响较小,该方法与全角度重建的结果几乎没有差别。这说明使用较少的散射场数据进行重建不仅可以加快全部散射场的重构速度,而且不会牺牲重建质量。这种方法在提高计算效率的同时,也保持了图像重建的高质量。
图7展示三维重建的结果图像。其中,图7(a)展示未经散射校正的切片图像,图7(b)展示利用插值法拟合散射信号后的散射校正切片图像,图7(c)是应用CS方法进行散射校正后的结果。图7(d)提供了图5中所选切片图像位置的示意图。通过比较各图像尤其是内弧区域的清晰度,可以明显看出CS方法在散射校正方面提供了更优越的效果。这种优化显著提高了图像的清晰度和可识别性,使得细节部分更加精确地被重建和展示。
2.2 数据分析
为了定量分析散射校正前后的去散射效果,采用灰度值变化和对比度噪声比(contrast-to-noise ratio,CNR)作为评价散射校正效果的关键指标。在第240层和第256层切片图像中,本文标定相同位置的两条线(黄色虚线),分别命名为Line 1和Line 2。进一步地,选定4个感兴趣区域及其相邻的背景区域,分别标记为Area 1、Area 2、Area 3和Area 4,用于计算CNR值。图8展示被标定的工件相关区域,具体标定情况如图8(a)和图8(b)所示。这种方法能够准确评估散射校正的效果,确保图像质量的显著提升。
根据散射校正理论,在散射校正后,工件区域的结构应更加清晰,对比度提高,相应的灰度值也得以提高。反映在灰度值变化上,校正后的灰度值曲线在工件部分的灰度值应明显高于校正前。
图9展示了线性灰度值变化的对比。图9(a)展现校正前后在Line 1位置的切片图像中灰度值的变化,图9(b)显示Line 2位置的相应变化。从图中可以观察到,在叶片区域,校正后的灰度值明显高于未校正的灰度值。在工件的边缘区域,灰度值的变化较为剧烈,表明图像的对比度提高,细节更加清晰可见。无论是从主观感受还是客观分析来看,图像中的伪影得到有效抑制,对比度也有所提升。与传统的插值法相比,采用CS方法的散射校正效果显著更佳。图9(c)呈现重建切片图像第225列的灰度值变化。结果显示,无论是角度插值方法还是全角度CS方法,所得图像的灰度值差异很小。与未进行散射校正的图像相比,去散射效果均表现出色。
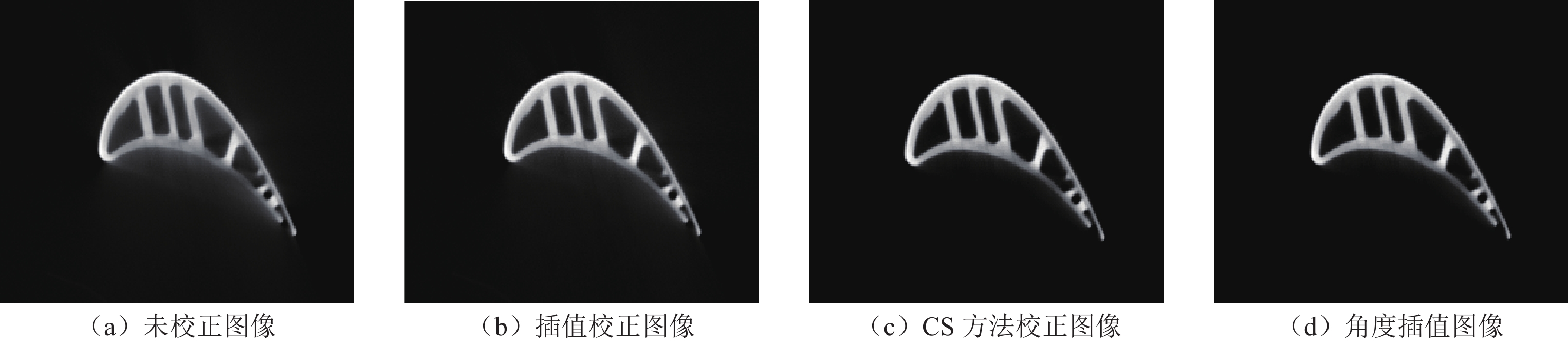
为了更好的比较散射校正效果,选取重建图像最中间层(第256层)作为比较对象。通过计算3组图像不同区域的CT值相对差异,来比较散射校正效果。CT值相对差异定义为:
$$ D = \frac{{\big| {{\mu _1} - {\mu _2}} \big|}}{{{\mu _2}}}, $$ (11) 其中
$ {\mu _1} $ 、$ {\mu _2} $ 为感兴趣区域的平均值。由于工件为均匀材质,工件各区域间灰度值理论上差距很小,因此,CT值相对差异越小,则说明该区域灰度值越均匀,即受到散射的影响越小,散射校正效果越好。选取工件均匀材质部分的两组感兴趣区域,分别标为红色和蓝色,如图5(a)~图5(c)所示。经过计算,未校正图像、插值校正图像、CS方法校正图像的CT值相对差异分别为21.90%、17.86%和13.45%,散射校正后CT值相对差异降低,同时所提方法的结果优于插值校正方法,证明本文所提散射校正方法的有效性。
对比度噪声比(contrast-to-noise ratio,CNR)是一个重要指标,用于衡量图像中感兴趣区域与背景之间的对比度。CNR值越高,表明感兴趣区域与背景的差异性越大,图像显示更为清晰和详细。CNR的定义为:
$$ {{\mathrm{CNR}}} = \frac{{{\mu _{\rm mat}} - {\mu _{\rm air}}}}{{\sqrt {\sigma _{\rm mat}^2 + \sigma _{\rm air}^2} }}, $$ (12) 其中
$\mu $ 为平均值,$\sigma $ 为工件和背景的5×5像素区域评估的灰度值的标准差。为了更精确地评估散射去除的效果,选择叶片内部作为感兴趣区域,并选取叶片边缘的高散射区域作为背景区域,而不是图像边缘处。这一选择依据散射信号的分布特性做出,因为散射信号主要集中在叶片及其周围区域,而边缘处的散射较少。选取叶片边缘的高散射区域能更有效地反映方法在去除散射方面的性能。
根据第240层和第256层切片图像的计算结果(分别展示在表3和表4中),数据分析显示,经过散射校正处理后,对比度噪声比平均分别提高了39.23%和46.01%。表明校正后的图像质量得到了改善,图像细节更加清晰可见。在CT扫描中,散射场的存在会覆盖图像中低对比度结构的细节,使得它们难以区分。通过散射校正将散射去除后,背景噪声减少,感兴趣区域的信号与周围结构的对比将更明显,对比度噪声比得以提升。同时,这也证明了CS方法在改善图像质量方面相较于传统插值方法具有更优的效果。
表 3 散射校正前后第240层的切片图像对比度噪声比Table 3. CNR of slice image from layer 240 before and after scattering correction散射拟合方法 CNR CNR提升百分比 Area 1 Area 2 Area 1 Area 2 原始投影 9.14 13.25 / / 插值方法 14.11 16.38 54.37 23.62 CS方法 14.77 17.28 61.60 30.42 表 4 散射校正前后第256层的切片图像对比度噪声比Table 4. CNR of slice image from layer 256 before and after scattering correction散射拟合方法 CNR CNR提升百分比 Area 1 Area 2 Area 1 Area 2 原始投影 21.26 6.45 / / 插值方法 23.76 9.43 11.76 46.20 CS方法 27.13 9.73 27.61 50.85 3. 结论
在本研究中,提出并验证了一种基于压缩感应理论的散射校正方法。这种方法结合BHA散射校正板与ADMM算法,用于处理离散数据并重建高质量的散射场图像用以散射校正。为了评估这种新方法的效果,通过与传统插值拟合散射场的方法进行了对比实验。实验结果显著地展示了新方法在减少图像散射伪影方面的优势,同时也有效地保留了图像的细节和边缘信息。在标定区域的测试中,对比度噪声比分别提高了39%和46%,证实了该方法在提升图像质量方面的显著有效性。为了提高散射场的重构效率,选用了仅占全角度1/17的投影图像来重构散射场图像,随后,通过角度插值方法,获取全角度的散射场图像。这种方法大幅提升了散射场重构的效率,同时确保了重构图像的完整性和精确性。
此外,本文所提方法通过提高离散数据的利用效率,实现了更精确的散射信号重构,从而达到了更优的散射校正效果。这对于基于压缩感知理论的锥束CT散射校正提供了一定参考价值。在未来的研究中,计划在散射校正过程中引入硬化校正,以便同时对散射和硬化造成的伪影进行有效抑制,进一步提升图像的清晰度和检测价值。
-
表 1 CT扫描参数
Table 1 CT scanning parameters
扫描电压/kV 扫描电流/μA FDD/mm FOD/mm 像素尺寸/mm 图像尺寸/(pixel×pixel) 430 1600 1158 500 0.2 1300 ×1300 表 2 BHA校正板参数
Table 2 Beam-hole array parameters
校正板高度/mm 校正板宽度/mm 校正板厚度/mm 孔洞直径/mm 垂直孔间距/mm 水平孔间距/mm 400 400 20 2 6 10.5 表 3 散射校正前后第240层的切片图像对比度噪声比
Table 3 CNR of slice image from layer 240 before and after scattering correction
散射拟合方法 CNR CNR提升百分比 Area 1 Area 2 Area 1 Area 2 原始投影 9.14 13.25 / / 插值方法 14.11 16.38 54.37 23.62 CS方法 14.77 17.28 61.60 30.42 表 4 散射校正前后第256层的切片图像对比度噪声比
Table 4 CNR of slice image from layer 256 before and after scattering correction
散射拟合方法 CNR CNR提升百分比 Area 1 Area 2 Area 1 Area 2 原始投影 21.26 6.45 / / 插值方法 23.76 9.43 11.76 46.20 CS方法 27.13 9.73 27.61 50.85 -
[1] HUANG K D, ZHANG H, SHI Y K, et al. Scatter correction method for cone-beam CT based on interlacing-slit scan[J]. Chinese Physics B, 2014, 23(9): 098106. DOI: 10.1088/1674-1056/23/9/098106.
[2] 刘建邦, 席晓琦, 韩玉, 等. 基于KN 模型的锥束 CT 散射伪影校正方法[J]. Acta Optica Sinica, 2018, 38(11): 1134001. DOI: 10.3788/AOS201838.1134001. LIU J B, XI X Q, HAN Y, et al. A new scattering artifact correction method based on K-N formula for cone-beam computed tomography[J]. Acta Optica Sinica, 2018, 38(11): 1134001. DOI: 10.3788/AOS201838.1134001. (in Chinese).
[3] 戎军艳, 刘文磊, 高鹏, 等. 锥束CT散射抑制方法综述[J]. CT理论与应用研究, 2016, 25(2): 235-250. DOI: 10.15953/j.1004-4140.2016.25.02.15. RONG J Y, LIU W L, GAO P. The review of scatter suppression methods in cone beam CT[J]. CT Theory and Applications, 2016, 25(2): 235-350. DOI:10.15953/j.1004-4140.2016.25.02.15. (in Chinese).
[4] 唐天旭, 段晓礁, 周志政, 等. 基于散射校正板的锥束微纳CT系统的散射校正[J]. 光学学报, 2019, 39(8): 0834001. DOI: 10.3788/AOS201939.0834001. TANG T, DUAN X, ZHOU Z, et al. Scatter correction based on beam stop array for cone-beam micro-computed tomography[J]. Acta Optica Sinica, 2019, 39(8): 0834001. DOI: 10.3788/AOS201939.0834001. (in Chinese).
[5] TSUJI Y, ARAKI K, ENDO A, et al. Scatter radiation and the effects of air gaps in cephalometric radiography[J]. Oral radiology, 2006, 22: 7-13. DOI: 10.1007/s11282-006-0038-7.
[6] LIU W, RONG J, GAO P, et al. Algorithm for X-ray beam hardening and scatter correction in low-dose cone-beam CT: Phantom studies[C]//Medical Imaging 2016: Physics of Medical Imaging. SPIE, 2016, 9783: 785-792.
[7] KWAN A L C, BOONE J M, SHAH N. Evaluation of X-ray scatter properties in a dedicated cone-beam breast CT scanner[J]. Medical Physics, 2005, 32(9): 2967-2975. DOI: 10.1118/1.1954908.
[8] SCHORNER K, GOLDAMMER M, STIERSTORFER K, et al. Scatter correction method by temporal primary modulation in X-ray CT[J]. IEEE Transactions on Nuclear Science, 2012, 59(6): 3278-3285. DOI: 10.1109/TNS.2012.2218127.
[9] SISNIEGA A, ZBIJEWSKI W, XU J, et al. High-fidelity artifact correction for cone-beam CT imaging of the brain[J]. Physics in Medicine & Biology, 2015, 60(4): 1415.
[10] ISKENDER B, BRESLER Y. Scatter correction in X-ray CT by physics-inspired deep learning[J]. IEEE Transactions on Computational Imaging, 2022, 8: 1074-1088. DOI: 10.1109/TCI.2022.3226300.
[11] 阳振宇, 吕杨, 赵俊. 基于蒙特卡罗法的三源锥束CT散射分析[J]. CT理论与应用研究, 2012, 21(1): 1-9. YANG Z Y, LV Y, ZHAO J. Analysis of scattering in triple-source cone-beam CT based on Monte Carlo method[J]. CT Theory and Applications, 2012, 21(1): 1-9. (in Chinese).
[12] CAI W, NING R, CONOVER D. Scatter correction using beam stop array algorithm for cone-beam CT breast imaging[C]//Medical Imaging 2006: Physics of Medical Imaging. SPIE, 2006, 6142: 1157-1165.
[13] SCHÖRNER K, GOLDAMMER M, STEPHAN J. Comparison between beam-stop and beam-hole array scatter correction techniques for industrial X-ray cone-beam CT[J]. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 2011, 269(3): 292-299. DOI: 10.1016/j.nimb.2010.11.053.
[14] ALTUNBAS C, KAVANAGH B, ALEXEEV T, et al. Transmission characteristics of a two dimensional antiscatter grid prototype for CBCT[J]. Medical Physics, 2017, 44(8): 3952-3964. DOI: 10.1002/mp.12346.
[15] 郭成龙, 倪培君, 齐子诚, 等. 基于斜孔散射校正板的锥束X射线CT散射校正方法[J]. 强激光与粒子束, 2024, 36(7): 074004-1-074004-9. GUO C L, NI P J, QI Z C, et al. Scattering correction method for cone-beam X-ray CT based on slanted-hole scattering correction plate[J]. High Power Lasep and Particle Beams, 2024, 36(7): 074004-1-074004-9. (in Chinese).
[16] 杨富强, 张定华, 黄魁东, 等. CT不完全投影数据重建算法综述[J]. 物理学报, 2014, 63(5): 058701. YANG F Q, ZHANG D H, HUANG K D, et al. Review of reconstruction algorithms with incomplete projection data of computed tomography[J]. Acta Physica Sinica, 2014, 63(5): 058701. (in Chinese).
[17] 张家浩, 乔志伟. 基于相对TV最小的CT图像重建方法[J]. CT理论与应用研究, 2023, 32(2): 153-169. DOI: 10.15953/j.ctta.2022.190. ZHANG J H, QIAO Z W. Computed tomography reconstruction algorithm based on relative total variation minimization[J]. CT Theory and Applications, 2023, 32(2): 153-169. DOI: 10.15953/j.ctta.2022.190. (in Chinese).
[18] YANG F, ZHANG D, HUANG K, et al. Scattering estimation for cone-beam CT using local measurement based on compressed sensing[J]. IEEE Transactions on Nuclear Science, 2018, 65(3): 941-949. DOI: 10.1109/TNS.2018.2803739.
[19] WAHLBERG B, BOYD S, ANNERGREN M, et al. An ADMM algorithm for a class of total variation regularized estimation problems[J]. IFAC Proceedings Volumes, 2012, 45(16): 83-88. DOI: 10.3182/20120711-3-BE-2027.00310.
[20] 宋洁. 基于ADMM的低剂量CT重建算法的研究[D]. 太原: 中北大学, 2019. [21] ZHU L, BENNETT N R, FAHRIG R. Scatter correction method for X-ray CT using primary modulation: Theory and preliminary results[J]. IEEE Transactions on Medical Imaging, 2006, 25(12): 1573-1587. DOI: 10.1109/TMI.2006.884636.




 下载:
下载: