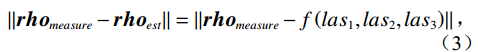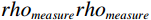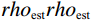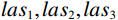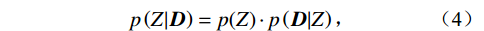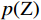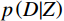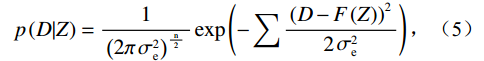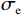Pre-stack Multidimensional Facies-controlled Thin Sandstone Prediction under Rock Physics Modeling of Coal-Bearing Strata in the Southern Ordos Basin
-
摘要:
鄂尔多斯盆地南部地区下石盒子组分流河道砂单层厚度薄，在有限的地震分辨率下，下伏山西-太原煤层反射的旁瓣与薄砂体的反射耦合在一起，难以对储层响应特征进行准确分析；此外，在进行岩石物理分析时，该地区还存在测井曲线质量差、横波资料不足等问题，导致储层定量预测存在一定困难。针对上述问题，本文在在Xu-White岩石物理模型的基础上，采用多参数拟合的曲线校正和分步融合的方法，建立一套砂、泥、煤三相岩石物理建模技术，有效改善测井曲线质量，并提高横波速度预测的精度，为后续反演提供合理的测井信息。此外，针对上述储层预测问题，本文提出一种适合研究区的多维相控叠前地质统计学反演方法：首先根据已有的地质认识和测井信息，分析与河道砂相关的地震属性，提取符合沉积变化规律的二维岩相概率密度作为石盒子组储层的平面约束；然后利用煤层反演体，结合贝叶斯判别原理，提取三维煤相概率密度作为下伏煤层的空间约束，最后同时综合二维和三维约束共同开展叠前地质统计学反演。上述方法的预测结果综合考虑下伏煤层和砂岩储层的耦合特征，有效降低薄储层预测的多解性，在实际应用效果较好，钻井吻合度得到明显提高。
Abstract:In the southern region of the Ordos Basin, the thin, single-layer distributary channel sands in the Lower Shihezi Formation cause coupling between the sidelobes of the underlying Shanxi-Taiyuan coal seam reflections and the reflections of thin sand bodies within a limited seismic resolution, making it difficult to accurately analyze the reservoir response characteristics. Additionally, challenges in petrophysical analysis arise owing to the poor quality of the logging curves and insufficient shear wave data in this area block, which impede quantitative reservoir prediction. To address these issues, this study proposes a set of sand, mud, and coal three-phase petrophysical modeling techniques based on the Xu–White petrophysical model, employing a multiparameter fitting curve correction and stepwise fusion method. This approach effectively improves the quality of logging curves and enhances the accuracy of shear wave velocity prediction, thereby providing reasonable logging information for subsequent inversions. Furthermore, to address the reservoir prediction problems mentioned above, this study introduces a multidimensional facies-controlled pre-stack geostatistical inversion method suitable for the study area. First, based on the existing geological understanding and well log information, seismic attributes related to channel sands were analyzed, and a two-dimensional lithofacies probability density conforming to sedimentary variation patterns was extracted as a planar constraint for the Shihezi Formation reservoir. Then, using the coal seam inversion volume combined with Bayesian discrimination principles, a three-dimensional coal facies probability density was extracted as a spatial constraint for the underlying coal seam. Finally, both two- and three-dimensional constraints were comprehensively integrated to conduct a pre-stack geostatistical inversion. The prediction results obtained using this method comprehensively considered the coupling characteristics of the underlying coal seams and sandstone reservoirs, effectively reducing the uncertainty in predicting thin reservoirs and demonstrating good practical application with significantly improved drilling concordance.
-
随着国内勘探开发的深入，储层和流体识别面临的问题越来越复杂，采用常规反演方法进行定量预测逐渐难以满足勘探开发的精度要求。鄂尔多斯南部地区二叠系下石盒子组辫状河三角洲平原分流河流相致密砂储层单层砂体薄,在有限的分辨率下，下伏山西-太原煤层反射的旁瓣与薄砂体的反射耦合在一起,对储层响应特征产生严重干扰；同时，在实际定量分析过程中，密度测井曲线受井眼的扩径和垮塌的影响，异常值较多；此外，该研究区域还存在横波资料严重不足等问题，上述因素导致对该区域进行精细的储层预测面临着较大的挑战。
岩石物理建模可以模拟各种岩石弹性参数和储层参数之间的联系，通过岩石物理模型正演出的弹性曲线更接近原状地层的岩石物理特征，目前利用Xu-White岩石物理建模预测横波在实际碎屑岩地层应用中效果较好[1-4]。后续也有许多学者对该岩石物理模型进行了改进，王金伟等[5]引入虚拟孔隙度变量优化Xu-White模型；杨志芳等[6]研究了纵波速度随含气饱和度的变化，同时建立低孔低渗储层含气饱和度定量预测模板；杨勤林等[7]引入虚拟岩性和误差融合方法，优化了横波速度预测过程；陈强等[8]提出了砂岩变孔隙结构的Xu-white岩石物理建模方法。
地质统计学反演将地震统计学与地震反演有机结合，在薄储层预测中应用较为广泛。该方法最早由Haas等[9]提出，通过综合地质、地震和测井等多种先验信息，可以有效提高纵向分辨率[10-12]。但与常规反演相比，地质统计学反演在测井、地震、地质数据等先验信息不足的情况下具有较强的多解性。针对该问题，近年来不少学者提出了基于相控的反演方法：闵小刚等[13]基于MCMC算法开展了成岩储集相控制的地质统计学反演；段新意等[14]提出在井网分布不均匀和地震资料品质较差的地区，开展高精度相控地质统计学反演。林利明等[15]将确定性反演得到的结果作为反演空间约束相，得到更加符合地质认识的结果。
考虑到研究区目的层含煤，本文在Xu-White理论模型和前人研究[16-18]基础上提出了多参数拟合的曲线校正和分步融合的砂、泥、煤三相岩石物理建模技术。此外，本文利用一种多维相约束的叠前地质统计学反演算法开展含煤地层的砂体预测。本文的结果如下：首先对岩石物理建模技术进行介绍，并给出多参数拟合曲线校正和分步融合的砂、泥、煤三相岩石物理建模技术流程，然后给出多维相约束的叠前地质统计学反演方法，最后将上述算法应用到鄂尔多斯盆地南部BC探区，并对预测结果进行分析与讨论。
1. 技术方法
1.1 砂-泥-煤三相岩石物理建模技术
在实际生产中，横波资料相对较少，岩石物理建模是较为常用的预测横波曲线的技术。Xu-White岩石物理建模利用孔隙度、饱和度、泥质含量、矿物和流体参数等估算砂泥岩纵横波速度，在常规砂泥岩横波预测应用效果较好。该岩石物理模型中，Kuster-Toksoz方程为：
$$ {K}_{\text{d}}-{K}_{\text{m}}=\frac{1}{3}({K}_{1}-{K}_{\text{m}})\frac{3{K}_{\text{d}}+4{\mu }_{m}}{3{K}_{\mu}+4{\text{μ} }_{m}}{\displaystyle \sum _{l=\text{s},c}{\phi}_{l}{T}_{iijj}({\alpha }_{l})} \text{，} $$ (1) $$\begin{split} {\mu _{\text{d}}} - {\mu _m} =\;& \frac{{\left( {{\mu _1} - {\mu _m}} \right)}}{5}\frac{{6{\mu _d}\left( {{K_m} + 2{\mu _m}} \right) + {\mu _m}\left( {9{K_m} + 8{\mu _m}} \right)}}{{5{\mu _m}\left( {3{K_m} + 4{\mu _m}} \right)}}\times \\ & \sum\limits_{l = {\text{s}},c} {{\phi _l}F({\alpha _l})} \text{，}\\[-1pt]\end{split} $$ (2) 其中：
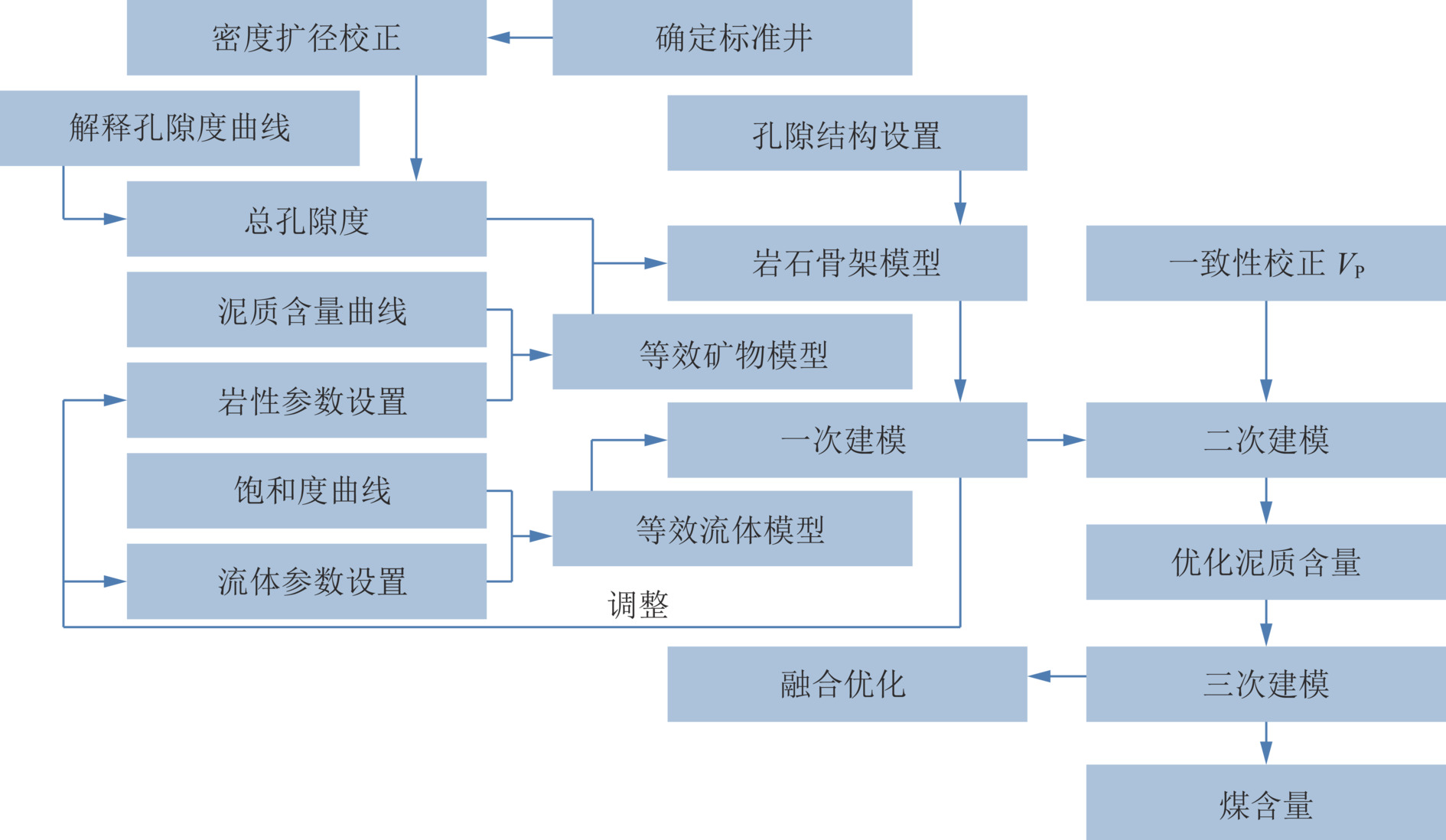
$ {K}_{d}{K}_{d} $ ，$ {K}_{m}{K}_{m} $ 和$ {K}_{1}{K}_{1} $ 分别为干岩石骨架、岩石矿物和孔隙流体体积模量，$ {\mu }_{d}{\mu }_{d} $ ，$ {\mu }_{m}{\mu }_{m} $ 和$ {\mu }_{1}{\mu }_{1} $ 分别为对应的剪切模量。$ F\left(\alpha \right)F\left(\alpha \right) $ ,$ {T}_{\text{iijj}}\left(\alpha \right){T}_{\text{iijj}}\left(\alpha \right) $ 和$ {T}_{\text{ijij}}\left(\alpha \right){T}_{\text{ijij}}\left(\alpha \right) $ 都是与孔隙纵横比$ \alpha \alpha $ 有关的函数。Kuster-Toksoz方程要求$ {\phi \mathord{\left/ {\vphantom {\phi \alpha }} \right. } \alpha } <<1 $ ，1995年，Xu等[19]利用差分等效介质理论拓展了这种假设。2002年Key等[20]又将该方程转化成为一个线性常微分方程组进行求解。当对上述方程进行求解之后，根据Gassmann方程计算出饱含流体的体积模量和剪切模量，最后通过这些模量参数得到纵波速度和横波速度。考虑到研究区目的层含煤，且存在大段扩径现象，针对该问题本文对Xu-White理论模型进行优化，提出了多参数拟合的曲线校正和分步融合的砂、泥、煤三相岩石物理建模技术进行横波曲线预测，整体流程如图1所示。在碎屑岩地层中，密度曲线往往受实际井眼扩径和垮塌的影响，存在异常值，因此首先要消除环境对测井曲线的影响。具体来说，通过分析不同井的曲线特征，将目的层段井径变化范围小，密度范围正常的井作为标准井；然后计算非扩径段密度测井曲线与其他曲线的相关性，优选相关性较高的曲线；再根据非线性优化算法求以下表达式的最小方差开展密度曲线拟合：
![]()
图 1 砂、泥、煤三相岩石物理建模技术路线图Figure 1. Flowchart of three-phase rock physical modeling technology of sand, mud, and coal$$ \left\| {{\boldsymbol{rh}}{{\boldsymbol{o}}_{measure}} -{\boldsymbol{ rh}}{{\boldsymbol{o}}_{est}}} \right\| = \left\| {{\boldsymbol{rh}}{{\boldsymbol{o}}_{measure}} - f\left( {la{s_1},la{s_2},la{s_3}} \right)} \right\| \text{，} $$ (3) 其中，
$ rh{o}_{measure}rh{o}_{measure} $ 为标准井标准段的实测密度，$ rh{o}_{\text{est}}rh{o}_{\text{est}} $ 为预测的密度，$ la{s_1},la{s_2},la{s_3} $ 为与密度相关性高的测井曲线。将密度预测的算法映射到其他扩径井，优化因扩径导致的测井曲线异常。完成多参数拟合的密度校正后，可以开展横波预测。首先，对于有横波测井曲线的井：
（1）针对非煤层段，根据加权平均法利用消除扩径影响的曲线反演出矿物和流体的密度，计算出总孔隙度；
（2）根据混合理论计算给定参数的石英、粘土基质矿物的等效体积模量（V-R-H模型）；
（3）利用孔隙度曲线和孔隙度纵横比，根据微分等效介质理论（DEM）计算干岩石的弹性模量；
（4）利用流体混合定律（Wood方程）计算孔隙流体的弹性模量；
（5）向孔隙系统中加入流体混合物，利用Gassmann方程计算饱含流体岩石的体积模量和剪切模量，并计算纵横波速度和密度；
（6）不断调整矿物和流体的模量，使得建模曲线与已知的测井曲线误差最小；
（7）结合测井纵波速度，对剩余误差开展泥质含量优化，进行二次建模，将因砂、泥孔隙度纵横比等参数所带入的误差等效为岩性的变化,来提高预测精度；
（8）在煤层段，利用解释的煤含量曲线代替泥质含量，优化矿物，开展3次建模；
（9）结合煤层和非煤层段，平滑局部优化，获得建模后的纵波速度、横波速度和密度曲线。
最后将矿物和流体参数应用到工区没有横波信息的井上，预测其他井的横波速度。整个过程中重点是对矿物和流体模量的确定。但该技术流程仅适用含煤地层的砂、泥、煤建模，对其他三相岩石物理建模的适用性待验证。合理的测井曲线是后续储层定量预测的基础。利用测井曲线开展储层弹性参数交会，可以确定储层弹性参数的范围；同时也需要利用测井曲线获得后续反演的统计学参数。
1.2 多维相控叠前地质统计学反演
针对于薄砂层的预测，可以开展地质统计学反演。该方法用概率的术语来描述问题，用统计学的方法来解决问题，可以获得高分辨率的反演结果。地质统计学反演将敏感弹性参数看作待求的未知数，先验信息为用概率密度函数、变差函数表达的地质信息和测井信息。贝叶斯推断是根据地震数据和先验信息，综合这些概率密度函数得到储层的后验概率分布函数。未知参数Z的后验概率密度可以表示为：
$$ p\left(Z|{\boldsymbol{D}}\right)=p(Z)\cdot p\left({\boldsymbol{D}}|Z\right) \text{，} $$ (4) 式中Z表示储层参数，D表示地震数据,
$ p({\text{Z}}) $ 表示先验概率密度，$ p\left( {D|Z} \right) $ 表示似然函数。假设噪声与模拟误差为标准的高斯分布，似然函数可以写为：$$ p\left( {D|Z} \right) = \frac{1}{{\mathop {\left( {2\pi \mathop \sigma \nolimits_{\text{e}}^2 } \right)}\nolimits^{\frac{{\text{n}}}{2}} }}\exp \left( { - \sum {\frac{{{{\left( {D - F\left( Z \right)} \right)}^2}}}{{2\mathop \sigma \nolimits_{\text{e}}^2 }}} } \right) \text{，} $$ (5) 其中，
$ \mathop \sigma \nolimits_{\text{e}} $ 表示方差，F表示正演算子。基于马尔科夫链-蒙特卡罗（Markov Chain Monte Carlo，MCMC）方法的地质统计学反演[21-24]可以根据实际的后验概率分布函数，通过Markov链进行抽样模拟得到统计意义上正确的随机样点分布。再基于这些样本，用Monte Carlo积分估计储层分布的期望值，从而得到储层的岩性和物性等储层参数。其中Markov链采用Metropolis-Hasting采样算法生成，其迭代步长随着迭代次数的增加而逐渐减小。
叠前地质统计学反演依赖地震数据和测井数据，对于少井的工区，结果随机性较大，存在一定误差。针对此问题发展起来的叠前相控地质统计学反演方法，通过结合已有的地质认识和测井资料，提取符合沉积的岩性变化规律，将其转化为不同的概率密度，并作为反演的约束条件，在一定程度上可以降低反演的多解性。但在实际鄂南地区中，由于下伏山西、太原组煤层的发育，在有限的分辨率下，煤层反射的旁瓣与砂体的反射耦合在一起，导致上伏石盒子组砂体地震波场特征较为复杂，储层特征不明显；同时下石盒子致密河道砂与下伏煤层具有不同的分布特征，常规相控方法难以实现对储层的精细预测。
因此，本文提出了基于多维相控的叠前地质统计学反演技术，对鄂南含煤地层中薄砂体进行预测。该方法采用不同维度相约束和随机函数参数，可以实现对上覆储层和下伏煤层的同时反演。由于上下两套地层采用了不同的约束方式，这就要求层位的解释相对准确。主要反演流程如图2所示，其中关键步骤如下：
![]()
图 2 多维相控叠前地质统计学反演流程图Figure 2. Flowchart of multidimensional phase-controlled pre-stack geostatistical inversion（1）多井测井岩石物理分析：对工区内所有井开展岩石物理分析，优选出对砂体敏感的弹性参数，为后续的反演奠定基础；
（2）多维岩相概率密度体构建：首先根据已有的地质认识和测井信息，分析与河道砂相关的地震属性，提取符合沉积变化规律的二维岩相概率密度作为石盒子组储层的平面约束；然后利用数据驱动的煤层反演体，结合贝叶斯判别原理，提取三维煤相概率密度作为下伏煤层的空间约束，最后基于建模曲线，综合二维和三维约束，共同开展两个层段的叠前地质统计学反演；
（3）统计学参数确定：变差函数既能描述区域化变量的空间结构性，也能描述其随机性，是地质统计学所特有的重要工具，与储层的非均质性相关。分析已有的地质和测井等先验信息，确定合理的统计学参数。
基于多维相控的叠前地质统计学反演的含煤地层薄砂体预测技术充分考虑下伏煤层和砂岩储层的耦合特征，降低地震数据的多解性，提高储层预测的精度，提供更具有地质概念的储层预测成果，具有较好的薄储层预测能力。
2. 应用实例
2.1 研究区地质概况
鄂尔多斯盆地南部BC探区山西-太原组为曲流河三角洲沉积，煤层厚度具有东部向西南逐渐减薄的特征，进入下石盒子组沉积期，区域沉积环境转变为辫状河三角洲沉积，其中分流河道岩性以砾岩、粗砂岩为主。主力层段为盒1段，砂体厚度薄，多在4~12 m。上古生界分流河道致密气藏具有埋深大、单层砂体薄，横向变化快，纵波阻抗对储层的区分度差等地质-岩石物理特征，在有限的地震分辨率下，下伏煤层反射的旁瓣与砂体的反射耦合在一起，为储层预测带来挑战。
2.2 砂-泥-煤三相岩石物理建模
通过对工区内井的纵波速度和密度的分布特征进行分析，发现纵波速度曲线整体分布较为合理，而密度测井曲线存在较多的异常值，考虑是碎屑岩地层中存在了扩径的影响（图3，图中不同颜色代表不同井的测井曲线）。本文优选W1井进行研究，该井整体上井径变化范围小，速度和密度范围基本正常，因此，将其作为标准井（图4）；其他几口井密度曲线与井径有明显相关关系，泥岩段密度受扩径影响大，存在较低的异常值，为扩径井（图5）。对标准井W1开展不同的测井曲线与密度的相关性分析，优选与密度相关性最高的曲线：伽马、声波、中子，利用这3条曲线进行非线性拟合预测密度曲线。图6（a）为标准井拟合前后对比，拟合后的密度与原始测井密度吻合程度较高。之后将该相关关系映射到扩径井中，对比结果如图6（b）所示。分析图6下扩径井，井径曲线整体变化较大，同时实测密度几乎整段都存在异常低的尖峰值，与井径曲线的变化有较大的相关性，而与标准井未扩径层段（图6（a））砂泥岩密度变化不大的特征相违背，因此认为该井存在大段的扩径，整体实测密度曲线较不可靠，局部井径变化不大的地方相对可靠。在图6（b）在井径变化小的层段，拟合密度与实测密度有较好的重合，验证了该方法的有效性。利用扩径校正后的密度曲线一方面进行解释孔隙度曲线的优化（实际解释孔隙度曲线仅在砂岩段有值，泥岩段无孔隙度值），另一方面为后续建模提供更为合理的密度曲线。
![]()
图 3 实测纵波速度（a）和密度（b）的分布Figure 3. Distribution of measured longitudinal wave velocity (a) and density (b)接下来根据上述三相岩石物理建模流程，对有横波曲线的井不断迭代，优化矿物、流体及骨架参数，进行3次建模和分步融合，获得了下石盒子组和山西组更加合理的建模曲线（图7（a））。预测结果与实测纵波速度、实测横波速度和校正密度吻合程度较高，说明了估算结果的可靠性以及估算方法的适用性。将优化后的矿物、流体及骨架参数应用到无横波井上，预测了横波速度曲线（图7（b））。后续的储层定量反演将采用该套横波估算曲线。
![]()
图 7 建模曲线与原始曲线对比注：黑线为原始，红线为建模Figure 7. Comparison between modeling curve and original curve2.3 多维相控叠前地质统计学反演及含煤地层薄砂体预测
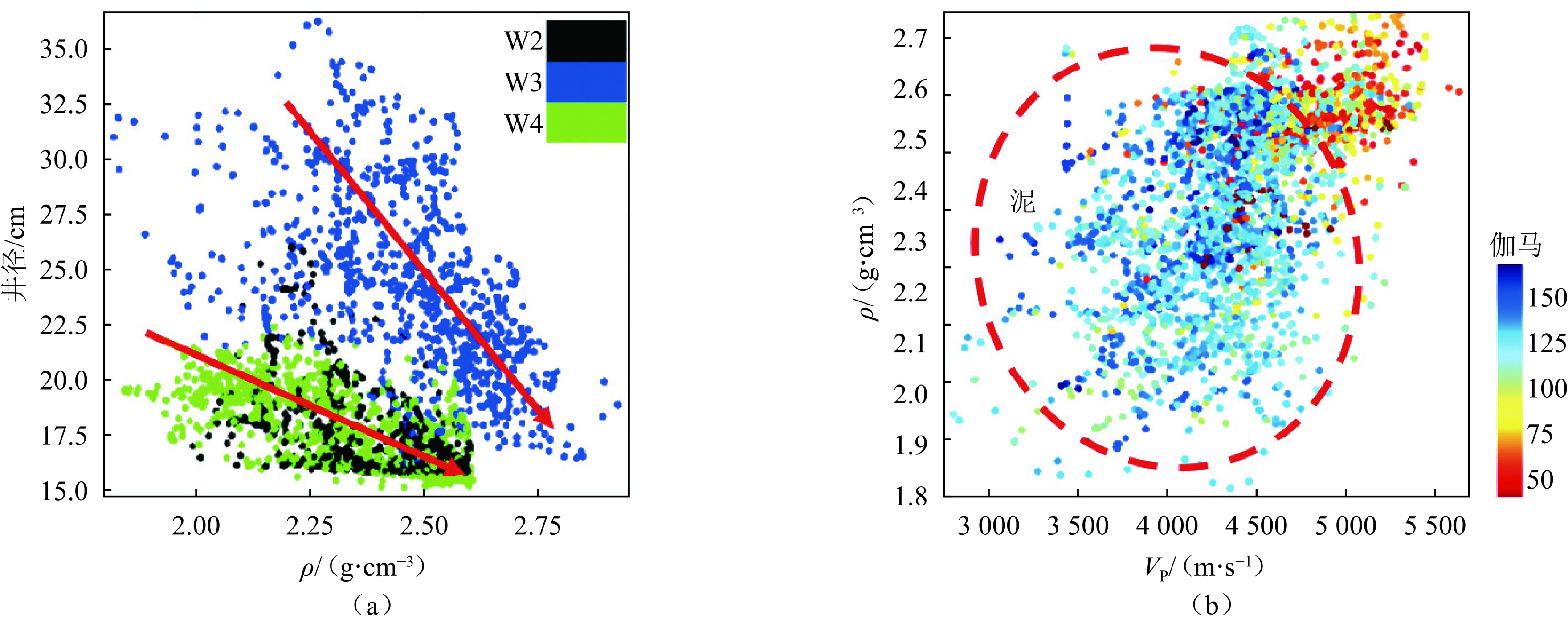
根据已有的测井解释成果和曲线，开展弹性参数交会分析（图8），结果表明，煤和砂、泥具有不同的特征，纵波阻抗值低于
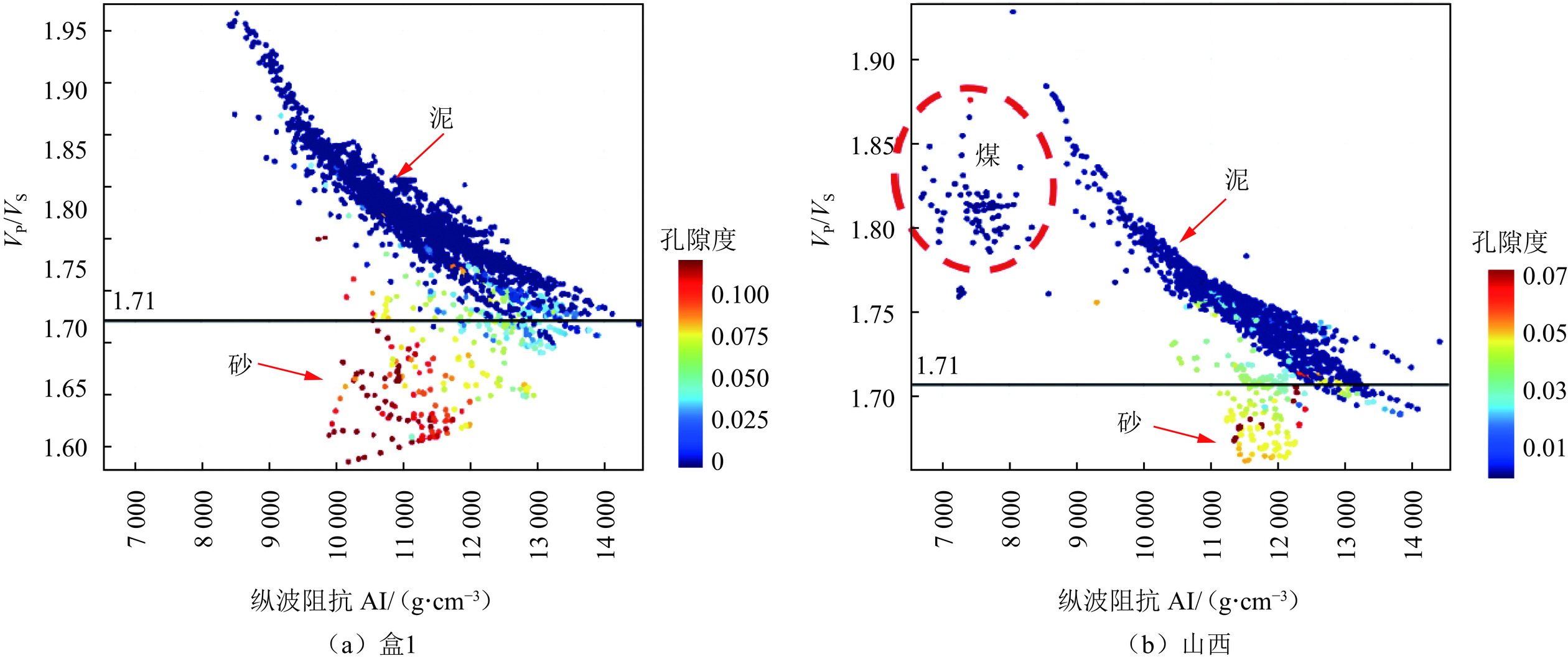
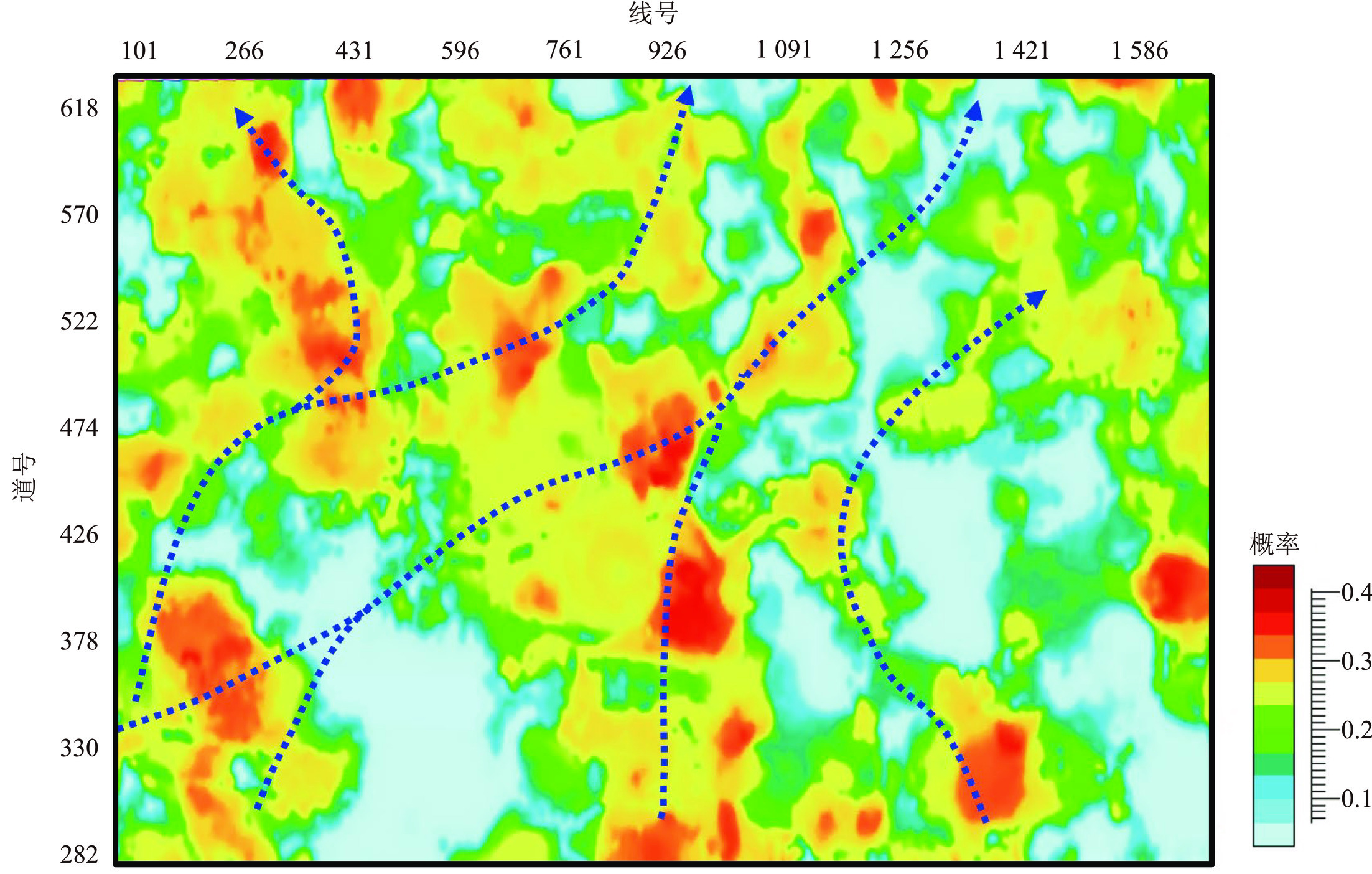
9000 （g/cm3*m/s）；盒1段砂体整体具有中-高纵波阻抗特征（纵波阻抗值范围9800 ~13500 （g/cm3*m/s）），随着物性变好纵波阻抗值会降低，与围岩的纵波阻抗区间存在叠置；纵横波速度比可以反映砂岩储层特征，当纵横波速度比小于1.71时为砂岩，大于1.71为泥岩。下石盒子组厚度相对稳定，分析盒1段的波形聚类属性，一定程度能够指示下石盒子组辫状河三角洲平原分流河道相带。结合地质先验认识和测井分析，利用该敏感属性，提取符合沉积变化规律的砂岩平面概率密度，作为反演过程中下石盒子组的二维约束（图9）。煤层具有低阻抗的特征，可利用地震数据叠后稀疏脉冲反演预测山西-太原煤层的分布，然后借助贝叶斯判别原理将结果转化为煤的三维岩相概率密度体，作为反演过程中山西-太原组的三维约束（图10）。
![]()
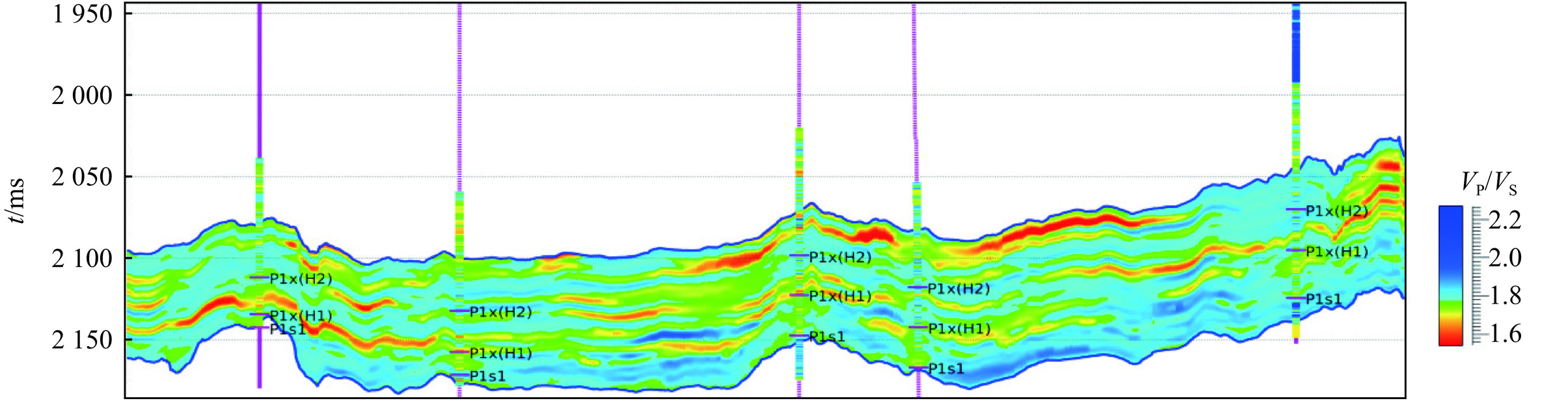
图 9 下石盒子组砂岩平面概率密度Figure 9. Probability density of sandstone plane in the Lower Shihezi Formation对叠前道集资料进行解释性优化，然后开展0~10°、10~20°、20~30°的分角度叠加，该3个叠加体作为后续反演的地震数据。通过对已知的钻井资料和地质信息的统计，获得各个层段不同岩性的变差函数等统计学参数，开展下石盒子组和山西-太原组岩石物理建模下的多维相控叠前地质统计学反演。经过多次随机结果分析得到了最终的预测结果。从反演的纵横波速度比剖面上看（图11），反演结果分辨率高，且有利的低速度比区域的横向连续性与盒1段河道砂体的快速相变特征一致。提取盒1段对应时窗内纵横波速度比小于1.71的时间厚度（图12），反映了研究区盒1段河道砂储层呈北东-南西向展布，与物源方向一致。预测得到的砂体厚度与井点实钻砂体厚度的符合率较高，达85%。有效地支撑了该地区开发井位部署，也证实了该方法预测结果的可靠性。
3. 结论
本文提出了一种针对鄂南地区含煤地层岩石物理建模下的叠前多维相控薄砂岩预测的方法。砂-泥-煤三相岩石物理建模是对常规Xu-White岩石物理建模过程的改进，适用于存在测井曲线扩径问题的含煤碎屑岩地层。在多参数拟合提高测井曲线质量的基础上，进行3次建模和分步融合预测横波速度，解决了实际工区横波资料不足的问题，曲线预测结果的精度较高，证明了该方法的有效性，同时也为后续反演提供了更非富的基础资料。基于多维相控的地质统计学反演综合利用了地震、地质和测井资料等先验信息，分别构建了与河道砂和下伏煤层有关的二维和三维约束，共同开展了叠前地质统计学反演，改善了常规地质统计学反演横向不确定性强的同时，也充分考虑了实际地区下伏煤层和砂岩储层的耦合特征。岩石物理建模下的叠前多维相控薄砂岩预测技术提高了含煤地层薄砂体预测的精度，预测结果与测井解释结论和地质认识能较好地吻合，在鄂南地区有较好的适用性，指导了该区下一步的勘探部署，也可以为其他类似地区的薄储层预测提供技术参考。
-
![]()
图 1 砂、泥、煤三相岩石物理建模技术路线图
Figure 1. Flowchart of three-phase rock physical modeling technology of sand, mud, and coal
![]()
图 2 多维相控叠前地质统计学反演流程图
Figure 2. Flowchart of multidimensional phase-controlled pre-stack geostatistical inversion
![]()
图 3 实测纵波速度（a）和密度（b）的分布
Figure 3. Distribution of measured longitudinal wave velocity (a) and density (b)
![]()
图 7 建模曲线与原始曲线对比
注：黑线为原始，红线为建模
Figure 7. Comparison between modeling curve and original curve
![]()
图 9 下石盒子组砂岩平面概率密度
Figure 9. Probability density of sandstone plane in the Lower Shihezi Formation
-
[1] 张杨. 利用Xu-White模型估算地震波速度[J]. 成都理工大学学报: 自然科学版, 2005, 32(2): 188-195. ZHANG Y. Xu White’s model for seismic wave velocity prediction[J]. Journal of Chengdu University of Technology: Science and Technology Edition, 2005, 32(2): 188-195. (in Chinese).
[2] 洪忠, 张猛刚, 朱筱敏. 基于岩石物理的致密碎屑岩气藏岩性及流体概率预测[J]. 石油物探, 2015, 54(6): 735-744. DOI: 10.3969/j.issn.1000-1441.2015.06.012. HONG Z, ZHANG M G, ZHU X M. Prediction of lithology and fluid probabilities of tight clastic gas reservoirs based on rock physics[J]. Geophysical Prospecting for Petroleum, 2015, 54(6): 735-744. DOI: 10.3969/j.issn.1000-1441.2015.06.012. (in Chinese).
[3] 边婧. 地震岩石物理分析在致密砂岩储层预测中的应用[J]. 东北石油大学学报, 2015, 39(5): 63-70. DOI: 10.3969/j.issn.2095-4107.2015.05.007. BIAN J. Application of rock physics to the prediction of tight sandstone reservoirs[J]. Journal of Northeast Petroleum University, 2015, 39(5): 63-70. DOI: 10.3969/j.issn.2095-4107.2015.05.007. (in Chinese).
[4] 窦龑, 高刚 梁琳 等. 基于Xu-White 模型的横波速度预测[J]. 新疆石油地质, 2016, 37(1): 83-87. DOU Y, GAO G, LIANG LET AL. Prediction of S-Wave velocity based on Xu-White model[J]. Xinjiang Petroleum Geology, 2016, 37(1): 83-87. (in Chinese).
[5] 王金伟, 张尔华, 谢春临. 虚拟孔隙度优化的Xu-White模型法预测横波速度[J]. 断块油气田, 2011, 18(4): 445-448. WANG J W, ZHANG E H, XIE C L. Prediction of shear wave velocity with optimized Xu-White model based on virtual porosity[J]. Fault-Block Oil & Gas Field, 2011, 18(4): 445-448. (in Chinese).
[6] 杨志芳, 曹宏, 姚逢昌, 等. 复杂孔隙结构储层地震岩石物理分析及应用[J]. 中国石油勘探, 2014, 19(3): 50-56. DOI: 10.3969/j.issn.1672-7703.2014.03.006. YANG Z F, CAO H, YAO F C, ET AL. Seismic rock physical analysis of complex porous reservoir and its application[J]. China Petroleum Exploration, 2014, 19(3): 50-56. DOI: 10.3969/j.issn.1672-7703.2014.03.006. (in Chinese).
[7] 杨勤林, 李洋, 曹少蕾, 等. 松辽盆地苏家屯区块致密砂岩岩石物理分析和含气性预测[J]. 天然气地球科学, 2020, 31(4): 578-585. YANG Q L, LI Y, CAO S L, ET AL. Rock physics analysis and gas-bearing prediction of tight clastic reservoir in Sujiatun Block, Songliao Basin[J]. Natural Gas Geoscience, 2020, 31(4): 578-585. (in Chinese).
[8] 陈强, 彭盛强, 赵光亮, 等. 地震岩石物理建模技术在迪北阿合组致密砂岩气中的应用[J]. 物探化探计算技术, 2024, 46(3): 315-323. DOI: 10.3969/j.issn.1001-1749.2024.03.08. CHEN Q, PENG S Q, ZHAO G L, ET AL. Application of seismic rock physical modeling technology in tight sandstone gas of Dibei Ahe Formation[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2024, 46(3): 315-323. DOI: 10.3969/j.issn.1001-1749.2024.03.08. (in Chinese).
[9] HAAS A, DUBRULE O. Geostatistical inversion: A sequential method of stochastic reservoir modelling constrained by seismic data[J]. First Break, 1994, 12(11): 561-569.
[10] 姜文龙, 杨锴. 岩石物理参数高分辨率地质统计学反演[J]. 石油物探, 2012, 51(6): 638-648. DOI: 10.3969/j.issn.1000-1441.2012.06.014. JIANG W L, YANG K. High-resolution geostatistical petrophysical parameter inversion[J]. Geophysical Prospecting for Petroleum, 2012, 51(6): 638-648. DOI: 10.3969/j.issn.1000-1441.2012.06.014. (in Chinese).
[11] 刘占族, 张雷, 霍丽娜, 等. 地质统计学反演在煤层气薄储层识别中的应用[J]. 石油地球物理勘探, 2012, 47(S1): 30-34. LIU Z, ZHANG L, HUO L N, ET AL. Identification of thin coalbed methane reservoirs using geostatistical inversion[J]. Oil Geophysical Prospecting, 2012, 47(S1): 30-34. (in Chinese).
[12] 赵晨, 张广智, 张佳佳, 等. 基于Metropolis优化的叠前全局迭代地质统计学反演方法[J]. 地球物理学报, 2020, 63(8): 3116-3130. DOI: 10.6038/cjg2020M0674. ZHAO C, ZHANG G Z, ZHANG J J, ET AL. Prestack global iteration geostatistical inversion method based on Metropolis sampling algorithm[J]. Chinese Journal of Geophysics, 2020, 63(8): 3116-3130. DOI: 10.6038/cjg2020M0674. (in Chinese).
[13] 闵小刚, 康安, 周守信. 基于相控地质统计学反演的薄储层岩性、物性预测[J]. 海洋地质前沿, 2015, 31(3): 27-32. MIN X G, KANG A, ZHOU S X. Lithological and physical properties prediction of thin reservoirs based on faciescontrolled geo-statistical inversion[J]. Marine Geology Frontiers, 2015, 31(3): 27-32. (in Chinese).
[14] 段新意, 李尧, 郭军, 等. 相控地质统计学反演方法及其在油田开发中的应用[J]. 断块油气田, 2021, 28(5): 683-690. DUAN X Y, LI Y, GUO J, ET AL. The facies-control geostatistical inversion method and its application in development stage of oilfield[J]. Fault-Block Oil and Gas Field, 2021, 28(5): 683-690. (in Chinese).
[15] 林利明, 郑颖, 史浩, 等. 基于相控地质统计学叠前反演的致密砂岩薄储层含气性预测——以鄂尔多斯盆地临兴中区为例[J]. 天然气工业, 2023, 43(2): 56-66. DOI: 10.3787/j.issn.1000-0976.2023.02.006. LIN L M, ZHENG Y, SHI H, ET AL. Gas-bearing prediction of thin tight sandstone reservoirs based on facies-controlled geostatistical pre-stack inversion: A case study of the middle Linxing Block in the Ordos Basin[J]. Natural Gas Industry, 2023, 43(2): 56-66. DOI: 10.3787/j.issn.1000-0976.2023.02.006. (in Chinese).
[16] 伊振林, 吴胜和, 张保国, 等. 一种新的测井曲线环境校正方法——在平湖油气田中的应用[J]. 天然气工业, 2010, 30(1): 39-41. DOI: 10.3787/j.issn.1000-0976.2010.01.010. YI Z L, WU S H, ZHANG B G, ET AL. Anewapproachto environmental correction of logs: Acase study in the Pinghu oil and gas field[J]. Natural Gas Industry, 2010, 30(1): 39-41. DOI: 10.3787/j.issn.1000-0976.2010.01.010. (in Chinese).
[17] 刘之的, 王剑, 杨秀春, 等. 密度测井扩径影响校正方法在煤层气储层中的适用性分析[J]. 地球物理学进展, 2014, 29(5): 2219-2223. DOI: 10.6038/pg20140534. LIU Z D, WANG J, YANG X C, ET AL. Applicability analysis of correction method for expanding diameter influence of density logging in coalbed methane reservoir[J]. Progress in Geophysics, 2014, 29(5): 2219-2223. DOI: 10.6038/pg20140534. (in Chinese).
[18] 王小玄, 肖程释, 郑翔天. 基于岩石物理分析的煤系地层测井曲线扩径影响校正[J]. 中国煤炭, 2016, 42(2): 22-26. DOI: 10.3969/j.issn.1006-530X.2016.02.006. WANG X X, XIAO C S, ZHENG X T. Expanding effect correction of coal measure strata logging curves based upon rock physics analysis[J]. China Coal, 2016, 42(2): 22-26. DOI: 10.3969/j.issn.1006-530X.2016.02.006. (in Chinese).
[19] XU S Y, WHITE R E. A new velocity model for clay-sand mixtures[J]. Geophysical Prospecting, 1995, 43(1): 91-118. DOI: 10.1111/j.1365-2478.1995.tb00126.x.
[20] ROBERT G, KEYS, XU S Y. An approximation for the Xu-White velocity model[J]. Geophysics, 2002, 65(5): 1406-1414.
[21] TORRES-VERDIN C, VICTORIA M, MERLETTI G, ET AL. Trace-based and geostatistical inversion of 3-D seismic data for thin-sand delineation: An application in San Jorge Basin, Argentina[J]. The Leading Edge, 1999, 18(9): 1070-1077. DOI: 10.1190/1.1438434.
[22] CONTRERAS A, TORRES-VERDIN C, KVIEN K, et al. AVA stochastic inversion of pre-stack seismic data and well logs for 3D reservoir modeling[C]//67th EAGE Conference & Exhibition. Madrid: European Association of Geoscientists & Engineers, 2005: cp-1-00310.
[23] 张广智, 王丹阳, 印兴耀, 等. 基于MCMC的叠前地震反演方法研究[J]. 地球物理学报, 2011, 54(11): 2926-2932. DOI: 10.3969/j.issn.0001-5733.2011.11.022. ZHANG G Z, WANG D Y, YIN X Y, ET AL. Study on prestack seismic inversion using Markov Chain Monte Carlo[J]. Chinese Journal of Geophysics, 2011, 54(11): 2926-2932. DOI: 10.3969/j.issn.0001-5733.2011.11.022. (in Chinese).
[24] 王丹阳. 基于MCMC方法的叠前反演方法研究[D]. 青岛: 中国石油大学(华东), 2012. WANG D Y. Pre-stack seismic inversion based on Markov Chain Monte Carlo Method[D]. Qingdao: China University of Petroleum (East China), 2012. (in Chinese).
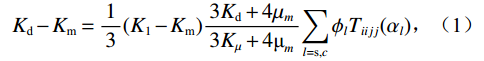
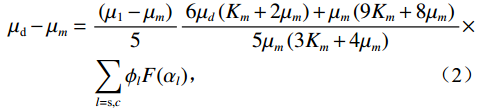
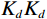
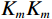
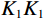
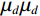
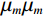
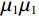
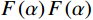
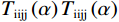
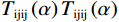
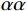
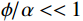
下载:
计量
- 文章访问数: 30
- HTML全文浏览量: 6
- PDF下载量: 5
