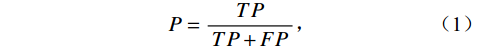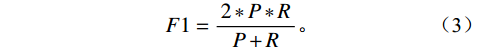Experimental Study on Long Short-term Memory Networks for Identifying P-wave Primary Phase
-
摘要:
初至震相的识别是地震数据处理中的基本内容。由于人工识别效率较低，且受到人为主观因素的影响，因此近年来陆续发展出许多自动识别初至震相的方法。然而，这些自动识别方法主要基于背景噪声和地震信号的差异，并且通常需要一个阈值，因此难以在复杂的地震区域实施或应对海量的地震数据。为克服这些不足，本文搭建7层基于长短期记忆网络（Lstm）的卷积循环神经网络，开展P波初至震相识别的实验研究，并利用南加州公开的数据集对新建的卷积循环神经网络进行训练和测试。通过与传统的卷积神经网络、自动识别算法、Pick-Net、EQtransformer网络等进行对比，本研究搭建的卷积循环神经网络的识别精度相对较高，因此可直接使用地震波形数据作为时间序列进行训练。此外，虽然本研究建立的卷积循环神经网络只有7层网络，但基本达到复杂网络模型的震相识别精度，充分说明卷积循环神经网络的优势。综上，本研究提出的基于时间序列卷积循环神经网络为P波初至震相的自动识别提供一种新思路，为快速精准的自动识别震相问题提供技术支持。
Abstract:Identifying primary phases of seismic waveforms is a routine task in seismic data processing. Owing to the low efficiency of manual identification and the influence of human subjective factors, many methods for the automatic identification of the primary phase have been developed in recent years. Most of these methods determine the arrival time based on the ratio between ambient noise and seismic signals. However, they typically require a threshold value, making their implementation in complex seismic regions and handling massive seismic data challenging. In this study, a seven-layer convolutional recurrent neural network based on long short-term memory (LSTM) network was constructed, and an experimental study was conducted to identify the P-wave primary phase. The network was trained and tested using a data set from Southern California. Compared with the traditional convolutional neural network, automatic identification algorithm, Pick-Net, and EQtransformer network, the recognition accuracy of our new convolutional recurrent neural network is relatively higher; therefore, the seismic waveform data can be directly used as a time series for training. Additionally, while the new convolutional recurrent neural network has only seven network layers, it achieves an accurate phase identification of complex network models, showcasing the strengths of convolutional neural networks. In summary, our study presents a convolutional recurrent neural network based on the LSTM, offers a new idea for the automatic identification of the primary phase, and provides technical support for the rapid and accurate automatic identification of the seismic phase.
-
地震初至震相识别和到时拾取不仅是地震数据处理的重要环节和开展后续成像工作的基础，而且也是地震资料解释的关键部分。随着全球地震台站及野外地震仪器布设的不断完善，如何更加高效的处理海量波形数据成了一个亟需解决的问题。
传统的震相识别和到时拾取主要包括人工标注和自动处理两种。人工标注即处理人员通过分析地震波形，对地震事件震相和到时进行手动拾取。虽然该方法的识别精度较高，但该精度更多地依赖于拾取者的经验，且当处理海量数据时更需要消耗大量的时间或人工成本，效率相对低下。相比之下，传统的自动处理方法主要基于波形互相关或自适应叠加等原理[1-4]，虽然相较于人工标注效率大大提高，但受机器性能、野外环境、震源复杂性等众多因素影响，仍存在稳定性较低、精度不高且灵敏度低等局限性。
相较于传统方法，作为一种新的数据驱动型技术，深度学习在地球物理学界引起了广泛的关注，并被用于解决传统方法所存在的瓶颈问题。
近几十年来，研究学者们已经提出了许多方法用以自动拾取地震事件的初至[5-11]。其中，短时长时能量比法（short term average/long term average，STA/LTA）是使用最广泛的方法之一。该方法首先计算短时间窗口与长时间窗口的移动平均能量比，然后选择大于用户定义阈值的最大值作为初至时刻。Baer等[5]通过将特征函数（characte riseitic function，CF）和动态峰值阈值整合到算法中，改进了STA/LTA的算法；Saragiotis等[6]在冗余小波变换域（redundant wavelet transform，R-WT）中使用高阶统计量（higher-order statistics，HOS）来自动拾取初至波；Zhang等[7]利用AIC准则自动检测和选择初至波。然而，上述这些方法由于效率问题难以应对海量地震数据的处理压力，且由于阈值要求，很难在复杂的地震区域实施。其他自动初至震相识别方法包括多窗口算法[8]、修正能量比法（modified energy ratio，MER）[9]、变换谱图法[10]、短期峰度与长期峰度比（S/L-Kurt）法[11]等。
相比较于其他的地震震相拾取方法，深度学习处理震相拾取问题通常被看做图像语义分割问题或者边界检测问题。Ma等[12]于2020年通过将地震信号转换为灰度图像，将初至震相识别问题转换为图像分割问题来研究，然后应用基于像素级CNN（convolutional neural networks）的U-net架构来拾取初至。与此类似，Fernhout等[13]部署了7层U-Net架构，并增加了用于识别的跳跃连接；Yuan等[14]使用U-net进行地震图像分割，并使用循环神经网络（recurrent neural network，RNN）进行到时拾取；Zheng等[15]的研究表明，在没有足够可用的训练数据的情况下，CNN与RNN架构的结合更适用于P波和S波的相位检测。
Ross等[16]探索了通过训练两个不同的CNN来对初动极性进行分类，该模型的预测精度达到了95%；Hollander等[17]提出了使用深度学习和传统拾取算法相结合的模型，先使用一个5层深度神经网络进行分类，再通过计算能量比属性捕捉到其最大值，在已识别窗口的边界内找到初至时刻的确切位置；Gao等[18]使用模糊C均值聚类算法研究了初至拾取，在研究中首先利用垂直和水平滑动窗口来确定初至时间的大致范围，然后利用模糊C-means聚类和粒子群优化（particle swarm optimization，PSO）定位初至时刻；Tsai等[19]使用变分自动编码器以及生成对抗网络，构建了在地震初至拾取的训练过程中与人工交互的模型；Duan等[20]提出了一种使用支持向量机（support vector machines，SVM）的初至拾取方法，以改善自动初至震相识别；Ma等[21]使用改进的二维像素卷积网络自动识别初至；Liao等[22]使用连续小波变换（continuous wavelet transform，CWT）作为 AlexNet，GoogleNet和SqueezeNet的输入特征，将迁移学习应用于初至拾取。
最近几年，许多优秀的神经网络模型应用到震相识别中来，比如Zhu等[23]提出一种基于DCNN的深度学习网络模型−相位解缠绕网络（PhastNet）完成相位解缠绕，将相位解缠绕建模成语义分割问题，PhaseNet将缠绕相位作为输入，缠绕数作为语义标签，此外还提出了一种基于聚类的后处理过程，结合了超过2π的不连续相位的位置信息；Wang等[24]提出了PickNet模型，将归一化的原始波形记录作为数据，输出一个类脉冲序列，序列最大值对应的时刻即为震相的到时。将地震波形序列映射为尖锐的到时脉冲序列，具有更高的拾取精度和泛化能力。使用VGG-16图像识别模型来识别P波和S波初至震相；Chai等[25]使用PhaseNet模型与双差层析成像相结合，以减少手动地震初至拾取的劳动力和成本；He等[26]使用从地震波形中提取的局部窗口提出了基于Faster R-CNN的P波拾取方法；Mousavi等[27]提出了一种用于地震探测和相位提取的深度学习模型，即EQtransfomer神经网络，将循环神经网络（RNN）的长短期记忆（LSTM）层与Transformer结构结合起来，由1个非常深的编码器和3个由1D卷积、双向和单向LSTM和自注意力层等组成的独立解码器。编码器在时域内消耗地震信号，并生成关于它们的时间依赖性的高级表示和上下文信息；解码器使用这些信息将高级特征映射到3个相关的概率序列：地震信号的准确性、P波初至和S波初至。该模型进一步大幅提升了对地震震相识别模型的准确性以及性能。
与STA/LTA和AIC拾取算法相比，这些网络具有显著的性能提升，且识别震相的准确率在90%左右，但大多数神经网络由于都是建立在卷积神经网络或循环神经网络模型之上。不可避免的是，地震波波形数据作为一维时间序列数据，而卷积神经网络和循环神经网络本身结构的有限性在对一维时间序列数据方面没有得到改善，RNN专门用于学习长期依赖性和顺序相关性，但不能很好地处理结构化信息，或者说更复杂的关系信息。CNN可以提取局部趋势的模式和在不同时间出现的相同模式，偏向于局部特征的提取。但CNN没有记忆功能且时间序列数据效果较差。
本文利用深度学习卷积神经网络（CNN）和循环神经网络（RNN）构建基于LSTM的卷积循环神经网络（CRNN），并使用南加州地震台网人工标定P波到时数据。选取均方误差和标准差作为训练结果的评价指标，对新建的神经网络进行训练，并与搭建的传统卷积神经网络、自动处理和较为成熟的深度网络选取准确率、召回率、F1分数等指标进行对比分析，以检验新搭建的CRNN网络的有效性。
1. 实验数据
1.1 数据与数据预处理
本研究所用的天然地震波形数据来源于南加州地震台网提供的地震数据集，包含数据集内人工标注的P波初至震相信息（表1）。
表 1 南加州地震台网地震数据信息Table 1. Information of Seismic Data from the Southern California Seismic Network震中距 通道 地震台数量 地震发生时间 波形数量 地震波类型 120 km内 NHZ、EHZ、HHZ 692 2000~2017年 3635436 P波 在使用地震数据集对神经网络进行训练之前，需要先进行数据预处理。本研究只对NHZ、EHZ、HHZ等通道的地震记录进行地震初至震相识别分析，将
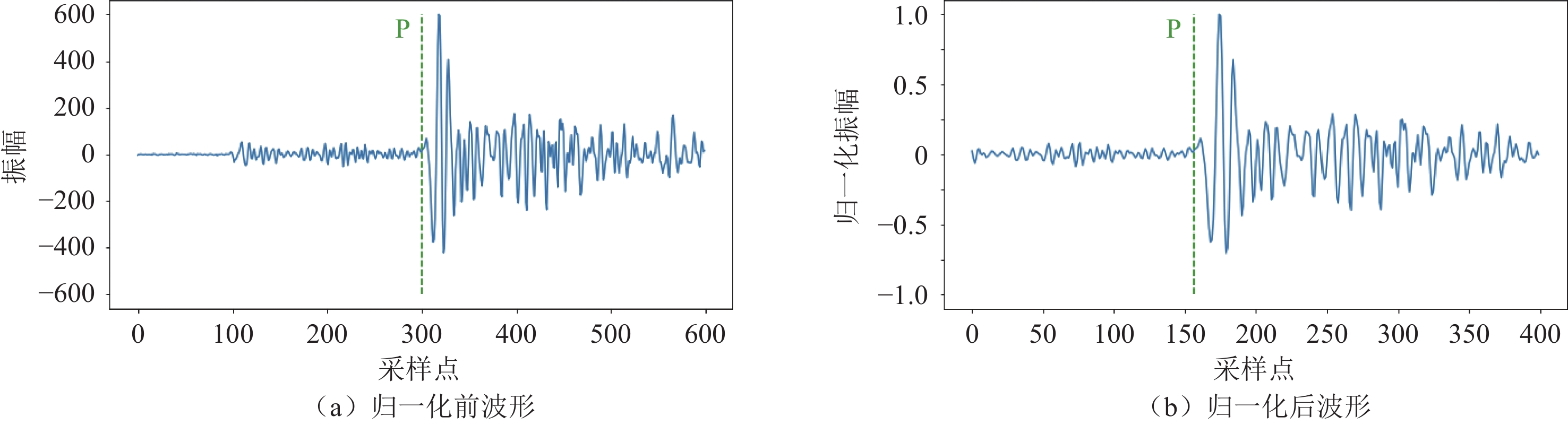
3635436 条波形记录的80%用作训练集，另外的20%数据用作测试集。南加州数据集已经进行了相关的预处理工作包括滤波等，本研究在数据集基础上进行了随机扰动和标准化等预处理工作。以人工手动标注的P波初至时刻作为中心点，在地震波形中截取±2.5 s长（总长5 s）的时间序列，采样频率为100 Hz。目前所有初至到时都处于第250个数据点处。
为了模拟实际情况，方便神经网络模型训练，需对初至到时进行随机变化。为每个地震信号都添加一个范围在[−50，50]的均匀随机整数，在时间序列上进行随机滑动。保留4 s长的数据序列，以保证P波初至时刻位于数据序列之内。同时保留均匀随机数，其中包含了初至到时信息。至此，地震初至震相识别问题被转换为一个自变量为400个数据点组成的数据序列，因变量为单个整数的非线性回归问题。
1.2 数据标准化
由于地震烈度不同，台站距离震中的距离也不同，因此观测到的地震资料差异较大，有的甚至相差数个量级。神经网络模型训练中要求使用的数据特征值相近，否则会严重影响梯度下降算法的收敛速度，所以有必要对数据进行归一化处理。常见的归一化方法有均值消减法、最大最小值缩放法、标准化法等。
当使用灰度图像进行训练时，每个像素点的数据压缩为[0，1]之间的浮点值。当使用8位彩色图像进行训练时，每个像素点表征为RGB三通道数据，每种颜色用[0，255]之间的自然数表示。
本文使用的地震信号数据为一维时间序列数据，在训练时作为时间序列直接输入到神经网络模型中，并采用最大最小值缩放法对数据进行标准化。首先计算每条地震信号的最大值和最小值，两者相减得出数据的宽度；然后根据数据宽度和最大值对序列中的每个数据进行缩放。这保证了标准化后每条地震信号的最大最小值都相同，其对神经网络的影响权重也相同。此外，训练集上每个输入变量的平均值接近于零，有助于提高收敛速度[28]。
图1展示了某示例波形数据归一化以及数据增强前后的效果，不仅均值接近零，而且很好地保留了地震信号的所有特征。
![]()
图 1 归一化前后天然地震波形示例，绿色虚线表示P波初至Figure 1. Example of the seismic waveform after normalization. The dashed green line shows the primary arrival of the P wave2. 实验方法
2.1 卷积神经网络
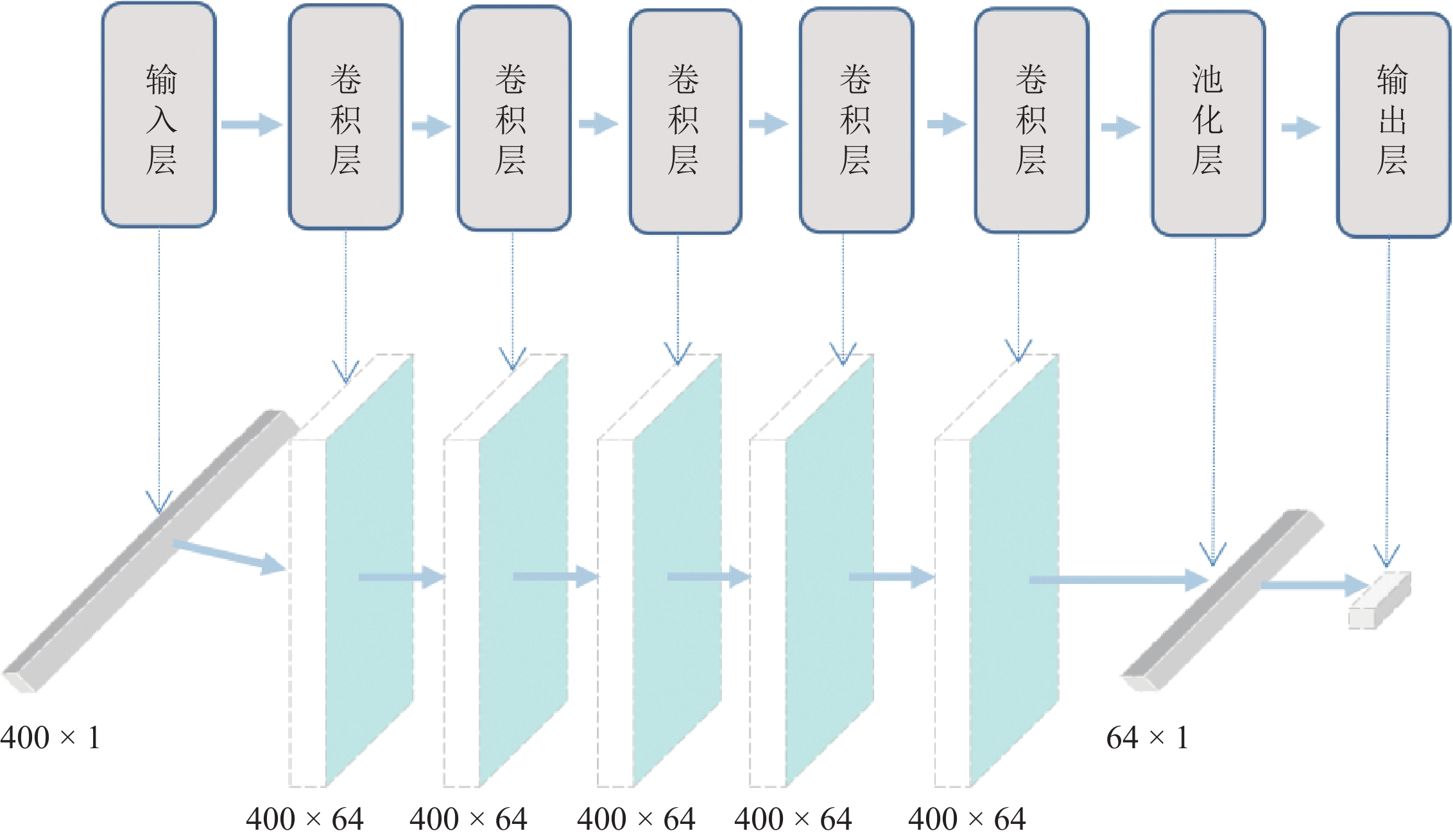
根据已有的CNN结构，本文确定卷积神经网络的总体结构，搭建包括5个卷积层、1个池化层和1个输出层（全连接层）的7层网络结构。其中：卷积层用于执行卷积操作，提取关键特征；池化层用于降采样操作，降低运算量，避免无关特征对结果的影响；全连接层用于对特征矩阵降维后输出结果。需要注意的是，卷积层的数量并不是越多越好，卷积神经网络的层数越大，其感受野就越大，但会面临梯度消失与梯度爆炸的风险。在目标检测领域，目标越大则需要越大的感受野。对于本实验而言，初至震相识别的目标大小仅有初至时刻附近十几个点，因此不需要过大的感受野就可以实现震相识别要求。
本实验搭建的CNN模型使用的5个卷积层均包含1个卷积核，其卷积核的大小为3×1，其步长为1，采用了相同填充（same padding）进行填充。每个卷积层后面都有一个正则化层，以避免过拟合问题的出现。正则化层后添加非线性激活函数。激活函数选择校正线性单元（ReLU）算法，比Sigmoid函数或Tanh函数计算效率更高，且有助于防止过拟合与梯度消失问题。
图2为本文所采用的CNN模型及各层输出矩阵维度示意图。如图所示，输入层的输入数据维度为400×1，经过5层卷积层的卷积操作后，输出数据维度为400×64，输入到池化层中进行降采样，并将特征图降为一维数据，池化层输出数据维度为64×1。最后全连接层作为输出层输出一个浮点值，此为初至震相预测结果。
![]()
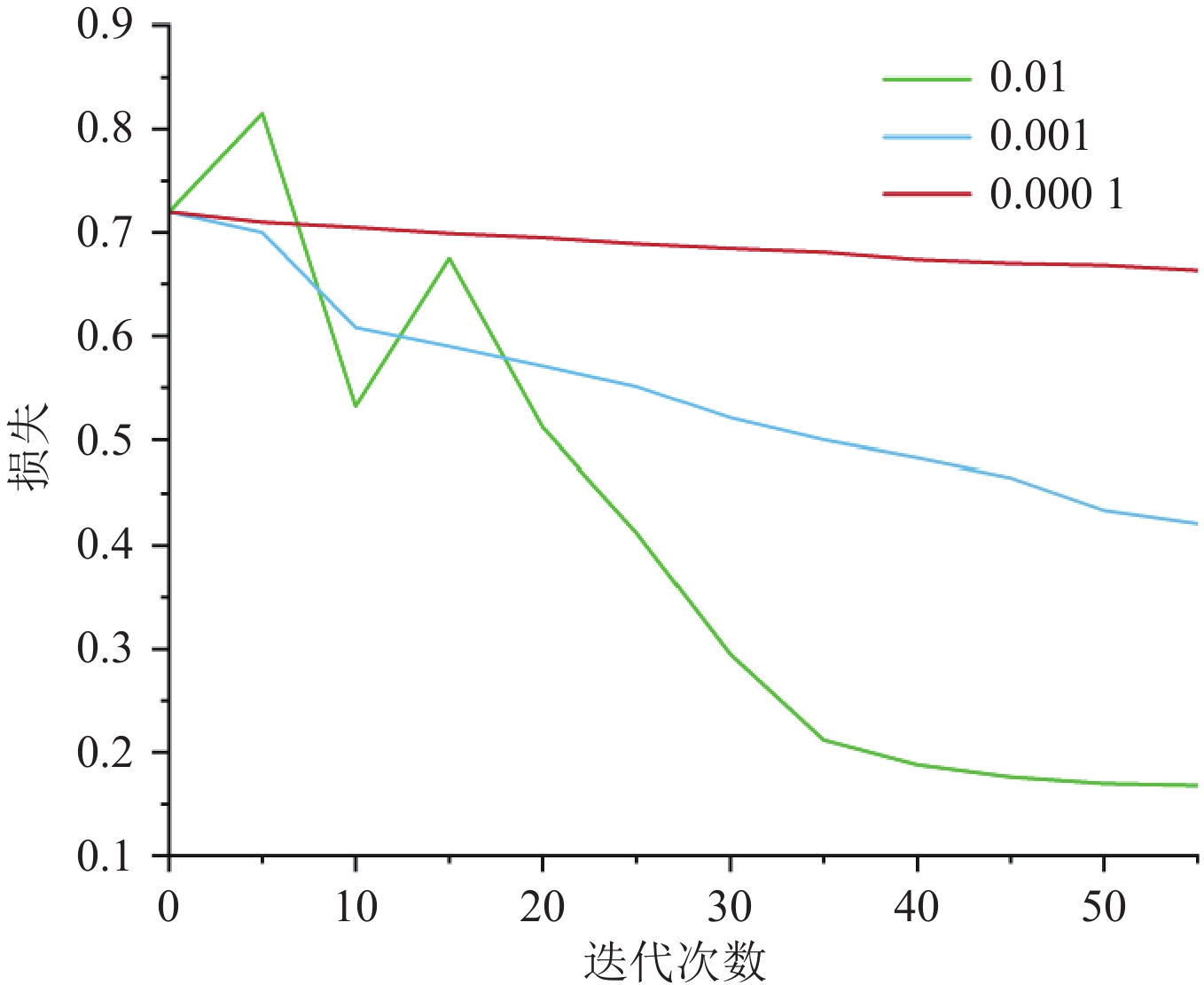
图 2 CNN模型及各层输出矩阵维度示意图Figure 2. Schematic of the CNN model and output matrix size of each layer学习率是深度神经网络的一个重要指标。如果数值设定的太小，尽管可以提高模型的稳定性，但很费时；如果设定过大，则会导致模型的收敛较慢，甚至会导致发散。学习率决定了参数按照梯度下降的方向进行更新的幅度大小。在不同的网络模型下，最佳的学习率不是固定不变的，通常设定在0.1~
0.0001 之间。图3为不同学习率下损失函数下降结果。本实验初始使用
0.0001 的学习率，训练过程中收敛缓慢，均方误差损失函数随着时间变化在缓慢降低，标准偏差也在小幅度变化，但速度缓慢，难以较快收敛。当使用0.01的学习率时，训练结果波动较大，可解释性差，均方误差与标准偏差都在较高范围来回波动，难以收敛。学习率一般以10的倍数关系进行调整，在使用0.001的学习率时，均方误差与标准偏差都能尽快实现收敛，且波动幅度小。![]()
图 3 不同学习率下损失函数下降结果Figure 3. Results of loss function reduction with different learning rates在训练神经网络时，在显存容许的情况下进行大批量训练可以有效地提高显存的使用效率。每次批量处理的样本量，即批次（Batch）大小决定着全部数据集完成训练所需的迭代次数。Batch值越大，梯度下降方向判断越准确，则训练震荡幅度也就越小。但盲目增大Batch大小会导致每次迭代耗时增加，参数修正缓慢，同时也会降低模型的泛化能力。在本实验中，使用了虚拟服务器，搭载的GPU加速器为NVIDIA Tesla V100，显存大小为32 GB。考虑到硬件设备与训练时间限制，本实验中Batch值设定为32。
优化方法选择Adam随机梯度下降法，是基于一阶梯度的随机损失函数优化算法。该方法易于实现，不受梯度的对角线重新缩放影响，并且非常适合参数量大的问题。Adam方法最大的特性是可以计算不同参数的自适应学习率。因此无需太多调整即可直接使用Adam算法。其计算效率很高，并且对内存的要求较小。
2.2 卷积循环神经网络
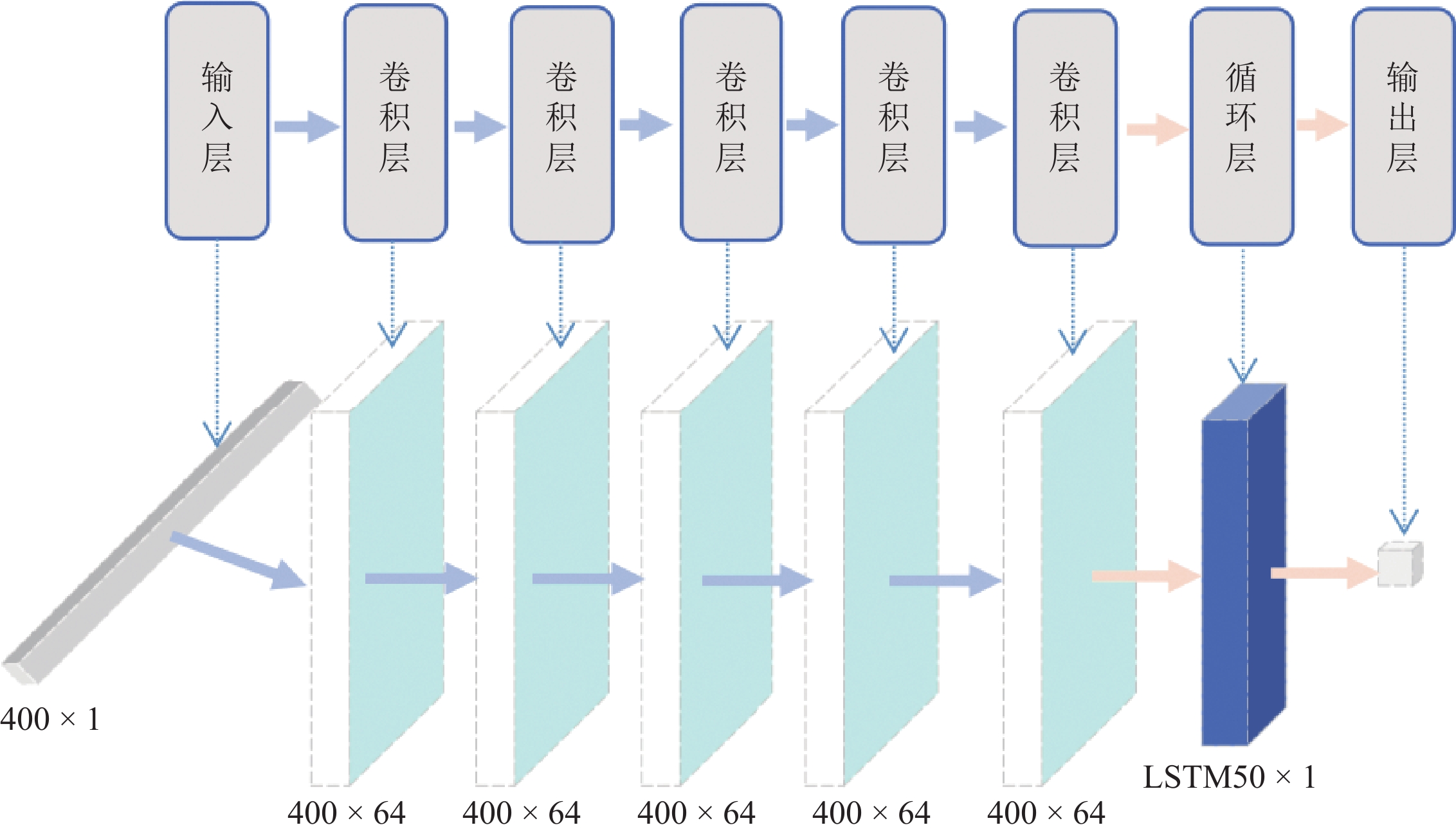
根据已有的RNN结构，并为了与卷积神经网络对比，本研究确定了卷积循环神经网络（CRNN）的总体结构，主要包括5层卷积层、1层循环层和1个输出层（全连接层）。与CNN模型不同的是，CRNN将其池化层替换成了一个循环层，该循环层选用对长序列有更好学习表现的长短期记忆（LSTM）层（图4）。
![]()
图 4 卷积循环神经网络（CRNN）结构及各层输出矩阵大小示意图Figure 4. Schematic diagram of the structure of the (CRNN) and the size of the output matrix of each layerCRNN模型的参数和算法的选取与CNN模型基本一样，每一层卷积层的结果输出到正则化层，用来避免和缓解过拟合问题。正则化层后添加ReLU激活函数用来控制向下一层的输出，在循环层的LSTM结构中使用了Sigmoid、Tanh激活函数。
如图4所示，输入层输入数据维度为400×1，经过5层卷积层的卷积操作后，输出结果维度为400×64，输出到LSTM层中进行训练，循环层的输出数据维度为50×1，最后全连接层作为输出层输出一个浮点值，此为初至震相预测结果。
为了更好地与CNN模型的实验结果进行对比，CRNN的各种超参数的设置和算法的选取与CNN模型完全一致：①损失函数选择均方误差（MSE）；②优化方法选择Adam随机梯度下降法；③学习率设置为0.001；④Batch值选择为32。两种网络模型中卷积层的卷积核大小也保持一致。
3. 实验结果与分析
3.1 自动处理算法（AR Picker）与CRNN实验对比
本研究选取相应的评估指标以及残差分布来作为衡量标准，对比自动处理算法（AR Picker）和CRNN模型的实验结果。将实验结果与Obspy中实现的开源“AR picker”[29]所获得的结果进行比较。表2展示了CRNN和AR picker的对比结果。
表 2 测试集P波评估指标对比结果Table 2. Comparison results of P-wave evaluation indices in the test set评估指标 AR picker CRNN 精确率P（Precision） 0.612 0.919 R（Recall） 0.612 0.796 F1分数 0.612 0.853 测试集标准偏差/s 0.127 0.072 对自动处理算法和CRNN模型选取了精确率、召回率、F1分数以及标准偏差作为衡量标准来进行实验对比。精确率P（Precision）是指在被所有预测为正的样本中实际为正样本的概率；召回率R（Recall）是指在实际为正的样本中被预测为正样本的概率。
$$ P = \frac{{TP}}{{TP + FP}} \text{，} $$ (1) $$ R=\frac{TP}{TP+FN}\text{。} $$ (2) F1分数是精确率和召回率的平衡标准，是同时考虑了精确率和召回率，让两者同时达到最高，取得平衡。
$$ F1 = \frac{{2 * P * R}}{{P + R}} 。 $$ (3) 由表2测试集P波评估指标对比结果可以看出，CRNN的精确率、召回率和F1分数都优于传统的自动拾取算法，在测试集标准偏差方面也有所提升，由
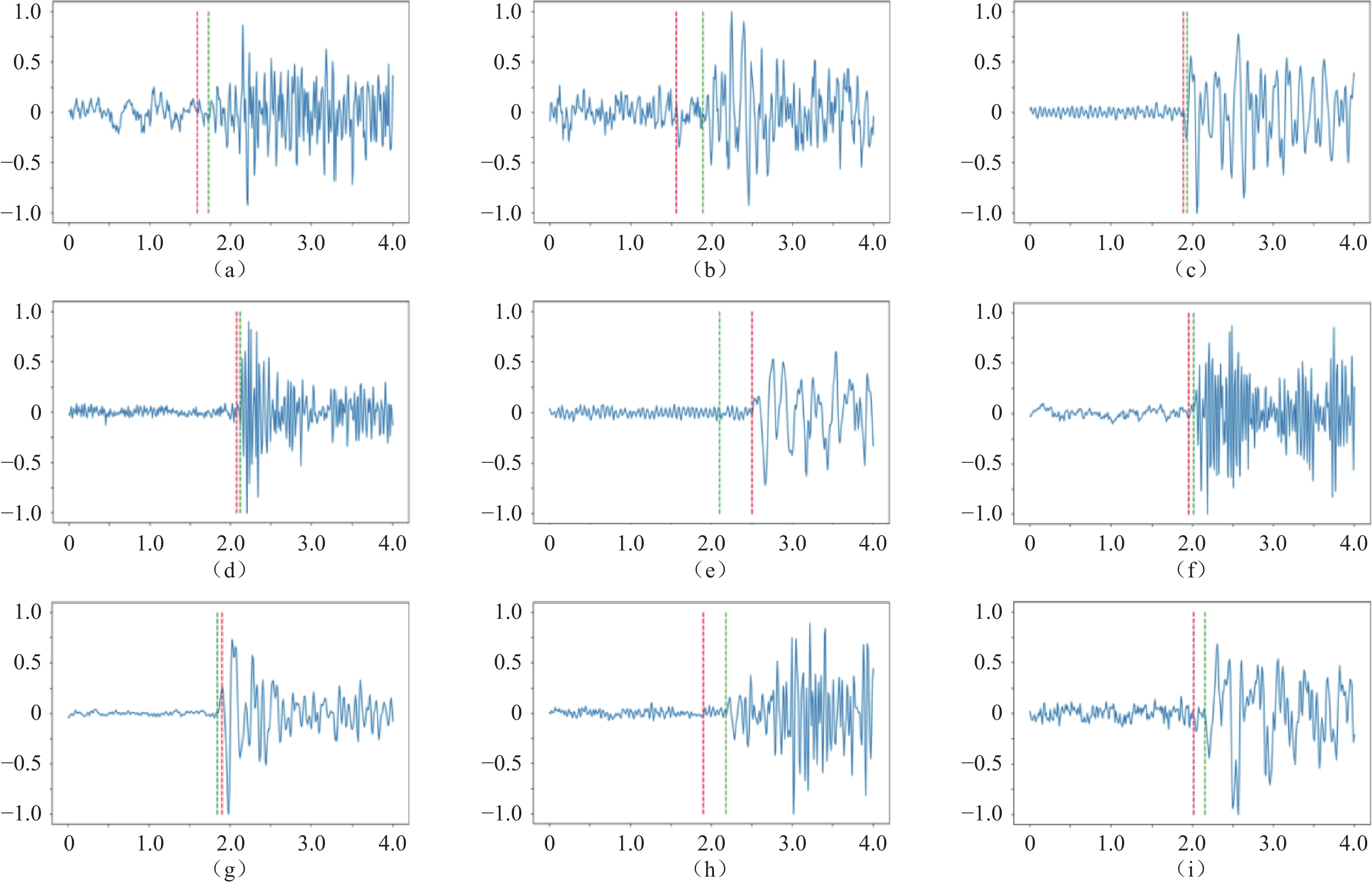
0.1269 s提升至0.0721 s。CRNN模型的性能与精度对比自动拾取算法有明显提高。图5显示了自动拾取算法与CRNN模型的走时残差分布的对比，由对比结果分析可知与自动拾取算法的结果相比，CRNN拾取器残差分布明显更窄，没有明显的偏差。
![]()
图 5 CRNN模型与自动处理算法走时残差对比Figure 5. Comparison of travel time residuals for CRNN and AR pickers3.2 CNN与CRNN实验对比
对CNN与CRNN使用
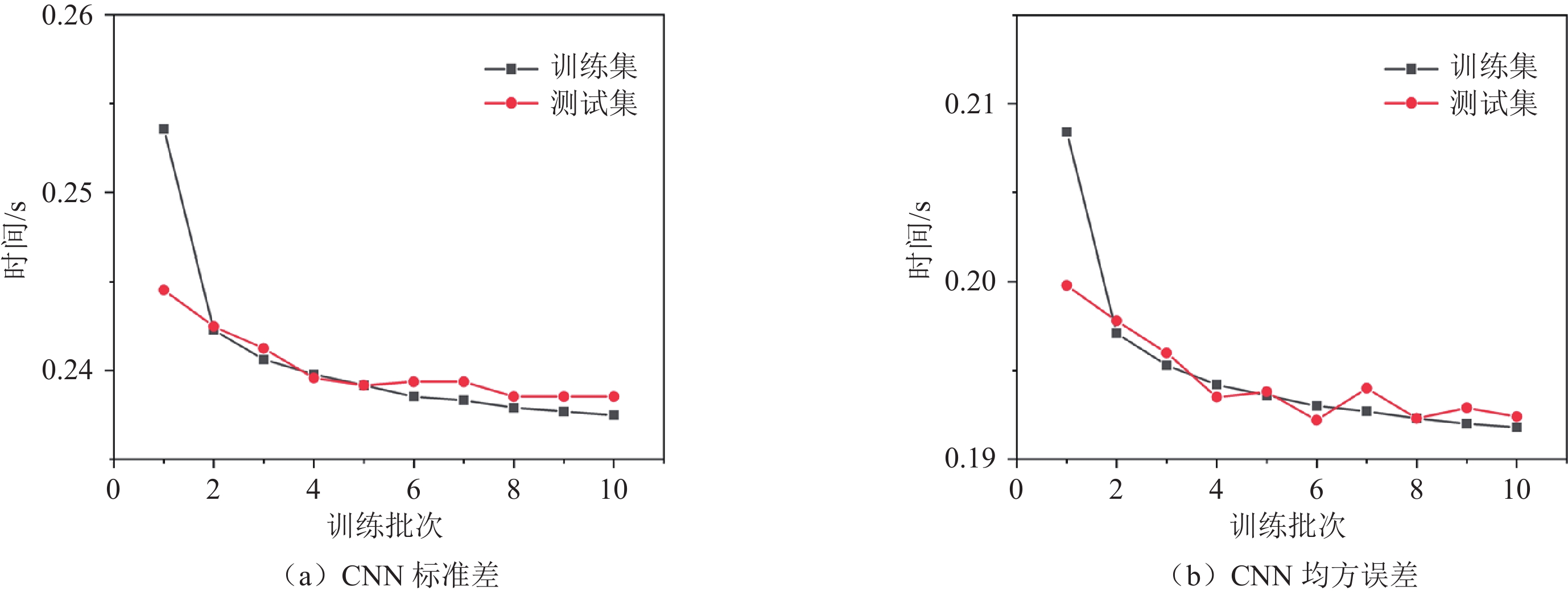
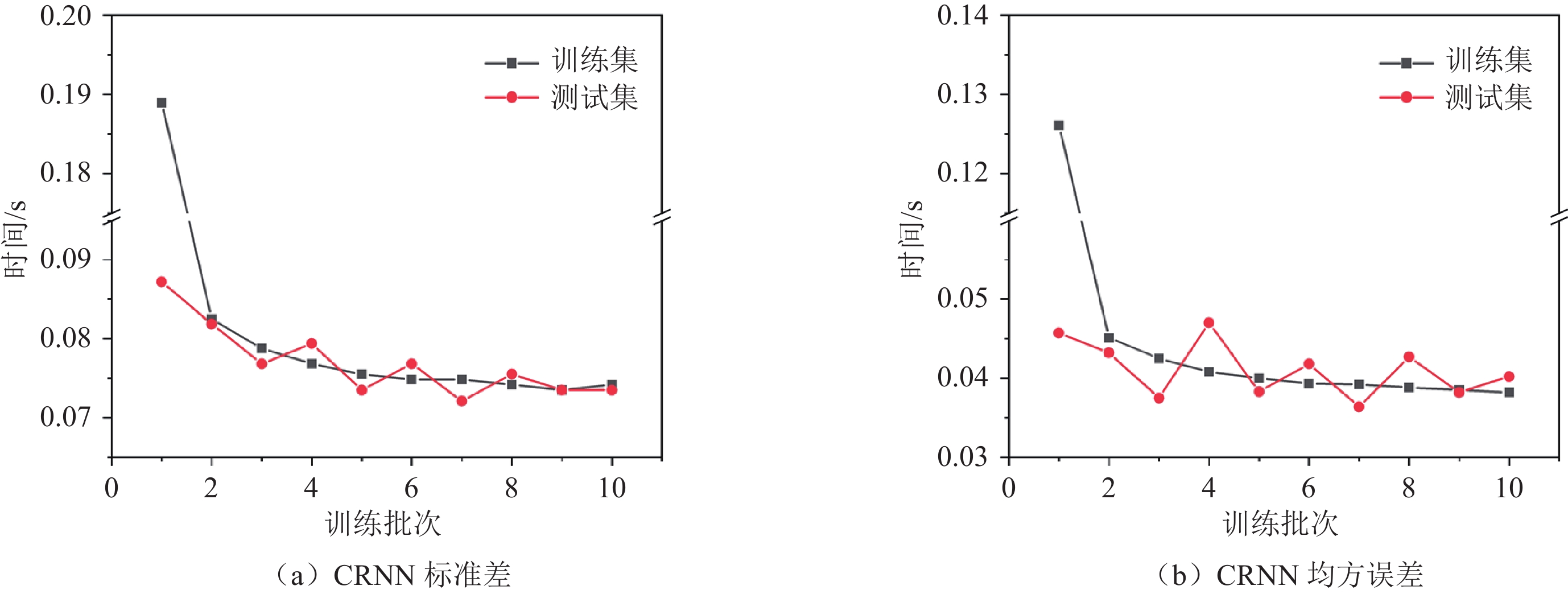
2908348 个波形作为训练集（总数据的80%），727088 个波形作为测试集（总数据的20%），共训练10个批次。图6和图7显示，两种神经网络的预测误差和标准偏差在第2个批次便得到大幅度降低，且测试集的预测结果与训练集的预测结果非常接近，有效地避免了过拟合，表现出较好的泛化能力。![]()
图 6 CNN模型训练时标准差和均方误差随着迭代次数变化情况Figure 6. Variations in standard deviation and mean square error of the CNN model with iterations![]()
图 7 CRNN模型训练时标准差和均方误差随着迭代次数变化情况Figure 7. Variations in the standard deviation and mean square error of the CRNN model with iterations值得注意的是：虽然两个模型的训练误差得到了有效的下降，但并未收敛到零值，这是神经网络模型训练中无法回避的问题。这可能是因为神经网络训练模拟的是人工拾取的结果，但人工拾取的初至时刻与真实的地震初至时刻并非完全符合，其中存在着误差，且不同数据处理人员拾取的结果也不尽相同，因此神经网络模型的训练误差不可能完全收敛到0。实际上，当网络模型不添加正则化层、失活层（Dropout）、池化层等操作时，神经网络模型在训练集上的误差可以尽可能地收敛于零值，但会导致其在测试集上的误差显著增加，即出现过拟合。此外，网络模型的深度问题也有可能影响误差大小，增加网络深度可以增大网络感受野，可以提取更高层次的特征。但一味地增大网络深度会引发梯度爆炸或梯度消失的风险，需要引进跳跃连接等结构改善该问题。本研究使用的是时间序列回归问题中常见的5层卷积层结构，深度适中。
表3展示CNN与CRNN的测试集实验结果。在准确度方面，CNN在测试集上的平均误差为
0.2375 s，标准偏差为0.1924 s；CRNN在测试集上的平均误差为0.0364 s，标准偏差为0.0721 s。CRNN方法的识别精度高于相同网络层数的CNN方法。在效率方面，当使用1块NVIDIA公司生产的Tesla V100图形处理单元（GPU），对CNN模型进行训练，每个批次大约需要6 min，对CRNN模型进行训练，每个批次大约需要35 min。CRNN模型批次训练时常较长的原因是由于模型中加入了循环层（LSTM），每一次步长（time step）计算都依赖上一层的计算和输出结果导致的。表 3 CNN与CRNN测试集实验对比结果Table 3. Comparison of testing results between CNN and CRNN模型 测试集平均
误差/s测试集标准
偏差/s每批次训练
时常/minCNN 0.2375 0.1924 6 CRNN 0.0364 0.0721 35 图8和图9分别显示了利用CNN和CRNN识别初至震相的部分波形结果示例。通过对比不难发现，CNN模型的预测结果误差较大，识别能力明显低于CRNN。相比之下，CRNN模型的预测结果非常接近人工识别到时，表现出较好的识别能力。图10为EQtransformer模型识别初至震相的波形结果，选取的波形到时和CRNN完全一致，可以看出CRNN识别效果接近EQtransformer模型。CRNN模型对于低信噪比的地震波形记录也可以拾取到P波，但拾取精度会有所下降。由对比结果可知CRNN模型有良好的识别能力。
![]()
图 8 CNN地震初至预测结果示例注：绿线表示人工到时，红线表示预测到时。Figure 8. Examples of prediction results for primary phase by CNN![]()
图 9 CRNN地震初至预测结果示例注：绿线表示人工到时，红线表示预测到时。Figure 9. Examples of the prediction results of the primary phase by CRNN![]()
图 10 EQtransformer地震初至预测结果示例注：绿线表示人工到时，红线表示预测到时。Figure 10. Examples of the prediction results of the primary phase using the EQtransformer3.3 CRNN与其它网络实验对比
为了进一步检验本研究提出的CRNN模型的有效性，本文将CRNN结果与Pick-Net等深度神经网络结果进行对比。选取了精确率、召回率、F1分数以及测试集标准偏差作为评估指标来对比结果。
表4和表5分别为CRNN网络与Pick-Net等深度神经网络的拾取结果与拾取误差范围对比。相较于传统的神经网络，本文新构建的CRNN网络精确率基本能达到90%以上，在拾取精度、召回率以及F1分数上与传统的深度神经网络近乎一致，而且在测试集标准偏差方面有所提升，拾取误差与传统的深层神经网络相接近。以上数据表明CRNN的拾取结果与PhaseNet、Pick-Net等成熟的深层神经网络效果比较接近，但与EQtransformer还有一定的差距。
表 4 测试集P波评估指标对比结果Table 4. Comparison of P-wave evaluation indices in the test set评估指标 EQtransformer PhaseNet CRNN PickNet 精确率P（Precision） 0.99 0.96 0.919 0.854 召回率R（Recall） 0.96 0.93 0.796 0.620 F1分数 0.97 0.94 0.863 0.719 测试集标准偏差/s 0.03 0.08 0.072 0.092 训练数据来源 全球 南加州 南加州 南加州 表 5 CRNN网络与成熟深层神经网络拾取误差范围的对比Table 5. Comparison of picking errors between the CRNN and previous deep neural networks拾取误差范围 CRNN Picknet EQtransformer PhaseNet 拾取精度 < 0.05 s 70.81% 73.91% 76.56% 70.21% 拾取精度 < 0.1 s 91.93% 85.41% 99.12% 95.89% 此外，本文构建的CRNN网络深度低于Pick-Net、PhaseNet等深度神经网络，且研究原理不同，相对而言还有增加深度以及添加跳跃连接和侧输出层的空间，以及对自注意力机制（self-attention）的应用。这也是本研究今后的优化方向。
4. 结论
本文基于长短期记忆网络搭建7层卷积循环神经网络，包括5层卷积层、1层循环层和1个全连接层，并利用南加州地震台网提供的地震数据集对新搭建的网络进行训练和测试。为了进行对比，本文搭建了相同层数的卷积神经网络，并使用相同的数据集和参数对搭建的两种网络进行对比实验。结果表明，本文搭建的卷积循环神经网络对地震初至震相识别精度有大幅度的提高。
本文还将卷积循环神经网络与目前已有的深层神经网络方法进行了实验对比，虽然架构原理不同，但识别的精度基本一致，说明本文提出的卷积循环神经网络算法是可行和有效的。但相对于EQtransformer神经网络来仍有一定的差距，将来有待进一步优化算法。
本文提出的基于时间序列的卷积循环神经网络为P波初至震相的自动识别提供了一种新思路，使得地震数据的识别和检测更加简易和智能化。
致谢：感谢南加州地震台网提供的地震数据集。论文实验使用的库和框架有Tensorflow、Obspy、Keras、NumPy、Scikit-Learn、Jupyter notebook等，文中图件使用Matplotlib、Visio 等软件进行绘制；Github网站提供的神经网络开源代码。
-
![]()
图 1 归一化前后天然地震波形示例，绿色虚线表示P波初至
Figure 1. Example of the seismic waveform after normalization. The dashed green line shows the primary arrival of the P wave
![]()
图 2 CNN模型及各层输出矩阵维度示意图
Figure 2. Schematic of the CNN model and output matrix size of each layer
![]()
图 3 不同学习率下损失函数下降结果
Figure 3. Results of loss function reduction with different learning rates
![]()
图 4 卷积循环神经网络（CRNN）结构及各层输出矩阵大小示意图
Figure 4. Schematic diagram of the structure of the (CRNN) and the size of the output matrix of each layer
![]()
图 5 CRNN模型与自动处理算法走时残差对比
Figure 5. Comparison of travel time residuals for CRNN and AR pickers
![]()
图 6 CNN模型训练时标准差和均方误差随着迭代次数变化情况
Figure 6. Variations in standard deviation and mean square error of the CNN model with iterations
![]()
图 7 CRNN模型训练时标准差和均方误差随着迭代次数变化情况
Figure 7. Variations in the standard deviation and mean square error of the CRNN model with iterations
![]()
图 8 CNN地震初至预测结果示例
注：绿线表示人工到时，红线表示预测到时。
Figure 8. Examples of prediction results for primary phase by CNN
![]()
图 9 CRNN地震初至预测结果示例
注：绿线表示人工到时，红线表示预测到时。
Figure 9. Examples of the prediction results of the primary phase by CRNN
![]()
图 10 EQtransformer地震初至预测结果示例
注：绿线表示人工到时，红线表示预测到时。
Figure 10. Examples of the prediction results of the primary phase using the EQtransformer
表 1 南加州地震台网地震数据信息
Table 1 Information of Seismic Data from the Southern California Seismic Network
震中距 通道 地震台数量 地震发生时间 波形数量 地震波类型 120 km内 NHZ、EHZ、HHZ 692 2000~2017年 3635436 P波 
下载: 导出CSV
表 2 测试集P波评估指标对比结果
Table 2 Comparison results of P-wave evaluation indices in the test set
评估指标 AR picker CRNN 精确率P（Precision） 0.612 0.919 R（Recall） 0.612 0.796 F1分数 0.612 0.853 测试集标准偏差/s 0.127 0.072
下载: 导出CSV
表 3 CNN与CRNN测试集实验对比结果
Table 3 Comparison of testing results between CNN and CRNN
模型 测试集平均
误差/s测试集标准
偏差/s每批次训练
时常/minCNN 0.2375 0.1924 6 CRNN 0.0364 0.0721 35
下载: 导出CSV
表 4 测试集P波评估指标对比结果
Table 4 Comparison of P-wave evaluation indices in the test set
评估指标 EQtransformer PhaseNet CRNN PickNet 精确率P（Precision） 0.99 0.96 0.919 0.854 召回率R（Recall） 0.96 0.93 0.796 0.620 F1分数 0.97 0.94 0.863 0.719 测试集标准偏差/s 0.03 0.08 0.072 0.092 训练数据来源 全球 南加州 南加州 南加州
下载: 导出CSV
表 5 CRNN网络与成熟深层神经网络拾取误差范围的对比
Table 5 Comparison of picking errors between the CRNN and previous deep neural networks
拾取误差范围 CRNN Picknet EQtransformer PhaseNet 拾取精度 < 0.05 s 70.81% 73.91% 76.56% 70.21% 拾取精度 < 0.1 s 91.93% 85.41% 99.12% 95.89%
下载: 导出CSV
-
[1] VanDECAR J C, CROSSON R S. Determination of teleseismic relative phase arrival times using multi-channel cross-correlation and leastsquares[J]. Bulletin of the Seismological Society of America, 1990, 80(1): 150-169. DOI: https://doi.org/10.1785/BSSA0800010150.
[2] CANSI Y. An automatic seismic event processing for detection and location: The P. M. C. C. method[J]. Geophysical Research Letters, 1995, 22(9): 1021-1024. DOI: 10.1029/95gl00468.
[3] VANDECAR J C, CROSSON R S. Determination of teleseismic relative phase arrival times using multi-channel cross-correlation and least squares[J]. Bulletin of the Seismological Society of America, 1990, 80(1): 150-169.
[4] VANDECAR J C, CROSSON R S. Determination of teleseismic rela-tive phase arrival times using multi-channel cross-correlation and leastsquares[J]. Bulletin of the Seismological Society of America, 1990, 80: 150-169.
[5] BAER M, KRADOLFER U. An automatic phase picker for local and teleseismic events[J]. Bulletin of the Seismological Society of America, 1987, 77(4): 1437-1445. DOI: 10.1785/BSSA0770041437.
[6] SARAGIOTIS C D, HADJILEONTIADIS L J, PANAS S M. A higher-order statistics-based phase identification of three-component seismograms in a redundant wavelet transform domain[C]//proceedings of the Proceedings of the IEEE Signal Processing Workshop on Higher-Order Statistics SPW-HOS'99, F, IEEE. 1999.
[7] ZHANG H, THURBER C, ROWE C. Automatic P-wave arrival detection and picking with multiscale wavelet analysis for single-component recordings[J]. Bulletin of the Seismological Society of America, 2003, 93(5): 1904-1912. DOI: 10.1785/0120020241.
[8] CHEN Z, STEWART R. Multi-window algorithm for detecting seismic first arrivals[C]//Proceedings of the Abstracts, CSEG National Convention, F. 2005.
[9] WONG J, HAN L, BANCROFT J, et al. Automatic time-picking of first arrivals on noisy microseismic data[J]. CSEG Recorder, 2009: 1-4.
[10] SONG F, KULELI H S, TOKSöZ M N, et al. An improved method for hydrofracture-induced microseismic event detection and phase picking[J]. Geophysics, 2010, 75(6): A47-A52. DOI: 10.1190/1.3484716.
[11] LI F, RICH J, MARFURT K J, et al. Automatic event detection on noisy microseismograms[C]//SEG Technical Program Expanded Abstracts. Society of Exploration Geophysicists: 2014: 2363-2367.
[12] MA Y, CAO S, RECTOR J W, et al. Automated arrival-time picking using a pixel-level network Arrival-time picking with U-Net[J]. Geophysics, 2020, 85(5): V415-V423. DOI: 10.1190/geo2019-0792.1.
[13] FERNHOUT C, ZWARTJES P, YOO J. Automatic first break picking with deep learning[J]. IOSR Journal of Applied Geology and Geophysics, 2020, 8(5): 24-36.
[14] YUAN P, WANG S, HU W, et al. A robust first-arrival picking workflow using convolutional and recurrent neural networks[J]. Geophysics, 2020, 85(5): U109-U119. DOI: 10.1190/geo2019-0437.1.
[15] ZHENG J, HARRIS J M, LI D, et al. SC-PSNET: A deep neural network for automatic P-and S-phase detection and arrival-time picker using 1C recordings deep learning for phase auto-pickers[J]. Geophysics, 2020, 85(4): U87-U98. DOI: 10.1190/geo2019-0597.1.
[16] ROSS Z E, MEIER M A, HAUKSSON E. P wave arrival picking and first-motion polarity determination with deep learning[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(6): 5120-5129. DOI: 10.1029/2017JB015251.
[17] HOLLANDER Y, MEROUANE A, YILMAZ O. Using a deep convolutional neural network to enhance the accuracy of first-break picking[C]//Proceedings of the 2018 SEG International Exposition and Annual Meeting, F. OnePetro. 2018.
[18] GAO L, JIANG Z Y, MIN F. First-arrival travel times picking through sliding windows and fuzzy c-means[J]. Mathematics, 2019, 7(3): 221. DOI: 10.3390/math7030221.
[19] TSAI K C, HU W, WU X, et al. Automatic first arrival picking via deep learning with human interactive learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 58(2): 1380-1391.
[20] DUAN X, ZHANG J. 2019 Multi-trace and multi-attribute analysis for first-break picking with the support vector machine[C]//SEG Technical Program Expanded Abstracts 2019. Society of Exploration Geophysicists: 2559-2563.
[21] MA Y, CAO S, RECTOR J W, et al. Automatic first arrival picking for borehole seismic data using a pixellevel network[C]//SEG Technical Program Expanded Abstracts 2019. Society of Exploration Geophysicists, 2019: 2463-2467.
[22] LIAO X, CAO J, HU J, et al. First arrival time identification using transfer learning with continuous wavelet transform feature images[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 17(11): 2002-2006.
[23] ZHU W, BEROZA G C. PhaseNet: A deep-neural-network-based seismicarrival-time picking method[J]. Geophys Int, 2018, 216: 261-273.
[24] WANG J, XIAO Z, LIU C, et al. Deep learning for picking seismic arrival times[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(7): 6612-6624. DOI: 10.1029/2019JB017536.
[25] CHAI C, MACEIRA M, SANTOS-VILLALOBOS H J, et al. Using a deep neural network and transfer learning to bridge scales for seismic phase picking[J]. Geophysical Research Letters, 2020, 47(16): e2020GL088651. DOI: 10.1029/2020GL088651.
[26] HE Z, PENG P, WANG L, et al. Enhancing seismic P-wave arrival picking by target-oriented detection of the local windows using faster-rcnn[J]. IEEE Access, 2020, 8: 141733-141747. DOI: 10.1109/ACCESS.2020.3013262.
[27] MOUSAVI S M, ZHU W Q, et al. Earthquake transformer: An attentive deep-learning model for simultaneous earthquake detection and phase picking[J]. Nature Communications, 2020, 11: 3952. DOI: 10.1038/s41467-020-17591-w.
[28] LECUN Y A, BOTTOU L, ORR G B, et al. Efficient backprop[M]. Neural Networks: Tricks of the Trade. Springer, 2012: 9-48.
[29] AKAZAWA T. T echnique for automatic detection of onset time of P- and S-phases in strong motion recordsin 13th World Conference onEarthquake Engineering[J]. Vancouver, 2004, 786: 786.
计量
- 文章访问数: 332
- HTML全文浏览量: 43
- PDF下载量: 33
