Q-factor Estimation Method Based on Time-varying Wavelet
-
摘要:
谱比法是估计Q值的常用方法，根据不同时刻地震子波对数谱比值与Q值之间的线性关系估算品质因子Q。时频域谱比法的基本思想是用时频谱分析提取不同时刻的频谱，代表对应时刻的地震子波频谱，忽略反射系数对地震子波的影响。由于受到局部反射系数的影响，时频谱比法求取Q时地震子波对数谱比往往具有复杂的多峰形态，偏离了对数谱比随频率线性变化的关系，线性拟合求取的Q值误差较大，不满足地层岩性解释和孔隙流体预测的要求。针对以上问题，将复赛谱分析与广义S变换相结合，提出一种消除反射系数影响的时变子波频谱提取方法，提高Q值估计的精度。利用广义S变换将地震记录变换到时频域，对地震记录的时频谱取对数，得到不同时刻地震记录的复赛谱。在复赛谱域子波位于低频段，反射系数位于中高频段。因此利用最小二乘法对低频段复赛谱进行平滑拟合，得到子波的复赛谱，再取复赛谱的指数，得到时变子波的频谱，通过相邻时刻子波的对数频谱比与Q值的线性关系计算Q值。模型测试结果验证时变子波提取的准确性以及估计Q值的可行性和抗噪性，东部某油田实际地震数据的应用结果验证该方法的有效性。
Abstract:The spectral ratio method is a technique commonly used for estimating Q values. It calculates the quality factor Q based on the linear relationship between the logarithmic spectral ratio of seismic wavelets at different times and the Q value. The core idea of the time-frequency domain spectral ratio method is to extract the spectral distribution at different moments via time-frequency spectrum analysis, representing the frequency spectrum of seismic wavelets at those moments while ignoring the influence of reflection coefficients. However, because of the impact of local reflection coefficients, the logarithmic spectral ratios of seismic wavelets obtained via the time-frequency spectral ratio method often exhibit complex multi-peak patterns, deviating from the linear relationship between logarithmic spectral ratios and frequency. This leads to significant errors in Q values derived from linear fitting, which fail to meet the requirements for lithological interpretation and pore fluid prediction. To address the issues, the present study combines cepstral analysis with the Generalized S-transform to propose a time-varying wavelet spectrum extraction method that eliminates the influence of reflection coefficients, thereby improving the Q estimation accuracy. First, the Generalized S-transform is applied to convert seismic records into the time-frequency domain. The logarithmic time-frequency spectrum of the seismic records is then computed to obtain their cepstra at different times. In the cepstral domain, the wavelet components reside in the low-frequency band, whereas reflection coefficients occupy the mid-to-high-frequency bands. By applying least-squares smoothing to the low-frequency cepstral components, the wavelet cepstrum is derived. Taking the exponential of the cepstrum reconstructs the spectrum of the time-varying wavelet. Finally, Q values are calculated using the linear relationship between the logarithmic spectral ratios of adjacent wavelets and the Q value. Model tests validate the accuracy of time-varying wavelet extraction, as well as the feasibility and noise resistance of Q estimation. Application to real seismic data from an oilfield in eastern China further confirms the effectiveness of the method.
-
由于地球介质的非完全弹性性质，地震波在实际地层中传播时往往发生显著的能量损失，引起地震子波的振幅衰减、主频降低以及频带宽度变窄[1]。吸收衰减特性是实际地球介质的固有特性，在地震勘探中一般用品质因子Q予以表征。
研究表明[2]，介质的吸收衰减特性受到多种因素的影响，介质的Q值与地层岩性、孔隙度、渗透率，以及孔隙流体类型等诸多岩石物理性质紧密相连。鉴于此，精确估计Q值，对于地层岩性精准识别、储层有效预测，乃至地震剖面分辨率的提升，都有着不可忽视的重要作用。
目前地震勘探中主要采用谱比法[3]进行Q值估算。为了避免传统频域率谱比法受时窗影响的局限性，谱比法已经发展到时频域。
Reine等[4]通过固定时窗的短时傅里叶变换、Gaber变换、变时窗的S变换和连续小波变换对比，发现变时窗的时频分析对于Q值的估计更加准确和稳定。但是时频域谱比法受噪声和频带宽度的选择影响较大，为进一步提高Q值提取的准确性和稳定性，许多学者对时频域谱比法进行了改进，其中改进Q值的计算方法和选取较高分辨率的时频分析方法是主要手段。朱耀旭等[5]依据子波Z变换的根关于单位圆移动与否构建遗传算法的编码链条，并利用全局优化算法估计了Q模型；陈文爽等[6]基于广义S变换，构建了时频域谱比斜率反演方程，通过方程组求解求取稳定的Q值；杨登锋等[7]提出了加权谱比法的Q值估计方法，降低了对频段选取的依赖性。
针对叠前数据，魏文等[8]提出小波域Q值求取方法；王小杰等[9-10]提出基于S变换Q值估计方法，后又针对不同频率的地震信号相互影响的问题，提出小波域分频Q值提取方法；李波等[11]结合Lucy-Richardson算法和广义S变换提高Q值估计的准确性；Li等[12]利用反演谱分解得到高分辨率时频谱，通过整形正则化来估计Q值；周东红等[13]基于复谱分解的高分辨率时频分析方法，通过井震联合估计Q值。
地下实际介质对振动能量的不断吸收衰减使得地震波中高频成分逐渐减少，使得地震子波具有时变特性，传统的平稳地震记录模型并不符合实际情况，于是有学者基于非平稳地震记录模型提出Q值估计方法。张繁昌等[14]通过对地震信号进行子波分解，将得到的匹配子波视为时变子波，以此来估计Q值；张瑾等[15]通过消除非本征衰减影响、结合双参考频段和频域平均化处理，提高了Q值估计精度；许李囡等[16]推导了非平稳地震记录模型在S变换域中的近似表示，并由此建立Q值和子波之间的优化函数，通过求解该优化函数估计Q值。
近年来，随着深度学习方法在地震勘探领域的发展，研究人员开展了基于深度学习的Q值估计方法研究。基于深度学习的Q值估计方法通过构建神经网络模型，直接从地震数据中学习Q值分布特征，避免了传统方法对时频变换的依赖。周晨[17]基于特征工程原则，构建了多输入单输出的深度神经网络，提高了Q值估计的精度和抗噪性；Wang等[18]提出了一种基于多任务学习的动态子波振幅谱提取方法，并将其应用于Q值估计；Li等[19]2024提出了一种基于全连接网络的VSP地震数据Q值提取方法。
实际地震数据可以看成时变子波与局部反射系数褶积后再叠加，从而使得地震记录的时频域振幅谱呈现复杂的多峰谱特性，这导致对数谱比与频率之间不再是严格的线性关系，严重影响了拟合的稳定性与Q值估计的精度。
为解决上述问题，本文基于非平稳地震道模型，通过广义S变换得到地震道时频谱，通过时频谱的对数计算，得到不同时刻地震记录的复赛谱。根据复赛谱域子波分布在低频段、反射系数位于高频段的特征，利用最小二乘法对低频段复赛谱进行平滑拟合，得到子波的复赛谱，消除了反射系数对时频振幅谱的影响，有效恢复了对数谱比与频率的线性关系。通过提取子波和理论子波的对比验证了复赛谱提取时变子波的准确性。与常规谱比法的对比表明了该方法具有更高的准确性和稳定性。
1. 方法原理
1.1 非平稳地震记录模型的广义S域表示
忽略噪声的影响，时间域的平稳地震记录模型可以表示为震源子波与反射系数的褶积。
$$ s(t) = w(t) * r(t) = \int\limits_{{{ - }}\infty }^\infty {w\left( {t - s} \right)} r(s){\mathrm{d}}s \text{，} $$ (1) 式中，
$ t $ 和$s$ 为时间变量，$s(t)$ 为平稳地震记录，$w(t)$ 为震源子波，$r(t)$ 为反射系数。平稳地震记录模型中初始子波与经过地层传播后的子波没有差别。考虑到实际地震波传播过程中的几何扩散、吸收衰减等效应，需引入衰减函数来描述子波的衰减。基于Aki常Q理论[20]的衰减函数表示为：$$ a(t,f) = {\text{exp}}\left( {\frac{{ - {\text{π}} ft}}{Q}} \right)\text{，} $$ (2) 式中
$ f $ 为频率，$Q$ 为品质因子。将平稳地震记录褶积模型转换到频率域，并引入衰减函数，推导出频率域非平稳地震记录褶积模型[21]：$$ s(f) = w(f)\int\limits_{ - \infty }^\infty {a\left( {t,f} \right)} r(t)\exp \left( { - 2{\text{π}} if} \right)t\;{\mathrm{d}}t。 $$ (3) 对地震信号
$ x(t) $ 的广义S变换[22]定义为：$$ \begin{gathered}{S_g}\left( {\tau ,f} \right) = \int\limits_{ - \infty }^\infty {x(t)} \frac{{\lambda {{\left| f \right|}^p}}}{{\sqrt {2{\text{π}} } }} \times\\ \exp \left( {\frac{{ - {\lambda ^2}{f^{2p}}{{\left( {\tau - t} \right)}^2}}}{2}} \right)\exp \left( { - i2{\text{π}} f} \right)t\;{\mathrm{d}}t \end{gathered} \text{，}$$ (4) 式中，
$ \tau $ 为滑动高斯窗函数中心点的时间；$ \lambda $ 和$ p $ 表示高斯窗函数的两个调节因子。广义S变换能够依据信号频率的动态变化，灵活地对窗函数的宽度实施精准调节。在检测信号频率的变化走向时，其表现更为出色，能够敏锐捕捉到细微的趋势变化。与传统变换方法相比[23]，广义S变换拥有多尺度的时频分辨率，这使其在不同频率段都能清晰呈现信号特征，而且还展现出了更高的时频聚焦性，意味着它能够将能量更为集中地聚焦于信号的关键时频区域，对非平稳信号频率变化的描绘更为细腻、精准，刻画能力相较于其他方法显著增强，能够有效提高非常规油气资源评价精度[24]，有效推动页岩油资源产业化发展。
将式（3）推广到广义S变换域中，推导可知非平稳地震记录所对应的广义S变换，近似等同于子波、衰减函数以及反射系数三者各自的广义 S 变换相互乘积：
$$ {S_g}\left( {\tau ,f} \right) \approx w(f)a\left( {\tau ,f} \right){R_g}\left( {\tau ,f} \right)\text{，} $$ (5) 式中，
${R_g}(\tau ,f)$ 表示反射系数的广义S变换，而$w(f)a(\tau ,f)$ 本质上是子波在经地层传播时间$\tau $ 后的傅里叶变换，将该项综合表示为时变子波：$$ {W_a}\left( {\tau ,f} \right) = w(f)a\left( {\tau ,f} \right)\text{。} $$ (6) 在广义S变换域，非平稳地震记录的时频谱近似表示为时变子波时频谱和反射系数时频谱的乘积：
$$ {S_g}\left( {\tau ,f} \right) \approx {W_a}\left( {\tau ,f} \right){R_g}\left( {\tau ,f} \right)。 $$ (7) 1.2 复赛谱域时变子波提取与Q值估计
基于反射系数谱为白谱的假设，认为反射系数影响地震记录振幅谱的细节，而子波决定地震记录振幅谱的大体形状，因此传统谱比法直接忽略反射系数的影响。但实际反射系数并不符合白谱的假设，子波与反射系数褶积后相互干涉、叠加使得地震记录振幅谱成为复杂的多峰谱。为摆脱反射系数的白谱假设，通过对地震记录的时频谱取对数将其转换至复赛谱域，从而利用复赛谱域子波分布在低频段这一特征提取时变子波的振幅谱。
式（7）给出了广义S域内非平稳地震记录在时频谱域的求取公式。仅考虑其振幅谱，将地震记录在每个时间点的振幅谱取对数后，得到时频域复赛谱，即非平稳地震记录的复赛谱：
$$ \ln \left| {{S_g}\left( {\tau ,f} \right)} \right| = \ln \big| {{W_a}\left( {\tau ,f} \right)} \big| + \ln \left| {{R_g}\left( {\tau ,f} \right)} \right| ，$$ (8) 其中，
$\ln \big| {{W_a}\left( {\tau ,f} \right)} \big|$ 表示时变子波的复赛谱，其在复赛时频域为光滑且连续的低频分量；$\ln \left| {{R_g}\left( {\tau ,f} \right)} \right|$ 则表示反射系数的复赛谱，其在复赛时频域为剧烈震荡的高频分量。在复赛谱域，根据反射系数和地震子波表现出的频率特征差异，可有效区分两者。通过对复赛谱进行平滑处理，便可提取出时变子波的振幅谱[20]。记非平稳地震记录的复赛时频谱为：
$$ {S_{\ln }}\left( {\tau ,f} \right) = \ln \left| {{S_g}\left( {\tau ,f} \right)} \right|\text{，} $$ (9) 然后通过最小二乘法拟合，平滑每个时间点的地震记录复赛谱：
$$ {S_{{\mathrm{fit}}}}\left( {\tau ,f} \right) = {\mathrm{fit}}\Big({S_{\ln }}\left( {\tau ,f} \right)\Big)\text{。} $$ (10) 在式（10）的基础上，时变子波的振幅谱可表示为：
$$ {W_a}\left( {\tau ,f} \right) = \exp \Big( {{S_{{\mathrm{fit}}}}\left( {\tau ,f} \right)} \Big)。 $$ (11) 通过上述流程，在保留时变效应的同时，可以提取到呈现平滑单峰特征的子波振幅谱。假设地震波传播到地层上下界面的旅行时为
${t_1}$ 和${t_2}$ ，取两个界面时变子波振幅谱比值的对数得到：$$ \ln \left(\frac{{{W_a}\left( {{t_2},f} \right)}}{{{W_a}\left( {{t_1},f} \right)}}\right) = - \frac{{{\text{π}} f\Delta t}}{Q} + C \text{，}$$ (12) 式中，
$\Delta t = {t_2} - {t_1}$ ，$C$ 表示与频率无关的量，式（12）中对数谱比与频率为线性关系，通过拟合得到其斜率$k = - {{\text{π}} }\Delta t/Q$ ，由此可计算Q值：$$ Q = - \frac{{{\text{π}} f\Delta t}}{k}。 $$ (13) 2. 模型测试
首先进行时频域复赛谱提取非平稳地震记录时变子波振幅谱的模型测试；然后对单道非平稳地震记录模型估计Q值，以验证复赛谱提取时变子波估计Q值的可行性与准确性；最后由含噪模型测试对比本文方法和常规方法的抗噪性。
2.1 复赛谱提取时变子波振幅谱
选取主频30 Hz的雷克子波作为震源子波，与如图1（a）所示随机反射系数序列褶积，得到平稳地震道如图1（b）所示。引入式（2）所示的衰减函数，设置其Q值为30，利用式（7）计算非平稳地震道，结果如图1（c）所示。
对比图1（b）和图1（c），明显可见在衰减函数的影响下，随着传播时间的增加，地震子波的振幅衰减，频率降低。
为了验证在复赛谱域进行非平稳地震数据子波振幅谱提取的准确性，采用广义S变化对地震数据进行时频分析，得到非平稳地震记录的时频谱如图2（a）所示。再将非平稳地震记录时频谱按式（8）取对数，得到非平稳地震记录的时频域复赛谱如图2（b）所示。图2（c）中，蓝线为某时间点的复赛谱，在复赛谱中，反射系数呈现震荡、高频特征。通过最小二乘法拟合来平滑复赛谱，其结果如图2（c）中红线所示，平滑后的结果提取出子波的复赛谱，消除了反射系数导致的剧烈波动。再对平滑结果按照式（11）计算得到该时间点子波的振幅谱。对每个时间点的复赛谱进行上述操作，得到非平稳地震道的时变子波时频振幅谱，其结果如图2（d）所示。
![]()
图 2 时频域复赛谱提取时变子波振幅谱Figure 2. Time-varying amplitude spectrum of the wavelet of cepstrum domain通过本文方法，反射系数导致的剧烈震荡现象被有效消除，可以更加清晰地展现出地震子波频谱随着传播时间的增加，振幅减小、主频降低且频带变窄的变化趋势，能够精确刻画地震子波的时变特性。
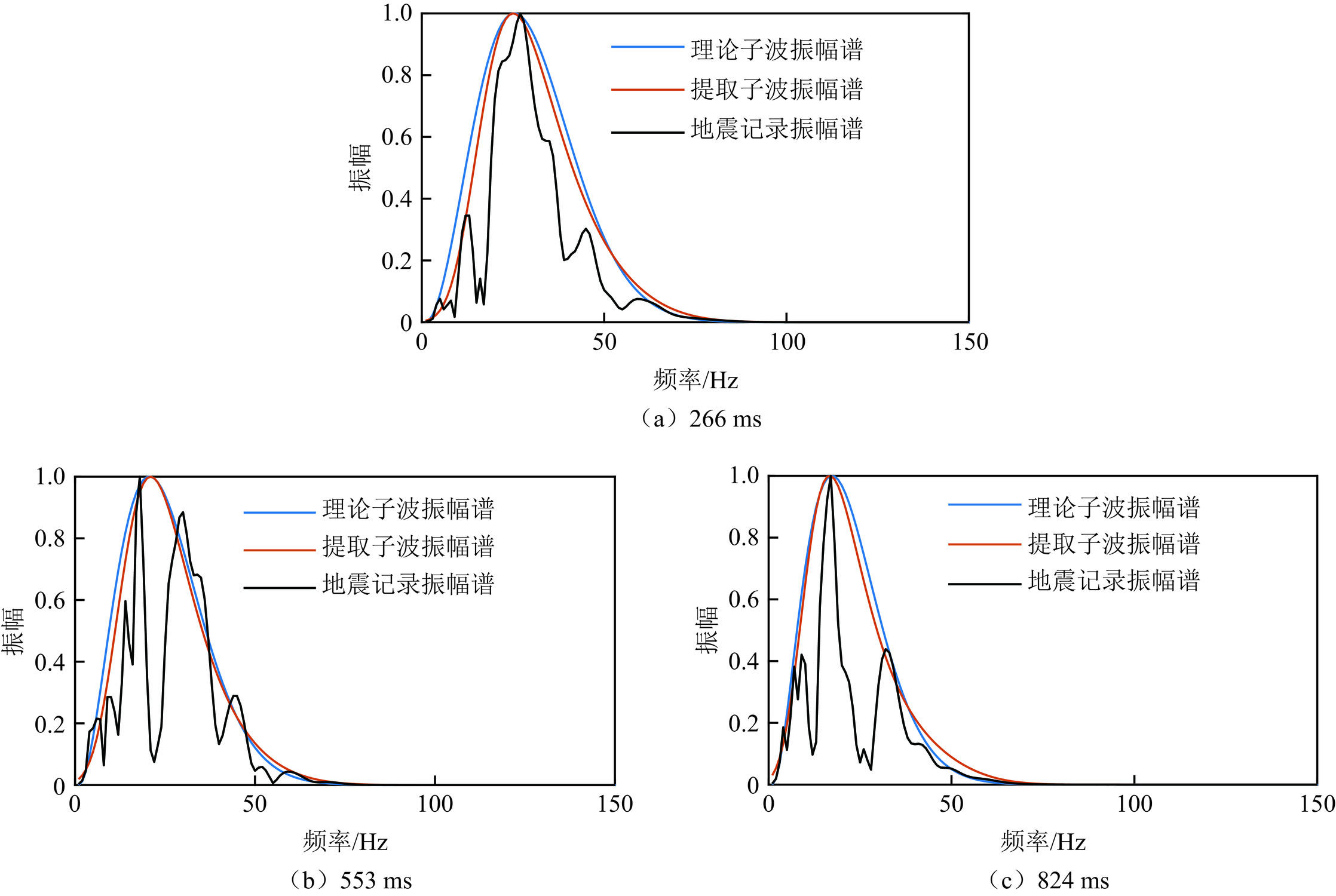
在随机反射系数序列（图1（a））中存在尖脉冲的时间点，对应如图2（a）所示的非平稳地震道时频谱的能量较为集中，选取266、553和824 ms 3个时间点，对应的非平稳地震道振幅谱、提取子波振幅谱和理论时变子波振幅谱对比结果如图3所示。图中黑线为原始的地震记录的振幅谱，因受到反射系数影响而产生很大的波动，成为复杂的多峰谱，图中红线为提取的时变子波振幅谱，蓝线为理论时变子波振幅谱，通过对比明显可见不同传播时刻的提取子波振幅谱与对应时刻的理论子波振幅谱均吻合，证明了利用复赛谱提取时变子波振幅谱方法的准确性。
2.2 无噪模型测试
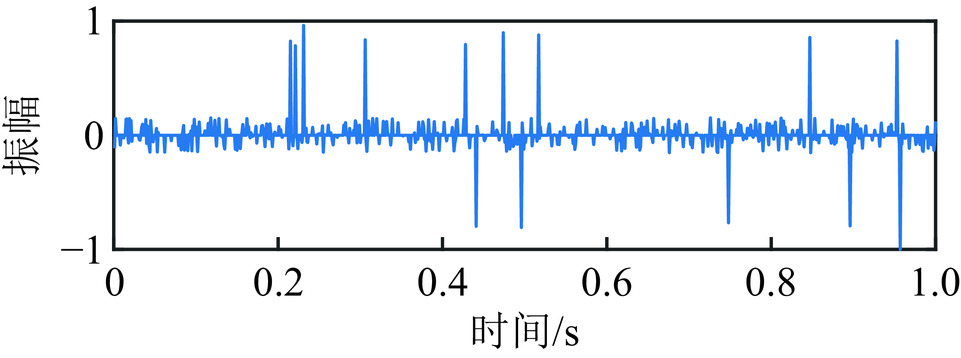
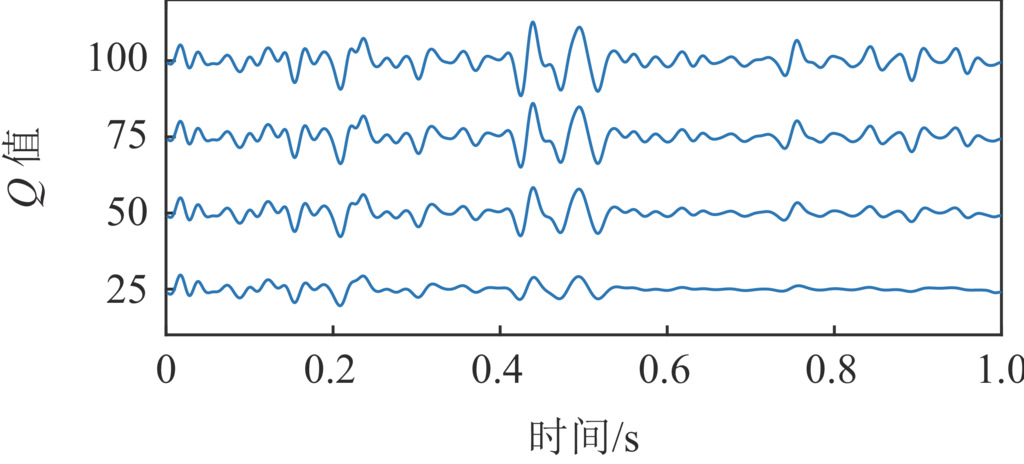
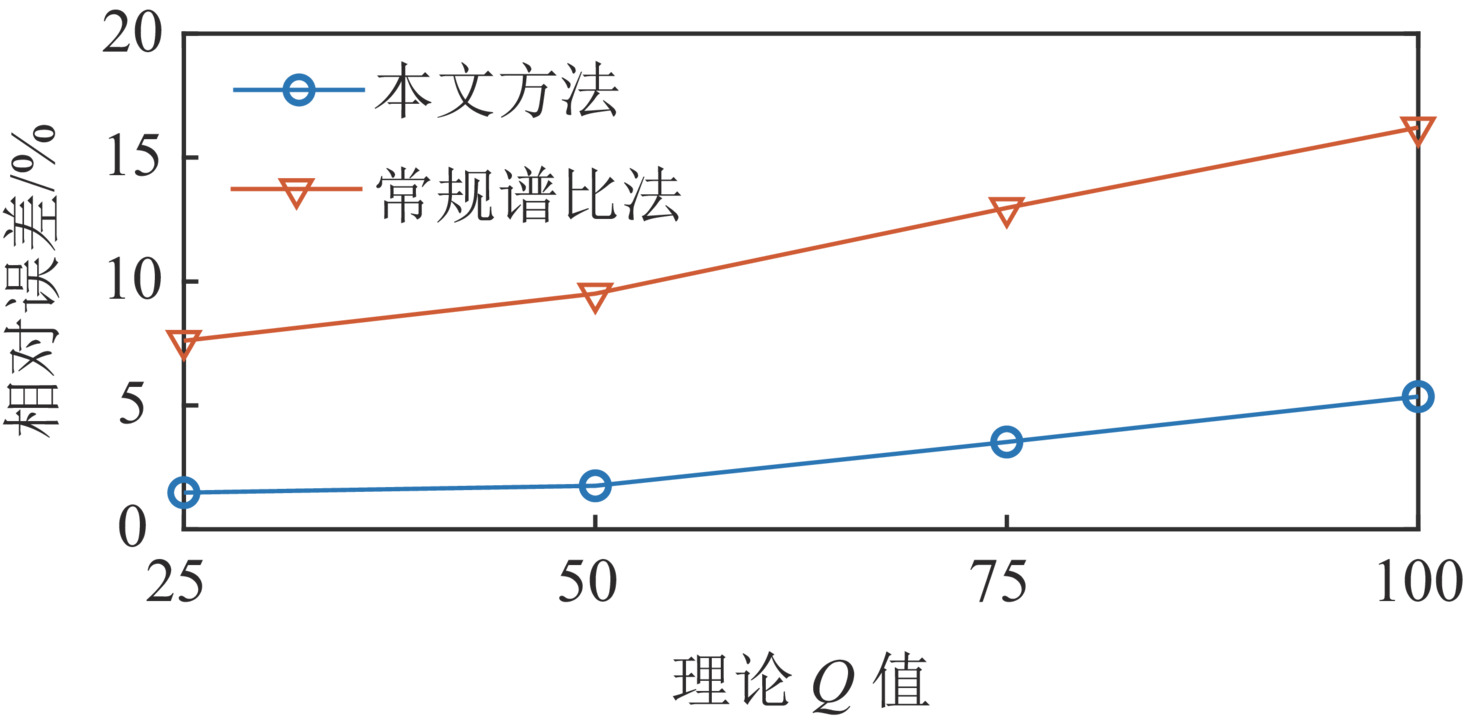
为验证本文方法估计Q值的有效性，选用无噪声模型进行测试。由图4所示的随机反射系数与30 Hz雷克子波生成地震记录，品质因子Q分别设置为25、50、75和100，得到的非平稳地震道模型如图5所示。对上述模型分别用本文方法和常规时频域谱比法估计Q值，两种方法均选择0.1 s处和0.5 s处的振幅谱进行谱比，然后拟合对数谱比曲线获得斜率，两种方法拟合斜率的频率段均选取10~70 Hz，再通过式（13）计算Q值。
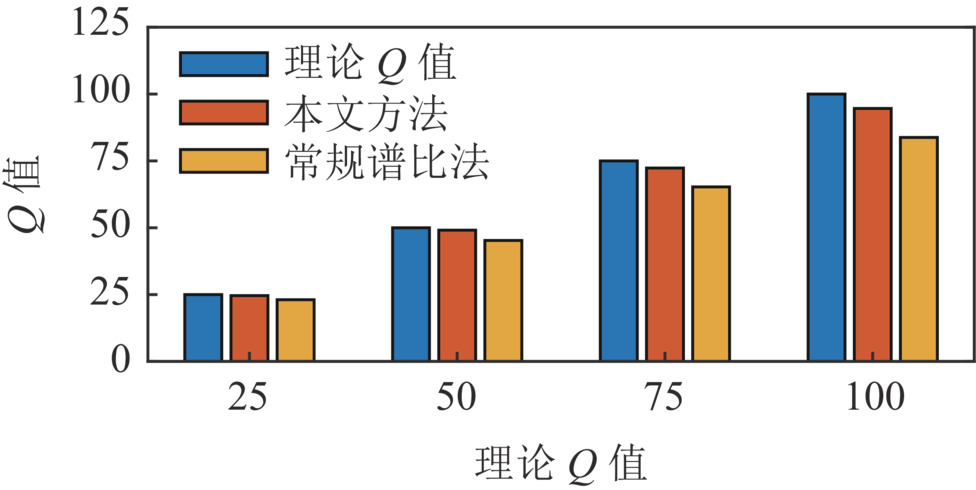
图6为两种方法估计Q值的结果。图7统计了不同方法估计Q值与理论Q值之间的误差。由图可知：对于不同Q值的模型，本文方法的结果比常规谱比法的结果更加接近理论值；本文方法结果的相对误差均小于常规谱比法结果的相对误差，且都小于6%。无噪声模型测试的结果表明：复赛谱提取时变子波Q值估计方法相较与常规谱比法具有更高的精确度。
![]()
图 6 本文方法与常规谱比法Q值估计结果Figure 6. Q estimation results of the proposed and the conventional spectral ratio methods![]()
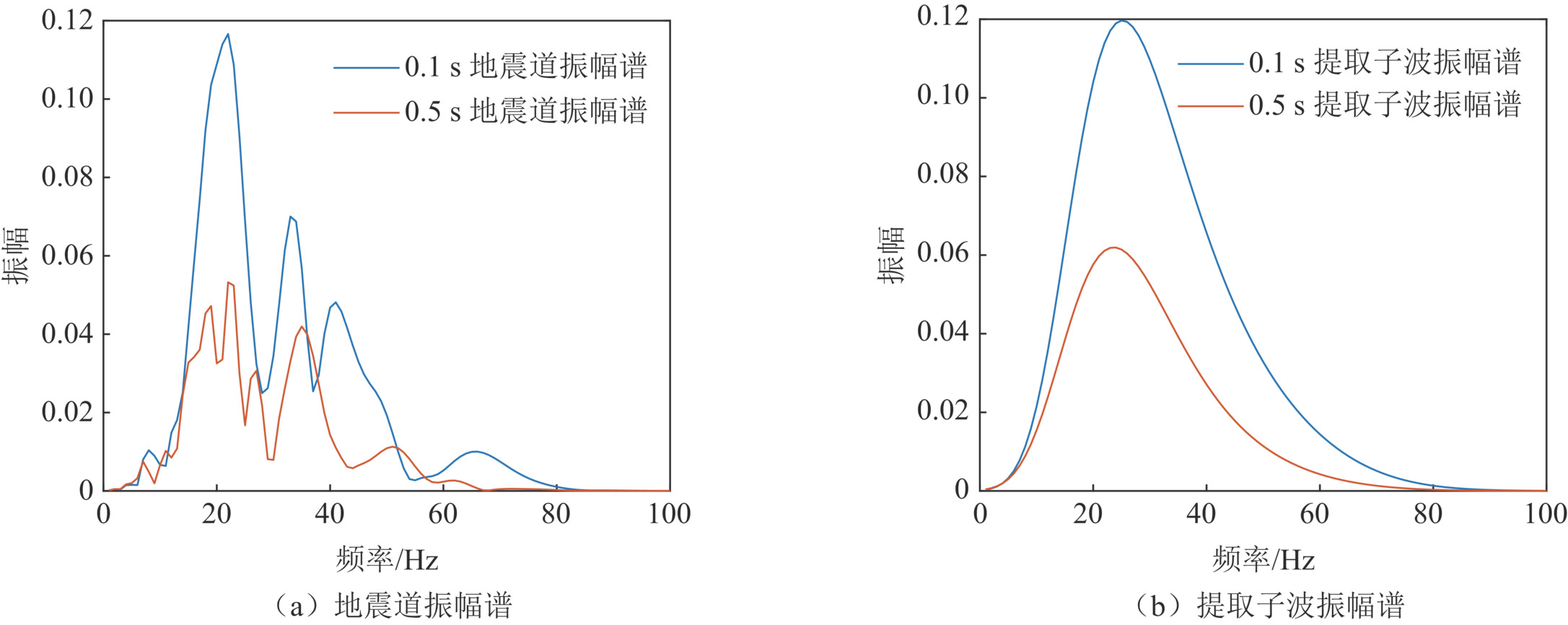
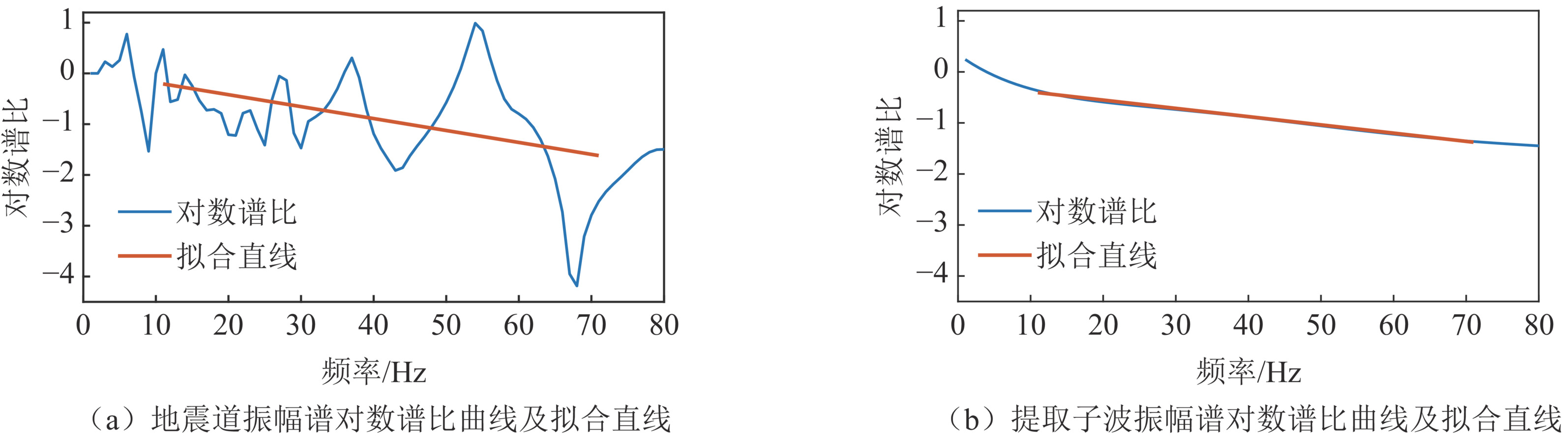
图 7 本文方法与常规谱比法Q值估计结果相对误差Figure 7. Relative error between the proposed and the conventional spectral ratio methods为进一步对比本文方法和常规时频域谱比法的差异，以Q值为100的非平稳地震道模型为例，图8（a）为未经过处理的瞬时地震道振幅谱。由图可见瞬时地震道振幅谱具有剧烈的波动，其形态复杂且有多个波峰，不同时刻的振幅谱形态具有较大的差异。对地震道瞬时振幅进行处理，得到其对数谱比曲线（图9（a））。由图可见对数谱比与频率的线性关系很差，这使得拟合直线的斜率与理论值有较大的偏差，由此斜率估计的Q值误差较大。图8（b）为经过复赛谱提取的时变子波瞬时振幅谱，振幅谱为光滑的单峰形态，0.5 s的子波振幅谱与0.1 s的子波振幅谱对比，其振幅峰值降低，主频减小且频带变窄，表明提取的子波振幅谱保留了时变特征。提取子波振幅谱的对数谱比曲线如图9（b）所示，可以明显看出对数谱比与频率之间的线性关系有了显著的增强。
2.3 含噪模型测试
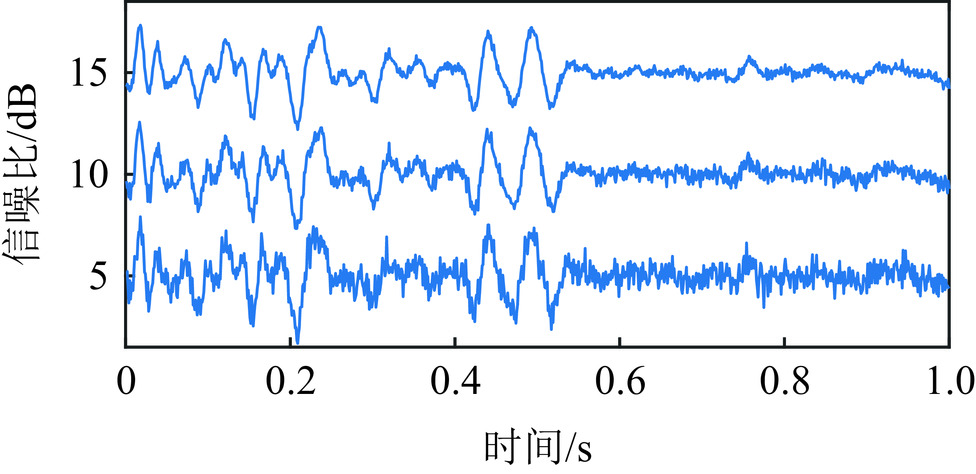
为对比研究本文方法与常规谱比法的抗噪性，本文进行了含噪声模型测试。选取图5中理论Q值为25的不含噪非平稳地震道模型，为其加入高斯白噪声合成含噪模型。在与无噪模型实验相同的条件下，通过本文方法和常规谱比法估计含噪模型的Q值。为分析不同强度的噪声对两种方法估计Q值的影响，设置含噪模型的信噪比为5、10和15 dB，不同信噪比的含噪模型如图10所示。用两种方法对不同信噪比的含噪模型各进行100次独立实验，每次实验所添加高斯白噪声是随机的，统计实验结果的均值和标准差。
本文方法和常规谱比法估计Q值的统计结果如表1所示，由表可知，地震数据的信噪比越高，两种方法Q值估计结果的精确度就越高；在不同强度的噪声影响下，本文方法Q值估计结果的精确度均高于常规谱比法Q值估计结果的精确度。
表 1 不同信噪比模型Q值估计统计结果Table 1. Statistical results of Q estimation for different signal-to-noise ratio models模型信噪比 5 dB 10 dB 15 dB 本文方法 均值 27.30 25.65 25.28 标准差 6.35 4.03 3.04 常规谱比法 均值 35.20 32.36 27.87 标准差 11.20 10.34 6.81 图11为本文方法对不同信噪比模型估计Q值的结果，由图可知，地震数据信噪比越高，本文方法估计Q值的结果就越接近理论Q值。由含噪模型测试结果可知，本文方法的准确性与稳定性均高于常规谱比法，具有更强的抗噪能力。
![]()
图 11 不同信噪比模型本文方法Q值估计结果Figure 11. Q estimation results of different signal-to-noise ratios using the proposed method3. 实际资料应用
将复赛谱域时变子波Q值估计方法应用于某工区的实际地震数据中。该工区整体为向斜构造，发育砂、泥岩互层沉积，主要形成砂岩上倾尖灭圈闭与砂岩透镜体圈闭。
如图12所示，选取工区内过井w1的地震剖面验证本文方法，将自然伽马测井曲线投影于该剖面（图中黑色曲线），黑圈所示位置为目的层，其岩性为砂岩。
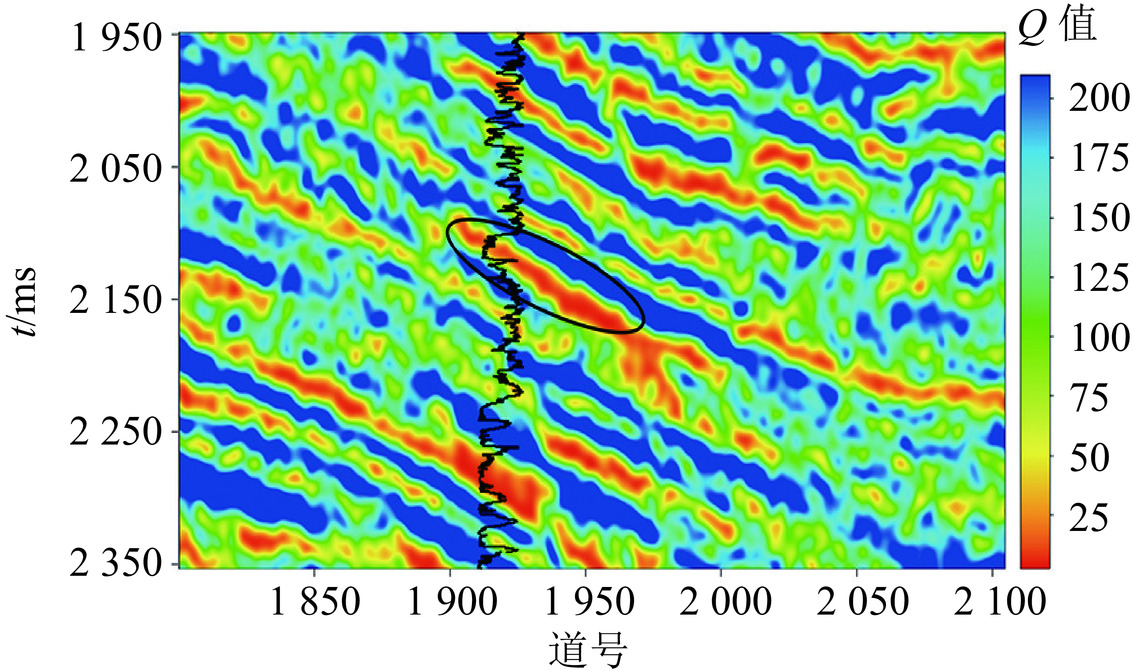
对该地震剖面估计Q值，图13是常规时频域谱比法估计的Q值剖面，图14是利用本文方法估计的Q值剖面。由图13和图14对比可见：常规时频域谱比法估计Q值剖面的高Q值区域与低Q值区域的边界不规则，存在较多零散分布的点状低Q值区域；本文方法估计的Q值剖面，其高Q值区域与低Q值区域之间的边界清晰。在图中黑色圆圈内，本文方法估计的Q值结果与目的层处测井曲线的自然伽马值相吻合，呈现低Q值特征。对比图15（a）与图15（b）可知，本文方法获得的Q值层次切片上低Q值更好地刻画了有效储层的空间展布。
![]()
图 13 常规时频域谱比法估计Q值剖面Figure 13. Q estimation profile obtained using the conventional spectral ratio method4. 结论
本文提出一种基于时频域复赛谱时变子波提取的Q值估计方法。该方法将地震记录时频谱变换为复赛谱，进行时变子波振幅谱提取，在此基础上应用时频域谱比法估计Q值。实验结果表明：
（1）复赛谱域提取子波方法能够准确提取非平稳地震记录不同时刻的子波振幅谱，提取的子波振幅谱摆脱了反射系数的白谱假设，保留了时变特性；
（2）相对于传统的时频域谱比法，本方法提取的时变子波振幅谱有效消除了反射系数对地震子波的影响，由子波振幅谱作比得到的对数谱比与频率之间的线性关系显著增强；
（3）与传统时频域谱比法相比，本文方法具有更高的准确性与抗噪性。实际数据测试结果表明本文方法能够有效的估计Q值，具有较好的适用性。
致谢：中石化胜利油田分公司物探研究院为本文研究提供了大量资料和基础数据。
-
![]()
图 2 时频域复赛谱提取时变子波振幅谱
Figure 2. Time-varying amplitude spectrum of the wavelet of cepstrum domain
![]()
图 6 本文方法与常规谱比法Q值估计结果
Figure 6. Q estimation results of the proposed and the conventional spectral ratio methods
![]()
图 7 本文方法与常规谱比法Q值估计结果相对误差
Figure 7. Relative error between the proposed and the conventional spectral ratio methods
![]()
图 11 不同信噪比模型本文方法Q值估计结果
Figure 11. Q estimation results of different signal-to-noise ratios using the proposed method
![]()
图 13 常规时频域谱比法估计Q值剖面
Figure 13. Q estimation profile obtained using the conventional spectral ratio method
表 1 不同信噪比模型Q值估计统计结果
Table 1 Statistical results of Q estimation for different signal-to-noise ratio models
模型信噪比 5 dB 10 dB 15 dB 本文方法 均值 27.30 25.65 25.28 标准差 6.35 4.03 3.04 常规谱比法 均值 35.20 32.36 27.87 标准差 11.20 10.34 6.81 
下载: 导出CSV
-
[1] FUTTERMAN W I. Dispersive body waves[J]. Journal of Geophysical Research, 1962, 7(13): 5279-5291.
[2] 李振春, 王清振. 地震波衰减机理及能量补偿研究综述[J]. 地球物理学进展, 2007, 22(4): 1147-1152. DOI: 10.3969/j.issn.1004-2903.2007.04.021. LI Z C, WANG Q Z. A review of research on mechanism of seismic attenuation and energy compensation[J]. Progress in Geophysics, 2007, 22(4): 1147-1152. DOI: 10.3969/j.issn.1004-2903.2007.04.021. (in Chinese).
[3] BATH M. Spectral analysis in geophysics[M]. New York: Elsevier Science Publication Limited Company, 1974: 1-50.
[4] REINE C, VAN D B M, CLARK R. The robustness of seismic attenuation measurements using fixed- and variable-window time-frequency transforms[J]. Geophysics: Journal of the Society of Exploration Geophysicists, 2009, 74(2): WA123-WA135.
[5] 朱耀旭, 包乾宗. 应用遗传算法估计非稳态地震数据的混合相位子波及Q值[J]. 石油地球物理勘探, 2024, 59(4): 763-770. ZHU Y X, BAO Q Z. Estimation of mixed-phase wavelet and Q value of nonstationary seismic data using genetic algorithm[J]. Oil Geophysical Prospecting, 2024, 59(4): 763-770. (in Chinese).
[6] 陈文爽, 管路平, 李振春, 等. 基于广义S变换的叠前Q值反演方法研究[J]. 石油物探, 2014, 53(6): 706-712. DOI: 10.3969/j.issn.1000-1441.2014.06.011. CHEN W S, GUAN L P, LI Z C, et al. Prestack Q-inversion based on generalized S transform[J]. Geophysical Prospecting for Petroleum, 2014, 53(6): 706-712. DOI: 10.3969/j.issn.1000-1441.2014.06.011. (in Chinese).
[7] 杨登锋, 刘军, 吴静, 等. 加权谱比法Q值估计[J]. 石油地球物理勘探, 2022, 57(3): 593-601. YANG D F, LIU J, WU J, et al. Q factor estimation by weighted spectral ratio me-thod[J]. Oil Geophysical Prospecting, 2022, 57(3): 593-601. (in Chinese).
[8] 魏文, 王小杰, 李红梅. 基于叠前道集小波域Q值求取方法研究[J]. 石油物探, 2011, 50(4): 355-360. DOI: 10.3969/j.issn.1000-1441.2011.04.007. WE W, WANG X J, LI H M. Study on extraction method for Q based on pre-stack gather in wavelet domain[J]. Geophysical Prospecting for Petroleum, 2011, 50(4): 355-360. DOI: 10.3969/j.issn.1000-1441.2011.04.007. (in Chinese).
[9] 王小杰, 印兴耀, 吴国忱. 基于S变换的吸收衰减技术在含气储层预测中的应用研究[J]. 石油物探, 2012, 51(1): 37-42. WANG X J, YIN X Y, WU G C. The application of an S transform based absorption and attenuation technique for prediction of gas-bearing reservoir[J]. Geophysical Prospecting for Petroleum, 2021, 51(1): 37-42. (in Chinese).
[10] 王小杰, 栾锡武. 基于小波分频技术的地层Q值提取方法研究[J]. 石油物探, 2015, 54(3): 260-266. DOI: 10.3969/j.issn.1000-1441.2015.03.003. WANG X J, LUAN X W. Q value extraction method based on wavelet frequency division technology[J]. Geophysical Prospecting for Petroleum, 2015, 54(3): 260-266. DOI: 10.3969/j.issn.1000-1441.2015.03.003. (in Chinese).
[11] 李波, 文晓涛, 张懿疆, 等. 基于Lucy-Richardson算法和广义S变换的Q值提取[J]. 石油物探, 2019, 58(5): 689-699. DOI: 10.3969/j.issn.1000-1441.2019.05.007. LI B, WEN X T, ZHANG Y J, et al. Combined generalized S transform and Lucy-Richardson algorithm for Q-value extraction[J]. Geophysical Prospecting for Petroleum, 2019, 58(5): 689-699. DOI: 10.3969/j.issn.1000-1441.2019.05.007. (in Chinese).
[12] LI B, WEN X T, NIE W L, et al. Pre-stack Q estimation based on inverse spectral decomposition[J]. Journal of Petroleum Science and Engineering, 2021, 205: 108775. DOI: 10.1016/j.petrol.2021.108775.
[13] 周东红, 段新意. 浅水环境下气云发育区高孔低胶结地层地震资料成像策略研究——以渤海莱北地区A油田为例[J]. 石油物探, 2023, 62(1): 105-118. DOI: 10.3969/j.issn.1000-1441.2023.01.009. ZHOU D H, DUAN X Y. Seismic data imaging strategy of high-porosity and low-cementation strata in the gas cloud development area of a shallow water environment: Case study of an oilfield in the Bohai Laibei area[J]. Geophysical Prospecting fortroleum, 2023, 62(1): 105-118. DOI: 10.3969/j.issn.1000-1441.2023.01.009. (in Chinese).
[14] 张繁昌, 张汛汛, 张立强, 等. 基于自适应子波分解的品质因子Q提取方法[J]. 石油物探, 2016, 55(1): 41-48. DOI: 10.3969/j.issn.1000-1441.2016.01.006. ZHANG F C, ZHANG X X, ZHANG L Q, et al. Extraction method of Q estimation based on adaptive wavelet decompensation[J]. Geophysical Prospecting for Petroleum, 2016, 55(1): 41-48. DOI: 10.3969/j.issn.1000-1441.2016.01.006. (in Chinese).
[15] 张瑾, 王彦国, 兰慧田, 等. 基于不同阶次泰勒级数展开的含非本征衰减频域振幅比平均的Q值估计方法[J]. 石油地球物理勘探, 2023, 58(6): 1423-1435. ZHANG J, WANG Y G, LAN H T, et al. Amplitude ratio average method in frequency domain for Q estimation of extrinsic attenuation based on Taylor series expansion with different orders[J]. Oil Geophysical Prospecting, 2023, 58(6): 1423-1435. (in Chinese).
[16] 许李囡, 高静怀, 杨阳, 等. 基于S变换和变分法的品质因子Q估计方法[J]. 石油地球物理勘探, 2022, 57(1): 82-90. XU L N, GAO J H, YANG Y, et al. Quality factor Q estimation based on S transform and variational method[J]. Oil Geophysical Prospecting, 2022, 57(1): 82-90. (in Chinese).
[17] 周晨. 基于深度学习的Q值估计和地震衰减补偿[D]. 北京: 中国石油大学(北京), 2023. [18] WANG J, LU W, LI Y. A multitask learning-based dynamic wavelet amplitude spectra extraction method and its application in Q estimation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 1-10.
[19] LI F, YU Z, MA J. An effective Q extraction method via deep learning[J]. Journal of Geophysics and Engineering, 2024, 21(2): 483-495. DOI: 10.1093/jge/gxae011.
[20] AKI K, RICHARDS P G. Quantitative Seismology: Theory and Methods[M]. San Francisco, CA: W. H. Freeman & Co. 1980.
[21] MARCRAVE G F, LAMOUREUX M P, HENLEY D C, et al. Gabor deconvolution: Estimating reflectivity by non-stationary deconvolution of seismic data[J]. Geophysics, 2011, 76(3): W15-W30. DOI: 10.1190/1.3560167.
[22] 刘俊杰, 陈学华, 吴昊杰, 等. 稀疏广义S变换及其在储层地震低频异常检测中的应用[J]. 石油地球物理勘探, 2023, 58(3): 690-699. LIU J J, CHENG X H, WU H J, et al. Sparse generalized S-Transform and its application to detection of low-frequency seismic anomalies in reservoirs[J]. Oil Geophysical Prospecting, 2023, 58(3): 690-699. (in Chinese).
[23] 刘春成, 周慰, 牛聪, 等. 基于改进广义S变换的复赛谱时频域反褶积方法[J]. 中国石油大学学报(自然科学版) 2018, 42(5): 57-64. LUD C C, ZHOU W, NU C, et al. Cepstral time-frequency domain deconvolution based on improved generalized S-transform[J]. Journal of China University of Petroleum (Edition of natural science), 2018, 42(5): 57-64. (in Chinese).
[24] 贾承造, 王祖纲, 姜林, 等. 中国页岩油勘探开发研究进展与科学技术问题[J]. 世界石油工业, 2024, 31(4): 1-11. DOI: 10.20114/j.issn.1006-0030.20240530001. JIA C Z, WANG Z G, JIANG L, et al. Progress and key scientific and technological problems of shale oil exploration and development in China[J]. World Petroleum Industry, 2024, 31(4): 1-11. DOI: 10.20114/j.issn.1006-0030.20240530001. (in Chinese).
计量
- 文章访问数: 55
- HTML全文浏览量: 9
- PDF下载量: 11
