Diagnostic Efficacy of Quantitative Computed Tomography in CTD-ILA/ILD
-
摘要:
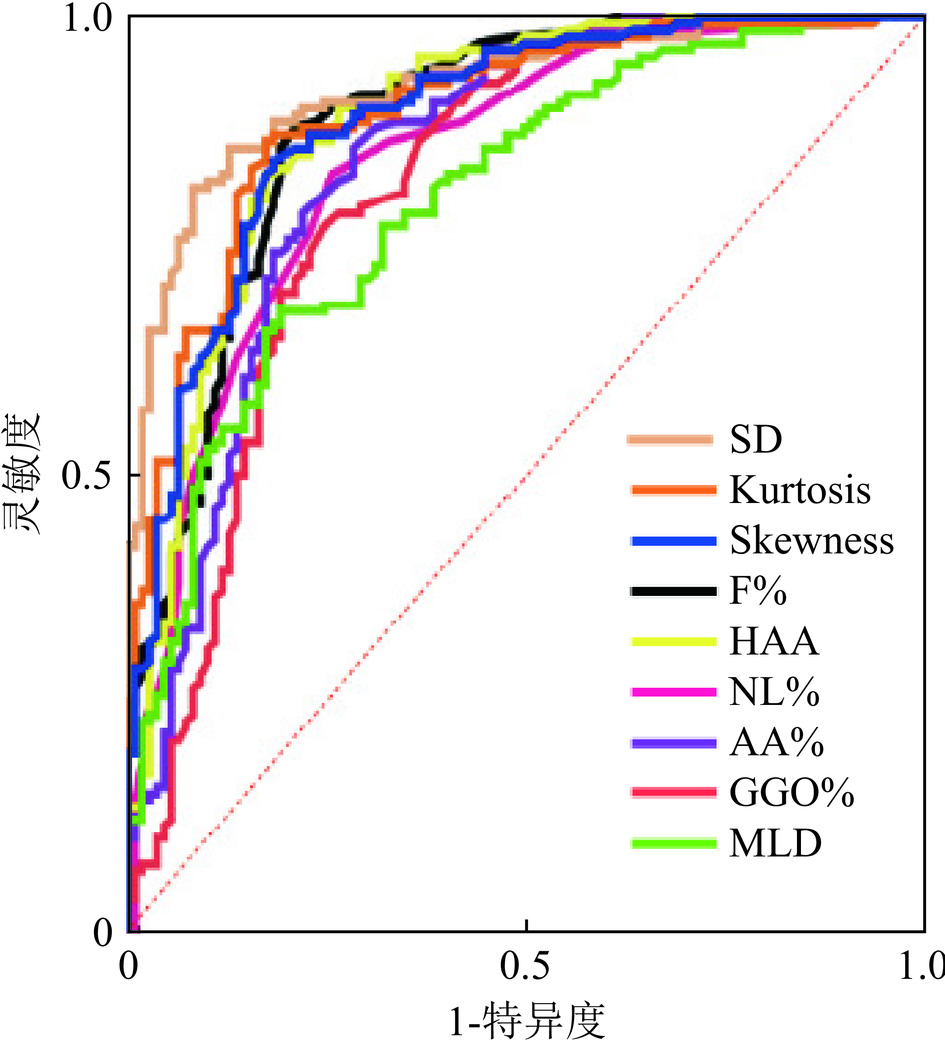
目的：评估定量CT在结缔组织病相关间质性肺异常（CTD-ILA）和结缔组织病相关间质性肺疾病（CTD-ILD）中的诊断效能，建立基于定量CT的结缔组织病（CTD）患者筛查方法。方法：纳入CTD-ILD患者140例、CTD-ILA患者33例、对照组109例，使用3D-Slicer获得定量指标。结果：各组间定量CT指标均存在差异；ROC分析显示，F%、GGO%、SD及Kurtosis是鉴别对照组与CTD-ILA/ILD的敏感指标，其中SD在早期诊断CTD-ILA（AUC=0.862）、CTD-ILD（AUC=0.923）时表现最佳，进一步区分CTD-ILA与CTD-ILD时，SD（AUC=0.649）和F%（AUC=0.617）展现出较强区分能力。多元逐步Logistic回归分析显示，F%、GGO%、SD和Kurtosis在区分对照组与CTD-ILA/ILD时具有统计学意义。结论：定量CT对于CTD-ILA/ILD早期诊断具有重要意义，基于定量CT构建CTD筛查流程有助实现患者精准管理。
Abstract:Objective: The aim of this study is to evaluate the diagnostic efficacy of quantitative computed tomography (CT) in differentiating between connective tissue disease-associated interstitial lung abnormalities (CTD-ILA) and connective tissue disease-associated interstitial lung disease (CTD-ILD), as well as to establish a screening protocol for connective tissue disease (CTD) patients based on quantitative CT. Methods: A total of 140 patients with CTD-ILD, 33 patients with CTD-ILA, and 109 healthy controls were enrolled. Quantitative indices were obtained using the 3D-Slicer software. Results: Significant differences in quantitative CT indices are observed among the groups. ROC analysis shows that the F%, GGO%, SD, and kurtosis are sensitive indicators for differentiating the control group from those with CTD-ILA/ILD. Notably, the best SD is demonstrated in the early diagnosis of both the CTD-ILA (AUC=0.862) and CTD-ILD (AUC=0.923) groups. Further distinguishing between CTD-ILA and CTD-ILD shows the strong discriminatory ability of the SD (AUC=0.649) and F% (AUC=0.617). Multivariable stepwise logistic regression analysis shows that F%, GGO%, SD, and kurtosis are statistically significant in differentiating the control group from the CTD-ILA/ILD groups. Conclusion: Quantitative CT is promising for the early diagnosis of CTD-ILA/ILD. Establishing a CTD screening protocol based on quantitative CT can facilitate precise patient management.
-
X射线计算机断层扫描技术（computed tomography，CT）作为一种重要的成像技术，在无损检测和材料分析领域起重要作用。在常规CT系统中，X射线是连续能谱的。当X射线穿过物体时，低能光子穿透能力弱，高能光子穿透能力强，低能射线相较于高能射线更容易衰减，通过物体后的平均能量比通过物体前的平均能量高，会出现“射束硬化”现象[1]。
射束硬化伪影校正是CT研究中的热点，实现方法通常可以分为两大类：硬件方法和软件方法[2]。硬件方法是指通过改进CT成像设备来减少射束硬化效应，其中典型的方法有滤波片校正、光子计数探测器等。滤波片校正法是对多能射线束进行滤波，可以在一定程度上抑制硬化伪影现象[3-4]。光子计数探测器可以通过合并一个较低阈值以上的光子，减少了较低能量光子的影响，从而降低射束硬化效应[5]。软件校正方法主要有深度学习法、迭代法、线性化法和多能成像法等[2]。
深度学习法对大规模样本进行训练，提取射束硬化伪影的特征并自动校正[6-8]，但需要标注大量数据，存在过拟合和泛化性差的问题。迭代法是一种不断用变量的旧值递推新值的过程。Brabant等[9]提出在迭代重建过程时，对射束硬化效应进行建模，将其融合到正投影过程中，达到消除伪影的目的。线性化法是通过线性变换对非线性数据进行校正，从而实现硬化伪影校正。通常可以利用多项式拟合将多能连续谱投影数据转化为单能投影数据，但该方法需要利用特定模体投影数据或其他先验信息进行估计，且难以适用于多材料构成的成像对象[10-12]。Ingacheva等[13]将投影数据进行单参数线性化，利用各角度下投影之和相同，通过求解参数最优解，对投影数据校正后进行重建。多能成像法是通过对多种不同能谱下的投影数据分解，获取基投影图像，进而合成出近似单能图像。对于物质成分已知且彼此不混合的被测物，罗婷等[14]把被检测物体的已知物质作为基材料，对CT投影数据采集过程进行数学建模，对基材料图像迭代求解，得到伪单能图像，可以显著地校正硬化伪影。Wei等[15-16]利用盲分解法，将能谱、材料信息作为未知变量，对多电压投影进行分解，得到基图像和能量，但该方法需要多个电压数据，不适用于单电压CT成像。Sajja等[17]改进了双能锥束CT技术，改善软组织对比度，减弱射束硬化伪影和金属伪影，该方法同样需要至少两个电压下的投影数据。
尽管多材料物体的射束硬化校正方法很多，但除深度学习法外，大多需要能谱信息，材料组分等作为先验信息。在这些先验信息未知条件下，则需要获取多电压投影。对此，本文提出一种单电压CT成像射束硬化伪影校正方法，适用于多材料物体成像，且不需要能谱、材料组分等先验信息。
1. 理论与方法
实际中X射线是连续能谱，然而传统CT重建算法是基于单能假设，导致重建图像中会出现硬化伪影。利用窄能谱X射线图像进行重建，可以减弱硬化伪影的影响。连续谱X射线图像可以看作是窄能谱X射线图像的线性组合，那么可以构建多能X射线透射率[18]分解模型。对X射线透射率模型进行求解，可以获取窄能谱X射线图像，从而实现硬化伪影校正。
1.1 多能X射线透射率分解模型
在实际应用中，X射线源发出的是连续能谱X射线，衰减系数不仅与位置相关，还与射线能量有关。根据Beer定理[19]：
$$ I=I_0\int\limits_0^{E_{\max}}S(E)\mathrm{exp}\left(-\int\limits_Lu(x,E)\mathrm{d}x\right)\mathrm{d}E\text{ }， $$ (1) 式中，I为探测器接收到的射线强度，I0为射线的初始强度，Emax表示成像电压下X射线最高能量。S(E)表示归一化等效能谱，与X射线能谱、探测器效率等因素有关，u(x,E)表示路径L上x处，能量为E时X射线的衰减系数。S(E)满足：
$$ 1 = \int\limits_0^{{E_{\max }}} {S(E){\mathrm{d}}E{\text{ }}}。 $$ (2) 对式（2）进行离散化，第r个窄能谱段能量近似为Er，可以得到：
$$ \frac{I}{{{I_0}}} = \sum\limits_{r = 1}^R {{s_r}{{\mathrm{exp}}\left({ - \sum\limits_{k = 1}^K {{u_{rk}}{d_k}} }\right)}} {\text{ }}, $$ (3) 其中，I/I0为X射线透射率，sr为第r个窄能谱段X射线透射率对应的加权系数，k表示第k种基材料或基效应。urk为第k种基材料在能量Er时的衰减系数，dk为X射线穿过路径上第k种基材料（效应）的等效长度。其中，
$$ 1 = \sum\limits_{r = 1}^R {{s_r}{\text{ }}} 。 $$ (4) 将投影图像中第m个像素对应的透射率记为fm，m=1, 2,
$\cdots ,$ M。由式（4），将所有像素的透射率写成矩阵形式为：$$ {\boldsymbol{F}} = {\boldsymbol{S}}{\exp \left({ - {\boldsymbol{UD}}}\right)}{\text{ }}, $$ (5) 其中，F=(f1, f2,
$\cdots$ , fM)，为投影图像各像素对应的X射线透射率构成的图像。S=(s1, s2,$\cdots $ , sR)，为构成X射线透射率图像的窄能谱图像加权系数。U=(urk)RK，U的一列对应一材料在各窄谱段的衰减系数，可以通过查询材料衰减系数数据库，得到各基材料在各能量段的衰减系数。D=(dkm)KM，D的一行是同种材料在各像素上的衰减长度。UD的每一行对应一个窄能谱投影。根据S，D的物理意义，S和D为非负矩阵，即S≥0，D≥0。由于各探元获得的测量值相互独立，所以考虑根据各探元对应的fm所服从的分布建立极大似然估计模型，对式（5）中的能谱权重矩阵S，各材料在各个像素中的衰减长度D进行估计。
X射线的成像过程中存在量子噪声、光子噪声和电子噪声。量子噪声是由于检测有限数量的X射线量子时的波动而出现的，是CT图像中的统计噪声产生的主要原因[20]。光子噪声是由于光子的随机到达引起的噪声，通常与光的粒子性相关。电子电路接收模拟信号的过程可能会受到一些噪声的影响，这些噪声被称为电子噪声。3种噪声都被认为是CT图像中的噪声，通常被认为服从加性高斯分布[20]，即：
$$ {f}_{m}\text{ }～\text{ }N({\tau }_{m},{\sigma }_{m}^{2})\text{ }, $$ (6) 式中，τm为fm的期望，σm为fm的标准差。将式（6）化为标准正态分布，可以得到：
$$ \frac{{f}_{m}-{\tau }_{m}}{{\sigma }_{m}}～\text{ }N(0,\text{ }1)\text{ }。 $$ (7) 概率分布函数为：
$$ \varphi\left(\frac{f_m-\tau_m}{\sigma_m}\right)=\frac{1}{\sqrt{2\text{π}}}\exp\left(-\frac{(f_m-\tau_m)^2}{2\sigma_m^2}\right)\text{ }。 $$ (8) 在fm已知的条件下，τm为第m探测单元上透射率的期望值[21]，即：
$$ {\tau _m} = \sum\limits_{r = 1}^R {{s_r}} {\exp\left({ - \sum\limits_{k = 1}^K {{u_{rk}}{d_{km}}} }\right)}{\text{ }}。$$ (9) 用ωm对式（8）中σm进行估计，ωm其中为各角度下每点的局部方差，计算过程如式（10）所示：
$$ {\omega _m} = \frac{{\displaystyle\sum\limits_{m \in \Theta } {{{\left(f(m) - \hat f(m)\right)}^2}} }}{N}{\text{ }}, $$ (10) 其中，f (m)代表X射线透射率图像中第m个像素的f值，
$ \hat{f}(m) $ 代表X射线透射率图像中以第m个像素点为中心，以N为窗口宽度的平均f值，Θ为像素点m所构成的集合。因此，建立高斯对数似然函数$$ \begin{gathered}L(s_r,d_{km})= -\frac{1}{2}m\ln(2{\text{π}})- \\ \frac{1}{2}\sum\limits_{m=1}^M\left(\frac{\Biggl(f_m-\sum\limits_{r=1}^Rs_r\exp\Big({-\sum\limits_{k=1}^Ku_{rk}d_{km}}\Big)\Biggl)}{\omega_m}\right)^2 。\end{gathered} $$ (11) 那么，式（11）可以转化为优化问题：
$$ \dfrac{\min \sum\limits_{m = 1}^M {{{\left( {{f_m} - \sum\limits_{r = 1}^R {{s_r}{\exp\Biggl({ - \sum\limits_{k = 1}^K {{u_{rk}}{d_{km}}} }\Biggl)}} } \right)}^2}}} {\omega _m^2{\text{ }}}。 $$ (12) 由于各像素点具有异方差性，可以使用加权最小二乘估计思想[21]对式（12）进行模型转化，进而对sr，dkm进行估计。结合式（4），得到优化模型如下：
$$ \begin{gathered}\min \left\| \frac{\boldsymbol{F}-\boldsymbol{S}\exp(-\boldsymbol{UD})}{\boldsymbol{\Omega}} \right\| _F^2 \\ \mathrm{s}.\mathrm{t}.\ \ S\ge0,\text{ }\boldsymbol{D}\ge0,\text{ }1=\sum\limits_{r=1}^Rs_r\text{ } \\ \end{gathered}， $$ (13) 其中，Ω=(ω1, ω2,
$\cdots $ , ωM)，为X射线透射率图像各角度下每点的局部方差矩阵。在单电压条件下，式（13）中的解具有不确定性，所以引入其它限制条件。1.2 基于积分不变性的多能X射线透射率分解模型
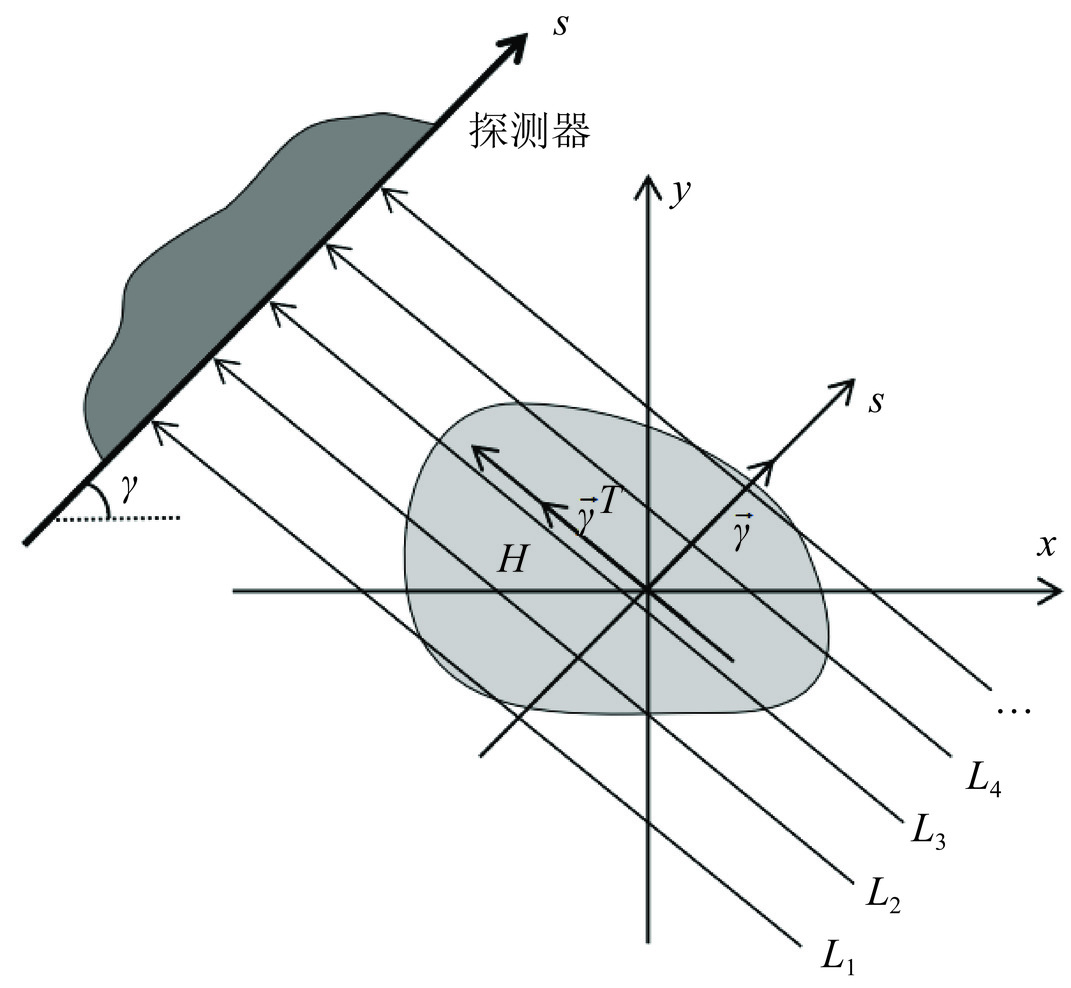
CT 成像扫描中物体本身是不变的，各材料的分布也是不变的。以二维CT成像为例，平行束X射线的投影过程如图1所示，图中阴影区域H表示一个单材料物体。以s表示探测器的坐标位置，射线路径可以表示为L(s)。射线沿着路径L(s)穿过物体时，穿过物体的长度记为d(s)，则d(s)对s的积分表示阴影区域H的面积S面积，即：
$$ S_{面积}=\displaystyle\int\limits_{-\infty}^{+\infty}d\left(s\right)\text{ }\text{d}s\ 。 $$ (14) 这一积分值与角度无关，由物体本身决定。对于单能X射线，如果衰减系数为u，则沿着路径L(s)的投影为ud(s)，从而：
$$ u{S}_{面积}={\displaystyle \int\limits_{-\infty }^{+\infty }ud\left(s\right)\text{ }}\text{d}s, $$ (15) 即uS面积与旋转角度无关，此为投影积分不变性[13,22-23]。同理，在多材料时，各材料对应的d(s)，其积分为各材料的面积，其值仅由物体本身决定。在不同角度下，是不变的。
假设第j个扫描角度下X射线投影像素数为Mj（
$j=1, 2,\cdots ,J$ ），将所有扫描角度下投影图像像素数之和记为M，则：$$ M=\sum\limits_{j=1}^JM_j\text{ }\ \ 。 $$ (16) 在平行束X射线成像下，对式（14），在离散情况下，积分变为求和，从而第k种材料在第j个角度下的面积可表示为：
$$ T_{kj}=\sum\limits_{i=1}^{M_j}d_{k\left(i+\sum\limits_{g=1}^{j-1}M_g\right)}\text{ }\ \ 。 $$ (17) 在不同角度下，该值均相等，因此有：
$$ T_{kj}=T_{k(j+1)},\;j=1,2,\cdots ,J-1,\;k=1,2,\cdots ,K \ 。 $$ (18) 在实际成像中，当X射线扇束角或锥角较小时，可近似看作平行束，用式（16）近似[13]。
由式（13）和式（16）及变量固有的非负性，可得X射线透射率分解模型如下：
$$ \begin{array}{c} \min \left\| \displaystyle\frac{{\boldsymbol{F}}-{\boldsymbol{S}}\exp\left({-{\boldsymbol{UD}}}\right)}{\Omega} \right\| _F^2 \\ {\mathrm{s.t}}.\; \; \text{ }{\boldsymbol{S}}\ge0\text{ }; \;\; {\boldsymbol{D}}\ge0\text{ ;}\;\; 1=\displaystyle\sum\limits_{r=1}^Rs_r\text{ ;} \\ T_{kj} = T_{k(j+1)},\;j = 1,2,\cdots,J - 1,\;\; k = 1,2,\cdots,K\end{array}。 $$ (19) 由于X射线透射率分解模型是一个具有非负约束的盲分离模型，仿照非负矩阵问题算法的求解方法，利用KKT条件对式（19）求解算法进行推导。在该模型中，将能谱段等间距划分，每个能量段以中间能量作参考，确定U值[16]。不考虑能谱归一化约束和积分不变性约束，可得S，D的迭代求解公式分别为：
$$ {\boldsymbol{S}} = {\boldsymbol{S}} \odot \displaystyle\frac{{\left( {\displaystyle\frac{{S\left( {{e^{ - UD}}} \right)}}{\Omega }} \right){{\left( {{{\mathrm{e}}^{ - {\boldsymbol{UD}}}}} \right)}^{\mathrm{T}}}}}{{\displaystyle\frac{{\boldsymbol{F}}}{{{{\boldsymbol{\Omega}} ^2}}}{{\left( {{{\mathrm{e}}^{ - {\boldsymbol{UD}}}}} \right)}^{\mathrm{T}}}}},\qquad $$ (20) $$ {\boldsymbol{D}}={\boldsymbol{D}}\odot\displaystyle\frac{{\boldsymbol{U}}^{\mathrm{T}}\left(\Biggl({\boldsymbol{S}}^{\mathrm{T}}\left(\displaystyle\frac{{\boldsymbol{S}}\left(e^{-{\boldsymbol{UD}}}\right)}{{\boldsymbol{\Omega}}^2}\right)\Biggl)\odot\left({\mathrm{e}}^{-{\boldsymbol{UD}}}\right)\right)}{{\boldsymbol{U}}^{\mathrm{T}}\left(\Biggl({\boldsymbol{S}}^{\mathrm{T}}\displaystyle\frac{{\boldsymbol{F}}}{{\boldsymbol{\Omega}}^2}\Biggl)\odot\left({\mathrm{e}}^{-{\boldsymbol{UD}}}\right)\right)}\text{ }\ 。 $$ (21) 在每次对S进行更新后，对其进行归一化，确保其满足式（4）约束。然后对D的值重新进行强制分配，使其尽量满足式（18）约束，具体为：
$$ d_{k\left(i+\sum\limits_{g=1}^{j-1}M_g\right)}=d_{k\left(i+\sum\limits_{g=1}^{j-1}M_g\right)}\left(\frac{\displaystyle\frac{1}{J}\displaystyle\sum\limits_{m=1}^Md_{km}}{\displaystyle\sum\limits_{i=1}^{M_j}d_{k\left(i+\sum\limits_{g=1}^{j-1}M_g\right)}}\right)\ \ 。 $$ (22) 由于X射线能谱的具体值是未知的，在某一能量段下，中间能量的强度比两端能量的强度相对较大，因此用二次函数作为能谱的近似。假定能谱等间隔划分为R段，划分能量为：
$$ 0 = {E_0} < {E_1} < \cdots < {E_R} = {E_{\max }}{\text{ }}, $$ (23) 则sr初始值取值为：
$$ {s_r} = \frac{{\displaystyle\int\limits_{{E_{r - 1}}}^{{E_r}} {E\left( {{E_{\max }} - E} \right)} {\text{ }}{\mathrm{d}}E}}{{\displaystyle\int\limits_0^{{E_{\max }}} {E\left( {{E_{\max }} - E} \right)} {\text{ }}{\mathrm{d}}E}}{\text{ }}, $$ (24) 对dkm初始值取值为：
$$ {d_{km}} = \frac{{{f_m}}}{{K{u_{\bar rk}}}},\;\;\bar r = \left[ {0.5 + \frac{R}{2}} \right]{\text{ }}, $$ (25) 其中“[ ]”表示取整。
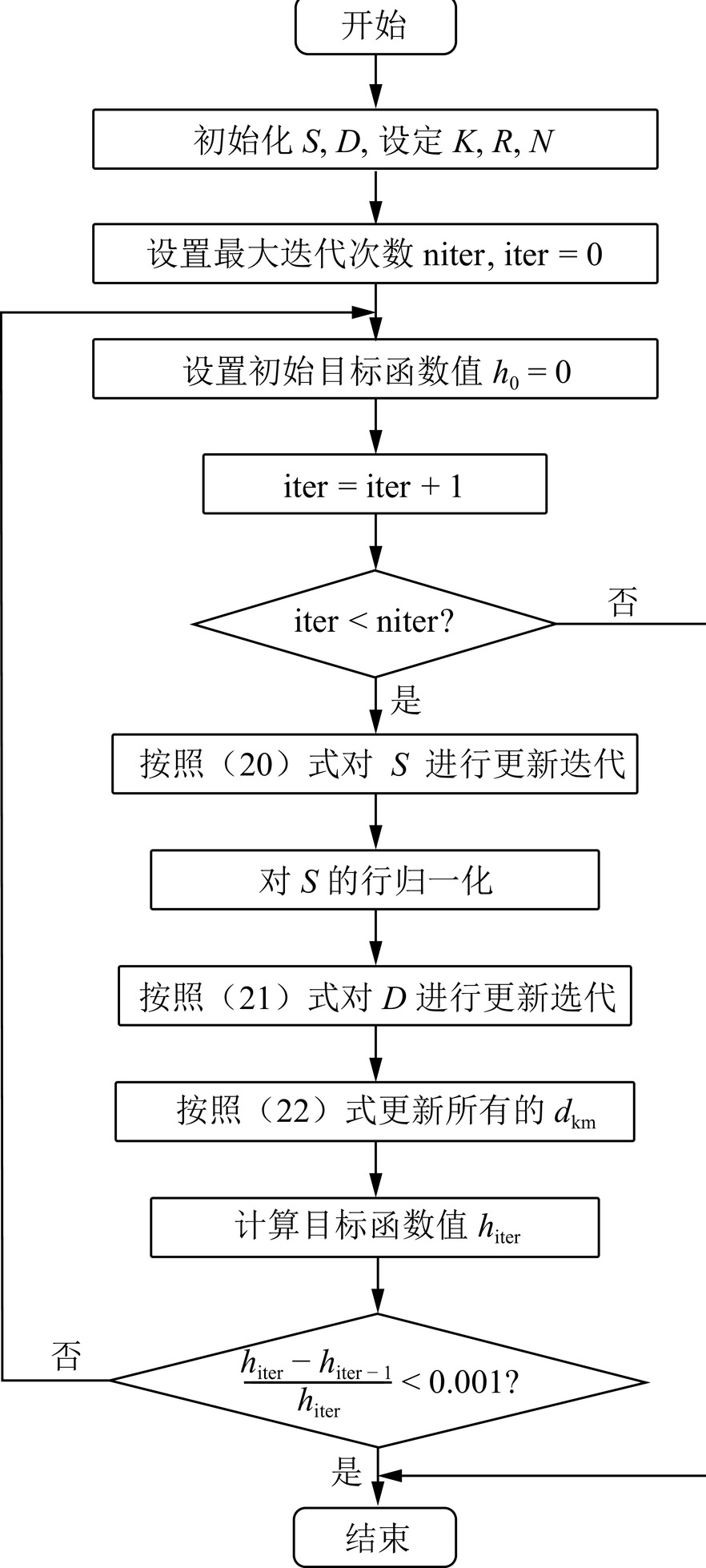
算法流程图如图2。
2. 实验结果
为了验证方法对射束硬化伪影的校正作用，分别使用双材料模体（钛合金与钢）、多材料模体（铝、氧化铝及氮化铝）进行实验验证。
第1个模体外部为钛合金材料，内部圆形区域为钢材料。钛合金部分的横截面为圆形的一部分，直径约为10.0 mm，钢部分直径约为2.5 mm。第2个模体铝、氧化铝及氮化铝3种材料横截面均为圆形，直径约为5.0 mm。
CT成像系统为中北大学智能探测技术与装备山西省重点实验室的YXLON FF20 CT系统，采用FBP算法进行重建。在单电压条件下，对于多材料物体的硬化伪影校正，文献[9]中的方法不需要能谱和材料信息，使用迭代重建算法，对硬化伪影进行校正；文献[13]中利用投影积分不变性对投影数据进行单参数线性化，校正后进行重建。所以选择文献[9]与文献[13]中方法重建结果与本算法重建结果、直接重建结果进行对比。
2.1 钛合金与钢实验
样品一实验中，管电压为160 kV，管电流为40 μA。射线源与物体中心的距离为200.000 mm，射线源与探测器的距离为779.577 mm，采样间隔为1°，采样角度为360°。
在上述距离条件下，X射线扇束角最大值为1.724°，可将扇形束投影数据近似看成是平行束投影数据。将能量范围等间隔划分为16个能量区间，记R=16，每个能量区间10 keV。选择光电效应和康普顿效应为基效应，记K=2。本实验中选择窗口宽度经验值为5，计算X射线透射率图像各角度下每点的局部方差，记N=5。分解后得到投影图像进行重建，重建图像大小为256×256，像素大小为0.045 mm×0.045 mm。为了方便进行对比，所以选择与直接重建图像灰度值相近的能量区间分解投影的重建图进行比较，此处选择第10能量区间下的投影重建图。对于文献[9]中的算法，参考文章中选取参数α=0.004，β=3。
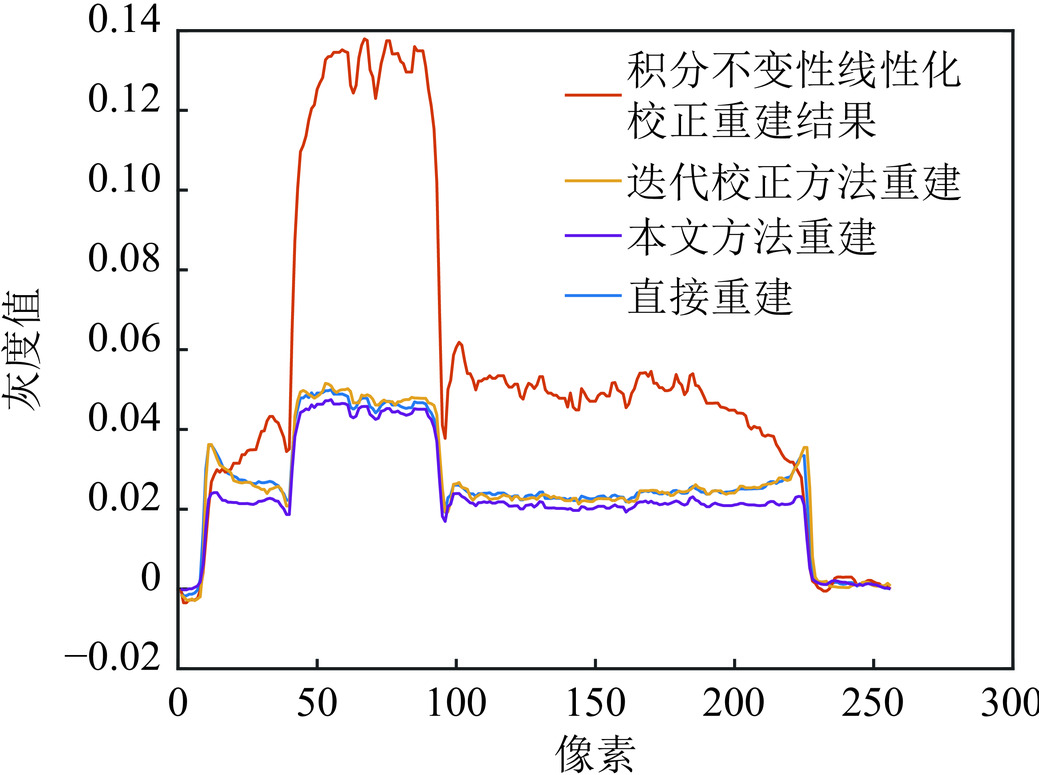
直接重建图像如图3（a）所示，积分不变性线性化校正方法重建图像如图3（b）所示，迭代校正方法重建图像如图3（c）所示，本文方法重建图像如图3（d）所示。不难发现，直接重建图像中，硬化伪影明显，尤其是钛合金区域，图像边缘像素灰度值高于中间部分。如图4所示，对比重建图像的同一列灰度值变化，本文方法硬化伪影校正后的重建图像，钛合金区域灰度值差异明显变小，优于直接重建图像和对比方法校正后的重建图像。
为了更加直观的观察伪影情况，对图像的伪彩色图进行对比。从图5（a）可知，直接重建的图像存在较为严重的硬化伪影，钛合金部分明显中间为黄绿色，边缘为红色，灰度值不均匀；从图5（b）观察，边缘亮度为蓝色，数值小于中间亮度，说明存在过校正现象；图5（c）观察发现，钛合金区域仍存在硬化伪影，校正效果不佳，表明迭代校正算法中，模型的参数选取对材料组分依赖性较强，文献中参数不适用于钛合金材料的伪影校正；相比之下，本文方法所得图像中间和边缘数值接近，图像更为均匀。
![]()
图 4 重建图像一列（图3（a）红线位置）灰度值变化Figure 4. Change in the grayscale values of a column (red line position in Fig.3 (a)) in the reconstruction result射束硬化伪影会导致重建图像的中间区域灰度值偏低，边缘区域灰度值偏高，极差值相对较大。极差均值比（extreme mean ratio，EMR）可以作为量化伪影的严重程度的指标，计算方法如公式（26）所示，
$$ \mathrm{EMR}=G_{\mathrm{region}}/\mu_{\mathrm{region}}\ \ ， $$ (26) 式中：Gregion为区域极差，μregion为区域均值。EMR越小，表示图像均匀性越好，像素值一致性越高。所以此处采用EMR对重建结果进行评价。表1展示了模体重建图像中钛合金和钢的极差、均值和EMR。
表 1 不同方法下极差均值比Table 1. Mean range ratio for different methods参数 直接重建 积分不变性线性化校正方法重建 迭代校正方法重建 本文方法重建 钛合金 钢 钛合金 钢 钛合金 钢 钛合金 钢 极差Gregion 0.161 0.169 0.309 0.355 0.236 0.156 0.118 0.149 均值μregion 0.183 0.259 0.656 0.654 0.270 0.264 0.157 0.245 EMR 0.881 0.655 2.119 0.543 0.875 0.591 0.750 0.607 本方法校正后，钛合金区域和钢的EMR值都低于直接重建图像的EMR值。尽管积分不变性线性化方法与迭代校正方法中对钢区域的射束硬化形成校正作用相对较好，但钛合金区域的EMR值高于本方法重建得到的钛合金区域的EMR值，说明图像的均匀性不佳。灰度值对比曲线、伪彩色图以及EMR值均表明，本方法对重建图像的射束硬化伪影现象具有一定抑制作用。
2.2 铝、氧化铝及氮化铝实验
样品二实验中，管电压为80 kV，管电流为40 μA。射线源与物体中心的距离为400.000 mm，射线源与探测器的距离为780.577 mm，采样间隔为1°，采样角度为360°。在上述距离条件下，X射线扇束角最大值为0.755°，可将扇形束投影数据近似看成是平行束投影数据。将能量范围等间隔划分为8个能量区间，记R=8，每个能量区间为10 keV。选择光电效应和康普顿效应为基效应，记K=2。本实验中选择窗口宽度经验值为5，计算X射线透射率图像各角度下每点的局部方差，记N=5。分解后得到投影图像，进行重建，重建图像大小为256×256，重建像素大小为0.064 mm×0.064 mm。对于文献[9]中的算法，参考文章中选取参数α=0.004，β=3。此处选择第5能量区间下的投影重建图与直接重建结果、积分不变性线性化校正[13]重建结果、迭代校正[9]重建结果进行对比（图6）。其中，左侧为铝，右侧上方为氮化铝，右侧下方为氧化铝。
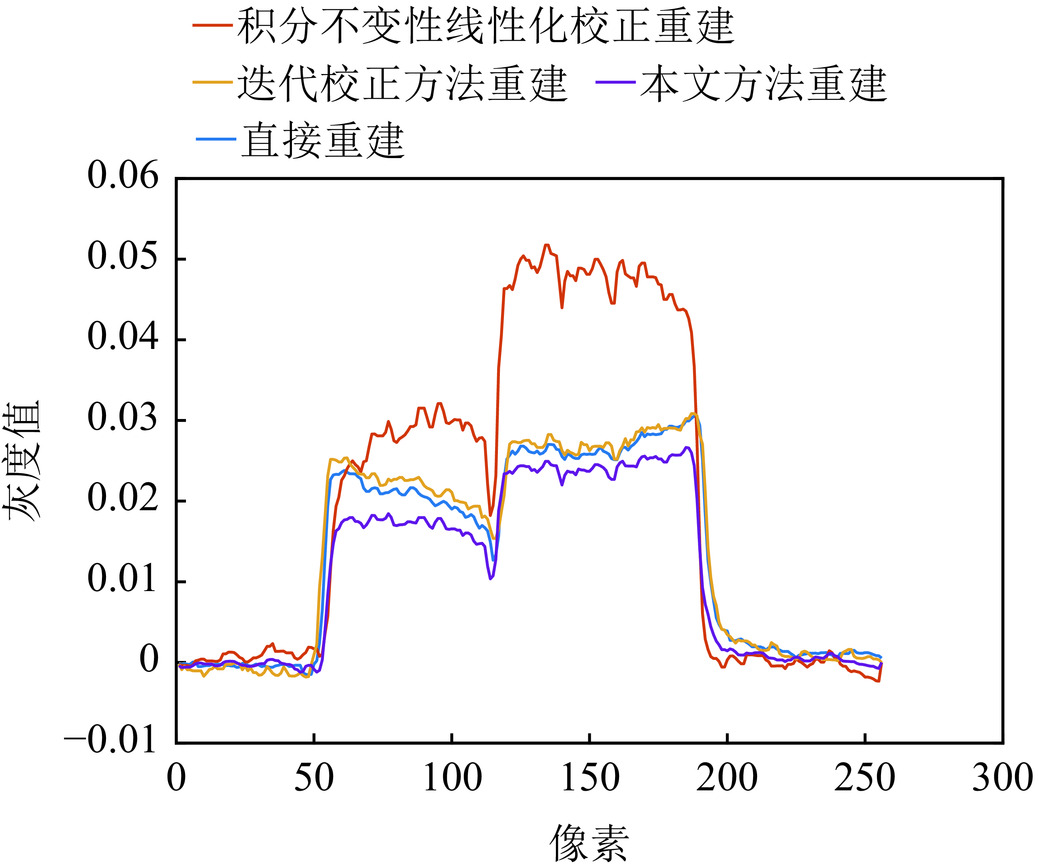
对比重建图像的同一条线上的灰度值变化（图7和图8），不难发现，本文方法硬化伪影校正后的重建图像，各材料的硬化伪影得到了很好的校正，边缘亮度，优于直接重建图像和积分不变性线性化方法与迭代校正方法校正后的重建图像。
![]()
图 7 重建图像一列（图6（a）红线位置）灰度值变化Figure 7. Change in the grayscale values of a column (red line position in Fig.6 (a)) in the reconstruction result![]()
图 8 重建图像一列（图6（a）绿线位置）灰度值变化Figure 8. Change in the grayscale values of a column (green line position in Fig.6 (a)) in the reconstruction result为了观察伪影情况，采用图像的伪彩色图进行对比（图9）。在直接重建图像中，可以观察到3种材料的边缘值均大于内部值，存在明显的硬化伪影。对比方法重建图像，均匀性不佳。相比之下，本文方法得到的图像同组分区域颜色相近，图像更为均匀，表明本方法对重建图像的射束硬化伪影现象具有抑制作用。
通过计算EMR值（表2）不难发现，对于多材料模体的硬化伪影校正，积分不变性线性化方法校正效果不佳，迭代校正方法对铝和氧化铝材料的硬化伪影可以起到校正效果，但对氮化铝材料不能进行硬化伪影校正。相比之下，本文方法的射束硬化形成校正作用明显，得到的图像均匀性更好。灰度值对比曲线与EMR值均表明，本方法对多材料模体重建图像的射束硬化伪影现象具有一定抑制作用。
表 2 不同方法下极差均值比Table 2. Mean range ratio under different methods项目 直接重建 积分不变性线性化校正方法重建 迭代校正方法重建 本文方法重建 铝 氧化铝 氮化铝 铝 氧化铝 氮化铝 铝 氧化铝 氮化铝 铝 氧化铝 氮化铝 极差Gregion 0.018 0.038 0.018 0.043 0.059 0.026 0.017 0.038 0.021 0.015 0.031 0.009 均值μregion 0.021 0.028 0.018 0.028 0.043 0.024 0.021 0.029 0.018 0.021 0.024 0.015 EMR 0.870 1.370 1.016 1.507 1.351 1.081 0.780 1.309 1.163 0.734 1.277 0.629 3. 结论
针对单电压条件下多材料物体CT成像中存在硬化伪影的问题，本文提出一种基于投影积分不变性约束的单电压CT图像硬化伪影校正方法。该方法以投影积分不变性作为约束条件，构建了X射线透射率分解模型，求解模型以获得窄能谱投影，进而重建得到硬化伪影校正的图像。实验结果中，该方法所得CT图像相比于直接重建、对比方法重建的CT图像，硬化伪影明显减弱。
理论上，单电压下，式（13）的优化模型必然是多解的，求解所得窄能谱投影未必是真正的窄能谱投影，并且其解会受到始值影响。利用投影积分不变性，约束了式（13）的优化模型解的结构，从而一定程度上达到硬化伪影校正的目的。
想要实现真正的窄能谱成像，仍然需要多个电压下的投影数据。此外，在实际成像中，对扇束和锥束可以近似转化为平行束的角度阈值界定，需要进一步研究。
-
![]()
图 1 CTD-ILA（a）和CTD-ILD（b）HRCT示例图
注：（a）一名59岁系统性红斑狼疮女性患者，按照指南诊断ILA，患者尚无呼吸系统症状。（b）一名66岁类风湿关节炎男性患者，按照指南诊断ILD，患者存在呼吸系统症状。
Figure 1. Representative HRCT images of CTD-ILA (a) and CTD-ILD (b)
![]()
图 3 密度阈值分割法示例图
注：（a）为CT横断位图，（b）为定量CT分割结果图。蓝色代表正常肺组织的百分比（NL%），橙色表示磨玻璃样混浊区域的百分比（GGO%），粉红色表示纤维化区域的百分比（F%），红色表示血管。磨玻璃样混浊区和纤维化区的百分比之和被设置为异常病变区的百分比（AA%）。
Figure 3. Schematic illustration of density threshold segmentation methodology
![]()
图 4 定量CT指标区分对照组与CTD-ILA ROC曲线
Figure 4. Receiver operating characteristic (ROC) curves of quantitative CT metrics for discriminating between control group and CTD-ILA patients
![]()
图 5 定量CT指标区分对照组与CTD-ILD ROC曲线
Figure 5. Receiver operating characteristic (ROC) curves of quantitative CT metrics for differentiating between control group from CTD-ILD patients
![]()
图 6 定量CT指标区分CTD-ILA与CTD-ILD ROC曲线
Figure 6. Receiver operating characteristic (ROC) curves of quantitative CT metrics for discriminating between CTD-ILA and CTD-ILD
表 1 患者临床资料表
Table 1 Demographic and clinical characteristics of study participants
项目 组别 统计检验 对照组（n=109） CTD-ILA（n=33） CTD-ILD（n=140） F/H P 性别（%） 14.52 0.001 男 19（17.3） 14（42.4） 53（37.9） 女 90（81.8） 19（57.6） 87（62.1） 年龄/岁 40（19） 64（11） 62.5（14） 104.52 ＜0.001 BMI/（kg/m2） 22.54（2.81） 21.89（3.08） 22.34（4.39） 0.29 0.864 病程 3（7） 5（11.25） 4（10.75） 3.25 0.187 CTD类型（%） 9.66 0.008 类风湿关节炎 63（57.3） 22（66.7） 67（47.9） 系统性红斑狼疮 24（21.8） 5（15.2） 10（7.1） 系统性硬化症 2（1.8） 2（6.1） 15（10.7） 干燥综合症 9（8.2） 2（6.1） 16（11.4） 皮肌炎 − 2（6.1） 8（5.7） 弥漫性结缔组织病 7（6.4） − 15（10.7） ANCA相关血管炎 4（3.6） 2（6.1） 9（6.4） CT分型（%） 1.12 0.291 普通型间质性肺炎 − 7（21.2） 41（29.3） 非特异性间质性肺炎 − 18（54.5） 71（50.7） 淋巴细胞性间质性肺炎 − 4（12.1） 22（15.7） 机化性肺炎 − 4（12.1） 6（4.3） 
下载: 导出CSV
表 2 各组间定量CT指标差异
Table 2 Intergroup differences in quantitative CT metrics among controls, CTD-ILA, and CTD-ILD cohorts
项目 组别 统计检验 对照组（n=109） CTD-ILA（n=33） CTD-ILD（n=140） F/H P NL% 74（7） 68.0（7.5）* 65.5（9）* 89.82 ＜0.001 GGO% 5.7（3.7） 11.3（8.75）* 12.65（9.1）* 76.00 ＜0.001 F% 2.9（1.25） 5.2（3.4）* 6.6（4.98）* 113.72 ＜0.001 AA% 8.8（4.9） 16.40（11.80）* 19.35（12.67）* 89.51 ＜0.001 HAA 4.04（2.18） 9.25±5.26* 9.44（6.92）* 114.05 ＜0.001 MLD −830.16（49.19） −777.08（59.02）* −768.19（93.69）* 70.18 ＜0.001 SD 179.94（16.38） 205.52（25.83）* 220.19（41.43）* 139.60 ＜0.001 Kurtosis 13.62±4.20 6.77（4.91）* 5.28（5.64）* 122.59 ＜0.001 Skewness 3.27（0.71） 2.34（0.74）* 2.19±0.60* 115.41 ＜0.001 注：*表示与对照组相比P＜0.05。NL%为正常肺区域百分比；GGO%为磨玻璃密度区域百分比；F%为纤维化区域百分比；AA%为异常病变区域百分比；HAA为高衰减区；MLD为平均肺密度；SD为标准差；Kurtosis为峰值；Skewness为偏度。
下载: 导出CSV
表 3 定量CT指标区分对照组与CTD-ILA的ROC曲线分析结果
Table 3 ROC curve analysis of quantitative CT metrics for discriminating control groups from CTD-ILA patients
项目 AUC P 最佳截断值 灵敏度 特异度 约登指数 NL% 0.770 ＜0.001 < 71.50 0.758 0.743 0.501 GGO% 0.774 ＜0.001 > 8.000 0.788 0.734 0.522 F% 0.814 ＜0.001 > 4.050 0.758 0.807 0.565 AA% 0.785 ＜0.001 > 12.20 0.788 0.762 0.549 HAA 0.830 ＜0.001 > 6.121 0.788 0.835 0.623 MLD 0.763 ＜0.001 > −800.9 0.697 0.798 0.495 SD 0.862 ＜0.001 > 191.2 0.849 0.817 0.665 Kurtosis 0.821 ＜0.001 < 9.615 0.727 0.844 0.571 Skewness 0.816 ＜0.001 < 2.795 0.788 0.817 0.604 注：NL% 为正常肺区域百分比；GGO%为磨玻璃密度区域百分比；F%为纤维化区域百分比；AA%为异常病变区域百分比；HAA为高衰减区；MLD为平均肺密度；SD为标准差； Kurtosis为峰值； Skewness为偏度。
下载: 导出CSV
表 4 定量CT指标区分对照组与CTD-ILD的ROC曲线分析结果
Table 4 ROC curve analysis of quantitative CT metrics for differentiating control groups from CTD-ILD patients
项目 AUC P 最佳截断值 灵敏度 特异度 约登指数 NL% 0.844 ＜0.001 < 71.50 0.829 0.743 0.572 GGO% 0.815 < 0.001 > 8.350 0.771 0.752 0.524 F% 0.886 < 0.001 > 4.050 0.727 0.807 0.535 AA% 0.843 < 0.001 > 11.30 0.857 0.716 0.573 HAA 0.885 < 0.001 > 6.205 0.727 0.844 0.571 MLD 0.801 < 0.001 > −798.2 0.636 0.826 0.462 SD 0.923 < 0.001 > 191.2 0.864 0.817 0.680 Kurtosis 0.896 < 0.001 < 11.74 0.818 0.706 0.525 Skewness 0.889 < 0.001 < 2.795 0.727 0.817 0.544 注：NL%为正常肺区域百分比；GGO%为磨玻璃密度区域百分比；F%为纤维化区域百分比；AA%为异常病变区域百分比；HAA为高衰减区；MLD为平均肺密度；SD为标准差； Kurtosis为峰值； Skewness为偏度。
下载: 导出CSV
表 5 定量CT指标区分CTD-ILA与CTD-ILD的ROC曲线分析结果
Table 5 ROC curve analysis of quantitative CT metrics for differentiating CTD-ILA from CTD-ILD
项目 AUC P 最佳截断值 灵敏度 特异度 约登指数 NL% 0.600 0.074 < 63.50 0.379 0.788 0.167 GGO% 0.544 0.435 > 12.10 0.536 0.576 0.112 F% 0.617 0.037 > 5.450 0.650 0.576 0.226 AA% 0.574 0.187 > 16.85 0.600 0.576 0.176 HAA 0.585 0.128 > 10.06 0.486 0.727 0.213 MLD 0.568 0.224 > −758.5 0.429 0.758 0.186 SD 0.649 0.008 > 219.1 0.529 0.758 0.286 Kurtosis 0.638 0.014 < 5.095 0.479 0.849 0.327 Skewness 0.614 0.042 < 1.932 0.364 0.879 0.243 注：NL%为正常肺区域百分比；GGO%为磨玻璃密度区域百分比；F%为纤维化区域百分比；AA%为异常病变区域百分比；HAA为高衰减区；MLD为平均肺密度；SD为标准差； Kurtosis为峰值； Skewness为偏度。
下载: 导出CSV
表 6 定量CT指标预测ILA与ILD多因素多元logistic回归结果
Table 6 Multivariate logistic regression analysis of quantitative CT metrics in predicting ILA vs. ILD
项目 β BE wald P OR 95% CI 下限 上限 ILA F% 0.620 0.225 7.629 0.006 1.859 1.197 2.887 GGO% −0.302 0.098 9.546 0.002 0.739 0.610 0.895 SD 0.015 0.006 6.784 0.009 1.016 1.004 1.027 Kurtosis −0.370 0.069 28.727 0.000 0.691 0.603 0.791 ILD F% 0.854 0.209 16.666 0.000 2.349 1.559 3.540 GGO% −0.454 0.092 24.385 0.000 0.635 0.530 0.760 SD 0.026 0.005 23.855 0.000 1.026 1.016 1.037 Kurtosis −0.439 0.062 50.962 0.000 0.645 0.571 0.727 注：GGO%为磨玻璃密度区域百分比；F%为纤维化区域百分比；SD为标准差； Kurtosis为峰值。
下载: 导出CSV
-
[1] TOMASSETTI S, POLETTI V, RAVAGLIA C, et al. Incidental discovery of interstitial lung disease: Diagnostic approach, surveillance and perspectives[J]. European Respiratory Review, 2022, 31(164): 210206. DOI: 10.1183/16000617.0206-2021.
[2] HATABU H, HUNNINGHAKE G M, RICHELDI L, et al. Interstitial lung abnormalities detected incidentally on CT: Position paper from the Fleischner Society[J]. The Lancet Respiratory Medicine, 2020, 8(7): 726-737. DOI: 10.1016/S2213-2600(20)30168-5.
[3] GARCíA MULLOR M M, ARENAS-JIMéNEZ J J, UREñA VACAS A, et al. Prevalence and prognostic meaning of interstitial lung abnormalities in remote CT scans of patients with interstitial lung disease treated with antifibrotic therapy[J]. Radiología (English Edition), 2024, 66: S10-S23. DOI: 10.1016/j.rxeng.2023.03.006.
[4] SEOK J, PARK S, YOON E C, et al. Clinical outcomes of interstitial lung abnormalities: A systematic review and meta-analysis[J]. Scientific Reports, 2024, 14(1): 7330. DOI: 10.1038/s41598-024-57831-3.
[5] AXELSSON G T, PUTMAN R K, ASPELUND T, et al. The associations of interstitial lung abnormalities with cancer diagnoses and mortality[J]. European Respiratory Journal, 2020, 56(6): 1902154. DOI: 10.1183/13993003.02154-2019.
[6] DONG H, JULIEN P J, DEMORUELLE M K, et al. Interstitial lung abnormalities in patients with early rheumatoid arthritis: A pilot study evaluating prevalence and progression[J]. European Journal of Rheumatology, 2018, 6(4): 193-198. DOI: 10.5152/eurjrheum.2019.19044.
[7] JEE A S, SHEEHY R, HOPKINS P, et al. Diagnosis and management of connective tissue disease‐associated interstitial lung disease in Australia and New Zealand: A position statement from the Thoracic Society of Australia and New Zealand[J]. Respirology, 2021, 26(1): 23-51. DOI: 10.1111/resp.13977.
[8] HU Z, WANG H, HUANG J, et al. Cardiovascular disease in connective tissue disease-associated interstitial lung disease: A systematic review and meta-analysis of observational studies[J]. Autoimmunity Reviews, 2024, 23(10): 103614. DOI: 10.1016/j.autrev.2024.103614.
[9] JEGANATHAN N, SATHANANTHAN M. Connective tissue disease-related interstitial lung disease: Prevalence, patterns, predictors, prognosis, and treatment[J]. Lung, 2020, 198(5): 735-759. DOI: 10.1007/s00408-020-00383-w.
[10] SPAGNOLO P, RYERSON C J, PUTMAN R, et al. Early diagnosis of fibrotic interstitial lung disease: Challenges and opportunities[J]. The Lancet Respiratory Medicine, 2021, 9(9): 1065-1076. DOI: 10.1016/S2213-2600(21)00017-5.
[11] PRITCHARD D, ADEGUNSOYE A, LAFOND E, et al. Diagnostic test interpretation and referral delay in patients with interstitial lung disease[J]. Respiratory Research, 2019, 20(1): 253. DOI: 10.1186/s12931-019-1228-2.
[12] CANO-JIMéNEZ E, VáZQUEZ RODRíGUEZ T, MARTíN-ROBLES I, et al. Diagnostic delay of associated interstitial lung disease increases mortality in rheumatoid arthritis[J]. Scientific Reports, 2021, 11(1): 9184. DOI: 10.1038/s41598-021-88734-2.
[13] PETNAK T, LERTJITBANJONG P, THONGPRAYOON C, et al. Impact of antifibrotic therapy on mortality and acute exacerbation in idiopathic pulmonary fibrosis[J]. Chest, 2021, 160(5): 1751-1763. DOI: 10.1016/j.chest.2021.06.049.
[14] GHAZIPURA M, MAMMEN M J, HERMAN D D, et al. Nintedanib in progressive pulmonary fibrosis: A systematic review and meta-analysis[J]. Annals of the American Thoracic Society, 2022, 19(6): 1040-1049. DOI: 10.1513/AnnalsATS.202103-343OC.
[15] DUBEY S, WOODHEAD F. Survival differences in rheumatoid arthritis interstitial lung disease and idiopathic pulmonary fibrosis may be explained by delays in presentation: Results from multivariate analysis in a monocentric UK study[J]. Rheumatology International, 2023, 44(1): 99-105. DOI: 10.1007/s00296-023-05505-0.
[16] HEWITT R J, BARTLETT E C, GANATRA R, et al. Lung cancer screening provides an opportunity for early diagnosis and treatment of interstitial lung disease[J]. Thorax, 2022, 77(11): 1149-1151. DOI: 10.1136/thorax-2022-219068.
[17] GUIOT J, MIEDEMA J, CORDEIRO A, et al. Practical guidance for the early recognition and follow-up of patients with connective tissue disease-related interstitial lung disease[J]. Autoimmunity Reviews, 2024, 23(6): 103582. DOI: 10.1016/j.autrev.2024.103582.
[18] KIM M S, CHOE J, HWANG H J, et al. Interstitial lung abnormalities (ILA) on routine chest CT: Comparison of radiologists’ visual evaluation and automated quantification[J]. European Journal of Radiology, 2022, 157: 110564. DOI: 10.1016/j.ejrad.2022.110564.
[19] CHAE K J, JIN G Y, GOO J M, et al. Interstitial lung abnormalities: What radiologists should know[J]. Korean Journal of Radiology, 2021, 22(3): 454. DOI: 10.3348/kjr.2020.0191.
[20] 杜雯娟, 赵祥博, 赵海峰, 等. 肺间质异常CT研究进展[J]. 生物医学工程与临床, 2025, 29(1): 129-133. DOI: 10.13339/j.cnki.sglc.20241220.009. DU W J, ZHAO X B, ZHAO H F, et al. Advances of computed tomography in interstitial lung abnormalities[J]. Biomedical Engineering and Clinical Medicine, 2025, 29(1): 129-133. DOI: 10.13339/j.cnki.sglc.20241220.009. (in Chinese).
[21] ALETAHA D, NEOGI T, SILMAN A J, et al. 2010 Rheumatoid arthritis classification criteria: An American College of Rheumatology/European league against rheumatism collaborative initiative[J]. Annals of the Rheumatic Diseases, 2010, 69(9): 1580-1588. DOI: 10.1136/ard.2010.138461.
[22] Van Den HOOGEN F, KHANNA D, FRANSEN J, et al. 2013 classification criteria for systemic sclerosis: An American college of rheumatology/European league against rheumatism collaborative initiative[J]. Annals of the Rheumatic Diseases, 2013, 72(11): 1747-1755. DOI: 10.1136/annrheumdis-2013-204424.
[23] LUNDBERG I E, TJäRNLUND A, BOTTAI M, et al. 2017 European league against rheumatism/American college of rheumatology classification criteria for adult and juvenile idiopathic inflammatory myopathies and their major subgroups[J]. Arthritis & Rheumatology, 2017, 69(12): 2271-2282. DOI: 10.1002/art.40320.
[24] ARINGER M, COSTENBADER K, DAIKH D, et al. 2019 European league against rheumatism/American college of rheumatology classification criteria for systemic lupus erythematosus[J]. Arthritis & Rheumatology, 2019, 71(9): 1400-1412. DOI: 10.1002/art.40930.
[25] SUPPIAH R, ROBSON J C, GRAYSON P C, et al. 2022 American college of rheumatology/European alliance of associations for rheumatology classification criteria for microscopic polyangiitis[J]. Annals of the Rheumatic Diseases, 2022, 81(3): 321-326. DOI: 10.1136/annrheumdis-2021-221796.
[26] SHIBOSKI C H, SHIBOSKI S C, SEROR R, et al. 2016 American college of rheumatology/European league against rheumatism classification criteria for primary sjögren’s syndrome: A consensus and data-driven methodology involving three international patient cohorts[J]. Arthritis & Rheumatology, 2017, 69(1): 35-45. DOI: 10.1002/art.39859.
[27] TANAKA Y, KUWANA M, FUJII T, et al. 2019 Diagnostic criteria for mixed connective tissue disease (MCTD): From the Japan research committee of the ministry of health, labor, and welfare for systemic autoimmune diseases[J]. Modern Rheumatology, 2021, 31(1): 29-33. DOI: 10.1080/14397595.2019.1709944.
[28] TRAVIS W D, COSTABEL U, HANSELL D M, et al. An official American thoracic society/European respiratory society statement: Update of the international multidisciplinary classification of the idiopathic interstitial pneumonias[J]. American Journal of Respiratory and Critical Care Medicine, 2013, 188(6): 733-748. DOI: 10.1164/rccm.201308-1483ST.
[29] WIJSENBEEK M, SUZUKI A, MAHER T M. Interstitial lung diseases[J]. The Lancet, 2022, 400(10354): 769-786. DOI: 10.1016/S0140-6736(22)01052-2.
[30] FISCHER A, BOIS R D U. Interstitial lung disease in connective tissue disorders[J]. The Lancet, 2012, 380(9842): 689-698. DOI: 10.1016/S0140-6736(12)61079-4.
[31] AHN Y, LEE S M, CHOI S, et al. Automated CT quantification of interstitial lung abnormality and interstitial lung disease according to the Fleischner Society in patients with resectable lung cancer: Prognostic significance[J]. European Radiology, 2023, 33(11): 8251-8262. DOI: 10.1007/s00330-023-09783-x.
[32] 杨凯, 张静平, 何立宇, 等. 基于定量CT评估多发性肌炎/皮肌炎相关间质性肺病患者肺部改变[J]. 中国临床医学影像杂志, 2024, 35(10): 694-699. YANG K, ZHANG J P, HE L Y, et al. Evaluation of pulmonary changes in patients with polymyositis/dermatomyositis-associated interstitial lung disease based on quantitative CT[J]. Journal of China Clinic Medical Imaging, 2024, 35(10): 694-699. (in Chinese).
[33] ZHANG H, LI X, ZHANG X, et al. Quantitative CT analysis of idiopathic pulmonary fibrosis and correlation with lung function study[J]. BMC Pulmonary Medicine, 2024, 24(1): 437. DOI: 10.1186/s12890-024-03254-9.
[34] JOHANNSON K A, CHAUDHURI N, ADEGUNSOYE A, et al. Treatment of fibrotic interstitial lung disease: Current approaches and future directions[J]. The Lancet, 2021, 398(10309): 1450-1460. DOI: 10.1016/S0140-6736(21)01826-2.
[35] 马震忠, 盛亚丹, 杨凯, 等. 皮肌炎/多发性肌炎相关间质性肺病高分辨率CT特征[J]. CT理论与应用研究(中英文), 2024, 33(4): 497-502. DOI: 10.15953/j.ctta.2023.131. MA Z Z, SHENG Y D, YANG K, et al. HRCT features of dermatomyositis-/polymyositis- associated interstitial lung disease[J]. CT Theory and Applications, 2024, 33(4): 497-502. DOI: 10.15953/j.ctta.2023.131. (in Chinese).
[36] 徐光兴, 俞咏梅 徐亮, 等. 皮肌炎/多发性肌炎并发间质性肺病的CT定量分析与肺功能的相关性研究[J]. 放射学实践, 2023, 38(5): 565-570. XU G X, YU Y M, XU L, et al. Correlation between CT quantitative analysis and pulmonary function of interstitial lung disease in derma-tomyositis/polymyositis[J]. Radiologic Practice, 2023, 38(5): 565-570. (in Chinese).
[37] GUISADO-VASCO P, SILVA M, DUARTE-MILLÁN M A, et al. Quantitative assessment of interstitial lung disease in Sjögren’s syndrome[J]. PLoS One, 2019, 14(11): e0224772. doi: 10.1371/journal.pone.0224772 GUISADO-VASCO P, SILVA M, DUARTE-MILLÁN M A, et al. Quantitative assessment of interstitial lung disease in Sjögren’s syndrome[J]. PLoS One, 2019, 14(11): e0224772. DOI: 10.1371/journal.pone.0224772.
[38] UFUK F, DEMIRCI M, ALTINISIK G. Quantitative computed tomography assessment for systemic sclerosis–related interstitial lung disease: Comparison of different methods[J]. European Radiology, 2020, 30(8): 4369-4380. DOI: 10.1007/s00330-020-06772-2.
[39] UFUK F, DEMIRCI M, ALTINISIK G, et al. Quantitative analysis of Sjogren’s syndrome related interstitial lung disease with different methods[J]. European Journal of Radiology, 2020, 128: 109030. DOI: 10.1016/j.ejrad.2020.109030.
[40] ALEVIZOS M K, DANOFF S K, PAPPAS D A, et al. Assessing predictors of rheumatoid arthritis-associated interstitial lung disease using quantitative lung densitometry[J]. Rheumatology, 2022, 61(7): 2792-2804. DOI: 10.1093/rheumatology/keab828.
[41] CHOI B, KAWUT S M, RAGHU G, et al. Regional distribution of high-attenuation areas on chest computed tomography in the multi-ethnic Study of atherosclerosis[J/OL]. European Respiratory Journal Open Research, 2020, 6(1). [2024-10-16]. https://openres.ersjournals.com/content/6/1/00115-2019. DOI: 10.1183/23120541.00115-2019.
[42] HASAN D, IMAM H, MEGALLY H, et al. The qualitative and quantitative high-resolution computed tomography in the evaluation of interstitial lung diseases[J]. Egyptian Journal of Radiology and Nuclear Medicine, 2020, 51(1): 135. DOI: 10.1186/s43055-020-00254-7.
[43] SHIRAISHI Y, TANABE N, SAKAMOTO R, et al. Longitudinal assessment of interstitial lung abnormalities on CT in patients with COPD using artificial intelligence-based segmentation: A prospective observational study[J]. BMC Pulmonary Medicine, 2024, 24(1): 200. DOI: 10.1186/s12890-024-03002-z.
计量
- 文章访问数: 99
- HTML全文浏览量: 13
- PDF下载量: 11
