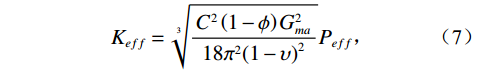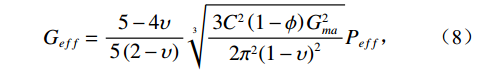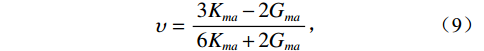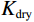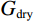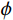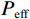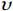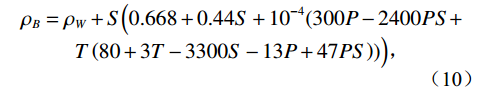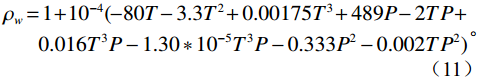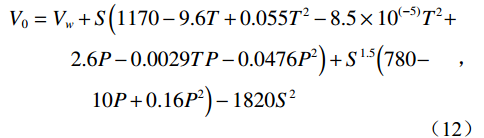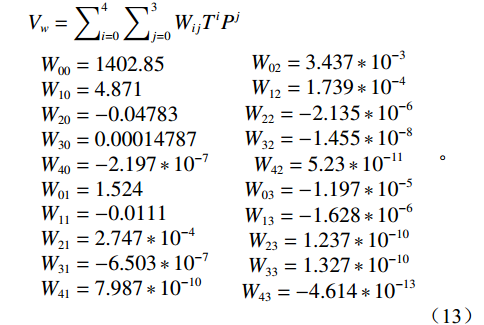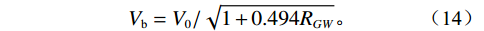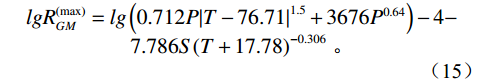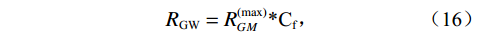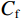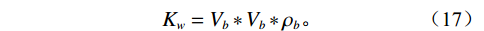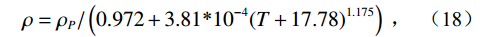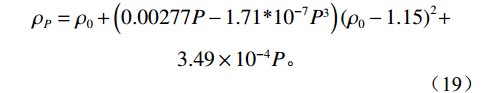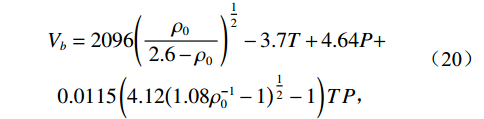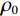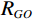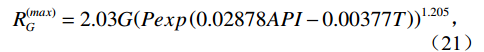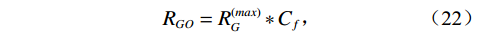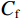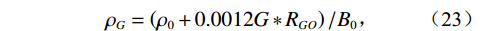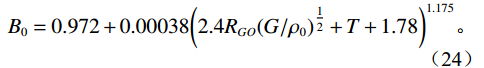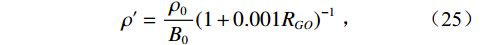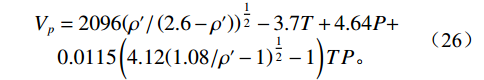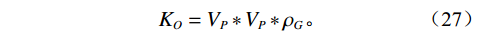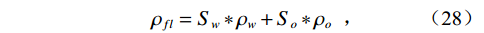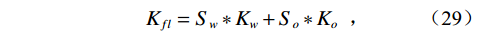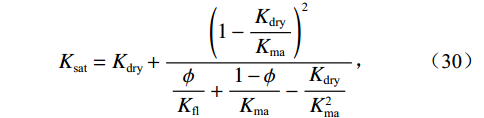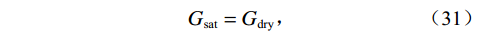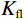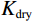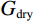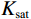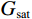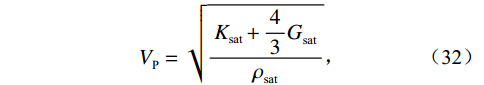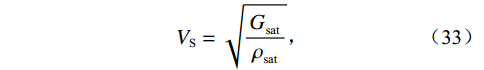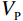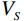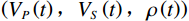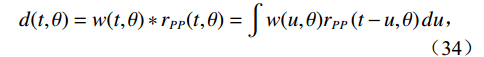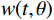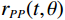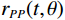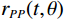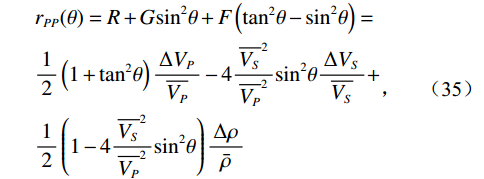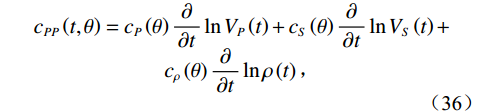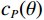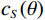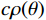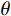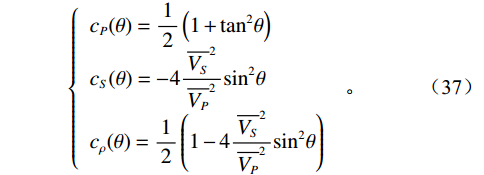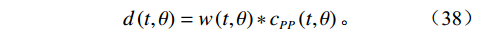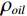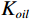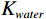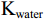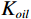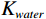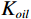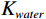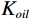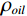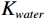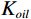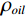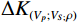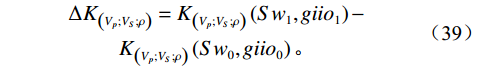Turbidite Sandstone Miscible Rock Physical Modeling and Time-lapse Seismic Forward Modeling Analysis
-
摘要:
深水浊积砂岩表现为高孔隙度、高渗透率，对油气生产和二氧化碳封存具有重要意义。在英国北海油田以及北美洲圭亚那油田深水浊积砂岩储层，开展了大量的时移地震开采开发工作。由于浊积砂岩的高孔隙度与低骨架模量特征，他们是开展时移地震的理想储层。较高的孔隙度，导致储层内流体的模量变化会对储层的弹性参数造成较大的影响，在实际油藏开采过程中，尤其是在注入流体的过程中，由于较高的孔隙压力，往往会出现混相的情况，气体会溶解于地层水和石油中进而导致流体的体积模量及密度发生变化。在时移地震剖面上引起干扰。因此，明确流体混相引起的储层弹性参数变化显得尤为重要。构建考虑流体混相的浊积砂岩储层地震岩石物理模型，建立浊积砂岩物性参数（孔隙度、饱和度）、混相流体参数以及地层压力与弹性参数（纵波速度、横波速度）之间的定量关系，为浊积砂岩的地震响应特征分析、储层预测、流体识别及勘探开发提供理论模型与技术支持。
Abstract:Gas injection technology enhances oil recovery by maintaining reservoir pressure and improving displacement efficiency. In deepwater turbidite sandstone reservoirs (characterized by high porosity, permeability, and pore pressure), fluid injection alters the elastic properties through gas dissolution in formation fluids, thereby affecting the accuracy of time-lapse seismic monitoring. This study established a rock physics model linking reservoir parameters (porosity and saturation), fluid mixing effects, and elastic moduli (P/S-wave velocities) in turbidite systems, providing a theoretical foundation for seismic response analysis and fluid identification in offshore exploration, particularly in North Sea and Guyana oilfields.
-
Keywords:
- turbidity sandstone /
- petrophysics /
- fluid miscibility /
- AVO Forward Simulation
-
地震岩石物理建模是连接地震弹性参数和储层物性参数的桥梁，为将弹性参数转化为物性参数奠定理论基础。通过地震岩石物理可以实现地震信息到岩性信息的转变或者定量化它们之间的不确定性关系。与致密砂岩气储层具有低孔、低渗的特征，发育裂缝的特征不同[1]。本文所研究的圭亚那深水浊积砂岩储层埋深较深，具有较高的孔隙压力与岩石敏感性。是开展时移地震技术的优势储层。且在实际的开采过程中，存在油气水混相的情况。气驱是提高油藏产量的一种重要采油手段，在油藏开采过程中被广泛应用。其优点是在开采过程中能使油藏始终保持高压条件。且在气体与石油接触并发生混相后，气体溶解于石油，除了会使原油的物性发生变化，还会改变原油体积且增强地层的弹性能量，注入气与原油会发生相间传质，使原油的粘度降低，增强原油在地层中的流动能力。提高原油的驱动效率。根据Stalkup[2]的定义，储层流体混相是指注入流体与储层流体在特定条件下达到无界面（即零界面张力）的状态，从而实现完全混合的驱替过程。换言之就是注入气体完全溶解于储层流体。Sequeira[3]介绍了气体溶解于流体的微观机理：气驱油时的蒸气化和冷凝/蒸气化机制，通过多接触过程逐渐提取原油中的轻质烃（C5-C30），同时自身冷凝将中间组分转移到油相，在一定的温度与压力条件下最终实现完全混合。
关于混相的研究已有大量成果。Coats[4]提出，根据界面张力的大小可以判断油藏是否为混相状态。常见的确定界面张力的方法包括经验公式（如Macleod-Sugden关联式）和实验测量。Todd等[5]通过一维细管实验，探讨了不同压力条件下的驱油效率，基于效率拐点来确定最小混相压力（MMP）。Srivastava[6]则通过数值模拟模型，研究了注采井间的压力分布及混相状态的演变，指出MMP是设计中的关键参数之一。刘玉章等[7]对影响气驱油混相条件的主要因素分析研究后认为岩石孔隙特征、地层压力以及注入流体的多少对多孔介质中最小混相压力有显著影响。在较小的压力范围内平均地层压力较低的油藏测量的最小混相压力值也较低。冉新权等[8]针对超低渗透油藏岩性致密、孔喉细微、物性差，注水开发提高单井产量难度大，提出气驱可降低注入介质与地层原油之间的界面张力和毛管阻力，提高微观驱油效率。吴忠宝等[9]对油气混相驱油机理和影响因素进行了系统研究，提出注入气发生混相提升采收率的原因是注入气溶解于原油中发生混相，增加了油藏的流动性，进而提高了油藏的采收率。在单一的注气井上，其产量往往可以增加一倍，且最终采收率也有所提高。Ahmadi等[10]通过岩心替换实验装置，研究了在驱替压力逐步增加的过程中，驱油效率的变化规律，将最小混相压力的85%定义为近混相压力。王锐等[11]认为气驱以其良好的注入性和驱油效果，成为低渗透油藏提高采收率的主要方法之一。一般注入气表现为较低的压力与温度，其在地层中处于超临界状态。因此在原油中就表现为高溶解性与高萃取性，较低的界面张力使其容易发生混相作用。注入气后原油粘度下降，且弹性能量发生改变。经实验室实验结果可知，当压力大于30 MPa时，混相程度可到达100%且在高压条件下，混相程度高，采收率高。袁舟等[12]基于相平衡理论和油藏数值模拟技术，研究了气驱过程中油藏流体的组分分布及界面张力的特征，提出了细化混相状态及波及系数的研究方法。他将混相状态进一步细分为完全混相、部分混相、近混相和非混相。并给出了区分标准。朱清源等[13]基于格子玻尔兹曼方法（LBM）揭示了驱动压力差影响气藏的微观分布,研究表明注气发生混相会使微观驱气效率达到42%~94%；且在含水饱和度较低区域，高压驱替效果更为显著。杨勇等[14]通过室内实验和现场实践发现在气驱过程中，地层压力在最小混相压力的1.2倍以上时，原油中的中重质成分混相能力显著提高，在较小孔隙中的原油流动性得到改善，气驱前缘及体积扩大，气驱效果更佳。本文主要研究是深水浊积砂岩，其储层表现为高压，故而研究主要是在高压条件下的的完全混相状态。
1. 浊积砂岩岩石物理模型构建及正演模拟
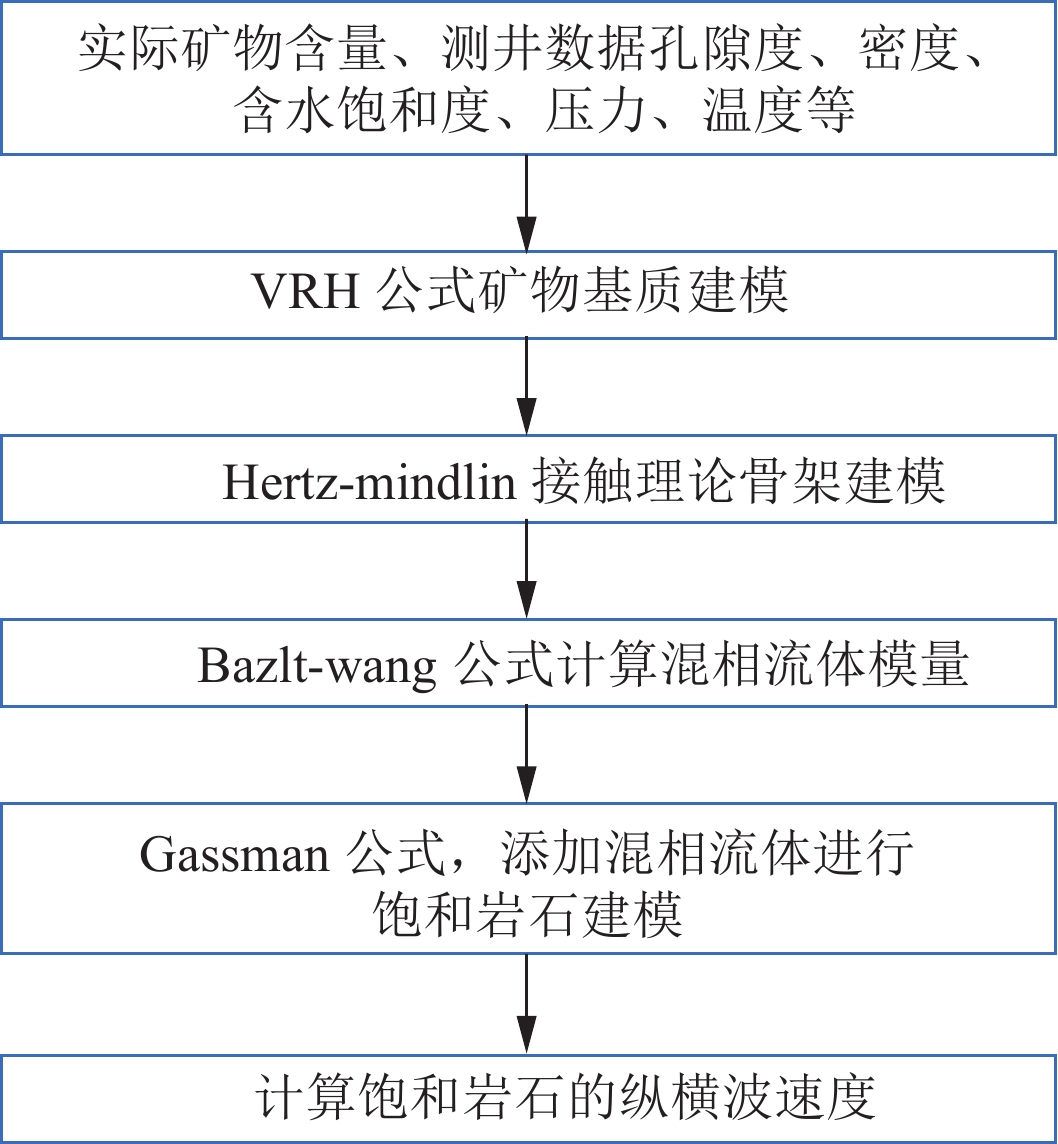
在实际油藏开采过程中，尤其是在注气开采过程中，往往会出现油气水三者混相的情况，气体会溶解于地层水和石油进而导致流体的体积模量及密度发生变化。常规岩石物理模型的构建步骤[15]包括使用计算矿物模量，计算流体模量，然后计算干岩石骨架，最后用Gassmann方程计算饱和流体的弹性模量。贾凌云等[16]总结了前人流体体积模量的各种计算方法，包括有Wood模型和Patchy模型。Wood模型适用于高孔高渗储层，假设流体均匀混合；而Patchy模型处理非均匀混相的情况，比如部分饱和的储层。但现有的理论方法对于流体混相的特殊物理情况难以刻画。根据Stalkup对混相的定义，流体混相是指注入气体完全溶解于流体，这不满足常规计算流体体积模量时均匀混合与非均匀混合的假设，故而利用Batzle-wang针对不同含气量的活油与含气地层水的体积模量计算公式得到混相流体模量，速度与密度进而计算饱和岩石的纵横波速度与密度。岩石物理建模首先用VRH公式构建岩石基质模型，利用Hertz-Mindlin接触理论计算骨架模型。然后采用流体模量计算公式计算不同含气量的储层各流体参数，进而使用Gassmann公式进行饱和岩石建模以及流体替换[17]。
具体步骤如下。
1.1 岩石基质建模
以实验数据和测井资料为基础，已知基质矿物组分与体积含量。且给定初始的岩石矿物模量，应用Voigt-Reuss-Hill平均方法计算岩石基质的体积模量和剪切模量。岩石基质建模：
$$ {K_{{\text{ma}}}} = \frac{1}{2}\left( {{K_V} + {K_R}} \right)\text{，} $$ (1) $$ {K_V} = V_{{\text{shale}}}^{}{K_{{\text{shale}}}} + \left( {1 - V_{{\text{shale}}}^{}} \right){K_{{\text{sand}}}}\text{，} $$ (2) $$ \frac{1}{{{K_R}}} = \frac{{V_{{\text{shale}}}^{}}}{{{K_{{\text{shale}}}}}} + \frac{{1 - V_{{\text{shale}}}^{}}}{{{K_{{\text{sand}}}}}}\text{，} $$ (3) $$ {G_{ma}} = \frac{1}{2}\left( {{G_V} + {G_R}} \right)\text{，} $$ (4) $$ {G_V} = V_{{\text{shale}}}^{}{G_{{\text{shale}}}} + \left( {1 - V_{{\text{shale}}}^{}} \right){G_{{\text{sand}}}}\text{，} $$ (5) $$ \frac{1}{{{G_R}}} = \frac{{V_{{\text{shale}}}^{}}}{{{G_{{\text{shale}}}}}} + \frac{{1 - V_{{\text{shale}}}^{}}}{{{G_{{\text{sand}}}}}}\text{，} $$ (6) 式中，
${V_{{\text{shale}}}}$ 为泥质含量；${K_{{\text{ma}}}}$ ，${K_{{\text{sand}}}}$ ，${K_{{\text{shale}}}}$ 分别是岩石基质以及砂质矿物组分和泥质矿物组分的体积模量；${G_{{\text{ma}}}}$ ，${G_{{\text{sand}}}}$ ，${G_{{\text{shale}}}}$ 分别是基质以及砂质矿物组分和泥质矿物组分的剪切模量。1.2 岩石骨架建模
浊积砂岩利用Hertz-Mindlin接触理论来计算岩石骨架的弹性模量，该理论是将岩石等效为一些颗粒的堆积，利用实际的测井数据验证该骨架模型的适用性，如图1所示，发现利用该模型中的下边界（软砂）能较好的表征纵波速度随孔隙度的变化。故而认为该模型对浊积砂岩是适用的。
![]()
图 1 测井数据实际骨架边界验证图Figure 1. Validation Diagram of Actual Skeleton Boundary from Logging Data接触模型骨架模量计算公式为：
$$ {K_{eff}} = \sqrt[3]{{\frac{{{C^2}\left( {1 - \phi } \right)G_{ma}^2}}{{18{\pi ^2}{{\left( {1 - \upsilon } \right)}^2}}}}}{P_{eff}} \text{，} $$ (7) $$ {G_{eff}} = \frac{{5 - 4\upsilon }}{{5\left( {2 - \upsilon } \right)}}\sqrt[3]{{\frac{{3{C^2}\left( {1 - \phi } \right)G_{ma}^2}}{{2{\pi ^2}{{\left( {1 - \upsilon } \right)}^2}}}}}{P_{eff}} \text{，} $$ (8) $$ \upsilon = \frac{{3{K_{ma}} - 2{G_{ma}}}}{{6{K_{ma}} + 2{G_{ma}}}}\text{，} $$ (9) 式中，
${K_{{\text{dry}}}}$ 和${G_{{\text{dry}}}}$ 分别为干岩石骨架的体积模量和剪切模量，$\phi $ 为孔隙度,${P_{{\text{eff}}}}$ 为有效压力，$ C $ 为配位数，一般为8~9，$ \upsilon $ 为颗粒矿物的泊松比。1.3 考虑混相的饱和岩石建模
模型的压力利用Batzle-Wang流体模型考虑压力和温度变化对流体的影响，针对油气水三流体混相特征，分别计算油和地层水以及含气石油与含气地层水的体积模量和密度。
1.3.1 含气地层水
地层水密度：
$$ \begin{array}{c}{\rho _B} = {\rho _W} + S\Big( 0.668 + 0.44S + {{10}^{ - 4}}( 300P - 2400PS + \\ T\left( {80 + 3T - 3300S - 13P + 47PS} \right) ) \Big)\text{，}\end{array} $$ (10) 其中，P为孔隙压力，T为温度，S为盐度。
纯水密度：
$$ \begin{gathered} {\rho _w} = 1 + {10^{ - 4}}( - 80T - 3.3{T^2} + 0.00175{T^3} + 489P - 2TP + \\ \quad\;\;\; 0.016{T^3}P - 1.30*{10^{ - 5}}{T^3}P - 0.333{P^2} - 0.002T{P^2}) \\ \end{gathered} 。 $$ (11) 地层水声波速度：
$$ \begin{gathered} {V_0} = {V_w} + S\Big( 1170 - 9.6T + 0.055{T^2} - 8.5 \times {{10}^{( - 5)}}{T^2} + \\ \qquad\quad 2.6P - 0.0029TP - 0.0476{P^2} \Big) + {S^{1.5}}\Big( 780 - \\ \qquad\qquad 10P + 0.16{P^2} \Big) - 1820{S^2} \\ \end{gathered} \text{，} $$ (12) 其中，
$$ \begin{gathered} {V_w} = \sum\nolimits_{i = 0}^4 {\sum\nolimits_{j = 0}^3 {{W_{ij}}{T^i}{P^j}} } \\ \begin{array}{*{20}{c}} \begin{gathered} {W_{00}} = 1402.85 \\ {W_{10}} = 4.871 \\ {W_{20}} = - 0.04783 \\ {W_{30}} = 0.00014787 \\ {W_{40}} = - 2.197*{10^{ - 7}} \\ {W_{01}} = 1.524 \\ {W_{11}} = - 0.0111 \\ {W_{21}} = 2.747*{10^{ - 4}} \\ {W_{31}} = - 6.503*{10^{ - 7}} \\ {W_{41}} = 7.987*{10^{ - 10}} \\ \end{gathered} &{\begin{array}{*{20}{c}} {{W_{02}} = 3.437 * {{10}^{ - 3}}} \\ {{W_{12}} = 1.739 * {{10}^{ - 4}}} \\ {{W_{22}} = - 2.135 * {{10}^{ - 6}}} \\ {{W_{32}} = - 1.455 * {{10}^{ - 8}}} \\ {{W_{42}} = 5.23 * {{10}^{ - 11}}} \\ {{W_{03}} = - 1.197 * {{10}^{ - 5}}} \\ {{W_{13}} = - 1.628 * {{10}^{ - 6}}} \\ {{W_{23}} = 1.237 * {{10}^{ - 10}}} \\ {{W_{33}} = 1.327 * {{10}^{ - 10}}} \\ {{W_{43}} = - 4.614 * {{10}^{ - 13}}} \end{array}} \end{array} \\ \end{gathered} 。 $$ (13) 气体溶解于地层水中，主要其声波速度发生改变，不同含气量情况下地层水的速度：
$$ {V_{\text{b}}} = {V_0}/\sqrt {1 + 0.494{R_{GW}}} 。 $$ (14) 气体在地层水中的最大溶解量：
$$ \begin{array}{c}lgR_{GM}^{(\max )} = lg\left( {0.712P{{\left| {T - 76.71} \right|}^{1.5}} + 3676{P^{0.64}}} \right) - 4 - \\ 7.786S{\left( {T + 17.78} \right)^{ - 0.306}}{\text{ }} 。 \end{array}$$ (15) 在实际情况中，我们用最大溶解量乘以地层水含气量来表示不同溶解气体的各种含气地层水的情况：
$$ {R_{{\text{GW}}}} = R_{GM}^{(\max )}{\text{*}}{{\text{C}}_{\text{f}}}\text{，} $$ (16) ${C_{\text{f}}}$ 为地层水含气量，为0~1的常数。至于地层水的密度，实验数据较少，但多数认为密度几乎与溶解气的含量无关。含气地层水的体积模量表示为：
$$ {K_w} = {V_b}*{V_b}*{\rho _b} 。 $$ (17) 1.3.2 含气石油
定义在常温标准大气压条件下，不溶解气体的石油称为死油，表征其参数如下：
密度是一个与压力及温度有关的函数：
$$ \rho = {\rho _P}/\left( {0.972 + 3.81{\text{*}}{{10}^{ - 4}}{{\left( {T + 17.78} \right)}^{1.175}}} \right){\text{ }} \text{，} $$ (18) 其中固定压力条件下的密度表示：
$$ \begin{array}{c}{\rho _P} = {\rho _0} + \left( {0.00277P - 1.71{\text{*}}{{10}^{ - 7}}{P^3}} \right){\left( {{\rho _0} - 1.15} \right)^2} + \\ 3.49 \times {10^{ - 4}}P 。\end{array} $$ (19) 速度：
$$ \begin{array}{c}{V_b} = 2096{\left( {\displaystyle\frac{{{\rho _0}}}{{2.6 - {\rho _0}}}} \right)^{\tfrac{1}{2}}} - 3.7T + 4.64P + \\ 0.0115\left( {4.12{{\left( {1.08\rho _0^{ - 1} - 1} \right)}^{\tfrac{1}{2}}} - 1} \right)TP \text{，}\end{array} $$ (20) 其中
${\rho _0}$ 为石油密度，T为温度，P为压力。定义有气体溶解的石油为活油，气体在石油中的溶解量受压力于温度关系较大。定义气油比
${R_{GO}}$ 标准大气压力和15.6℃温度条件下释放的气体体积与剩余原油体积之比。原油中最大可溶解的气量：
$$ R_G^{(max)} = 2.03G{\left( {Pexp\left( {0.02878API - 0.00377T} \right)} \right)^{1.205}} \text{，} $$ (21) $$ {R_{GO}} = R_G^{(max)}*{C_f} \text{，} $$ (22) ${C_{\text{f}}}$ 为石油含气量，为0~1的常数。含气石油的密度：$$ {\rho _G} = \left( {{\rho _0} + 0.0012G*{R_{GO}}} \right)/{B_0} \text{，} $$ (23) $$ {B_0} = 0.972 + 0.00038{\left( {2.4{R_{GO}}{{\left( {G/{\rho _0}} \right)}^{\tfrac{1}{2}}} + T + 1.78} \right)^{1.175}} 。 $$ (24) 含气石油的速度要用准密度来计算：
$$ {\rho'} = \frac{{{\rho _0}}}{{{B_0}}}{\left( {1 + 0.001{R_{GO}}} \right)^{ - 1}}{\text{ }} \text{，} $$ (25) $$ \begin{array}{c}{V_p} = 2096{\left( {\rho '/\left( {2.6 - \rho '} \right)} \right)^{\tfrac{1}{2}}} - 3.7T + 4.64P +\\ 0.0115\left( {4.12{{\left( {1.08/\rho ' - 1} \right)}^{\tfrac{1}{2}}} - 1} \right)TP 。 \end{array}$$ (26) 活油的体积模量表示为：
$$ {K_O} = {V_P}*{V_P}*{\rho _G} 。 $$ (27) 混合流体密度为：
$$ \begin{array}{*{20}{c}} {}&{{\rho _{fl}} = {S_w}*{\rho _w} + {S_o}*{\rho _o}} \end{array} \text{，} $$ (28) 混合流体体积模量为非均匀混合：
$$ \begin{array}{*{20}{c}} {}&{{K_{fl}} = {S_w}*{K_w} + {S_o}*{K_o}} \end{array} \text{，} $$ (29) 应用Gassmann方程，计算饱和岩石的体积模量和剪切模量：
$$ {K_{{\text{sat}}}} = {K_{{\text{dry}}}} + \displaystyle\frac{{{{\left( {1 - \displaystyle\frac{{{K_{{\text{dry}}}}}}{{{K_{{\text{ma}}}}}}} \right)}^2}}}{{\displaystyle\frac{\phi }{{{K_{{\text{fl}}}}}} + \displaystyle\frac{{1 - \phi }}{{{K_{{\text{ma}}}}}} - \displaystyle\frac{{{K_{{\text{dry}}}}}}{{K_{{\text{ma}}}^{\text{2}}}}}}\text{，} $$ (30) $$ {G_{{\text{sat}}}} = {G_{{\text{dry}}}}\text{，} $$ (31) 式中，
${K_{{\text{fl}}}}$ 为混合流体体积模量，${K_{{\text{dry}}}}$ ，${G_{{\text{dry}}}}$ 为干岩石骨架的体积模量和剪切模量；${K_{{\text{sat}}}}$ ，${G_{{\text{sat}}}}$ 为流体饱和岩石的体积模量和剪切模量。根据纵、横波速度公式，计算岩石物理流体替换后等效流体饱和岩石的纵波速度和横波速度：
$$ V_{\text{P}}^{} = \sqrt {\frac{{K_{{\text{sat}}}^{} + \displaystyle\frac{4}{3}G_{{\text{sat}}}^{}}}{{\rho _{{\text{sat}}}^{}}}} \text{，} $$ (32) $$ {V_{\text{S}}} = \sqrt {\frac{{G_{{\text{sat}}}^{}}}{{\rho _{{\text{sat}}}^{}}}} \text{，} $$ (33) 式中，
$V_{\text{P}}^{}$ 和$V_S^{}$ 分别为流体饱和岩石的纵波速度和横波速度，${\rho _{{\text{sat}}}}$ 为流体饱和岩石的密度。1.4 正演模拟
地震记录可以近似地表示为地震子波和反射系数的褶积，即层界面弹性对比的反射率大小。地震反射系数取决于地下界面上下各层的弹性特性。各向同性弹性介质完全由3个材料参数描述，例如纵波和横波速度和密度
$ \left({V}_{P}\left(t\right)，{V}_{S}\left(t\right)，\rho \left(t\right)\right) $ ，其中t为地震双向传播时间[18]。$$ d(t,\theta ) = w(t,\theta )*{r_{PP}}(t,\theta ) = \int w (u,\theta ){r_{PP}}\left( {t - u,\theta } \right)du \text{，} $$ (34) 式中
$w(t,\theta )$ 为子波，${r_{PP}}(t,\theta )$ 为反射系数。反射系数${r_{PP}}(t,\theta )$ 可以使用Zoeppritz方程精确计算。作为时间的函数t和反射角度θ或可以使用线性近似准确近似小反射角度和小变化的弹性在界面处反射系数${r_{PP}}(t,\theta )$ 的近似为:$$ \begin{gathered} {r_{PP}}(\theta ) = R + G{\sin ^2}\theta + F\left( {{{\tan }^2}\theta - {{\sin }^2}\theta } \right) = \\ \frac{1}{2}\left( {1 + {{\tan }^2}\theta } \right)\frac{{\Delta {V_P}}}{{\overline {{V_P}} }} - 4\frac{{{{\overline {{V_S}} }^2}}}{{{{\overline {{V_P}} }^2}}}{\sin ^2}\theta \frac{{\Delta {V_S}}}{{\overline {{V_S}} }} + \\ \frac{1}{2}\left( {1 - 4\frac{{{{\overline {{V_S}} }^2}}}{{{{\overline {{V_P}} }^2}}}{{\sin }^2}\theta } \right)\frac{{\Delta \rho }}{{\bar \rho }} \\ \end{gathered} \text{，} $$ (35) 其中θ是反射角，为了简化符号，省略了旅行时变量t。式（35）中的单界面反射系数可扩展为连续时间的反射率函数为：
$$ \begin{array}{c}{c_{PP}}\left( {t,\theta } \right) = {c_P}\left( \theta \right)\displaystyle\frac{\partial }{{\partial t}}\ln {V_P}\left( t \right) + {c_S}\left( \theta \right)\displaystyle\frac{\partial }{{\partial t}}\ln {V_S}\left( t \right) +\\ {c_\rho }\left( \theta \right)\displaystyle\frac{\partial }{{\partial t}}\ln \rho \left( t \right)\text{，} \end{array}$$ (36) 其中
${c_P}(\theta )$ ，${c_S}(\theta )$ 和$c\rho (\theta )$ 是依赖于反射角$ \theta $ 和平均速度的系数：$$ \left\{ {\begin{array}{*{20}{l}} {{c_P}(\theta ) = \displaystyle\frac{1}{2}\left( {1 + {{\tan }^2}\theta } \right)} \\ {{c_S}(\theta ) = - 4\displaystyle\frac{{{{\overline {{V_S}} }^2}}}{{{{\overline {{V_P}} }^2}}}{{\sin }^2}\theta } \\ {{c_\rho }(\theta ) = \displaystyle\frac{1}{2}\left( {1 - 4\frac{{{{\overline {{V_S}} }^2}}}{{{{\overline {{V_P}} }^2}}}{{\sin }^2}\theta } \right)} \end{array}} \right.{\text{ }}。 $$ (37) 因此，如果已知层的弹性性质，即纵波、横波速度和密度，则可计算地震响应：
$$ d\left( {t,\theta } \right) = w\left( {t,\theta } \right)*{c_{PP}}\left( {t,\theta } \right)。 $$ (38) 2. 实际应用
该研究区位于南美洲北部的圭亚那，毗邻委内瑞拉西北部，南部与巴西接壤，东部与苏里南相邻，东北方向与大西洋接壤。圭亚那盆地自西向东横跨圭亚那、苏里南和法属圭亚那等国家，盆地长约930 km，宽约150 km。地层沉积较为连续，泥页岩、深水浊积砂岩发育良好。区块南部浅水区与陆架交界处，断层与裂缝构成油气垂直运移的主要通道，储层主要由新生代砂岩构成；而在盆地的深水区，晚白垩世期间发育了多期次重叠的深水浊积水道体系，这些体系广泛分布，海底扇沉积具有高孔隙度和渗透性，主要通过上白垩统砂岩组合成藏。其中，Liza油田的主要储层平均孔隙度为25%，平均渗透率达到
5000 mD。同时储层表现出的高孔隙度与高渗透率使得储层对流体模量的变化较为敏感，因此，精细描述气体溶解于地层水与石油的混相现象对储层描述有重要意义。2.1 浊积砂岩储层混相岩石物理特征分析
研究工区浊积砂岩储层矿物成分主要为石英，长石，和粘土，通过实际测井数据发现，在实际注气开采过程中，出现气体不同程度的溶解于石油与地层水中。
对流体进行不同含气量的替换测试，预估各流体在不同含气情况下的体积模量与密度及速度的变化情况对岩石物理模型进行不同饱和度与不同含气量下的流体替换模拟，预测在注气开采实际过程中，流体饱和度变化与注气混相同时发生的情况。流体混相表现为气体与石油及地层水不是常规的均匀混合与非均匀混合，而是溶解于流体中，示意图如图2。
对各流体进行不同含气情况下流体速度、密度、模量的分析，进而模拟在不同含气情况下，饱和岩石纵横波速度密度变化情况[19]。由图3可知，随着流体含气量的提升，地层水速度与体积模量下降，变化量分别为0.18 km/s、0.6 GPa,含气地层水的密度不随着含气量的增加而变化。石油随着含气量的变化表现为随着含气量的增加，速度、密度、体积模量均降低，气体溶解于流体后，会导致流体速度降低，进而影响流体体积模量降低。
![]()
图 3 不同流体模量参数随含气量变化图Figure 3. Variation of different fluid modulus parameters with gas content有关混相流体的模量计算，例如国外学者Kama[20]等系统介绍了油气溶解度受到储层条件的影响，如储层压力、温度和含水量等，这些变化影响石油的体积系数和流动性，从而影响油气的开采和运输，研究发现在砂岩储层中溶解气体会降低流体密度，Konstantin等[21]提到了当液体中溶解气体时，溶解气体通过改变液体的分子间作用力和有效体积来影响流体模量，使之显著降低。这与本文结论相符，气体溶解于流体会导致流体体积模量与密度均降低，含气地层水由于溶解气含量微弱，故而密度几乎不变。
建立计算纵横波速度密度流程如图4所示：
![]()
图 4 考虑混相的浊积砂岩岩石物理模型流程图Figure 4. Flow chart of miscible turbidite sandstone rock physical mode如图5所示，蓝色曲线为模型预测结果，红色曲线为注气井（部分段）实际曲线，绿色为注气前测井数据。可以看出，该模型对于注气后储层弹性参数拟合较好。精度较高。
![]()
图 5 混相浊积砂岩岩石物理模型横波预测结果Figure 5. S-wave prediction results of miscible turbidite sandstone rock physics model针对浊积砂岩岩石物理模型进行含气量在不同流体中变化对弹性参数影响分析。使用如表1参数对模型进行验证，分析流体含气量对流体模量的影响。
表 1 混相模型参数Table 1. Mixed-phase model parameters储层参数 油藏参数 孔隙压力 69 MPa 温度 114℃ 上覆压力 95 MPa 含油饱和度 80% 泥质含量 22% 石油重量 34（API重量） 含水饱和度 20% 气体重量 0.76 孔隙度 23% 盐度 20083 ppm如图6所示，当石油含气量增加时，含气石油的密度
${\rho _{oil}}$ 会随之降低，且体积模量${K_{oil}}$ 随之降低，因此饱和岩石纵波速度随之降低；横波速度增加；当地层水含气量增加时，含气地层水的密度${\rho _{water}}$ 不变，但含气地层水的体积模量${K_{water}}$ 随之降低，故而饱和岩石纵波速度增加（微弱）几乎不变，横波速度不变。![]()
图 6 饱和岩石弹性参数随流体含气量变化图Figure 6. Variation of elastic parameters of saturated rock with gas content of fluid2.2 不同混相情况对储层影响分析
在注气开采过程中，气体会溶解于石油与含气地层水，其最大溶解量我们可计算得知，但受储层条件复杂影响下，气体溶解与石油与地层水的含量往往是复杂多变的，随着注气开采过程进行，时移地震响应受流体含气量的变化较大，因此明确不同流体含气情况对时移地震响应分析具有重要意义，现介绍三类储层流体含气情况（极限情况）：
① 气体同时溶解与石油于地层水；
② 气体大量溶解于石油，而几乎不溶解于地层水；
③气体大量溶解于地层水，而几乎不溶解于石油。
考虑含水饱和度与流体含气量共同变化时，饱和岩石的弹性参数变化有：
如图7所示第1行为气体只溶解于石油时纵横波波速度密度变化值，随着流体含气量的增加，在含水饱和度较低时纵波速度与密度降低，横波速度增加；含水饱和度变化引起的纵横波速度密度差异变大。
如图7所示第2行为气体只溶解于地层水时纵横波波速度密度变化值，随着流体含气量的增加纵波速度降低，密度与横波速度保持不变；
如图7所示第3行为气体同时溶解于地层水与石油时纵横波波速度密度变化值，随着流体含气量的增加，纵波速度降低，横波速度增加，密度降低；
纵向对比3类情况，当气体同时溶解于水和油时，含油饱和度变化引起的纵波速度变化小于气体只溶解于油时；随着石油含气量的增加，含油饱和度变化引起的纵波速度变化增加。这是因为气体同时溶解于油和水时，
${{\text{K}}_{{\text{water}}}}$ 下降，${K_{oil}}$ 也下降，油水弹性模量差异相对不变，所以含油饱和度变化引起速度差异大。气体只溶解于油时，${K_{water}}$ 不变${K_{oil}}$ 下降，油水弹性模量差异更大，所以含水饱和度变化引起速度差异更大；当气体只溶解于水时，含油饱和度变化引起的纵波速度变化小于气体同时溶解油和水。当气体同时溶解于油和水时，${K_{water}}$ 下降，${K_{oil}}$ 也下降，油水弹性模量差异相对不变，所以含油饱和度变化引起速度差异大，气体溶于水密度保持不变，${\rho _{water}}$ 不变${\rho _{oil}}$ 也下降，油水密度差异相对变大，横波速度主要受密度影响，油水密度差异相对变大。当气体只溶解于水时，${K_{water}}$ 下降${K_{oil}}$ 不变，油水弹性模量差异变小，所以含油饱和度变化引起速度差异小，${\rho _{water}}$ 不变，${\rho _{oil}}$ 不变，油水密度差异相对变小。Attia等[22]研究了气体注入储层后弹性参数的变化，纵波速度与密度降低，横波速度的微弱变化仅由密度变化引起，剪切模量保持不变，这与本文结论一致。虽然其没有具体考虑气体是否溶解于储层流体中，但气体注入导致储层流体模量变化仍有指示作用。三种情况下的弹性参数差异值随着饱和度变化与流体含气量变化如图8所示，弹性参数差异值$ \Delta {K_{({V_p};{V_{S;}}\rho )}} $ ：![]()
图 8 弹性参数差异随含水饱和度与流体含气量变化图Figure 8. Variation of elastic parameter difference with water saturation and fluid gas content$$\begin{array}{c} \Delta {K_{\left( {{V_p};{V_S};\rho } \right)}} = {K_{\left( {{V_p};{V_S};\rho } \right)}}\left( {S{w_1},gii{o_1}} \right) - \\ {K_{\left( {{V_p};{V_S};\rho } \right)}}\left( {S{w_0},gii{o_0}} \right) 。 \end{array}$$ (39) 如图8所示，①为气体大量溶解于石油而几乎不溶解于地层水；②为气体同时溶解于石油与地层水；③为气体大量溶解于地层水而几乎不溶解于石油。当气体只溶解于石油时引起的纵波速度大于气体同时溶解于地层水与石油大于气体只溶解于地层水，气体只溶解于石油时，密度差异值等于气体同时溶解于地层水和石油，大于气体只溶解于地层水，由于饱和岩石横波速度主要受密度的影响。故而其结论与密度一致，表现为气体只溶解于石油时，横波速度差异值等于气体同时溶解于地层水和石油，大于气体只溶解于地层水。
3. 正演模拟
在常规情况下，孔隙度扰动对岩石弹性性质的影响要远远高于流体饱和度[23]。但时移地震主要关注储层流体的动态变化与压力变化[24]。为了验证在实际注水注气开采过程中流体不同含气量情况下储层特征。结合实际开采情况，我们利用建立的岩石物理模型计算在注水与注气时的速度，以及储层流体不同类型溶解气体的情况建立如图的四类速度模型，进行正演模拟。针对所设计模型的厚度较薄，正演模拟采用90°相移技术。能有效避免使用零相位子波产生的干涉现象。对于90°相位子波，当层厚小于λ后，来自上下界面产生的反射波发生干涉形成对称型，当厚度很薄时，只用一个波峰或者波谷就代表了“层”。选用30 Hz雷克子波进行正演模拟[25]（图9）。
如图9所示，从上至下分别是速度模型、正演模拟记录和时移地震模拟记录，其中速度模型分为①为气体仅溶解与油；②气体仅溶解与水，③为气体同时溶解与油和水；正演模拟记录为M0时期与M1和M2时期的正演模拟结果；时移地震记录为模拟时移地震记录M1-M0与M2-M0。分析正演模拟，气体仅溶解于油时，时移地震差异最大，大于同时溶解于水和油时，大于仅溶解水时。这与岩石物理分析得到的结论一致。
4. 结论
本文从常规的岩石物理建模流程出发，总结了流体混相的微观构造成岩，对比前人各类流体体积模量的各种计算方法，难以对流体混相情况进行准确描述，故而利用Batzle-wang针对不同含气量活油与含气地层水的体积模量计算公式得到混相流体模量完成岩石物理模型，利用岩石物理模型与实际测井数据进行对比，发现使用该方法能较好的描述流体混相。且岩石物理响应特征分析与前人针对流体混相的总结规律相符。进一步验证了本文方法的准确性。之后利用岩石物理模型进行岩石物理响应分析与正演模拟分析，研究发现，随着含气量的增加，饱和岩石的纵波速度和密度降低，而横波速度增加。此外，流体含气量会影响含水饱和度在相同变化范围内引起的饱和岩石弹性参数的差异值。这对时移地震检测地下储层变化有着重要意义。在含水饱和度变化一致时，气体仅溶解于石油时的纵波速度差异值大于气体同时溶解于地层水和石油时，且均大于气体仅溶解于地层水时；气体溶解于石油时的密度差异值等于同时溶解于地层水和石油时，且均大于气体仅溶解于地层水时。由于横波速度不受流体直接影响，其变化仅由饱和岩石密度的变化引起。
-
![]()
图 1 测井数据实际骨架边界验证图
Figure 1. Validation Diagram of Actual Skeleton Boundary from Logging Data
![]()
图 3 不同流体模量参数随含气量变化图
Figure 3. Variation of different fluid modulus parameters with gas content
![]()
图 4 考虑混相的浊积砂岩岩石物理模型流程图
Figure 4. Flow chart of miscible turbidite sandstone rock physical mode
![]()
图 5 混相浊积砂岩岩石物理模型横波预测结果
Figure 5. S-wave prediction results of miscible turbidite sandstone rock physics model
![]()
图 6 饱和岩石弹性参数随流体含气量变化图
Figure 6. Variation of elastic parameters of saturated rock with gas content of fluid
![]()
图 8 弹性参数差异随含水饱和度与流体含气量变化图
Figure 8. Variation of elastic parameter difference with water saturation and fluid gas content
表 1 混相模型参数
Table 1 Mixed-phase model parameters
储层参数 油藏参数 孔隙压力 69 MPa 温度 114℃ 上覆压力 95 MPa 含油饱和度 80% 泥质含量 22% 石油重量 34（API重量） 含水饱和度 20% 气体重量 0.76 孔隙度 23% 盐度 20083 ppm
下载: 导出CSV
-
[1] 聂南方, 郭智奇, 刘财. 改进的地震AVAZ裂缝弱度反演方法及其在致密砂岩储层中的应用[J]. 地球与行星物理论评(中英文), 2024, 55(3): 358-368. DOI: 10.19975/j.dqyxx.2023-2025. NIE N F, GUO Z Q, LIU C. Application of the improved seismic AVAZ inversion method for fracture characterization of a tight sandstone gas reservoir in the Ordos Basin[J]. Reviews of Geophysics and Planetary Physics, 2024, 55(3): 358-368. DOI: 10.19975/j.dqyxx.2023-2025. (in Chinese).
[2] KULKARNI, MADHAV M. Multiphase mechanisms and fluid dynamics in gas injection enhanced oil recovery processes[M] LSU Doctoral Dissertations. 2005, DOI: 62.10.31390/gradschool_dissertations.62.
[3] SEQUEIRA DL. Compositional Effects on Gas-Oil Interfacial Tension and Miscibility at Reservoir Conditions[D]. Louisiana State University and Agricultural and Mechanical College 2006.
[4] COATS K H. An equation of state compositional model[J]. Society of Petroleum Engineers Journal, 1980, 20(5): 363-376. DOI: 10.2118/8284-PA.
[5] TODD M R, LONGSTAFF W J. The development, testing, and application of a numerical simulator for predicting miscible flood performance[J]. Journal of Petroleum Technology, 1972, 24(7): 874-882 DOI: 10.2118/3484-PA.
[6] SRIVASTAVA N K, Effect of pressure gradient on displacement performance for miscible/near miscible gas flooding[D]. Stanford University, 2004.
[7] 刘玉章, 陈兴隆, 低渗油藏CO_2驱油混相条件的探讨[J]. 石油勘探与开发, 2010, (4): 466-470. LIU Y Z, CHEN X L. Miscible conditions of CO2 flooding technology used in low permeability reserviors[J]. Petroleum Exploration and Development, 2010, 37(4): 466-470. (in Chinese).
[8] 冉新权, 赵继勇, 何永宏, 等, 超低渗透油藏CO_2驱混相范围确定新方法[J]. 西南石油大学学报(自然科学版) 2011, (5): 89-93. RAN X Q, ZHAO J Y, HE Y H, et al. A new method for determining the miscible range of CO₂ flooding in ultra-low permeability reservoirs[J]. Journal of Southwest Petroleum University (Natural Science Edition), 2011, (5): 89-93. (in Chinese).
[9] 吴忠宝, 甘俊奇, 曾倩, 等. 低渗透油藏二氧化碳混相驱油机理数值模拟[J]. 油气地质与采收率 2012, (3): 67-70. WU Z B, GAN J Q, ZENG Q, et al. Numerical simulation of CO₂ miscible flooding mechanism in low permeability reservoirs[J]. Petroleum Geology and Recovery Efficiency, 2012, (3): 67-70. (in Chinese).
[10] AHMADI A M, HASANVAND Z M, SHOKROLAHZADEH S. Technical and economic feasibility study of flue gas injection in an Iranian oil field[J]. Petroleum, 2015, 1(3): 217-222. DOI: 10.1016/j.petlm.2015.07.010.
[11] 王锐, 吕成远, 伦增珉, 等, 低渗透油藏CO_2驱替过程中的混相特征实验研究[J]. 陕西科技大学学报(自然科学版), 2015, 33(3): 105-108. WANG R, LYU C Y, LUN Z M, et al. Experimental study on miscibility characteristics during CO₂ flooding in low permeability reservoirs[J]. Journal of Shaanxi University of Science and Technology (Natural Science Edition), 2015, 33(3): 105-108. (in Chinese).
[12] 袁舟, 廖新维, 赵晓亮, 等. 砂岩油藏CO2驱替过程中溶蚀作用对储层物性的影响[J]. 油气地质与采收率, 2020, 27(5): 97-104. YUAN Z, LIAO X W, ZHAO X L, et al. Sandstone reservoir CO2Effect of dissolution on reservoir physical properties during displacement[J]. Petroleum Geology and Recovery Efficiency, 2020, 27(5): 97-104. (in Chinese).
[13] 朱清源, 吴克柳, 张晟庭, 等. 致密砂岩气藏注CO_2提高天然气采收率微观机理[J]. 天然气工业, 2024, 44(4): 135-145. ZHU Q Y, WU K L, ZHANG S T, et al. Microscopic mechanism of CO2 injection to enhance gas recovery in tight sandstone gas reservoirs[J]. Natural Gas Industry, 2024, 44(4): 135-145. (in Chinese).
[14] 杨勇, 张世明, 曹小朋, 等. 胜利油田CO_2高压混相驱油与封存理论技术及矿场实践[J/OL]. 石油勘探与开发, 2024, 51(5): 1080-1091. YANG Y, ZHANG S M, CAO X P, et al. CO2 high-pressure miscible flooding and storage technology and its application in Shengli Oilfield, East China[J]. Petroleum Exploration and Development, 2024, 51(5): 1080-1091. (in Chinese).
[15] 吕其彪, 孙作兴. 岩石物理模版在储层定量解释中的应用[J]. 地球物理学进展, 2012, 27(2): 610-618. LV Q B, SUN Z X. Application of rockphysics chart to quantitative reservoir interpretation[J]. Progress in Geophysics, 2012, 27(2): 610-618. (in Chinese).
[16] 贾凌云, 李琳, 王千遥, 等. 流体体积模量计算方法研究[J]. 地球物理学进展, 2018, 33(1): 223-227. JIA L Y, LI L, WANG Q Y, et al. Research on calculation methods of fluid bulk modulus[J]. Progress in Geophysics, 2018, 33(1): 223-227. (in Chinese).
[17] 张佳佳, 李宏兵, 刘怀山, 等. 几种岩石骨架模型的适用性研究[J]. 地球物理学进展, 2010, 25(5): 1697-1702. DOI: 10.3969/j.issn.1004-2903.2010.05.024. ZHANG J J, LI H B, LIU H S, et al. Accuracy of dry frame models in the study of rock physics[J]. Progress in Geophysics, 2010, 25(5): 1697-1702. DOI:10.3969/j.issn.1004-2903.2010.05.024. (in Chinese).
[18] Dario Grana, Seismic Reservoir Modeling, Theory, Examples, and Algorithms[M]. 2021.
[19] 马凌波, 张佳佳, 张广智, 等. 基于岩石物理模型的碳酸盐岩物性参数替换方法[J]. CT理论与应用研究(中英文), 2024, 33(3): 273-288. DOI: 10.15953/j.ctta.2023.185. MA L B, ZHANG J J, ZHANG G Z, et al. Carbonate rock physical property parameter substitution method based on rock physics models[J]. CT Theory and Applications, 2024, 33(3): 273-288. DOI: 10.15953/j.ctta.2023.185.
[20] KAMAL I, SALIH M N, MARTYUSHEV A D. Correlations between petroleum reservoir fluid properties and amount of evolved and dissolved natural gas: Case study of transgressive–regressive-sequence sedimentary rocks[J]. Journal of Marine Science and Engineering, 2023, 11(10).
[21] TROYAKOV K V, KAVERZINA A S, RYBIN V V, et al. Effect of undissolved gas on fluid bulk modulus[J]. E3S Web of Conferences, 2024, 471. DOI: 10.1051/e3sconf/202447102019.
[22] AL HAGREY SA, KÖHN D, RABBEL W. Geophysical assessments of renewable gas energy compressed in geologic pore storage reservoirs[J]. Springer Plus, 2014, 3(1): 267. DOI: 10.1186/2193-1801-3-267.
[23] 胡华锋, 张立强, 孙振涛. 衰减岩石物理模型驱动的流体饱和度地震反演方法[J]. 石油地球物理勘探, DOI: 10.13810/j.cnki.issn.1000-7210.20240179. HU H F, ZHANG L Q, SUN Z T. Seismic inversion for fluid saturation based on attenuated rock physics model[J]. Oil Geophysical Prospecting, 2025, 60(2): 474-485 DOI:10.13810/j.cnki.issn.1000-7210.20240179. (in Chinese).
[24] 吴思, 韩波, 纪利祥, 等. 利用叠前AVO反演预测砂岩储层有效压力[J]. 石油地球物理勘探, 2024, 59(5): 1165-1173. DOI: /10.13810/j.cnki.issn.1000-7210.2024.05.020. WU S, HAN B, JI L X, et al. Pre-stack AVO inversion for estimating effective pressure in sandstone reservoirs[J]. Oil Geophysical Prospecting, 24, 59(5): 1165-1173. DOI:10.13810/j.cnki.issn.1000-7210.2024.05.020. (in Chinese).
[25] 桂志鹏, 邵奇奇, 张军华, 等. 2024. 含强屏蔽滩坝砂储层正演模拟分析及描述[J]. 地球物理学进展, 2024, 39(5): 1911-1922. DOI: 10.6038/pg2024HH0357. GUI Z P, SHAO Q Q, ZHANG J H, et al. 2024. Forward modeling analysis and description of beach-bar sand reservoir with strong shielding[J]. Progress in Geophysics, 2024, 39(5): 1911-1922. DOI: 10.6038/pg2024HH0357.
计量
- 文章访问数: 32
- HTML全文浏览量: 3
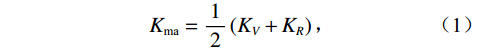
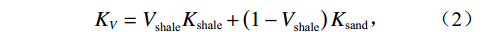
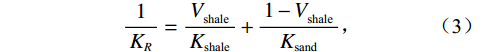
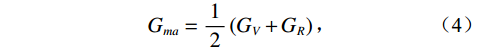
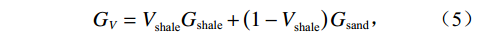
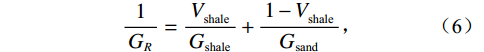
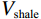
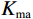
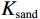
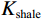
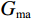
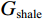
- PDF下载量: 5
