Dual-view CT Reconstruction Algorithm Based on Gradient Information Constraints
-
摘要:
计算机断层成像(CT)技术凭借其无损检测、分辨率高和可视化等特点,在工业检测领域展现出显著应用价值。然而,在某些工业检测场景中,极端受限的扫描条件导致投影数据获取难度大,传统重建方法应用受限。为应对这一挑战,本研究提出一种适用于快速CT成像的正交双视角三维重建网络。提出的方法基于编解码架构,并使用二维卷积代替三维卷积,用特征通道维度推断CT体积的深度,提高模型的推理速度。同时引入梯度信息、梯度损失来增强网络对边缘的恢复能力。该方法在核桃和引信数据集上进行验证,实验结果表明,重建分辨率为128的体积仅需0.19 s,且重建图像的结构相似性高于0.98。该方法从双视角2D投影中推断出3D CT体积的有效能力,展现其在快速CT成像中的未来潜力。
Abstract:Computed tomography (CT) technology has demonstrated significant application value in industrial inspection owing to its non-destructive testing capabilities, high resolution, and visualization features. However, in certain industrial inspection scenarios, extremely limited scanning conditions pose substantial challenges for projection data acquisition, restricting the application of traditional reconstruction methods. To address this challenge, this study proposes an orthogonal dual-view 3D reconstruction network tailored for rapid CT imaging. The proposed method employs an encoder–decoder architecture, utilizing 2D convolutions instead of 3D convolutions to infer the depth dimension of CT volumes through feature channels, thereby enhancing model inference speed. Additionally, gradient information and gradient loss are introduced to strengthen the edge recovery capability of the network. The method is validated on walnut and Fuze datasets. Experimental results showed that reconstructing a volume with a resolution of 128 required only 0.19 s, and the structural similarity of the reconstructed images was higher than 0.98. This approach demonstrates effective capability in inferring 3D CT volumes from dual-view 2D projections, revealing its future potential in rapid CT imaging.
-
计算机断层成像(computed tomography,CT)技术凭借其非破坏性、高效、非接触等特点,在工业中具有广阔的应用空间[1-2]。目前CT成像技术主要分为传统重建和深度学习重建两大类别。
传统重建方法大致可以分为两类:解析重建算法和迭代重建算法。通过数百个X射线投影,传统重建算法可以近似地重建CT体积。之后有学者把压缩感知引入到CT重建中开发了基于正则化的重建方法[3],把先验信息整合到重建模型中,成功减少了所需投影图像的数量。然而在一些条件受限的应用场景中,只能获取非常有限的投影图像,如工业产品在线检测、瞬态毁伤动态测试等,依靠传统方法和正则化方法无法获得高质量的结果。因此,从超稀疏采样的投影中重建图像以加快CT成像过程成为研究的热点问题。超稀疏视角CT成像可突破传统采样定理限制,实现重建效率的阶跃式提升。
近来,随着深度学习的快速发展,数据驱动的单/双视角CT重建算法应运而生[4]。在卷积神经网络(convolutional neural networks,CNN)领域,Li等[5]通过编解码网络并结合跳跃连接,实现了从单视角X射线投影重建3D CT体积;Tan等[6]在特征提取的过程中加入注意力机制和多尺度特征提取模块将2D特征转换为3D特征,并与相应的3D生成模块进行特征融合,实现利用单个2D影像生成3D体积数据;Liu等[7]设计了混合网络HybRecon,用于微小缺陷恢复,将CT重建任务分解为3个子任务,对应于3个不同的模块,并且3个模块的训练有先后顺序;Sun等[8]的X-ray2 CTNet,借助密集连接与跳跃连接,成功实现了基于双视角投影的固体火箭发动机药柱燃面的三维重建。尽管CNN在图像重建方面取得了显著进展,但随着研究的深入和应用需求的不断提升,新的技术方向也应运而生。
生成对抗网络(generative adversarial network,GAN)以其独特的对抗训练机制,为图像重建领域带来了新的思路。Ying等[9]提出的X2CT-GAN模型通过2D到3D跨维映射、特征编解码、特征融合和对抗性训练,实现双视角医学图像重建;Huang等[10]提出了3DSP-GAN模型,通过构建3D-3D的生成器网络来减少跨维图像的语义差距,并提出由3D软池化操作组成的下采样模块,成功实现了肺部CT高质量重建。然而,基于GAN的方法在应用过程中暴露出两大主要问题,一方面,训练过程稳定性欠佳;另一方面,生成的内容可能出现虚假结构。这些问题促使研究人员不断探索新的技术。
随着Transformer架构的突破,其强大的特征提取和建模能力也逐渐引起了图像重建领域学者的关注。Shi等[11]提出了名为XRayWizard的新型模型,它使用Vision Transformer块来编码2D X射线图像,并在每个Transformer Block的末尾引入一个池化层来提取特征信息,成功实现单个2D 胸部X射线图像重建3D肺体积;Wang等[12]提出了采用Transformer网络模块来增强X射线图像特征表示的TRCTGAN,用于从双平面X射线图像重建胸部CT体积。然而,Transformer架构高模型复杂度的固有局限限制了其在实际场景中的广泛应用。
尽管基于深度学习的单/双视角CT重建算法已取得显著进展,但当前该类三维CT重建算法普遍将三维卷积作为核心运算单元,通过三维卷积的空间维度感知特性实现从投影数据到体素空间的特征映射。然而,级联形式的三维卷积会致使参数量急剧增加,显存消耗显著,严重制约了重建体素维度与重建速率[13]。在2D X射线投影到3D CT重建的任务中,使用两个从正交方向捕获的投影,可以实现信息互补,帮助模型获得更准确的结果。
在此背景下,本文提出适用于快速CT成像的双视角三维重构网络。该网络基于编解码架构,利用特征通道维度推断CT体积的深度,从而避免解码阶段使用级联的三维卷积带来的显存急剧消耗。同时为提高对先验信息的利用和加快模型的收敛速度,该模型还引入了梯度损失函数。本文的工作点总结如下。
(1)设计一个基于正交双视角投影的快速三维重建网络,仅需要正交双视角投影,便可以快速准确地推断CT体积,为投影采集受限的场景提供应用的可能性。
(2)为避免级联的三维卷积对显存和计算速度产生严重制约,网络采用二维卷积替代三维卷积,将通道维度编码为深度维度,利用特征通道推断CT体积深度。这一做法可以在保证重建质量的同时减少计算量。
(3)引入梯度图像和梯度损失提高网络对先验信息的利用,加快模型的收敛速度,增强网络对边缘的恢复能力。
1. 网络架构
通常来说,一张投影图像只包括该投影方向上的对象信息,通过传统CT重建方法无法重建出高质量的结果。深度学习方法通过不断优化模型参数来拟合投影到体积的映射函数。该方法使用由投影图像和对应的全视角CT重建体积组成的数据对进行训练,在训练过程中它可以不断地获取先验信息。
本文构建一个基于正交双视角投影的快速三维重建网络。网络基于编解码架构,采用二维卷积替代三维卷积,利用特征通道推断CT体积深度,提高3D CT重建速度。同时引入梯度图像和梯度损失,加快模型的收敛速度,增强网络对边缘的恢复能力。
首先计算正交双视角投影图像的梯度,随后将原图像、梯度图像以及二者之和进行拼接。然后进行通道数扩展操作,完成后进行维度对齐操作,接着再输入到编解码网络中。最后通过特征重构恢复出目标体积数据。所提出的网络模型可分为4个模块:维度扩展模块、编码器模块、解码器模块、特征重构模块,对应的数学模型分别为
$ {F_{{\mathrm{de}}}} $ 、$ {F_{{\mathrm{encoder}}}} $ 、$ {F_{{\mathrm{decoder}}}} $ 、$ {F_{{\mathrm{fr}}}} $ 。网络模型拟合的2D投影图像到3D CT体积的映射函数$ F $ 可以描述为式1所示,$$ F = {F_{{\mathrm{fr}}}}\left( {{F_{{\mathrm{de}}}} \otimes {F_{{\mathrm{encoder}}}} \otimes {F_{{\mathrm{decoder}}}}} \right) \text{,} $$ (1) 其中
$ \otimes $ 表示网络模型级联。通过对投影图像进行预处理得到一个包含梯度信息和原始先验信息的多通道数据。接着再进行通道扩展和对齐操作,得到匹配目标CT体积深度的中间体积数据。然后输入到编码器中得到一个低维度高级特征[14],再通过解码器逐步重构高维特征。最后借助特征重构模块输出目标CT体积,实现3D CT重建。
网络整体架构图如图1所示,该模型各模块的设计如下。
1.1 维度扩展模块
为了充分利用先验信息和增强模型对边缘的恢复能力,本文使用投影图像、梯度图像和二者之和作为输入。首先计算投影图像
$ \left\{{I}_{1},{I}_{2}\right\}\in {R}^{H\times W\times 1} $ 的Scharr梯度,得到$ \left\{{I}_{3},{I}_{4}\right\}\in {R}^{H\times W\times 1} $ 。Scharr梯度计算公式如下:$$ \begin{aligned} & G_x=\left[\begin{array}{*{20}{c}}-3 & 0 & 3 \\ -10 & 0 & 10 \\ -3 & 0 & 3\end{array}\right]\otimes\boldsymbol{A} \\ & G_y=\left[\begin{array}{*{20}{c}}-3 & -10 & -3 \\ 0 & 0 & 0 \\ 3 & 10 & 3\end{array}\right]\otimes\boldsymbol{A}\end{aligned}\ \ , $$ (2) $$ \begin{aligned} & G(i,j) = \sqrt {{{\Big( {G_x^{}(i,j)} \Big)}^2} + {{\left( {G_y^{}(i,j)} \right)}^2}} \\ & \theta (i,j) = \arctan \left( {\frac{{{G_y}(i,j)}}{{{G_x}(i,j)}}} \right) \end{aligned} \text{,} $$ (3) 其中,
$ {\boldsymbol{A}} $ 表示待处理的图像,$ \otimes $ 表示卷积,$ {G_x} $ 表示水平方向的梯度,$ {G_y} $ 表示垂直方向的梯度,$ G $ 表示梯度幅值,$ \theta $ 表示梯度方向。Scharr梯度能够更精确地近似图像的真实梯度,而且在计算梯度时考虑了更多的邻域信息,对噪声具有一定的鲁棒性。然后求投影图像和梯度图像的和,得到
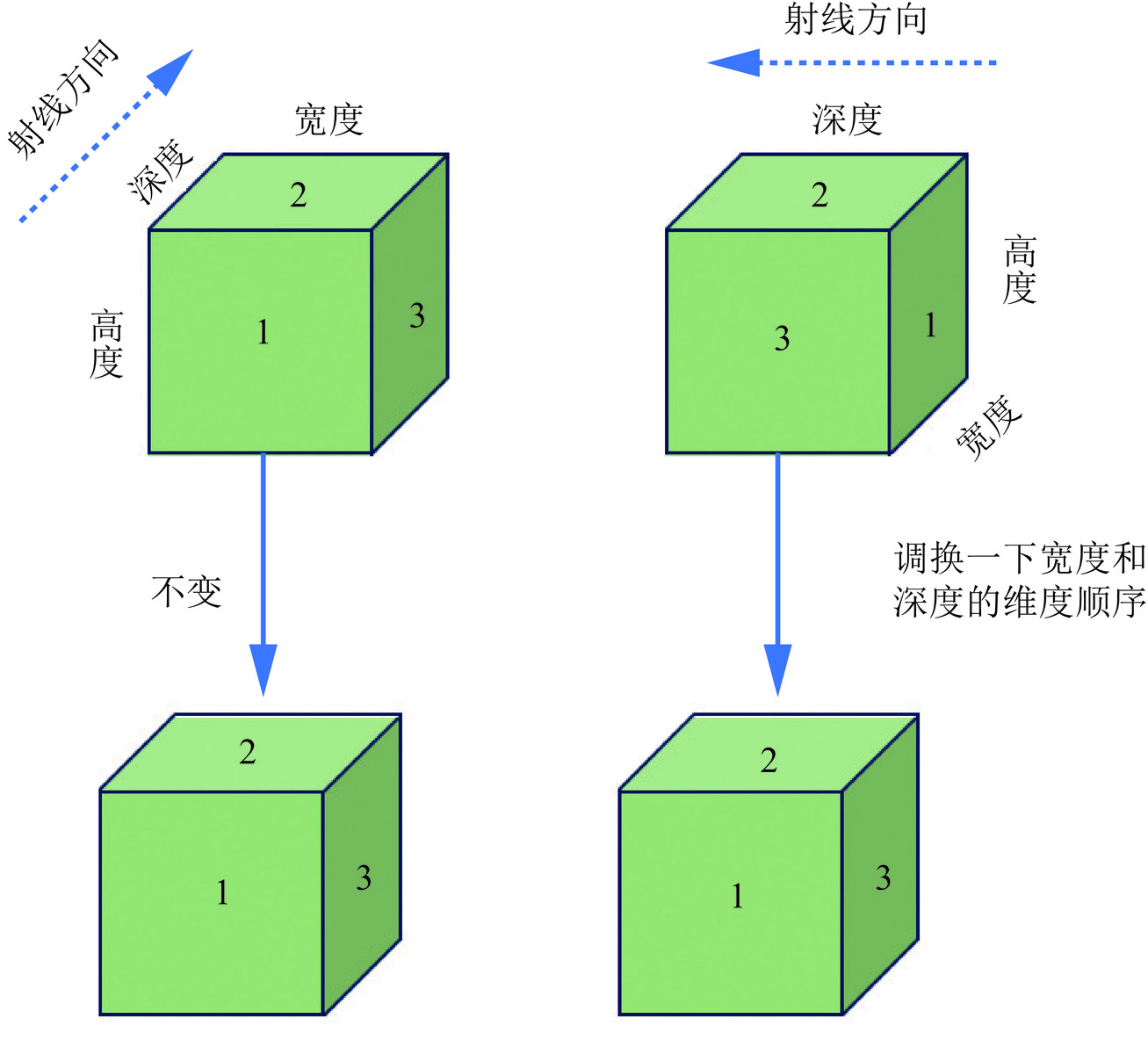
$ \{{I}_{1}+{I}_{3}, {I}_{2}+{I}_{4}\}\in {R}^{H\times W\times 1} $ 。最后将它们在通道维度上进行拼接,生成3通道初始数据$ \left\{{I}_{5},{I}_{6}\right\}\in {R}^{H\times W\times 3} $ 。接着对初始数据进行通道数扩展操作,把通道维度编码为深度维度,利用特征通道推断CT体积深度。通道数扩展由4个级联的ResBlock块组成。随着ResBlock块的逐步执行,特征图的通道数呈阶梯式增长,依次为3→16→32→64→128。在此过程中,网络持续探索深度信息,并将3D信息逐步嵌入特征图的不同通道内。最后再通过对齐操作,实现维度的统一。对齐操作示意图如图2所示。1.2 编码模块
编码器将经过通道数扩展的初始3D体积数据作为输入,逐步对高维特征图进行压缩编码。随着下采样的进行,特征图的尺寸不断被压缩,但特征通道数保持不变,一直匹配目标CT体积数据的深度。在此过程中,感受野会逐渐扩大,可以感知到更多的低频信息[15]。在编码过程中,通过跳跃连接将不同级别特征信息直接传递给解码器,以共享特征信息加强信息利用。
编码器由4个级联的下采样块组成。其中,每个下采样块由“2D ResBlock layer→2D ResBlock layer→pooling layer”组成。通过逐步的下采样操作,特征图尺寸逐步为128→64→32→16→8。
1.3 解码模块
解码器将经过编码的低维高级特征作为输入,逐步重构高维特征并恢复图像细节[16]。解码器由4个拼接融合操作和4个上采样模块组成,每个上采样块由一组“2D Deconvolution layer→2D ResBlock layer→2D ResBlock layer”组成。通过逐步的上采样操作,特征图尺寸依次为8→16→32→64→128,但特征图通道数保持不变。
随着上采样的进行,模型将解码器自身的信息和来自编码器对应层级的特征信息一步一步融合,充分利用多尺度的信息,逐渐恢复目标图像的结构和细节。
1.4 特征重构模块
将两个解码器的结果与特征重构模块自身的结果在通道维度上进行拼接,随后使其通过二维卷积操作,以此实现特征信息的有效融合[17]。特征重构模块由4个简单上采样块组成。每个简单上采样块由一组“Concat→2D Conv layer→2D Deconvolution layer→2D Conv layer→2D Batch Normalization layer→ReLU layer”组成。
通过逐步的简单上采样操作,特征图尺寸依次为8→16→32→64→128,但特征图通道数仍然保持不变。最后再通过1个拼接操作和2个二维卷积输出目标CT体积。
2. 训练和推理细节
本文提出的网络模型采用正交投影图像、对应的梯度图像和二者的和作为输入。首先通过维度扩展得到匹配目标CT体积数据深度的初始体积数据,然后经过对齐操作实现维度统一,接着再输入到编解码网络中,最后通过特征重构模块输出预测CT体积。为了提升重建速度并降低显存需求,本文网络使用特征通道推断CT体积深度。整个网络以端到端的方式进行优化,模型各层参数结构如表1所示。
表 1 模型各层参数结构Table 1. Parameter structure of each layer of the model层 参数 输出尺寸(H×W×C格式) 维度扩展×2 2D ResBlock×4 128×128×128 编码网络×2 Downsampling 64×64×128 Downsampling 32×32×128 Downsampling 16×16×128 Downsampling 8×8×128 解码网络×2 Upsampling+Concat+2D Conv 16×16×128 Upsampling+Concat+2D Conv 32×32×128 Upsampling+Concat+2D Conv 64×64×128 Upsampling+Concat+2D Conv 128×128×128 特征重构模块 Simple Upsampling 16×16×128 Simple Upsampling 32×32×128 Simple Upsampling 64×64×128 Simple Upsampling 128×128×128 Concat + 2D Conv + 2D Conv 128×128×128 网络采用adam优化器进行优化,初始学习率设置为
0.0001 ,并设置动量参数$ {\beta _1} $ 为0.9,$ {\beta _2} $ 为0.99。随着epoch数量的增加,学习率采用线性衰减策略,降低到10−8。本文实验设置批次处理大小为12,训练周期总数为150。通过Tensorflow2.4平台实现了该网络,并在配备了NVIDIA Tesla V100图形显卡的计算设备上进行训练、验证和测试。3. 实验
3.1 数据集
为了训练本文提出的网络,构建了一个包含有4个核桃的数据集,该数据集由2D投影图像和3D体积数据组成。对于每个核桃,使用微焦点CT系统YXLON FF 20(图3)获得全视图投影(
1200 张)和真值CT体积图像(使用周向投影数据通过FDK算法重建得到的)。将两张正交2D投影图像和对应的3D CT体积命名一组数据,总计4×1200 /2=2400 组数据。表2汇总所用的投影数据采集参数。按照8∶1∶1的比例划分数据集,分别用于训练,验证和测试。投影数据的维度大小为128×128,体积数据维度大小为128×128×128。为了更好的训练和加速拟合,对投影数据和体积数据进行了归一化处理。
表 2 FF 20微焦点CT系统的数据采集参数Table 2. Data acquisition parameters of the FF 20 microfocus CT system参数 数值 X射线源到探测器的距离 780.577 mm X射线源到旋转中心的距离 155.22 mm 管电压 120 kV 管电流 40 μA X射线源焦点尺寸 1 μm 探元尺寸 0.127 mm 探测器分辨率 1122 ×1122 3.2 损失函数
为有效提升重建质量与精度,增强模型鲁棒性,本文构建了一个多维度约束的损失函数。该函数由重建损失、结构相似性损失和梯度损失3部分构成,具体内容如下。
(1)重建损失。使用均方误差(mean squared error,MSE)作为重建损失函数。该损失是一种体素损失,用于约束体素的结构一致性[18],确保模型在空间上重建出尽可能准确的3D模型。重建损失定义如下,
$$ {L_{{\mathrm{RE}}}}\Big({Y_{{\mathrm{pred}}}},{Y_{{\mathrm{truth}}}}\Big) = \| {Y_{{\mathrm{pred}}}} - {Y_{{\mathrm{truth}}}}\|_2^2 \text{,} $$ (4) 其中,
$ {Y_{{\mathrm{pred}}}} $ 表示网络模型预测的体积数据,$ {Y_{{\mathrm{truth}}}} $ 表示真实的体积数据。(2)结构相似性损失。结构相似性(structural similarity,SSIM)是衡量两幅图像相似度的指标,综合比较亮度、对比度和结构相似度,关注于图像的视觉质量和结构一致性[19]。因此,引入基于SSIM的结构相似性损失,损失函数定义为,
$$ {L_{{\mathrm{SSIM}}}}\Big({Y_{{\mathrm{pred}}}},{Y_{{\mathrm{truth}}}}\Big) = 1 - {\mathrm{SSIM}}\Big({Y_{{\mathrm{pred}}}},{Y_{{\mathrm{truth}}}}\Big) \text{,} $$ (5) 其中,
$ {Y_{{\mathrm{pred}}}} $ 表示网络模型预测的体积数据,$ {Y_{{\mathrm{truth}}}} $ 表示真实的体积数据。(3)梯度损失。为了更好地恢复图像的结构信息和边缘细节,本文引入了梯度损失。梯度损失关注图像的边缘和纹理信息,可以在预测过程中保持图像的整体结构,避免出现模糊现象。定义如下,
$$ {\mathrm{MS}}{{\mathrm{E}}_x} = \frac{1}{{DHW}}{\sum\limits_{d = 1}^D \sum\limits_{h = 1}^H \sum\limits_{w = 1}^W \Big({\nabla _x}{Y_{{\mathrm{pred}}}} - {\nabla _x}{Y_{{\mathrm{truth}}}}\Big)^2} \text{,} $$ (6) $$ {\mathrm{MS}}{{\mathrm{E}}_y} = \frac{1}{{DHW}}{\sum\limits_{d = 1}^D \sum\limits_{h = 1}^H \sum\limits_{w = 1}^W \Big({\nabla _y}{Y_{{\mathrm{pred}}}} - {\nabla _y}{Y_{{\mathrm{truth}}}}\Big)^2} \text{,} $$ (7) $$ {L_{{\mathrm{GL}}}}\Big({Y_{{\mathrm{pred}}}},{Y_{{\mathrm{truth}}}}\Big) = \frac{{{\mathrm{MSE}}_x + {\mathrm{MSE}}_y}}{2} \text{,} $$ (8) 其中,
$ {Y_{{\mathrm{pred}}}} $ 表示网络模型预测的体积数据,$ {Y_{{\mathrm{truth}}}} $ 表示真实的体积数据,$ {\mathrm{MSE}}_x $ 为$ x $ 方向梯度的均方误差,$ {\mathrm{MSE}}_y $ 为$ y $ 方向梯度的均方误差。综上,总的优化目标定义如下,
$$ {L_{{\mathrm{total}}}} = {\lambda _1}{L_{{\mathrm{RE}}}} + {\lambda _2}{L_{{\mathrm{SSIM}}}} + {\lambda _3}{L_{{\mathrm{GL}}}} \text{,} $$ (9) 其中,
$ {\lambda _1} $ 、$ {\lambda _2} $ 和$ {\lambda _3} $ 控制不同损失项的相对重要性。在本文的重建任务中优先考虑体素一致性,故本文实验设置$ {\lambda _1} =1$ ,$ {\lambda _2}=0.1 $ ,$ {\lambda _3} =0.1$ 。3.3 对比方法
为了验证本文模型的有效性,选取了PatRecon[20]和X2CT-GAN模型展开对比分析。
PatRecon通过在通道维度上拼接正交双视角投影图像,然后经过表示网络、转换模块和生成网络来实现正交双视角CT重建。表示网络用2D卷积残差块从2D投影中提取语义特征;转换模块通过卷积和反卷积操作跨维度转换特征;生成网络基于3D反卷积块生成3D CT体积。X2CT-GAN则借助生成对抗网络,运用正交双视角投影图像生成3D医学解剖体积。并且该模型采用了一种创新的融合方法,能够有效整合双视角投影携带的信息。
4. 结果
4.1 视觉比较
为了公平起见,本文提出的模型和对比模型均采用128×128的投影图像重建分辨率为128的CT体积。PatRecon和X2CT-GAN的架构与对应论文中的基本一致,只改变了模型的输入和输出数据的维度,以匹配本文的数据集。核桃的真实数据(使用周向投影数据通过FDK算法重建得到的)、测试结果和二者差异的切片图如图4所示。为了增强差异图的呈现效果,本文将差异图的像素值放大3.5倍。
可以看出本文模型和对比模型都重建出令人满意的轮廓,但从效果增强后的差异图可以看出PatRecon重建的结果与真值的差异最大,X2CT-GAN次之。并且PatRecon和X2CT-GAN模型重建结果的图像纹理效果不如本文模型。同时在一些细小裂缝处(图4的红色方框),本文模型重建的更清晰、更准确。
实验结果表明本文所提出的重建模型表现更为出色,能够高效且精准地重建3D CT体积图像。
4.2 定量比较
本文选取均方根误差(root mean squared error,RMSE)、峰值信噪比(peak signal-to-noise ratio,PSNR)和结构相似性指数(SSIM)作为评估重建质量的指标。此外,对于相同的测试集,给出了测试阶段不同模型的推理时间。
所有实验在配备NVIDIA Tesla V100 GPU(32 G)显卡的Ubuntu 16.04系统上进行,定量结果如表3所示。可以看出本文模型在这4个指标上均优于PatRecon和X2CT-GAN。实验结果显示出本文模型从双视角2D投影中快速准确推断出3D CT体积的有效能力。
表 3 定量比较结果Table 3. Quantitative comparison results模型 RMSE SSIM PSNR Testing time/s 本文方法 0.011 0.988 38.942 0.19 X2CT-GAN 0.013 0.975 37.583 0.63 PatRecon 0.015 0.961 36.763 2.75 4.3 复杂度比较
本文还比较了这3种模型的参数量和浮点运算数(表4)。本文模型避免了级联的三维卷积,使用特征通道推断CT体积深度,在模型复杂度和计算复杂度方面都呈现出一定的优势。
表 4 模型参数量和FLOPs比较结果Table 4. Comparison results of the number of model parameters and FLOPs模型 Param./(×107) FLOPs/(×109) 本文方法 1.69 179.44 X2CT-GAN 7.28 392.88 PatRecon 58.86 1304.12 在模型复杂度方面,本文模型展现出显著的轻量化特性,其参数量只有16.9 M,远远低于PatRecon。在计算复杂度方面,本文模型的浮点运算量为179.44×109,低于PatRecon和X2CT-GAN模型。结果表明,本文模型具有很小的模型参数量和很低的计算资源消耗,为快速准确三维重建提供了更优的方案。
4.4 鲁棒性验证
为了验证本文模型的鲁棒性,还构建了一个包含有6种引信装配情况的数据集。该数据集一共有6×
1080 /2=3240 组数据。按照8∶1∶1的比例划分数据集,分别用于训练,验证和测试。其中一种引信装配情况的测试结果切片图如图5所示。第1行是真实数据(使用周向投影数据通过FDK算法重建得到的)3个维度方向的切片图,第2行是测试结果的切片图。可以看出本文模型重建出了正确的撞针方向,同时其整体几何构型与真实数据也高度一致。结果表明,本文模型在引信数据上取得了良好的效果,验证了该模型的鲁棒性。
4.5 模型结构选择
为了进一步展现利用二维卷积替代三维卷积的优势,本文还构建了一个特殊的双视角重建网络。该网络的架构和上面的图1基本一致,只是在编解码和特征重构模块中用三维卷积替代了二维卷积。之后,在相同的软硬件配置下,使用同样的数据集和损失函数,进行训练、验证和测试。表5展示了对比结果。
表 5 模型对比结果Table 5. Comparison results of models模型 SSIM PSNR Param./(×107) FLOPs/(×109) Testing time/s 本文模型(二维卷积) 0.988 38.942 1.69 179.44 0.19 本文模型(三维卷积) 0.985 38.175 0.89 488.15 0.87 可以看出两个模型的重建质量基本一致,但使用二维卷积替代三维卷积可以在测试时间上带来很大的提升。由于二维卷积模型需要用通道数维度推测深度维度,在特征编解码和特征重构阶段必须保持128个通道数不变,而三维卷积模型无此约束,因此二维卷积模型的参数量要高于三维卷积模型。结果表明,为了进行快速高质量CT重建,利用二维卷积替代三维卷积这一思路很有优势。
5. 结论与讨论
综上所述,本研究提出的正交双视角三维重构网络有效解决了极端受限扫描条件下CT重建的不适定性难题,在重建速度、图像质量、模型参数量和计算复杂度方面都展现出一定优势。
使用二维卷积替代三维卷积,利用特征通道维度推断CT体积的深度维度,可以减小模型的推理时间。引入梯度信息、梯度损失,可以加快模型的收敛速度,增强网络对边缘的恢复能力。将该算法与PatRecon和X2CT-GAN算法进行比较,实验结果表明该算法具有更好的重建效果、较低的模型参数量和较快的重建速度。
今后仍需要在该研究的基础上,继续深入开展后续研究,引入神经辐射场的思想,着重提升模型的泛化性。将物体的密度场建模为隐函数,构建坐标到CT密度场的隐式表征,实现2D投影图像中像素和3D CT体积中体素的对应。并且加入符合CT扫描物理原理的损失函数,让网络学习CT成像的物理过程,增强模型的泛化性和可解释性。
-
表 1 模型各层参数结构
Table 1 Parameter structure of each layer of the model
层 参数 输出尺寸(H×W×C格式) 维度扩展×2 2D ResBlock×4 128×128×128 编码网络×2 Downsampling 64×64×128 Downsampling 32×32×128 Downsampling 16×16×128 Downsampling 8×8×128 解码网络×2 Upsampling+Concat+2D Conv 16×16×128 Upsampling+Concat+2D Conv 32×32×128 Upsampling+Concat+2D Conv 64×64×128 Upsampling+Concat+2D Conv 128×128×128 特征重构模块 Simple Upsampling 16×16×128 Simple Upsampling 32×32×128 Simple Upsampling 64×64×128 Simple Upsampling 128×128×128 Concat + 2D Conv + 2D Conv 128×128×128 表 2 FF 20微焦点CT系统的数据采集参数
Table 2 Data acquisition parameters of the FF 20 microfocus CT system
参数 数值 X射线源到探测器的距离 780.577 mm X射线源到旋转中心的距离 155.22 mm 管电压 120 kV 管电流 40 μA X射线源焦点尺寸 1 μm 探元尺寸 0.127 mm 探测器分辨率 1122 ×1122 表 3 定量比较结果
Table 3 Quantitative comparison results
模型 RMSE SSIM PSNR Testing time/s 本文方法 0.011 0.988 38.942 0.19 X2CT-GAN 0.013 0.975 37.583 0.63 PatRecon 0.015 0.961 36.763 2.75 表 4 模型参数量和FLOPs比较结果
Table 4 Comparison results of the number of model parameters and FLOPs
模型 Param./(×107) FLOPs/(×109) 本文方法 1.69 179.44 X2CT-GAN 7.28 392.88 PatRecon 58.86 1304.12 表 5 模型对比结果
Table 5 Comparison results of models
模型 SSIM PSNR Param./(×107) FLOPs/(×109) Testing time/s 本文模型(二维卷积) 0.988 38.942 1.69 179.44 0.19 本文模型(三维卷积) 0.985 38.175 0.89 488.15 0.87 -
[1] 刘勇, 曾理. 工业CT图像的管道圆柱度误差测量[J]. 计算机工程与应用, 2011, 47(13): 199-200, 233. DOI: 10.3778/j.issn.1002-8331.2011.13.056. LIU Y, ZENG L. Cylindricity error evaluation of pipe in industrial CT images[J]. Computer Engineering and Applications, 2011, 47(13): 199-200, 233. DOI: 10.3778/j.issn.1002-8331.2011.13.056. (in Chinese).
[2] 汤戈, 赵欣雨, 王宇翔, 等. 工业CT技术在地球科学中的应用[J]. CT理论与应用研究(中英文), 2024, 33(1): 119-134. DOI: 10.15953/j.ctta.2023.091. TANG G, ZHAO X Y, WANG Y X, et al. Applications of industrial computed tomography technology in the geosciences[J]. CT Theory and Applications, 2024, 33(1): 119-134. DOI: 10.15953/j.ctta.2023.091. (in Chinese).
[3] 邸江磊, 林俊成, 钟丽云, 等. 基于深度学习的稀疏或有限角度CT重建方法研究综述[J]. 激光与光电子学进展, 2023, 60(8): 32-69. DOI: 10.3788/LOP230488. DI J L, LIN J C, ZHONG L Y, et al. Review of sparse-view or limited-angle CT reconstruction based on deep learning[J]. Laser & Optoelectronics Progress, 2023, 60(8): 32-69. DOI:10.3788/LOP230488. (in Chinese).
[4] 樊雪林, 文昱齐, 乔志伟. 基于Transformer增强型U-net的CT图像稀疏重建与伪影抑制[J]. CT理论与应用研究(中英文), 2024, 33(1): 1-12. DOI: 10.15953/j.ctta.2023.183. FAN X L, WEN Y Q, QIAO Z W. Sparse reconstruction of computed tomography images with transformer enhanced U-net[J]. CT Theory and Applications, 2024, 33(1): 1-12. DOI: 10.15953/j.ctta.2023.183. (in Chinese).
[5] LI X, WANG S, CHEN P, et al. 3-D inspection method for industrial product assembly based on single X-ray projections[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-14.
[6] TAN Z, LI J, TAO H, et al. XctNet: Reconstruction network of volumetric images from a single X-ray image[J]. Computerized Medical Imaging and Graphics, 2022, 98: 102067. DOI: 10.1016/j.compmedimag.2022.102067.
[7] LIU X, YU J, SUN Y, et al. Tiny defect oriented single-view CT reconstruction based on a hybrid framework[J]. IEEE Transactions on Instrumentation and Measurement, 2024.
[8] SUN X, LI X, CHEN P. An ultra-sparse view CT imaging method based on X-ray2CTNet[J]. IEEE Transactions on Computational Imaging, 2022, 8: 733-742. DOI: 10.1109/TCI.2022.3201390.
[9] YING X, GUO H, MA K, et al. X2CT-GAN: Reconstructing CT from biplanar X-rays with generative adversarial networks[C]//Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2019: 10619-10628.
[10] HUANG C, LI K, FANG J, et al. 3DSP-GAN: A 3D-to-3D network for CT reconstruction from biplane X-rays[C]//2024 IEEE 7th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC). IEEE, 2024, 7: 931-935.
[11] SHI Z, GENG K, ZHAO X, et al. XRayWizard: Reconstructing 3-D lung surfaces from a single 2-D chest X-ray image via Vision Transformer[J]. Medical Physics, 2024, 51(4): 2806-2816. DOI: 10.1002/mp.16781.
[12] WANG Y, SUN Z L, ZENG Z, et al. TRCT-GAN: CT reconstruction from biplane X-rays using transformer and generative adversarial networks[J]. Digital Signal Processing, 2023, 140: 104123. DOI: 10.1016/j.dsp.2023.104123.
[13] 孙雪琴. 基于超稀疏视角CT成像的固体火箭发动机燃面退移测试方法研究[D]. 太原: 中北大学, 2024. DOI: 10.27470/d.cnki.ghbgc.2024.000018. SUN X Q. Testing method of solid rocket motor burning surfaceregression based on ultra-sparse view CT imaging[D]. Taiyuan: North University of China, 2024. DOI:10.27470/d.cnki.ghbgc.2024.000018. (in Chinese).
[14] 杨甜添. 基于多尺度特征和自注意力机制的MRI心脏图像分割算法研究[D]. 武汉: 武汉纺织大学, 2024. DOI: 10.27698/d.cnki.gwhxj.2024.000395. YANG T T. Research on MRI Heart Image segmentationalgorithm based on multi-scale features and self-attention mechanism[D]. Wuhan: Wuhan Textile University, 2024. DOI:10.27698/d.cnki.gwhxj.2024.000395. (in Chinese).
[15] 邱怡, 包乾宗, 马铭, 等. 基于U-Net网络的二维小波域地震数据随机噪声衰减[J]. 石油物探, 2023, 62(5): 878-890. DOI: 10.12431/issn.1000-1441.2023.62.05.007. QIU Y, BAO Q Z, MA M, et al. Seismic data random noise attenuation using U-Net network in the 2D discrete wavelet domain[J]. Geophysical Prospecting for Petroleum, 2023, 62(5): 878-890. DOI: 10.12431/issn.1000-1441.2023.62.05.007. (in Chinese).
[16] 孙卓群, 赵加祥. 基于多尺度注意力小波网络的可适应病变规模超声乳腺图像分割[J]. 微电子学与计算机, 2023, 40(12): 45-52. DOI: 10.19304/J.ISSN1000-7180.2022.0901. SUN Z Q, ZHAO J X. Adaptive lesion scale ultrasound breast image segmentation based on multi-scale attention wavelet network[J]. Microelectronics & Computer, 2023, 40(12): 45-52. DOI: 10.19304/J.ISSN1000-7180.2022.0901. (in Chinese).
[17] 苏申申, 周卫, 周淋芋, 等. 基于MobileViT轻量化网络的蘑菇图像分类算法改进[J]. 现代计算机, 2024, 30(21): 69-73. [18] 王苏恺. 基于深度学习的稀疏角CT重建算法研究[D]. 太原: 中北大学, 2022. DOI: 10.27470/d.cnki.ghbgc.2022.001319. WANG S K. Research on sparse-view CT reconstructionalgorithm based on deep learning[D]. Taiyuan: North University of China, 2022. DOI:10.27470/d.cnki.ghbgc.2022.001319. (in Chinese).
[19] 向锐. 基于边缘和结构一致性的红外−可见光图像转换算法研究[D]. 武汉: 华中科技大学, 2023. DOI: 10.27157/d.cnki.ghzku.2023.003074. XIANG R. Research on infrared-visible image conversion algorithm based on edge and structure consistency[D]. Wuhan: Huazhong University of Science and Technology, 2023. DOI:10.27157/d.cnki.ghzku.2023.003074. (in Chinese).
[20] SHEN L, ZHAO W, XING L. Patient-specific reconstruction of volumetric computed tomography images from a single projection view via deep learning[J]. Nature Biomedical Engineering, 2019, 3(11): 880-888. DOI: 10.1038/s41551-019-0466-4.











 下载:
下载: