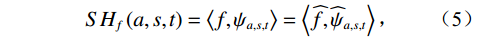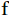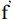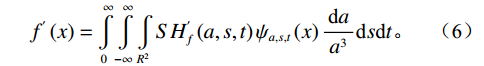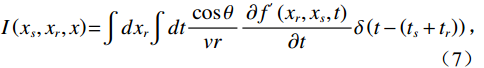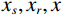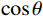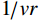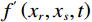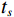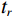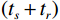Eight Directional Acoustic Logging Remote Detection Reflection Wave Imaging Technology: A Collaborative Imaging Framework Combining Shear Wave Transformation and Kirchhoff Migration
-
摘要:
随着非常规油气藏精细勘探的深入开展，对井旁复杂构造（如裂缝和溶洞）高分辨率成像的需求日益迫切。针对常规声波测井仪器分辨率不足的问题，本文依托新研制的八方位声波测井仪器，提出一种适用于复杂储层的基于剪切波变换和克希霍夫积分偏移协同成像方法。该方法具有多尺度稀疏表示能力，可以有效提取信道中微弱的反射波信号，并实现反射波能量的准确成像归位。通过理论模拟及实测井资料处理，验证所提方法对溶洞系统和双倾斜界面的识别能力，结果表明：该方法可提升反射波识别准确度与构造成像分辨率。研究成果为八方位测井仪器在复杂储层地质环境中的应用提供了技术支撑。
Abstract:As fine-scale exploration of unconventional oil and gas reservoirs advances, the need for high-resolution imaging of complex structures, such as fractures and cavities, near boreholes has become increasingly critical. To address the limited resolution of conventional acoustic logging tools, this paper presents a collaborative imaging method based on shear wave transformation and Kirchhoff integral migration. The approach is tailored for complex reservoirs and leverages a newly developed eight-directional acoustic logging instrument. The proposed method features multi-scale sparse representation capabilities, enabling effective extraction of weak reflected wave signals within the borehole environment and accurate imaging and localization of reflected wave energy. Its ability to identify karst cave systems and double-inclined interfaces has been validated through both theoretical simulations and real well data analysis. Results demonstrate that the method enhances the accuracy of reflected wave identification and improves the resolution of structural imaging. These findings offer technical support for the application of eight-directional logging instruments in geologically complex reservoir settings.
-
随着非常规油气资源的持续推进，深层、致密及构造复杂储层（如缝洞型碳酸盐岩、裂缝性页岩等）的探测需求日益迫切[1-2]。这类储层通常具有显著的非均质性、低孔隙度和渗透率、空间展布不连续、波阻抗突变频繁等地质特征。这些特征使得传统声波测井技术在探测深度和分辨率方面难以满足井周微小地质体（如裂缝和溶洞）的高精度成像需求[3-4]。为了实现更大探测范围、更高构造辨识精度的目标，发展具备远探测能力的高分辨声波成像技术，已成为提升储层表征效率与精度的关键突破口[5-6]。
在此背景下，本文基于新研制的八方位声波测井仪器，开发一种面向复杂储层的远探测反射波成像框架。声波远探测成像的核心在于从单极子纵波信号中提取微弱反射波，并将其准确归位于地下真实界面。然而在复杂储层条件下，该任务面临诸多挑战：一方面，滑行纵波与反射纵波在低频段的视速度差异较小，使得基于频-波数域的滤波方法在分离反射波时往往伴随着有效信号的能量损失，导致反射信息提取精度下降[7-8]。另一方面，井径变化与仪器旋转引起的直达波周期性改变会干扰常规中值滤波方法的准确性，进而影响反射波的识别与提取[9]，导致恢复构造复杂区域特征时产生“划弧”类伪影，显著干扰反射界面的真实刻画[9-11]。这些因素共同限制了声反射成像测井技术在非常规储层中的应用效果与推广范围。
针对上述问题，本文聚焦八方位测井仪器数据的处理流程，提出一种融合剪切波变换与克希霍夫积分偏移的远探测反射波协同成像方法。该方法充分结合剪切波变换在弱信号提取方面的多尺度稀疏表示能力[12-15]以及克希霍夫积分偏移在反射能量成像归位方面的高精度波动方程求解特性[16-18]。在处理八方位测井仪器数据时，该方法能够有效表征地质信号中的非线性与局部特征，通过将信号分解为不同尺度和方向的剪切波基函数，使得反射波与滑行波的高效分离，显著增强对高倾角裂缝等复杂构造的识别能力，实现对微弱反射信号的显著增强与背景干扰的有效抑制，将反射能量精准归位至实际地质界面。该方法在面对横向速度变化和仪器偏心等复杂工况时具有良好的稳定性，有效抑制由此带来的成像畸变。
本研究为实现八方位声波测井仪器的全方位远探测成像提供理论支撑和实验验证基础，拓展声波测井技术在复杂储层中的应用深度与适用性。
1. 方法原理
声反射成像测井资料处理技术由两大核心部分构成：反射波提取与偏移成像。在反射波提取环节，本文采用了剪切波变换技术，从阵列波形中提取反射波信息。进一步地，基于获得的反射波数据判断反射体所在的空间方位。在此基础上，对确定的反射体方位实施偏移成像处理，通过应用克希霍夫积分偏移方法，成功获取了井外反射体与井孔之间的相对位置。以下将详细阐述各部分方法的具体原理。
连续剪切波变换基本思想是通过尺度矩阵与剪切矩阵乘积构成剪切波序列函数。因此，连续剪切波变换依赖于缩放参数a，剪切参数s以及平移参数t。其连续变换形式如下所示：
$$ {\psi _{a,s,t}}(x) = {a^{ - \tfrac{3}{4}}}\psi \left( {{\rm A}_a^{ - 1}S_s^{ - 1}\left( {x - t} \right)} \right),\;a \in {R^ + },\;s \in R,\;t \in {R^2} \text{，} $$ (1) 其中，A和S对应于尺度矩阵和剪切矩阵，二者的具体形式如下：
$$ {A_a} = \left( {\begin{array}{*{20}{c}} a&0 \\ 0&{\sqrt a } \end{array}} \right),\;\;{S_s} = \left( {\begin{array}{*{20}{c}} 1&s \\ 0&1 \end{array}} \right) \text{，} $$ (2) 母函数
$ \psi $ 在傅里叶域的表达形式如下：$$ {\widehat \psi _{a,s,t}}(\omega ) = {a^{\tfrac{3}{4}}}{e^{ - 2\pi i\left\langle {\omega ,t} \right\rangle }}{\widehat \psi _1}(a{\omega _1}){\widehat \psi _2}\left( {{a^{ - \tfrac{1}{2}}}\left( {s + \frac{{{\omega _1}}}{{{\omega _2}}}} \right)} \right) \text{，} $$ (3) 则母函数
$ \widehat \psi $ 被定义为如下形式：$$ \widehat \psi \left( {{\xi _1},{\xi _2}} \right) = {\widehat \psi _1}\left( {{\xi _1}} \right){\widehat \psi _2}\left( {\frac{{{\xi _2}}}{{{\xi _1}}}} \right) \text{，} $$ (4) 其中，
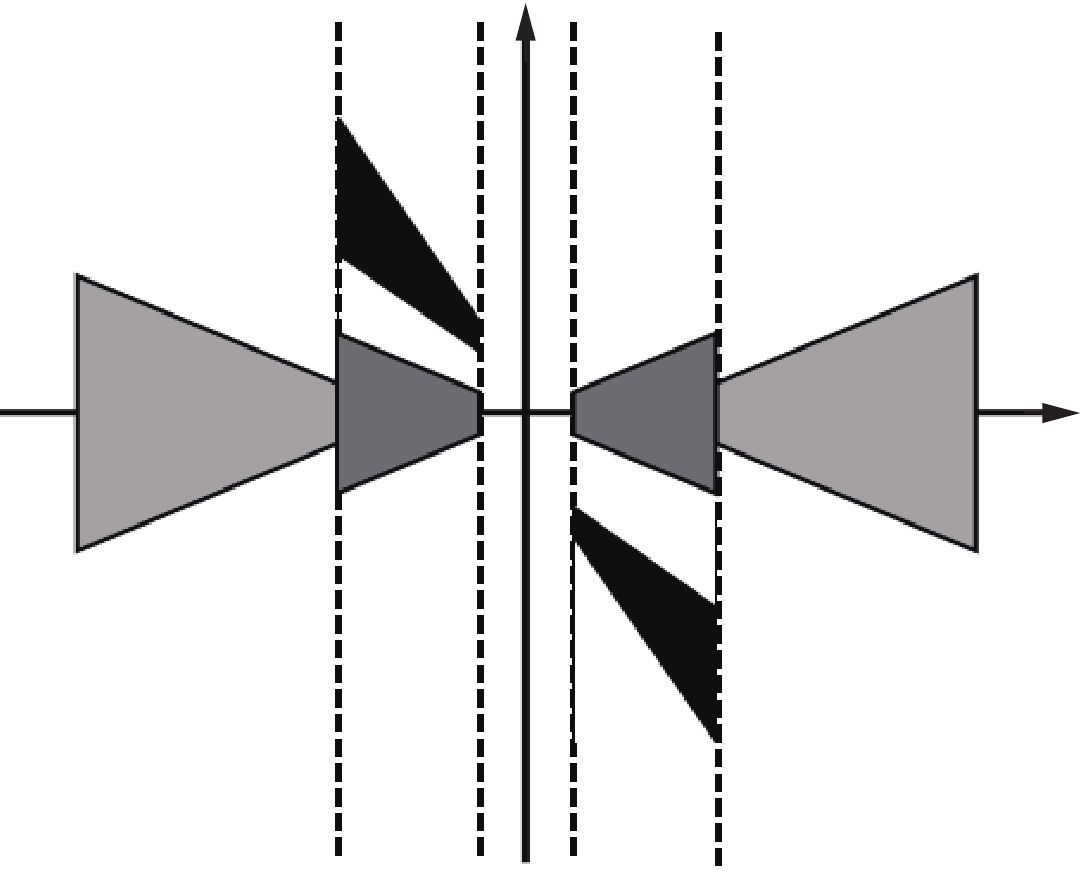
$ {\widehat \psi _1} $ 为连续小波函数，$ {\widehat \psi _2} $ 为bump函数，二者在频率域内均具有紧支撑结构。连续剪切波变换在频率域的剖分如图1所示。对于平方可积函数，定义其连续剪切波变换为：
$$ S{H_f}\left( {a,s,t} \right) = \left\langle {f,{\psi _{a,s,t}}} \right\rangle = \left\langle {\widehat f,{{\widehat \psi }_{a,s,t}}} \right\rangle \text{，} $$ (5) 其中，
$ \text{f} $ 为原始输入信号，SHf为剪切波系数。对剪切波系数进行阈值滤波等操作后得到所需的剪切波系数，随后通过剪切波逆变换重构得到输出信号$ {\text{f}}^{\text{'}} $ ：$$ {f^{'}}\left( x \right) = \int\limits_0^\infty {\int\limits_{ - \infty }^\infty {\int\limits_{{R^2}}^{} {SH_f^{'}\left( {a,s,t} \right){\psi _{a,s,t}}\left( x \right)\frac{{{\text{d}}a}}{{{a^3}}}{\text{d}}s{\text{d}}t} } } 。 $$ (6) 经剪切波变换处理后的稀疏反射波分量，将作为克希霍夫积分偏移的输入数据。这一数据流动过程，实现了“反射信号提取→反射信号成像”的首尾闭环，确保协同成像流程的信息传递与动态耦合。随后，输入至克希霍夫积分偏移的反射波数据，依据已知的速度模型，采用高频近似下的克希霍夫积分理论，逐点进行波场时空映射。该环节本质上依据地震波的传播机理，对剪切波变换提取的反射能量进行空间归位和叠加成像，从而实现井外复杂结构的高分辨率恢复。
克希霍夫积分解是波动方程解法的其中一种求解形式，实际上是基于惠更斯波动原理发展出的一种基于波动力学的数学解。该表达式描绘了由点源发出的波的传播特性，涵盖了波的传播时间、空间位置等关键信息，实际表达形式如下：
$$ I\left( {{x_s},{x_r},x} \right) = \int {d{x_r} \int {dt\frac{{\cos \theta }}{{vr}}} } \frac{{\partial {f^{'}}\left( {{x_r},{x_s},t} \right)}}{{\partial t}}\delta \left( {t - \left( {{t_s} + {t_r}} \right)} \right) \text{，} $$ (7) 其中，I为偏移成像结果，
$ {x_s},{x_r},x $ 分别为声源、接收器和井外成像点位置，$ \cos \theta $ 为倾角因子，$ {1 \mathord{\left/ {\vphantom {1 {vr}}} \right. } {vr}} $ 为球面波散射因子，$ {f^{'}}\left( {{x_r},{x_s},t} \right) $ 为由剪切波变换得到的阵列反射信号，$ {t_s} $ 和$ {t_r} $ 分别表示弹性波从声源传播至成像点和从成像点传播至接收器所需的时间。根据式（7）可知，克希霍夫积分偏移公式包括两个过程：一是根据速度场计算井外各空间点的走时信息，二是对阵列波形上$ \left( {{t_s} + {t_r}} \right) $ 时刻的振幅进行加权求和。本文提出的八方位声波测井仪器数据处理框架如图2所示，该框架不仅涵盖了剪切波变换方法与克希霍夫积分偏移成像技术，还根据实际需求，融入了方位矫正与波形合成处理等技术。
![]()
图 2 八方位声波测井仪器数据处理流程Figure 2. Data processing flow of eight directional acoustic logging instruments2. 数值实验
本文利用有限差分算法计算单极源声波测井模型。阵列接收器一组共13个，间距为
0.1524 m，距离声源3 m处为第一个接收器，共接收40组信号。为贴合生产现场，声源中心频率设置为f0=10 kHz[19-20]。该参数设置与后文实测数据所使用的仪器参数保持一致。2.1 多反射体模型
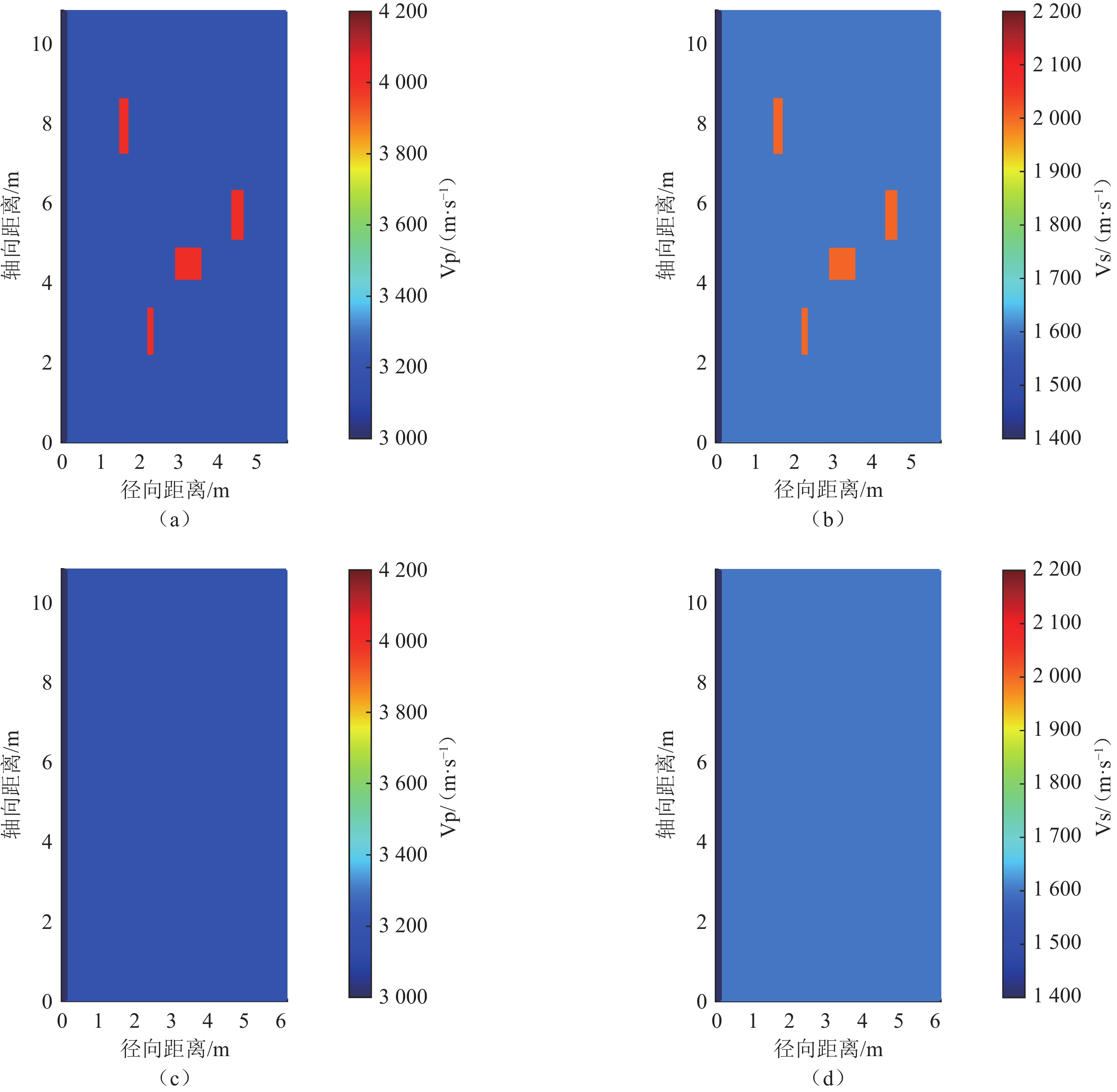
图3（a）和图3（b）为井外存在多个反射体的纵横波速度模型，背景纵横速度分别为
3300 m/s和1600 m/s，反射体的纵横波速度分别取4000 m/s和2000 m/s。图3（c）和图3（d）为均质模型，其速度与真实模型背景速度一致。通过有限差分方法分别计算在真实地层结构与均质结构中测井仪器接收到的波形信号，并对两者进行差值计算，从而得到由于反射界面存在而产生的反射波信号。![]()
图 3 井外含有多反射体时的（a）纵波和（b）横波速度模型，以及没有反射体时的均质模型（c）纵波和（d）横波均质模型Figure 3. (a) Longitudinal and (b) transverse wave velocity models with multiple reflectors outside the well as well as (c) longitudinal and (d) transverse wave homogenization models without reflectors.图4（a）展示了全波信号以及经过差值计算得到的真实反射波信号。由于反射体距离井轴位置较近，部分反射波信号与首波和导波发生了混叠，这将增加反射波提取的难度。图4（b）则展示了基于真实反射波数据应用克希霍夫积分偏移技术得到的成像结果，该结果与反射体的实际位置高度吻合，验证了克希霍夫积分偏移方法在构建井外模型方面的准确性。图4（c）对比了真实反射波信号与采用剪切波变换法提取的反射波信号。在信号重叠区域，反射波的提取质量欠佳，但后续部分的提取成效显著。对比图4（b）和图4（d），可以观察到经剪切波变换处理的反射波偏移成像结果与实际情况相近，但在能量强度上有所减弱。这表明剪切波变换法在反射波提取中具有一定的有效性，特别是在定位反射体位置方面表现良好，但在保持信号强度方面存在一定的局限性。
![]()
图 4 （a）全波波形与真实的反射波信号以及（b）利用真实的反射波信号偏移成像的结果；（c）真实的反射波信号与剪切波变换法提取的反射波信号以及（d）利用剪切波变换法提取的反射波信号偏移成像的结果Figure 4. (a) Full wave waveform and real reflected wave signal. (b) Results of imaging using the real reflected wave signal offset. (c) Real reflected and reflected wave signals extracted using the shear wave transformation method. (d) Offset imaging result of the reflected wave signal extracted using the shear wave transformation method2.2 倾斜界面模型
图5（a）和图5（b）分别展示了井外真实的纵横波速度结构，其中在距离井轴3.5 m和5 m的位置存在反射界面，地层纵波速度从左往右依次为
3300 m/s，3600 m/s和4000 m/s，横波速度为1600 m/s，1800 m/s和2000 m/s，其均质模型与算例一相同。![]()
图 5 井外存在双倾斜界面时的（a）纵波和（b）横波速度模型Figure 5. The velocity models of (a) longitudinal waves and (b) transverse waves when there is a double inclined interface outside the well图6（a）中，展示了在双层倾斜界面模型下计算获得的全波信号及其中的真实反射波信号。该模型中，反射界面被设定在距离井轴较远的位置，因此反射波信号未与纵波首波发生混叠，但仍有部分与横波首波及导波信号相混叠。尽管如此，相较于算例一，整体混叠程度有所减轻。图6（b）则揭示了克希霍夫积分偏移技术利用真实反射波数据得到的成像效果。结果显示，在反射体的实际位置附近，反演出较强的能量，表明成像技术有效。图6（c）通过对比，展示了真实反射波信号与采用剪切波变换法提取的反射波信号之间的差异。与算例一相比，在时间较晚的部分，由于混叠部分的减少，剪切波变换法提取的反射波效果更佳。对比图6（b）与图6（d），可以观察到，经过剪切波变换处理的反射波偏移成像结果与实际情况颇为接近，进一步验证了剪切波变换在反射波信号处理及成像中的有效性。
![]()
图 6 （a）全波波形与真实的反射波信号以及（b）利用真实的反射波信号偏移成像的结果；（c）真实的反射波信号与剪切波变换法提取的反射波信号以及（d）利用剪切波变换法提取的反射波信号偏移成像的结果Figure 6. (a) Full wave waveform and real reflected wave signal. (b) Results of imaging using the real reflected wave signal offset; (c) Real reflected and reflected wave signals extracted using the shear wave transformation method. (d) Offset imaging result of the reflected wave signal extracted using the shear wave transformation method3. 实测数据
为验证本文方法的有效性，选取枣新一井现场实测资料，对井深
1785 ~1820 m区段进行成像分析。该井段地层属于软地层，纵波速度介于2500 ~2800 m/s之间。成像处理中采用持续时间为8 ms的数据作为计算基础。图7（a）为滤波前的实测数据原始波形，可以看出信号中存在大量的噪声，反射波与直达波混叠，难以区分。经过剪切波变换滤波处理后，反射波与模式波得到了有效分离，波形更加清晰，反射波的特征更加明显。
![]()
图 7 实测数据（a）滤波前的波形；（b）滤波后的波形Figure 7. The waveform of the measured data (a) before filtering; (b) The filtered waveform图8（a）展现
1785 ~1820 m深度范围反射体方位随深度的变化趋势，包含10个接收器的综合结果。可以看出反射体在1785 ~1815 m深度主要集中在井旁90°左右，即井孔正东方；反射体在1815~1820 m深度方位略有所改变。上述结果为地质构造的识别提供了直观的依据。图8（b）中以井旁的径向位置作为横轴，深度作为纵轴，构建了直观的地层剖面图像。利用不同的颜色对井周地质构造进行刻画，红色表示该位置具有较强的反射体，深蓝色表示该位置存在较弱或者不存在反射体。根据方位识别结果绘制了井旁方位3（90°）的反射体成像结果，成像范围包括轴向45 m径向5 m的空间。在轴向距离约为1805 m和1823 m的位置附近，观察到两个强度尤为突出的能量区域（黄色线框）。这些区域靠近井轴，因此其反射波强度更大，初步判断为潜在的射孔区域。在图像的右上方，一个由白色线框界定的范围内，其成像结果与多反射体数值算例反射结果相似，判断该处为速度异常介质。![]()
图 8 （a）反射体方位识别结果与（b）对应方位成像结果Figure 8. (a) Reflector orientation recognition results and (b) corresponding orientation imaging results4. 讨论
本文提出的基于剪切波变换与克希霍夫积分偏移的协同成像方法，具有较好的成像精度。然而，在实际应用中，该方法对强噪声背景或极薄层结构的处理仍受限于信号能量衰减，导致分辨率不足。对此，可结合VMD与剪切波变换构建多层次信号分解框架，利用VMD的模态分离优势增强反射波提取的鲁棒性；或引入卷积神经网络优化剪切波变换的尺度参数，适应复杂井况下的信号特征。针对低信噪比问题，可开发基于物理约束的自适应正则化算法，或利用多分量数据联合反演策略，提升成像稳定性。此外，克希霍夫积分偏移的计算复杂度较高，在三维大规模成像任务中，计算效率成为制约其实时应用的瓶颈。可探索并行计算框架（如GPU加速）或量子计算技术，通过量子算法优化矩阵运算和积分迁移过程，大幅降低计算成本。这些改进将推动方法在深层致密储层、碳酸盐岩储层等非常规油气勘探中的广泛应用。
5. 结论
本文围绕远探测反射波成像问题，依托新研制的八方位声波测井仪器，构建了一种融合剪切波变换与克希霍夫积分偏移的协同成像框架，为复杂储层条件下的高精度油气勘探提供了坚实的技术支撑。本文研究工作为八方位全覆盖成像奠定了理论与实验基础。在数值模拟方面，本文设计了多反射体模型与倾斜界面模型两种典型构造情形进行验证。在多反射体模型中，反射波与直达波、导波信号混叠显著，增加了波场分离的难度。即便如此，本文提出的协同成像方法仍能有效提取反射波信号，且得到的成像结果与模型实际构造较为一致。在倾斜界面模型中，混叠程度相对减弱，反射波提取效果较为理想，偏移结果亦展现出良好的反演精度，进一步验证了该协同成像方法的稳健性与普适性。在实际测井数据处理中，本文提出的方法将反射波与模式波的分离，偏移成像结果可识别井旁反射体的空间分布，重建了地层构造剖面，显示出良好的应用效果。综上所述，本文提出的协同成像方法在井旁复杂构造识别中具备较高的精度与稳定性，为声反射成像测井技术在深层及非常规油气储层中的推广应用奠定了基础。
-
![]()
图 2 八方位声波测井仪器数据处理流程
Figure 2. Data processing flow of eight directional acoustic logging instruments
![]()
图 3 井外含有多反射体时的（a）纵波和（b）横波速度模型，以及没有反射体时的均质模型（c）纵波和（d）横波均质模型
Figure 3. (a) Longitudinal and (b) transverse wave velocity models with multiple reflectors outside the well as well as (c) longitudinal and (d) transverse wave homogenization models without reflectors.
![]()
图 4 （a）全波波形与真实的反射波信号以及（b）利用真实的反射波信号偏移成像的结果；（c）真实的反射波信号与剪切波变换法提取的反射波信号以及（d）利用剪切波变换法提取的反射波信号偏移成像的结果
Figure 4. (a) Full wave waveform and real reflected wave signal. (b) Results of imaging using the real reflected wave signal offset. (c) Real reflected and reflected wave signals extracted using the shear wave transformation method. (d) Offset imaging result of the reflected wave signal extracted using the shear wave transformation method
![]()
图 5 井外存在双倾斜界面时的（a）纵波和（b）横波速度模型
Figure 5. The velocity models of (a) longitudinal waves and (b) transverse waves when there is a double inclined interface outside the well
![]()
图 6 （a）全波波形与真实的反射波信号以及（b）利用真实的反射波信号偏移成像的结果；（c）真实的反射波信号与剪切波变换法提取的反射波信号以及（d）利用剪切波变换法提取的反射波信号偏移成像的结果
Figure 6. (a) Full wave waveform and real reflected wave signal. (b) Results of imaging using the real reflected wave signal offset; (c) Real reflected and reflected wave signals extracted using the shear wave transformation method. (d) Offset imaging result of the reflected wave signal extracted using the shear wave transformation method
![]()
图 7 实测数据（a）滤波前的波形；（b）滤波后的波形
Figure 7. The waveform of the measured data (a) before filtering; (b) The filtered waveform
-
[1] 张银涛, 林承焰, 罗枭, 等. 深层缝洞体地震特征提取与能量脊线追踪[J]. 石油地球物理勘探, 2024, 59(5): 1132-1140. DOI: 10.13810/j.cnki.issn.1000-7210.2024.05.017. ZHANG Y T, LIN C Y, LUO X, et al. Method for extracting seismic features and tracing energy ridges in deep fractured-vuggy reservoirs[J]. Oil Geophysical Prospecting, 2024, 59(5): 1132-1140. DOI: 10.13810/j.cnki.issn.1000-7210.2024.05.017.
[2] 李宇航, 张宏, 张军华, 等. 油页岩勘探开发现状及进展[J]. CT理论与应用研究, 2014, 23(6): 1051-1063. LI Y H, ZHANG H, ZHANG J H, et al. The present situation and progress of oil shale exploration and exploitation[J]. CT Theory and Applications, 2014, 23(6): 1051-1063. (in Chinese).
[3] 张恒荣, 肖立志, 曾少军, 等. 基于裂缝柔度和地应力模型的声电测井正、反演方法及应用[J]. 石油地球物理勘探, 2023, 58(2): 431-442. DOI: 10.13810/j.cnki.issn.1000-7210.2023.02.020. ZHANG H R, XIAO L Z, ZENG S J, et al. Forward and inversion methods and application of acoustoelectric logging based on fracture compliance and crustal stress model[J]. Oil Geophysical Prospecting, 2023, 58(2): 431-442. DOI: 10.13810/j.cnki.issn.1000-7210.2023.02.020.
[4] 罗辉, 沈金松, 张文学, 等. 裂缝性储层阵列声波成像测井响应模拟及速度频散特征研究[J]. CT理论与应用研究(中英文), 2024, 33(6): 747-760. DOI: 10.15953/j.ctta.2024.107. LUO H, SHEN J S, ZHANG W X, et al. Study on the numerical simulation of array sonic logging responses and their velocity dispersion characteristics in fractured formation[J]. CT Theory and Applications, 2024, 33(6): 747-760. DOI: 10.15953/j.ctta.2024.107.
[5] 李超, 岳文正, 金行林, 等. 声反射成像测井数据处理研究进展[J]. 测井技术, 2013, 37(1): 13-20. DOI: 10.16489/j.issn.1004-1338.2013.01.003. LI C, YUE W Z, JIN X L, et al. Progresses of Data processing methods for acoustic reflection lmaging logging[J]. Well Logging Technology, 2013, 37(1): 13-20. DOI: 10.16489/j.issn.1004-1338.2013.01.003. (in Chinese).
[6] 张承森, 肖承文, 刘兴礼, 等. 远探测声波测井在缝洞型碳酸盐岩储集层评价中的应用[J]. 新疆石油地质, 2011, 32(3): 325-328. ZHANG C S, XIAO C W, LIU X L, et al. Application of Remote Detection Acoustic Reflection Logging to Fractured-Vuggy Carbonate Reservoir Evaluation[J]. Xinjiang Petroleum Geology, 2011, 32(3): 325-328. (in Chinese).
[7] HORNBY B E. Imaging of near-borehole structure using full-waveform sonic data[J]. Geophysics, 1989, 54(6): 747-757. DOI: 10.1190/1.1442702.
[8] 王兵, 陶果, 王华, 等. 阵列声波测井中反射纵波和横波信号提取方法[J]. 中国石油大学学报(自然科学版), 2011, 35(2): 57-63. DOI: 10.3969/j.issn.1673-5005.2011.02.010. WANG B, TAO G, WANG H, et al. Extraction method of P and S reflection waves from array acoustic logging data[J]. Journal of China University of Petroleum, 2011, 35(2): 57-63. DOI: 10.3969/j.issn.1673-5005.2011.02.010.
[9] 张恒. 偶极远探测反射波提取及成像方法研究[D]. 北京: 中国石油大学(北京), 2021. ZHANG H. The study of reflection extraction and imaging methods of dipole array acoustic logging[D]. Beijing: China University of Petroleum (Beijing), 2021. (in Chinese).
[10] 杨晓东, 秦宁, 王延光. 常用叠前深度偏移方法特点分析与实例对比[J]. 地球物理学进展, 2015, 30(2): 740-745. DOI: 10.6038/pg20150235. YANG X D, QING N, WANG Y G. Analysis and examples of commonly used prestack depth migration methods[J]. Progress in Geophysics, 2015, 30(2): 740-745. DOI: 10.6038/pg20150235. (in Chinese).
[11] TANG X M, PATTERSON D J. Single-well S-wave imaging using multicomponent dipole acoustic-log data[J]. Geophysics, 2009, 74(6): WCA211-WCA223. DOI: 10.1190/1.3227150.
[12] CHEN J, YUE W, LI C, et al. Extracting reflected waves from acoustic logging data based on the shearlet transform[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(11): 1688-1692. DOI: 10.1109/LGRS.2019.2908286.
[13] WANG X, LIU S. Noise suppressing and direct wave arrivals removal in GPR data based on Shearlet transform[J]. Signal processing, 2017, 132: 227-242. DOI: 10.1016/j.sigpro.2016.05.007.
[14] ASSOUS S, ELKINGTON P. Shearlets and sparse representation for microresistivity borehole image inpainting[J]. Geophysics, 2018, 83(1): D17-D25. DOI: 10.1190/geo2017-0279.1.
[15] HÄUSER S, STEIDL G. Fast finite shearlet transform[J]. arXiv preprint arXiv: 1202.1773, 2012. DOI: 10.48550/arXiv.1202.1773.
[16] Pu Y, Liu G, Wang D, et al. Wave-equation traveltime and amplitude for Kirchhoff migration[C]//First International Meeting for Applied Geoscience & Energy. Society of Exploration Geophysicists, 2021: 2684-2688.
[17] YUE Y, LIU Y, GRAY S H. Accelerating least-squares Kirchhoff time migration using beam methodology[J]. Geophysics, 2021, 86(3): S221-S234. DOI: 10.1190/geo2020-0629.1.
[18] TANG X M, PATTERSON D J. Single-well S-wave imaging using multicomponent dipole acoustic-log data[J]. Geophysics, 2009, 74(6): WCA211-WCA223. DOI: 10.1190/1.3227150.
[19] ARIAN A, ALTHOFF G, VARSAMIS G L, et al. A new MWD full wave dual mode sonic tool design and case histories[C]//SPWLA Annual Logging Symposium. SPWLA, 1999: SPWLA-1999-F.
[20] MARKET J, BILBY C. Introducing the first LWD crossed-dipole sonic imaging service[C]//SPWLA Annual Logging Symposium. SPWLA, 2011: SPWLA-2011-DDD.
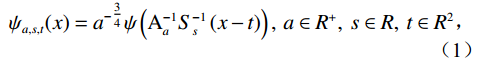
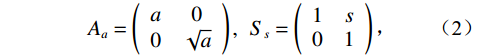
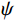
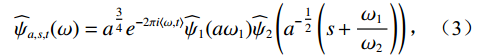
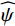
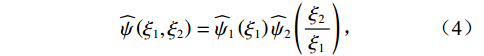
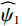
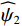
下载:
计量
- 文章访问数: 55
- HTML全文浏览量: 5
- PDF下载量: 7
