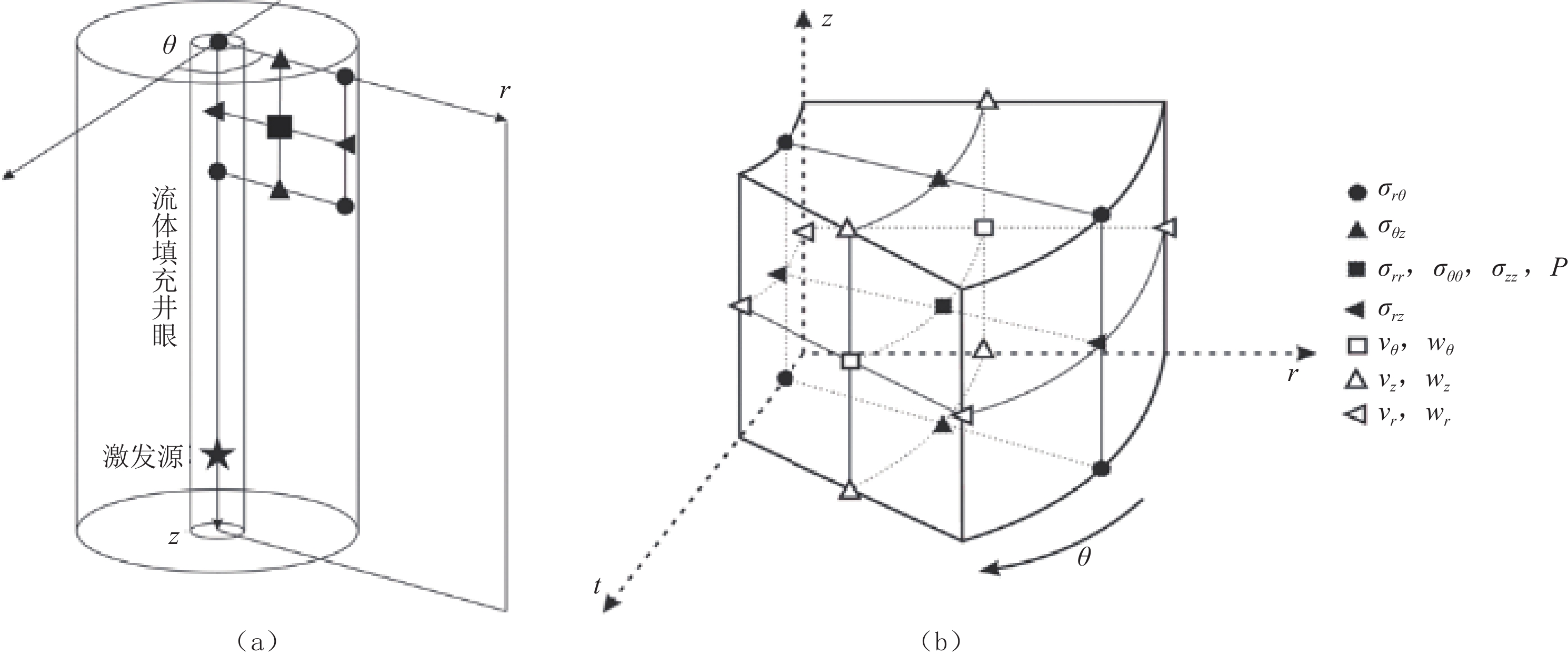
Study on the Numerical Simulation of Array Sonic Logging Responses and Their Velocity Dispersion Characteristics in Fractured Formation
-
摘要:
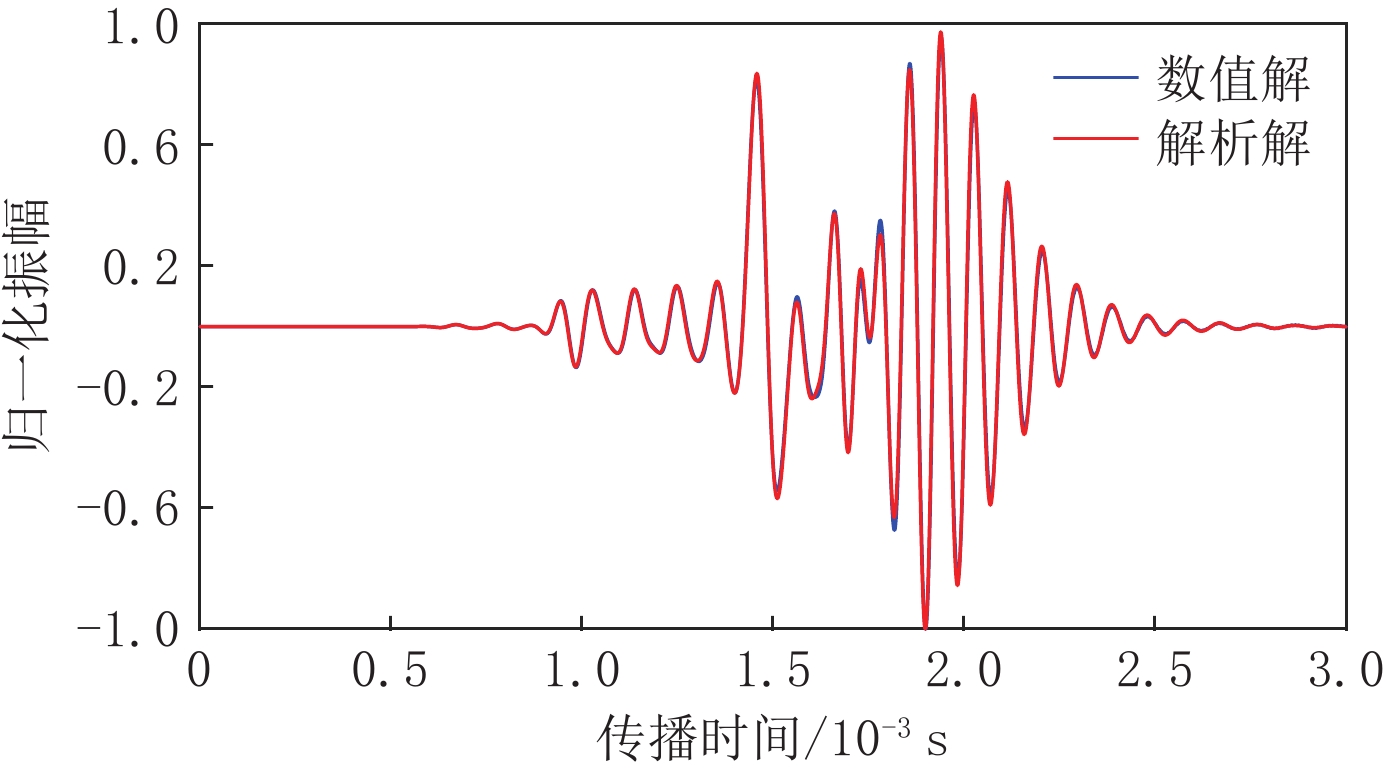
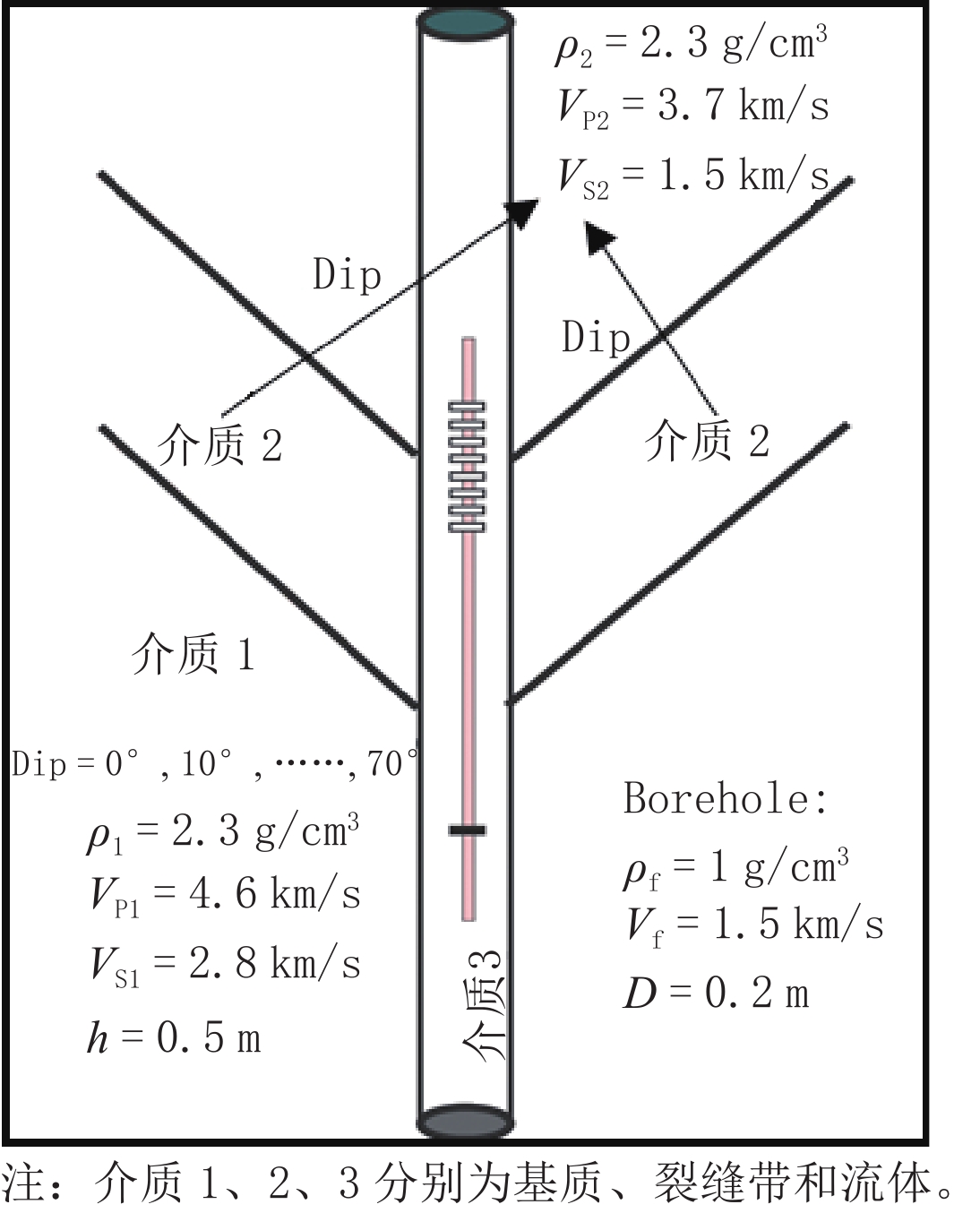
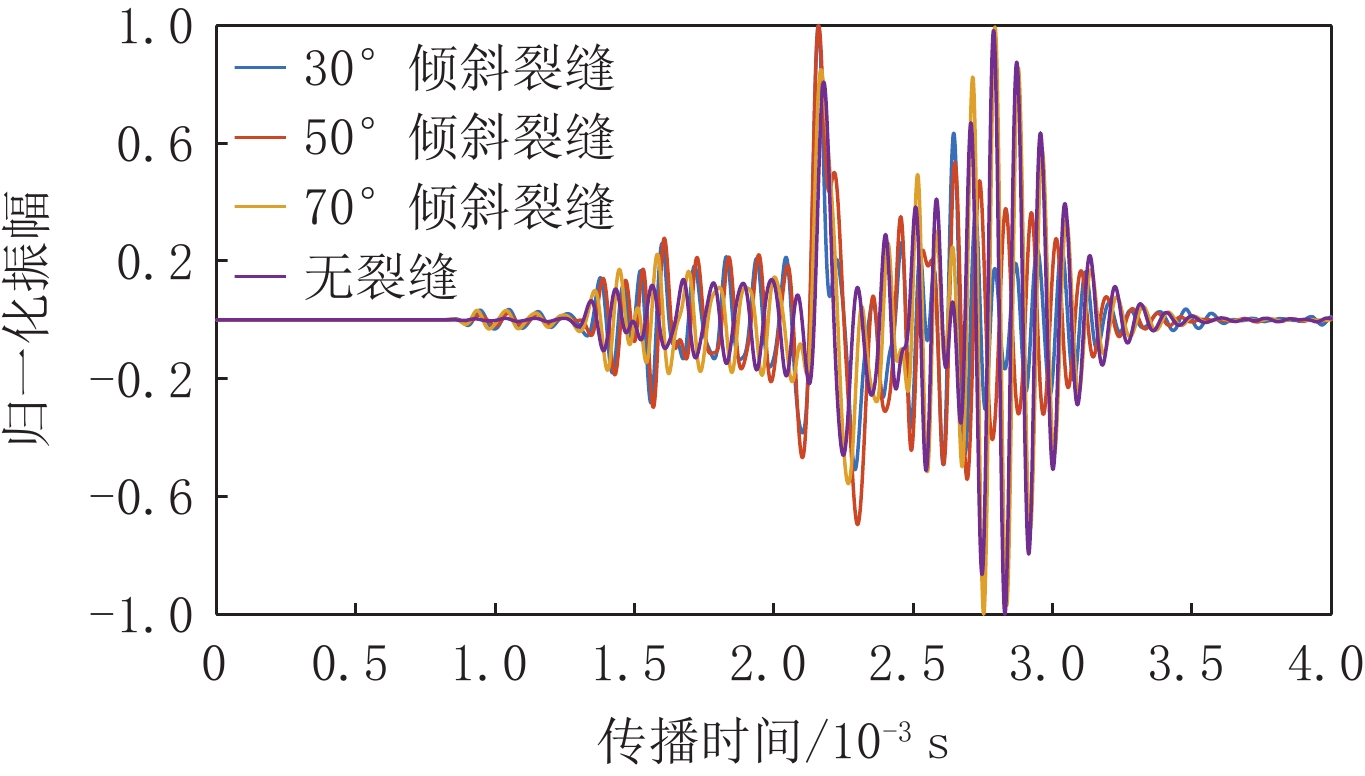
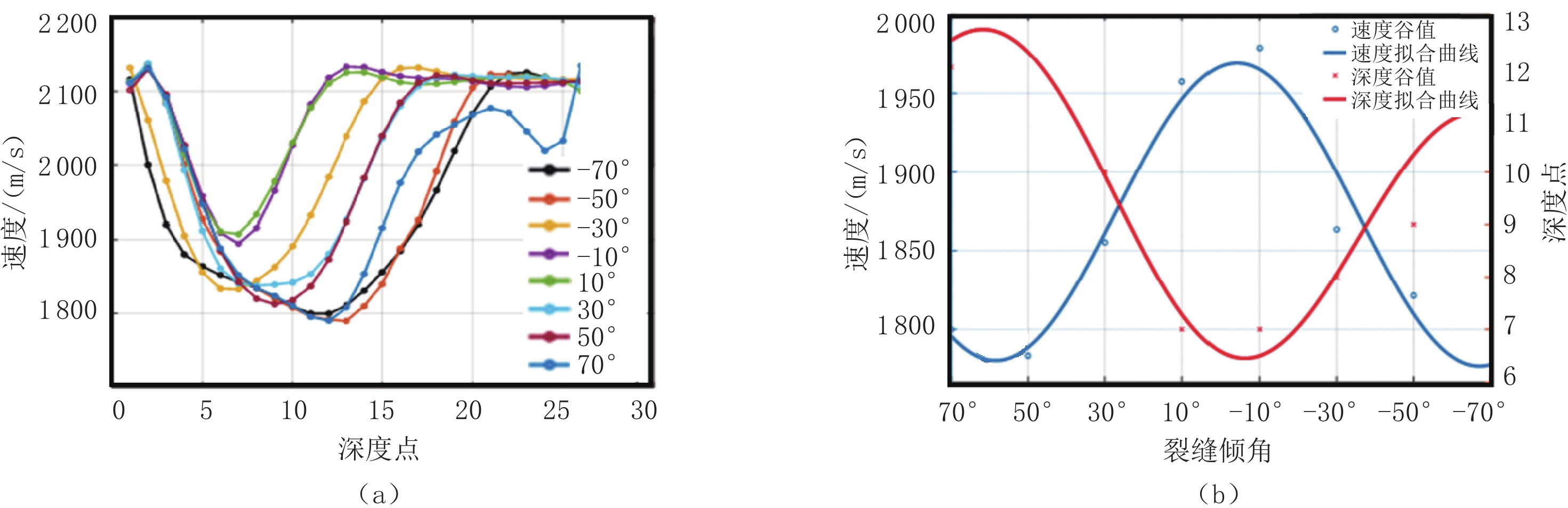
为分析裂缝性储层中裂缝发育带对阵列声波测井响应的影响，本文采用交错网格有限差分算法实现孔弹介质阵列声波测井波列响应的数值模拟。通过对模拟波形速度频散信息的提取，总结裂缝发育带与扩径井段不同模式波的吸收衰减与速度频散响应特征的差异性。首先基于Biot孔弹介质模型导出柱坐标下弹性波的速度-应力方程；其次，用交错网格有限差分方法对孔弹波动方程进行离散化，为提高模拟算法效率与精度，使用高阶差分格式与NPML；最后，基于含倾斜裂缝带模型与井壁坍塌地层模型的响应模拟，用前后向振幅相位估计法分析阵列声波的波形幅度相位响应特征与速度频散的差异性。结果表明，低速裂缝带纵横波波场时差会增大，且衰减幅度随裂缝带倾角变化；井壁塌陷在径向与轴向上扩大时，会增强斯通利波与伪瑞利波衰减。声波纵横波时差、速度频散与幅度衰减均可反映一定的裂缝带特征，这些影响对评价和开发裂缝性储层具有重要意义。
Abstract:To understand the effects of fractured formation on the responses of array sonic logging, the wave propagation of array acoustic logging was simulated based on the staggered grid finite difference method and poroelastic theory. Methods of velocity dispersion analysis and attenuation estimation were carried out on simulated sonic waveforms, and the differences of velocity dispersion and wave amplitude attenuation among these wave modes were summarized. First, the velocity-stress equation in cylindrical coordinates was deduced for the Biot poroelastic model. Next, the velocity-stress wave equation was discretized by using the staggered grid finite difference method. Furthermore, the higher order finite difference format and nearly perfect match layer (NPML) were adopted to improve the efficiency and accuracy of the finite difference method. Finally, simulated sonic waveforms in formation models with a tilted fracture zone and collapsed interval were applied to the velocity dispersion analysis by using forward and back amplitudes and the phase estimation method. The results show that the time difference of the P and S wave field in the low-velocity fracture zone increases and that the attenuation amplitude changes with the dip angle of the fracture zone. The attenuation of Stoneley waves and pseudo-Rayleigh waves is enhanced when the shaft collapse expands in the radial and axial directions. The time difference of acoustic waves, velocity dispersion, and amplitude attenuation can reflect the characteristics of the fracture zone, which is of great significance to the evaluation and development of fractured reservoirs.
-
![]()
图 2 轴向对称性地层的配置（a）与非轴对称空间域离散化的交错网格剖分示意图（b）
Figure 2. Scheme of formation with (a) axial symmetric and (b) asymmetric staggered grids in a three-dimensional discretized space domain
![]()
图 7 有限差分数值解与经典波数积分解结果对比
Figure 7. Comparisons between FD numerical simulation results and those of a classic wave number integral
![]()
图 9 （a）基质地层，（b）30°，（c）50°，（d）70°倾斜裂缝带地层模型的波场模拟结果
Figure 9. (a) No slow formation, (b) inclined slow formation (dip = 30), (c) inclined slow formation (dip = 50), (d) inclined slow formation (dip = 70)
![]()
图 10 源处于5 m处时7.59 m处第1个接收器在4个模型中的全波波形
Figure 10. Waveforms of the first receiver when the source is at 5.0 and the receiver is at 7.59 m in four models
![]()
图 11 含50°倾角裂缝带与基质地层在7.59 m处的频率-慢度图
Figure 11. Dispersion plot velocity slowness at 7.59 m, (a) formation with an inclined fracture zone （dip=50） and （b） matrix formation
![]()
图 12 8个不同倾角裂缝带地层模型的模拟波形用STC方法提取横波速度谷值点随倾角与深度的变化
注：（a）速度随裂缝带倾角与深度的变化，（b）速度谷值点随裂缝带倾角与深度的变化。
Figure 12. STC analysis of simulated scenarios with different inclined sediments
![]()
图 13 8个不同倾角裂缝带地层模型的模拟波形用STC方法提取纵波速度谷值点随倾角与深度的变化
注：（a）速度随裂缝带倾角与深度的变化，（b）速度谷值点随裂缝带倾角与深度的变化。
Figure 13. STC analysis of simulated scenarios with different inclined sediments
![]()
图 14 含径向（a）和纵向（b）扩径模拟地层配置示意图
Figure 14. Scheme of simulated formation configurations with radial borehole enlargement (a) and vertical borehole enlargement (b)
![]()
图 15 （a）无扩径，（b）0.2 m扩径，（c）0.4 m扩径，（d）0.6 m扩径全波列数据
Figure 15. Full waveform data of (a) no enlargement, and with enlargement of (b) 0.2 m, (c) 0.4 m and (d) 0.6 m
![]()
图 17 （a）无扩径，（b）扩径范围0.4 m，（c）扩径范围0.8 m，（d）扩径范围1.2 m全波列数据
Figure 17. Full waveform data with (a) no enlargement and enlargement of (b) 0.4 m, (c) 0.8 m and (d) 1.2 m
![]()
图 16 （a）0.2 m扩径，（b）0.6 m扩径在8.59 m处的FBAPES结果
Figure 16. FBAPES results at 8.59 m of (a) 0.2 m and (b) 0.6 m
表 1 含倾斜慢速地层模型物性参数
Table 1 Simulated parameters of inclined slow formation
分区介质 分层位置 固相参数 流相参数 耦合参数 耗散参数 A11 A13 A44 ρ11 R ρ22 Q ρ12 b 井中流体 0.1 R/m 2.25 2.25 0 1.00 0 1.00 0 0 0 基质地层 3.0 R/m 43.39 13.62 14.89 2.27 0.30 0.16 1 -0.06 1 慢速地层 -6.7 Z/m 8.00 2.24 2.88 2.08 0.30 0.16 1 -0.06 1 
下载: 导出CSV
表 2 阵列声波测井模拟参数
Table 2 Simulated schematic for array sonic logging
参数 取值 起始深度/m -11 结束深度/m -6 深度间隔/m 0.2 源类型 单极子源 子波类型 Ricker子波 采样点数 12000 采样间隔/μs 0.47 首接收器与源的距离/m 2.59 接收器间隔/m 0.152 接收器数量 8
下载: 导出CSV
表 3 阵列声波测井模拟参数
Table 3 Simulated parameters of inclined slow formation
分区介质 分层位置 固相参数 流相参数 耦合参数 耗散参数 A11 A13 A44 ρ11 R ρ22 Q ρ12 b 井中流体 0.1 R/m 2.25 2.25 0 1.00 0 1.00 0 0 0 快速地层 3.0 R/m 43.39 13.62 14.89 2.27 0.30 0.16 1 -0.06 1 坍塌填充 -7.0 Z/m 2.25 2.25 0 1.00 0 1.00 0 0 0
下载: 导出CSV
-
[1] 漆立新. 塔里木盆地顺托果勒隆起奥陶系碳酸盐岩超深层油气突破及其意义[J]. 中国石油勘探, 2016, 21(3): 38-51. QI L X. Oil and gas break through in ultra-deep ordovician carbonate formations in Shuntuoguole, Uplift Tarim Basin[J]. China Petroleum Exploration, 2016, 21(3): 38-50. (in Chinese).
[2] 焦方正. 塔里木盆地顺北特深碳酸盐岩断溶体油气藏发现意义与前景[J]. 石油与天然气地质, 2018, 39(2): 207-216. JIAO F Z. Significance and prospect of ultra-deep carbonate fault karst reservoirs in Shunbei area, Tarim Basin[J]. Oil & Gas Geology, 2016, 39(2): 207-216. (in Chinese).
[3] 苏可嘉, 秦臻, 邓呈祥, 等. 致密砂岩裂缝填充识别及其测井响应特征——以鄂尔多斯盆地镇泾油田延长组为例[J]. 科学技术与工程, 2022, 22(21): 9095−9104. DOI: 10.3969/j.issn.1671-1815.2022.21.011. SU K J, QIN Z, DENG C X, et al. Fracture filling identification and logging response characteristics of tight sandstone: A case study of Yanchang Formation in Zhenjing oilfield, Ordos Basin[J]. Science Technology and Engineering, 2022, 22(21): 9095−9104. DOI: 10.3969/j.issn.1671-1815.2022.21.011. (in Chinese).
[4] 唐晓明, 魏周拓. 利用井中偶极声源远场辐射特性的远探测测井[J]. 地球物理学报, 2012, 55(8): 2798-2807. TANG X M, WEI Z T. Single-well acoustic reflection imaging using far-field radiation characteristics of a borehole dipole source[J]. Chinese Journal of Geophysics, 2012, 55(8): 2798-2807. (in Chinese).
[5] 陆云龙, 崔云江, 关叶钦, 等. 基于阵列声波测井的裂缝有效性定量评价方法[J]. 测井技术, 2022, 46(1): 64−70. LU Y L, CUI Y J, GUAN Y Q, et al. Quantitative evaluation method of fracture effectiveness based on array acoustic logging[J]. Well Logging Technology, 2022, 46(1): 64−70. (in Chinese).
[6] 张波, 李超, 张晋言, 等. 三维声波测井探测特性分析与处理技术应用[J]. 应用声学, 2021, 40(5): 774−784. ZHANG B, LI C, ZHANG J Y, et al. Analysis of detecting characteristics and application of data processing technology for 3D array acoustic logging[J]. Journal of Applied Acoustics, 2021, 40(5): 774−784. (in Chinese).
[7] 本建林, 车小花, 乔文孝, 等. 方位反射声波成像测井技术在井旁地质体评价中的应用[J]. 测井技术, 2021, 45(1): 23−29. BEN J L, CHE X H, QIAO W X, et al. Application of near borehole geologic reflector evaluation using azimuthal acoustic reflection imaging logging[J]. Well Logging Technology, 2021, 45(1): 23−29. (in Chinese).
[8] 楚泽涵, 徐凌堂, 尹庆文, 等. 远探测反射波声波测井方法实验研究进展[J]. 测井技术, 2005, 29(2): 98−101. DOI: 10.3969/j.issn.1004-1338.2005.02.003. CHU Z H, XU L T, YIN Q W, et al. Progress of lab study on remote exploration acoustic reflection logging methods[J]. Well Logging Technology, 2005, 29(2): 98−101. DOI: 10.3969/j.issn.1004-1338.2005.02.003. (in Chinese).
[9] 乔文孝, 车小花, 李刚, 等. 反射声波成像测井的物理模拟[J]. 石油物探, 2004, (3): 294-297. QIAO W X, CHE X H, LI G, et al. The physical modeling of acoustic reflection image logging[J]. Geophysical Prospecting for Petroleum, 2004, 43(3): 294-297. (in Chinese).
[10] 陶果, 何峰江, 王兵, 等. 声反射成像测井在地层中的三维波场模拟方法研究[J]. 中国科学(D辑: 地球科学), 2008, 38(S1): 166−173. TAO G, HE J F, WANG B. Study on numerical modeling of three-dimension wave field of acoustic reflection image logging in formation[J]. Science in China: Esrarth Science, 2008, 38(S1): 166−173. (in Chinese).
[11] TANG X M. Imaging near-borehole structure using directional acoustic-wave measurement[J]. Geophysics, 2004, 69(6): 1378−1386. DOI: 10.1190/1.1836812.
[12] TANG X M, PATTERSON D J. Single-well S-wave imaging using multicomponent dipole acoustic-log data[J]. Geophysics, 2009, 74(6): WCA211−WCA223. DOI: 10.1190/1.3227150.
[13] NOLTE B, CHENG A. Estimation of nonorthogonal shear wave polarizations and shear wave velocities from four-component dipole logs[R]. USA: The Annual Technology Report of The Earth Resources Laboratory (ERL), MIT, 1996.
[14] NOLTE B, RAO R, HUANG X J. Dispersion analysis of split flexural waves[R]. USA: The Annual Technology Report of the Earth Resources Laboratory (ERL), MIT, 1997.
[15] LI W, TAO G, MATUSZYK J P, et al. Forward and backward amplitude and phase estimation method for dispersion analysis of borehole sonic measurements[J]. Geophysics, 2015, 80(3): D295−D308. DOI: 10.1190/geo2014-0298.1.
[16] 王瑞甲, 乔文孝, 鞠晓东. 一种多通道声波测井信号频散分析方法[J]. 测井技术, 2012, 36(2): 135−140. DOI: 10.3969/j.issn.1004-1338.2012.02.006. WANG R J, QIAO W X, JU X D. A multi-channel acoustic logging signal dispersion analysis method[J]. Well Logging Technology, 2012, 36(2): 135−140. DOI: 10.3969/j.issn.1004-1338.2012.02.006. (in Chinese).
[17] 刘航, 陈彦竹, 姚梦麟, 等. 基于纵波频散谱的缝洞碳酸盐岩储层有效性评价[J]. 测井技术, 2021, 45(3): 330−335. LIU H, CHEN Y Z, YAO M L, et al. Effectiveness evaluation of fractured vuggy carbonate reservoir based on P-wave dispersion spectrum[J]. Well Logging Technology, 2021, 45(3): 330−335. (in Chinese).
[18] ZHANG C, CHEN D, HU H S, et al. A method for transforming aliased modes to true modes based on density clustering and Riemann sheets selection in acoustic logging dispersion inversion[J]. Geophysics, 2024, 89(1): D15−D29. DOI: 10.1190/geo2022-0706.1.
[19] CHEN D, GUAN W, ZHANG C, et al. High-resolution inversion for dispersion characteristics of acoustic logging waveforms[J]. Journal of Geophysics and Engineering, 2020, 17(3): 439−450. DOI: 10.1093/jge/gxaa003.
[20] GUAN W, HU H S, HE X. Finite-difference modeling of the monopole acoustic logs in a horizontally stratified porous formation[J]. Journal of the Acoustical Society of America, 2009, 125(4): 1942−1950. DOI: 10.1121/1.3081518.
[21] LI X F. PML absorbing boundary condition for seismic numerical modeling by convolutional differentiator in fluid-saturated porous media[J]. Journal of Earth Science, 2011, (22): 377−385.
[22] GUAN W, HU H S. The parameter averaging technique in finite-difference modeling of elastic waves in combined structures with solid, fluid and porous subregions[J]. Communications in Computational Physics, 2011, 10(3): 695-715.
[23] COLLINO F, TSOGKA C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 2001, 66(1): 294−307. DOI: 10.1190/1.1444908.
[24] PAN C D, ABUBAKAR A, HABASHY T M. An effective perfectly matched layer design for acoustic fourth-order frequency-domain finite-difference scheme[J]. Geophysical Journal International, 2012, 188(1): 211−222. DOI: 10.1111/j.1365-246X.2011.05244.x.
[25] WANG H, TAO G, SHANG X F, et al. Stability of finite difference numerical simulations of acoustic logging-while-drilling with different perfectly matched layer schemes[J]. Applied Geophysics, 2013, 10: 384−396. DOI: 10.1007/s11770-013-0400-6.
[26] 李宁, 王克文, 刘鹏, 等. 不同裂缝条件下斯通利波幅度衰减实验[J]. 石油勘探与开发, 2021, 48(2): 258−265. DOI: 10.11698/PED.2021.02.03. LI N, WANG K W, LIU P, et al. Experimental study on attenuation of Stoneley wave under different fracture factors[J]. Petroleum Exploration and Development, 2021, 48(2): 258−265. DOI: 10.11698/PED.2021.02.03. (in Chinese).
[27] 聂南方,郭智奇,刘财. 改进的地震AVAZ裂缝弱度反演方法及其在致密砂岩储层中的应用[J]. 地球与行星物理论评(中英文), 2024, 55(3): 358−368. DOI: 10.19975/j.dqyxx.2023-02. DOI: 10.19975/j.dqyxx.2023-025. Nie N F, Guo Z Q, Liu C. Application of the improved seismic AVAZ inversion method for fracture characterization of a tight sandstone gas reservoir in the Ordos Basin[J]. Reviews of Geophysics and Planetary Physics, 2024, 55(3): 358-368. DOI: 10.19975/j.dqyxx.2023-025. (in Chinese).
[28] 王晨光, 蔺学旻, 周显华, 等. 基于地震多属性融合的断层识别与评价——以塔里木盆地SHB地区碳酸盐岩缝洞型储层为例[J]. CT理论与应用研究, 2021, 30(1): 35−48. DOI: 10.15953/j.1004-4140.2021.30.01.04. WANG C G, LIN X M, ZHOU X H, et al. Fault detection and evaluation based on fusion of multiple seismic attributes——An example of fractured and vuggy carbonate formation in SHB area,tarimu basin[J]. CT Theory and Applications, 2021, 30(1): 35-48. DOI: 10.15953/j.1004-4140.2021.30.01.04. (in Chinese).
[29] 徐冰, 李文博, 王易安, 等. 不规则井眼的斯通利波反射数值模拟[J]. 科学技术与工程, 2012, 20(9): 2029-2032. XU B, LI W B, WANG Y, et al. Numerical simulation of stonely wave reflection in irregular borehole[J]. Science Technology and Engineering, 2012, 12(9): 2029-2032. (in Chinese).
-
期刊类型引用(1)
1. 李振宇，何碧竹，贠晓瑞，蔡志慧，张盛生，刘若涵，马绪宣，陈希节. 共和盆地东北部花岗岩型干热岩井下裂缝系统及其构造成因. 岩石学报. 2024(12): 3964-3983 . 
百度学术
其他类型引用(0)
