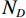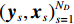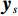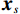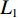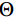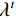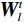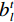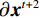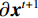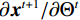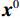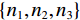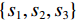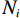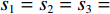Research on Material Decomposition of Dual-energy CT Image Based on Iterative Residual Network
-
摘要:
双能计算机断层成像技术(DECT)由于其材料分解能力,在高级成像应用中发挥着重要作用。图像域分解直接对CT图像进行线性矩阵反演,但分解后的材料图像会受到噪声和伪影的严重影响。虽然各种正则化方法被提出来解决这个问题,但它们仍然面临着两个挑战: 繁琐的参数调整和过度平滑导致的图像细节损失。为此,本文提出一种基于迭代残差网络的双能CT图像材料分解算法,直接求逆作为初始基图像,利用堆叠的双通道卷积神经网络替换迭代分解模型中的正则化项,构成深度迭代分解网络,该方法同时实现了材料分解和噪声抑制。实验结果表明,本文提出的迭代残差网络优于其他对比方法,能够在保持基图像边缘细节信息的同时有效抑制噪声和伪影。
Abstract:Dual energy computed tomography (DECT) plays an important role in the application of advanced imaging due to its material decomposition capability. Image domain decomposition can directly invert CT images through by linear matrix, but the decomposed material images will be seriously affected by noise and artifacts. Although various regularization methods have been proposed to solve this problem, they still face two challenges: tedious parameter adjustment and the loss of image details resulted from over-smoothing. Therefore, in this paper we proposes a dual energy CT image material decomposition algorithm based on iterative residual network. Direct inversion is used as the initial base image, and a stacking two-channel convolutional neural network is used to replace the regularization items in the iterative decomposition model to form a deep iterative decomposition network. This method can realize material decomposition and noise suppression simultaneously. Experimental results show that the iterative residual network proposed in this paper is superior to other comparison methods and can effectively suppress noise and artifacts while maintaining the edge details of the base image.
-
Keywords:
- computed tomography /
- dual-energy CT /
- residual network /
- noise suppression
-
双能CT(dual energy CT, DECT)广泛的应用于医学成像、公共安全和工业无损检测等领域[1-2],具有重要应用潜力和研究价值。与计算机断层成像技术(computed tomography, CT)相比,双能CT技术可以利用两种不同的光谱获得额外的诊断信息[3]。因此,DECT可以分解特定材料的图像,还能得到关于被成像物体原子序数和电子密度的分布图。
在材料分解方面,双能图像直接求逆分解(DIMD)易引起噪声放大,为提高图像质量,发展了许多基于正则项约束的分解算法。Xue等[4]在双能CT图像分解中添加了额外的约束(体积守恒和质量守恒),提出一种图像域多材料分解算法(DECT-EP),提高了分解精度;利用全变分(TV)正则化的方法在DECT图像分解中取得了成功[5-6]。虽然这些基于全变分的方法在DECT图像重建中得到了广泛的应用,但是通常会产生阶梯效应,导致图像细节模糊。受字典学习的启发,Li等[7-8]结合传统的惩罚加权最小二乘估计(PWLS),提出稀疏变换(DECT-ST)和学习变换混合集(DECT-MULTRA)的正则化方法, 此方法大大提高了材料分解精度,但是存在调节参数繁琐和迭代时间长的缺点,且需要一个良好的初始基图像。上述迭代优化方案面临计算成本高、繁琐的调参和图像平滑造成的图像细节缺失等问题。因此,为了进一步提高材料分解精度,必须发展更先进的方法。
近年来,深度学习算法在医学图像处理领域得到了广泛的应用[9-11]。特别地,将深度学习技术与迭代重建算法结合,迭代神经网络已成功的应用于多种逆成像问题[12-14]。受迭代神经网络良好性能的启发,本文从图像域出发,提出一种深度迭代残差网络(IR-Net)用于DECT材料分解。本文将迭代过程展开为递归残差网络,其中正则化项和相关参数被堆叠的卷积神经网络(CNN)替代,在训练阶段自适应调节正则化参数,同时实现图像分解和噪声抑制。利用每次迭代的数据保真项,训练样本数量并不需要很大。实验表明,该方法可以在较短时间内完成分解,并有效抑制基图像噪声和伪影,提高材料分解精度。
1. 双能CT图像域材料分解模型
在图像域材料分解理论中,将基材料图像中像素值的线性组合近似为CT图像中每个像素的线性衰减系数。在本文中,假定这个近似是准确的,首先将不同能量下的重建图像组成一个堆叠的双通道图像向量
${{\boldsymbol{y}}}=\Big({\boldsymbol{y}}_{H}^{{\rm{T}}},{{{\boldsymbol{y}}}}_{L}^{{\rm{T}}}\Big)\in {R}^{2{N}_{p}}$ ,其中${{{\boldsymbol{y}}}}_{H}$ 和${{{\boldsymbol{y}}}}_{L}$ 分别是高能量和低能量下的衰减图像,$ {N}_{p} $ 是图像的像素总数。${{\boldsymbol{x}}}=\Big({{{\boldsymbol{x}}}}_{H}^{{\rm{T}}},{{{\boldsymbol{x}}}}_{L}^{{\rm{T}}}\Big)\in {R}^{2{N}_{p}}$ 表示未知的材料密度图像,${{{\boldsymbol{x}}}}_{m}=\left({{\boldsymbol{x}}}_{m1},\cdots ,{{\boldsymbol{x}}}_{mn},\cdots , {{\boldsymbol{x}}}_{m{N}_{p}}\right)\in {R}^{2{N}_{p}}$ 代表L种材料图像。它们的关系可以表示为${{\boldsymbol{y}}}\approx {\boldsymbol{A}}{{\boldsymbol{x}}}$ ,其中A为质量衰减系数矩阵,它由${{\boldsymbol{A}}}_{0}$ 和单位矩阵I的 Kronecker组成。${{\boldsymbol{A}}}_{0}$ 是一个$ 2\times 2 $ 的材料分解矩阵:$$ {{\boldsymbol{A}}_0} = \left( {\begin{array}{*{20}{c}} {{\omega _{1H}}}&{{\omega _{2H}}} \\ {{\omega _{1L}}}&{{\omega _{2L}}} \end{array}} \right) \text{,} $$ (1) 其中,
$ {\omega }_{lH}={\mu }_{lH}/{\rho }_{l} $ 和$ {\omega }_{lL}={\mu }_{lL}/{\rho }_{l} $ 分别为第l种材料在高能量和低能量时的质量衰减系数,$ {\mu }_{lH} $ 和$ {\mu }_{lL} $ 分别为第l种材料在高能量和低能量下的线性衰减系数,$ {\rho }_{l} $ 第l种材料的密度。水和骨头的材料密度分别用理论值1 g/cm−3和1.92 g/cm−3。为了得到$ {\mu }_{lH} $ 和$ {\mu }_{lL} $ ,本方法在${{\boldsymbol{y}}}_{H}$ 和${{\boldsymbol{y}}}_{L}$ 中手动选择两个包含材料的均匀区域,然后计算这两个区域的平均像素值。直接矩阵反演得到的基材料图像信噪比严重退化,不利于物质识别。为提高基材料图像质量,本文采用正则化的方法求解:
$$ \mathop {\min }\limits_{x \in {\mathbb{R}^{2{N_p}}}} \Bigg(\frac{\;\lambda \;}{2}\big\| {{{{\boldsymbol{y}}}} - {\boldsymbol{{\boldsymbol{A}}}}{{{{{\boldsymbol{x}}}}}}} \big\|_2^2 + R\Big( {{{\boldsymbol{x}}}} \Big) \Bigg),$$ (2) 其中
$\dfrac{\;\lambda \;}{2}{\big\|{{\boldsymbol{y}}}-{\boldsymbol{A}}\boldsymbol{x}\big\|}_{2}^{2}$ 为数据保真项,$R\left({{{{\boldsymbol{x}}}}}\right)$ 为正则项,$ \lambda $ 参数控制数据保真项和正则化之间的平衡。2. 双能CT图像迭代分解网络
2.1 迭代网路架构
近年来深度学习的方法广泛应用于图像处理,具有时间短、良好的去噪能力等优点。本文提出使用基于深度学习的正则化项来降低基材料图像的噪声,建立的目标函数如下:
$$ \mathop {\min }\limits_{{\text{x}} \in {R^{2{N_p}}}} \left(\frac{\;\lambda \;}{2}\big\| {{{{\boldsymbol{y}}}} - {\boldsymbol{A}}{\boldsymbol{x}}} \big\|_2^2 + \sum\limits_{k = 1}^K {{\varphi _k}\Big({{\boldsymbol{G}}_k}{{{\boldsymbol{x}}}}\Big)}\right) {\text{ , s}}{\text{.t}}{\text{. }}{\boldsymbol{x}} \ge 0\text{,} $$ (3) 其中
$ K $ 是正则化的数量,${{\boldsymbol{G}}}_{k}$ 是大小为$ {N}_{f} $ 的转化矩阵,它可以看作是CT图像的卷子算子,$ {\varphi }_{k} $ 是势函数。${{\boldsymbol{G}}}_{k}$ 和${\varphi }_{k}$ 可以从数据中学习得到。为求解式(3)本文方法使用梯度下降算法,更新过程如下:
$$ \begin{split} {{\boldsymbol{x}}^{t + 1}} = {{{{\boldsymbol{x}}}}^t} - \left( {{\lambda ^t}{{\boldsymbol{A}}^{\rm{T}}}\Big( {{\boldsymbol{A}}{{\boldsymbol{x}}^t} - {\boldsymbol{y}}} \Big) + \sum\limits_{k = 1}^K {{{\Big( {{\boldsymbol{G}}_k^t} \Big)}^{\rm{T}}}\gamma _k^t\Big( {{\boldsymbol{G}}_k^t{{{{\boldsymbol{x}}}}^t}} \Big)} } \right) \text{,}\end{split} $$ (4) 更新式(4)中T是矩阵的转置,
$\gamma \left(\cdot \right)={\varphi }'\left(\cdot \right)$ 。其中(4)式中的正则项可以看作是一个CNN,${{\boldsymbol{G}}}_{k}$ 和${\left({{\boldsymbol{G}}}_{k}\right)}^{{\rm{T}}}$ 视为卷积层中的卷积,$ {\gamma }_{k}^{t} $ 为网络中的激活函数。将正则项展开为一个堆叠的CNN:
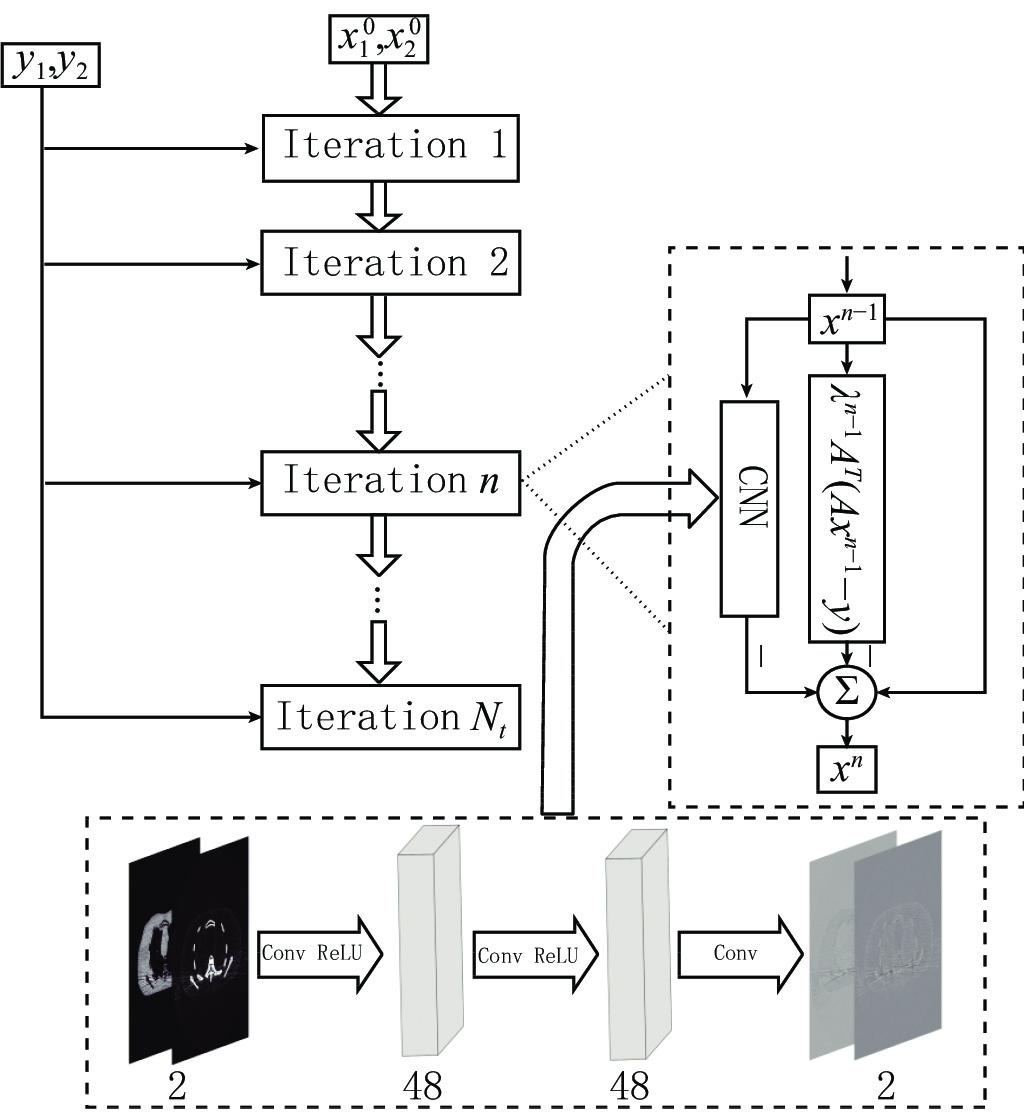
$$ \begin{array}{*{20}{l}} &Q\left( {{{\boldsymbol{x}}^t}} \right) = f_L^t \Biggl({18}{{\rm{ReLU}}\bigg( {f_{L - 1}^t\bigg( { \cdots {\rm{ReLU}}\Big( {f_1^t} \Big)} \bigg)} \Bigg)} \Biggr)\\ &f_1^t = {\boldsymbol{W}}_1^t * {{\boldsymbol{x}}^t} + {\boldsymbol{b}}_1^t{\text{ }} \\ &f_l^t = {\boldsymbol{W}}_l^t\Bigg( {{\rm{ReLU}}\bigg( {f_{l - 1}^t} \bigg)} \Bigg) + {\boldsymbol{b}}_l^t\;\;\;\;{\text{ }}\Big( {l = 2,3, \cdots ,L} \Big) \end{array}, $$ (5) ${\boldsymbol{W}}_{l}^{t}(l=\mathrm{1,2,}\cdots ,L)$ 是包含$ {n}_{l} $ 个卷积核的权重,其中卷积核大小为$ {\mathit{s}}_{l} $ ,${\boldsymbol{b}}_{l}^{t}$ 是偏置。$ * $ 和ReLU(·)分别为卷积运算和激活函数,L为网络的层数。图1显示了本文的深度迭代框架。${\lambda }^{t-1}{{\boldsymbol{A}}}^{{\rm{T}}}({\boldsymbol{A}}{\boldsymbol{x}}^{t-1}-{\boldsymbol{y}})$ 对应于数据保真项,${\boldsymbol{x}}^{t-1}$ 和${\boldsymbol{x}}^{t}$ 之间利用shortcut连接,整体的架构是一个保留结构细节并加速训练的残差网络。2.2 网络训练
IR-Net以监督学习的方式训练网络,训练集包含
$ {N}_{D} $ 对图像${({\boldsymbol{y}}_{s},{\boldsymbol{x}}_{s})}_{s=1}^{{N}_{D}}$ ,其中$ {{{\boldsymbol{y}}}}_{s} $ 是双能重建图像,${\boldsymbol{x}}_{s}$ 是对应标签图像。通过$ {L}_{1} $ 损失(最小绝对值误差)建立了以下训练模型:$$ \left\{ {\begin{split} &{\mathop {\min }\limits_\Theta L(D;\Theta ) = \frac{1}{\;{2{N_D}hwd}\;}\big| {{{{{\boldsymbol{x}}}}^{{N_t}}}\left({{{{\boldsymbol{y}}}}_s},\Theta \right) - {{{{\boldsymbol{x}}}}_s}} \big|} \\ &{{\rm{s.t.}}\left\{ {\begin{split} &{{{{\boldsymbol{x}}}}_s^{t + 1} = {{{\boldsymbol{x}}}}_s^t \;-\; \bigg({\lambda ^t}{{\boldsymbol{A}}^{\rm{T}}}\Big({\boldsymbol{A}}{{{\boldsymbol{x}}}}_s^t \;-\; {{{{\boldsymbol{y}}}}_s}\Big) \;+\; M\Big({{{\boldsymbol{x}}}}_s^t\Big)\bigg)} \\ &{t = 0,1,2, \cdots ,{N_t} - 1{\text{ }}} \end{split}} \right.} \end{split}} \right. \text{,} $$ (6) 其中h,w和d分别代表输入的基材料图像的长、宽和深度,
$ \mathrm{\Theta } $ 代表网络中可训练的参数,包括正则项参数$ {\lambda }^{t} $ ,卷积核参数${{{\boldsymbol{W}}}}_{l}^{t}$ 和偏置$ {\mathit{b}}_{l}^{t} $ 。采用Adam优化算法寻找最优参数,而执行反向传播过程的关键是梯度计算,本文给部分梯度计算示例:$$ \frac{\;{\partial {L_h}\;}}{{\partial {\Theta ^i}}} = \frac{\;{\partial {{{{\boldsymbol{x}}}}^{t + 1}}\;}}{{\partial {\Theta ^t}}} \cdot \frac{\;{\partial {{{{\boldsymbol{x}}}}^{t + 1}}\;}}{{\partial {{{{\boldsymbol{x}}}}^{t + 1}}}} \cdots \frac{{\partial {{{{\boldsymbol{x}}}}^{{N_t}}}}}{\;{\partial {{{{\boldsymbol{x}}}}^{{N_t} - 1}}\;}} \cdot \frac{{\partial L}}{\;{\partial {{{{\boldsymbol{x}}}}^{{N_t}}}}\;} \,, $$ (7) 其中
$\partial {{{\boldsymbol{x}}}}^{t+2}$ /$\partial {{{\boldsymbol{x}}}}^{t+1}$ 的梯度:$$ \frac{\;{\partial {{{{\boldsymbol{x}}}}^{t + 2}}\;}}{{\partial {{{{\boldsymbol{x}}}}^{t + 1}}}} = I - \left( {{\lambda ^{t + 1}}{{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{A}} + \frac{\;{\partial R\left( {{{{{\boldsymbol{x}}}}^{t + 1}}} \right)\;}}{{\partial {{{{\boldsymbol{x}}}}^{t + 1}}}}} \right) , $$ (8) $\partial {{{\boldsymbol{x}}}}^{t+1}/\partial {{\Theta }}^{t}$ 的梯度可以分成3部分:$$ \frac{{\;\partial {{{{\boldsymbol{x}}}}^{i + 1}}}\;}{{\partial {\lambda ^i}}} = - {\bigg( {{{\boldsymbol{A}}^{\rm{T}}}\Big( {A{{{\boldsymbol{x}}}}_s^i - {{{{\boldsymbol{y}}}}_s}} \Big)} \bigg)^{\rm{T}}},{\text{ }} \frac{{\;\partial {{{{\boldsymbol{x}}}}^{i + 1}}\;}}{{{\boldsymbol{W}}_1^i}} = - \frac{{\;\partial R\left( {{{{{\boldsymbol{x}}}}^i}} \right)\;}}{{{\boldsymbol{W}}_1^i}},\frac{{\;\partial {{{{\boldsymbol{x}}}}^{i + 1}}\;}}{{{\boldsymbol{b}}_1^i}} = - \frac{\;{\partial R\left( {{{{{\boldsymbol{x}}}}^i}} \right)\;}}{{{\boldsymbol{b}}_1^i}}{\text{。}} $$ (9) 网络训练中以直接求逆的结果作为初始基图像
${\boldsymbol{x}}^{0}$ 。迭代次数为200次,前100次学习率为10−4,后100次迭代学习率为10−5。使用神经网络工具箱MatConvNet进行了训练。算法编程环境为:Ubuntu 16,处理器为3颗Intel(R) xeon(R) E5-2640 v4 @ 2.40 GHz,内存32 G,显卡为Tesla K80。影响分解质量的参数包括卷积核$ \left\{{n}_{1},{n}_{2},{n}_{3}\right\} $ 的数量、卷积核的大小$ \left\{{s}_{1},{s}_{2},{s}_{3}\right\} $ ,以及总迭代次数$ {N}_{i} $ 。上述所有参数在本实验中均手动设置。本文中,通过固定其他参数,扰动其中一个参数来得到合适的网络配置为$ {n}_{1}={n}_{2}= 48$ ,${n}_{3}=2$ ,${s}_{1}= {s}_{2}= {s}_{3}=$ 3×3,$ {N}_{i}= 13$ 。3. 实验
3.1 实验数据和网络参数
为了评估所提出的迭代残差网络在双能CT图像域材料分解的性能,本文分别进行了仿真实验和临床数据的测试,本文使用Duke大学提供的基于真实患者的XCAT仿真人体模型数据来获得双能CT图像用于训练和测试。实验中,使用GE LightSpeed X-ray CT扇形系统,模拟得到模体在140 kVp和80 kVp下大小为888×984的投影,并在投影数据中添加泊松噪声,噪声方差为5。采用滤波反投影重建算法(FBP)重建双能CT图像,重建图像大小为512×512,物理尺寸是每个像素0.98 mm×0.98 mm。
在训练IR-Net网络时,为保证网络测试结果的公正有效,挑选数据时遵循交叉验证原则。从XCAT模体中随机选取70张切片,其中50张作为训练集,剩余20张作为测试集。此外,本文还使用XCAT模体训练的结果通过一组腹部双能CT图像[15]来进一步验证IR-Net网络的实用性,这组图像的原始图像是通过单能扫描得到,然后使用SpekCalc软件生成140 kVp和80 kVp下的能谱,模拟得到双能扫描下的投影并添加了泊松噪声,采用滤波反投影重建算法法(FBP)重建双能CT图像。
3.2 仿真实验
为了直观的说明IR-Net网络的去噪性能,本文选取不同于训练数据的切片77来作测试,图2显示了该切片重建的高低能图像和材料密度图像。在仿真实验中将与DIMD、DECT-ST、DECT-MULTRA进行比较,同时使用均方根误差(RMSE)、峰值信噪比(PSNR)和结构相似度(SSIM)等指标定量的分析不同算法的分解效果。
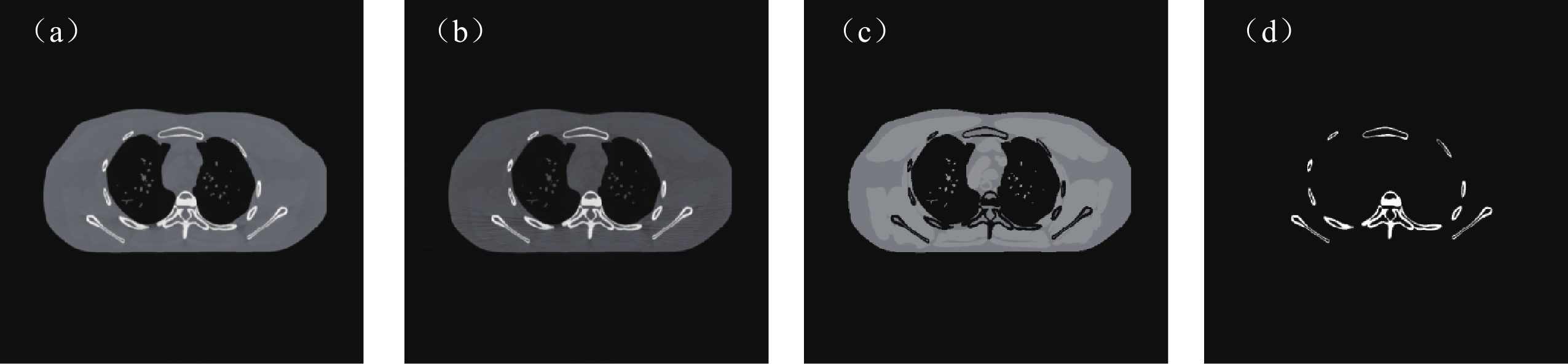
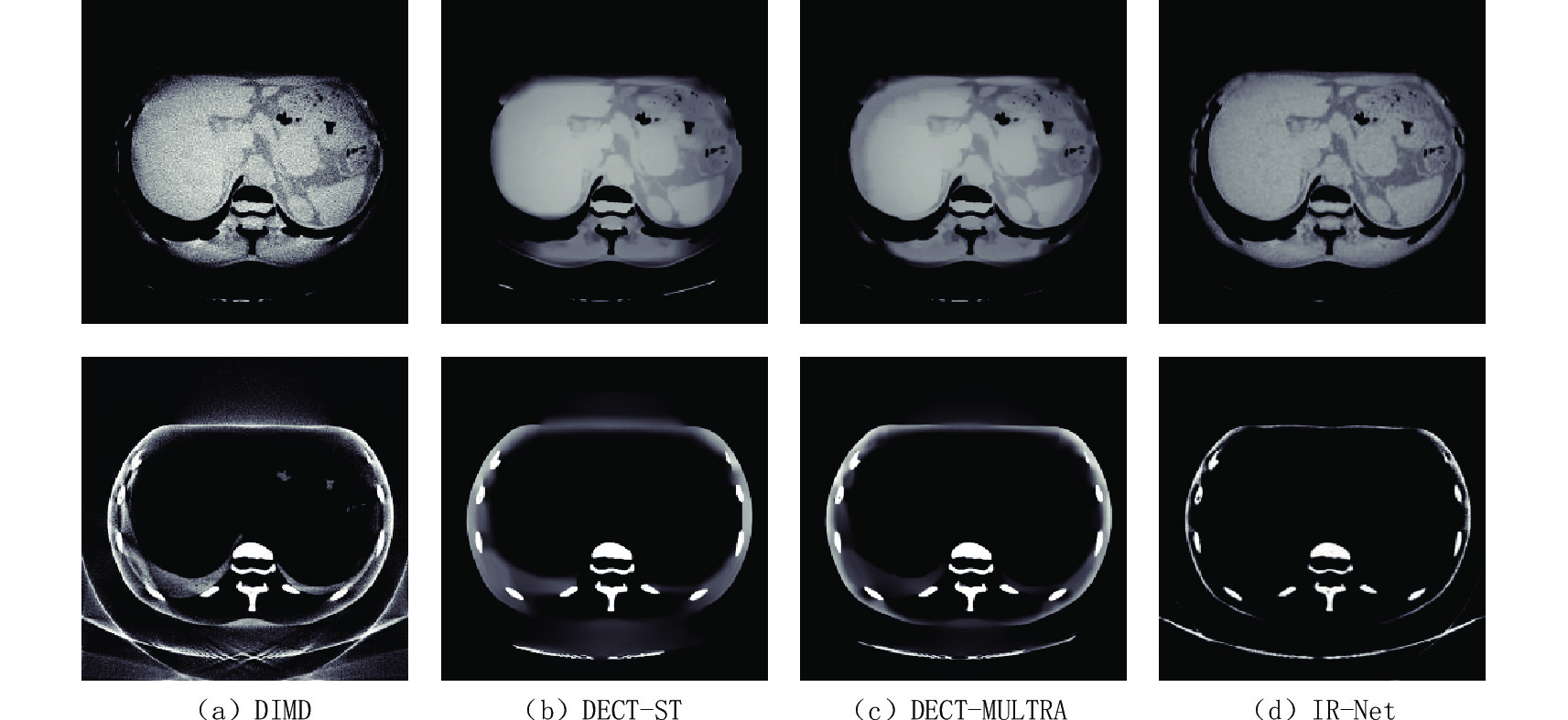
图3为不同算法下的两种基材料分解结果,水和骨的显示窗口分别为[0.7 1.3] g/cm-3和[0 0.8] g/cm-3。由图3可知,DIMD分解得到的基图像含有大量噪声,不能显示任何有用的诊断信息,其他3种方法均能有效抑制噪声和伪影。相比于DIMD,DECT-ST、DECT-MULTRA和本文方法抑制了大量的噪声,且图像清晰,边缘完整。但是由于过度平滑,软组织细节放大处可以观察到DECT-MULTRA模糊掉组织的一些细节信息。此外,DECT-MULTRA和DECT-ST需要以DECT-EP迭代500次的结果作初始基图像,调节参数繁琐,运行时间超过1 h,而本文方法运行测试图像只需要7 s。
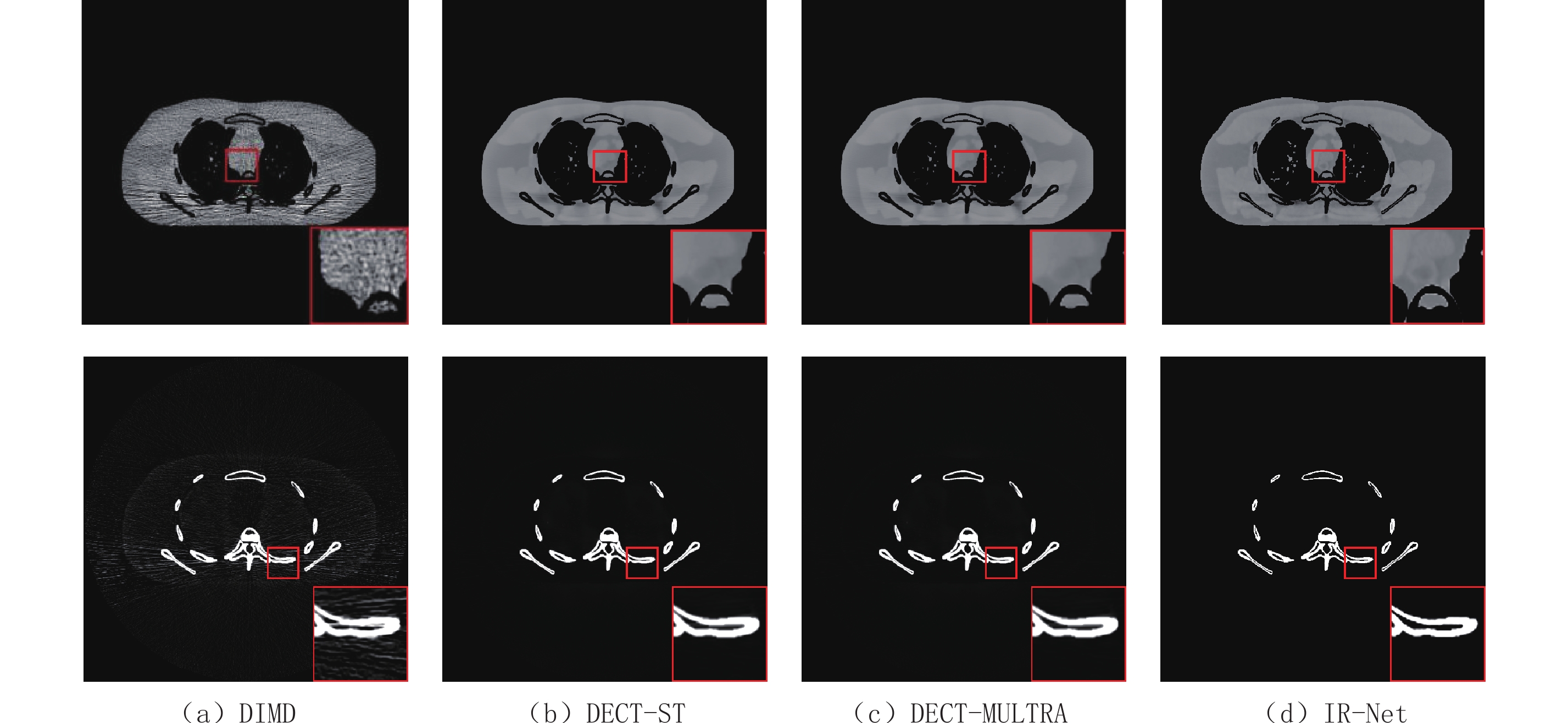
为了进一步评价所提方法的优点,图4显示了分解结果偏差的绝对值,提供了视觉上的噪声抑制性能比较,每种基材料的显示窗口为[0 0.3] g/cm-3。通过对比可知,本文方法对分解结果的偏差最小。总的来说,IR-Net网络避免了繁琐的参数调节,提高了材料分解精度,保持了图像边缘清晰。
为了定量评价IR-Net网络在材料分解中的性能,分别计算每种方法下基图像的RMSE、PSNR和SSIM,其结果如表1。由表1知,DIMD获得的两种基材料图像的RMSE值很大,PSNR和SSIM值都很小,说明DIMD材料分解精度最低。与DIMD、DECT-ST和DECT-MULTRA各图像指标相比,IR-Net网络骨和水的基图像的RMSE值最小,说明IR-Net网络分解精度最高;SSIM值最大,证明IR-Net网络分解后的基图像在所有对比算法中与理想图像最相似;此外,其PSNR值均较大,可知IR-Net网络去噪效果好。通过定量综合分析知,IR-Net网络优于其他3种算法,在保持细微结构的同时,能更有效的抑制图像噪声。
表 1 不同算法的定量评估结果Table 1. Quantitative evaluation results of different algorithmsMateria Index DIMD DECT-ST DECT-MULTRA IR-Net RMSE 0.0815 0.0500 0.0341 0.0169 water PSNR 21.7735 26.0188 29.3327 35.4356 SSIM 0.4201 0.9276 0.9112 0.9937 RMSE 0.0786 0.0554 0.0440 0.0150 bone PSNR 22.0949 25.1253 27.1373 36.4688 SSIM 0.3399 0.8148 0.8949 0.9995 3.3 腹部数据实验
为进一步验证IR-Net网络的实用性,采用直接分解做初始迭代点,各类算法对临床腹部数据进行比较。图4显示了腹部数据的高低能图像和对比分解基材料图像,软组织和骨的显示窗口分别为[0.5 1.5] g/cm-3和[0 0.8] g/cm-3。
腹部数据添加了泊松噪声,相对于XCAT模体数据的噪声水平更高。为了适用于临床图像,网络应具有较好鲁棒性,本实验选择以软组织和骨作基材料。由图5可得DIMD获得的基图像含噪声最多;DECT-ST和DECT-MULTRA减少了噪声,但是图像过于平滑,导致一些图像细节的缺失;IR-Net网络降噪能力明显强于前3种,去除了一些较强的噪声,同时保护了图像的结构和边缘信息。总之,IR-Net网络能够抑制图像噪声,提高材料分解精度。
4. 结论
本文针对双能CT分解两种材料存在噪声大、精度低等问题,提出一种基于迭代残差网络的双能CT材料分解算法,利用先验知识改善图像质量,使用堆叠的CNN代替正则化项和相应参数,展开为深度残差网络,提高材料分解精度。因此,该算法可以自适应学习正则化项,避免了繁琐的参数调整和图像过度平滑,降低噪声并保护图像细节。使用XCAT模体和腹部数据进行的实验表明,该算法在噪声抑制、定量和定性评价方面具有普遍优势。
-
1 不同算法的定量评估结果
Materia Index DIMD DECT-ST DECT-MULTRA IR-Net RMSE 0.0815 0.0500 0.0341 0.0169 water PSNR 21.7735 26.0188 29.3327 35.4356 SSIM 0.4201 0.9276 0.9112 0.9937 RMSE 0.0786 0.0554 0.0440 0.0150 bone PSNR 22.0949 25.1253 27.1373 36.4688 SSIM 0.3399 0.8148 0.8949 0.9995 表 1 不同算法的定量评估结果
Table 1 Quantitative evaluation results of different algorithms
Materia Index DIMD DECT-ST DECT-MULTRA IR-Net RMSE 0.0815 0.0500 0.0341 0.0169 water PSNR 21.7735 26.0188 29.3327 35.4356 SSIM 0.4201 0.9276 0.9112 0.9937 RMSE 0.0786 0.0554 0.0440 0.0150 bone PSNR 22.0949 25.1253 27.1373 36.4688 SSIM 0.3399 0.8148 0.8949 0.9995 -
[1] JOHNSON T R, KRAU B, SEDLMAIR M, et al. Material differentiation by dual energy CT: Initial experience[J]. European Radiology, 2007, 17(6): 1510-1517.
[2] 王文杰, 陈平, 潘晋孝, 等. 基于参考组分的双能CT成像方法[J]. CT理论与应用研究, 2021,30(1): 61−69. DOI: 10.15953/j.1004-4140.2021.30.01.06. WANG W J, CHEN P, PAN J X, et al. Dual-energy CT imaging method based on reference components[J]. CT Theory and Applications, 2021, 30(1): 61−69. DOI: 10.15953/j.1004-4140.2021.30.01.06. (in Chinese).
[3] 王李磊. 双能CT 图像重建算法研究[D]. 郑州: 解放军信息工程大学, 2016. WANG L L. Research on dual energy CT image reconstruction algorithm[D]. Zhengzhou: PLA University of information engineering, 2016. (in Chinese).
[4] XUE Y, RUAN R S, HU X H, et al. Statistical image-domain multimaterial decomposition for dual-energy CT[J]. Medical Physics, 2017, 44(3): 886−901. doi: 10.1002/mp.12096
[5] XUE D, NIU T Y, ZHU L. Combined iterative reconstruction and image-domain decomposition for dual energy CT using total-variation regularization[J]. Medical Physics, 2014, 41(5): 051909. DOI: 10.1118/1.4870375.
[6] DING Q Q, NIU T Y, ZHANG X Q, et al. Image-domain multi-material decomposition for dual-energy CT based on prior information of material images[J]. Medical Physics, 2018: 45. DOI: 10.1002/mp.13001.
[7] LI Z, RAVISHANKAR S, YONG L, et al. Image-domain material decomposition using data-driven sparsity models for dual-energy CT[C]//2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018). IEEE, 2018.
[8] LI Z P, RAVISHANKAR S, LONG Y, et al. DECT-MULTRA: Dual-energy CT image decomposition with learned mixed material models and efficient clustering[J]. IEEE Transactions on Medical Imaging, 2020, 39(4): 1223−1234. DOI: 10.1109/TMI.2019.2946177.
[9] ZHANG J L, GU Y B, TANG H, et al. Compressed sensing MR image reconstruction via a deep frequency-division network[J]. Neurocomputing, 2020, 384: 346−355. doi: 10.1016/j.neucom.2019.12.011
[10] CHEN H, ZHANG Y, KALRA M K, et al. Low-dose CT with a residual encoder-decoder convolutional neural network (RED-CNN)[J]. IEEE Transactions on Medical Imaging, 2017, 36(99): 2524−2535.
[11] SU T, SUN X, ZHANG Y, et al. DIRECT-net: A unified mutual-domain material decomposition network for quantitative dual-energy CT imaging[J]. 2020.
[12] CHEN H, ZHANG Y, CHEN Y, et al. LEARN: Learned experts' assessment-based reconstruction network for sparse-data CT[J]. IEEE Transactions on Medical Imaging, 2018, (99): 1−1.
[13] YANG Y, SUN J, LI H, et al. ADMM-CSNet: A deep learning approach for image compressive sensing[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020: 521−538.
[14] ADLER J, OKTEM O. Learned primal-dual reconstruction[J]. IEEE Transactions on Medical Imaging, 2017: 1322−1332.
[15] XU Y F, YAN B, ZHANG J F, et al. Image decomposition algorithm for dual-energy computed tomography via fully convolutional network[J]. Computational & Mathematical Methods in Medicine, 2018: 2527516. DOI: 10.1155/2018/2527516.
-
期刊类型引用(4)
1. 张然,孔慧华,李佳欣,宋一娇. 基于残差挤压激励神经网络的材料分解. CT理论与应用研究(中英文). 2025(01): 117-128 .  百度学术
百度学术
2. 张然,孔慧华,宋一娇,杜晓双,赵效荷. 基于改进U-Net网络的双能CT材料分解方法. 计算机测量与控制. 2025(01): 252-260 .  百度学术
百度学术
3. 吴凡,金潼,詹郭睿,解晶晶,刘进,张谊坤. 基于多通道交叉卷积UCTransNet的双能CT基材料分解方法. 光学学报. 2024(05): 136-150 .  百度学术
百度学术
4. 郭俏,姚旭峰. 双能CT图像域基材料分解算法的研究进展. CT理论与应用研究. 2023(01): 139-146 .  本站查看
本站查看
其他类型引用(0)






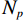



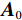
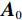


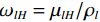

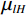

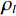
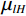
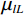
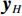
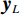

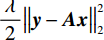
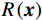


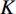
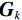
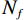
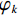

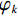

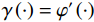
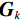
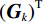
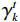

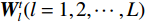
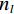
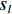
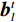
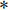
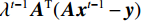
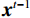
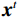
 下载:
下载: