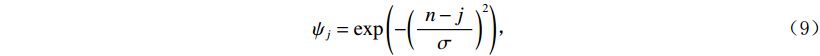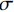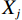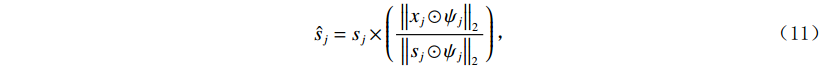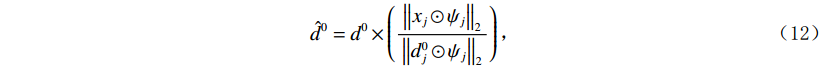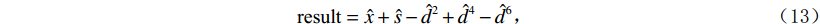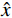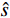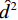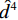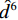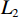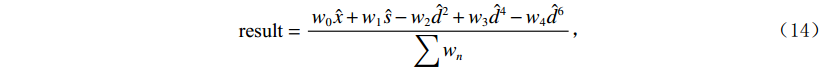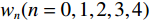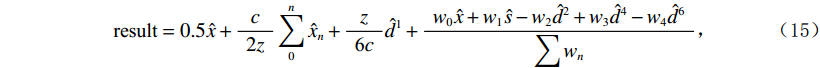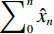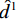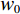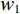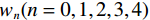Research and Application of Seismic Frequency Extension technology Based on Ghost Wave Attenuation and Non-stationary Multi-order Differential Algorithm
-
摘要: 高分辨率地震资料可以达到更精细的井震标定结果，能更清晰地进行构造解释与储层刻画，同时对薄层具有更好的识别能力。为提高地震分辨率，需要对地震数据进行拓频处理。常规地震拓频方法通常在频率域进行，易受到高频噪音影响，降低资料可靠性。本文提出一种基于鬼波处理与多阶差分结合的时域拓频技术，仅通过原始地震道数次积分与差分运算便能拓宽地震频带，积分及差分结果在高斯窗口内进行振幅匹配以保证处理前后振幅一致性。与差分结果进行加权融合，高阶差分设置较小权值以避免高频噪声的影响，提高算法的抗噪性。本理论模型及实际地震资料处理分析结果表明，该方法能有效提高地震资料分辨率。Abstract: High-resolution seismic data can realize better well seismic calibration results,clearer structural interpretation and reservoir characterization, and also hold better identification ability of thin layers. In order to improve seismic resolution, it is necessary to carry out frequency extension processing on seismic data. The conventional seismic spectral broadening method used to be carried out in the frequency domain is susceptible to high-frequency noise and thus reduces the reliability of the data. In this paper we propose a time-domain frequency extension technology which is based on the combination of ghost wave processing and non-stationary multi-order differential resolution. The sesmic spectral can be broaded merely through multiple times of integration and differential operation, whose results are performed amplitude matching at Gaussian window to ensure the consistency of the amplitude before and after the processing. Weighted fusion is performed on the difference results, the high-order difference is assigned a smaller weight to avoid the influence from the high-frequency noise, and thus improve the anti-noise performance of the algorithm. The theoretical models and processing results of the field seismic data show that the algorithm can effectively improve the resolution of seismic data.
-
Keywords:
- de-ghosting /
- differential /
- spectral broaden /
- Gaussian window
-
高分辨率地震数据对地震解释至关重要，从中可以提取更有效的构造及沉积信息。但是地震成果资料的分辨率受很多因素影响，如地震采集参数[1-2]、处理技术[3-4]、成像技术等。另外地层的特异性也对分辨率造成影响，如大地滤波效应、浅层气吸收衰减[5]。在偏移后资料上有多种方法可以提高地震分辨率，如谱白化、谱蓝化、反Q滤波及各种形式的反褶积技术[6]。按照实现原理可以归纳为3类，分别为基于频谱重构的频率域方法、基于子波压缩类的反褶积方法及基于子波分解的分频数据重构方法。
就频谱重构方法而言，反Q滤波及谱整形较为常见有效。反Q滤波是一种补偿大地吸收衰减效应技术，它可以补偿振幅衰减和频率损失，并恢复地震记录的相位特性，从而改善地震同相轴的连续性，提高弱反射波的能量和地震资料的信噪比、分辨率。使用反Q滤波进行振幅补偿时，由于振幅补偿算子为频率与走时的指数函数，在深层易出现高频噪音。改进方法为使用约束反Q补偿方法，如时变Q补偿门限[7]、基于最小二乘的贝叶斯估计[8]、频谱连续性约束[9]。谱整形方法通过在频率域设计振幅谱形态，而相位谱不变，然后作反傅氏变换得到谱整形后记录。谱整形技术虽应用广泛，但存在一些问题：对频率内所有成分校正，噪音有可能放大；整形谱由用户定义，人为控制因素多，可能会产生假象。
基于子波压缩类的反褶积方法可以分为确定性反褶积方法及统计性反褶积方法，其主要差别之一在于求取反褶积时的约束方法不同。地震波场可以假设为震源响应、接收器响应、鬼波、多次波及地层反射因子的褶积模型，若已知震源子波，则可以通过确定性反褶积消除震源子波的影响[10]。震源子波可以通过统计方法得到[11]，这些方法通常假设地层反射系数为白信号[12]。在鬼波衰减中，通常使用特定的海水面反射系数及鬼波延迟时间设计鬼波衰减因子进行确定性反褶积[13]。统计性反褶积指使用统计约束方法对反褶积方法进行约束，如假设反射系数满足稀疏性[14]、使用基于泊松约束的R-L反卷积方法[15]、基于最大后验概率（MPM）的盲卷积[16]。
基于子波分解的分频数据重构方法主要包括基于小波分解及基于希尔伯特-黄变换的谱白化方法。基于小波分解的谱白化方法主要通过小波变换将信号分解至不同尺度，再利用谱白化对尺度信号进行频率补偿[17]。希尔伯特-黄变换（HHT）与小波变换类似，其与小波变换的差异在于它没有固定的先验基函数。其核心思想是将时间序列资料通过经验模态分解（EMD）分解成数个固有模态函数（IMF），然后利用希尔伯特变换构造解析信号，得出资料的瞬时频率和振幅[18]。
以上方法在实际应用中效果都比较好，但计算均较复杂。本文提出一种基于低阶鬼波衰减[19]与多阶差分组合的提频技术[20-21]，该方法将积分、差分通过线性关系组合，在时间域实现频谱白化处理，并通过低频增强及高阶差分权重处理提高抗噪性。
1. 基于低阶鬼波衰减的低频增强技术
鬼波是海上地震中特有的干扰波，一般分为炮鬼波、检波点鬼波、炮-检波点鬼波。鬼波有关的反射波与有效反射波相干，其在频率域的陷波点频率可以表示为：
$$ {f}_{n}=\frac{nc}{2z}\text{，}n=0,1,2,\cdots \text{，} $$ (1) 其中c为海水速度，z为水深，陷波点与水深z相关。因此鬼波会减弱固定频率处的振幅能量，通常有效振幅位于第1个陷波点与第2个陷波点之间。
若只考虑检波点端的鬼波，那么其鬼波响应函数可以表示为：
$$ G\Big({k_x},{k_y},k,z\Big) = 1 - {r_0}\exp \Big(2i{k_z}z\Big)\text{，} $$ (2) 其中
${k_z} = \sqrt {{k^2} - k_x^2 - k_y^2}$ 为垂直平面的波数，$k = \omega /c$ 为波数的角频率$\omega = 2{\text π} f$ ，f为频率，${k_x}、{k_y}$ 为与x、y方向相关的水平波数，${r_0}$ 为鬼波在海水面的振幅反射率，以下将假设其等于1。为简化表达式，假设地震波场在垂直平面内传播，则
${k_x}{\text{ = }}{k_y}{\text{ = 0}}$ ，鬼波影响函数可以改写为：$$ G\Big({k_x} = {k_y} = 0,\;k,\;z\Big) = G(k,\;z) = 1 - \exp \Big(2ikz\Big)。 $$ (3) 进一步推导，可得鬼波影响因子的频谱响应为：
$$ \Big|\;G\Big({k_x} = {k_y} = 0,\;k,\;z\Big)\;\Big| = \Big| {\;2\sin (kz)} \;\Big|。 $$ (4) 可见鬼波对所有频率范围内的振幅均有影响，只是在陷波点的影响最大，去除鬼波的影响则是需要将鬼波因子在所有频率上的振幅因子去除，本文只讨论检波点鬼波衰减。
在理想情况下，可以通过在频率-波数域除以鬼波的响应因子来衰减鬼波影响，鬼波响应因子的倒数可以简化为：
$$ \frac{{\text{1}}}{{\;G\Big({k_x} = {k_y} = 0,\;k,\;z\Big)\;}} = \frac{1}{{\;1 - \exp \Big(2ikz\Big)\;}}{\text{ = }}\;\frac{1}{2}\;\Big( {1 + i\cot (kz)} \Big)。 $$ (5) 去鬼波方法通常在炮域进行，在共检波点域、共反射点域均可以进行，甚至适用于零相位化后道集，鬼波衰减后子波宽度被压缩，低频增加，高频拓宽。但鬼波衰减对参数z及海水面反射系数敏感，每道的延迟时间不同，会使鬼波衰减效果不理想，若直接乘以上式易引入不可估计的误差，故这里使用级数展开为，并只保留2阶级数项，则（5）式可以改写为：
$$ \frac{{\text{1}}}{{\;G\Big({k_x} = {k_y} = 0,\;k,\;z\Big)\;}} = \;\frac{1}{2}\;\Bigg(1 + i\frac{{\;\cos (kz)\;}}{{\sin (kz)}}\Bigg) \approx \frac{{\text{1}}}{{\text{2}}}\Bigg(1 + i\frac{1}{{\;kz\;}} - \frac{{\;ikz\;}}{3}\Bigg)。 $$ (6) 那么鬼波衰减后的波场的频率-波数域形式可以表达为：
$$ {U^{DG}}(w,z) \approx \frac{1}{\;2\;}\Bigggr({18}1 + i\Bigg(\frac{1}{{kz}} - \frac{{kz}}{{\text{3}}}\Bigg)\Bigggr){18}*U(w,z)\text{，} $$ (7) 其中
$\;{U^{DG}}(w,z)\;$ 为鬼波衰减后的波场的频率-波数域表达，$U(w,z)\;$ 为原始接收波场的频率-波数域表达。将其变换至时域：
$$ {U^{DG}}(t,z) \approx {\frac{1}{\;2\;}U(t,z)} + {\frac{c}{\;2z\;}}\int\limits_0^t {{\rm{d}}{t'}U({t'},z)} + {\frac{z}{{\;\text{6}}c\;}}{\partial _t}U(t,z)。$$ (8) 该方法在雷克子波上有较好的效果（图1）。雷克子波主频为25 Hz，地震采样率为2 ms，鬼波延迟时间为20 ms，则鬼波引起的第2个陷频点位于50 Hz。经过低阶鬼波衰减以后，鬼波的旁瓣振幅明显减弱，其低频及高频能量均得到增强，但低频能量增强幅度更大。
2. 基于非平稳多阶差分的高分辨率处理技术
非平稳多阶差分提频技术（differential resolution，DR）在原始地震道集的基础上添加平滑成分、二阶、四阶及六阶差分成分。每种高阶差分代表一种高频信号，而平滑成分代表了低频信号，通过多种频率成分组合，达到提高地震分辨率的目的。
理论上每一步差分均会引入 -90° 相移，因此四阶差分的相移为360°，其极性为正，但是二阶差分及六阶差分的极性为负，因此在应用过程中乘以 -1。由于差分的振幅与原始地震的振幅差异较大，所以每个差分均与原始地震进行振幅匹配处理。在此处使用高斯移动窗口对原始地震及差分结果的振幅进行匹配处理，如下式所示：
$$ {\psi _j} = {\exp\left({ - {{\left( {\dfrac{\;{n - j\;}}{\sigma }} \right)}^2}}\right)}\text{，} $$ (9) $$ {X_j} = tr \odot {\psi _j}\text{，} $$ (10) 其中
${\psi _j} $ 表示高斯滑动窗口，其样点数为n，j为当前处理校点位置，$\sigma $ 为高斯函数的方差，表示窗口的尖锐程度，${X_j}$ 为高斯窗口处理后的地震。高斯窗口大小不易过小，也不易过大，本文中以25个样点长度为默认值。对于地震数据的平滑项（即低频成分），此处使用15点Hanning滤波器，那么最终的低频成分可以表示为：
$$ {\hat s_j} = {s_j} \times \left( {\frac{{{{\left\| {{x_j} \odot {\psi _j}} \right\|}_2}}}{{{{\left\| {{s_j} \odot {\psi _j}} \right\|}_2}}}} \right)\text{，} $$ (11) $$ \hat d_{}^0 = d_{}^0 \times \left( {\frac{{{{\left\| {{x_j} \odot {\psi _j}} \right\|}_2}}}{{{{\left\| {d_j^0 \odot {\psi _j}} \right\|}_2}}}} \right) \text{，} $$ (12) $$ \text{result} = \hat x + \hat s - {\hat d^2} + {\hat d^4} - {\hat d^6}\text{，} $$ (13) 其中
$\;\hat x\;$ 表示原始数据项，$\hat s\;$ 表示平滑项，${\hat d^2}\;$ 表示二阶差分项，${\hat d^4}\;$ 表示4阶差分项，${\hat d^6}\;$ 表示6阶差分项。${\left\| {\cdot} \right\|_2}$ 表示对经平滑或差分处理后的地震道在高斯窗口内进行${\;L_2\;}$ 范数振幅匹配。当地震数据信噪比较低时，其高阶差分项受噪音影响可靠度较低，故此处对各频率成分的地震数据添加权重因子，高阶差分分配较小权重，如下式所示：
$$ \text{result} = \frac{{{w_0}\hat x + {w_1}\hat s - {w_2}{{\hat d}^2} + {w_3}{{\hat d}^4} - {w_4}{{\hat d}^6}}}{{\displaystyle\sum {{w_n}} }}\text{，} $$ (14) 其中
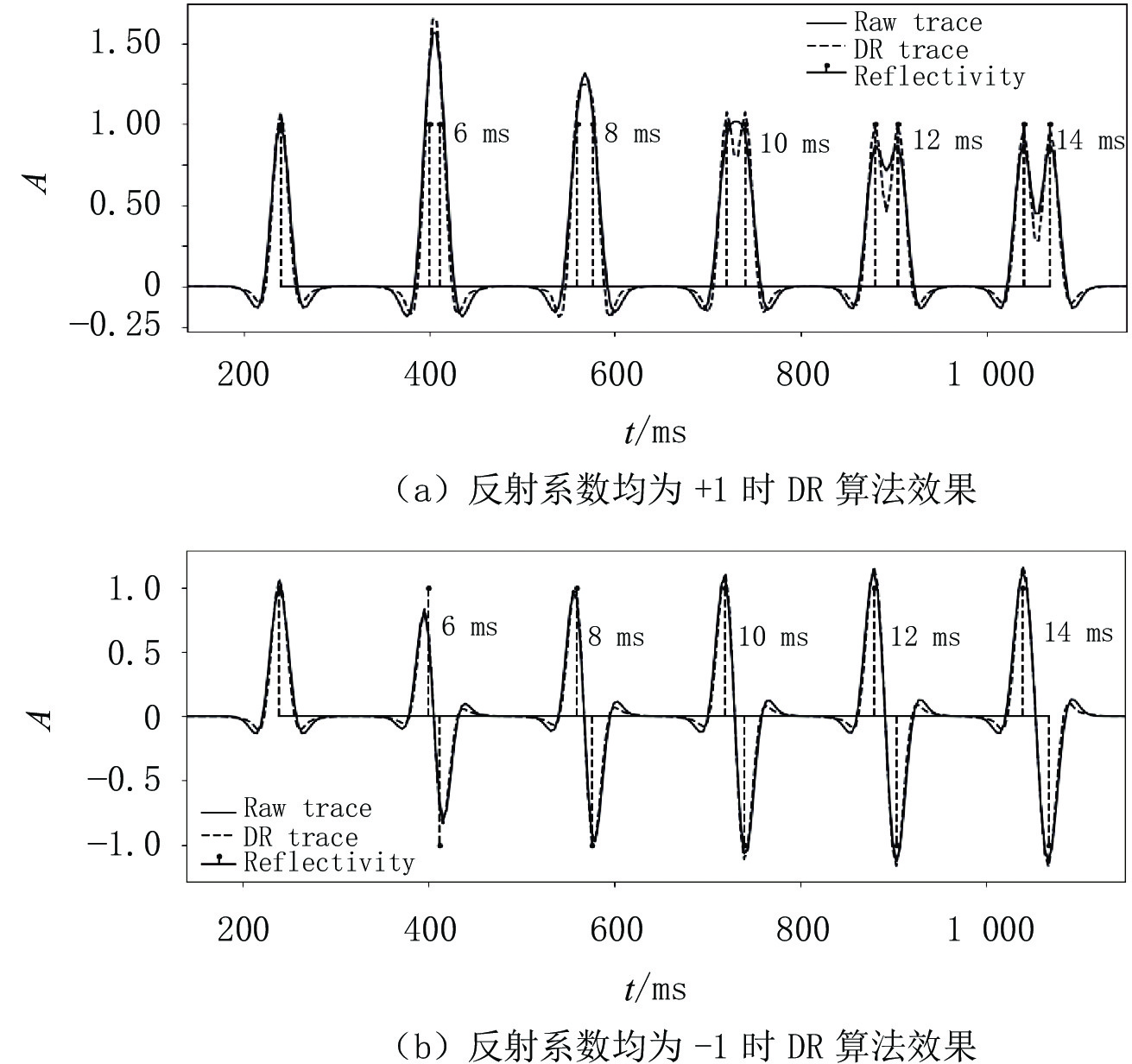
$\;{w}_{n}(n=0,1,2,3,4)\;$ 表示各项权重系数。上图中使用子波为雷克子波，主频25 Hz，黑色垂直虚线表示反射系数，各反射点间隔均为0、6、8、10、12和14 ms。从图2（a）中可以看出，经过处理后的地震数据分辨率明显提高，原始数据上10 ms反射系数点处波峰为平点，DR算法结果将2个反射信号明显分开，且在8 ms反射系数点处波峰值变为类平点，对于12 ms和14 ms反射系数点处的分辨度也明显提高。图2（b）中负反射系数的处理效果与原始地震基本一致，但DR算法的旁瓣能量较原始地震稍弱。
![]()
图 2 DR算法处理前后对比图Figure 2. Comparison of raw data and DR results on the opposite-polarity and negative-polarity synthetic trace将低阶鬼波衰减与多阶差分算法结合（low deghosting and differential resolution，LDDR），便可综合低阶鬼波低频增强及多阶差分高分辨率处理的优势，联合公式（8）及公式（14）可得
$$ \text{result} = 0.5\hat x + \frac{c}{{\;2z\;}}\sum\limits_0^n {{{\hat x}_n}} + \frac{z}{\;{{\text{6}}c\;}}{\hat d^{\text{1}}} + \frac{\;{{w_0}\hat x + {w_1}\hat s - {w_2}{{\hat d}^2} + {w_3}{{\hat d}^4} - {w_4}{{\hat d}^6}}\;}{{\displaystyle\sum {{w_n}} }}\text{，} $$ (15) 其中
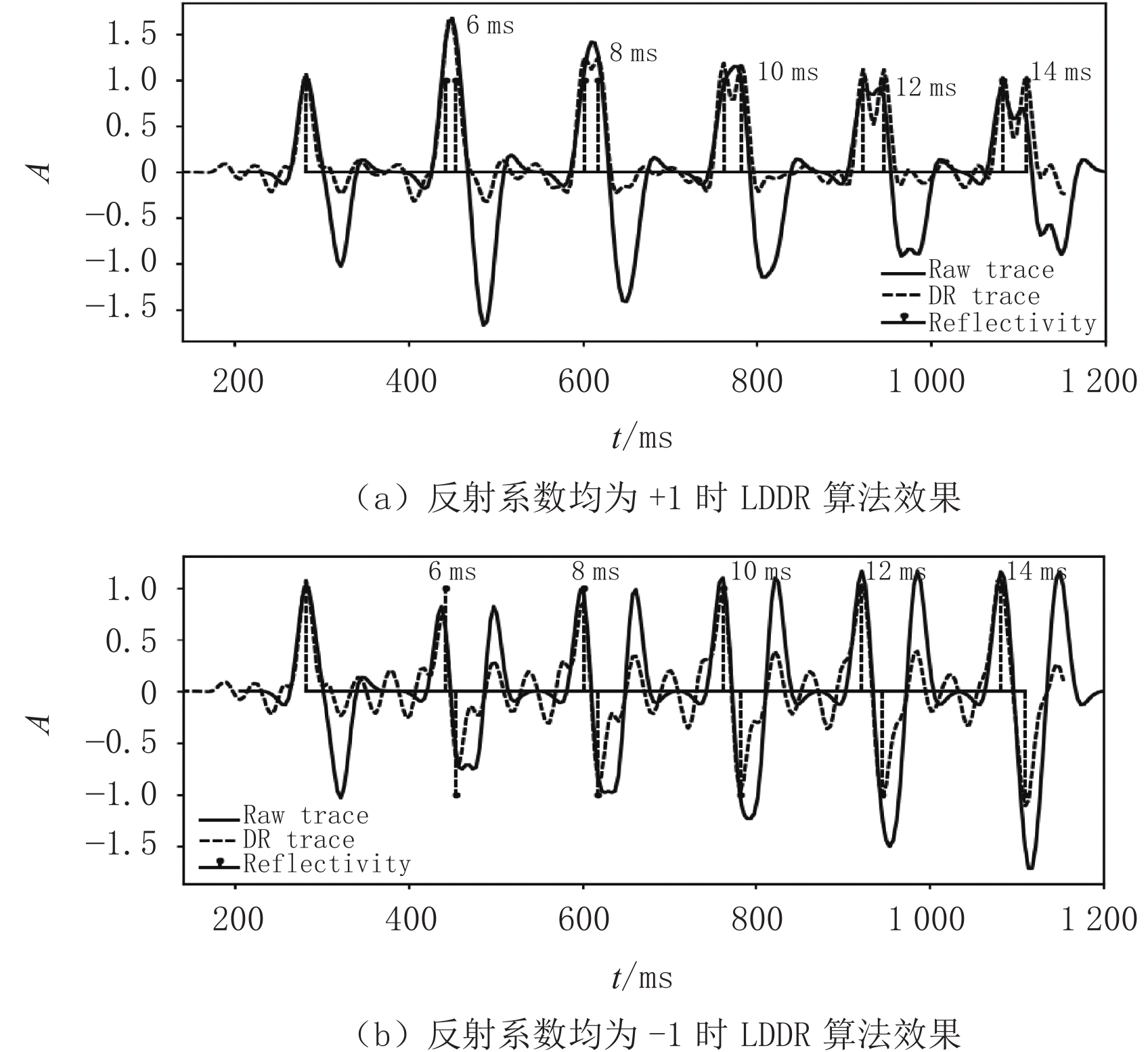
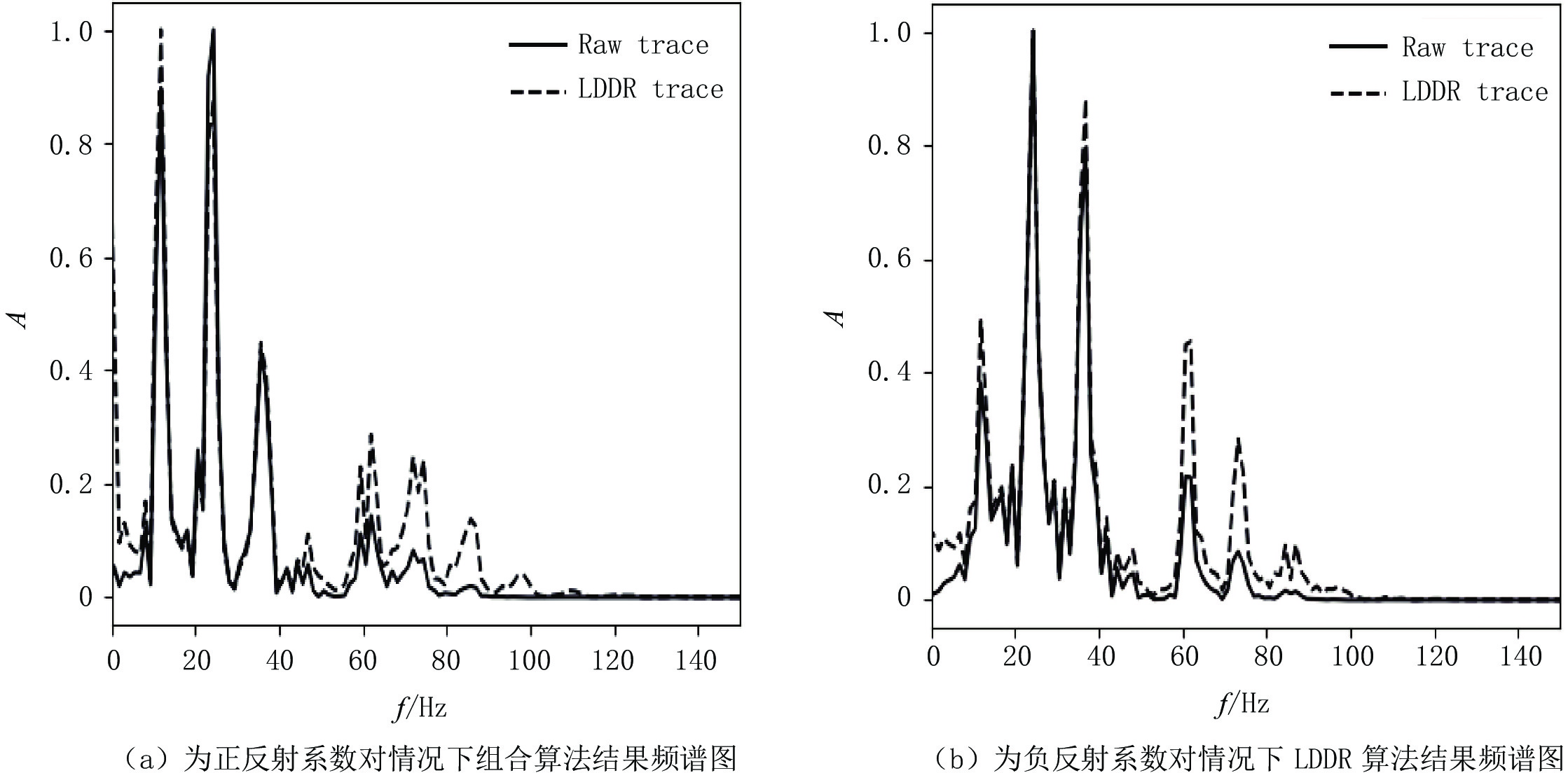
$\displaystyle\sum\nolimits_0^n {{{\hat x}_n}}$ 表示第n个采样点处积分，${\hat d^{\text{1}}}\;$ 表示一阶差分项。使用低阶鬼波衰减与多阶差分组合算法LDDR，在正反射系数与负反射系数对正演数据上进行了测试。如图3（a）所示鬼波影响基本被衰减，对于8 ms反射系数点处识别效果较图2（a）好，这与鬼波导致低频降低有关，但对于12 ms和14 ms反射系数点处两波峰间波谷的振幅较2（a）高。图3（b）中负反射系数的处理效果与原始地震存在一定差距，DR算法结果在负反射系数点处的绝对振幅更弱，但与正反射系数处振幅更一致，而原始地震的负反射系数点处绝对振幅随反射系数间隔增大而增大。从图4知经过LDDR算法处理后，地震信号的低频及高频信号均得到了增强。
![]()
图 3 LDDR算法处理前后对比图Figure 3. Comparison of ghost data and combined algorithm results on the opposite-polarity and negative-polarity synthetic trace![]()
图 4 图2及图3中LDDR算法结果频谱Figure 4. The spectrum of LDDR algorithm results in Fig.2 and Fig.33. 西湖凹陷某工区资料处理
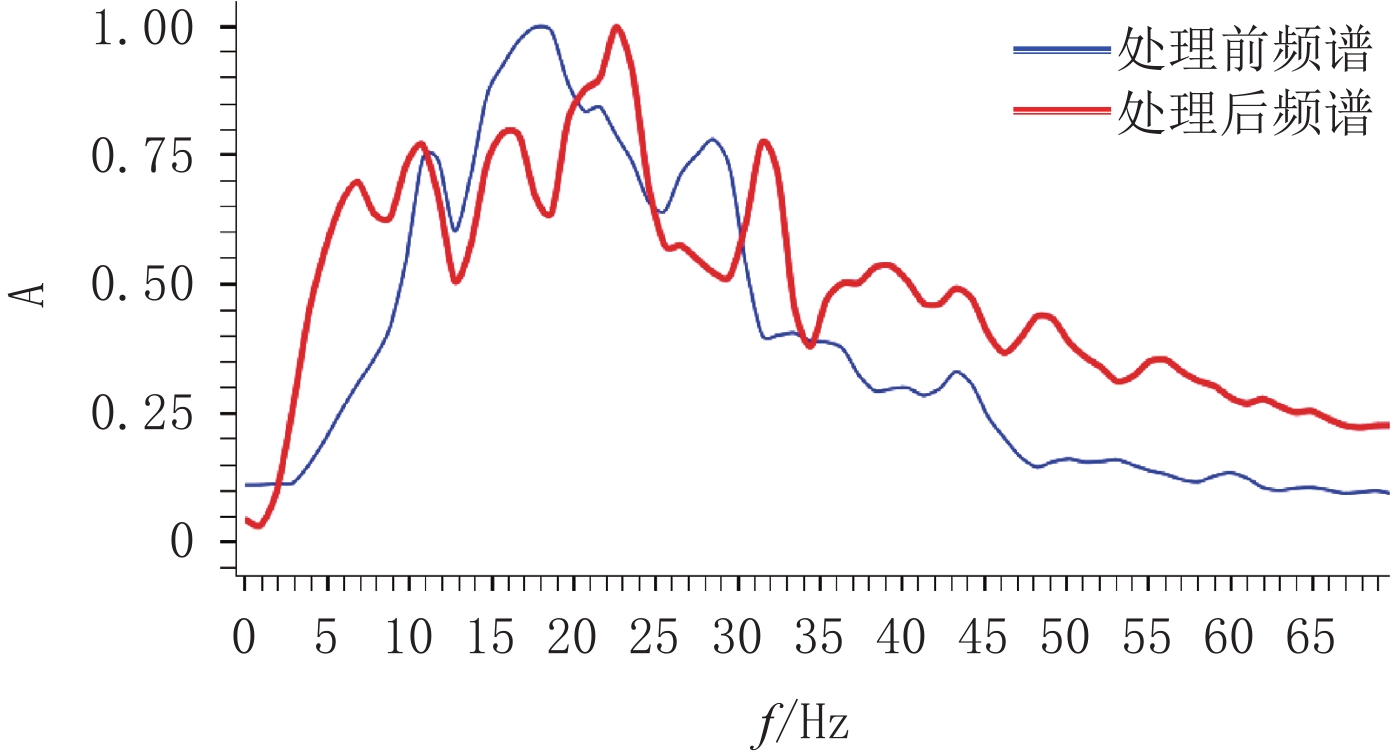
该实际资料位于东海西湖凹陷某油气田，其电缆沉放深度为7 m，最大偏移距为6000 m。在处理过程中并未进行鬼波衰减处理，道集目的层低频较弱，其频谱宽度仅10～30 Hz，主频为18 Hz，严重制约了对薄层的分辨能力。如图5中3060 ms处的薄泥岩夹层，在原始道集中基本无响应，影响其上覆砂体的储层落实。
该资料电缆沉放深度较浅，其第二理论陷波点位置应在75 Hz处，位于有效频带之外，故本方法鬼波衰减补偿0 Hz处振幅，公式（15）中c/2z设置为 13 ms，其高频端能量则利用非平稳差分技术进行增强处理，式（15）差分项中
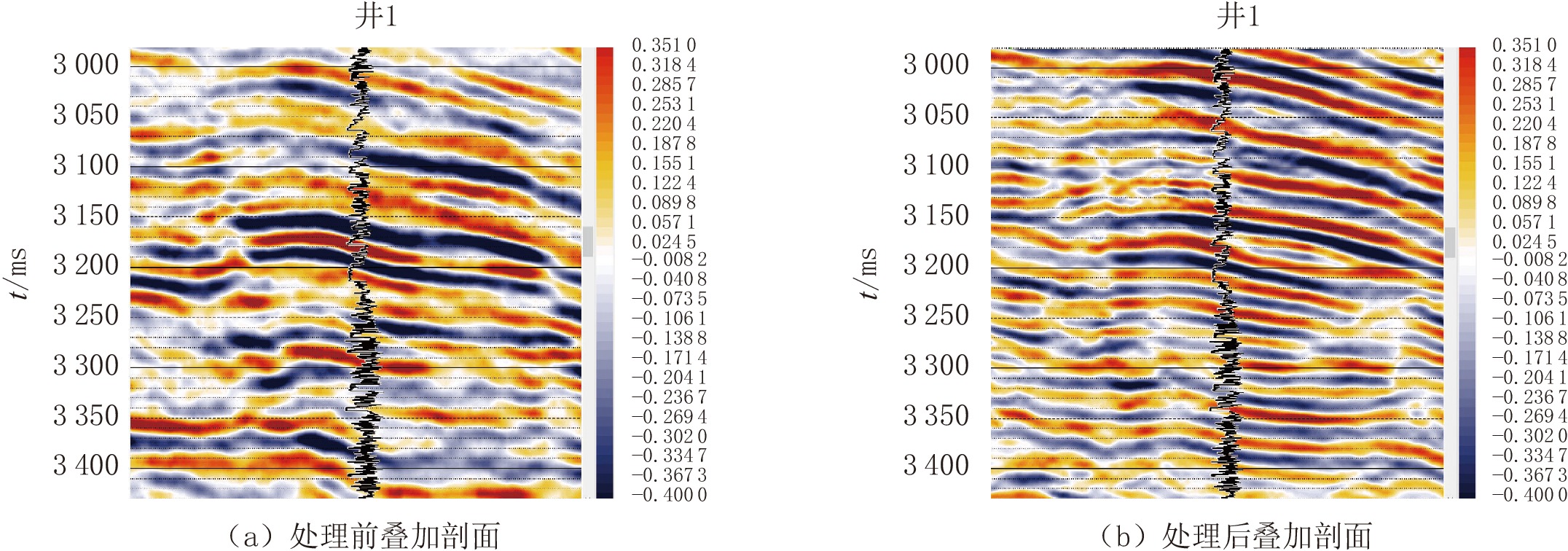
$\;{w_0}\;$ 与$\;{w_{\text{1}}}\;$ 设置较低权重值。考虑到信噪比对高阶差分的影响较大，高频能量增强以二阶差分及四阶差分为主，以六阶差分为辅。通过效果测试，${w}_{n}(n=0,1,2,3,4)\;$ 分别为5、1、22、20和12。如图5（b）所示，LDDR算法对弱振幅能量有较好的增强效果，如2930 ms处弱波峰在处理后波形更加清晰，与周边道集同相轴的匹配度更高。如图6处理前后频谱对比，LDDR算法处理后的道集频谱宽度为4～33 Hz，低频端较处理前明显拓宽，而高频端（35～70 Hz）能量较处理前提高近一倍。![]()
图 6 本文方法处理前后道集频谱Figure 6. The comparison of spectrum befrore and after processing by the method in this paper处理后资料叠加剖面的分辨率有明显改善。如图7所示，原始剖面上较为模糊的地层反射在处理后形成2套或多套反射，其地质信息更加丰富，与伽马曲线吻合度更高。如3115 ms附近的弱负振幅与泥岩背景特征一致，其下砂岩的顶底反射也更清晰（砂顶反射对应负振幅，砂底对应正波峰），而在处理前剖面上顶底反射不明显，3320 ms处的20 m薄砂岩在原叠加剖面上无响应，处理后剖面上砂体反射清晰。该井3080 ms处砂体为10 m薄气层，基于该处理成果，该砂体上倾方向有变厚趋势，为下一步的勘探方向提供了有力支撑。
4. 结论
（1）拓频处理是地震资料解释中常用的手段，本文利用低阶鬼波衰减及非平稳差分技术综合了两种方法的优势，能够更合理地提高低、高频端振幅能量。
（2）鬼波衰减中，炮点、检波点的沉放深度对鬼波衰减效果影响较大，细微的偏差会导致第二陷波点处振幅畸变，但对0 Hz处第一陷波点影响较小。本文推导的低阶鬼波衰减方法利用该特性能有效提高低频端能量，在理论模型及实际资料测试中均有较好的低频增强效果，具有较广的适用性。
（3）非平稳差分技术通过基于高斯窗的振幅匹配方法，解决了差分运算中振幅异常问题，使不同波组振幅更具一致性及对比性，具有更好的适用性。鬼波处理后资料低频能量更强，信噪比更高，在此资料基础上，非平衡差分技术具备更强的抗噪能力。
（4）LDDR算法中的低阶鬼波衰减及非平稳差分技术无运算复杂度低，仅需在时间域单道上进行1次积分与6次差分计算，计算效率高。
-
![]()
图 2 DR算法处理前后对比图
Figure 2. Comparison of raw data and DR results on the opposite-polarity and negative-polarity synthetic trace
![]()
图 3 LDDR算法处理前后对比图
Figure 3. Comparison of ghost data and combined algorithm results on the opposite-polarity and negative-polarity synthetic trace
![]()
图 4 图2及图3中LDDR算法结果频谱
Figure 4. The spectrum of LDDR algorithm results in Fig.2 and Fig.3
![]()
图 6 本文方法处理前后道集频谱
Figure 6. The comparison of spectrum befrore and after processing by the method in this paper
-
[1] FENG X K, WANG Y F, WANG X J, et al. The application of high-resolution 3D seismic acquisition techniques for carbonate reservoir characterization in China[J]. The Leading Edge, 2012, 31(2): 168−179. DOI: 10.1190/1.3686914.
[2] MOLDOVEANU N, COMBEE L, EGAN M, et al. Over/under towed-streamer acquisition: A method to extend seismic bandwidth to both higher and lower frequencies[J]. The Leading Edge, 2007, 26(1): 41−58. DOI: 10.1190/1.2431831.
[3] AMUNDSEN L, ZHOU H, REITAN A, et al. On seismic deghosting by spatial deconvolution[J]. Geophysics, 2013, 78(6): V267−V271. DOI: 10.1190/geo2013-0198.1.
[4] 刘建磊, 王修田. 海上地震虚反射相位剔除法反褶积[J]. 海洋地质与第四纪地质, 2002,22(4): 117−122. DOI: 10.16562/j.cnki.0256-1492.2002.04.018. LIU J L, WANG X T. Deconvolution by phase spectrum deghosting in marine seismic survey[J]. Marine Geology & Quaternary Geology, 2002, 22(4): 117−122. DOI: 10.16562/j.cnki.0256-1492.2002.04.018. (in Chinese).
[5] 夏同星, 刘垒, 明君, 等. 渤海湾 X 油田气云区地震资料关键处理技术研究[J]. 石油物探, 2018,57(2): 283−291. DOI: 10.3969/j.issn.1000-1441.2018.02.014. XIA T X, LIU L, MING J, et al. Key processing technologies of seismic data for a gas cloud area in the X oilfield, Bohai Bay Basin[J]. Geophysical Prospecting for Petroleum, 2018, 57(2): 283−291. DOI: 10.3969/j.issn.1000-1441.2018.02.014. (in Chinese).
[6] 韦红, 宋俊亭, 田涛, 等. 基于相控的振幅补偿法在渤海 B 油田储层预测中的应用[J]. CT理论与应用研究, 2021,30(6): 681−690. DOI: 10.15953/j.1004-4140.2021.30.06.03. WEI H, SONG J T, TIAN T, et al. Application of Amplitude compensation method based on phase control in reservoir prediction of Bohai B Oil[J]. CT Theory and Applications, 2021, 30(6): 681−690. DOI: 10.15953/j.1004-4140.2021.30.06.03. (in Chinese).
[7] ZHANG X W, HAN L G, ZHANG F J, et al. An inverse Q-filter algorithm based on stable wavefield continuation[J]. Applied Geophysics, 2007, 4(4): 263−270. DOI: 10.1007/s11770-007-0040-9.
[8] ZHANG C, ULRYCH T J. Seismic absorption compensation: A least squares inverse scheme[J]. Geophysics, 2007, 72(6): R109−R114. DOI: 10.1190/1.2766467.
[9] ZHANG G L, WANG X M, HE Z H. A stable and self-adaptive approach for inverse Q-filter[J]. Journal of Applied Geophysics, 2015, 116: 236−246. DOI: 10.1016/j.jappgeo.2015.03.012.
[10] CHENG Q S, CHEN R, LI T. Simultaneous wavelet estimation and deconvolution of reflection seismic signals[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(2): 377−384. DOI: 10.1109/36.485115.
[11] Van der BAAN M, PHAM D T. Robust wavelet estimation and blind deconvolution of noisy surface seismic[J]. Geophysics, 2008, 73(5): V37−V46. DOI: 10.1190/1.2965028.
[12] ROSA A L R, ULRYCH T J. Processing via spectral modeling[J]. Geophysics, 1991, 56(8): 1244−1251. DOI: 10.1190/1.1443144.
[13] 管西竹, 陈宝书, 符力耘, 等. 基于波动方程的上下缆地震数据鬼波压制方法研究[J]. 地球物理学报, 2015,58(10): 3746−3757. DOI: 10.6038/cjg20151025. GUAN X Z, CHEN B S, FU L Y, et al. The study of a deghosting method of over/under streamer seismic data based on wave equation[J]. Chinese Journal of Geophysics, 2015, 58(10): 3746−3757. DOI: 10.6038/cjg20151025. (in Chinese).
[14] DANILO R V. Stochastic sparse-spike deconvolution[J]. Geophysics, 2008, 73(1): R1−R9. DOI: 10.1190/1.2790584.
[15] LU W K, LI F Y. Seismic spectral decomposition using deconvolutive short-time Fourier transform spectrogram[J]. Geophysics, 2013, 78(2): V43−V51. DOI: 10.1190/geo2012-0125.1.
[16] RAM I, COHEN I, RAZ S. Multichannel deconvolution of seismic signals using statistical MCMC methods[J]. IEEE Transactions on Signal Processing, 2010, 58(5): 2757−2770. DOI: 10.1109/tsp.2010.2042485.
[17] 陈传仁, 周熙襄. 小波谱白化方法提高地震资料的分辨率[J]. 石油地球物理勘探, 2000,35(6): 703−709. doi: 10.3321/j.issn:1000-7210.2000.06.003 CHEN C R, ZHOU X X. Improving resolution of seismic data using wavelet spectrum whitening[J]. Oil Geophysical Prospecting, 2000, 35(6): 703−709. (in Chinese). doi: 10.3321/j.issn:1000-7210.2000.06.003
[18] 计子琦, 张学强, 张海江, 等. 基于VMD的随掘地震超前探测信号谱白化方法研究[J]. CT理论与应用研究, 2021,30(2): 148−160. DOI: 10.15953/j.1004-4140.2021.30.02.02. JI Z Q, ZHANG X Q, ZHANG H J, et al. Research on spectral whitening method of seismic while drilling ahead detection signals based on VMD[J]. CT Theory and Applications, 2021, 30(2): 148−160. DOI: 10.15953/j.1004-4140.2021.30.02.02. (in Chinese).
[19] AMUNDSEN L, ZHOU H. Low-frequency seismic deghosting[J]. Geophysics, 2013, 78(2): WA15−WA20. DOI: 10.1190/geo2012-0276.1.
[20] SAJID M, GHOSH D. A fast and simple method of spectral enhancement[J]. Geophysics, 2014, 79(3): V75−V80. DOI: 10.1190/geo2013-0179.1.
[21] SAJID M, GHAZALI A R. Nonstationary differential resolution: An algorithm to improve seismic resolution[J]. Geophysics, 2018, 83(3): V149−V156. DOI: 10.1190/geo2016-0614.1.
-
期刊类型引用(1)
1. 朱焱辉. 基于压缩感知的地震频带拓宽方法——以珠江口盆地东部惠州地区为例. 中外能源. 2023(06): 44-52 . 
百度学术
其他类型引用(0)
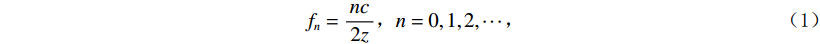
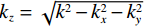
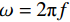
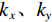
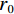
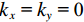
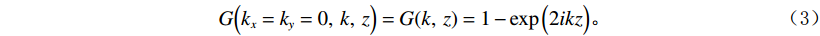
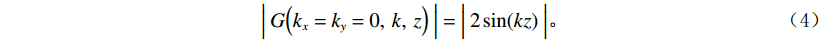
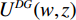
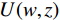
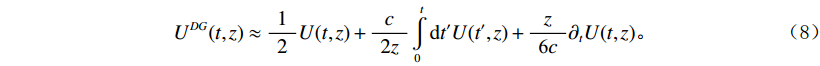
下载:
计量
- 文章访问数: 415
- HTML全文浏览量: 154
- PDF下载量: 36
- 被引次数: 1
