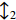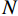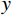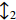Sparse CT Reconstruction Based on Adversarial Residual Dense Deep Neural Network
-
摘要: 针对计算机断层成像稀疏重建过程中产生条状伪影的问题,本文提出一种基于对抗式残差密集深度神经网络的CT图像高精度稀疏重建方法。设计一种耦合残差连接、密集连接、注意力机制和对抗机制的UNet网络,以含条状伪影图像和高精度图像作为训练样本,通过大规模训练数据,对该网络进行训练,使其具有压制条状伪影的能力。首先,利用滤波反投影算法从稀疏投影中重建出含条状伪影的CT图像;接着,将其输入深度网络,通过网络压制条状伪影;最后,得到高精度的重建图像。实验结果表明,相比于现有的若干深度学习算法,提出的新型网络重建出的图像精度更高,可以更好地压制条状伪影。Abstract: To solve the problem of severe streak artifacts in sparse-view computed tomography (CT) reconstruction, in this paper we propose a method which is based on the adversarial residual dense deep neural network to acquire high-quality sparse-view CT reconstruction. The UNet that combines residual connectioin, dense connection, adversarial mechanism and attention mechanism is designed, which is trained through large-scale training data composed of streak artifact images and high-quality images to suppress streak artifacts. First, the filtered back projection (FBP) algorithm is used to reconstruct CT images with streak artifacts from sparse projections, then these images are inputed into the deep network, which can suppress streak artifacts to output high-quality images. The experimental results show that, compared with the existing deep learning algorithms, the image reconstructed by the proposed new network possesses higher accuracy and can suppress streak artifacts better.
-
Keywords:
- sparse reconstruction /
- CT /
- UNet /
- adversarial mechanism /
- attention mechanism
-
计算机断层成像(computed tomography,CT)是应用最为广泛的医学成像模态,由于其过高的X射线辐射剂量可能存在诱发癌症的风险。因此,低剂量CT成为当前研究的热点。目前,低剂量CT有两种实现方法,一种是降低每个投影角度下的辐射剂量,另一种是在稀疏角度下减少投影个数。在稀疏投影角度下重建的图像就是稀疏重建,其中以滤波反投影(filtered back projection,FBP)[1]算法为代表的解析法,是一类经典的CT图像重建算法。然而FBP算法稀疏重建的图像产生严重的条状伪影,可能导致出现错误的疾病判读,基于此,研究者们开始设计新的高精度稀疏重建算法,以压制条状伪影。
CT稀疏重建方法大致分为两类。一类方法是基于压缩感知(compressed sensing,CS)[2]的迭代法,2006年以来,Sidky等[3-4]提出了扇束和锥束CT的总变差(total variation,TV)最小算法,实现了高精度CT稀疏重建。随后,研究者们在TV算法的基础上,提出了自适应加权TV(adaptive-weighted total variation,awTV)[5]、保边TV(edge-preserving TV,EPTV)[6]、各向异性TV(anisotropic TV,aTV)[7]、高阶TV(high order TV,HOTV)[8]、非局部TV(non-local TV,NLTV)[9]及TpV(total p-variation,TpV)[10-11]等算法,进一步提高了重建精度,有力地推动了CT稀疏重建的发展。此外,其他基于压缩感知的重建算法也得到了深入研究,如基于字典学习的方法[12]和基于秩最小的方法[13]。
另一类方法是深度学习法。Chen等[14]提出的RED-CNN网络,结合了反卷积[15]和残差学习[16],在CT稀疏重建方面取得了不错的效果。Wolterink等[17]使用生成式对抗网络(generative adversarial networks,GAN)[18]在CT稀疏重建问题上也获得了很大的提升。Han等[19]证明学习条状伪影比学习原始信号更加简单,并提出了基于Unet网络[20-21]的深度残差学习方法来估计条状伪影,然后通过输入的含条状伪影的CT图像减去估计的条状伪影来获得高质量的CT图像。Jin等[22]提出的FBPConvNet网络将残差UNet网络和FBP算法结合起来解决稀疏重建中出现的条形伪影问题,并将该方法与传统的TV方法进行对比,取得了不错的效果。
Zhang等[23]提出的DD-Net网络结合密集连接[24]和反卷积,通过特征复用克服了梯度消失和梯度爆炸以及模型参数大小增加等问题,让网络结构进一步的压缩从而更容易训练,提高了网络训练的性能。Han等[25]揭示了Unet网络可能会产生模糊边缘的缺陷,提出了基于UNet的多分辨率深度学习网络结构:多级结构UNets和轻量级结构UNets,增强了图像的高频特征,并论证了该网络压制伪影的性能优于传统的TV算法。Steven等[26]提出的FD-UNet网络在UNet网络的收缩和扩展路径中均引入密集连接来抑制条状伪影,进一步实现高精度稀疏重建。
在这些利用深度学习的图像处理中,ResNet网络中残差连接可以在训练更深网络的同时,又能保证良好的性能。一定程度上解决了深度神经网络存在的退化问题和梯度消失、梯度爆炸的问题[16]。密集连接增加了浅层网络的特征映射在深层网络中的复用,提升了网络的表达能力[24];注意力机制通过对空间或通道信息进行加权,强调有用信息,提升了网络性能[27];对抗机制通过两个不同网络的博弈达到纳什均衡,在计算机视觉方面取得了良好的效果[18]。
本文拟在经典UNet网络的基础上,引入残差连接、密集连接、注意力机制和对抗机制,提出一种对抗式残差密集深度神经网络,用于压制由解析法FBP稀疏重建产生的条状伪影,以期进一步提高CT稀疏重建的精度。
1. GAN模型
GAN[18]网络被广泛应用于图像处理的各个领域。GAN由生成网络G(generator,G)和判别网络D(discriminator,D)两个网络构成,生成网络G用来生成图像,判别网络D用来判别图像的真假。标准GAN模型的目标函数为:
$$ \underset{G}{{\rm{min}}}\;\underset{D}{{\rm{max}}}V(D,G)={E}_x\sim{P}_{{\rm{data}}}\left(x\right)\Big(\mathit{{\rm{log}}}D\left(x\right)\Big)+{E}_z\sim{P}_{z}\left(z\right)\bigg(\mathit{{\rm{log}}}\Big(1-D\big(G\left(z\right)\big)\Big)\bigg), $$ (1) 其中
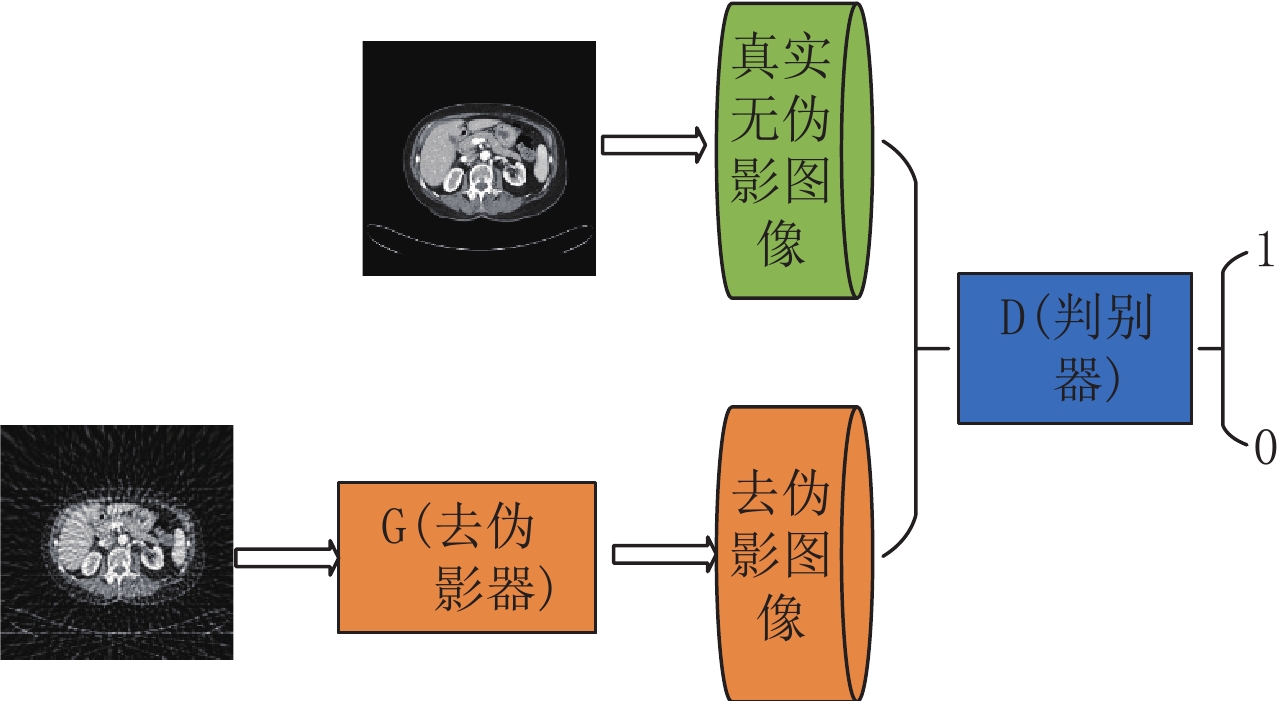
$G$ 为生成器;$ D $ 为判别器;$ z $ 为噪声,服从高斯分布;${P}_{{\rm{data}}}\left(x\right)$ 为真实数据$ x $ 服从的概率分布;$ {P}_{z}\left(z\right) $ 为$ z $ 服从的概率分布;$ {E}_{x} $ 和$ {E}_{z} $ 为期望值。对抗式残差密集网络的框架图如图1所示。在训练过程中,对抗式残差密集网络分别迭代训练残差密集生成网络和判别网络,从而达到纳什均衡,以压制条状伪影。2. 网络结构设计
2.1 残差密集生成网络结构
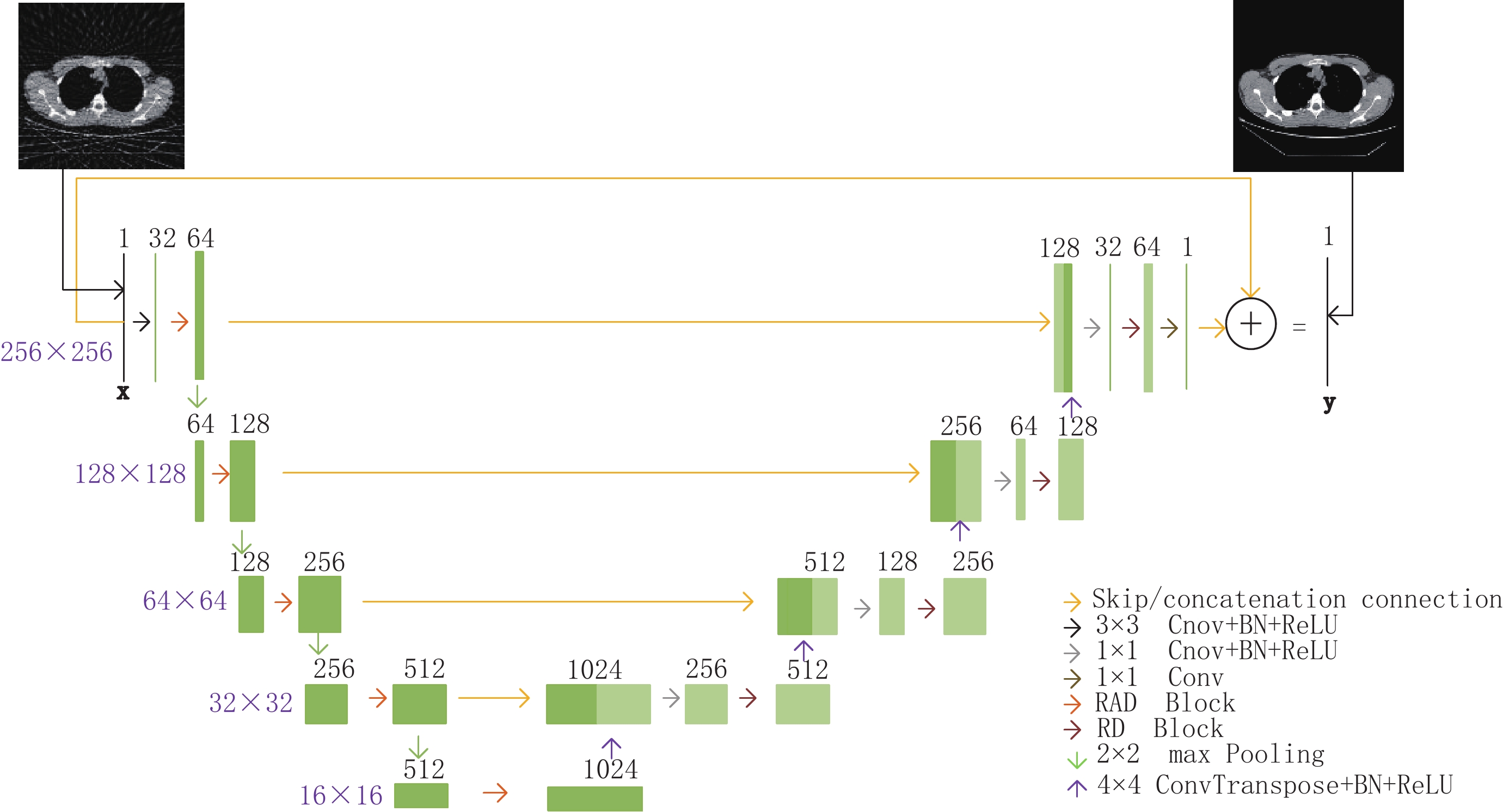
残差密集生成网络原理是将FBP算法稀疏重建的含条状伪影的CT图像作为输入,经过残差密集生成网络训练后,得到高精度CT图像。残差密集生成网络基于经典UNet进行了改进,残差密集生成网络结构如图2所示,网络结构以大小为256×256的CT图像作为输入,在U型结构的左侧,第1个卷积单元(这里将每次下采样后到下一次下采样之前的卷积操作称作1个卷积单元)包含一个通道数为32的3×3卷积层、BN(batch normalization)层、ReLU (Rectified linear unit)激活层和RAD块(residual attention-based dense block)等操作,其余4个卷积单元只包含RAD块操作。
在U型结构的右侧,每一次上采样之后的输出与U型结构左侧相同大小的特征映射图进行拼接,之后进行1×1卷积层、BN层、ReLU激活层和RD块(residual dense block)等操作。1×1卷积将输入的特征图的通道数减少为原来的1/4倍,RD块操作将输入的特征图通道数转换为原来的2倍。其中,上采样过程中转置卷积操作卷积核大小为4×4,步长为2,padding为1。
最后一个卷积单元的最后一层是通道数为1的1×1卷积层,用来输出图像。在U型结构的输入和输出之间加入了残差连接。这样,整个深度网络实际上是在学习含条状伪影图像到条状伪影图像的映射。
一种输入为32通道输出为64通道的RAD块如图3所示,它是整个网络第1单元中的RAD块,其余单元中的RAD块有类似结构。在图3中,RAD块包含6个单元。前4个单元构成密集连接块,具体的特征映射图变化流程如图3所示。
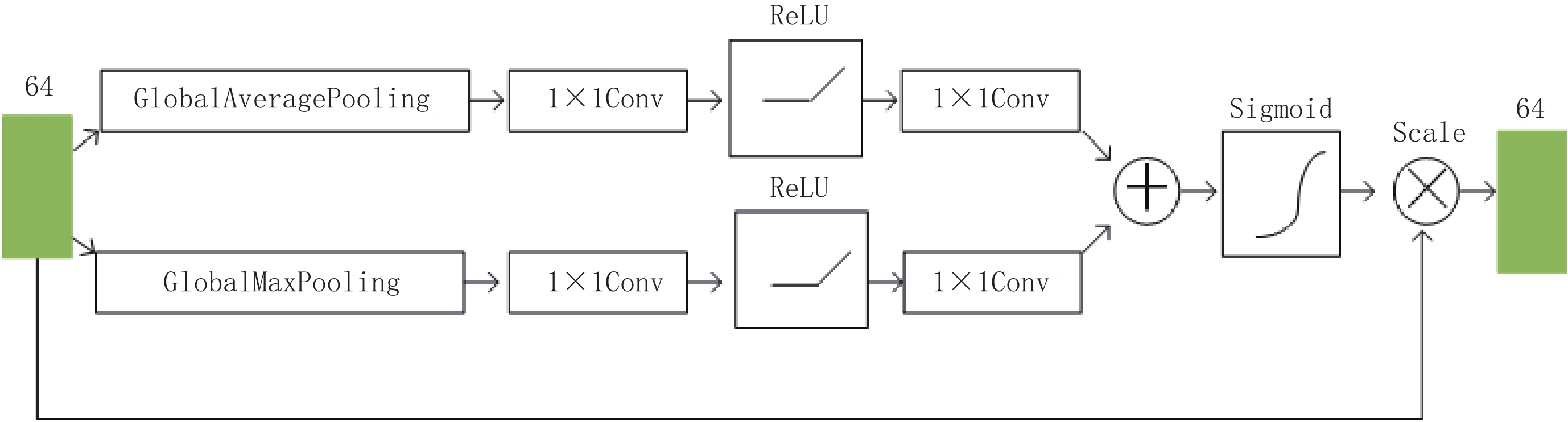
第5个单元是一个通道注意力模块,如图4所示。它通过学习到一个64×1的通道注意力权重,并将之与输入的通道数为64的特征映射图相乘,获得特定通道被加强的特征映射图。第6个单元是1×1卷积层,并在第4个单元与第6个单元之间加入了残差学习。RD块与RAD块的区别是没有第5个单元即注意力模块。
2.2 判别器结构
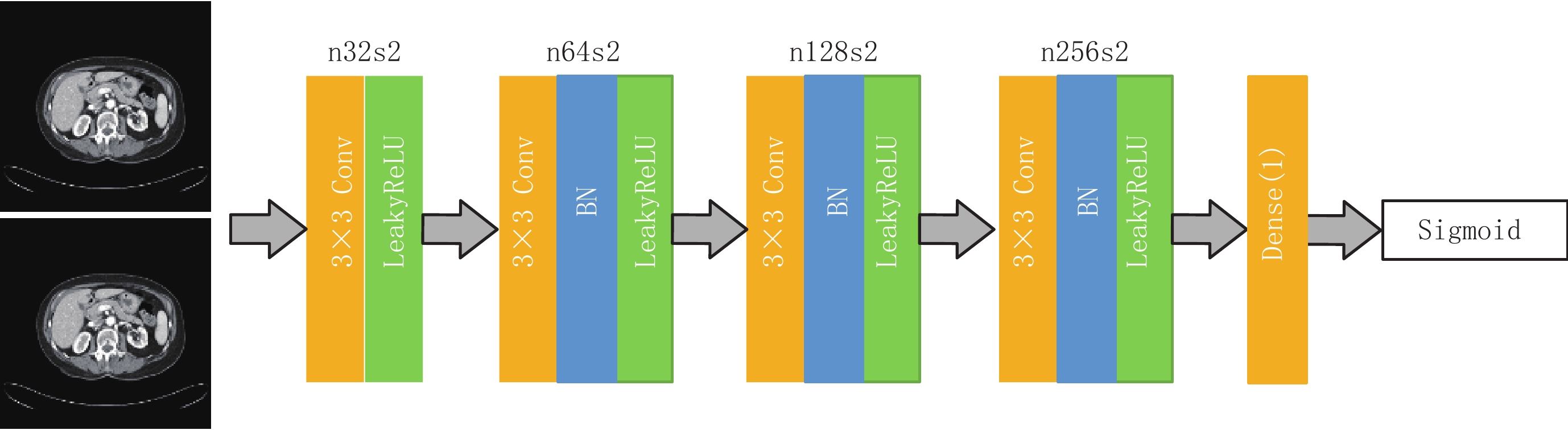
判别网络结构图如图5所示。判别网络采用4个卷积层,将大小为256×256的高精度CT图像和残差密集生成网络重建的CT图像分别作为网络的输入,然后进行4个卷积操作,4个卷积操作使用3×3大小的卷积核,步长为2。最后一个卷积操作将通道数转换为1,进行输出,通过这样训练的时候可以获取到更多的图像细节。图中n32s2代表卷积层的卷积核的数量为32,步长为2。
2.3 损失函数
本文对抗式残差密集网络采用原始GAN中的交叉熵二分类作为对抗损失,本文的对抗式残差密集网络的损失函数采用内容损失和对抗损失的加权和,内容损失使用
$ {\mathcal{l}}_{2} $ 损失可以获取到更好的效果。内容损失表示为:$$ {L}_{{\rm{Con}}}=\frac{1}{N}\sum _{i=0}^{N}{({y}_{i}-{x}_{i})}^{2}, $$ (2) 其中,
$ i $ 表示图像中像素的索引,$ N $ 为图像的大小, x为残差密集生成网络生成的CT图像,$ y $ 为相对应的高精度CT图像。本文损失函数表示为:$$ L={L}_{{\rm{Con}}}+{L}_{{\rm{adv}}} 。$$ (3) 3. 实验结果与分析
本节主要介绍数据集,网络训练参数设定,以及实验对比分析。实验选取经典的RED-CNN网络、FBPConvNet和FD-UNet网络3种算法作为稀疏重建的算法,来与本文算法进行对比。
3.1 数据集的创建
本文选取了2015幅不同的CT图像进行训练,来自TCIA数据集(https://www.cancerimagingarchive.net/),其中50幅为测试集,50幅为验证集。图像大小为256×256像素。含条状伪影的CT图像通过对高精度CT图像进行Radon变换得到相对应的稀疏投影图像,其中每幅CT图像选择60个投影进行稀疏重建。
3.2 网络训练超参数设定
在实验中,RED-CNN网络、FBPConvNet网络和FD-UNet网络使用
$ {\mathcal{l}}_{2} $ 损失函数。本文提出的对抗式残差密集网络使用$ {\mathcal{l}}_{2} $ 损失与对抗损失加权,其他参数保持一致。其中,所有的网络都使用Adam优化器,epoch为80,学习率为0.0002,batch_size为8。所有的卷积和反卷积滤波器都以均值为0、标准差为0.01的随机高斯分布初始化。3.3 实验平台
实验配置CPU是Inter(R) Xeon(R) CPU E5-2620 v4 @ 2.10 GHz,GPU是NVIDIA Geforce GTX 1080 Ti,使用Keras库,在Python上进行训练,训练时间约为4 h。
3.4 实验结果及分析
3.4.1 稀疏重建算法对比分析
该实验中,输入是在[0,π]范围内等间隔采集60个角度下的投影数据进行稀疏重建的CT图像。在测试集中分别选取两幅CT图像不同算法测试结果如图6和图7所示,将本文提出的方法与经典的RED-CNN、FBPConvNet和FD-UNet三种算法进行实验对比,实验结果表明,FBP稀疏重建的CT图像具有明显的条状伪影,其他3种经典稀疏重建算法都有效地压制了条状伪影,并取得了较好的效果,但图像中仍然存在一些明显的条状伪影,而本文提出的对抗式残差密集网络重建图像较为清晰,在去掉条状伪影的同时保留了更多的图像细节。
对于定量分析,本文采用峰值信噪比(PSNR)、均方根误差(RMSE)和结构相似性(SSIM)作为CT图像稀疏重建效果的评价指标,结果如表1所示。本文方法与经典的RED-CNN、FBPConvNet和FD-UNet三种方法相比,第1幅CT图像PSNR 高出 FBPConvNet网络大概1 dB,RMSE降低了将近0.002,与FD-UNet网络相比,SSIM略微领先。第2幅CT图像中本文方法指标也优于其他的稀疏重建方法。实验结果表明,本文提出的方法与经典的RED-CNN、FBPConvNet和FD-UNet三种算法相比,该方法保留的细节信息更多,重建出的CT图像精度更高。
表 1 稀疏重建结果的RMSE、SSIM和PSNR分析Table 1. RMSE, SSIM and PSNR analysis of sparse-view reconstruction results重建方法 FBP RED-CNN FBPConvNet FD-UNet 本文方法 PSNR 22.230 28.800 34.440 35.180 35.240 RMSE 0.077 0.036 0.019 0.017 0.017 SSIM 0.645 0.923 0.967 0.969 0.970 PSNR 19.740 27.210 35.660 35.930 36.150 RMSE 0.103 0.044 0.016 0.016 0.016 SSIM 0.593 0.941 0.981 0.979 0.981 3.4.2 本文算法在不同稀疏情形下的性能分析
为了探索本文提出的对抗式残差密集网络在不同稀疏情形下的重建图像算法的性能,在[0,π]范围内等间隔分别采集15、30和90个角度下的投影数据进行稀疏重建的CT图像作为本文算法的输入进行训练,并进行定性和定量分析。
实验结果如图8所示,在稀疏度为15时,该对抗式残差密集网络稀疏重建的CT图像效果最差,稀疏度为30时重建的图像仍然存在明显的条状伪影,稀疏度为60时,保留的细节信息明显增加,从图8(i)可以看出,90个投影角度下保留的细节信息更多,纹理结构更加明显。对于定量分析,比较结果如表2所示,在90个稀疏角度下重建出的CT图像PSNR比60个稀疏度下重建的CT图像高出将近0.2 dB。实验结果表明,在深度学习去条状伪影过程中,稀疏角度越多的CT图像,在该网络中越容易训练出高精度CT图像。
表 2 不同稀疏度下重建图像的PSNR值、SSIM值、RMSE值Table 2. RMSE, SSIM and PSNR analysis of reconstruction results under different sparsity投影个数 15 30 60 90 PSNR 29.770 31.450 34.690 34.810 RMSE 0.032 0.027 0.018 0.018 SSIM 0.908 0.930 0.964 0.964 4. 结语
在本文提出的对抗式残差密集深度神经网络中,将残差密集生成网络基于经典UNet进行了改进,判别网络提高了网络的表达能力。与经典的RED-CNN、FBPConvNet和FD-UNet三种稀疏重建算法相比,该算法能够有效地恢复图像细节,且重建出的CT图像精度更高。与此同时,稀疏角度越多,该网络越容易训练出高精度CT图像,说明该网络在提高CT图像高精度稀疏重建方面具有很大的潜力。
未来的研究方向将基于此网络架构的压制条状伪影网络进行改进,进一步提高CT图像稀疏重建的精度。现在,我们正将此网络应用于电子顺磁共振稀疏重建中,评估其在此成像模态下的性能。
-
表 1 稀疏重建结果的RMSE、SSIM和PSNR分析
Table 1 RMSE, SSIM and PSNR analysis of sparse-view reconstruction results
重建方法 FBP RED-CNN FBPConvNet FD-UNet 本文方法 PSNR 22.230 28.800 34.440 35.180 35.240 RMSE 0.077 0.036 0.019 0.017 0.017 SSIM 0.645 0.923 0.967 0.969 0.970 PSNR 19.740 27.210 35.660 35.930 36.150 RMSE 0.103 0.044 0.016 0.016 0.016 SSIM 0.593 0.941 0.981 0.979 0.981 表 2 不同稀疏度下重建图像的PSNR值、SSIM值、RMSE值
Table 2 RMSE, SSIM and PSNR analysis of reconstruction results under different sparsity
投影个数 15 30 60 90 PSNR 29.770 31.450 34.690 34.810 RMSE 0.032 0.027 0.018 0.018 SSIM 0.908 0.930 0.964 0.964 -
[1] PAN X, SIDKY E Y, VANNIER M. Why do commercial CT scanners still employ traditional, filtered back-projection for image reconstruction?[J]. Inverse Problems, 2008, 25(12): 1230009.
[2] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289−1306. doi: 10.1109/TIT.2006.871582
[3] SIDKY E Y, KAO C M, PAN X. Accurate image reconstruction from few-view limited-angle data in divergent-beam CT[J]. Journal of X-ray Science and Technology, 2006, 14(2): 119-139.
[4] SIDKY E Y, PAN X. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization[J]. Physics in Medicine & Biology, 2008, 53(17): 4777−4807. doi: 10.1088/0031-9155/53/17/021
[5] LIU Y, MA J, FAN Y, et al. Adaptive-weighted total variation minimization for sparse data toward low-dose X-ray computed tomography image reconstruction[J]. Physics in Medicine & Biology, , 2012, 57(23): 7923-7956.
[6] STRONG D, CHAN T. Edge-preserving and scale-dependent properties of total variation regularization[J]. Inverse Problems, 2003, 19(6): 165−187. doi: 10.1088/0266-5611/19/6/059
[7] XIN J, CHEN Z, XING Y. Anisotropic total variation minimization method for limited-angle CT reconstruction[C]//proceedings of the Spie Optical Engineering + Applications, F, 2012.
[8] ZHANG Y, ZHANG W H, CHEN H, et al. Few-view image reconstruction combining total variation and a high-order norm[J]. International Journal of Imaging Systems & Technology, 2013, 23(3): 249−255.
[9] ZHANG H, YAN B, WANG L, et al. Sparse-view image reconstruction with nonlocal total variation[C]//Proceedings of the 2014 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), F, 2014.
[10] SIDKY E Y, REISER I, NISHIKAWA R M, et al. Practical iterative image reconstruction in digital breast tomosynthesis by non-convex TpV optimization[J]. Proceedings of SPIE — The International Society for Optical Engineering, 2008: 6913(1): 691328-691324 .
[11] 闫慧文, 乔志伟. 基于ASD-POCS框架的高阶TpV图像重建算法[J]. CT理论与应用研究, 2021, 30(3): 279-289. DOI: 10.15953/j.1004-4140.2021.30.03.01. YAN H W, QIAO Z W. High order TpV image reconstruction algorithms based on ASD-POCS framework[J]. CT Theory and Applications, 2021, 30(3): 279-289. DOI:10.15953/j.1004-4140.2021.30.03.01. (in Chinese).
[12] LI S, CAO Q, CHEN Y, et al. Dictionary learning based sinogram inpainting for CT sparse reconstruction[J]. Optik - International Journal for Light and Electron Optics, 2014, 125(12): 2862−2867. doi: 10.1016/j.ijleo.2014.01.003
[13] ZHU J, CHEN C W. A compressive sensing image reconstruction algorithm based on low-rank and total variation regularization[J]. Journal of Jinling Institute of Technology, 2015, 31(4): 23-26.
[14] CHEN H, ZHANG Y, KALRA M K, et al. Low-dose CT with a residual encoder-decoder convolutional neural network (RED-CNN)[J]. IEEE Transactions on Medical Imaging, 2017, 36(12): 2524-2535.
[15] XU L, REN J, LIU C, et al. Deep convolutional neural network for image deconvolution[J]. Advances in neural information processing systems, 2014, 27(2): 1790−1798.
[16] HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]// Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, F, 2016.
[17] WOLTERINK J M, LEINER T, VIERGEVER M A, et al. Generative adversarial networks for noise reduction in low-dose CT[J]. IEEE Transactions on Medical Imaging, 2017, 36(12): 2536−2545. doi: 10.1109/TMI.2017.2708987
[18] GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial networks[J]. Advances in Neural Information Processing Systems, 2014, 3(11): 2672−2680.
[19] HAN Y S, YOO J, YE J C. Deep residual learning for compressed sensing CT reconstruction via persistent homology analysis[J]. 2016.
[20] RONNEBERGER O, FISCHER P, BROX T. U-Net: Convolutional networks for biomedical image segmentation[J]. Springer International Publishing, 2015, 9351: 234-241.
[21] 陈康, 狄贵东, 张佳佳, 等. 基于改进U-Net卷积神经网络的储层预测[J]. CT理论与应用研究, 2021, 30(4): 403-416. DOI:10.15953/j.1004-4140.2021.30.04.01. CHEN K, DI G D, ZHANG J J, et al. Reservoir prediction based on improved U-net convolutional neural network[J]. CT Theory and Applications, 2021, 30(4): 403-416. DOI:10.15953/j.1004-4140.2021.30.04.01. (in Chinese).
[22] JIN K H, MCCANN M T, FROUSTEY E, et al. Deep convolutional neural network for inverse problems in imaging[J]. IEEE Transactions on Image Processing, 2016, 26(9): 4509−4522.
[23] ZHANG Z, LIANG X, XU D, et al. A sparse-view CT reconstruction method based on combination of densenet and deconvolution[J]. IEEE Transactions on Medical Imaging, 2018, 37(6): 1407-1417.
[24] GAO H, ZHUANG L, MAATEN L V D, et al. Densely connected convolutional networks[J]. IEEE Computer Society, 2017: 2261-2269.
[25] HAN Y, YE J C. Framing U-Net via deep convolutional framelets: Application to sparse-view CT[J]. IEEE Transactions on Medical Imaging, 2018, 37(6): 1418−1429.
[26] STEVEN, GUAN, AMIR, et al. Fully dense UNet for 2D sparse photoacoustic tomography artifact removal[J]. IEEE Journal of Biomedical & Health Informatics, 2019, 24(2): 568-576.
[27] JIE H, LI S, GANG S, et al. Squeeze-and-excitation networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 42(8): 2011−2023.



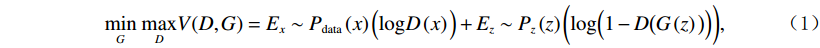








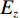
 下载:
下载: