Dense Reconstruction Algorithm of Sparse Light-field Based on Optical Flow Method
-
摘要: 光场成像在三维重建、合成孔径去遮挡和全息成像等应用中具有重要作用。光场稠密重建算法能够弥补光场成像硬件的不足，实现稀疏光场的稠密重建。本文从二维光流基本原理出发，以光场双平面模型为基础，提出一种新的四维光场光流约束方程数学模型，利用该约束方程求解得到的光场光流确定新视角的位置坐标，并通过插值计算及图像反演逐点获得新坐标的强度值，最终获得高质量的新视角合成图像。实验结果表明，本文方法能够对长基线场景中的纹理、阴影及色彩等信息进行高质量重建，定量评价结果表明该算法能够完成复杂场景的光场稠密重建任务。本文算法仅适用于线性光场光流的约束以及一维视角光场的情形，后续相关研究将围绕非线性光流约束以及多维视角光场的情形展开。Abstract: Light field imaging plays a vital role in three-dimensional reconstruction, synthetic aperture de occlusion, and holographic imaging. The light field dense reconstruction algorithm can make up for the shortage of light field imaging hardware and realize the dense reconstruction of the sparse light field. Based on the basic principle of two-dimensional optical flow and the light field biplane model, a new mathematical model of a four-dimensional light field optical flow constraint equation is proposed in this paper. The position coordinates of the new viewing angle are determined by using the light field optical flow solved by the constraint equation, and the intensity values of the new coordinates are obtained point by point through interpolation calculation and image inversion, so as to finally obtain a high-quality new viewing angle synthetic images. The experimental results show that the proposed method can realize high-quality reconstruction of the texture, shadow, and color information in the extended baseline scene. The quantitative evaluation results show that the algorithm can accomplish the task of dense light field reconstruction in complex settings. This algorithm in this paper is only applicable to the case of linear optical flow constraint and one-dimensional viewing angle light field. The subsequent related research will focus on the case of nonlinear optical flow constraint and multi-dimensional viewing angle light field.
-
Keywords:
- light field /
- light field reconstruction /
- LK optical flow method
-
光场成像由于能够记录场景中光线的4D空间角度信息而成为一种很有前途的三维渲染和显示技术[1]。目前光场相机主要有基于微透镜阵列式光场相机（又称全光相机）[2]与相机阵列[3]两种，全光相机通过在主透镜和传感器之间插入一组微透镜阵列实现对四维光场的采集，但是由于传感器分辨率的限制，全光相机通常以牺牲空间分辨率来换取角度分辨率。与此相比，阵列相机能够在一定空间区域内设置足够多的高空间分辨率的相机来提高光场的角度分辨率，但是在实际应用中，增多相机阵列数量面临成本增多、系统复杂度提高、多相机同步困难等问题，所以对低数量相机阵列获取的稀疏光场进行稠密化重建具有重要的现实意义。因此，相关研究人员以较低的价格且易于设置的稀疏相机阵列为基础，试图将稀疏相机阵列采集的稀疏光场通过图像处理算法重建为稠密光场。
目前学者们的研究方案主要对深度信息的依赖状况进行区分[4-5]。基于深度的图像渲染（depth image based rendering，DIBR）算法[6]虽然能够较好地完成重建任务，但由于重建质量非常依赖深度信息的计算精度，计算量大且构建的图像易出现重影，裂纹等现象。不依赖于深度信息的重建方案目前主要有基于压缩感知[7-8]和深度学习[9]两种，基于压缩感知的重建方案虽然利用信号在变换域的稀疏性达到了良好的计算重构效果，但是编码掩膜对像素点的透光率不同会对光线产生一定的阻碍，使得采集得到的光场丢失了部分的原始光场信号，导致重建图片信噪比较低，重建质量下降。基于深度学习的重建方案的目标是通过特征学习使合成视图与真实视图的误差达到最小，进而实现稠密重建的目的，但是特征提取过程中的上采样操作大大增加了计算开销，同时使得重建结果出现可见的重建伪影。
近年来，Flynn等[10]利用深度学习的方法对DIBR算法求取深度图不精确的问题进行了完善，他们提出了一种新的端到端的深度架构，虽然能够将场景中相邻视图的像素通过网络直接生成待重建视图的像素，但这种合成方式会丢失场景大量的原始信息。李坤等[11]利用卷积神经网络从输出视图估计出新视角的深度信息，将深度估计与视点合成有机结合，相互优化，虽然极大改善了现有算法的问题，但依然面临求取深度图不精确的问题，多种算法综合使用大大提高了计算开销。
本文提出一种新的基于四维光流约束方程的实现稀疏光场尤其是一维稀疏采样条件下的稠密重建方法，首先从二维光流约束方程出发，结合光场采集过程中光线位置的微小移动，将二维光流约束方程推广到四维光场光流约束方程中，将二维光流能够保持数据间的连续性与相关性的特性与四维光场图像数据间的关系有机结合；然后通过求解四维光流约束方程，得到光场数据间点对点的光流，合理保持了光场光线的连续性，既省去了提取深度图的繁琐步骤，又避免了现有算法中的空洞、裂纹等问题[12]；最后利用较为简单的插值算法，对以四维光流约束方程计算得到的光场光流为基础确定的待重建的光场坐标位置进行逐点插值，利用图像反演逐点求取得到待重建光场的强度值，并在不同基线场景上均呈现出较好的结果，验证了基于四维光流约束方程算法的合理性及优越性。
1. 基本原理
光流是Gibson在1950年为描述图像模式运动的速度首先提出来的[13]，光流场是图像上物体点运动的速度场，空间中的运动场转移到图像上就表示为光流场[14]。而光流法是基于光流提出的一种计算机视觉操作，旨在计算视频序列中两帧连续的特征的表观运动[15]。二维光流的算法[16]能够有效保持像素数据间的连续性和关联性，同时光流场能够有效表示像素在连续图像之间的运动，而光场稠密重建在重建过程中恰好要求保持光场数据间的连续性和关联性，使得生成的子孔径图像更加接近真实采集的子孔径图像，所以光流场的特性为将其应用于光场重建中提供了强有力的理论支撑。
1.1 Lucas-Kanada光流法算法原理
LK算法基于3点假设[17]：①灰度一致。图像场景中目标在帧间运动时像素亮度不变。②时间连续或运动是“小运动”。③空间一致。该像素点与邻域内的点具有相似运动。
假设在时间
$ t $ ，点$ (x,y) $ 处的像素灰度值为$I\big(x,y,t\big)$ ，在时间$ t + \Delta t $ ，位置$\big(x,y\big)$ 移动到位置$\big(x + \Delta t,\;y + \Delta y\big)$ ，此时的像素灰度值为$I\big(x + \Delta t,\;y + \Delta y,\;t + \Delta t\big)$ 。根据灰度一致假设，即像素的灰度在瞬时运动中应该保持一致。满足条件$\displaystyle\frac{{\;\;{\rm{d}}I(x,y,t)\;\;}}{{{\rm{d}}t}} = 0$ ，因此有：$$ I\big(x,y,t\big) = I\big(x + \Delta x,\;y + \Delta y,\;t + \Delta t\big) \text{，} $$ (1) 将上式泰勒展开：
$$ I\big(x + \Delta x,\;y + \Delta y,\;t + \Delta t\big) = I\big(x,y,t\big) + \frac{{\partial I}}{{\;\partial x\;}}\Delta x + \frac{{\partial I}}{{\;\partial y\;}}\Delta y + \frac{{\partial I}}{\;{\partial t\;}}\Delta t + o\big(\rho \big) \text{，} $$ (2) 忽略上式中的高无穷小项：
$$ \frac{{\partial I}}{{\;\partial x\;}}\Delta x + \frac{{\partial I}}{{\;\partial y\;}}\Delta y + \frac{{\partial I}}{{\;\partial t\;}}\Delta t = 0 \text{，} $$ (3) 方程两边同时除以
${\rm{d}}t$ 得：$$ \frac{{\partial I}}{{\;\partial x\;}}\frac{{{\rm{d}}x}}{{{\rm{d}}t}} + \frac{{\partial I}}{{\;\partial y\;}}\frac{{{\rm{d}}y}}{{{\rm{d}}t}} + \frac{{\partial I}}{{\;\partial t\;}} = 0 \text{，} $$ (4) 定义：
${I_x} = \displaystyle\frac{{\partial I}}{{\;\partial x\;}},{\text{ }}{I_y} = \frac{{\partial I}}{{\;\partial y\;}},{\text{ }}{I_t} = \frac{{\partial I}}{{\;\partial t\;}},{\text{ }}{V_x} = \frac{{\;{\rm{d}}x\;}}{{{\rm{d}}t}},{\text{ }}{V_y} = \frac{{\;{\rm{d}}y\;}}{{{\rm{d}}t}}$ ，则方程（4）可以写成：
$$ {I_x}{V_x} + {I_y}{V_y} = - {I_t} 。 $$ (5) 方程（5）就是基本的光流约束方程，LK光流法假设邻域内其他像素的位移矢量和中心像素相同，然后通过加权最小二乘法对邻域内的所有像素点进行计算。假设在一个小邻域空间
$ \omega $ 内包括$ n $ 个像素点${q_1},{q_2}, \cdots ,{q_n}(n \geq 2)$ ，那么可得线性方程组为：$$ \left\{ {\begin{aligned} & {{I_x}\big({q_1}\big){V_x} + {I_y}\big({q_1}\big){V_y} = - {I_t}\big({q_1}\big)} \\ & {{I_x}\big({q_2}\big){V_x} + {I_y}\big({q_2}\big){V_y} = - {I_t}\big({q_2}\big)} \\ & \qquad\qquad\qquad \vdots \\ & {{I_x}\big({q_n}\big){V_x} + {I_y}\big({q_n}\big){V_y} = - {I_t}\big({q_n}\big)} \end{aligned}} \right. 。 $$ (6) 关于每个像素的速度值
$ {V_x} $ 和$ {V_y} $ 的线性超定方程组的最小二乘解为：$$ {\Big({V_x},{V_y}\Big)^{\rm{T}}} = {\Big({\boldsymbol{A}}{}^{\rm{T}}{\boldsymbol{A}}\Big)^{ - 1}}{{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{b}} \text{，} $$ (7) 其中
${ \boldsymbol{A}} = \left( {\begin{array}{*{20}{c}} {{I_x}\big({q_1}\big)}&{{I_y}\big({q_1}\big)} \\ {{I_x}\big({q_2}\big)}&{{I_y}\big({q_2}\big)} \\ \vdots & \vdots \\ {{I_x}\big({q_n}\big)}&{{I_y}\big({q_n}\big)} \end{array}} \right) $ ，$ { \boldsymbol{b}} = - \left( {\begin{array}{*{20}{c}} {{I_t}\big({q_1}\big)} \\ {{I_t}\big({q_2}\big)} \\ \vdots \\ {{I_t}\big({q_n}\big)} \end{array}} \right) $ 。1.2 基于LK光流法四维光场重建算法理论
如图1，传统计算二维光流约束方程是建立在图1（a）传统单相机二维积分成像中，而本文算法以图1（b）利用相机阵列采集的四维光场为基础，这就要求我们将二维光流约束方程推广到四维空间中。
![]()
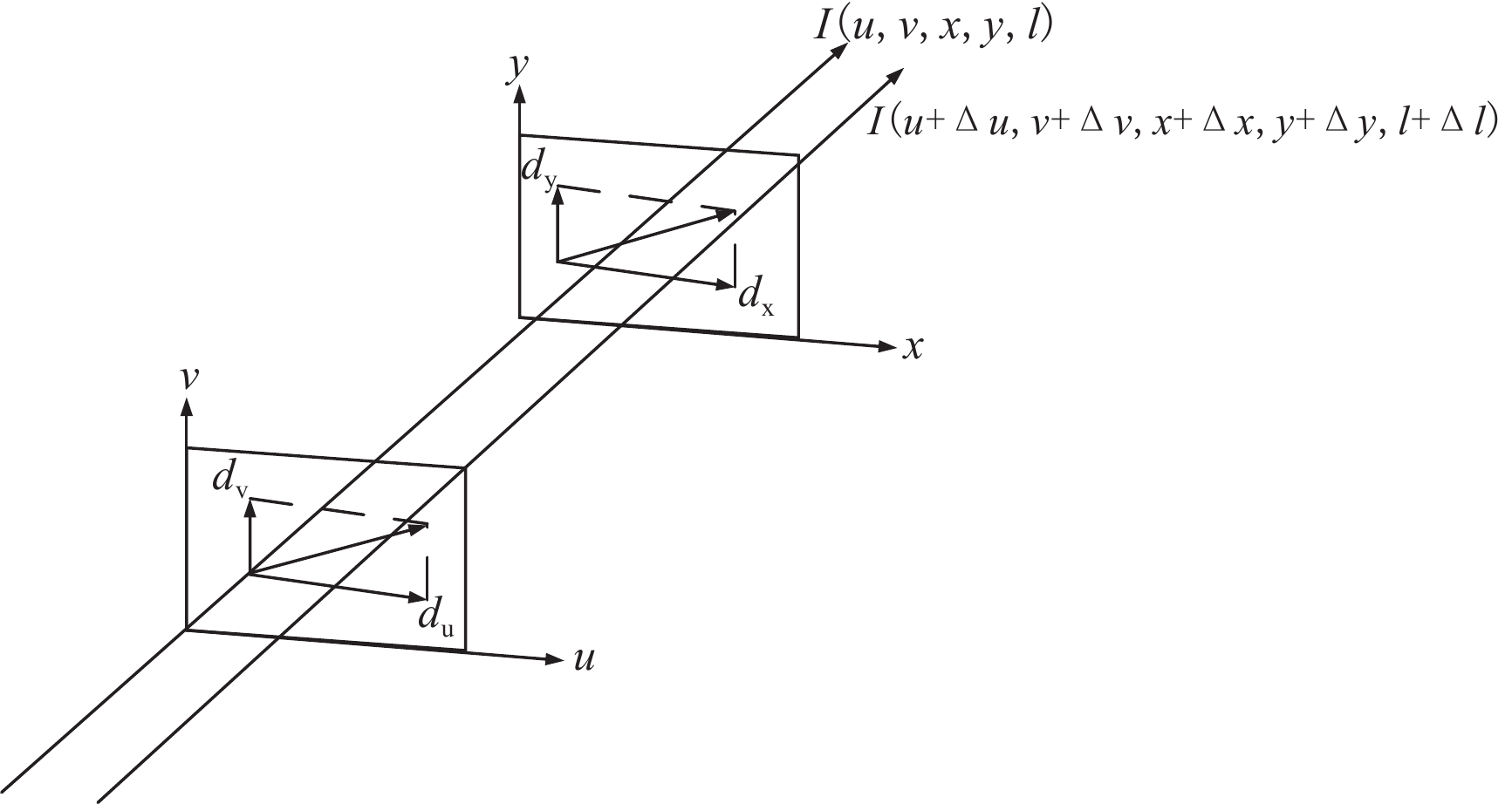
图 1 二维成像到四维成像扩展Figure 1. Extension of two-dimensional imaging to four-dimensional imaging如图2光场成像双平面表示法[18]中在位置l的强度值为
$ I\big(u,v,x,y,l\big) $ ，其中$ \big(u,v\big) $ 平面为镜头中心所在平面，图1（b）中的相机阵列的不同位置的相机就对应$\big(u,v\big) $ 平面上的不同采样点，即光场图像的角度分辨率；$ \big(x,y\big) $ 平面为成像平面，用来描述光场光线在传感器上的采样，即光场图像的空间分辨率，此时光场在所求两个平面4个方向上的光流分量为：$$ {{{{d}}}_u} = \frac{{\;{\rm{d}}u\;}}{{{\rm{d}}l}},\;{{{d}}_v} = \frac{{\;{\rm{d}}v\;}}{{{\rm{d}}l}},\;{{{d}}_x} = \frac{{\;{\rm{d}}x\;}}{{{\rm{d}}l}},\;{{{d}}_y} = \frac{{\;{\rm{d}}y\;}}{{{\rm{d}}l}} 。 $$ (8) 如图2所示，光场采集过程中，光线由位置
$ l $ 变化到位置$ l + \Delta l $ ，根据灰度一致假设，即光线位置发生微小变化过程中，光场的强度值应保持一致。满足条件$\displaystyle\frac{{\;{\rm{d}}I(u,v,x,y,l)\;}}{{{\rm{d}}l}} = 0$ ，因此有：$$ I\big(u,v,x,y,l\big) = I\big(u + \Delta u,\;v + \Delta v,\;x + \Delta x,y + \Delta y,\;l + \Delta l\big) \text{。} $$ (9) 此时，在光线位置发生微小变化时，利用泰勒公式对函数
$I\big(u + \Delta u,\;v + \Delta v,\;x + \Delta x, $ $ y + \Delta y,\;l + \Delta l\big)$ 进行展开：$$ \begin{aligned} &\qquad\qquad\qquad\qquad I\big(u + \Delta u,\;v + \Delta v,\;x + \Delta x,\;y + \Delta y,\;l + \Delta l\big) \\ & = I\big(u,v,x,y,l\big) + \frac{{\partial I}}{{\;\partial u\;}}\Delta u + \frac{{\partial I}}{{\;\partial v\;}}\Delta v + \frac{{\partial I}}{{\;\partial x\;}}\Delta x + \frac{{\partial I}}{{\;\partial y\;}}\Delta y + \frac{{\partial I}}{{\;\partial l\;}}\Delta l + o\big(\rho \big) \end{aligned} \text{，} $$ (10) 代入（9）式，则有：
$$ \frac{{\partial I}}{{\;\partial u\;}}\Delta u + \frac{{\partial I}}{{\;\partial v\;}}\Delta v + \frac{{\partial I}}{{\;\partial x\;}}\Delta x + \frac{{\partial I}}{{\;\partial y\;}}\Delta y + \frac{{\;\partial I\;}}{{\partial l}}\Delta l + o\big(\rho \big)=0 \text{，} $$ (11) 忽略（11）式的高阶无穷小项得：
$$ \frac{{\partial I}}{{\;\partial u\;}}\Delta u + \frac{{\partial I}}{{\;\partial v\;}}\Delta v + \frac{{\partial I}}{{\;\partial x\;}}\Delta x + \frac{{\partial I}}{{\;\partial y\;}}\Delta y{\text{ = }} - \frac{{\partial I}}{{\;\partial l\;}}\Delta l \text{，} $$ (12) 方程两边同时除以
${\rm{d}}l$ 得：$$ - \frac{{\;\partial I\;}}{{\partial l}} = \frac{{\partial I}}{{\;\partial u\;}}\frac{{{\rm{d}}u}}{{{\rm{d}}l}} + \frac{{\partial I}}{{\;\partial v\;}}\frac{{{\rm{d}}v}}{{{\rm{d}}l}} + \frac{{\partial I}}{{\;\partial x\;}}\frac{{{\rm{d}}x}}{{{\rm{d}}l}} + \frac{{\partial I}}{{\;\partial y\;}}\frac{{{\rm{d}}y}}{{{\rm{d}}l}} \text{，} $$ (13) 此时可得光场四维光流基本约束方程为：
$$ {I_u}{d_u} + {I_v}{d_v} + {I_x}{d_x} + {I_y}{d_y} = - {I_l} $$ (14) 其中：
${I_u} = \displaystyle\frac{{\partial I}}{{\;\partial u\;}},{\text{ }}{I_v} = \frac{{\partial I}}{{\;\partial v\;}},{\text{ }}{I_x} = \frac{{\partial I}}{{\;\partial x\;}},{\text{ }}{I_y} = \frac{{\partial I}}{{\;\partial y\;}},{\text{ }}{I_l} = \frac{{\;\partial I\;}}{{\partial l}}$ 。由二维LK光流法第三个假设，即空间一致。该像素点与邻域内的点具有相似运动。此时假定光场中的小邻域
$ \omega $ 中包含$ n $ 个点${q_1},{q_2}, \cdots ,{q_n}(n \geq 4)$ ，它们具有相同的运动，即得如下线性方程组：$$ \left\{ {\begin{array}{*{20}{c}} {{I_u}\big({q_1}\big){d_u} + {I_v}\big({q_1}\big){d_v} + {I_x}\big({q_1}\big){d_x} + {I_y}\big({q_1}\big){d_y} = - {I_l}\big({q_1}\big)} \\ {{I_u}\big({q_2}\big){d_u} + {I_v}\big({q_2}\big){d_v} + {I_x}\big({q_2}\big){d_x} + {I_y}\big({q_2}\big){d_y} = - {I_l}\big({q_2}\big)} \\ \vdots \\ {{I_u}\big({q_n}\big){d_u} + {I_v}\big({q_n}\big){d_v} + {I_x}\big({q_n}\big){d_x} + {I_y}\big({q_n}\big){d_y} = - {I_l}\big({q_n}\big)} \end{array}} \right. 。 $$ (15) 利用最小二乘法对关于
$\big({d_u},{d_v},{d_x},{d_y}\big)$ 的超定线性方程组（15）进行求解，最终可得最小二乘解为：$$ \big({d_u},{d_v},{d_x},{d_y}\big) = {\Big({\boldsymbol{A}}{}^{\rm{T}}{\boldsymbol{A}}\Big)^{ - 1}}{{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{b}} \text{，} $$ (16) 其中：
$ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{I_u}\big({q_1}\big)}&{{I_v}\big({q_1}\big)}&{{I_x}\big({q_1}\big)}&{{I_y}\big({q_1}\big)} \\ {{I_u}\big({q_2}\big)}&{{I_v}\big({q_2}\big)}&{{I_x}\big({q_2}\big)}&{{I_y}\big({q_2}\big)} \\ \vdots & \vdots & \vdots & \vdots \\ {{I_u}\big({q_n}\big)}&{{I_v}\big({q_n}\big)}&{{I_x}\big({q_n}\big)}&{{I_y}\big({q_n}\big)} \end{array}} \right],\;\;{\boldsymbol{b}} = - \left[ {\begin{array}{*{20}{c}} {{I_l}\big({q_1}\big)} \\ {{I_l}\big({q_2}\big)} \\ \vdots \\ {{I_l}\big({q_n}\big)} \end{array}} \right] $ 。传统的LK光流算法是依赖周围小块的邻域像素来求解的，如果两帧间物体的运动速度大，算法的误差就会增大。为解决这一问题，针对物体快速运动的情况建立图像金字塔[19]，虽然快速移动会导致原始图像中对象的大偏移，但是在相应的高层图像中可以假设缓慢移动，因此，可以确保光流方法的3个假设。
图像金字塔的具体流程是先对图像进行金字塔分层。上层每次缩放为下层的一半，将分辨率低的图像分配在最顶层，原始图像
$ {L_0} $ 分配在最底层。从顶层$ {L_m} $ 也就是分辨率低的图片开始，递归求解到原始图片为止。将其应用在光场中，设第$ L $ 层的损失函数为：$$ \begin{aligned} &\qquad \qquad \qquad \qquad \qquad \qquad \qquad e({{\boldsymbol{d}}^L}) = e\left( {{d_u^L},{d_v^L},{d_x^L},{d_y^L}} \right)= \hfill \\ & \sum\limits_{u = x_u^L - {\omega _u}}^{x_u^L + {\omega _u}} {\sum\limits_{v = x_v^L - {\omega _v}}^{x_v^L + {\omega _v}} {\sum\limits_{x = x_x^L - {\omega _x}}^{x_x^L + {\omega _x}} {\sum\limits_{y = x_y^L - {\omega _y}}^{x_y^L + {\omega _y}} {{{\Bigg( {{I^L}\Big(u,v,x,y\Big) - {J^L}\bigg( {u + g_u^L + d_u^L,v + g_v^L + d_v^L,x + g_x^L + d_x^L,y + g_y^L + d_y^L} \bigg)} \Bigg)}^2}} } } } \hfill \\ \end{aligned} \text{，} $$ (17) 其中，
$ {J^L} $ 表示匹配到位置$ l $ 最优的点的亮度，${{\boldsymbol{g}}^L} = \Big(g_u^L,g_v^L,g_x^L,g_y^L\Big)$ 表示亮度点在第$ L $ 层的迭代运算中的光流初值，${{\boldsymbol{d}}^L} = \Big(d_u^L,d_v^L,d_x^L,d_y^L\Big)$ 表示亮度点在第$ L $ 层迭代运算中的光流误差。其中${{\boldsymbol{d}}^L} $ 通过上述标准的LK光流法计算式（16）得到，$ {{\boldsymbol{g}}^L} $ 通过下式计算得到：$$ {{\boldsymbol{g}}^L} = 2\Big({g^{L{\text{ + }}1}} + {d^{L + 1}}\Big) 。 $$ (18) 在最高层
$ {L_m} $ 处，定义$ {{\boldsymbol{g}}^{{L_m}}} = {\big[\begin{array}{*{20}{c}} 0&0&0&0 \end{array}\big]^{\rm{T}}} $ ，重复上述计算过程逐层迭代计算。最终，金字塔最底层的光流为：$$ {\boldsymbol{d}} = {{\boldsymbol{g}}^0}{\text{ + }}{{\boldsymbol{d}}^0} 。 $$ (19) 假设待重建的光场为
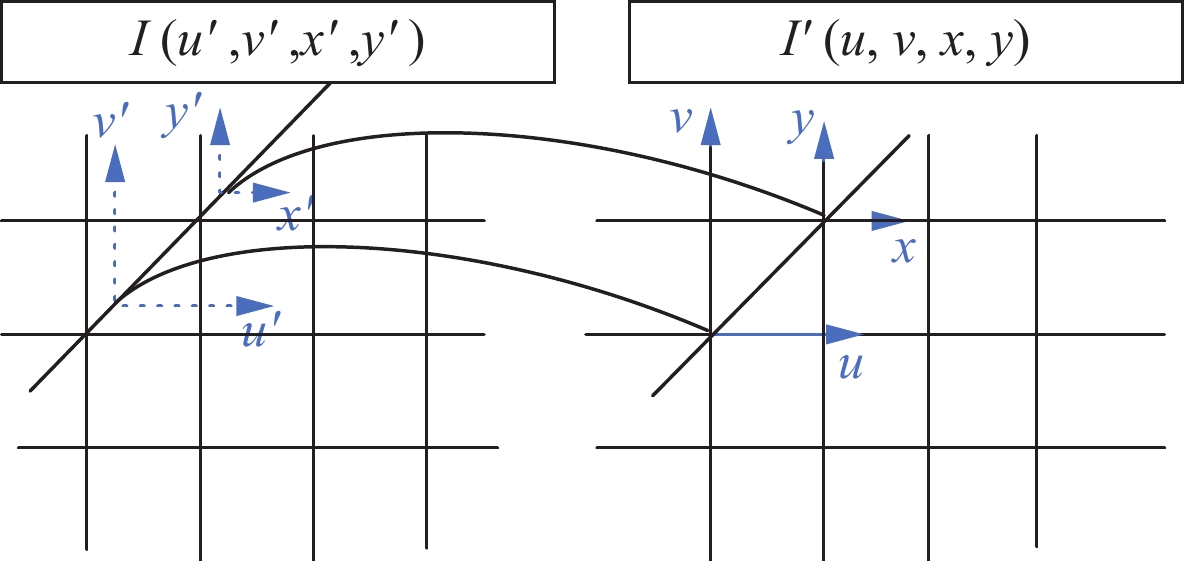
${I^\prime }\Big(u,v,x,y\Big)$ ，假设$ \lambda $ 为光场视角间的距离参数，待重建光场中对应原光场的坐标变化可表示为：$$ \Big(u,v,x,y\Big) \mapsto \left( {u + \frac{{{d_u}}}{\lambda },v + \frac{{{d_v}}}{\lambda },x + \frac{{{d_x}}}{\lambda },y + \frac{{{d_y}}}{\lambda }} \right) = \Big(u',v',x',y'\Big) 。 $$ (20) 由于坐标
$\big (u',v',x',y'\big) $ 均不是整数值，所以对应的强度值无法直接得到，如图3，利用插值方法计算坐标$ \big(u',v',x',y'\big) $ 的强度值$ I\big(u',v',x',y'\big) $ ，进而通过像素映射得到待重建光场的强度值${I'}\big(u,v,x,y\big)$ 。二维插值能够在合理保持各分量的比重、非零元素的位置及其强度值之间的相互约束下，合理地为基向量的权重进行赋值。假设双线性插值算子为$\varGamma$ ，则待重建的光场可以表示为：$$I'\big(u,v,x,y\big) = I\big(u',v',x',y'\big) = \varGamma {\text{ }}I\big(u,v,x,y\big) 。 $$ (21) 具体算法流程图如图4所示，通过线性相机阵列采集到特定场景的稀疏光场，选取稀疏光场中任意视点的两帧光场图像,利用金字塔对四维光场光流约束方程进行求解，得到已知两视点的光流，加入适当的光场视角间的距离参数λ，以此获得待重建光场的位置坐标；通过已知的所选的任一视点的强度值进行插值运算，并通过图像反演得到新视点下坐标位置对应的强度值，完成稀疏光场稠密重建任务。
2. 实验与讨论
实验采用康坦茨大学和海德堡大学的HCI实验室联合提供的光场数据集[20]。该数据集提供了精心设计合成、密集采样的具有高度精确的视差真实度的4D光场，为目前最完善的光场图像合成数据集。本文从该数据集中的28个9×9个场景中选择9个场景进行了实验。由于自然场景的相似性，对场景中包含的遮挡与自遮挡信息、明显的视觉信息、丰富的高低频、颜色与阴影等信息的恢复，能够有效验证算法的有效性。
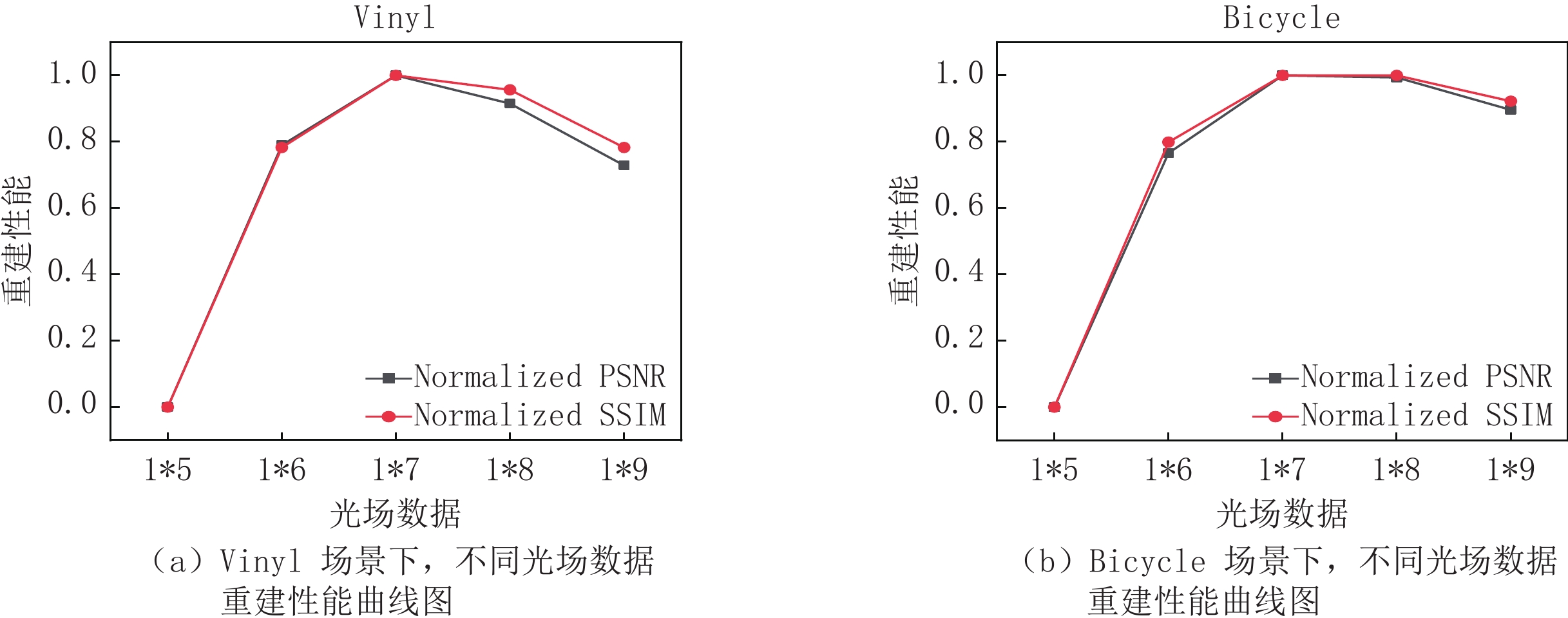
（1）为了选取合理规模的光场数据进行重建实验，需要对两个或以上差别较大的虚拟视角进行重建并与目标视角进行比较，所以选择的光场数据不应少于1×5；由于所选数据集中光场规模的限制，所选光场数据最大为1×9。分别选择两个特征丰富的自然场景Vinyl与Bicycle进行实验，选取场景中的1×5，1×6，1×7，1×8，1×9的光场数据对同一视点进行恢复，量化结果由峰值信噪比（peak signal to noise ratio，PSNR）以及结构相似性（structural similarity index，SSIM）[21]来表征，峰值信噪比是基于对应像素点之间的误差，即基于误差敏感的图像质量评价指标，峰值信噪比的值越大，说明重建图像失真越小。结构相似性是一种衡量两张数字图像相似度的指标，它分别从亮度、对比度、结构3方面度量图像的相似性，更加符合人眼对图片质量的判断，结构相似性的取值范围为[0,1]，值越大，失真越小。为了易于观察重建性能随光场数据的变化趋势，从而便于对光场数据进行合理取值，对原始实验数据进行了归一化处理。
如图5所示，不同场景下的PSNR值与SSIM值均在光场数据为1×7时取得最大值，由此说明本文算法选择光场数据为1×7时重建性能最优，重建效果最好，更能解决光场成像面临的角度分辨率与空间分辨率的制约问题，提高了光场成像的角度分辨率，进而更好地满足实际应用中的要求，所以综合考虑算法的重建性能以及运算效率，本文算法选取场景中的1×7的光场数据为稠密光场，并可以选取任一视角作为待重建视角。
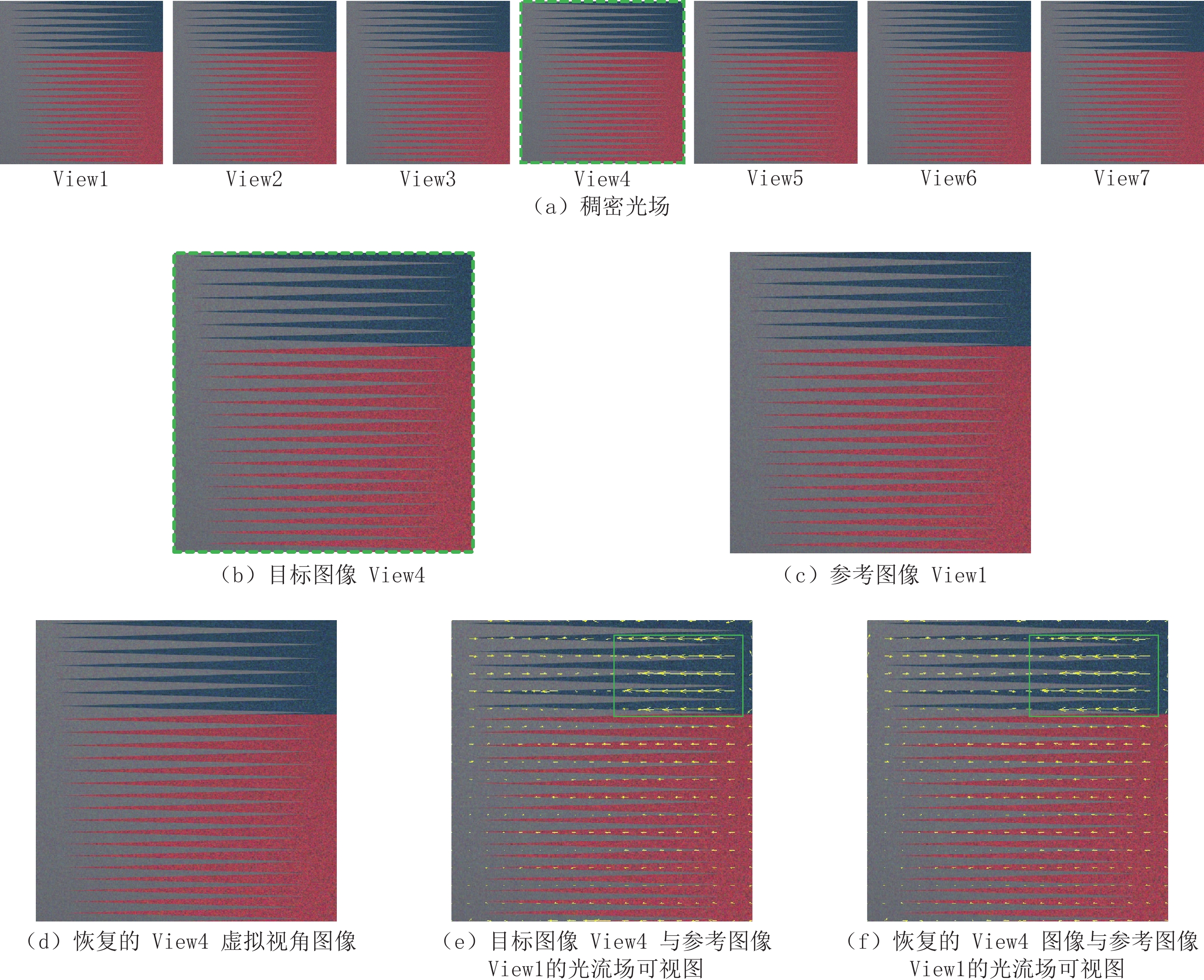
（2）为验证光流算法在稀疏光场稠密重建算法中的可行性，选取数据集中的backgammon场景进行实验。
图6（a）为1×7的稠密光场，图6（b）为待重建中间虚拟视角View4图像，即为目标图像，图6（c）为参考图像View1，图6（d）为本文算法恢复的虚拟视角View4图像，即为重建图像，图6（e）为参考图像View1与目标图像View4的光流场可视图，图6（f）为参考图像View1与重建图像View4的光流场可视图。参考图像与目标图像View4的光流场可视图表明，由视角View4到视角View1光流运动的矢量图说明场景整体向左移动（相机视角的左），在绿色框划定的视差较大的区域，光流的变化较大，视差较小的区域，光流的变化较小，光流可视图体现了场景间视差信息的变化。参考图像与重建图像View4的光流场可视图和参考图像与目标图像View4的光流场可视图基本吻合，证明了算法能够较好地恢复光场的视差信息，说明光流算法在稀疏光场稠密重建是有效的。
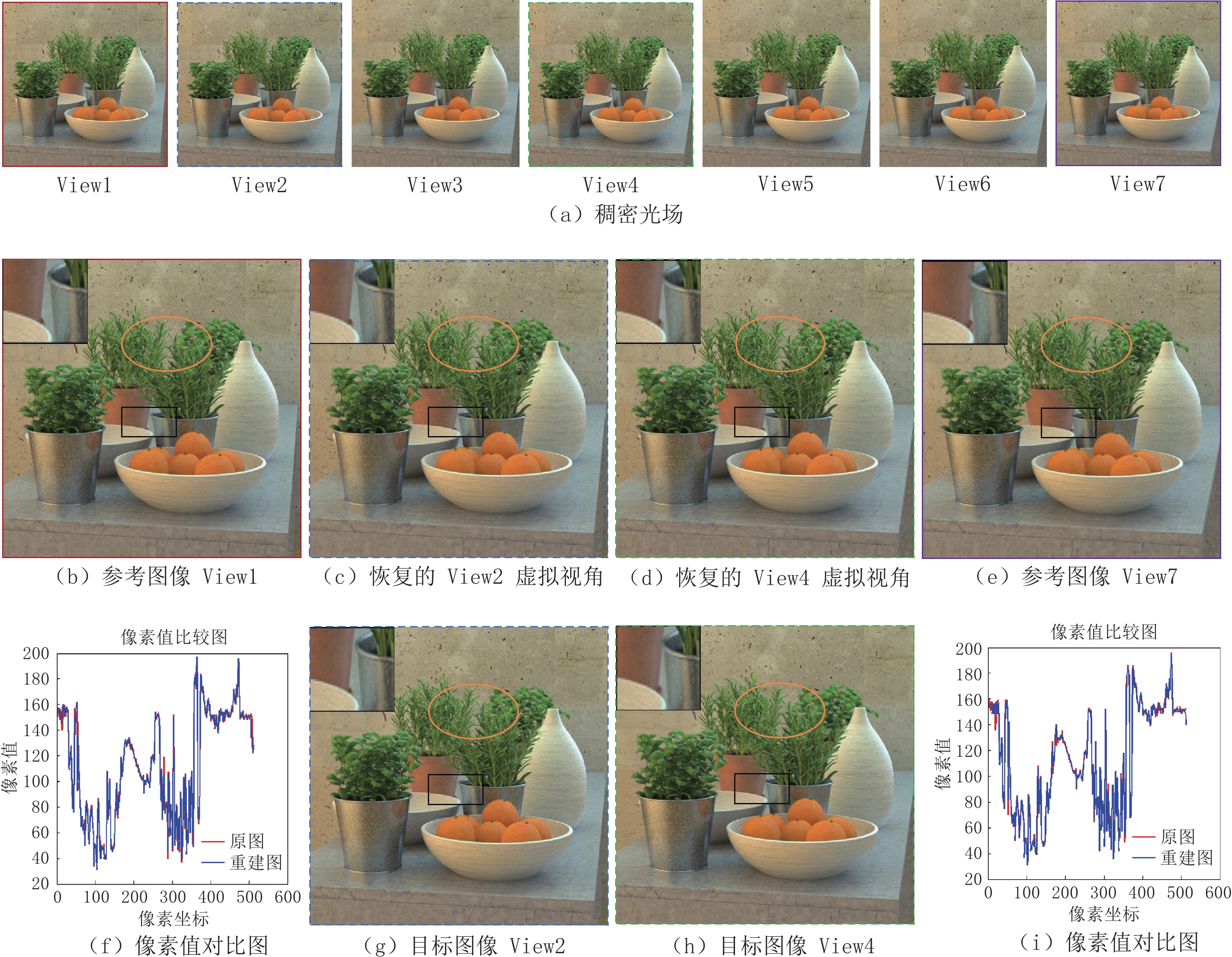
（3）为了验证算法对遮挡、自遮挡与视差信息等恢复的有效性，选取数据集中包含明显遮挡与自遮挡区域的场景herbs进行重建。
图7（a）为1×7的稠密光场，保持了光场空间和角度的连续性。图7（b）和图7（e）为光场两端视角的参考图像。场景中白色花盆为前景目标，其对后景橙色花盆造成了明显遮挡；场景中包含复杂交错及具有细长结构的树叶，层次分明，明显遮挡及自遮挡信息明显。图7（c）和图7（d）为目标图像，图7（g）和图7（h）为恢复的两个虚拟视角图像。从图中的左上角黑色方框放大区域可以明显地看到算法准确恢复了场景中局部区域被遮挡的目标的信息；图中橙色椭圆所示位置表明算法对具有细长结构且自遮挡明显的树叶的边缘信息恢复较为清晰并有效地保持了图像局部颜色一致性。恢复的两个虚拟角度图像之间具有明显视差，表明算法能够有效地恢复光场间的视差信息。图7（f）和图7（i）分别为目标视角View2和View4与其对应重建图的像素值对比图，图中看出，信息丰富的中轴线的重建像素值与目标图基本吻合，从数值方面说明重建效果好。总体说明本文算法能对特征相似、深度不同且视差明显的复杂场景进行高质量重建。
（4）选取包含高低频信息的greek场景进行实验，并与优于DIBR算法且低计算开销的基于字典学习的稠密光场算法重建结果[22]进行比较。
图8（a）为1×7稠密光场，图8（b）和图8（d）为光场两端视角的参考图像。图8（c）为待恢复视角图像，图8（e）本文算法恢复虚拟视角图像，图8（f）为基于字典学习的稠密光场算法恢复的虚拟视角图像。由于本文算法使用了光流法映射坐标，重建位置信息获取准确，逐点匹配的强度信息完整，能够有效且完整地恢复虚拟视点图像，图中黄色框内放大区域表明本文算法准确且完整恢复了虚拟视点的信息，而基于字典学习的算法所恢复的图像出现了失真现象，即在包含高频信息丰富的男性雕塑头部出现区域模糊现象。图8（g）为本文算法重建图、基于字典学习算法重建图与原目标图的像素值对比图，像素值对比图表明本文算法的重建图与原目标图像的像素值基本一致，而基于字典学习的像素值与原目标图像的像素值相差甚远，说明本文算法能对高频信息丰富的场景进行高质量重建。
![]()
图 8 包含高低频信息场景的稠密光场重建Figure 8. Dense light field reconstruction of scenes containing high and low frequency information为验证算法对不同场景的适应性，通过与基于字典学习的稠密重建算法比较对同一视点恢复的PSNR值与SSIM值，本文算法对多种不同场景的1×9和1×7的光场数据进行稠密重建实验，重建结果如表1与表2所示，本文算法的重建结果优于基于字典学习的算法重建结果；将选取的1×9和1×7的光场数据的实验结果进行对比，虽然PSNR值与SSIM值基本接近，但是本文算法对1×7的光场数据适应性更强，重建性能更好。总体的量化结果表明本文算法能够对不同基线长度、不同复杂程度以及不同空间结构的场景进行高质量重建。
表 1 不同场景稠密光场重建PSNR值对比结果Table 1. Comparison of PSNR values of dense light field reconstruction in different scenes场景 Table Bicycle Town Boardgames Rosemary Vinyl 文献22算法 34.865 30.773 34.015 30.813 35.367 34.614 本文算法1*9 39.326 34.817 38.979 44.117 41.105 46.855 本文算法1*7 40.074 35.030 39.780 44.228 42.412 47.389 表 2 不同场景稠密光场重建SSIM值对比结果Table 2. Comparison of SSIM values of dense light field reconstruction in different scenes场景 Table Bicycle Town Boardgames Rosemary Vinyl 文献22算法 0.932 0.886 0.947 0.934 0.970 0.942 本文算法1*9 0.960 0.958 0.982 0.993 0.987 0.994 本文算法1*7 0.963 0.959 0.984 0.994 0.988 0.995 3. 结论
传统的光流法能够根据各个像素点的速度矢量特征对图像进行分析，从而实现对目标的运动检测，本文提出基于光流法的稀疏光场稠密重建的方法，将二维光流特性与光场进行有机结合，提出四维光流约束方程模型，利用点对点求取的四维光场光流实现对光场数据的逐点重建，较好地恢复了场景的视差、遮挡、自遮挡等信息，尤其避免了重建过程中容易出现的空洞、裂纹、重影等问题。实验结果表明，本文方法对多种不同基线的场景都有较好的重建性能，且能较好保留场景的纹理、轮廓、阴影等细节信息。
本文目前只针对线性相机阵列采集的一维视角稀疏光场进行稠密重建，在接下来的研究中，将围绕非线性相机采集的多维视角光场进行展开。
-
![]()
图 1 二维成像到四维成像扩展
Figure 1. Extension of two-dimensional imaging to four-dimensional imaging
![]()
图 8 包含高低频信息场景的稠密光场重建
Figure 8. Dense light field reconstruction of scenes containing high and low frequency information
表 1 不同场景稠密光场重建PSNR值对比结果
Table 1 Comparison of PSNR values of dense light field reconstruction in different scenes
场景 Table Bicycle Town Boardgames Rosemary Vinyl 文献22算法 34.865 30.773 34.015 30.813 35.367 34.614 本文算法1*9 39.326 34.817 38.979 44.117 41.105 46.855 本文算法1*7 40.074 35.030 39.780 44.228 42.412 47.389 
下载: 导出CSV
表 2 不同场景稠密光场重建SSIM值对比结果
Table 2 Comparison of SSIM values of dense light field reconstruction in different scenes
场景 Table Bicycle Town Boardgames Rosemary Vinyl 文献22算法 0.932 0.886 0.947 0.934 0.970 0.942 本文算法1*9 0.960 0.958 0.982 0.993 0.987 0.994 本文算法1*7 0.963 0.959 0.984 0.994 0.988 0.995
下载: 导出CSV
-
[1] IHRKE I, RESTREPO J, MIGNARD-DEBISE L. Principles of light field imaging: Briefly revisiting 25 years of research[J]. IEEE Signal Processing Magazine, 2016, 33(5): 59−69. doi: 10.1109/MSP.2016.2582220
[2] REN N, LEVOY M, BREDIF M, et al. Light field photography with a hand-held plenoptic camera[J]. Stanford University Cstr, 2005, 2(1): 1−11.
[3] WILBURN B, JOSHI N, VAISH V, et al. High performance imaging using large camera arrays[J]. ACM Transactions on Graphics, 2005, 24(3): 765−776. doi: 10.1145/1073204.1073259
[4] STA B, LU Z, WZA B, et al. Quality assessment of DIBR-synthesized views: An overview[J]. Neurocomputing, 2021, 423: 158−178. doi: 10.1016/j.neucom.2020.09.062
[5] ZHOU W, LIU G, SHI J, et al. Depth-guided view synthesis for light field reconstruction from a single image[J], Image and Vision Computing, 2020, 95(c): 103874.
[6] JING X, MA Y, ZHAO Q, et al. Light field reconstruction using dynamically generated filters[J]. Springer, Cham, 2020: 3−13.
[7] 焦鹏飞, 李亮, 赵骥. 压缩感知在医学图像重建中的最新进展[J]. CT理论与应用研究, 2012,21(1): 133−147. JIAO P F, LI L, ZHAO J. New advances of compressed sensing in medical image reconstruction[J]. CT Theory and Applications, 2012, 21(1): 133−147. (in Chinese).
[8] CAO X, GENG Z, et al. Dictionary-based light field acquisition using sparse camera array[J]. Optics Express, 2014, 22(20): 24081−24095. doi: 10.1364/OE.22.024081
[9] 王飞, 王昊, 卞耀明, 等. 深度学习在计算成像中的应用[J]. 光学学报, 2020,40(1): 0111002. doi: 10.3788/AOS202040.0111002 WANG F, WANG H, BIAN Y M, et al. Applications of deep learning in computational imaging[J]. Acta Optica Sinica, 2020, 40(1): 0111002. (in Chinese). doi: 10.3788/AOS202040.0111002
[10] FLYNN J, NEULANDER I, PHILBIN J, et al. Deep stereo: Learning to predict new views from the world's imagery[C]//IEEE Computer Society, 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Washington D C, USA: 2016: 5515-5524.
[11] 李坤, 毛亚丽, 马健, 等. 稀疏光场的密集重建方法[J]. 中国科技论文, 2018,13(20): 2317−2322. doi: 10.3969/j.issn.2095-2783.2018.20.006 LI K, MAO Y L, MA J, et al. Dense reconstruction for sparsely-sampled light field[J]. China Sciencepapter, 2018, 13(20): 2317−2322. (in Chinese). doi: 10.3969/j.issn.2095-2783.2018.20.006
[12] 王伟健. 基于DIBR的虚拟视点合成算法研究[D]. 武汉: 华中科技大学, 2016. [13] GIBSON J J. The perception of the visual world[M]. Oxford, England: Houghton Mifflin, 1950.
[14] 都雪静, 张美欧. 基于光流法与背景建模法融合的车道线识别算法研究[J]. 重庆理工大学学报(自然科学), 2021,35(3): 29−35, 99. DU X J, ZHANG M O. Based on fusing optical flow method and background, odeling for lane line recognition[J]. Journal of Chongqing University of Technology (Natural Science), 2021, 35(3): 29−35, 99. (in Chinese).
[15] HARTMANN C, WANG J, OPRISTESCU D, et al. Implementation and evaluation of optical flow methods for two-dimensional deformation measurement in comparison to digital image correlation[J]. Optics & Lasers in Engineering, 2018, 107(aug.): 127−141.
[16] 於小杰, 贺勇, 刘盛华. 一种用于无人机室内定位的改进ORB光流算法[J]. 计算机工程与应用, 2021, 57(4): 266-271. SHI X J, HE Y, LIU S H. An improved orb optical flow algorithm for UAV indoor positioning[J]. Computer Engineering and Applications, 2021, 57(4): 266-271. (in Chinese).
[17] GANG Z, TANG S, LI J. Face landmark point tracking using LK pyramid optical flow[C]//Tenth International Conference on Machine Vision (ICMV 2017). 2018.
[18] 赵于平, 金熙, 赵松年. 光场成像中的景深扩展方法与信息处理[J]. 现代电子技术, 2016,39(4): 102−107. ZHAO Y P, JING X, ZHAO S N. Scene depth extension method and information processing in light field imaging[J]. Modern Electronics Technique, 2016, 39(4): 102−107. (in Chinese).
[19] 李亚楠, 赵耀, 林春雨, 等. 基于图像分割的金字塔Lucas-Kanade光流法提取深度信息[J]. 铁道学报, 2015,37(1): 63−68. doi: 10.3969/j.issn.1001-8360.2015.01.010 LI Y N, ZHAO Y, LIN C Y, et al. Depth information extraction with pyramid lucas-kanade optical flow method based on image segmentation[J]. Journal of the China Railway Society, 2015, 37(1): 63−68. (in Chinese). doi: 10.3969/j.issn.1001-8360.2015.01.010
[20] HONAUER K, JOHANNSEN O, KONDERMANN D, et al. A dataset and evaluation methodology for depth estimation on 4d light fields[M]. Asian Conference on Computer Vision, 2016: 19-34.
[21] 佟雨兵, 张其善, 祁云平. 基于PSNR与SSIM联合的图像质量评价模型[J]. 中国图象图形学报, 2006,11(12): 1758−1763. doi: 10.11834/jig.2006012307 TONG Y B, ZHANG Q S, QI Y P. Image quality assessing by combining PSNR with SSIM[J]. Journal of Image and Graphics, 2006, 11(12): 1758−1763. (in Chinese). doi: 10.11834/jig.2006012307
[22] 夏正德, 宋娜, 刘宾, 等. 基于字典学习的稠密光场重建算法[J]. 物理学报, 2020,69(6): 064201. doi: 10.7498/aps.69.20191621 XIA Z D, SONG N, LIU B, et al. Dense light field reconstruction algorithm based on dictionary learning[J]. Acta Physica Sinica, 2020, 69(6): 064201. (in Chinese). doi: 10.7498/aps.69.20191621
-
期刊类型引用(5)
1. 詹林，潘剑伟，高健，张成丽，杨晨，钱伦，槐玉鹿. 基于局部加密的非结构化网格SNMR方法二维Occam反演研究. 地球物理学进展. 2024(03): 1089-1101 . 
百度学术
2. 闫建波，余永鹏，杨彦成，王嘉文，谭浩，李昱霖. 采煤工作面地下水分布变化的综合物探应用研究. 煤炭技术. 2024(10): 96-101 . 百度学术
3. 唐塑，武银婷，邢浩，娄雪聪，石海涛. 高密度电法与瞬变电磁法在戈壁区找水的联合应用. CT理论与应用研究. 2023(01): 27-34 . 本站查看
4. 卢向星，陈慈河，孙旭，杨晨，钱伦，潘剑伟. 高密度电阻率法联合自然电场法在滑坡探测中的应用研究. 中国水运. 2023(05): 150-152 . 百度学术
5. 彭菁. 单套制趋势下长航局系统电子会计凭证报销入账归档研究. 中国水运. 2023(09): 150-152 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 554
- HTML全文浏览量: 279
- PDF下载量: 52
- 被引次数: 7
