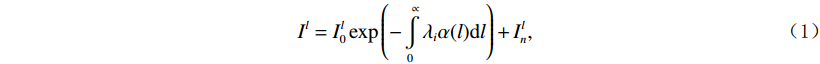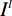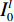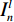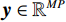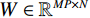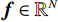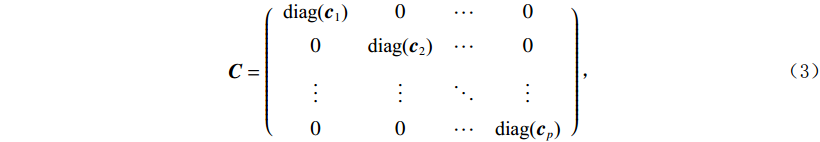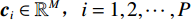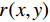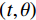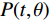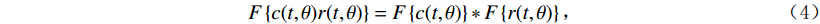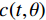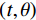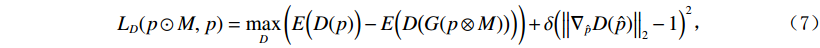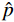Coded Aperture Computed Tomography Via Generative Adversarial U-net
-
摘要: 针对编码孔径CT成像非连续稀疏采样只能通过代数类迭代重建算法的缺点,本文提出一种基于U型生成对抗网络的编码孔径CT成像方法。通过构建基于U型生成对抗网络的非连续稀疏投影的动态博弈模型,结合联合损失函数,预测正弦图的结构性缺失,实现编码孔径CT成像分析类(非迭代)快速重建。实验结果表明,在辐射剂量降低95% 的条件下,基于U型生成对抗网络的编码孔径CT成像方法实现了峰值信噪比大于30 dB @ 256×256的高质量重建。相比于目前最先进的编码孔径CT成像方法,其重建时间降低了约两个数量级。Abstract: Generative adversarial U-net for coded aperture computed tomography (CT) is proposed in this paper to alleviate the tradeoff between the non-continuous sparse projections and the ill-posedness iterative reconstruction problem. A non-continuous sparse projection model is presented based on generative adversarial U-net and the corresponding joint penalty function is formulated. Simulations using real datasets show that CT images with 256×256 pixels can be reconstructed with peak signal-to-noise ration more than 30 dB at only 5% transmittance. Furthermore, the computational time in the reconstructions is reduced by two orders of magnitude when compared with the state-of-the-art iterative algorithms in coded aperture computed tomography.
-
Keywords:
- computed tomography /
- coded aperture /
- generative adversarial net
-
X射线计算机断层成像(computed tomography,CT)因其独特的三维层析能力与密度分辨力优势,在医学诊断、手术导航、精准医疗等方面得到了广泛的应用[1]。然而,CT成像中X射线产生的电离辐射可能诱发基因突变,增大了癌症等疾病的风险[2]。自CT成像技术问世以来,研究人员一直致力于降低成像所需射线的剂量,主要方法包括高灵敏度探测技术、高效率扫描机制、新型信号处理技术等[3-5]。得益于上述技术的进步,目前主流的胸部CT的辐射剂量约为7 mSv,腹盆CT增强检查的辐射剂量约为20 mSv,均低于100 mSv/年的安全阈值[1]。另一方面,X射线辐射的随机性效应决定了癌症的患病概率会随着辐射剂量的增加而增加,因此,进一步降低成像所需的最小剂量仍然是CT成像技术的重点问题[6]。
近年来,随着新型光电成像技术与信号处理理论的发展,Brady小组[7]在2009年首先提出了编码孔径CT成像的概念,通过放置于X射线源前的编码掩膜板降低CT成像投影之间的结构性冗余,结合信号稀疏测量理论,可以有效提高采样效率,降低辐射剂量。该文分析4种不完全采样条件下的X射线CT成像策略,实验结果表明,在X射线辐射剂量相同的条件下,随机分布探测器的采样策略在稀疏测量与重建的理论框架内性能最优。相比于传统扇形扫描和锥形束扫描CT成像,在重建质量相同的条件下,可降低90% 以上的辐射剂量;而相比于目前辐射剂量较低的CT成像方法,例如基于稀疏约束的有限(稀疏)角度CT成像方法,在重建质量相同的条件下,可降低30%~50% 的辐射剂量[8-12]。
2017年Mojica等[13]提出了超分辨率编码孔径X射线CT成像,利用低分辨率的X射线探测器测量经高分辨率编码掩膜板调制的X射线投影,结合压缩感知重建算法,从低分辨率、高信噪比的测量中恢复出高分辨率、高信噪比的三维CT图像。
2019年Cuadros等[14]提出了编码孔径X射线光谱CT成像,该编码孔径CT成像系统利用X射线K边缘能谱特性,通过设计合适的编码掩膜板产生特定的空间-光谱X射线投影,实现对四维目标(三维空间+光谱)的线性多路复用测量,并通过交替方向乘子法重建出四维断层图像(三维空间+光谱)。2021年,Cuadros等[15-16]首次通过实验验证了编码孔径X射线CT成像,在3D打印形成的0-1随机分布的二值图案中,使用钨粉末填充非闭合元素,并通过环氧树脂密封,最终形成X射线波段的编码掩膜板。实验表明,放置于X射线源之前的0-1分布的编码掩膜板并不会导致金属伪影,但X射线经过编码掩膜板会产生一定的散射伪影,可以通过掩膜校正抑制该伪影[17]。
此外,现阶段编码孔径CT成像重建算法的研究主要集中于通过优化编码掩膜板中非闭合元素的分布,结合稀疏测量与重建理论,通过迭代运算,提高重建质量。其主要方法包括基于有限等距性质(restricted isometry property,RIP)的随机梯度下降算法[18],基于均匀采样(uniform sensing)策略的优化算法[19-20]和基于稀疏主成分分析(sparse principle component analysis,SPCA)的快速搜索算法[21]。
虽然上述工作大幅度降低了CT成像所需的辐射剂量,但极度欠定采样的策略与目前的主流的解析类CT重建框架并不兼容,重建与优化均是建立在代数类重建框架内,算法复杂度高,重建时间长,难以满足临床需求。本文提出基于U型生成对抗网络的编码孔径CT成像方法,本方法通过构建编码孔径CT成像的非连续性投影数据动态博弈模型,利用医学图像的高维稀疏特性,预测欠定采样策略下非连续性CT投影的缺失数据,使其与解析类CT重建框架兼容,实现高质量的快速CT图像重建。
1. 原理与方法
1.1 编码孔径CT成像
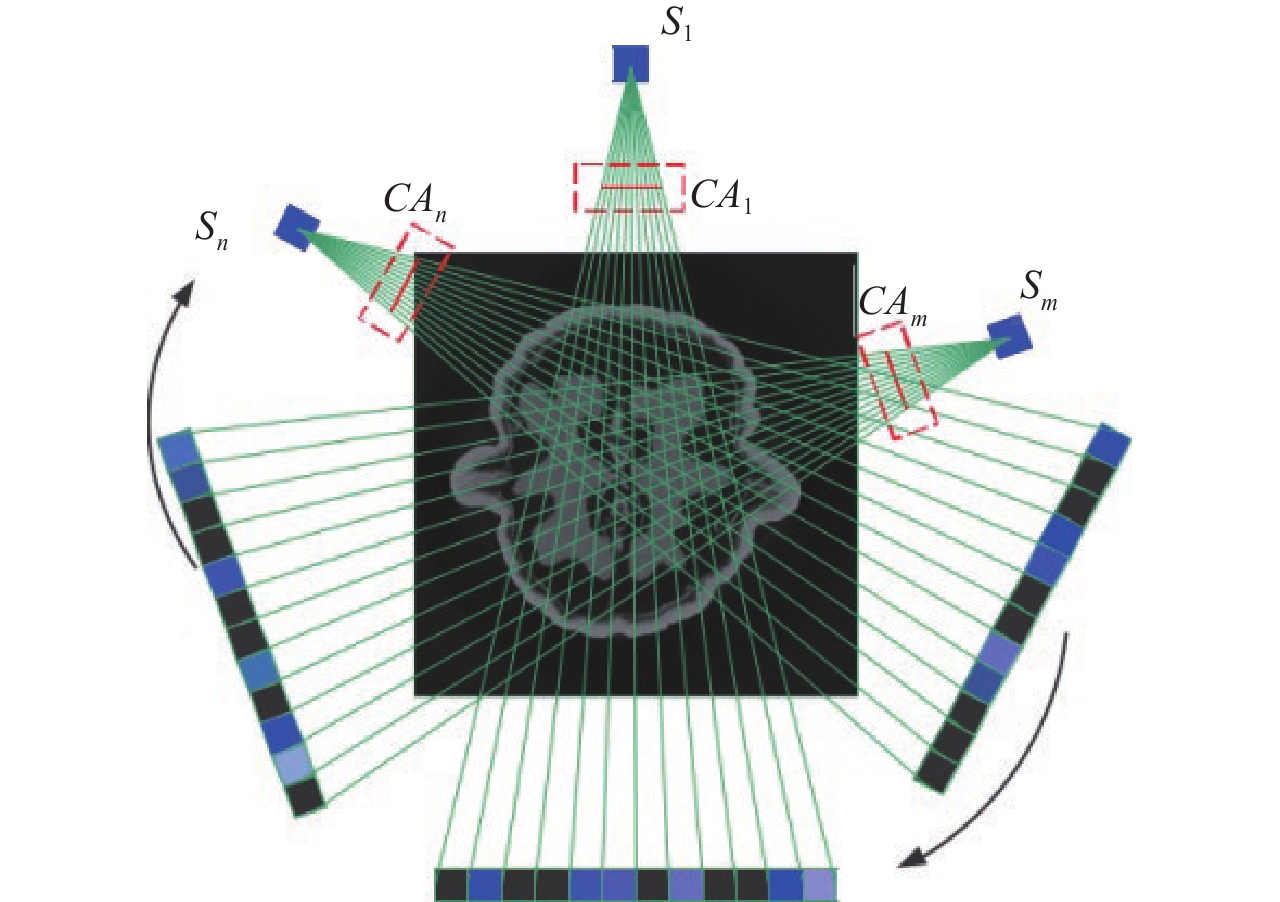
编码孔径CT成像的光学结构与传统CT成像类似,这里我们以扇形X射线束照明,平板型探测器测量的扇形编码孔径CT成像结构为例,其光学几何结构如图1所示。编码掩膜板
$ {\lambda _i} \in {\mathbb{R}^M} $ ,$ i = 1,2, \cdots ,M $ ,放置于扇形X射线光源与目标之间,并且编码掩膜板上的像素与线性探测器上的像素一一对应。其中,M是编码掩膜板中元素的数量。经过编码掩膜板调制与目标吸收衰减的 X射线投影被平板型探测器测量,探测器每个像素所测得的X射线强度是其与X射线光源所构成直线上所有点的衰减的积分;X射线光源和对应的探测器绕着待测目标旋转P个角度,$ {S_1} $ ,$ {S_2} $ $, \cdots,$ $ {S_P} $ ,测量得到不同角度下的目标X射线投影。根据Beer-Lamber定理[22],X射线在路径l的衰减可以描述为:$$ {I^l} = I_0^l\exp \left( { - \int\limits_0^{\; \propto } {{\lambda _i}\alpha (l)} {\rm{d}}l} \right) + I_n^l , $$ (1) 这里,
$ {I^l} $ 是探测器的测量值,$ I_0^l $ 是单色X射线光源的强度,$ I_n^l $ 是X射线CT成像的系统噪声,α是沿路径l的线性衰减系数。式(1)通过对数运算可以变形为线性方程组,以矩阵形式可以表示为:
$$ {\boldsymbol{y}} = {\boldsymbol{CWf}} 。 $$ (2) 详细推导过程可以参考本课题组前期工作[23]。其中,
${\boldsymbol{y}} \in {\mathbb{R}^{MP}}$ 是向量化的通过对数运算得到的测量值,其可以通过探测器的测量值和X射线的强度计算得到;$ W \in {\mathbb{R}^{MP \times N}} $ 是结构矩阵,${\boldsymbol{f}} \in {\mathbb{R}^N}$ 是向量化的线性衰减系数。具体的,编码矩阵可以表示为:$$ {\boldsymbol{C}} = \left( {\begin{array}{*{20}{c}} {{\text{diag(}}{{\boldsymbol{c}}_1}{\text{)}}}&0& \cdots &0 \\ 0&{{\text{diag(}}{{\boldsymbol{c}}_2}{\text{)}}}& \cdots &0 \\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &{{\text{diag(}}{{\boldsymbol{c}}_p}{\text{)}}} \end{array}} \right) \text{,} $$ (3) 其中,编码掩膜板
${{\boldsymbol{c}}_i} \in {\mathbb{R}^M},i = 1,2, \cdots ,P$ 。从式(3)可以看出,X射线编码孔径CT成像是对X射线CT成像在空域的0-1随机采样,根据傅里叶切片定理,即物体
$ r(x,y) $ 在方向$ (t,\theta ) $ 上的投影$ P(t,\theta ) $ 的一维傅里叶变换变为:$$ F\left\{ {c(t,\theta )r(t,\theta )} \right\} = F\left\{ {c(t,\theta )} \right\} * F\left\{ {r(t,\theta )} \right\} \text{,} $$ (4) 其中,
$ c(t,\theta ) $ 是方向$ (t,\theta ) $ 上的编码掩膜板分布。从式(4)可以看出,经过编码掩膜板,投影变换的频域混叠严重,并不满足解析类重建算法的基本要求。同时,X射线编码孔径CT成像中的编码矩阵C的对角向量是一个 0-1向量,其采样频率远小于传统X射线CT成像乃至有限角度X射线CT成像。因此,FBP算法等解析重建算法无法直接应用于X射线编码孔径CT成像。
1.2. 基于U型生成对抗网络的正弦图重建
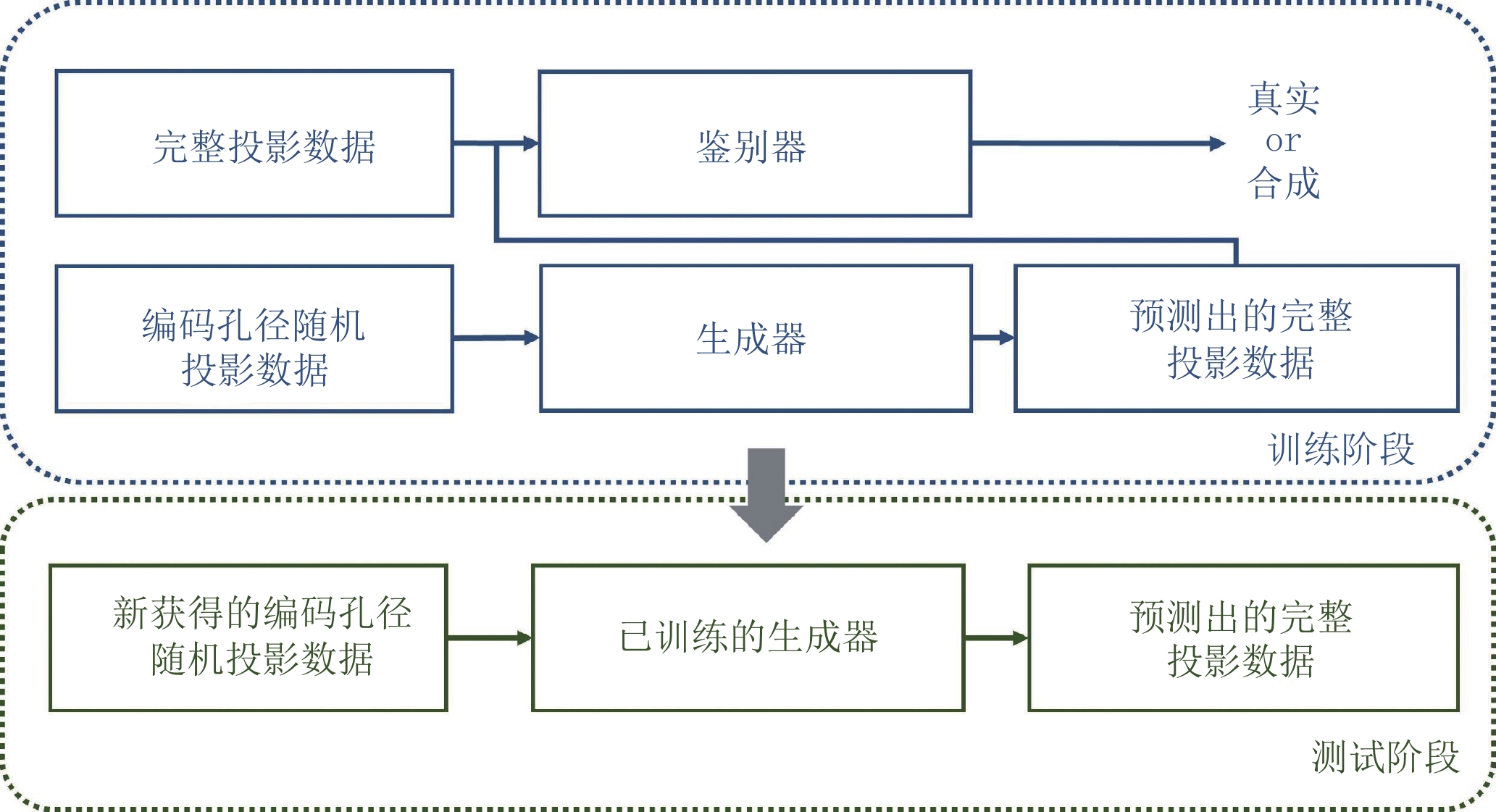
如图2所示,与传统CT成像不同,编码孔径的引入使得其正弦图具有两大特征:非连续性和稀疏性。本文提出一种基于U型生成对抗网络的非连续正弦图重建模型,以解决在不连续、稀疏条件下编码孔径正弦图的反演问题。该方法的核心思想是生成对抗网络[24],包括训练模型和测试模型两个模块。在训练模型中,构建U型编解码全卷积网络作为训练模型的生成器,将编码孔径CT成像系统的随机投影数据作为输入图像对生成器网络进行训练。
如图3所示,生成器网络的主要作用是对输入的非连续投影数数据进行预测,随后用预测的投影数据结果和完整投影数据对鉴别网络进行训练,鉴别器网络的作用是估计生成器网络所生成的投影数据是否为真实的概率。同时在整个训练过程加入联合损失函数以保证编码孔径投影数据和完整投影数据的一致性。在测试阶段,主要是将新获得的编码孔径随机投影数据输入至测试阶段训练好的生成器中得到预测的非连续的投影数据,从而得到预测的完整投影数据。
1.3 U型生成对抗网络
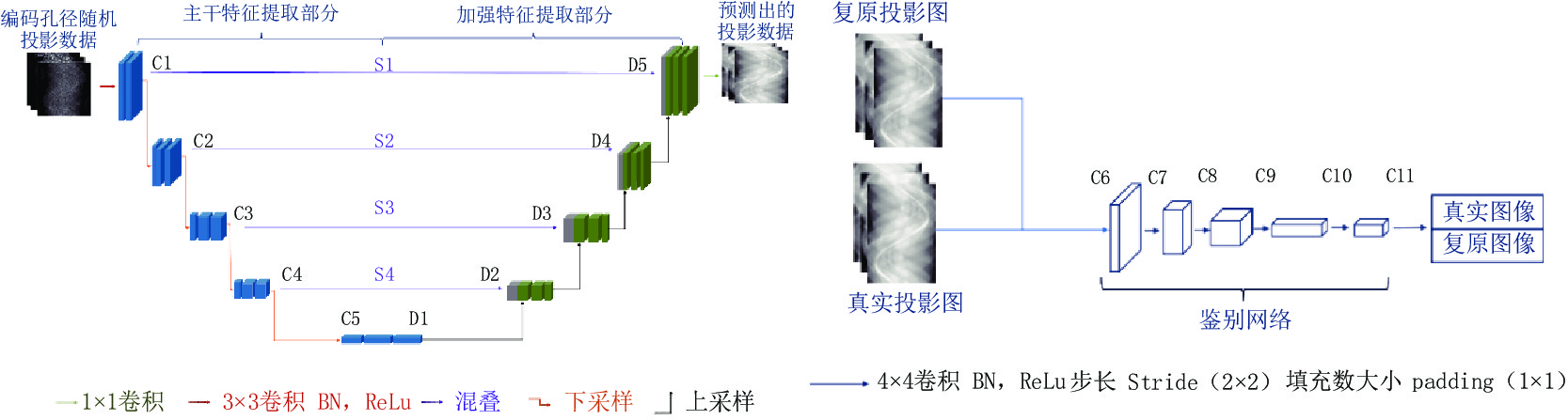
本文拟采用如图4所示的U型生成对抗网络,包括生成网络(图4(a)所示)和鉴别网络(图4(b))所示。生成网络分为主干特征提取网络、加强特征提取网络和预测网络3个部分。生成网络的输入为一系列大小为512×512大小的投影数据;主干特征提取网络分为5层,由1层输入块C1和4层下采样块C2~C5组成。输入块C1对输入图像进行2次3×3的卷积、归一化和整流线性单位,进而生成特征图谱。每个下采样块C2~C5由两组3×3卷积层-批标准化层-ReLU激活函数层和一组2×2的最大池化层组成,增加特征通道的数量,以便获得4个初步有效特征层,在图中依次表示为S1至S4。同时,下采样模块可以使得网络更具有鲁棒性,抑制过拟合发生的概率。
加强特征提取网络由4个上采样块组成。每个上采样块由两组3×3卷积层-批标准化层-ReLU激活函数层和一组最近邻采样层组成,其作用是将下采样降级的图像特征还原至原始图像大小。在加强特征提取部分中,利用主干特征提取获得的初步有效特征层S1至S4,进行4次上采样块操作,并进行特征融合。最后,在预测网络部分利用一个1×1的卷积进行通道调整,将获得的最后一个有效特征层对每一个特征点进行分类,获得预测结果。
鉴别器网络结构与生成器结构相近,该结构由5个卷积层C6~C10以及1个输出层C11组成。其中,每个卷积层包括卷积运算-批标准化层-LeakyReLU激活函数层。为了避免棋盘效应以及过拟合现象,每层卷积核的大小设定为4×4,横轴与纵轴方向步长均设置为2个像素值,填充数为1个像素。鉴别器将生成器预测出的结果及对应的真实数据作为输入,其输出是预测出来的结果被鉴别为真实数据的概率,值为0到1之间,值越接近1,代表预测出的数据越接近为真实数据。
1.4 联合损失函数
在训练过程中,对于生成器输入的编码正弦图,其重建损失函数Lrec可以为:
$$ {L_{{\rm{rec}}}}\Big( {G(p \odot M),\,p} \Big) = {\Big\| {\varphi \Big( {G(p \odot M)} \Big) - \varphi (p)} \Big\|_2} \text{,} $$ (5) 其中,G表示训练时使用的生成器,p表示完整的正弦图,M表示编码掩膜板,⊙表示哈达玛积,φ为使用基于 Image-Net训练权重的VGG16网络第4组卷积网络的第3层输出特征图。同时,本文采取Wasserstein距离作为其的对抗性损失函数
$$ {L_G}(p \odot M,\,p) = \mathop {\max }\limits_G \bigg( {{{E}}\Big( {{{D}}\big( {{G}(p \odot M)} \big)} \Big)} \bigg) \text{,} $$ (6) $$ {L_D}(p \odot M,\,p) = \mathop {\max }\limits_D \bigg( {E\Big( {D(p)} \Big) - E\Big( {D\big(G(p \otimes M)\big)} \Big)} \bigg) + \delta {\Big( {{{\left\| {{\nabla _{\hat p}}D(\hat p)} \right\|}_2} - 1} \Big)^2} \text{,} $$ (7) 其中,
$ \hat p $ 表示随机噪声,D表示鉴别器,δ表示梯度惩罚。损失函数LG的主要目的是使鉴别器对合成数据判定概率尽可能的接近 1,提高生成器输出图像的质量。LD的主要目的是提高鉴别器对真实数据判定概率并降低预测数据的判定概率,以此来鉴别真实数据和预测数据。通过生成器与鉴别器训练过程中的互相博弈,使得预测图像的数据分布接近于真实图像的数据分布。2. 实验结果
本文采用课题组前期工作的编码孔径CT成像的光学几何结构[20,22],CT图像分辨率为256×256,探测器分辨率为512×1,扫描次数为512。因此,正弦图的空间分辨率为512×512。本文选用北美放射协会(Radiological Society of North America,RSNA)的2500张颅内出血CT图像作为数据集并将其空间分辨率缩放至256×256。其中,选取2000张用于测试CT图像及其对应的编码正弦图进行训练,500张CT图像及其对应的编码正弦图。
训练参数上的设置:Batch Size大小4,训练epoch数115,学习率0.0001。训练平台intel i9 9900 k,GeForce RTX 2080 Ti,128 GB RAM。由于在神经网络的训练过程中,当预测图像的准确度出现震荡或loss不再下降时,进行适当的学习率衰减可以有效提高准确率。因此,本文在训练过程中加入学习率衰减函数且在训练15个epoch后执行学习率衰减函数,可以使训练结果达到最佳。由于经过U型生成对抗网络的编码孔径CT成像的正弦图在空间域上是连续的,因此,本文可以采用滤波反投影算法进行重建。相比于代数类重建算法和稀疏约束重建算法,滤波反投影算法在内存需求上可以降低2~3个数量级,重建算法复杂度可以降低2~3个数量级。
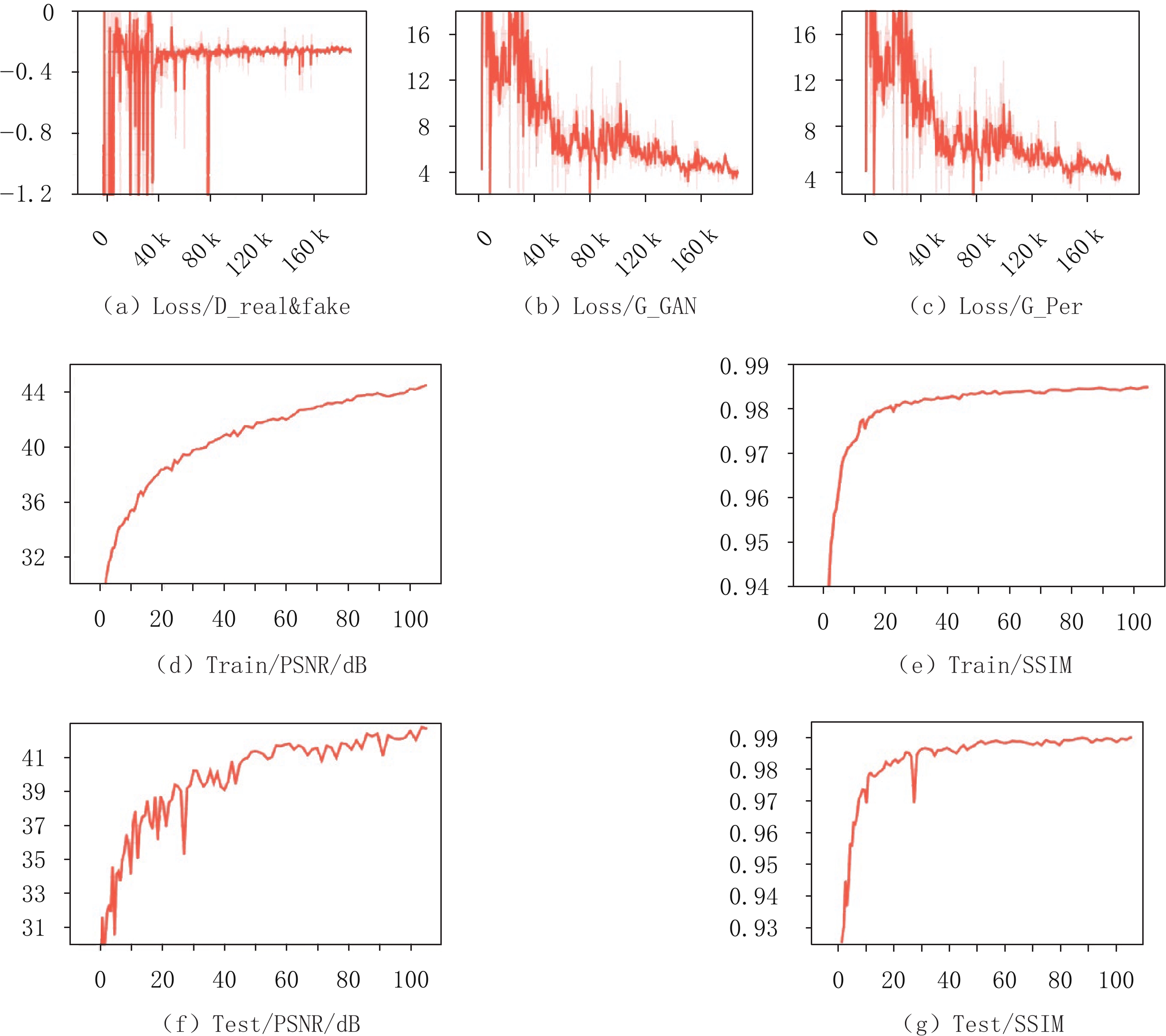
图5表示编码掩膜板透过率为20%,训练次数为115个epoch的训练结果图。其中,图5(a)~图5(c)表示对抗性损失函数曲线图,在经过80 k的迭代之后,损失函数逐渐收敛,趋于稳定。图5(d)~图5(g)表示10% 透过率下每个epoch训练和测试的峰值信噪比(peak signal-to-noise ratio,PSNR)和结构相似性(structural similarity,SSIM),从图中可以看出,测试集重建图像质量略有下降,但整体质量较好(PSNR>40 dB,SSIM>0.98)。其中,利用训练好的网络从编码正弦图反演完整的正弦图,运算时间为1~2 s,滤波反投影算法运算时间为1~2 s。而同等分辨率条件下,编码孔径CT成像方法迭代反演方法需要十多分钟。因此,相比于目前已有的编码孔径CT成像方法,本文所提出的方法可以将重建时间降低约两个数量级。
图6表示编码掩膜板透过率为25% 时,基于U型生成对抗网络的编码孔径CT成像的结果图。其中(a)为原始图像,(b)编码掩膜板,(c)为编码孔径CT成像的正弦图,(d)是经过U型生成对抗网络反演预测的正弦图,(e)为预测的正弦图(d)经FBP重建算法反演的CT图像。这里,经网络预测的正弦图与真实正弦图的PSNR分别为35.2 、46.5 和46.3 dB,SSIM分别为0.98、0.98和0.99;而根据预测的正弦图经FBP重建算法反演的CT图像与原始图像的PSNR分别为41.6 、38.3 和36.1 dB,SSIM分别为0.96、0.94和0.90。实验结果表明,基于U型生成对抗网络的编码孔径CT成像可以在兼顾大幅度降低辐射剂量(仅25% 的透过率)和保证重建效率(预测正弦图<2 s)的情况下,高质量的重建出CT图像(PSNR>35 dB,SSIM>0.9)。
图7表示编码掩膜板透过率为5%、15% 以及25% 时,基于U型生成对抗网络的编码孔径CT成像的结果图。其中(a)为原始图像,(b)是透过率为5%、15% 和25% 的编码掩膜板,(c)为编码孔径CT成像的正弦图,(d)是经过U型生成对抗网络反演预测的正弦图,(e)为预测的正弦图(d)经FBP重建算法反演的CT图像。这里,经网络预测的正弦图与真实正弦图的PSNR分别为40.8 、41.9 和45.2 dB,SSIM分别为0.99、0.98和0.98;而根据预测的正弦图经FBP重建算法反演的CT图像与原始图像的PSNR分别为38.7 、41.3 和41.6 dB,SSIM分别为0.95、0.96和0.96。实验结果表明,基于U型生成对抗网络的编码孔径CT成像方法鲁棒性较强,在编码掩膜板透过率5% 时仍可以较高质量的重建CT图像。
表1表示在不同编码掩膜板透过率下,测试集中预测的正弦图和CT重建图像的平均值。其中,编码掩膜板透过率5%~25% 的CT重建图像平均PSNR仅相差3.3 dB @ PSNR>30 dB,平均SSIM仅相差0.03 @ SSIM>0.87。因此,基于U型生成对抗网络的编码孔径CT成像方法对于编码掩膜板透过率的变化鲁棒性较好,在实际应用中可以尽可能的降低编码掩膜板的透过率,进一步降低辐射剂量。
表 1 不同编码掩膜板透过率下,测试集中预测的正弦图和CT重建图像的平均值Table 1. The average results of sonograms and CT reconstructions at different transmission rates测试数据集 图像质量评价指标 编码掩膜板透过率 5% 10% 15% 20% 25% 预测的正弦图 PSNR/dB 39.1 41.6 40.9 42.6 43.8 SSIM 0.98 0.97 0.98 0.99 0.98 CT重建图像 PSNR/dB 33.7 32.0 33.5 35.3 33.6 SSIM 0.88 0.88 0.89 0.91 0.90 3. 结论
本文提出一种基于U型生成对抗网络的编码孔径CT成像方法。通过构建基于U型生成对抗网络的非连续稀疏投影的动态博弈模型,结合联合损失函数,预测正弦图的结构性缺失,实现编码孔径CT成像分析类(非迭代)快速重建。实验结果表明,相比于编码孔径CT成像目前使用的迭代类算法,基于U型生成对抗网络的编码孔径CT成像方法可以将重建时间降低约两个数量级。同时,在辐射剂量降低95% 的条件下,仍然可以获得峰值信噪比大于30 dB @ 256×256的高质量重建结果。该方法对于下一代低剂量CT成像设备的研究具有一定的理论基础和参考依据。
-
表 1 不同编码掩膜板透过率下,测试集中预测的正弦图和CT重建图像的平均值
Table 1 The average results of sonograms and CT reconstructions at different transmission rates
测试数据集 图像质量评价指标 编码掩膜板透过率 5% 10% 15% 20% 25% 预测的正弦图 PSNR/dB 39.1 41.6 40.9 42.6 43.8 SSIM 0.98 0.97 0.98 0.99 0.98 CT重建图像 PSNR/dB 33.7 32.0 33.5 35.3 33.6 SSIM 0.88 0.88 0.89 0.91 0.90 -
[1] KALENDER W A. Computed tomography: Fundamentals, system technology, image quality, applications[M]. John Wiley & Sons, 2011.
[2] KALENDER W A. X-ray computed tomography[J]. Physics in Medicine & Biology, 2006, 51(13): R29.
[3] WILLEMINK M J, PERSSON M, POURMORTEZA A, et al. Photon-counting CT: Technical principles and clinical prospects[J]. Radiology, 2018, 289(2): 293−312. doi: 10.1148/radiol.2018172656
[4] FUCHS T, KACHELRIE M, KALENDER W A. Technical advances in multi-slice spiral CT[J]. European Journal of Radiology, 2000, 36(2): 69−73. doi: 10.1016/S0720-048X(00)00269-2
[5] ZHU Z, WAHID K, BABYN P, et al. Improved compressed sensing-based algorithm for sparse-view CT image reconstruction[J]. Computational and Mathematical Methods in Medicine, 2013: 185750:1−185750:15.
[6] MCCOLLOUGH C H, LENG S, YU L, et al. CT dose index and patient dose: They are not the same thing[J]. Radiology, 2011, 259(2): 311−316. doi: 10.1148/radiol.11101800
[7] CHOI K, BRADY D J. Coded aperture computed tomography[C]//International Society for Optics and Photonics. Adaptive Coded Aperture Imaging, Non-Imaging, and Unconventional Imaging Sensor Systems. 2009, 7468: 74680B.
[8] JEREZ A, MARQUEZ M, ARGUELLO H. Adaptive coded aperture design for compressive computed tomography[J]. Journal of Computational and Applied Mathematics, 2021, 384: 113174. doi: 10.1016/j.cam.2020.113174
[9] ZHANG T, ZHAO S, MA X, et al. Nonlinear reconstruction of coded spectral X-ray CT based on material decomposition[J]. Optics Express, 2021, 29(13): 19319−19339. doi: 10.1364/OE.426732
[10] YAN K, LI D, HOLMGREN A, et al. Compressed sampling strategies for tomography[J]. Journal of the Optical Society of America A, 2014, 31(7): 1369−1394. doi: 10.1364/JOSAA.31.001369
[11] ZHAO Q, MA X, CUADROS A, et al. Single-snapshot X-ray imaging for nonlinear compressive tomosynthesis[J]. Optics Express, 2020, 28(20): 29390−29407. doi: 10.1364/OE.392054
[12] TZOUMAS S, VERNEKOHL D, XING L. Coded-aperture compressed sensing X-ray luminescence tomography[J]. IEEE Transactions on Biomedical Engineering, 2017, 65(8): 1892−1895.
[13] MOJICA E, PERTUZ S, ARGUELLO H. High-resolution coded-aperture design for compressive X-ray tomography using low resolution detectors[J]. Optics Communications, 2017, 404: 103−109. doi: 10.1016/j.optcom.2017.06.053
[14] CUADROS A, MA X, ARCE G R. Compressive spectral X-ray tomography based on spatial and spectral coded illumination[J]. Optics Express, 2019, 27(8): 10745−10764. doi: 10.1364/OE.27.010745
[15] CUADROS A P, MA X, RESTREPO C M, et al. Static code CT: Single coded aperture tensorial X-ray CT[J]. Optics Express, 2021, 29(13): 20558−20576. doi: 10.1364/OE.427382
[16] CUADROS A P, LIU X, PARSONS P E, et al. Experimental demonstration and optimization of X-ray static code CT[J]. Applied Optics, 2021, 60(30): 9543−9552. doi: 10.1364/AO.438727
[17] MA X, YUAN X, FU C, et al. LED-based compressive spectral-temporal imaging[J]. Optics Express 2021, 29(7): 10698-10715.
[18] CUADROS A P, ARCE G R. Coded aperture optimization in compressive X-ray tomography: A gradient descent approach[J]. Optics Express, 2017, 25(20): 23833−23849. doi: 10.1364/OE.25.023833
[19] CUADROS A P, PEITSCH C, ARGUELLO H, et al. Coded aperture optimization for compressive X-ray tomosynthesis[J]. Optics Express, 2015, 23(25): 32788−32802. doi: 10.1364/OE.23.032788
[20] MEJIA Y, ARGUELLO H. Binary codification design for compressive imaging by uniform sensing[J]. IEEE Transactions on Image Processing, 2018, 27(12): 5775−5786. doi: 10.1109/TIP.2018.2857445
[21] MAO T, CUADROS A P, MA X, et al. Fast optimization of coded apertures in X-ray computed tomography[J]. Optics Express, 2018, 26(19): 24461−24478. doi: 10.1364/OE.26.024461
[22] SWINEHART D F. The beer-lambert law[J]. Journal of Chemical Education, 1962, 39(7): 333. doi: 10.1021/ed039p333
[23] MAO T, CUADROS A P, MA X, et al. Coded aperture optimization in X-ray tomography via sparse principal component analysis[J]. IEEE Transactions on Computational Imaging, 2019, 6: 73−86.
[24] YI X, WALIA E, BABYN P. Generative adversarial network in medical imaging: A review[J]. Medical Image Analysis, 2019, 58: 101552. doi: 10.1016/j.media.2019.101552
-
期刊类型引用(0)
其他类型引用(1)



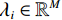

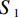
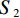

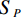
 下载:
下载: