Coded Aperture Computed Tomography Via Generative Adversarial U-net
-
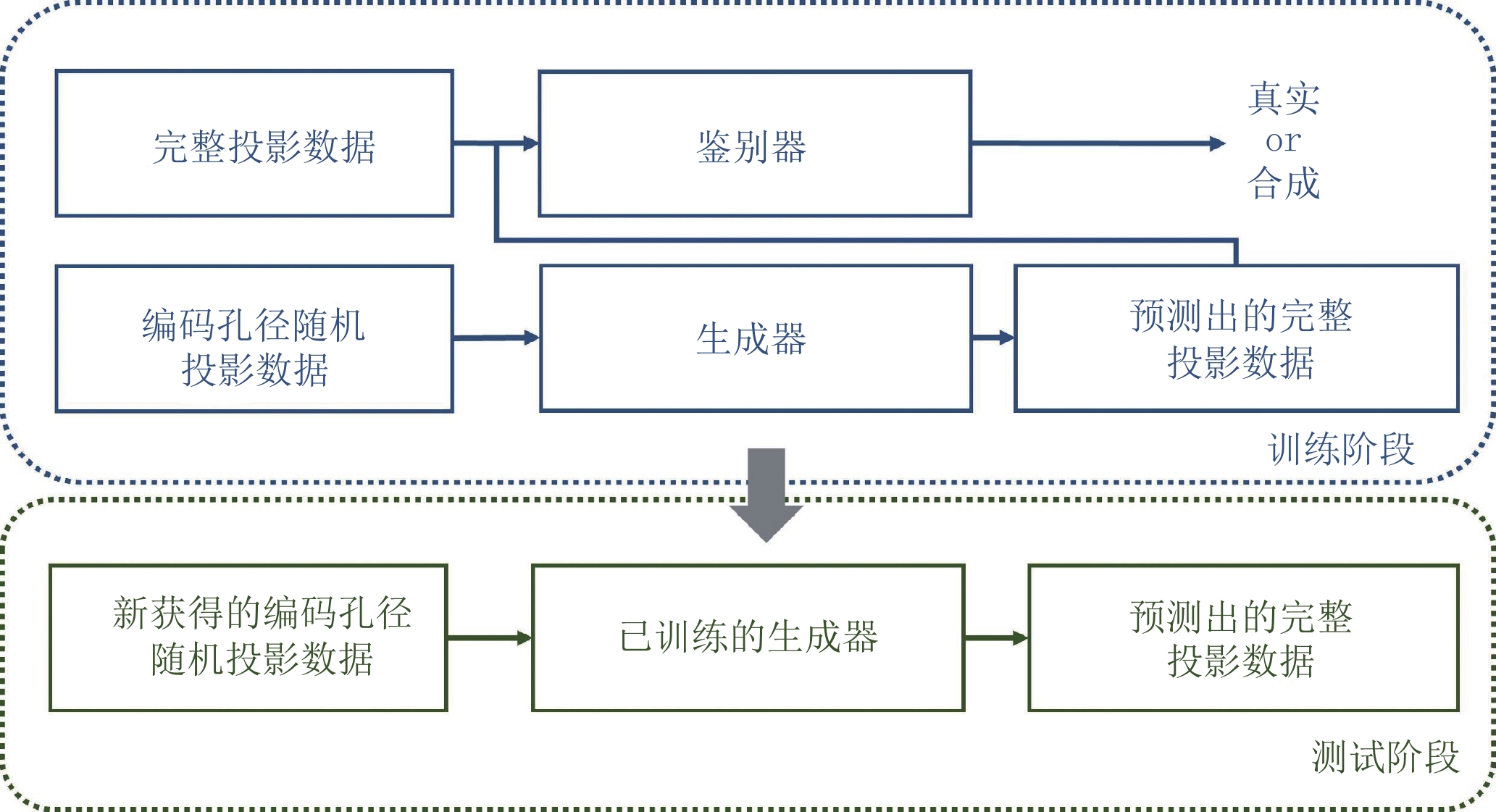
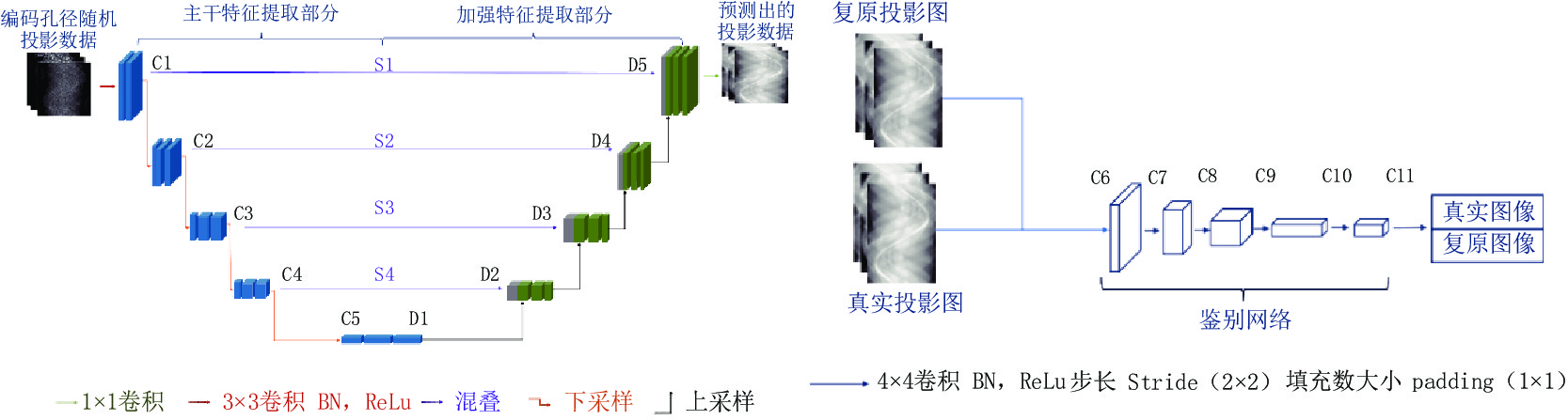
摘要: 针对编码孔径CT成像非连续稀疏采样只能通过代数类迭代重建算法的缺点，本文提出一种基于U型生成对抗网络的编码孔径CT成像方法。通过构建基于U型生成对抗网络的非连续稀疏投影的动态博弈模型，结合联合损失函数，预测正弦图的结构性缺失，实现编码孔径CT成像分析类（非迭代）快速重建。实验结果表明，在辐射剂量降低95％ 的条件下，基于U型生成对抗网络的编码孔径CT成像方法实现了峰值信噪比大于30 dB @ 256×256的高质量重建。相比于目前最先进的编码孔径CT成像方法，其重建时间降低了约两个数量级。Abstract: Generative adversarial U-net for coded aperture computed tomography (CT) is proposed in this paper to alleviate the tradeoff between the non-continuous sparse projections and the ill-posedness iterative reconstruction problem. A non-continuous sparse projection model is presented based on generative adversarial U-net and the corresponding joint penalty function is formulated. Simulations using real datasets show that CT images with 256×256 pixels can be reconstructed with peak signal-to-noise ration more than 30 dB at only 5% transmittance. Furthermore, the computational time in the reconstructions is reduced by two orders of magnitude when compared with the state-of-the-art iterative algorithms in coded aperture computed tomography.
-
Keywords:
- computed tomography /
- coded aperture /
- generative adversarial net
-
伦琴于1895年发现X射线，而后英国工程师Hounsfield基于X射线发明出计算机断层成像（computed tomography，CT）机。自CT机问世几十年来，无论是在硬件性能（X光机、探测器）、扫描方式，还是重建算法上都获得了长足发展，在医疗、工业和安全检查等领域发挥着重要作用。更短的扫描和重建时间，以及更好的成像质量成为该领域研究人员追求的目标[1]。
双能CT是由Alvarez[2]在1976年首次提出，可以获取物体的等效原子序数和电子密度信息，从而更加准确地识别物质。多能谱CT是在双能CT的基础上，增加了参与扫描和重建的能区数量，引入了更多能谱信息，重建结果更加准确。
随着高计数率电子元器件的迅速发展，以光子计数探测器为核心的多能谱X射线成像技术成为射线检测领域的重要发展方向[3-4]。与传统能量积分探测器相比，光子计数探测器可以通过设置能量阈值来选择不同能区的信号，同时它将每个光子当作独立事件进行统计，一次扫描便能得到多段能谱，减小了辐射剂量[5]。但在实际的应用上也存在多能段光子数减少、信噪比下降，探测器性能不足造成的噪声等问题[6]，对影响光子计数X射线CT成像精度的因素及其规律进行基础性研究十分必要。
本文对系统能谱的获取、模体的扫描和重建过程进行仿真实验，以重建得到的等效原子序数和电子密度的标准差作为成像质量的评价标准，得出探测器能量分辨率、能谱阈值和能谱范围等因素对成像精度影响的有关结论，为后续相关技术的工程应用化提供参考。
1. 双能重建基本原理
本文主要研究探测器能量分辨率、能谱阈值和能谱范围等对重建图像精度的影响规律。以双能重建为例，根据光子计数探测原理[7]，进行双能成像的模拟。双能CT成像的重点研究内容之一是双能分解方法，常见的双能分解方法包含投影域前处理、图像域后处理和迭代方法[8]。
考虑到未来的工程化需求，本文选择的双能重建方法为基于基材料模型的双能投影预处理分解方法，基材料选取的是碳和铝。
材料模型公式：
$$ \mu \left(E\right)={{b}}_{1}{\mu }_{1}\left(E\right)+{{b}}_{2}{\mu }_{2}\left(E\right) \text{，} $$ (1) $ {\mu }_{1} $ (E)、$ {\mu }_{2} $ (E)分别为两种基材料的线性衰减系数；$ {b}_{1}$ 、$ {b}_{2}$ 对应两种基材料的分解系数，对于某一固定的物质，$ {b}_{1}$ 、$ {b}_{2}$ 是两个常数。双能分解即求解如下的双能投影积分方程组：
$$ \left\{\begin{aligned} {P}_{L}=\;& -{\ln}\bigg(\int \mathit{{S}_{L}} (E)\exp \Big({-{B}}_{1}{\mu }_{1}({E})-\\& {{B}}_{2}{\mu }_{2}({E})\Big){\rm d}{E}\bigg)+{\ln}\int \mathit{{S}_{L}}(E){\rm d}E\\ {P}_{H}=\;&-{\ln}\bigg(\int \mathit{{S}_{H}}(E) \exp \Big(-{{B}}_{1}{\mu }_{1}({E})-\\ & {{B}}_{2}{\mu }_{2}({E})\Big){\rm d}{E}\bigg)+{\ln}\int \mathit{{S}_{H}}(E){\rm d}E\end{aligned}\right. \text{，} $$ (2) 其中，SH、SL分别为高低能能谱，纵坐标记录的是光子数，PH、PL分别为高低能投影，
$ {{B}}_{1}=\displaystyle \int {{b}}_{1}\mathrm{d}{l}， {{B}}_{2}=\displaystyle \int {{b}}_{2}\mathrm{d}{l} $ 。求解
$ {B}_{1}$ 、$ {B}_{2}$ 的这个过程被称为投影分解过程。由于$ {B}_{1}$ 、$ {B}_{2}$ 为$ {b}_{1}$ 、$ {b}_{2}$ 的线积分投影值，求解出$ {B}_{1}$ 、$ {B}_{2}$ 后，根据CT重建的原理，利用滤波反投影重建算法[9]，便可计算出$ {b}_{1}$ 和$ {b}_{2}$ ，由此可以计算材质的等效原子序数和电子密度信息，以完成材料的探测识别。计算公式：$$ {Z}_{\rm{eff}}={\left(\frac{{b}_{1}{\rho }_{e1}{Z}_{1}^{n}+{b}_{2}{\rho }_{e2}{Z}_{2}^{n}}{{b}_{1}{\rho }_{e1}+{b}_{2}{\rho }_{e2}}\right)}^{\tfrac{1}{n}} \text{，} $$ (3) $$ {\rho }_{e}={{b}_{1}\rho }_{e1}+{{b}_{2}\rho }_{e2} ， $$ (4) 式（3）和式（4）中Z1、Z2分别为两种基材料的原子序数，ρe1、ρe2分别为两种基材料的电子密度，n一般取在3~4之间。
2. 光子计数CT成像系统能谱仿真
在Ubuntu系统下利用Geant 4软件，模拟高速电子撞击靶材射出X射线的过程。真空管内靶材为1 cm厚的钨，靶面倾角为25°，射线源射出能量为160 keV的电子，滤波片为2.5 mm厚的铝，射线穿过区域皆为真空，光子穿过虚拟探测器后被记录能量，得到射线源入射能谱。图1为能谱发射的几何示意，图2为得到的入射能谱。
通过对入射能谱与基于能量分辨率高斯函数的卷积来模拟探测器能量分辨率的影响，得到系统能谱[10]。后续实验所需的高低能能谱均基于系统能谱得到。探测器能量分辨率R通常用半高全宽（full width at half maximum，FWHM）W表示，定义：
$$ R=\frac{W}{E}\text{，} $$ (5) 其中，E是相对应的能量。W可以通过标准差σ与高斯分布的关系计算得到：
$$ W=2.355\;\sigma 。 $$ (6) 因此，标准差可以表示为：
$$ \sigma =\frac{R\times E}{2.355} 。 $$ (7) 根据探测器指定能量下的标准能量分辨率R0和能量E0，可由式（8）获得其他能量下的能量分辨率。由式（7）获得每个能量点下的标准差σ，并使用该标准差对原始入射能谱进行高斯模糊[11]。
$$ R={R}_{0}\sqrt{\frac{{E}_{0}}{E}} 。 $$ (8) 3. 投影数据加噪仿真
由于光子计数的特性遵循泊松分布[12-13]，所以本文为投影数据添加泊松噪声，用于模拟真实环境。泊松分布的概率函数见式（9），该函数表示在给定时间间隔或空间区域内发生k次事件的概率，其中，
$ \lambda $ 是泊松分布的均值和方差。$$ P\Big(X=k\Big)=\frac{{\lambda }^{k}{\exp}{(-\lambda )}}{k!} 。 $$ (9) 具体加噪过程。
（1）光子穿过模体后的衰减规律：
$$ {n}=\int S\left(E\right){\exp}{\left(\int -l\mu \left(E\right)\mathrm{d}l\right)}\mathrm{d}E \text{，} $$ (10) 其中，n为入射后探测器接收到的光子数，S(E)为系统能谱，exp为自然常数，l表示射线穿过模体的厚度，μ(E)为水模的线性衰减系数。
将各个单能（E1、E2、E3、···）下的光子数ni=
$ S\left({E}_{\mathrm{i}}\right){\exp}{\left(\int -l\mu \left({E}_{\mathrm{i}}\right)\mathrm{d}l\right)} $ 分别代入式（9）中的$ \lambda $ ，将对应泊松分布下生成的随机数作为该能量下加噪后的光子数ni_noise。（2）将能谱各单能段加噪后的光子数ni_noise累加，并与入射前探测器接收到的光子数n0按下式进行变换，便可得到加噪后的投影Pnoise：
$$ {P}_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}=\mathrm{l}\mathrm{n}\left(\frac{{n}_{0}}{{n}_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}}\right) \text{，} $$ (11) 其中，入射前探测器接收到的光子数
$ {n}_{0}= \displaystyle \int S\left(E\right)\mathrm{d}E $ 。4. 实验仿真和结果分析
4.1 实验模体和成像几何
设置的仿真模体为一圆柱状物体，材料为钙（原子序数20，密度1.55 g/cm3），半径为3 cm，模体截面如图3所示。
进行扫描仿真实验的探测系统几何结构如图4所示。射线源为扇形束，扇束张角为22.6°；探测器线性等距排列，共256个探测单元，总长512 mm；射线源、模体、探测器中心位于同一条直线；射线源到模体中心和探测器中心的距离分别为640 mm和
1280 mm；每隔1° 扫描一次模体，每次扫描发射的光子数为105。4.2 能量分辨率的影响
市场上性能相对较好的光子计数探测器材料为碲锌镉（CZT），其在60~100 keV下的能量分辨率大约是10%。因此参考碲锌镉材料的分辨率作为最优值，从10% @ 100 keV到40% @ 100 keV依次递减能量分辨率，间隔10%取4组能量分辨率进行实验，并配以理想能量分辨率（0%）作为对比，高低能能量阈值选为80 keV，各实验组参数见表1。各实验组高斯模糊化之后的高低能能谱见图5。
表 1 能量分辨率实验对照表Table 1. Experimental comparison table of energy resolution编号 能量分辨率 低能区光子数 高能区光子数 1 0% @ 100 keV 82978 17286 2 10% @ 100 keV 82964 17271 3 20% @ 100 keV 82964 17218 4 30% @ 100 keV 82963 17132 5 40% @ 100 keV 82932 17005 穿过模体的光子由所设能量阈值被划入不同的能量通道，从而得到高低能投影数据。为投影数据添加泊松噪声后，进行双能重建[14-15]。
上述实验组的成像结果见表2。不同能量分辨率下的重建结果标准差曲线如图6所示。
表 2 能量分辨率实验成像结果表Table 2. Imaging results of energy resolution experiment编
号能量
分辨率等效原子
序数等效原子
序数标准差电子密度 电子密
度标准差1 0% @
100 keV19.538647 0.268186 1.518764 0.039321 2 10% @
100 keV19.549584 0.291602 1.517544 0.042370 3 20% @
100 keV19.544331 0.295689 1.518037 0.042150 4 30% @
100 keV19.544904 0.313434 1.518503 0.044175 5 40% @
100 keV19.570808 0.350212 1.515818 0.048496 ![]()
图 6 不同能量分辨率下的成像结果对比Figure 6. Comparison of imaging results at different energy resolutions上述结果表明，随着探测器能量分辨率的提高，成像结果受噪声影响程度下降，等效原子序数相较电子密度而言，受噪声影响程度更大。不难分析，光子计数探测器能量分辨率越低，表示其对目标能区光子的统计区域越大，这会使得能谱重叠范围增加，不利于能量分解。但研究发现，能量分辨率在30%甚至40%的情况下，密度和原子序数的标准差变化并不十分明显。
图7是不同探测器能量分辨率的重建结果对比图，电子密度图的灰度显示窗口为[1.44 1.60]，等效原子序数图的灰度显示窗口为[18.3 20.7]。图8为同一排像素灰度曲线比较。
![]()
图 7 不同能量分辨率的重建结果对比Figure 7. Comparison of reconstruction results at different energy resolutions4.3 能量阈值及能量范围的影响
本部分考察的是高低能能谱重合程度对于成像的影响，在探测器能量分辨率相同的条件下，通过选取不同能量阈值，改变能量范围，可以得到重合度不一的高低能能谱，重合度的定义为：
$$ {\text{重合度}} = \frac{\text{能谱重叠部分面积}}{\text{全能谱范围面积}}。 $$ (12) 探测器能量分辨率选用30% @ 100 keV，具体对照实验见表3。各实验组能谱对比见图9。
表 3 能量范围实验对照表Table 3. Experimental comparison table of energy range编号 低能范围EL 高能范围EH 重合度Overlap_ratio 低能段光子数 高能段光子数 1 0~70 keV 110~160 keV 0.0025 74978 4419 2 0~80 keV 100~160 keV 0.0134 82323 7438 3 0~80 keV 80~160 keV 0.0648 82963 17132 4 0~100 keV 60~160 keV 0.1526 62561 37533 实验结果见表4，图10为重建结果的均值变化。图11为重建切片图，电子密度图的灰度显示窗口为[1.41 1.61]，等效原子序数图的灰度显示窗口为[18.6 20.5]。图12为同一排像素的灰度比较。
表 4 能量范围实验结果Table 4. Results of energy range experiment编号 重合度Overlap_ratio 等效原子序数 等效原子序数标准差 电子密度 电子密度标准差 1 0.0025 19.550129 0.316059 1.517544 0.049246 2 0.0134 19.551358 0.298083 1.517176 0.043675 3 0.0648 19.544904 0.313434 1.518503 0.044175 4 0.1526 19.554059 0.409670 1.517345 0.055390 ![]()
图 10 不同能谱重合度下的成像结果对比Figure 10. Comparison of imaging results at different energy overlap-ratios![]()
图 11 不同能量范围的重建结果对比Figure 11. Comparison of reconstruction results within different energy ranges从结果可以看出，设置能谱阈值改变能谱范围，使得高低能能谱重合度发生改变，会对成像质量造成影响。盲目减小高低能能谱重合度，并不一定使重建结果更好，因为当光子数减少时，噪声会增大。如何平衡能谱重合度和噪声是下一步的研究工作。
5. 小结
光子计数探测器作为多能谱成像的关键器件，成为研究能谱成像的一个重要内容。本文通过实验，模拟光子计数探测器在不同能量分辨率、不同能谱阈值和能量范围下的成像实验。通过比较重建的等效原子序数图和电子密度图的标准差，评价成像结果的好坏，得到上述因素对光子计数X射线CT成像精度的影响规律。
（1）针对安检CT中常用的160 kV射线源能量，光子计数探测器能量分辨率越高，成像效果越好，但是能量分辨率对于材料的分辨差异并不显著。
（2）在探测器能量分辨率确定的情况下，恰当选取能谱阈值对于成像很有帮助。通过设置合适的阈值，使高低能能谱重合度减小，往往可以得到更好的成像结果。但是随着能谱变窄、重合度下降，噪声也会加大，需要平衡这两种因素，否则更低的能谱重合度也有可能带来更差的成像结果。
本文的研究成果将有助于能谱CT系统的总体设计，如从双能成像材料分辨的角度，并不一定过高追求能量分辨率，这对于能量成像CT系统的硬件选型具有积极的指导意义。
-
![]()
图 3 本文提出的非连续性投影数据训练和测试框架
Figure 3. The framework of training and testing for discrete projection data
![]()
图 4 U型生成对抗网络结构图
Figure 4. Generative Adversarial U-Net for coded aperture computed tomography
![]()
图 5 编码掩膜板透过率为20％，训练次数为115个epoch的结果图
Figure 5. The results for coded apertures at 20％ transmittance
![]()
图 6 编码掩膜板透过率为25％ 时基于U型生成对抗网络的编码孔径CT成像结果
Figure 6. The reconstructed images for coded apertures computed tomography at 25％ transmittance
![]()
图 7 编码掩膜板透过率为5％、15％ 和25％时基于U型生成对抗网络的编码孔径CT成像结果
Figure 7. The reconstructed images for coded apertures computed tomography at 5％, 15％ and 25％ transmittance, respectively
表 1 不同编码掩膜板透过率下，测试集中预测的正弦图和CT重建图像的平均值
Table 1 The average results of sonograms and CT reconstructions at different transmission rates
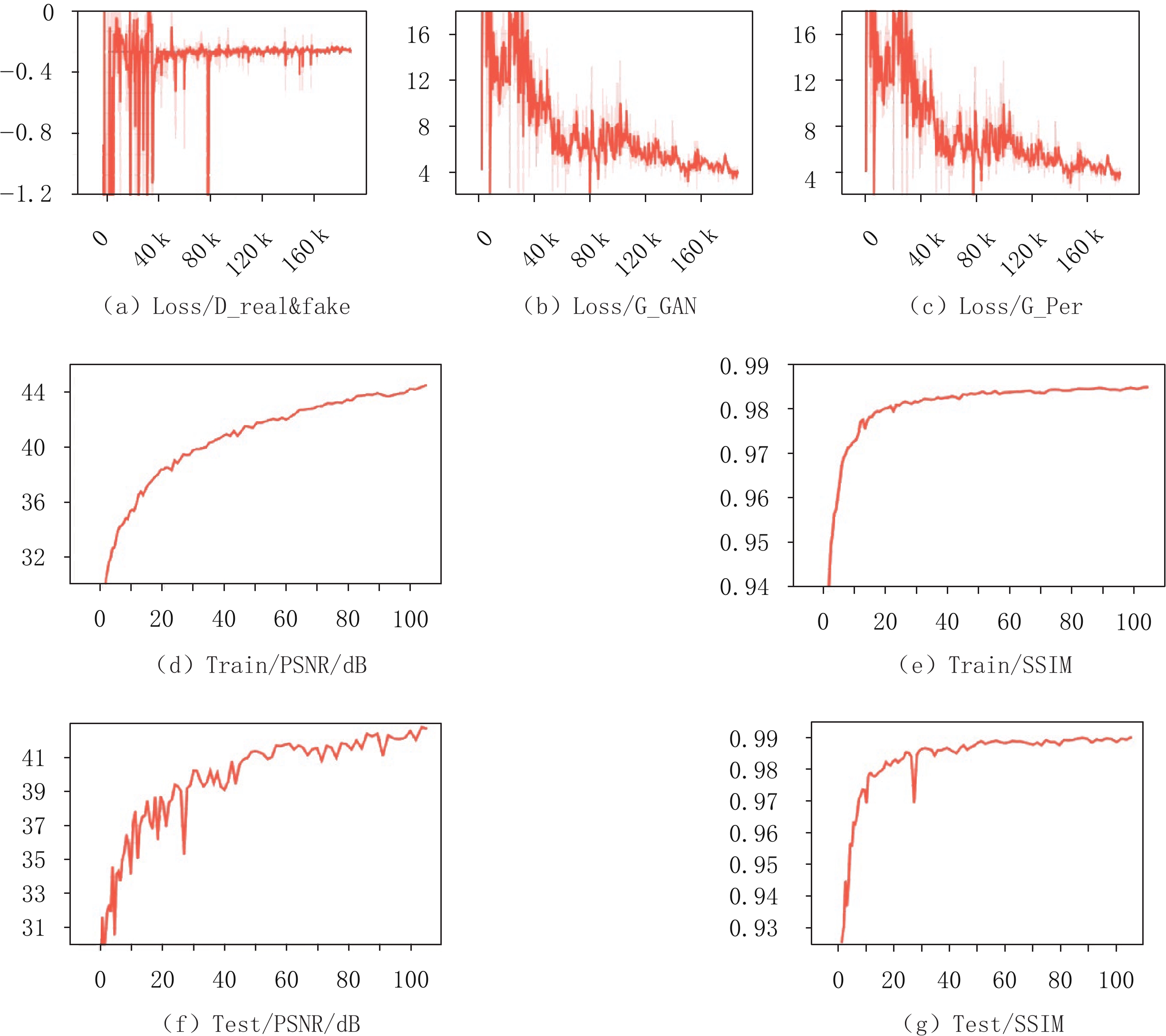
测试数据集 图像质量评价指标 编码掩膜板透过率 5％ 10％ 15％ 20％ 25％ 预测的正弦图 PSNR/dB 39.1 41.6 40.9 42.6 43.8 SSIM 0.98 0.97 0.98 0.99 0.98 CT重建图像 PSNR/dB 33.7 32.0 33.5 35.3 33.6 SSIM 0.88 0.88 0.89 0.91 0.90 
下载: 导出CSV
-
[1] KALENDER W A. Computed tomography: Fundamentals, system technology, image quality, applications[M]. John Wiley & Sons, 2011.
[2] KALENDER W A. X-ray computed tomography[J]. Physics in Medicine & Biology, 2006, 51(13): R29.
[3] WILLEMINK M J, PERSSON M, POURMORTEZA A, et al. Photon-counting CT: Technical principles and clinical prospects[J]. Radiology, 2018, 289(2): 293−312. doi: 10.1148/radiol.2018172656
[4] FUCHS T, KACHELRIE M, KALENDER W A. Technical advances in multi-slice spiral CT[J]. European Journal of Radiology, 2000, 36(2): 69−73. doi: 10.1016/S0720-048X(00)00269-2
[5] ZHU Z, WAHID K, BABYN P, et al. Improved compressed sensing-based algorithm for sparse-view CT image reconstruction[J]. Computational and Mathematical Methods in Medicine, 2013: 185750:1−185750:15.
[6] MCCOLLOUGH C H, LENG S, YU L, et al. CT dose index and patient dose: They are not the same thing[J]. Radiology, 2011, 259(2): 311−316. doi: 10.1148/radiol.11101800
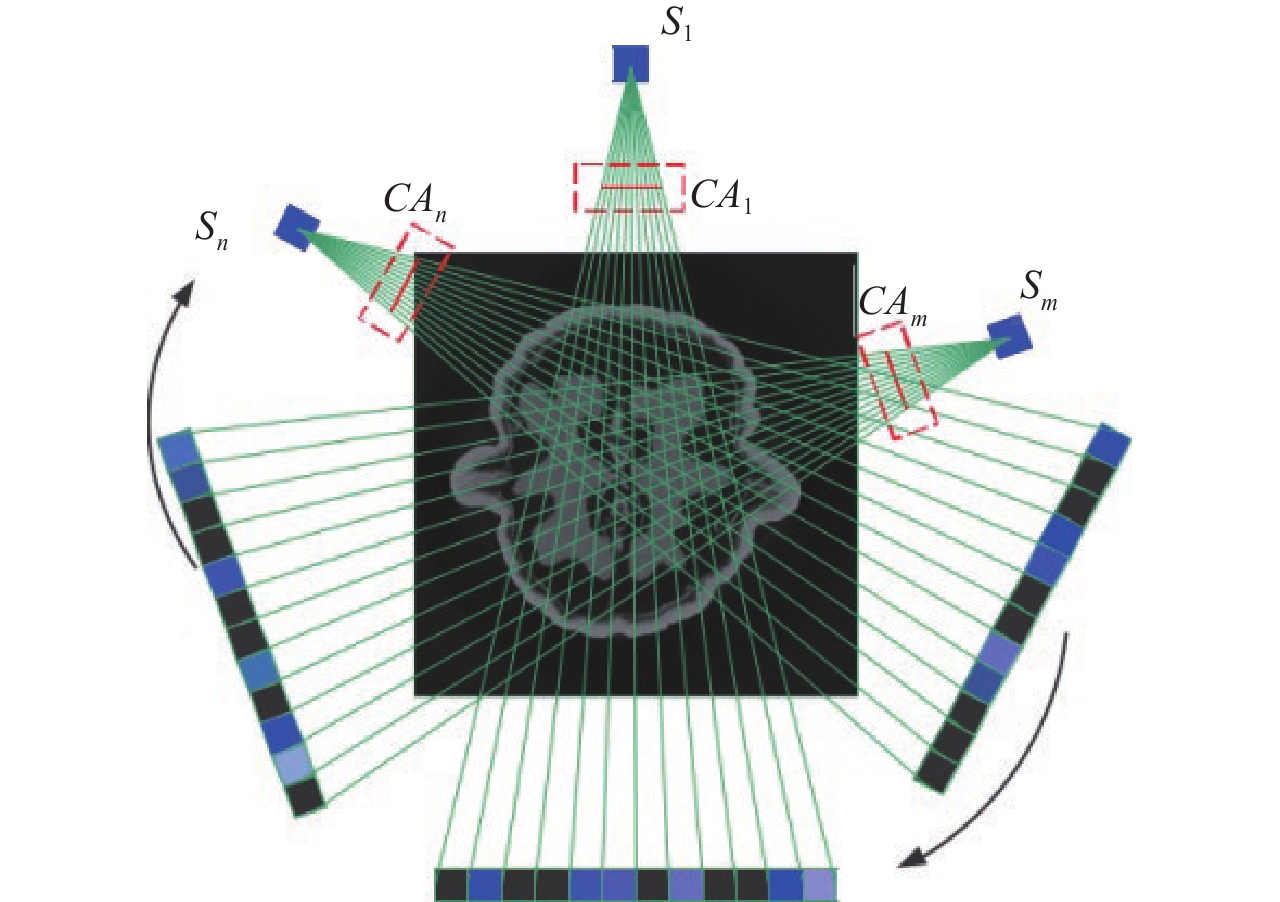
[7] CHOI K, BRADY D J. Coded aperture computed tomography[C]//International Society for Optics and Photonics. Adaptive Coded Aperture Imaging, Non-Imaging, and Unconventional Imaging Sensor Systems. 2009, 7468: 74680B.
[8] JEREZ A, MARQUEZ M, ARGUELLO H. Adaptive coded aperture design for compressive computed tomography[J]. Journal of Computational and Applied Mathematics, 2021, 384: 113174. doi: 10.1016/j.cam.2020.113174
[9] ZHANG T, ZHAO S, MA X, et al. Nonlinear reconstruction of coded spectral X-ray CT based on material decomposition[J]. Optics Express, 2021, 29(13): 19319−19339. doi: 10.1364/OE.426732
[10] YAN K, LI D, HOLMGREN A, et al. Compressed sampling strategies for tomography[J]. Journal of the Optical Society of America A, 2014, 31(7): 1369−1394. doi: 10.1364/JOSAA.31.001369
[11] ZHAO Q, MA X, CUADROS A, et al. Single-snapshot X-ray imaging for nonlinear compressive tomosynthesis[J]. Optics Express, 2020, 28(20): 29390−29407. doi: 10.1364/OE.392054
[12] TZOUMAS S, VERNEKOHL D, XING L. Coded-aperture compressed sensing X-ray luminescence tomography[J]. IEEE Transactions on Biomedical Engineering, 2017, 65(8): 1892−1895.
[13] MOJICA E, PERTUZ S, ARGUELLO H. High-resolution coded-aperture design for compressive X-ray tomography using low resolution detectors[J]. Optics Communications, 2017, 404: 103−109. doi: 10.1016/j.optcom.2017.06.053
[14] CUADROS A, MA X, ARCE G R. Compressive spectral X-ray tomography based on spatial and spectral coded illumination[J]. Optics Express, 2019, 27(8): 10745−10764. doi: 10.1364/OE.27.010745
[15] CUADROS A P, MA X, RESTREPO C M, et al. Static code CT: Single coded aperture tensorial X-ray CT[J]. Optics Express, 2021, 29(13): 20558−20576. doi: 10.1364/OE.427382
[16] CUADROS A P, LIU X, PARSONS P E, et al. Experimental demonstration and optimization of X-ray static code CT[J]. Applied Optics, 2021, 60(30): 9543−9552. doi: 10.1364/AO.438727
[17] MA X, YUAN X, FU C, et al. LED-based compressive spectral-temporal imaging[J]. Optics Express 2021, 29(7): 10698-10715.
[18] CUADROS A P, ARCE G R. Coded aperture optimization in compressive X-ray tomography: A gradient descent approach[J]. Optics Express, 2017, 25(20): 23833−23849. doi: 10.1364/OE.25.023833
[19] CUADROS A P, PEITSCH C, ARGUELLO H, et al. Coded aperture optimization for compressive X-ray tomosynthesis[J]. Optics Express, 2015, 23(25): 32788−32802. doi: 10.1364/OE.23.032788
[20] MEJIA Y, ARGUELLO H. Binary codification design for compressive imaging by uniform sensing[J]. IEEE Transactions on Image Processing, 2018, 27(12): 5775−5786. doi: 10.1109/TIP.2018.2857445
[21] MAO T, CUADROS A P, MA X, et al. Fast optimization of coded apertures in X-ray computed tomography[J]. Optics Express, 2018, 26(19): 24461−24478. doi: 10.1364/OE.26.024461
[22] SWINEHART D F. The beer-lambert law[J]. Journal of Chemical Education, 1962, 39(7): 333. doi: 10.1021/ed039p333
[23] MAO T, CUADROS A P, MA X, et al. Coded aperture optimization in X-ray tomography via sparse principal component analysis[J]. IEEE Transactions on Computational Imaging, 2019, 6: 73−86.
[24] YI X, WALIA E, BABYN P. Generative adversarial network in medical imaging: A review[J]. Medical Image Analysis, 2019, 58: 101552. doi: 10.1016/j.media.2019.101552
-
期刊类型引用(2)
1. 李梦雨，段诗苗，张雷，周咏春. 提高肺SBRT精度的多窗位动态组合诊疗手段. 中国CT和MRI杂志. 2024(04): 63-65 . 
百度学术
2. 李玉辉，刘龙进，徐乐意，刘远高. 胸部CT不同图像算法对人工智能辅助诊断软件肺结节检出效果的影响研究. 中国医学装备. 2023(12): 10-14 . 百度学术
其他类型引用(3)
计量
- 文章访问数: 674
- HTML全文浏览量: 158
- PDF下载量: 92
- 被引次数: 5
