Combined Boundary of CPML and Feature Analysis within Frequency-Space Domain
-
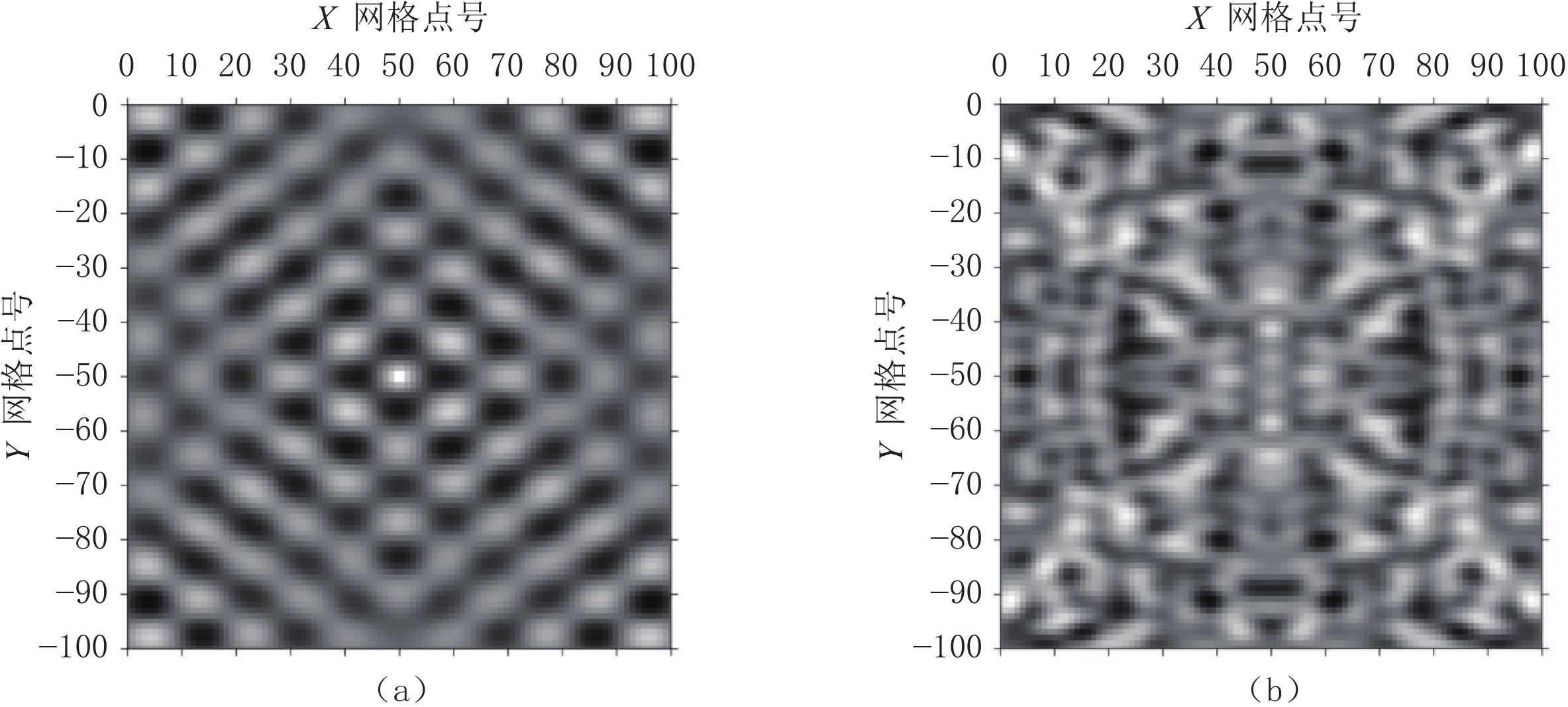
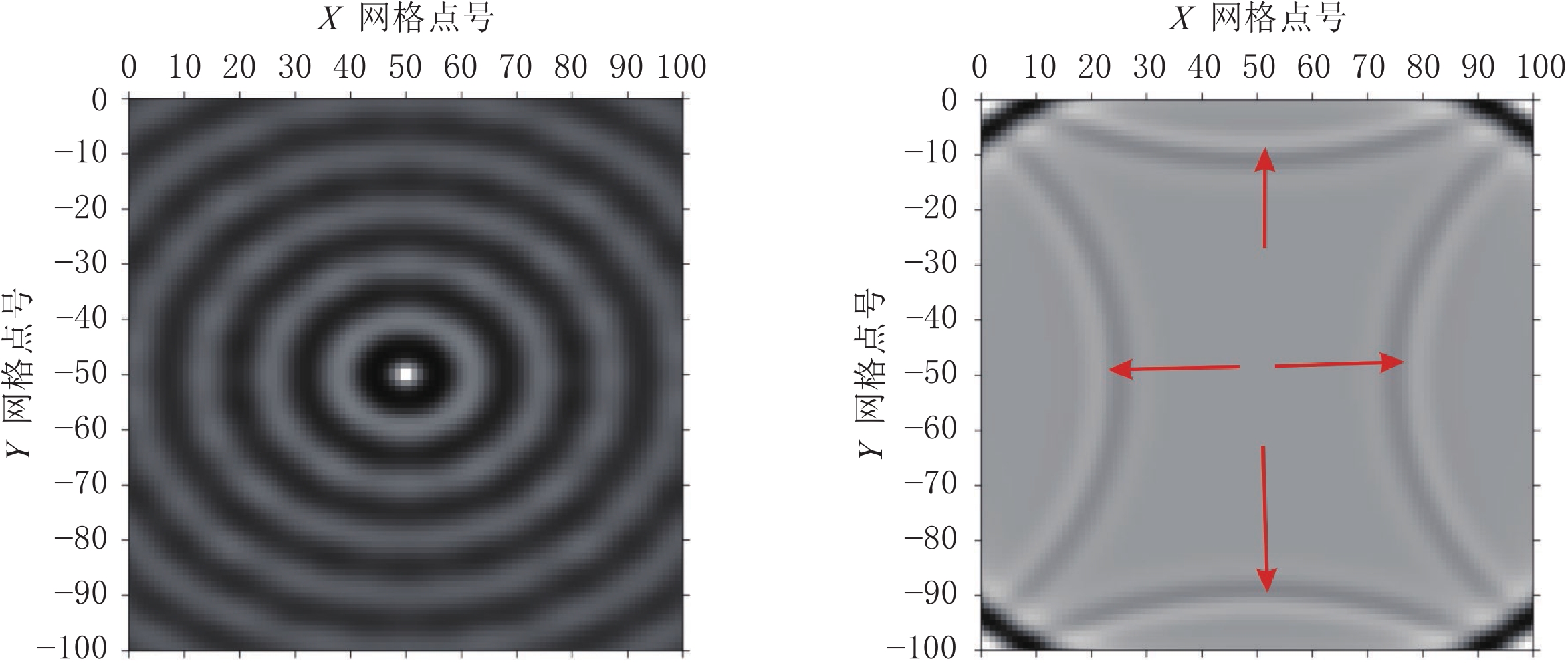
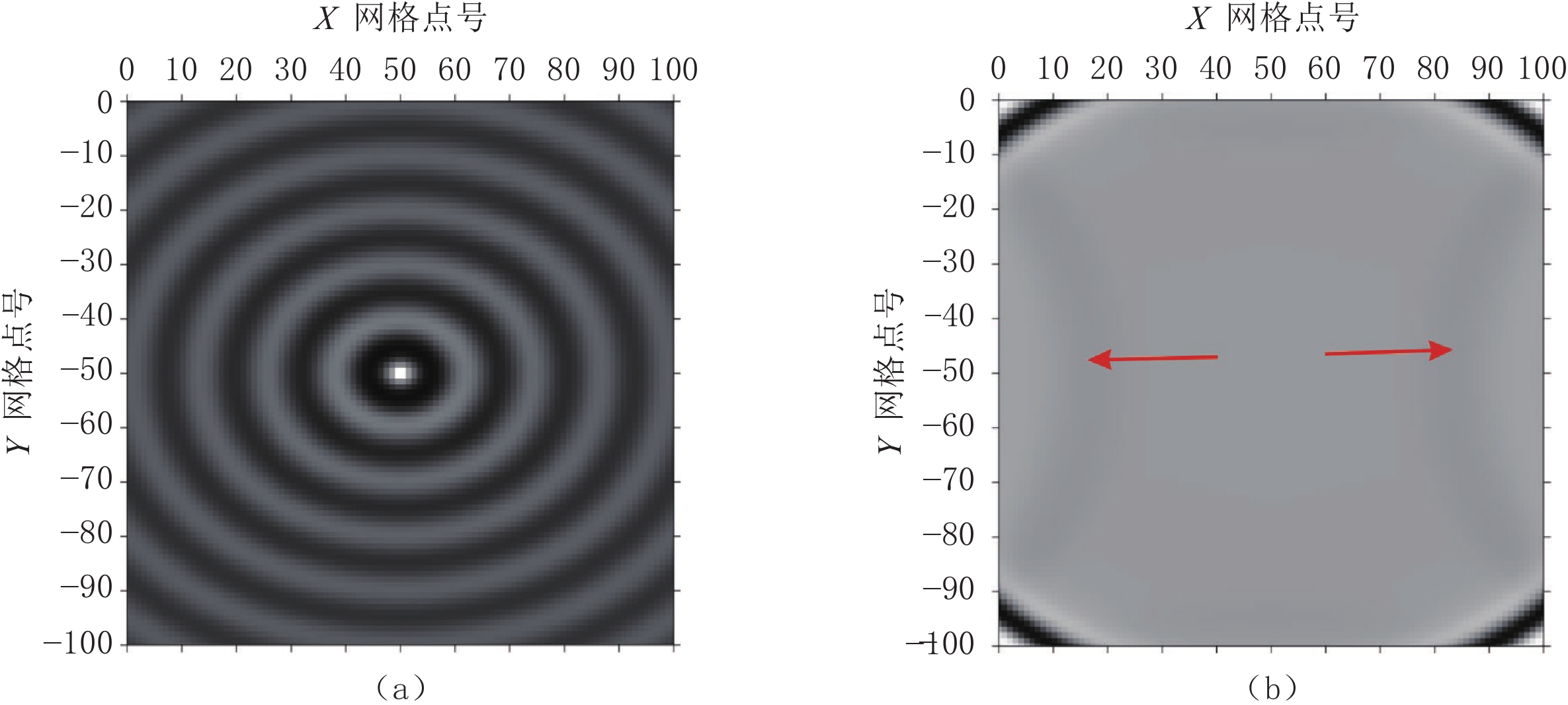
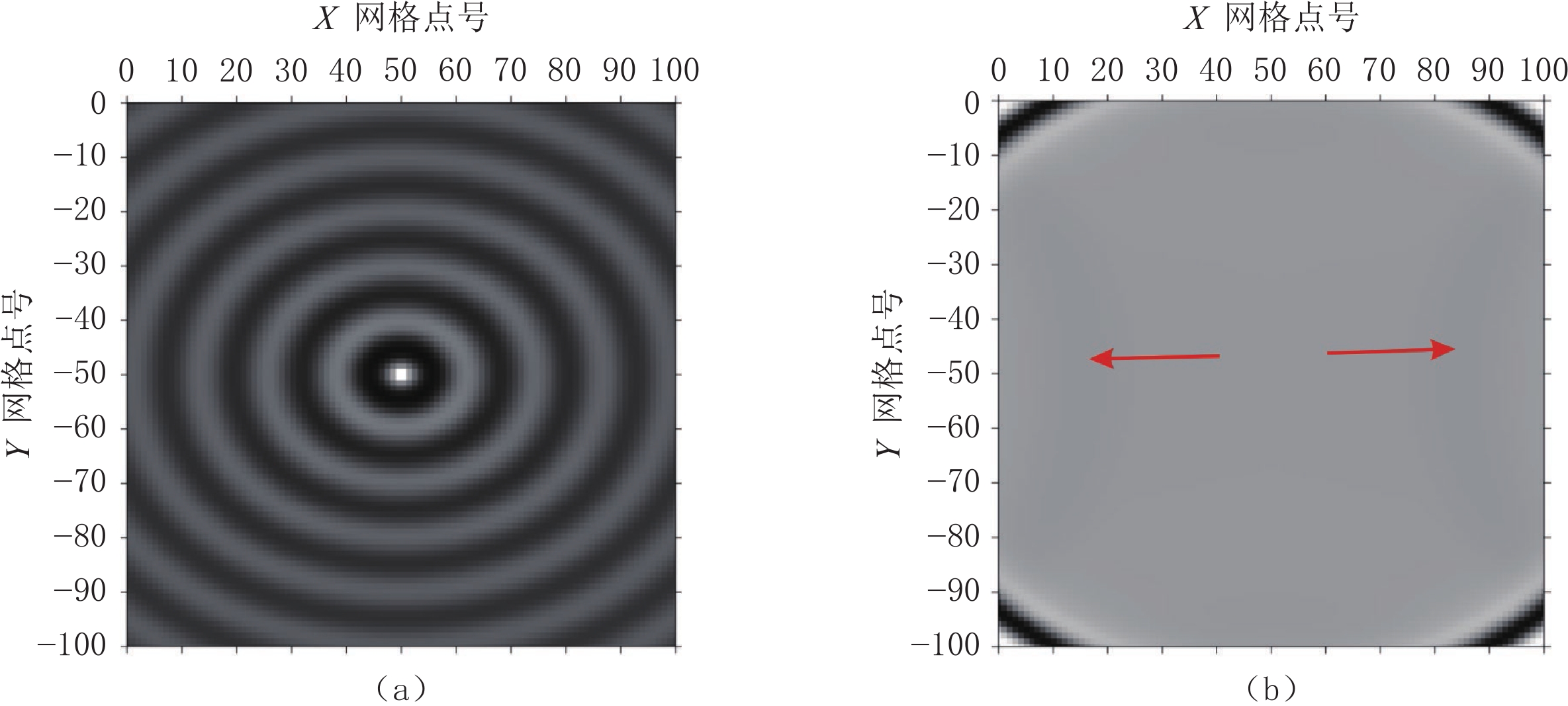
摘要: 在地震波场数值模拟过程中，边界反射是影响其模拟结果的一个重要因素。实际地下介质具有各向异性特征，传统的完全匹配层边界（PML）对于小入射角地震波具有良好效果，但该方法并不能有效地吸收低频波和大角度入射波。针对VTI介质边界反射的问题，本文提出在频率-空间域有限差分法数值模拟中采用卷积完全匹配层（CPML）和特征分析法的组合边界条件，并对该组合边界条件进行数值模拟实验和边界反射吸收效果分析，验证所提方法是一种可靠的人工吸收边界条件，能够有效地压制波场模拟过程中产生的边界反射。Abstract: In the process of numerical simulation, boundary reflection is an important factor which affect the numerical simulation results. The actual underground medium holds anisotropic characteristics. The traditional perfectly matched layer boundary (PML) shows good effect on small incident angle seismic waves, yet it can not effectively absorb low-frequency waves and large angle incident waves. To solve the problem of boundary reflection, in this paper, we propose a combined boundary condition using convolution perfectly matched layer (CPML) and eigenvalue analysis method to be applied in the numerical simulation of finite difference method in frequency space domain. The numerical simulation experiment and boundary reflection absorption effect analysis of the combined boundary condition verify that the proposed method is a reliable artificial absorption boundary condition, which can effectively suppress the boundary reflection generated in the process of wave field simulation.
-
地震波场数值模拟过程中产生的边界反射会影响模拟的结果。由于计算能力所限，用于实现地震波场数值模拟的计算空间是有限的，所以需要在计算区域的周围施加人工吸收边界条件来降低边界反射。目前广泛应用于地震波场数值模拟的人工边界条件有两种，一是海绵吸收边界，二是傍轴近似吸收边界。
海绵吸收边界指通过在边界周围设置粘滞边界，通过粘滞边界衰减边界处的入射地震波[1]，达到吸收和压制边界反射的目的。完全匹配层边界（perfectly matched layers，PML）是由Berenger[2-4]提出并应用在电磁场模拟中的一种经典的海绵吸收边界条件，理论上PML边界能吸收任意角度和频率的连续波场[5-9]。在之后的研究中，学者们在此基础上进行改进，使其变得更加有效。1994年Chew和Weedon引入复伸展坐标系，将PML边界总结为具体公式。1996年Chew等[10]将PML边界应用于弹性动力学；2003年Wang等[11]将非分裂PML方法应用在弹性波有限差分数值模拟中。然而离散化的数值模拟会降低PML边界的吸收效果，特别是对于近切入射波场和低频波场[12]。基于传统的PML方法，1996年Kuzuoglu等[13]提出了应用于电磁波模拟的复频移 PML方法；2000年Roden等[14]引入递归卷积技术，提出卷积完全匹配层边界（CPML），相比于传统的PML边界条件，CPML边界条件增加了额外的控制参数，能很好地吸收低频反射，具有良好的吸收效果；2007年Drossaert等[15-16]将非分裂式CPML方法应用到一阶波动方程的弹性波数值模拟中；2014年Chen等[17]将CPML应用到粘弹性和孔隙弹性波场等各种地震波场数值模拟。Ma等[18-20]结合辛方法将非分裂复频移完全匹配层应用到地震波波动方程中。
另一方面，结合特征分析法分离出地震波场中的单程波，并根据不同边界区域构造各自的吸收边界条件，用于衰减波场模拟过程中产生的边界反射。吴国忱等[21-22]和董良国[23]的研究表明该方法可在一定程度上改善成像效果。基于此，本文在前人的研究基础上，利用频率-空间域波动方程进行数值模拟，在该过程中采用CPML吸收边界和特征分析法相结合的组合边界条件，并对组合边界的效果进行验证和效果分析，数值模拟的结果表明该组合边界条件对数值模拟过程中的边界反射有较好的压制和吸收效果。
1. VTI介质波动方程
根据本构方程，运动微分方程和柯西方程可得出VTI介质弹性波波动方程：
$$ \left\{ {\begin{aligned} & {{C_{11}}\frac{{{\partial ^2}u}}{{\partial {x^2}}} + {C_{66}}\frac{{{\partial ^2}u}}{{\partial {y^2}}} + {C_{44}}\frac{{{\partial ^2}u}}{{\partial {z^2}}} + \Big({C_{12}} + {C_{66}}\Big)\frac{{{\partial ^2}v}}{{\partial x\partial y}} + \Big({C_{13}} + {C_{44}}\Big)\frac{{{\partial ^2}w}}{{\partial x\partial z}} + \rho {f_x} = \rho \frac{{{\partial ^2}u}}{{\partial {t^2}}}} \\ & {{C_{66}}\frac{{{\partial ^2}v}}{{\partial {x^2}}} + {C_{11}}\frac{{{\partial ^2}v}}{{\partial {y^2}}} + {C_{44}}\frac{{{\partial ^2}v}}{{\partial {z^2}}} + \Big({C_{12}} + {C_{66}}\Big)\frac{{{\partial ^2}u}}{{\partial x\partial y}} + \Big({C_{13}} + {C_{44}}\Big)\frac{{{\partial ^2}w}}{{\partial y\partial z}} + \rho {f_y} = \rho \frac{{{\partial ^2}v}}{{\partial {t^2}}}} \\ & {{C_{44}}\frac{{{\partial ^2}w}}{{\partial {x^2}}} + {C_{44}}\frac{{{\partial ^2}w}}{{\partial {y^2}}} + {C_{33}}\frac{{{\partial ^2}w}}{{\partial {z^2}}} + \Big({C_{13}} + {C_{44}}\Big)\frac{{{\partial ^2}v}}{{\partial x\partial y}} + \Big({C_{13}} + {C_{44}}\Big)\frac{{{\partial ^2}v}}{{\partial y\partial z}} + \rho {f_z} = \rho \frac{{{\partial ^2}w}}{{\partial {t^2}}}} \end{aligned}} \right.\text{，} $$ (1) 其中
${C_{11}}$ 、${C_{12}}$ 、${C_{13}}$ 、${C_{33}}$ 、${C_{44}}$ 、${C_{66}}$ 为弹性参数；$u$ 、$v$ 、$w$ 为位移；${f_x}$ 、${f_y}$ 、${f_z}$ 为体力项；$\rho $ 为介质密度。将平面波方程
$\boldsymbol U = {\boldsymbol{A}}\;{\exp{\Big(i({k_x}x + {k_y}y + {k_z}z - \omega t)\Big)}}$ 代入VTI介质弹性波波动方程（1）。化简可得Kelvin-Christoffel方程，其中${\boldsymbol{U}}$ 为位移；${\boldsymbol{A}}$ 为振幅；${k_x}$ 、${k_y}$ 、${k_z}$ 为波数；$\omega $ 为圆频率；$t$ 为时间。Kelvin-Christoffel方程的矩阵形式为：
$$ \left( {\begin{array}{*{20}{c}} {{\varGamma _{11}} - \rho {\omega ^2}}&{{\varGamma _{12}}}&{{\varGamma _{13}}} \\ {{\varGamma _{12}}}&{{\varGamma _{22}} - \rho {\omega ^2}}&{{\varGamma _{23}}} \\ {{\varGamma _{13}}}&{{\varGamma _{23}}}&{{\varGamma _{33}} - \rho {\omega ^2}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{A_x}} \\ {{A_y}} \\ {{A_z}} \\ \end{array}} \right) = 0\text{，} $$ (2) 其中
${\varGamma _{11}}$ 、${\varGamma _{12}}$ 、${\varGamma _{13}}$ 、${\varGamma _{22}}$ 、${\varGamma _{23}}$ 、${\varGamma _{33}}$ 为弹性参数的函数；$$ \left\{ {\begin{aligned} & {\varGamma _{11}} = {C_{11}}k_x^2 + {C_{66}}k_y^2 + {C_{44}}k_z^2 \\ & {\varGamma _{12}} = \Big({C_{12}} + {C_{66}}\Big){k_x}{k_y}\\ & {\varGamma _{13}} = \Big({C_{13}} + {C_{44}}\Big){k_x}{k_z}\\ & {\varGamma _{22}} = {C_{66}}k_x^2 + {C_{11}}k_y^2 + {C_{44}}k_z^2\\ & {\varGamma _{23}} = \Big({C_{13}} + {C_{44}}\Big){k_y}{k_z}\\ & {\varGamma _{33}} = {C_{44}}k_x^2 + {C_{11}}k_y^2 + {C_{33}}k_z^2 \end{aligned}} \right.。 $$ (3) 矩阵方程（2）中系数矩阵的矩阵行列式等于零，即可求得该系数矩阵特征值和特征向量，即：
$$ \begin{gathered} \quad \det \varGamma = \left| {\begin{array}{*{20}{c}} {{\varGamma _{11}} - \rho {\omega ^2}}&{{\varGamma _{12}}}&{{\varGamma _{13}}} \\ {{\varGamma _{12}}}&{{\varGamma _{22}} - \rho {\omega ^2}}&{{\varGamma _{23}}} \\ {{\varGamma _{13}}}&{{\varGamma _{23}}}&{{\varGamma _{33}} - \rho {\omega ^2}} \end{array}} \right|= \hfill \\ \;\;\; \Big({\varGamma _{11}} - \rho {\omega ^2}\Big)\Big({\varGamma _{22}} - \rho {\omega ^2}\Big)\Big({\varGamma _{33}} - \rho {\omega ^2}\Big) + 2{\varGamma _{12}}{\varGamma _{23}}{\varGamma _{13}} - \hfill \\ \Big({\varGamma _{11}} - \rho {\omega ^2}\Big)\varGamma _{23}^2 - \Big({\varGamma _{22}} - \rho {\omega ^2}\Big)\varGamma _{13}^2 - \Big({\varGamma _{33}} - \rho {\omega ^2}\Big)\varGamma _{12}^2 = 0 \end{gathered} 。 $$ (4) 在方程（4）中，根据Thomsen参数可以得出Thomsen参数与弹性参数之间的关系，Thomsen参数包括
${V_{{\rm{P}}0}}$ ，${V_{{\rm{S}}0}}$ ，$\varepsilon $ ，$\gamma$ ，$\delta $ 共5个量；$$ \left\{ {\begin{aligned} & {V_{{\rm{P}}0}} = \sqrt {\frac{{{C_{33}}}}{\rho }} \\ &{V_{{\rm{S}}0}} = \sqrt{ \frac{{{C_{55}}}}{\rho } }\\ & \varepsilon = \frac{{{C_{11}} - {C_{33}}}}{{2{C_{33}}}}\\ & \gamma = \frac{{{C_{66}} - {C_{44}}}}{{2{C_{44}}}} \\ &\delta = \frac{{{{({C_{13}} + {C_{44}})}^2} - {{({C_{33}} - {C_{44}})}^2}}}{{2{C_{33}}({C_{33}} - {C_{44}})}} \end{aligned}} \right.\text{，} $$ (5) 式中
$\rho $ 表示介质密度；${V_{{\rm{P}}0}}$ 为准P波在垂直方向上传播的速度；${V_{{\rm{S}}0}}$ 为准S波在垂直方向上传播的速度；$\varepsilon $ 、$\gamma$ 、$\delta $ 为衡量VTI介质中各向异性程度的Thomsen参数。设横波速度
${V_{{\rm{S}}0}}$ 等于零，则Thomsen参数表征VTI介质中的弹性参数的公式为：$$ \left\{ {\begin{aligned} & {\varGamma _{11}} = \rho V_{{\rm{P}}0}^2(1 + 2\varepsilon )k_x^2 \\ &{{\varGamma _{12}} = \rho V_{{\rm{P}}0}^2(1 + 2\varepsilon ){k_x}{k_y}} \\ &{{\varGamma _{13}} = \rho V_{{\rm{P}}0}^2\sqrt {1 + 2\delta } {k_x}{k_z}} \\ & {\varGamma _{22}} = \rho V_{{\rm{P}}0}^2(1 + 2\varepsilon )k_y^2 \\ & {{\varGamma _{23}} = \rho V_{{\rm{P}}0}^2\sqrt {1 + 2\delta } {k_y}{k_z}} \\ & {\varGamma _{33}} = \rho V_{{\rm{P}}0}^2k_z^2 \end{aligned}} \right.。 $$ (6) 将方程组（6）代入系数矩阵（4）中，整理可得到准P波的频散方程：
$$ {\omega ^4} = {\omega ^2}\Big( {V_{{\rm{P}}0}^2(1 + 2\varepsilon )k_x^2 + V_{{\rm{P}}0}^2(1 + 2\varepsilon )k_y^2 + V_{{\rm{P}}0}^2k_z^2} \Big) - 2(\varepsilon - \delta )V_{{\rm{P}}0}^4k_y^2k_z^2 - 2(\varepsilon - \delta )V_{{\rm{P}}0}^4k_z^2k_x^2。 $$ (7) 引入参数
$\textit{χ} = 1 + 2\varepsilon ，\eta = \varepsilon - \delta$ ，将其转化到频率-空间域二维情况下可得 Ⅶ 介质波动方程为：$$ {\omega ^4}F + \textit{χ} V_{{\rm{P}}0}^2{\omega ^2}\frac{{{\partial ^2}F}}{{\partial {x^2}}} + V_{{\rm{P}}0}^2{\omega ^2}\frac{{{\partial ^2}F}}{{\partial {z^2}}} + 2\eta V_{{\rm{P}}0}^4\frac{{{\partial ^4}F}}{{\partial {x^2}\partial {z^2}}} = 0， $$ (8) 其中
$F$ 为准P波的波场。2. 吸收边界原理
2.1 CPML吸收边界原理
传统PML边界的复频伸展函数定义为：
$$ \left\{ {\begin{aligned} &{{e_x} = {a_x} - \frac{{i{\sigma _x}}}{\omega }} \\ &{{e_z} = {a_z} - \frac{{i{\sigma _z}}}{\omega }} \end{aligned}} \right.\text{，} $$ (9) 其中在匹配层区域，
${a_x}$ 、${a_z}$ 为尺度因子，虚数部分起衰减作用；在非匹配层区域，${a_x} = $ $ {a_z} = 1$ ，虚数部分为0，不发生衰减作用；衰减函数${\sigma _x}$ 、${\sigma _z}$ 分别为：$$ {\sigma }_{x}=\left\{\begin{array}{c}2 \pi {a}_{0}{f}_{0}{\left(\displaystyle\dfrac{{x}_{i}}{{L}_{{\text{PML}}}}\right)}^{2},（匹配层区域）\\ \begin{array}{cccc}& \begin{array}{cc}& 0\end{array}& & \end{array},（非匹配层区域）\end{array}\right. \text{，} {\sigma }_{z}=\left\{\begin{array}{c}2\pi {a}_{0}{f}_{0}{\left(\displaystyle\dfrac{{z}_{i}}{{L}_{{\text{PML}}}}\right)}^{2},（匹配层区域）\\ \begin{array}{cccc}& \begin{array}{cc}& 0\end{array}& & \end{array},（非匹配层区域）\end{array} \right.。 $$ (10) 在（10）式中，
${a_0}$ 一般取值为1.79[24]；${L_\text{PML}}$ 是匹配层的厚度；${f_0}$ 是震源主频；${x_i}$ 、${z_i}$ 分别是计算网格点到匹配层与非匹配层边界的横向距离和垂向距离。采用CPML边界的复频伸展函数为[25]：
$$ \left\{ {\begin{aligned} &{{e_x} = {\kappa _x} + \frac{{{\sigma _x}}}{{{a_x} + i\omega }}} \\ &{{e_z} = {\kappa _z} + \frac{{{\sigma _z}}}{{{a_z} + i\omega }}} \end{aligned}} \right.。 $$ (11) 在式（11）中：
${\kappa _x}$ 、${\kappa _z}$ 、${a_x}$ 、${a_z}$ 为辅助衰减系数，且${\kappa _x} \geq1$ ，${\kappa _z} \geq 1$ ，${a_x} \geq0$ ，${a_z} \geq0$ 。如果设定${\kappa _x} = 1$ ，${\kappa _z} = 1$ ，${a_x} = 0$ ，${a_z} = 0$ ，方程（11）就会变成传统的PML吸收边界条件。图1为在计算区域的周围施加CPML边界示意图，其中：
（1）标号④的区域为非匹配层区域，标号①、②、③为匹配层区域；
（2）在①区域内，
${\sigma _x} \ne 0$ ，${\sigma _z} \ne 0$ ；（3）在②区域内，
${\sigma _x} = 0$ ，${\sigma _z} \ne 0$ ；（4）在③区域内，
${\sigma _x} \ne 0$ ，${\sigma _z} = 0$ 。结合衰减函数
${\sigma _x}$ 、${\sigma _z}$ 和VTI介质弹性波动方程，得到二维VTI介质准P波波动方程为：$$ {\omega ^4}F + \frac{{(1 + 2\varepsilon )V_{{\rm{P}}0}^2{\omega ^2}}}{{e_x^2}}\frac{{{\partial ^2}F}}{{\partial {x^2}}} + \frac{{V_{{\rm{P}}0}^2{\omega ^2}}}{{e_z^2}}\frac{{{\partial ^2}F}}{{\partial {z^2}}}+ \frac{{2(\varepsilon - \delta )V_{{\rm{P}}0}^4}}{{e_x^2e_z^2}}\frac{{{\partial ^4}F}}{{\partial {x^2}\partial {z^2}}} = 0。 $$ (12) 2.2 特征分析法边界原理
二维时间-空间域VTI介质准P波波动方程为：
$$ \left\{ {\begin{aligned} &{\frac{{{\partial ^2}{u_x}}}{{\partial {t^2}}} = \frac{{{C_{11}}}}{\rho }\frac{{{\partial ^2}{u_x}}}{{\partial {x^2}}} + \frac{{{C_{44}}}}{\rho }\frac{{{\partial ^2}{u_x}}}{{\partial {z^2}}} + \frac{{({C_{13}} + {C_{44}})}}{\rho }\frac{{{\partial ^2}{u_z}}}{{\partial x\partial z}}} \\ & {\frac{{{\partial ^2}{u_z}}}{{\partial {t^2}}} = \frac{{({C_{13}} + {C_{44}})}}{\rho }\frac{{{\partial ^2}{u_x}}}{{\partial x\partial z}} + \frac{{{C_{44}}}}{\rho }\frac{{{\partial ^2}{u_z}}}{{\partial {x^2}}} + \frac{{{C_{33}}}}{\rho }\frac{{{\partial ^2}{u_z}}}{{\partial {z^2}}}} \end{aligned}} \right.\text{，} $$ (13) 其中
${u_x}$ 和${u_z}$ 分别是$X$ 方向和$Z$ 方向的位移。弹性参数用Thomsen参数表征，同时令${V_{{\rm{S}}0}} = 0$ ，则弹性参数为：$$ \left\{ {\begin{aligned} &{{C_{11}} = \rho (1 + 2\varepsilon )V_{{\rm{P}}0}^2 = \rho v_1^2} \\ & {{C_{13}} = \rho \sqrt {1 + 2\delta } V_{{\rm{P}}0}^2 = \rho v_2^2} \\ & {C_{33}} = \rho V_{{\rm{P}}0}^2 = \rho v_3^2 \\ & {C_{44}} = 0 \end{aligned}} \right.\text{，} $$ (14) 其中：
$$ \left\{ {\begin{aligned} & {{v_1} = {V_{{\rm{P}}0}}\sqrt {1 + 2\varepsilon } } \\ & {{v_2} = {V_{{\rm{P}}0}}\sqrt[4]{{1 + 2\delta }}} \\ & {v_3} = {V_{{\rm{P}}0}} \end{aligned}} \right.。 $$ (15) 设
${v_x}$ 和${v_z}$ 分别是$X$ 方向和$Z$ 方向的位移速度，${\sigma _{xx}}$ 和${\sigma _{zz}}$ 分别是$X$ 方向和$Z$ 方向的正应力，则由运动微分方程和几何方程简化后得速度应力场的关系式：$$ \left\{ {\begin{aligned} &\frac{{\partial {v_x}}}{{\partial t}} = \frac{1}{\rho }\frac{{\partial {\sigma _{xx}}}}{{\partial x}} \\ &\frac{{\partial {v_z}}}{{\partial t}} = \frac{1}{\rho }\frac{{\partial {\sigma _{zz}}}}{{\partial z}} \\ & {\frac{{\partial {\sigma _{xx}}}}{{\partial t}} = \rho v_1^2\frac{{\partial {v_x}}}{{\partial x}} + \rho v_2^2\frac{{\partial {v_z}}}{{\partial z}}} \\ & {\frac{{\partial {\sigma _{zz}}}}{{\partial t}} = \rho v_2^2\frac{{\partial {v_x}}}{{\partial x}} + \rho v_3^2\frac{{\partial {v_z}}}{{\partial z}}} \end{aligned}} \right.。 $$ (16) 令
$\boldsymbol U = {({v_x},{v_z},{\sigma _{xx}},{\sigma _{zz}})^{\rm{T}}}$ ，则上式可写成矩阵形式：$$ \frac{{\partial \boldsymbol U}}{{\partial t}} = {\boldsymbol{A}}\frac{{\partial \boldsymbol U}}{{\partial x}} + {\boldsymbol{B}}\frac{{\partial \boldsymbol U}}{{\partial z}}\text{，} $$ (17) 其中：
$$ {\boldsymbol{A}} = \left( {\begin{array}{*{20}{c}} 0&0&{\displaystyle\dfrac{1}{\rho }}&0 \\ 0&0&0&0 \\ {\rho v_1^2}&0&0&0 \\ {\rho v_2^2}&0&0&0 \end{array}} \right)\text{，}{\boldsymbol{B}} = \left( {\begin{array}{*{20}{c}} 0&0&0&0 \\ 0&0&0&{\displaystyle\dfrac{1}{\rho }} \\ 0&{\rho v_2^2}&0&0 \\ 0&{\rho v_3^2}&0&0 \end{array}} \right)。 $$ (18) 将
${\boldsymbol{A}}\displaystyle\frac{{\partial U}}{{\partial x}}$ 分解为左行波和右行波，并求解矩阵${\boldsymbol{A}}$ 的特征值得${\lambda _1} = {v_1}$ ,${\lambda _2} = 0$ ,${\lambda _3} = 0$ ,${\lambda _4} = - {v_1}$ ，其中${\lambda _1}$ 和${\lambda _2}$ 代表准P波沿$X$ 轴负方向和正方向传播的特征速度[24]。设${\boldsymbol{ \varLambda} _{\boldsymbol{A}}}$ 为矩阵${\boldsymbol{A}}$ 的相似对角矩阵，矩阵${\boldsymbol{P}}$ 为特征向量组成的矩阵，则矩阵${\boldsymbol{A}}$ 可以表示为：$$ {\boldsymbol{A}} = {\boldsymbol{P}}_{\boldsymbol{A}}^{{{ - 1}}}{{\boldsymbol{\varLambda }}_{\boldsymbol{A}}}{{\boldsymbol{P}}_{\boldsymbol{A}}}\text{，} $$ (19) $$ {{\boldsymbol{\varLambda }}_{\boldsymbol{A}}} = {\boldsymbol{\varLambda }}_{\boldsymbol{A}}^{\boldsymbol{ + }} + {\boldsymbol{\varLambda }}_{\boldsymbol{A}}^{\boldsymbol{ - }}\text{，} $$ (20) $$ {({\boldsymbol{\varLambda }}_{\boldsymbol{A}}^{\boldsymbol{ + }})_{ij}} = \frac{{{{({{\boldsymbol{\varLambda }}_{\boldsymbol{A}}})}_{ij}} + \left| {{{({{\boldsymbol{\varLambda }}_{\boldsymbol{A}}})}_{ij}}} \right|}}{2}\text{，} $$ (21) $$ {({\boldsymbol{\varLambda }}_{\boldsymbol{A}}^ - )_{ij}} = \frac{{{{({{\boldsymbol{\varLambda }}_{\boldsymbol{A}}})}_{ij}} - \left| {{{({{\boldsymbol{\varLambda }}_{\boldsymbol{A}}})}_{ij}}} \right|}}{2}。 $$ (22) 同理矩阵
${\boldsymbol{B}}$ 也有类似的形式，则方程（17）可写成：$$ \frac{{\partial {\boldsymbol{U}}}}{{\partial t}} = \Big({\boldsymbol{P}}_{\boldsymbol{A}}^{ - 1}{\boldsymbol{\varLambda }}_{\boldsymbol{A}}^{\boldsymbol{ + }}{{\boldsymbol{P}}_{\boldsymbol{A}}} + {\boldsymbol{P}}_{\boldsymbol{A}}^{ - 1}{\boldsymbol{\varLambda }}_{\boldsymbol{A}}^{\boldsymbol{ - }}{{\boldsymbol{P}}_{\boldsymbol{A}}}\Big)\frac{{\partial {\boldsymbol{U}}}}{{\partial x}} + \Big({\boldsymbol{P}}_{\boldsymbol{B}}^{ - 1}{\boldsymbol{\varLambda }}_{\boldsymbol{B}}^{\boldsymbol{ + }}{{\boldsymbol{P}}_{\boldsymbol{B}}} + {\boldsymbol{P}}_{\boldsymbol{B}}^{ - 1}{\boldsymbol{\varLambda }}_{\boldsymbol{B}}^{\boldsymbol{ - }}{{\boldsymbol{P}}_{\boldsymbol{B}}}\Big)\frac{{\partial {\boldsymbol{U}}}}{{\partial z}}。 $$ (23) 将上式等号右边第1项分解为
${\boldsymbol{P}}_{\boldsymbol{A}}^{ - 1}{\boldsymbol{\varLambda }}_{\boldsymbol{A}}^{\boldsymbol{ + }}{{\boldsymbol{P}}_{\boldsymbol{A}}}\displaystyle\dfrac{{\partial {\boldsymbol{U}}}}{{\partial x}}$ 和${\boldsymbol{P}}_{\boldsymbol{A}}^{ - 1}{\boldsymbol{\varLambda }}_{\boldsymbol{A}}^{\boldsymbol{ - }}{{\boldsymbol{P}}_{\boldsymbol{A}}}\displaystyle\dfrac{{\partial {\boldsymbol{U}}}}{{\partial x}}$ ，表示了准P波向$X$ 轴负方向和正方向传播的左行准P波和右行准P波。则左边界条件为：
$$ \frac{{\partial {\boldsymbol{U}}}}{{\partial t}} = {{\boldsymbol{A}}}+\frac{{\partial {\boldsymbol{U}}}}{{\partial x}} + {\boldsymbol{B}}\frac{{\partial {\boldsymbol{U}}}}{{\partial z}}。 $$ (24) 将公式（24）消去
${\sigma _{xx}}$ 和${\sigma _{zz}}$ ，并根据${v_x} = {{\partial {u_x}} \mathord{\left/ {\vphantom {{\partial {u_x}} {\partial t}}} \right. } {\partial t}}$ 和${v_z} = {{\partial {u_z}} \mathord{\left/ {\vphantom {{\partial {u_z}} {\partial t}}} \right. } {\partial t}}$ ，可以得出：$$ \left\{ {\begin{aligned} & {\frac{{{\partial ^2}{u_x}}}{{\partial {t^2}}} = {v_1}\frac{{{\partial ^2}{u_x}}}{{\partial x\partial t}} + \frac{{v_2^2}}{2}\frac{{{\partial ^2}{u_z}}}{{\partial x\partial z}}} \\ & {\frac{{{\partial ^2}{u_z}}}{{\partial {t^2}}} = \frac{{v_2^2}}{{{v_1}}}\frac{{{\partial ^2}{u_x}}}{{\partial z\partial t}} + v_3^2\frac{{{\partial ^2}{u_z}}}{{\partial {z^2}}}} \end{aligned}} \right.。 $$ (25) 方程组（25）中代入平面波方程
$U = A{\exp\Big({i({k_x}x + {k_z}z - \omega t)}}\Big)$ ，可得：$$ \left( {\begin{array}{*{20}{c}} {{v_1}\omega {k_x} - {\omega ^2}}&{\displaystyle\frac{{v_2^2}}{2}{k_x}{k_z}} \\ {\displaystyle\frac{{v_2^2}}{{{v_1}}}\omega {k_z}}&{v_3^2k_z^2 - {\omega ^2}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{A_x}} \\ {{A_z}} \\ \end{array}} \right) = 0。 $$ (26) 求解方程（26）可得：
$$ {\omega ^4} = {v_1}{\omega ^3}{k_x} + v_3^2{\omega ^2}k_z^2 - \frac{{2v_1^2v_3^2 - v_2^4}}{{2{v_1}}}\omega {k_x}k_z^2。 $$ (27) 对方程（27）两边乘以准P波的频率-波数域波场值
$p({k_x},{k_z},\omega )$ ，再对方程两边进行${k_x}$ 和${k_z}$ 的傅里叶逆变换，可得左边界的频率-空间域吸收边界条件：$$ {\omega ^4}F + i{\omega ^3}{v_1}\frac{{\partial F}}{{\partial x}} + v_3^2{\omega ^2}\frac{{{\partial ^2}F}}{{\partial {z^2}}} + i\omega \frac{{2v_1^2v_3^2 - v_2^4}}{{2{v_1}}}\frac{{{\partial ^3}F}}{{\partial x\partial {z^2}}} = 0。 $$ (28) 同理可得其余3条边界和4个角点的边界条件方程：
$$ \left\{\begin{aligned} &{\omega }^{4}F-i{\omega }^{3}{v}_{1}\frac{\partial F}{\partial x}+{v}_{3}^{2}{\omega }^{2}\frac{{\partial }^{2}F}{\partial {z}^{2}}-i\omega \frac{2{v}_{1}^{2}{v}_{3}^{2}-{v}_{2}^{4}}{2{v}_{1}}\frac{{\partial }^{3}F}{\partial x\partial {z}^{2}}=0\text{，}右边界\\ &{\omega }^{4}F+{\omega }^{2}{v}_{1}^{2}\frac{\partial F}{\partial x}+i{v}_{3}{\omega }^{3}\frac{\partial F}{\partial z}+i\omega \frac{2{v}_{1}^{2}{v}_{3}^{2}-{v}_{2}^{4}}{2{v}_{1}}\frac{{\partial }^{3}F}{\partial {x}^{2}\partial z}=0\text{，}上边界\\ &{\omega }^{4}F+{\omega }^{2}{v}_{1}^{2}\frac{\partial F}{\partial x}-i{v}_{3}{\omega }^{3}\frac{\partial F}{\partial z}-i\omega \frac{2{v}_{1}^{2}{v}_{3}^{2}-{v}_{2}^{4}}{2{v}_{1}}\frac{{\partial }^{3}F}{\partial {x}^{2}\partial z}=0\text{，}下边界\\ &{\omega }^{4}F+i{\omega }^{3}{v}_{1}\frac{\partial F}{\partial x}+i{v}_{3}{\omega }^{3}\frac{\partial F}{\partial z}-{\omega }^{2}\frac{2{v}_{1}^{2}{v}_{3}^{2}-{v}_{2}^{4}}{2{v}_{1}}\frac{{\partial }^{2}F}{\partial x\partial z}=0\text{，}左上角\\ &{\omega }^{4}F-i{\omega }^{3}{v}_{1}\frac{\partial F}{\partial x}+i{v}_{3}{\omega }^{3}\frac{{\partial }^{2}F}{\partial {z}^{2}}+{\omega }^{2}\frac{2{v}_{1}^{2}{v}_{3}^{2}-{v}_{2}^{4}}{2{v}_{1}}\frac{{\partial }^{2}F}{\partial x\partial z}=0\text{，}右上角\\ &{\omega }^{4}F+i{\omega }^{3}{v}_{1}\frac{\partial F}{\partial x}-i{v}_{3}{\omega }^{3}\frac{{\partial }^{2}F}{\partial {z}^{2}}+{\omega }^{2}\frac{2{v}_{1}^{2}{v}_{3}^{2}-{v}_{2}^{4}}{2{v}_{1}}\frac{{\partial }^{2}F}{\partial x\partial z}=0\text{，}左下角\\ &{\omega }^{4}F-i{\omega }^{3}{v}_{1}\frac{\partial F}{\partial x}-i{v}_{3}{\omega }^{3}\frac{{\partial }^{2}F}{\partial {z}^{2}}-{\omega }^{2}\frac{2{v}_{1}^{2}{v}_{3}^{2}-{v}_{2}^{4}}{2{v}_{1}}\frac{{\partial }^{2}F}{\partial x\partial z}=0\text{，}右下角\end{aligned} 。\right. $$ (29) 3. 数值模拟实例与边界效果分析
为了验证边界条件的效果，建立均匀VTI介质模型，模型参数设置如下：模型大小700 m×700 m，准P波速度
${V_{{\rm{P}}0}}$ =2500 m/s，网格间距10 m，时间采样间隔2 ms，时间采样点数512，震源位于（350 m，350 m），采用50 Hz雷克子波，边界厚度100 m，$\rho $ 为1.7，$\varepsilon $ 为0.255，$\delta $ 为0.32。采用频率-空间域有限差分法对设定的模型进行地震波场数值模拟，并在匹配层区域同时施加CPML吸收边界和特征分析法边界形成组合边界来压制边界反射。图2为未加边界时50 Hz单频波快照图2（a）和150 ms时间域波前快照图2（b）。由图2可以看出，未施加边界条件时产生了强烈的边界反射，由于入射波和产生的边界反射相互影响，单频波快照中波形抖动剧烈，时间域波前快照中无法明确地显示出波前。
![]()
图 2 未加边界时的50 Hz单频波快照（a）和时间域150 ms波前快照（b）Figure 2. 50 Hz single frequency snapshot (a) and 150 ms wavefront snapshot (b) without boundary attenuation in time domain图3为施加特征分析法边界后的50 Hz单频波快照图3（a）和150 ms时间域波前快照图3（b）。由图3可以看出，在施加吸收边界之后，在单频波快照中可以看到抖动现象，时间域波前快照中箭头所指位置可以看到明显的边界反射。
![]()
图 3 施加特征分析法边界衰减后的50 Hz单频波快照（a）和150 ms时间域波前快照（b）Figure 3. 50 Hz single frequency snapshot (a) and 150 ms wavefront snapshot (b) with the boundary attenuation of characteristic analysis method in time domain图4为施加PML与特征分析法的组合边界后50 Hz单频波快照图4（a）和150 ms时间域波前快照图4（b），由图4可以看出，单频波快照中的抖动现象很弱，几乎看不到抖动，时间域波前快照上箭头所指位置能看到边界反射减弱。
![]()
图 4 施加PML和特征分析组合边界后的50 Hz单频波快照（a）和150 ms时间域波前快照（b）Figure 4. 50 Hz single frequency snapshot (a) and 150 ms wavefront snapshot (b) with the combination absorption boundary of PML and characteristic analysis method in time domain图5为施加CPML与特征分析法的组合边界条件后的50 Hz单频波快照图5（a）和150 ms时间域波前快照图5（b），由图5可以看出，当采用本文所提的组合边界时，单频波快照更清晰光滑，时间域波前快照上基本看不到边界反射回来的能量。
![]()
图 5 施加CPML和特征分析的组合边界后的50 Hz单频波快照（a）和150 ms时间域波前快照（b）Figure 5. 50 Hz single frequency snapshot (a) and 150 ms wavefront snapshot (b) with the combination absorption boundary of CPML and characteristic analysis method in time domain4. 结论
本文提出CPML与特征分析法结合的组合边界条件，并将此组合边界应用在VTI介质准P波的频率-空间域数值模拟中，通过模拟实验可以得出该组合边界能有效地减少边界反射，提高数值模拟精度，证明该组合边界是一种适合频率域数值模拟的吸收边界条件。
-
![]()
图 2 未加边界时的50 Hz单频波快照（a）和时间域150 ms波前快照（b）
Figure 2. 50 Hz single frequency snapshot (a) and 150 ms wavefront snapshot (b) without boundary attenuation in time domain
![]()
图 3 施加特征分析法边界衰减后的50 Hz单频波快照（a）和150 ms时间域波前快照（b）
Figure 3. 50 Hz single frequency snapshot (a) and 150 ms wavefront snapshot (b) with the boundary attenuation of characteristic analysis method in time domain
![]()
图 4 施加PML和特征分析组合边界后的50 Hz单频波快照（a）和150 ms时间域波前快照（b）
Figure 4. 50 Hz single frequency snapshot (a) and 150 ms wavefront snapshot (b) with the combination absorption boundary of PML and characteristic analysis method in time domain
-
[1] 戚艳平. 三维VTI介质qP波正演方法研究[D]. 东营: 中国石油大学(华东), 2008. QI Y P. The Study on qP wave forward modeling methods in 3D VTI media[D]. Dongying: China University of Petroleum (East China), 2008. (in Chinese).
[2] BERENGER J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185−200. doi: 10.1006/jcph.1994.1159
[3] BERENGER J P. Application of the CFS-PML to the absorption of evanescent waves in waveguides[J]. IEEE Microwave and Wireless Components Letters, 2002, 12(6): 218−220. doi: 10.1109/LMWC.2002.1010000
[4] BERENGER J P. Numerical reflection from FDTD-PMLs: A comparison of the split PML with the unsplit and CFS PMLs[J]. IEEE Transactions on Antennas and Propagation, 2002, 50(3): 258−265. doi: 10.1109/8.999615
[5] 罗玉钦, 刘财. 近似完全匹配层边界条件吸收效果分析及衰减函数的改进[J]. 石油地球物理勘探, 2018,53(5): 903−913,879. DOI: 10.13810/j.cnki.issn.1000-7210.2018.05.003. LUO Y Q, LIU C. Absorption effects in nearly perfectly matched layers and damping factor improvement[J]. Oil Geophysical Prospecting, 2018, 53(5): 903−913,879. DOI: 10.13810/j.cnki.issn.1000-7210.2018.05.003. (in Chinese).
[6] 李青阳, 吴国忱, 梁展源. 基于PML边界的时间高阶伪谱法弹性波场模拟[J]. 地球物理学进展, 2018,33(1): 228−235. LI Q Y, WU G C, LIANG Z Y. Time domain high-order pseudo spectral method based on PML boundary for elastic wavefield simulation[J]. Progress in Geophysics, 2018, 33(1): 228−235. (in Chinese).
[7] 谢志南, 郑永路, 章旭斌, 等. 弱形式时域完美匹配层—滞弹性近场波动数值模拟[J]. 地球物理学报, 2019,62(8): 3140−3154. XIE Z N, ZHENG Y L, ZHANG X B, et al. Weak-form time-domain perfectly matched layer for numerical simulation of viscoelastic wave propagation in infinite-domain[J]. Chinese Journal of Geophysics, 2019, 62(8): 3140−3154. (in Chinese).
[8] 张衡, 刘洪, 李博, 等. VTI介质声波方程非分裂式PML吸收边界条件研究[J]. 石油物探, 2016,55(6): 781−792. ZHANG H, LIU H, LI B, et al. The research on unsplit PML absorbing boundary conditions of acoustic equation for VTl media[J]. Geophysical Prospecting for Petroleum, 2016, 55(6): 781−792. (in Chinese).
[9] 马锐, 邹志辉, 芮拥军,等. 基于SPML和海绵边界的伪谱法弹性波模拟复合吸收边界条件[J]. 石油物探, 2018,57(1): 94−103. MA R, ZOU Z H, RUI Y J, et al. A composite absorbing boundary based on the SPML and sponge absorbing boundary for pseudo-spectral elastic wave modeling[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 94−103. (in Chinese).
[10] CHEW W C, LIU Q H. Perfectly matched layers for elastodynamics: A new absorbing boundary condition[J]. Journal of Computational Acoustics, 1996, 4(4): 341−359. doi: 10.1142/S0218396X96000118
[11] WANG T L, TANG X M. Finite-difference modeling of elastic wave propagation: A nonsplitting perfectly matched layer approach[J]. Geophysics, 2003, 68(5): 1749−1755. doi: 10.1190/1.1620648
[12] 方修政, 钮凤林. 二阶声波方程非分裂式CPML实施新方法[J]. 中国科学: 地球科学, 2021,51(8): 1341−1354. doi: 10.1360/SSTe-2021-0012 FANG X Z, NIU F L. A new implementation method of non splitting CPML for second-order acoustic equation[J]. Scientia Sinica Terrae, 2021, 51(8): 1341−1354. (in Chinese). doi: 10.1360/SSTe-2021-0012
[13] KUZUOGLU M, MITTRA R. Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers[J]. IEEE Microwave and Wireless Components Letters, 1996, 6(12): 447−449.
[14] RODEN J A, GEDNEY S D. Convolution PML (CPML): An efficient FDTD implementation of the CFS-PML for arbitrary media[J]. Microwave and Optical Technology Letters, 2000, 27(5): 334−339. doi: 10.1002/1098-2760(20001205)27:5<334::AID-MOP14>3.0.CO;2-A
[15] DROSSAERT F H, GIANNOPOULOS A. A nonsplit complex frequency-shifted PML based on recursive integration for FDTD modeling of elastic waves[J]. Geophysics, 2007, 72(2): T9−T17. doi: 10.1190/1.2424888
[16] DROSSAERT F H, GIANNOPOULOS A. Complex frequency shifted convolution PML for FDTD modelling of elastic waves[J]. Wave Motion, 2007, 44(7): 593−604.
[17] CHEN H M, ZHOU H, LI Y Q. Application of unsplit convolutional perfectly matched layer for scalar arbitrarily wide-angle wave equation[J]. Geophysics, 2014, 79(6): T313−T321. doi: 10.1190/geo2014-0103.1
[18] MA X, YANG D H, HUANG X Y, et al. Nonsplit complex-frequency shifted perfectly matched layer combined with symplectic methods for solving second-order seismic wave equations — Part 1: Method[J]. Geophysics, 2018, 83(6): T301−T311. doi: 10.1190/geo2017-0603.1
[19] MA X, YANG D H, HE X J, et al. Nonsplit complex-frequency-shifted perfectly matched layer combined with symplectic methods for solving second-order seismic wave equations — Part 2: Wavefield simulations[J]. Geophysics, 2019: T167−T179.
[20] MA X, LI Y J, SONG J X. A stable auxiliary differential equation perfectly matched layer condition combined with low-dispersive symplectic methods for solving second-order elastic wave equations[J]. Geophysics, 2019: T193−T206.
[21] 吴国忱, 梁锴. VTI介质准P波频率空间域组合边界条件研究[J]. 石油物探, 2005,44(4): 301−307, 15. WU G C, LIANG K. Combined boundary conditions of quasi-P wave within frequency-space domin in VTI media[J]. Geophysical Prospecting for Petroleum, 2005, 44(4): 301−307, 15. (in Chinese).
[22] 吴国忱. 各向异性介质地震波传播和成像[M]. 东营: 中国石油大学出版社, 2006. WU G C. Seismic wave propagation and imaging in anisotropic media[M]. Dongying: China University of Petroleum Press, 2006. (in Chinese).
[23] 董良国. 地震波数值模拟与反演中的几个关键问题研究[D]. 上海: 同济大学, 2003. DONG L G. Research on several key problems in seismic wave numerical simulation and inversion[D]. Shanghai: Tongji University, 2003. (in Chinese).
[24] 李桂花, 林年添, 杨思通, 等. 井间地震高分辨率数值模拟方法及波场特征研究[M]. 徐州: 中国矿业大学出版社, 2017. LI G H, LIN N T, YANG S T, et al. Study on high resolution numerical simulation method and wave field characteristics of crosswell seismic[M]. Xuzhou: China University of mining and Technology Press, 2017. (in Chinese).
[25] 张奎涛, 顾汉明, 刘少勇, 等. 基于CPML-RML组合边界条件粘弹TTI介质旋转交错网格有限差分正演模拟[J]. 石油物探, 2019,58(2): 187−198, 218. ZHANG K T, GU H M, LIU S Y, et al. Rotated staggered grid finite difference forward modeling for wave propagation in viscoelastic TTI media based on CPML-RML combined boundary condition[J]. Geophysical Prospecting for Petroleum, 2019, 58(2): 187−198, 218. (in Chinese).
下载:
计量
- 文章访问数: 364
- HTML全文浏览量: 137
- PDF下载量: 63
