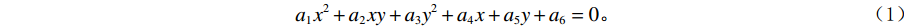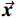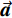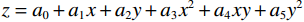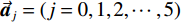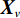随着工业技术与数字技术的不断发展，在工业4.0建设要求的不断推进下，传统的生产模式已经发生了根本性的变化，在生产过程中对产品进行实时数字化观察显得十分重要，工业用X射线计算机断层成像（X-ray computed tomography，X-CT），在晶体生长、工件装配等领域都有着重要的应用。

在晶体生长领域，单晶体的制备过程主要采用Bridgman晶体生长方法^[1]，由于锥部生长过程中晶界的出现和冷却过程中裂纹的出现，使大尺寸、高纯单晶沿选择取向生长极为困难。对于这些问题，Tandjaoui等^[2]开发了一种使用X射线成像技术观察多晶硅生成过程中的固液界面的装置，在ESRF（欧洲同步辐射装置）的BM05光束线上用同步辐射X射线照相术研究了固/液界面的形态，图像空间的分辨率为15 μm；Dong等^[3]利用X光成像技术对铝锌合金定向凝固过程中固液界面形态转变过程进行了二维和三维原位观察。

X-CT技术是一种集自动控制、机械、光电、计算机图像处理等于一体的无损检测技术，它以图像方式，直观、清晰地呈现被测物质（体）的内部结构等信息，用于检测物体内部的缺陷，如空洞、裂隙等，在材料科学、航空航天、核工业、机械工业、地质及考古等领域具有重要的应用价值。在测量方面，工业CT也可以无损地获取物体的内部形态，有助于获取内部的几何参数。

二次曲面是在三维坐标系(x,y,z)下三元二次代数方程对应的所有图形的统称。在欧氏三维空间里坐标x, y, z之间的二次方程（系数为实数，且二次项系数不全为零）所表示的曲面，最常见的二次曲面是球面、直圆柱面和直圆锥面，此外，二次曲面还包括椭球面、双曲面和抛物面。二次曲面也是工程中常见的一种曲面，例如在晶体生长中，因为晶体的类型、生长工艺以及相关因素影响，界面呈现微凸^[4]或者微凹^[5]的曲面形式。

在二次曲面拟合方面，曹冰等^[6]利用基于曲率小波变换的多尺度分析方法，消除大量冗余信息，提高轮廓的提取效率，为三维重构提供了条件。传统曲面拟合算法一般采用Lukács等^[7]提出的针对给定类型的二次曲面拟合方法，使用迭代法最小化目标函数进行求解，迭代速度较慢。邹斌等^[8]提出了工业CT图像管道拟合，利用Facet模型提取管道边缘的基础上，将三维圆柱面、椭圆柱面管道的拟合转化为中心轴截面上的二维轮廓曲线圆、椭圆的拟合，得到了较好的结果。

在用序列断层图像重构工业CT三维图像的过程中，一般要把目标物体从断层图像中分离出来，然后重构物体的三维模型^[9]，因此，能否准确分割目标物体会直接影响到三维重构图像的质量。目前人们已经提出了各种类型的分割方法，比较常用的方法有阈值比较法^[10]、区域生长法^[11]、像素迭代聚类法^[12]等。近年来，卷积神经网络在计算机视觉方面取得了重大进展，Shelhamer等^[13]提出了全卷积神经网络（fully convolutional network，FCN）之后，基于此网络的各种变形，U-net^[14]、PSPNet^[15]、Deeplab^[16-18]等网络解决了FCN存在的细节不清晰、缺乏空间一致性等问题，其中U-net在医学图像分割领域表现出了强大的实力。

本文提出一种用于工业CT图像的二次曲面拟合算法，并通过实验证明所提出的方法的有效性。

1.   方法

1.1   模体设计及实验方法

为了研究用于工业CT图像的二次曲面拟合算法，实验中使用X射线CT系统对二次曲面进行观察。要想得到较好的观察结果，需要射线具有足够高的能量保证能够穿透样品。经过计算，采用最高电压为450 kV的X射线源工业CT。

本文通过仿真进行前期验证。设计感兴趣区域为直径150 mm，高14.6 mm，曲面曲率为1/200的球弧面，感兴趣区域上方为线吸收率与感兴趣区域相差较小的背景物质，二者由厚度为15 mm的外围材料紧密包裹，最外层为5 mm厚的高吸收率物质。创建三维模体模拟这个系统，模体中每个体素的值为该位置元素的吸收率，具体数值与每个体素对应的实际大小有关，在本次仿真中，为获得较好的效果，设置每个体素对应0.1 mm。模体如图1所示。

图  1  模体示意图

Figure  1.  Schematic of the model

下载: 全尺寸图片 幻灯片

1.2   二次曲面提取与拟合

在CT重建出包含物体内部信息的三维图像序列后，感兴趣区域与背景之间的分界面为需要拟合的二次曲面。为了在三维空间获得完整的二次曲面，需要对CT重建出的图像序列进行分割。

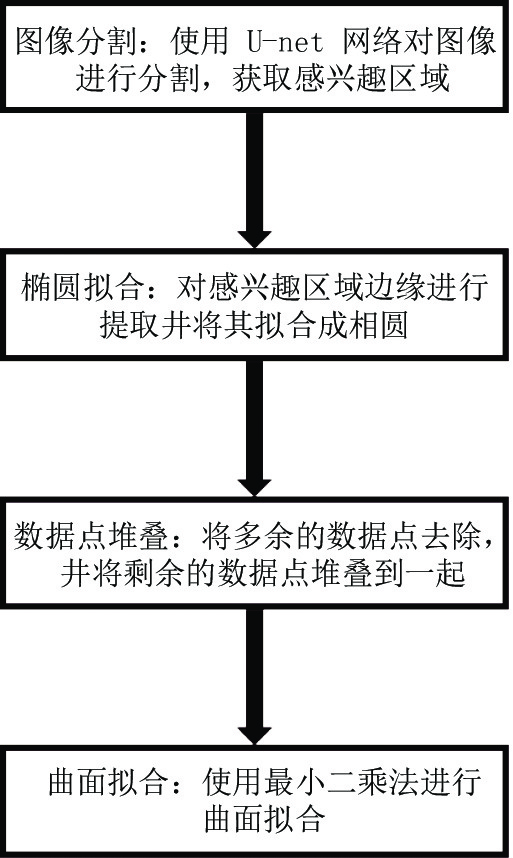
受CT成像分辨率和部分容积效应的影响，难以精确定位二次曲面的最高点，而曲面中远离最高点的部位重建相对准确，因此这里避开二次曲面的最顶端，重点采集下部的数据，使用基于最小二乘法的曲面拟合算法将曲面拟合成一个多项式，这样可以利用除顶部之外部分的信息来推断整个曲面的形态信息。如图2所示，整个拟合流程分为以下4个步骤。

图  2  拟合流程图

Figure  2.  Fitting process

下载: 全尺寸图片 幻灯片

（1）图像分割：将三维图像序列中每一层的感兴趣区域分割出来，得到二值化分割图。

（2）椭圆拟合：使用边界跟踪算法提取每层分割图中感兴趣区域的边缘，对提取到的边缘使用基于直接最小二乘椭圆拟合算法，得到每层拟合的椭圆边界点。

（3）数据点堆叠：精简椭圆边界数据，剔除误差过大的数据点。保留下来的椭圆数据是一组二维序列图，需要根据1 mm的层间距给每层赋以高度值，最终得到二次曲面的三维点集。

（4）曲面拟合：使用基于最小二乘法的曲面拟合算法获得二次曲面。

在工业应用中，需要检测的材料往往尺寸较大且密度较高，X射线难以穿透，导致CT重建图像噪声较高，且工件装配中结合紧密，传统算法（如阈值分割法、区域生长法等）难以很好地将外壳与材料分开。当前各种基于深度学习的图像处理方法成为研究热点，在图像分割领域，卷积神经网络（convolutional neural networks，CNNs）具有许多传统算法不具备的优势，其中U-net是一种效果优异的轻量化卷积网络，可以实现对二次曲面快速准确分割。

考虑到不同层的CT图像可能会受到不同程度噪声的干扰，因此在拟合出每层的椭圆数据点之后需要对数据进行精简。针对本文任务，这里设计了一种剔除重复与病态数据的精简算法，在提高拟合精度的同时大大降低了计算复杂度，精简算法在2.1节中详细介绍。

1.3   U-net图像分割网络

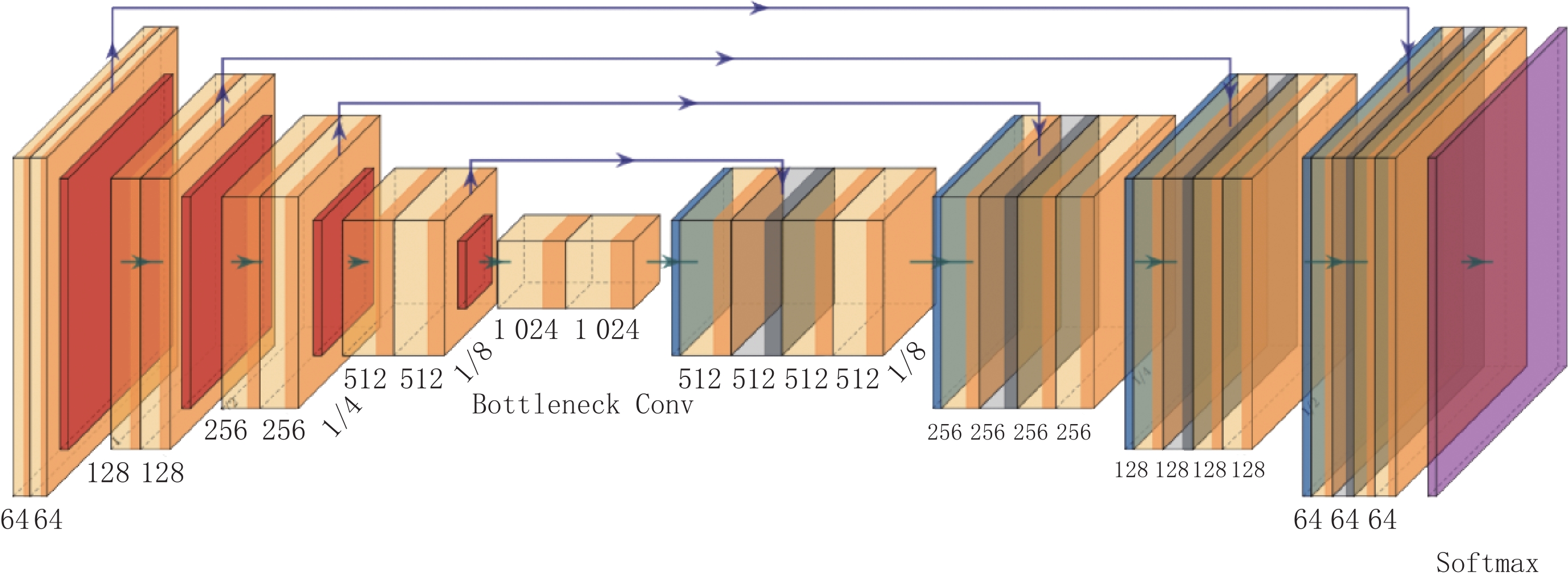
U-net网络在FCN基础上发展来，本文研究工作使用的U-net网络的结构如图3所示。U-net由下采样和上采样两部分组成，其中VGG16作为下采样的骨干网络，每步下采样由一组卷积（由两个不进行填充的3×3卷积层组成）、一个激活函数和一个步长为2的2×2最大池化层组成，其中激活函数通常使用ReLU（rectified linear unit，ReLU）。这样，每对特征图进行一步下采样操作，特征图的分辨率都会下降一倍，通道数提升一倍。在进行4次下采样后，采用1×1卷积代替VGG16中的全连接层，经过两次1×1卷积层后进行上采样。上采样可以看作是下采样的逆运算，使用反卷积代替下采样过程中的最大池化层，实现特征图分辨率的倍增。与此同时，U-net网络将上下采样过程中尺寸相同的特征图进行跨越连接，能够有效避免训练过程中的梯度消失。

图  3  U-net网络结构图

Figure  3.  U-net network structure diagram

下载: 全尺寸图片 幻灯片

对于语义分割网络来说，网络的结构越复杂，特征提取能力越强，能够获得更大的感受野。一般来说，网络的浅层部分更容易关注输入图像的纹理信息，而深层部分会获取更加高维的特征信息。在本文任务中，纹理信息更为重要，利用跨越连接的结构可以让网络在上采样过程中依然能够关注到纹理信息。众所周知，当卷积网络进行下采样时，一定会损失某些纹理信息，丢失的信息无法在上采样过程中获得，但是U-net网络的跨越连接能够使特征图在上采样过程中不断地从前序网络中获得丢失的纹理信息。

本文所涉及到的图像语义内容较为简单，不同图像中的物体组成结构比较固定，不需要对信息进行过多的过滤，所有细节信息的重要程度大致相同，使用跨越连接结构可以将高级和低级的特征都利用上。同时网络结构较为简单，在面对较小的数据集时基本不会出现过拟合。

1.4   最小二乘法拟合

最小二乘法（least square method，LSM）通过最小化误差的平方和寻找数据的最优函数匹配。本文使用最小二乘法进行椭圆拟合与曲面拟合^[19]。

椭圆方程可以用以下二阶多项式来表示：

令$ \vec {\boldsymbol{a}} = \left( {{a_1},\;{a_2},\;{a_3},\;{a_4},\;{a_5},\;{a_6}} \right) $，$\vec {\boldsymbol{x}} = {\left( {{x^2},\,xy,\;{y^2},\;x,y,\;1} \right)^{\rm{T}}}$，方程可以表示为$\vec {\boldsymbol{a}}\vec {\boldsymbol{x}} = 0$，所以拟合椭圆的最优化问题可以表示为：

其中$\vec {\boldsymbol{x}}$表示数据样本集合，矩阵维度为6×n，每列表示1个样本。$\vec {\boldsymbol{a}}$表示椭圆方程的参数。为了避免出现$\vec {\boldsymbol{a}} = \vec 0$这种无意义的解，需要对参数添加约束条件。

在拟合曲面时，选择二次方程$z = {a_0} + {a_1}x + {a_2}y + {a_3}{x^2} + {a_4}xy + {a_5}{y^2}$作为待拟合曲面的标准方程。对样本数据集中观测点计算误差平方并求和为：

为了寻找最优化的多项式参数${\vec {\boldsymbol{a}}_j} = \left( {j = 0,1,2,\cdots,5} \right)$估计值，对于给定的观测点求解误差平方和取最小值的参数。通过构建对应的范德蒙矩阵${{\boldsymbol{X}}_v}$，利用矩阵运算求得所求的参数：

2.   实验与结果讨论

2.1   数据采集与处理

仿真实验参考COMET MXR-451 X射线管（管电压450 kV，钨阳极，固有过滤量为2.3 mm Fe和1.0 mm Cu，光子能量主要分布在200 keV到450 keV^[20]），这里选择多个能级进行仿真，每个能级的光子数由射线源的光子光谱决定。探测器采用像素宽度为2 mm的线阵探测器，射线源到物体中心点的距离为1650 mm，射线源到探测器的距离为1950 mm，等效像素大小约为0.167 mm。采样间隔为1°，采样角度为360°。仿真实验采用扇形束，通过上下移动射线源与探测器进行多次扫描，获取三维物体不同位置的断层图像，每次移动间隔1 mm，从上到下共获取20组投影。为模拟实际情况，需要在投影数据中添加噪声，首先在正弦图中添加泊松噪声，模拟光子受量子效应到达探测器表面的统计涨落；在正弦图中添加高斯噪声，模拟探测器电路的电子噪声。

CT图像使用滤波反投影重建算法（filtered back projection，FBP）进行重建，每层图像的大小为2048×2048，共20层。

对模体进行多次仿真扫描和重建，使用其中一组数据对U-net网络进行训练。为了增强网络训练的鲁棒性，需要对训练数据进行预处理。

预处理流程如图4所示，首先对图像按照随机比例进行缩放，缩放的比例从0.5到2.0按步长0.25随机挑选；之后对图像进行随机翻转（random flip），一般来讲有两种翻转方式，水平翻转与上下翻转；最后对图像进行随机裁剪（random crop），目的是使得输入到网络中的图像固定在相同大小。

图  4  数据预处理流程图

Figure  4.  Data preprocessing process

下载: 全尺寸图片 幻灯片

通过上述数据预处理对训练数据进行扩充，共计得到1120张训练图。设置批大小（batch-size）为8，初始学习率（learning-rate，LR）为0.01，使用poly学习率降低策略，经过14000个循环的训练后，网络收敛，在随机划分的测试集上平均交并比（mIoU）达到了0.9439，在另外两组数据上测试，网络泛化性较好。

由于CT成像分辨率和部分容积效应的影响，在重建靠近曲面顶部的区域时会出现严重的误差。同时，由于系统误差和随机误差的影响，获得的CT数据包含一定的噪声与伪影，所以在进行数据点堆叠的时候，如果不将干扰过大的数据去除，那么拟合出来的曲面参数将会受到很大影响。为了保证能够将受到干扰的数据排除在拟合数据之外，对CT每层拟合出的椭圆参数进行比较，处理流程如下：

（1）对所有椭圆的圆心坐标求取平均值。

（2）将圆心偏离平均圆心坐标值过大的层去除。

（3）椭圆的长短轴长度由上而下逐渐增大，求每两层之间椭圆长短轴长度的差值，当某层与上一层的差值小于一定像素，且与后续层数之间均小于一定像素时，视为达到最大直径，将后续层数的数据去除。

2.2   实验结果

使用训练好的U-net图像分割网络对获取的断层图像进行分割，以第9层CT图像以及纵向剖面图为例，分割结果如图5所示。

图  5  U-net分割结果图

Figure  5.  U-net segmentation result

下载: 全尺寸图片 幻灯片

通过观察分割得到的图像与原图的叠加结果，发现网络的分割效果较好，可以完整地将感兴趣区域分割出来。

区域生长法是一种经典的图像分割算法，下面使用区域生长算法与U-net进行比较。分别设置生长的阈值为2、3和4，得到分割结果如图6所示。

图  6  区域生长分割结果图

Figure  6.  Region growing segmentation results

下载: 全尺寸图片 幻灯片

可以看到阈值的选取对区域生长算法结果影响较大，其分割效果和算法普适性均不如U-net。分割结果为二值化灰度图，使用Canny算子对图像进行边缘检测。得到边缘检测结果如图7所示。

图  7  边缘检测结果图

Figure  7.  Edge detection result graphs

下载: 全尺寸图片 幻灯片

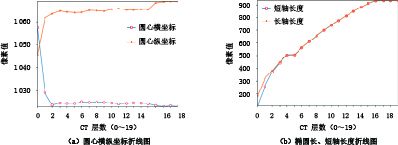
对边缘检测得到的数据点进行椭圆拟合，使用基于最小二乘法的椭圆拟合算法，将每层模体的边缘拟合成椭圆，得到每层椭圆的圆心位置与长、短轴长度，统计如图8所示。

图  8  椭圆拟合结果图

Figure  8.  Ellipse fitting result diagrams

下载: 全尺寸图片 幻灯片

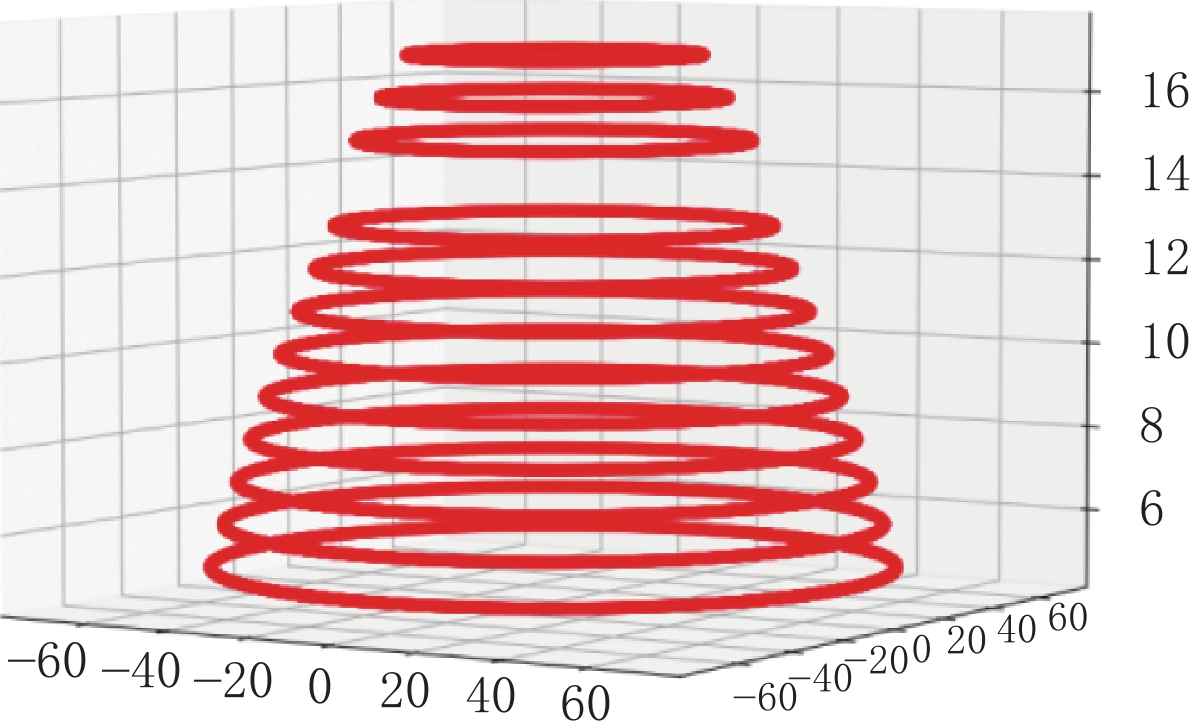
可以看到，每层椭圆的圆心位置基本不变，且离心率都接近于0，椭圆的长短轴长度逐层加，最终趋于不变，但在中间层也出现了长度不变的情况（不变层），因此在堆叠数据时需要对其进行精简。同时模体底部为柱状稳定层，会影响拟合精度，因此需要去除，然后得到堆叠后的三维点集如图9所示。

图  9  三维点集图

Figure  9.  3D point set diagram

下载: 全尺寸图片 幻灯片

对三维点集进行最小二乘曲面拟合，对比不进行中间不变层去除和不进行底部稳定层去除的曲面拟合结果，得到结果如表1所示。

表  1  拟合结果

Table  1.  Fitting results

数据精简方式	曲面高度Δh/mm				曲面曲率δ/％
	模体值	拟合值	相对误差/％		模体值	拟合值	相对误差/％
进行异常数据剔除	14.6	14.67	0.40		0.0973	0.0978	0.40
不进行不变层去除	14.6	15.04	3.01		0.0973	0.1002	3.01
不进行稳定层去除	14.6	13.39	8.29		0.0973	0.0892	8.29

下载: 导出CSV 

| 显示表格

拟合结果与实际曲面的误差在1％ 以内。误差可能由几种原因造成：①由于模型的尺寸较大且所用的材料吸收率较高，X射线难以穿透导致重建图噪声较大，对图像处理过程产生了一定影响；②U-net网络的分割仍然存在一定的误差，并且误差在后续的边缘检测与椭圆拟合中会逐渐累加；③数据精简过程虽然可以剔除病态数据并保留有效数据，但是由于对每层数据进行分类，所以仍有部分有效数据被丢弃而病态数据被保留。

3.   总结与展望

本文为解决以工业CT序列图像为基础的物体内部二次曲面的提取与拟合问题，设计了一套算法。采用深度学习方法对CT图像进行分割，再对拟合出的椭圆形边界进行数据精简，在不过多降低曲面信息的同时剔除了干扰数据。通过仿真模拟，验证了该处理流程的有效性，与实际曲面的误差在1％ 以内，符合预先的设计要求。

为了应对更多不同吸收率差距的内外材料，我们将在后期实际实验数据处理中进一步优化该算法流程，改进分割网络，加入领域自适应等算法，提高该算法的泛化性。