The Lithospheric Structure of the Middle Solonker−Xar Moron Suture by Surface-wave Tomography
-
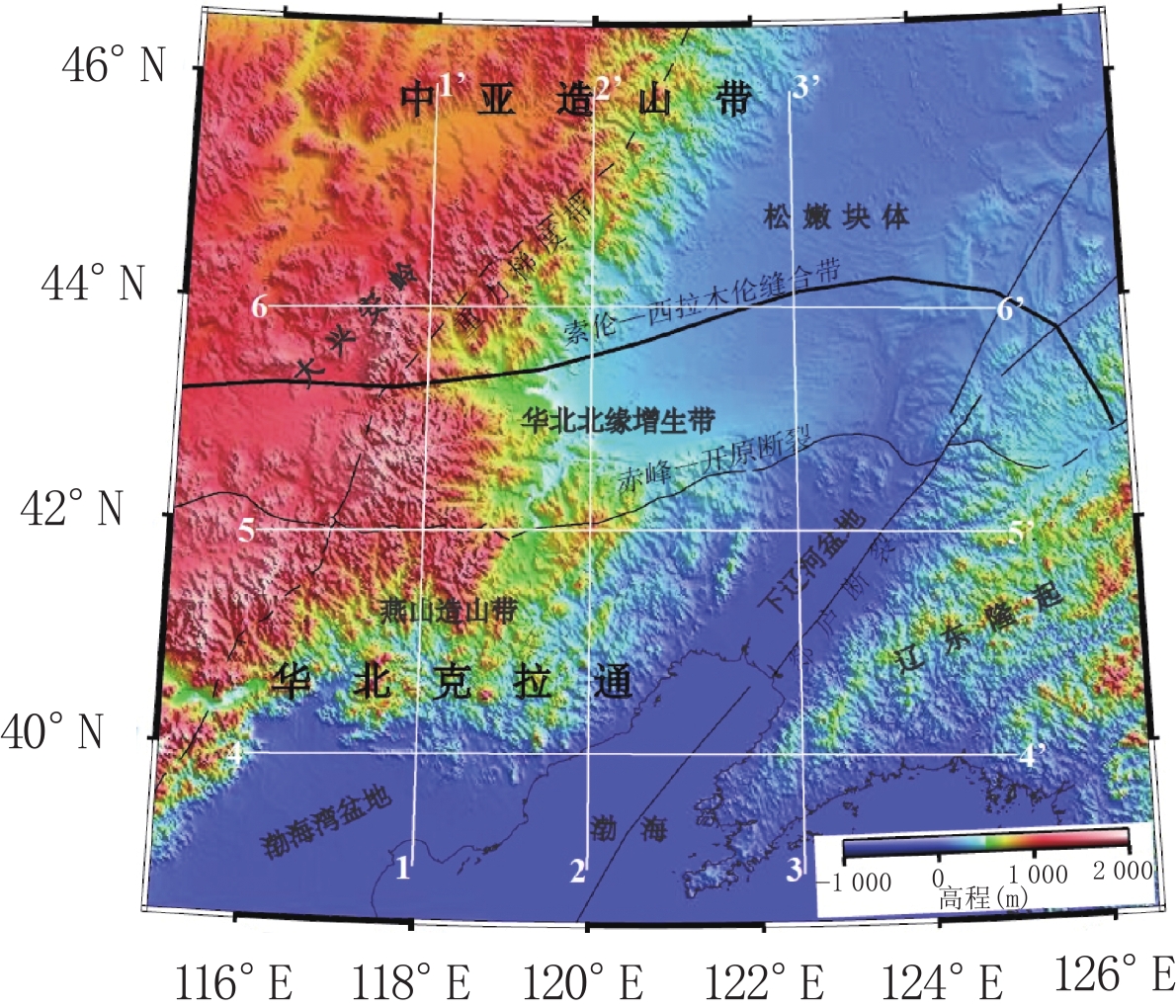
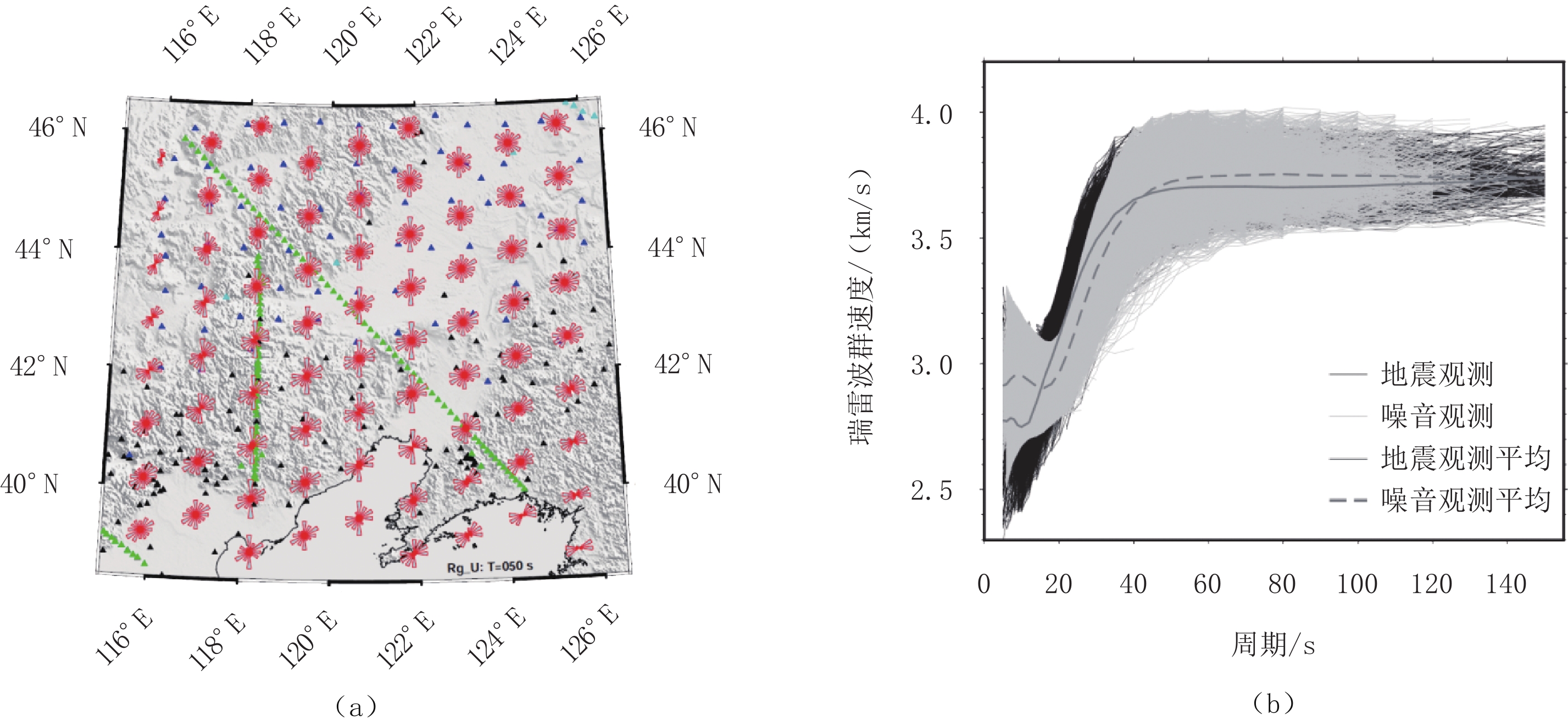
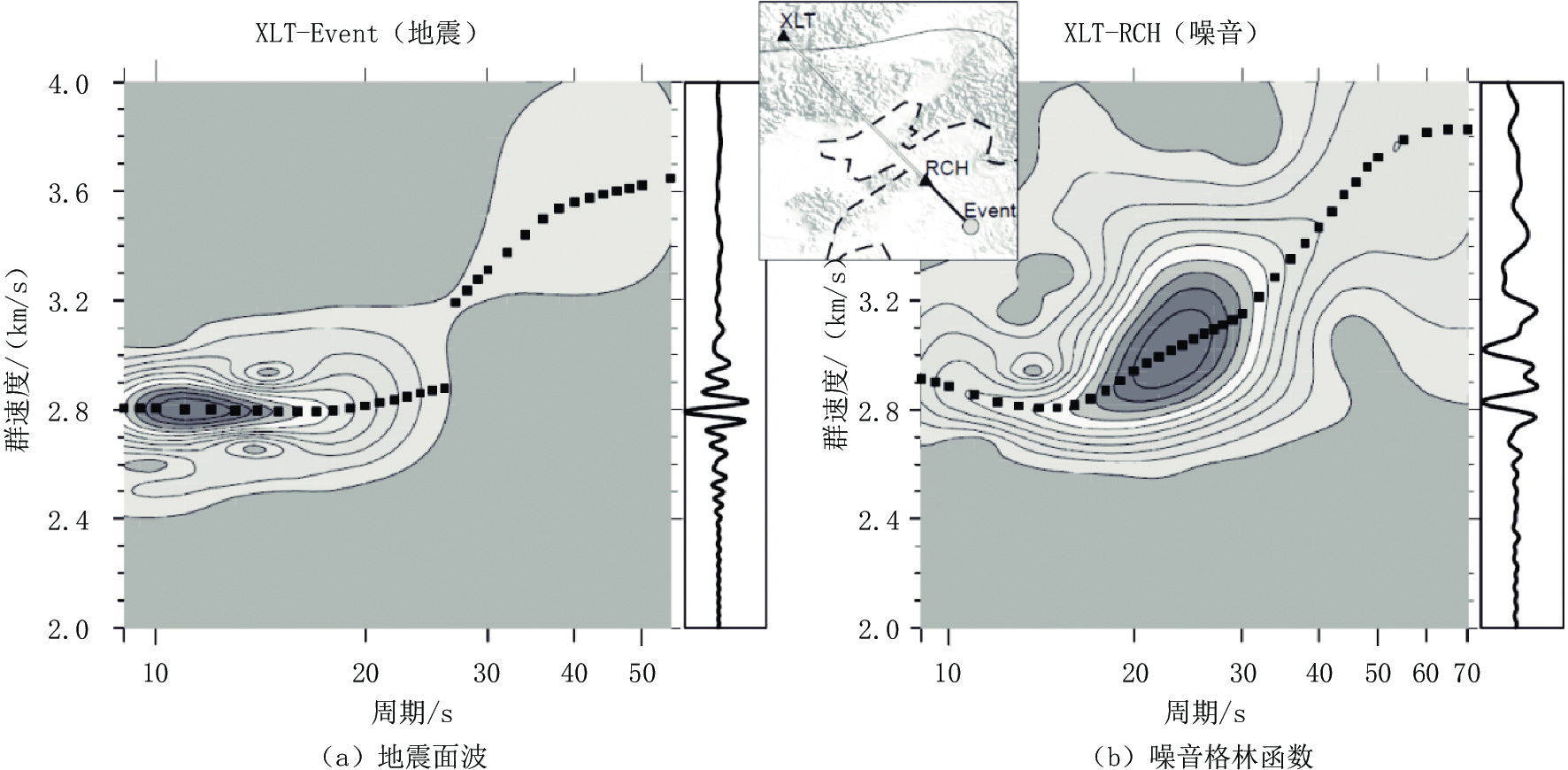
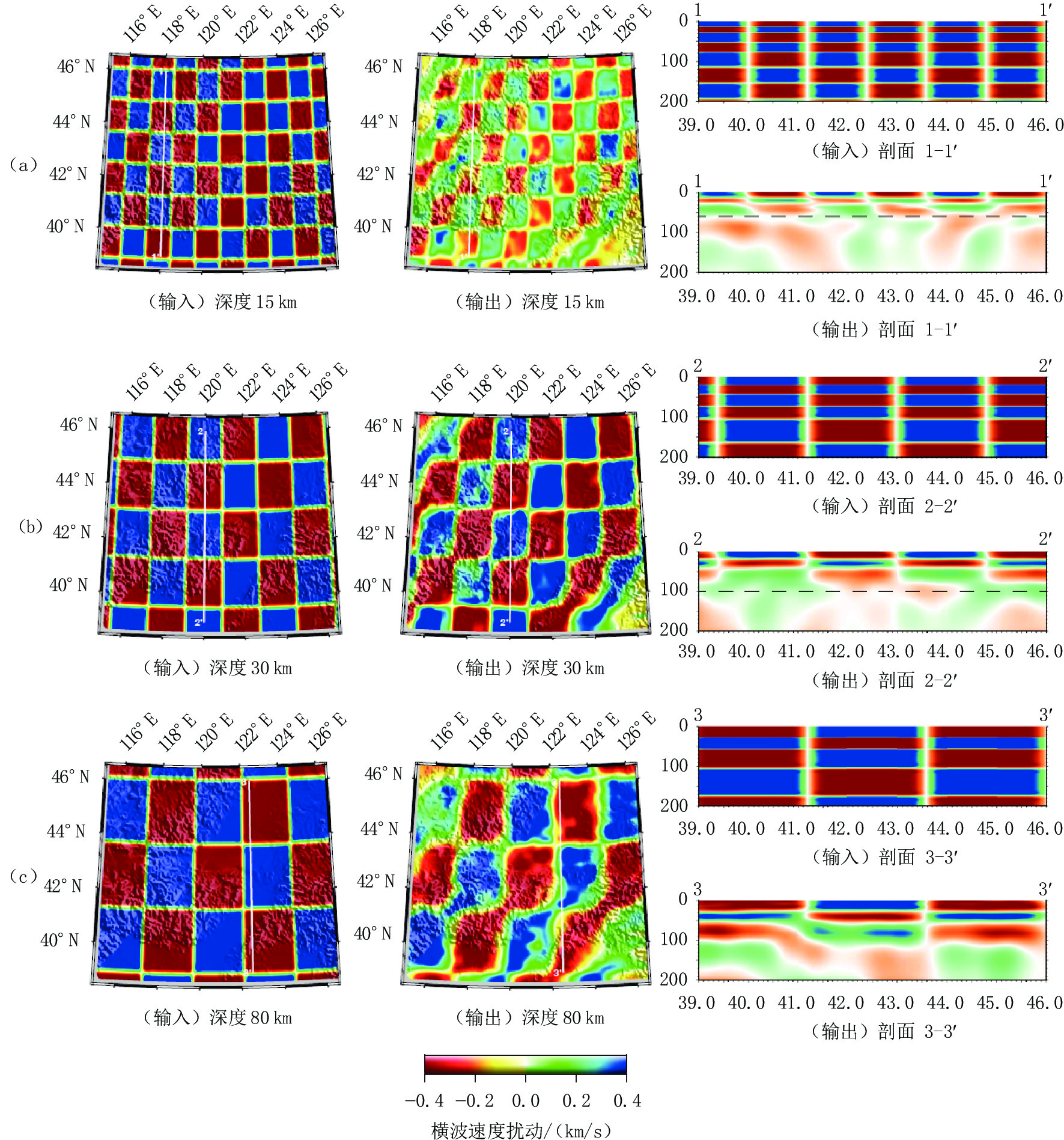
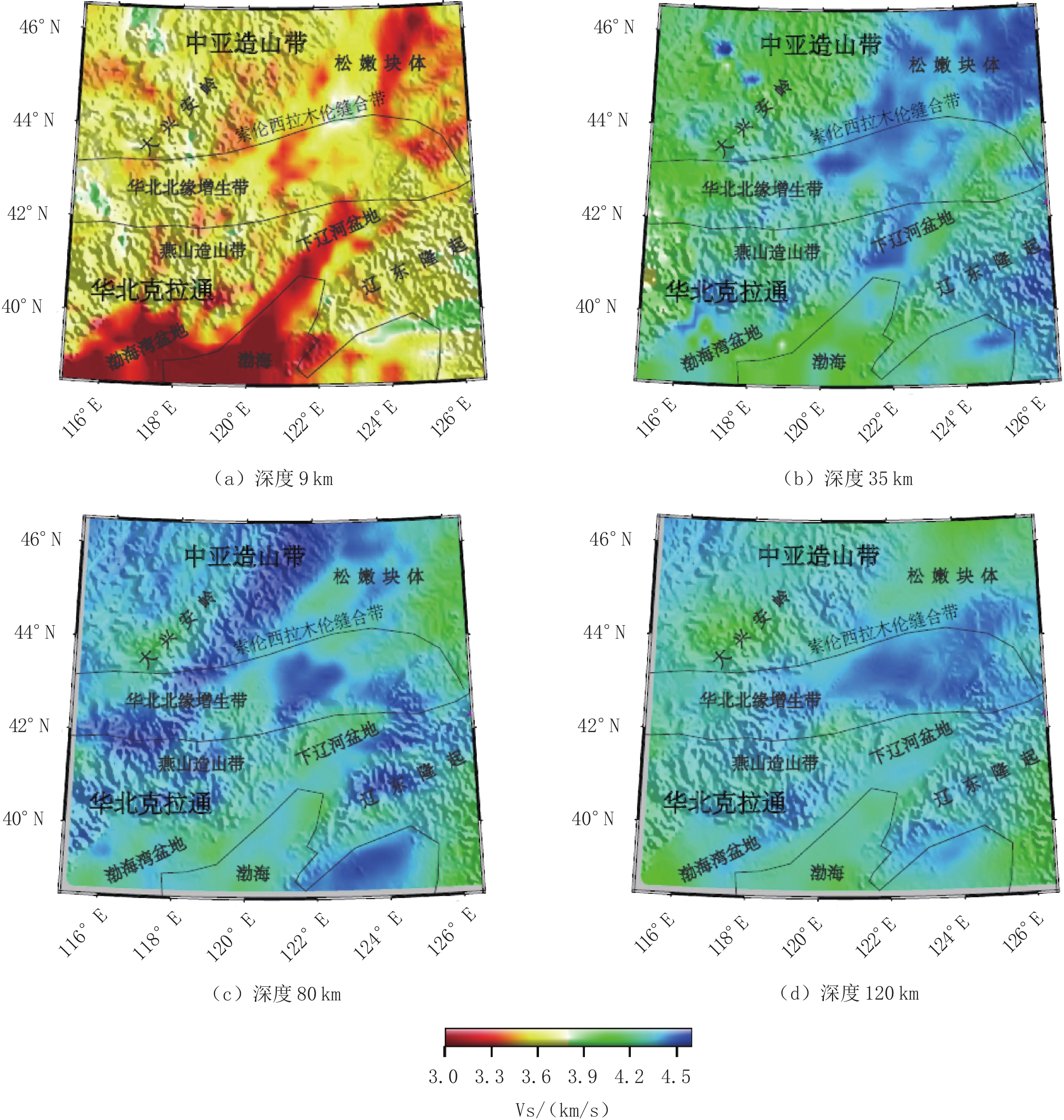
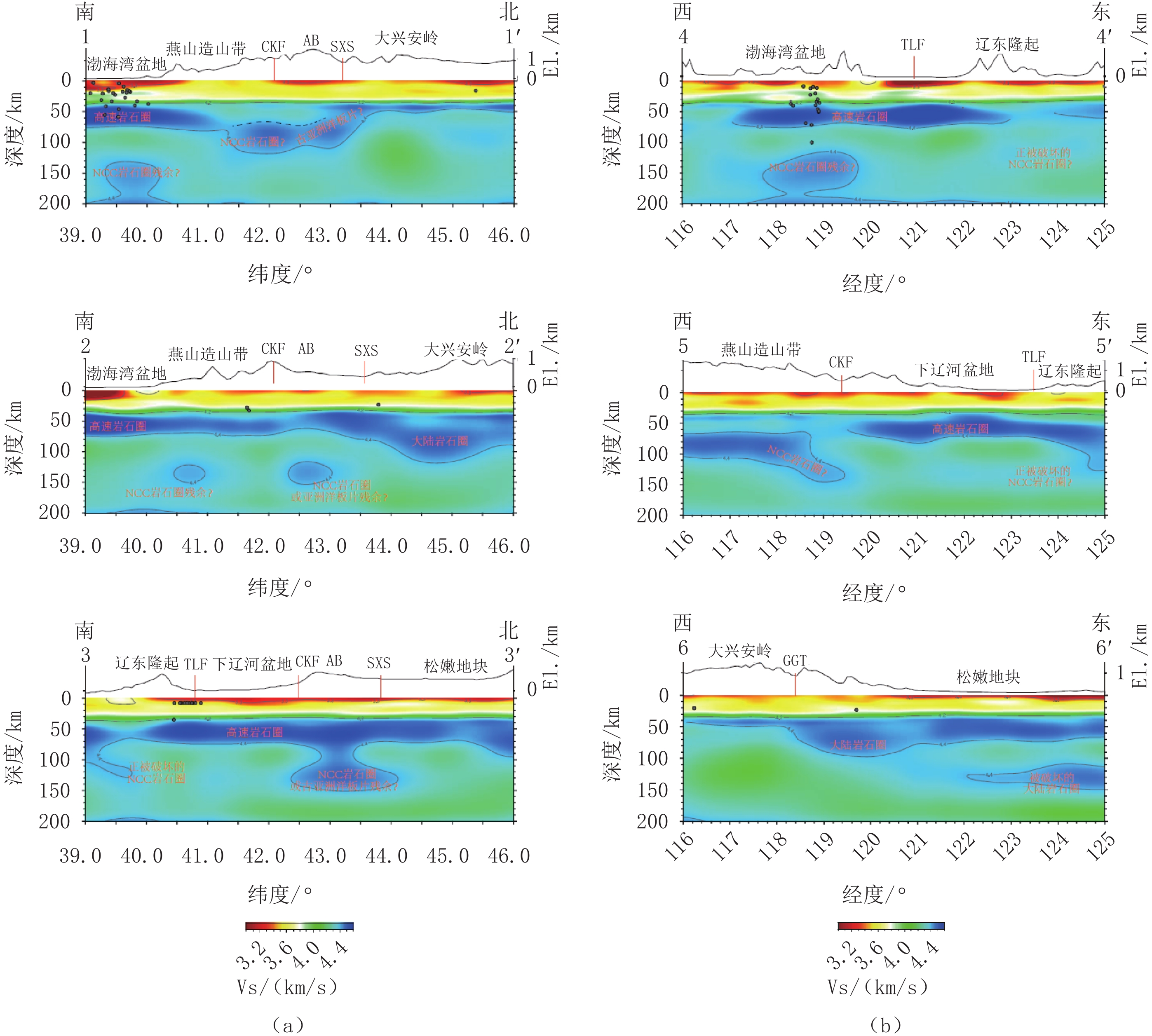
摘要: 索伦-西拉木伦缝合带中段及周边区域先后经历了古生代古亚洲洋闭合、中生代蒙古鄂霍茨克洋闭合和中新生代太平洋俯冲等构造复合叠加，导致该区深部构造异常复杂。本研究从该区近年来累积的宽频地震探测资料的地震面波和环境噪音互相关格林函数中提取瑞雷波群速度频散，并据此反演区域尺度的三维横波速度。结果发现：区域地壳厚度横向变化不大，松辽盆地和下辽河盆地地壳比大兴安岭薄，地壳厚度与地形吻合表明这些地区基本达到重力均衡状态；而辽东隆起和渤海湾盆地地壳厚度与地形高度呈反相关，表明这些地区可能仍处于构造改造过程中。在80 km深度之下，波速分布则呈现与索伦-西拉木伦缝合带走向近似平行的东西向展布。以索伦-西拉木伦缝合带为界，南北两侧横波速分布复杂程度明显不同且南侧的东西两部分复杂程度也不同。这些结果表明区域受太平洋俯冲体系冲破坏程度存在明显差异，同时索伦-西拉木伦缝合带以南可能仍有古亚洲洋板片残留。
-
关键词:
- 面波层析成像 /
- 三维横波速度 /
- 索伦-西拉木伦缝合带 /
- 华北克拉通 /
- 中亚造山带东段
Abstract: The middle section of the Solonker-Xar Moron suture and its surrounding areas have successively been affected by the closure of the Paleo-Asian Ocean during the Paleozoic, the closure of the Mongolian-Okhotsk Ocean during the Mesozoic, and the subduction of the Pacific Ocean plate since the Meso-Cenozoic, resulting in very complex, deep structures in this area. We conducted a regional-scale three-dimensional S-wave velocity tomographic study of the area. To do this, we used surface waves from earthquake data and ambient noise data recorded in recent years. The lithospheric tomographic model shows that the regional crustal thickness does not vary considerably, but the crust in the Songliao and the Lower Liaohe basins is thinner than that in the Daxing'an Mountains. The fact that the crustal thickness remains consistent with changes in topography indicates that these areas have reached gravitational equilibrium. However, the crustal thickness of the Liaodong uplift and the Bohai Bay Basin is inversely related with topography, indicating that these areas may still be in a tectonically active state. At depths greater than 80 km, the S-wave velocities spread in an east-west direction approximately parallel to the Solonker-Xar Moron suture. The complexity of the upper-mantle velocity distribution to the north of the Solonker-Xar Moron suture differs significantly from that to its south. Furthermore, south of the Solonker-Xar Moron suture, the complexity of the velocity distribution in the east differs considerably from that in the west. This implies that the destruction resulting from the Pacific Ocean subduction system varies significantly within the study region, and remnants of the paleo-Asian ocean slab may still exist in the south. -
页岩气是一种蕴藏在页岩层中的天然气。20世纪中期美国的“页岩气革命”，通过大规模开采和使用页岩气，大大降低其国内能源价格和对进口石油的依赖，带动了美国经济的发展，同时也对世界能源格局产生了深远的影响。近年来，页岩气已经成为许多国家能源结构调整的重要组成部分[1-2]。我国也很早就布局页岩气的勘探和开采，目前查明的资源储量主要分布在重庆市与四川省两个地区。
页岩孔隙结构是它的类型、大小、形状和分布会影响页岩储层的储集性能、渗流能力和页岩气产能，因此是页岩储层评价的核心内容。获取孔隙结构信息的常见方法包括扫描电镜法（scanning electron microscope，SEM）、X射线CT法、高压压泵法、气体吸附法等[3]，其中，微纳米CT成像（Micro-/Nano-CT）是常用的无损探测方法[4-5]。
Micro-CT具有较广的空间分辨率范围，最高达300 nm，该方法适合表征微米尺度和更大尺度的结构，如有机质空间分布模式、矿物空间分布特征与微裂缝三维结构特征等；Nano-CT方法分辨率范围一般为30~150 nm，适合表征亚微米尺度的孔隙结构（如不同类型的孔隙结构）。另一类获得高分辨率图像的方法是扫描电镜法，该方法可以获取高分辨率的图像，使得纳米级别微观结构和孔隙形态清晰可见。但是SEM图像存在复杂的纹理和噪声等干扰，准确地自动分析仍然是一个具有挑战性的问题[6-7]。
为了解决这一问题，图像分割方法被应用于页岩孔隙识别。图像分割是将数字图像分成多个区域的过程，目的是简化或改变图像的表示形式，使某些特征在同一区域内表现出一致性或相似性，在不同区域间则明显不同，从而使图像更容易理解和分析。通过图像分割，页岩孔隙图像中的各类孔隙和非孔隙区域被分开，从而获取准确的孔隙信息，认识页岩的孔隙结构。传统的分割方法，如阈值分割、基于聚类的分割、基于边缘检测的分割，在处理复杂的页岩图像时面临如孔隙灰度阈值差异、孔隙类别划分规则等复杂问题的挑战。此外，分割图像的孔隙信息，还要依靠人为主观判断，从而限制了对大量页岩样本的快速、准确分析。
深度学习方法最近几年在迅速地改变计算机视觉领域的发展，为解决人脸识别、自动驾驶、医疗影像检测等复杂问题提供了更为可靠快速的解决方案[8-9]。例如图像语义分割是计算机视觉社区中广泛应用的像素化的密集分类方法（pixel-wise classification），但重大突破是在深度学习方法的融入后才出现[10-11]。
目前基于深度学习的语义分割在地学领域的应用并不多见，主要集中在对矿物、断层、孔隙等目标的识别方面[12-14]。在这些应用中，多数研究者通过监督学习来训练模型的手段，即将所有用于训练的数据进行人工标注，再让模型来拟合数据与标签。但对于大的数据集而言，语义分割任务需要为每张图像的每一个像素点分配标签，时间成本非常高昂，这与人工智能解放人力工作的初衷相违背。而半监督学习利用未标记的数据辅助训练，具有数据利用率高、成本降低、泛化能力强等优势[15-19]。
本研究采用SEM图像进行神经网络训练，通过生成伪标签的方法实现半监督学习，同时通过集成学习提升模型的精度。本研究的方法将为页岩气勘探和开采提供更精准的页岩孔隙结构信息，并为提高页岩气勘探和开发效率提供技术支持。
1. 数据和方法
1.1 数据和处理流程
四川盆地及其周边地区的龙马溪组页岩是中国四川盆地的一个主要页岩气藏层，具有巨大的页岩气资源潜力，是中国最具有开发价值的页岩气层之一[20-22]。本研究使用重庆龙马溪组页岩储层SEM黑白图像，每张尺寸为
2538 ×1106 像素，共251张，图像示例见图1。部分图像中含有灰边和不属于样本的区域，为了让模型能够更好地对抗噪声干扰，这些区域并未被去除。图像预处理。首先，对原始图像进行随机切割、翻转等操作以获得数据增强，最终得到
1000 张448×448像素图像构成的数据集。然后，选择其中100张图像，对图中的有机孔、无机孔、有机质、黏土矿物基质、自生矿物（主要为黄铁矿）和脆性矿物（如石英）、样本外区域（包含图像灰边）共6类进行人工标注，将其中50张有标注的图像作为测试集，剩余50张有标注的图像和其它900张未标注图像作为训练集。最终训练集和测试集占比分别为95% 和5%。1.2 方法概述
语义分割是图像分割的常见目标是为输入图像的每一个像素分配一个类别标签。给定尺寸为
$ m \times n $ 的输入图像$ {\boldsymbol{X}} $ 和一组预定义的$ k $ 个类别标签集合$ L = \{ {l_1},l{}_2, \cdots ,{l_k}\} $ ，需要找到一个从输入图像$ {\boldsymbol{X}} $ 到输出图像$ {\boldsymbol{Y}} $ 的映射$ {\boldsymbol{F}} $ ，即：$$ {\boldsymbol{Y}} = {\boldsymbol{F}}({\boldsymbol{X}})\text{，} $$ (1) 其中，
$ {\boldsymbol{Y}} $ 也是一个$ m \times n $ 的图像，每个像素$ {\boldsymbol{Y}}(i,j) $ 为对应输入图像像素$ {\boldsymbol{X}}(i,j) $ 的类别标签。传统的语义分割方法大多简单容易实现，但是很难处理复杂的纹理和噪点。例如阈值分割采用阶梯函数来为输入图像的像素分配标签，在很多情况下，不同的类别会具有相同的像素值导致阈值分割失效。与之相比，深度学习方法可以学习图像中的特征，并在不同层次上对图像进行分割，因此可以获得更高的准确度。此外，深度学习方法可以将这些特征应用于不同的图像分割任务，具有更强的泛化能力。
深度学习基于深度神经网络训练模型：
$$\begin{aligned} &{\boldsymbol{Y}} =\\& {f^{(T)}}\Bigg( {{f^{(T - 1)}}\bigg( {, \cdots ,{f^{(2)}}\left( {{f^{(1)}}\left( {{\boldsymbol{X}};{{\boldsymbol{\theta }}_1}} \right);{{\boldsymbol{\theta}} _2}} \right), \cdots ,{{\boldsymbol{\theta}} _{T - 1}}} \bigg);{{\boldsymbol{\theta}} _T}} \Bigg)\text{，} \end{aligned}$$ (2) 或简写为：
$$ {\boldsymbol{Y}} = F\Big({\boldsymbol{X}};{\boldsymbol{\varTheta}} \Big)\text{，} $$ (3) 其中，
$ {\boldsymbol{F}}( \cdot ) = {f^{(T)}}\bigg({f^{(T - 1)}}, \cdots ,{f^{(2)}}\Big({f^{(1)}}( \cdot )\Big) \bigg)$ 表示层数为$ T $ 的神经网络结构，$f$ 表示多项式函数（如线性多项式），$ {\boldsymbol{\varTheta }} = \Big({{\boldsymbol{\theta }}_1},{{\boldsymbol{\theta }}_2}, \cdots ,{{\boldsymbol{\theta }}_T}\Big) $ 为网络各层的参数集。深度学习的最终目标是找到使给定损失函数$ L $ 最小化的参数集。深度学习的核心要素包含神经网络结构、训练策略和超参数，合理地设计这些内容对于模型性能和训练效率至关重要。由于本研究中数据集难以标注的性质，我们将侧重于自动生成标签训练策略的探究。
1.3 神经网络结构
语义分割往往采用由编码器和解码器构成的神经网络。编码器用于提取图像特征，通常使用卷积神经网络（convolutional neural networks，CNN）。解码器将编码器提取出的特征进行还原，生成与原图大小相同的分割结果，通常采用上采样、反卷积等方法。本文分别使用VGG 16和ResNet 34作为编码器、全卷积网络（fully convolutional network，FCN）和金字塔场景解析网络（pyramid scene parsing network, PSPNet）作为解码器，并对比测试它们的性能。
FCN通过上采样将特征图还原到原始图像大小，生成分割结果，并且使用跳跃连接方法，即在编码器中的每个池化层之后添加一个反池化层，将低分辨率的特征图还原到原始分辨率，然后将其与解码器中对应层次的特征图进行拼接[10]。FCN的一个缺点是处理细节的能力较差，而PSPNet在FCN的基础上引入更多上下文信息，通过金字塔型特征结构的全局均值池化操作（global average pooling）和特征融合，提取不同尺度的特征，在保留空间信息的同时，增强了图像的语义信息[23]。
如图2所示，PSPNet先用一个CNN对输入图像进行特征提取，这个CNN被称为主干网络。这个过程会生成一个特征图，其中包含了图像的低级和高级特征信息。为了捕捉不同尺度的上下文信息，PSPNet使用金字塔池化模块，这个模块包括一系列的自适应平均池化层，每一层具有不同的池化窗口大小。这些池化层会将特征图分别缩放到不同的尺寸，从而捕捉不同尺度的上下文信息。经过金字塔池化模块处理后，每个池化层的输出特征图需要进行反卷积以实现上采样，从而恢复到原始特征图的大小。然后，所有上采样后的特征图和原始特征图相叠加，即可实现多尺度特征的融合。然后PSPNet通过一个卷积层对融合后的特征图进行进一步处理。这个卷积层的输出通道数等于目标类别数量，用于为每个像素预测其所属的类别。最后，PSPNet使用像素级的Softmax函数将实数值转换成概率分布，即利用：
$$P\left({v}_{i}|u\right)={\mathrm{Softmax}}\left({v}_{i}\right)= \frac{\exp\Big(h\left(u,{v}_{i}\right)\Big)}{\displaystyle\sum\limits _{j=1}^{N} \exp\Big(h\left(u,{v}_{j}\right)\Big)} ， $$ (4) 计算每个像素属于各个类别的概率，概率最高的类别被认为是该像素的预测类别。
在这个Softmax函数表达式中，
$ N $ 是类别总数，$ h(u,{v}_{i}) $ 表示当前状态$ u $ 和像素$ {v}_{i} $ 之间相似度关系的函数，是给定像素$ u $ 的情况下，该像素属于类别$ {v}_{i} $ 的概率。通过上述运作过程，PSPNet可以有效地捕捉并融合多尺度上下文信息，从而在语义分割任务上取得优异的性能。
1.4 训练策略
神经网络的训练流程如图3所示。首先，我们通过已标注数据
$ {D_T} = \{ {{\boldsymbol{x}}_{{T_i}}},{{\boldsymbol{y}}_{{T_i}}}\} $ 训练出教师模型，令教师模型对未标记数据$ {D_U} = \{ {{\boldsymbol{x}}_{{U_i}}}\} $ 进行预测生成伪标签$ {\tilde D_U} = \{ {{\boldsymbol{x}}_{{U_i}}},{{\boldsymbol{\tilde y}}_{{U_i}}}\} $ ，然后令包含真实标签或伪标签的数据共同训练出学生模型。学生模型训练完成后令其作为教师模型对伪标签进行更新，训练出下一个学生模型。学生模型的更新重复迭代3次。
1.4.1 伪标签
伪标签方法的实质是让模型去自行生成标签[15-16]。首先，在已标记的数据上训练出教师模型，然后将教师模型来预测对未标记的数据进行预测，得到一组伪标签。将伪标签和有标签的数据混合，再次训练模型，使其逐步改进并提高性能。通常，这个过程需要迭代多次，每次都会产生新的伪标签和更新的模型。在训练过程中，伪标签最初是很不可靠的，但是随着迭代次数增加，会渐渐变得可靠。正因如此，我们引入一个正则化参数
$ \alpha $ ，代表无标签数据的更新权重。给定损失函数$ L({{\cdot}}) $ ，训练学生模型时采用的总损失函数为：$$ L({\boldsymbol{\theta }}) = {L_\theta }({\boldsymbol{y}},{\boldsymbol{z}}) + \alpha {L_\theta }({\boldsymbol{y}}',{\boldsymbol{z}}')\text{，} $$ (5) 其中，
$ {\boldsymbol{\theta}} $ 为网络模型参数，$ {\boldsymbol{z}} $ 表示标签数据的输出类，$ {\boldsymbol{y}} $ 表示标签数据的真实类，$ {{\boldsymbol{z}}}'$ 表示无标签数据的输出类，$ {{\boldsymbol{y}}}'$ 表示无标签数据的伪标签，${L_\theta }({\boldsymbol{y}},{\boldsymbol{z}})$ 为教师模型预测标记数据的监督损失，${L_\theta }({\boldsymbol{y}}',{\boldsymbol{z}}')$ 为学生模型预测未标记数据的无监督损失。在训练过程中，由于学生模型逐渐变得精确，$ \alpha $ 值应当逐渐升高以增强学生模型损失函数的权重。伪标签方法的优点是可以利用未标记的数据，增加训练数据集的大小，从而提高模型的性能。它可以在有限的标记数据情况下获得更好的模型性能，还可以扩大模型的应用范围。但是，伪标签方法也存在一些问题，如伪标签的质量可能不如真实标签，对模型的影响不确定，可能会导致模型性能下降。
1.4.2 集成学习
对于监督学习算法而言，集成学习是一种能有效改进预测准确率的方法。在集成学习中，会训练多个模型，并将这些模型组合为一个预测模型，以此降低模型的偏倚和方差。集成学习的方式通常包括Bagging、Boosting和Stacking等，但是由于标记数据的样本量等原因，上述方法对本研究的半监督学习并不适用。
我们采用了一种更加直接的集成学习策略：基于软投票法的模型平均。对于同一个训练集，以不同的随机初始参数训练出多个模型，并简单地对这些模型的预测概率取平均值，得到最终的模型。对于任意一个样本，假如有
$ N $ 个模型$ {C_1},{C_2},{C_3},\cdots,{C_N} $ ，则集成后的预测结果为：$$ {y_{{\text{ensemble}}}} = \arg\max\limits _{i = 1}^m\left( {\sum\limits_{j = 1}^N {\left( {\frac{1}{N}{{\hat y}_{ji}}} \right)} } \right)\text{，} $$ (6) 其中，
$ m $ 为类别数，$ {\hat y_{ji}} $ 为第$ j $ 个模型预测样本属于类别$ i $ 的概率，这里每一个样本对应图像的一个像素。经验表明，当所有的神经网络具有相同的结构、对相同的数据集训练使用相同的标准训练算法，即随机梯度下降学习速率和相同的正则化，只有随机初始参数不同时，集成学习可以有效降低模型的方差，且集成后模型的表现大概率优于每一个集成前模型。
1.5 损失函数
对于多类别的语义分割问题，传统的损失函数包括有多类别交叉熵（categorical cross entropy，CCE）和聚焦损失（focus loss，FL）等。对于本研究中的问题而言，由于不同类别的像素数量占比非常不均衡，因此我们对CCE进行按类别加权，设计出一种加权多类别交叉熵（weighted categorical cross entropy，WCCE）损失函数，将有机孔和无机孔分类错误的代价大幅增加，使分类的应用效果更好。通过CCE和WCCE构建的损失函数分别如下：
$$ {L_{{\text{CCE}}}} = - \frac{1}{n}\sum\limits_{i = 1}^n {\left( {\sum\limits_{j = 1}^m {\Big( {{y_{ij}}\log {{\hat y}_{ij}}} \Big)} } \right)} \text{，} $$ (7) $$ {L_{{\text{WCCE}}}} = - \frac{1}{n}\sum\limits_{i = 1}^n {\left( {\sum\limits_{j = 1}^m {\Big( {{w_j}{y_{ij}}\log {{\hat y}_{ij}}} \Big)} } \right)} \text{，} $$ (8) 其中，
$ n $ 为样本容量，$ m $ 为类别数，$ {y_{ij}} $ 为判断样本$ i $ 预测是否与标签（或伪标签）一致的符号函数，$ {w_j} $ 为第$ j $ 种类别的自定义权重，$ {\hat y_{ij}} $ 为模型预测样本$ i $ 属于类别$ j $ 的概率。1.6 训练步骤
我们通过Tensorflow 2深度学习框架搭建上述神经网络，通过调参得到以下超参数设置：验证集划分比例设为20%，训练批次大小设为5，初始学习率设为0.001，学习率衰退因子设为0.001。由于学生模型继承教师模型的权值可能导致陷入局部最优，所有网络的权值初始化都采用随机初始化。
最后一次训练学生模型时，通过不同的随机初始化训练出10个模型，将这10个模型集成为最终的模型。在预测时，分别将图像输入至10个模型中，通过式（6）得到最终的预测结果。
2. 实验结果与讨论
2.1 不同方法孔隙分割效果
图4是不同的神经网络结构和训练策略的语义分割效果示例。预测结果中，白色表示脆性矿物和碎屑矿物，黑色表示无机孔，红色表示有机孔，浅蓝色表示黏土矿物基质，深蓝色表示有机质，绿色（图4（b）左上区域）表示样本外区域。可以看出，每种神经网络和训练策略都能对图像中的矿物和孔隙进行大致的区分，但是在细节上存在着一定的差异。视觉上，PSPNet+ResNet34的预测结果（图4（c）和图4（e））要好于FCN-8+VGG16（图4（b）和图4（d））。在页岩孔隙图像中，上下文关系不匹配对于复杂场景的理解会造成普遍的影响。
传统的FCN模型缺乏收集上下文信息的能力，会增加误分类的可能性。在FCN的观测结果中，有很多预测错误要被归咎于不合适的，而PSPNet可以有效改善这一点[23]。
使用不同的损失函数也会对语义分割的效果产生影响。以FCN-8+VGG16的监督学习结果为例，和输入图像（图5（d））相比，CCE损失函数的预测结果（图5（a））未能有效识别右侧的脆性矿物和自生矿物，而使用参数为2的FL损失函数的预测效果更差（图5（c））。考虑到样本的类别不平衡可能会影响模型性能，我们对CCE进行调整，大幅提高了误判孔隙的交叉熵权重，得到WCCE函数。采用这种WCCE作为损失函数可以取得更好的预测结果（图5（b））。
2.2 模型的性能评估
传统的深度学习方法往往用像素准确率（pixel accuracy）评价模型的性能。然而，在图像分割问题中，由于各类别的像素占比极其不均衡，准确率并非一个良好的评价指标。这里对于具体的某个物体，我们可以从预测框与真实框的贴合程度判断检测的质量，这个指标就是交并比（mean intersection over union，MIoU），用于量化两个框的贴合程度。MIoU的计算方式为：
$$ {\text{MIoU}} = \frac{1}{{k + 1}}\sum\limits_{i = 0}^k {\left( {\frac{{{p_{ii}}}}{{\sum\limits_{j = 0}^k {{p_{ij}} + \sum\limits_{j = 0}^k {{p_{ji}} - {p_{ii}}} } }}} \right)} \text{，} $$ (9) 其中，
$ {p_{ij}} $ 表示将类别$ i $ 预测为类别$ j $ 的像素个数，$ k $ 为样本的类别数。对于每种训练方案，我们从目标迭代轮次开始，向后继续迭代并保存20个模型，并统计其MIoU，结果表1和图6所示。
表 1 各模型和训练策略的MIoU（$ \pm $ 标准差）Table 1. MIoU of different models and training strategies ($ \pm $ standard variation)模型 监督学习 5% 半监督学习 监督学习+10次集成 5% 半监督学习+
10次集成FCN8+VGG16 0.620$ \pm $0.012 0.660$ \pm $0.012 0.649$ \pm $0.008 0.690$ \pm $0.010 FCN8+ResNet34 0.641$ \pm $0.011 0.672$ \pm $0.015 0.696$ \pm $0.012 0.715$ \pm $0.008 PSPNet+VGG16 0.646$ \pm $0.009 0.652$ \pm $0.013 0.683$ \pm $0.010 0.701$ \pm $0.010 PSPNet+ResNet34 0.654$ \pm $0.013 0.660$ \pm $0.013 0.694$ \pm $0.012 0.728$ \pm $0.012 ![]()
图 6 各类模型和训练策略的MIoU折线图Figure 6. Line graph of MIoU for different models and training strategies表1中，第2列为仅用监督学习（不采用伪标签）的结果，第3列为采用5% 真实标签与95% 伪标签的半监督学习的结果，第4列为监督学习+集成学习的结果，第5列为半监督学习+集成学习的结果。
图6中，①表示真实标签训练；②表示伪标签训练；③表示集成学习。实验结果表明，在标签数据有限的情况下，伪标签方法和集成学习对于神经网络的性能有一定的提升。在本实验中，对于相同的神经网络结构，同时采用伪标签方法和集成学习能将模型的MIoU提升大约7%。
2.3 算法优劣对比及检验
通过表1和图6，我们可以直观认为模型之间存在性能的差异，我们需要通过假设检验才能在统计学意义上确认不同算法的优劣。虽然我们得到每种算法的MIoU均值和方差，但由于我们无法确定MIoU的真实分布，这里应该采取非参数统计方法中的比较检验。对于同一数据集上的多组算法，可以先用Friedman检验判断算法之间是否性能都相同，再用Nemenyi检验对算法进行排序。
我们将从训练策略和神经网络结构这两个维度进行分析。以训练策略的比较为例，对于神经网络结构相同且迭代轮次顺序相同的一组MIoU，我们记录每种训练策略的序值，MIoU最高的策略其序值记为1，第2高的策略序值记为2，以此类推。假如出现性能完全并列的情况，则按照平均值来记录，如二者并且最高则分别记为1.5。每种算法的平均序值记为
$ {r_i} $ ，则变量：$$\begin{aligned} {\tau _{{\chi ^2}}} =\;& \frac{{k - 1}}{k} \cdot \frac{{12N}}{{{k^2} - 1}}{\sum\limits_{i = 1}^k {\left( {{r_i} - \frac{{k + 1}}{2}} \right)} ^2} =\\ &\frac{{12N}}{{k(k + 1)}}\left( {\sum\limits_{i = 1}^k {r_i^2 - \frac{{k{{(k + 1)}^2}}}{4}} } \right)\text{，}\end{aligned} $$ (10) 在
$k$ 和$N$ 都较大时，服从自由度为$k - 1$ 的${\chi ^2}$ 分布，其中$k$ 为算法数量，$N$ 为样本量。这里我们采用改进后的计算方式，变量：$$ {\tau _F} = \frac{{(N - 1){\tau _{{\chi ^2}}}}}{{N(k - 1) - {\tau _{{\chi ^2}}}}}\text{，} $$ (11) 服从自由度为
$ k - 1 $ 和$ (k - 1)(N - 1) $ 的$ F $ 分布。经过计算得出，不同训练策略间的P$ \approx 5.5 \times {10^{ - 12}} $ ，不同神经网络结构间的P$ \approx 6.3 \times {10^{ - 7}} $ ，可以认为算法之间均存在显著性能差异。后续，我们用Nemenyi事后检验对算法进行比较。我们先计算临界值域，
$$ {\mathrm{CD}} = {q_\alpha }\left( {\frac{{k(k + 1)}}{{6N}}} \right) \text{，} $$ (12) 其中，
$ {q_\alpha } $ 是Tukey分布的临界值。如果两个算法$ i,j $ 的平均序值之差$ \left| {{\tau _i} - {\tau _j}} \right| >CD $ ，则以置信度$ 1 - \alpha $ 拒绝“两个算法性能相同”这一假设。我们借助R语言，对多种假设在不同显著性水平下进行检验（表2）。为了提高结论的可重复性，我们采用
$ \alpha = 0.005 $ 作为统计显著性的阈值。注意到PSPNet比FCN-8性能更好这一假设在$ \alpha = 0.005 $ 被拒绝，但我们并不能否定神经网络结构对性能的影响，只是在本研究中这两种解码器的差异还不够大。我们可以接受的结论是，采用合理的训练策略可以有效提升模型的性能。表 2 算法性能比较的假设检验Table 2. Hypothesis testing for algorithm performance comparison算法 $ \alpha = 0.002\,5 $ $ \alpha = 0.005 $ $ \alpha = 0.01 $ 半监督学习+集成 > 监督学习+集成 T T T 监督学习+集成 > 半监督学习 T T T 半监督学习 > 监督学习 T T T ResNet34 > VGG16 F T T PSPNet > FCN-8 F F T 2.4 研究的局限性和未来展望
虽然我们通过训练策略改善了过拟合、人工标注误差等问题，但我们最终得到的模型仍然是个黑箱系统，缺乏可解释性。我们很难真正理解模型是如何作出预测的，只能通过实验尽量让其预测地更准确。在语义分割领域，相比于自动驾驶这类已被广泛应用的任务，页岩孔隙更具有多样性和复杂性，且类别区分度低，我们仍未能有效解决数据与岩性之间的复杂关系。
我们采用的两种训练策略——伪标签方法和集成学习，仍有许多改进空间。伪标签方法最致命的问题是错误传播问题。如果模型对未标记数据的预测不准确，错误的伪标签可能会被引入训练过程，导致模型性能下降。在本研究中，我们对页岩孔隙图像进行人工标注时，可能会对部分像素的类别判断错误，这可能会降低伪标签的准确程度。如果未标记数据中的类别分布与已标记数据不同，伪标签技术可能导致类别不平衡问题，进而影响模型性能。此外，伪标签学习通常需要多次迭代训练，每次迭代都需要使用模型对未标记数据进行预测并更新伪标签。这会增加训练时间和计算资源的消耗。尽管如此，以伪标签方法为代表的半监督学习可以显著降低语义分割人工标注成本，已经成为深度学习的主流技术路线之一。
本研究中，我们以不同初始化的方法进行了模型层面的集成。在单个模型性能有限的情况下，这种方法可以平衡各自模型的优缺点，减轻了过拟合的影响。而我们采用的投票法是相对容易实现的方法，与现有的监督学习算法结合，无需对原本的模型做出大幅的改动。但是集成学习的训练时间和计算复杂度会倍增。我们只采用了较小的数据集，所以这类问题并不严重。但在使用大量数据或复杂模型时，计算资源的消耗可能会成为一个问题。另外，对于投票法而言，在调用集成后的模型进行预测时，本身也要调用每个参与集成的模型进行投票，这会增加预测消耗的时间。
在集成学习的领域，本研究还有如下改进空间。
（1）对于不同损失函数进行集成。我们对CCE函数的不同类别进行加权得到最终的WCCE损失函数，但是这些权重本身就存在过拟合的问题。如果将不同权重的WCCE进行模型平均或投票集成，有可能会得到表现更好的模型。
（2）对于不同学习率进行集成。深度学习会让模型收敛到一个局部最优解，使用不同的学习率意味着模型将以不同的速度进行学习和优化。一些学习率可能使模型快速收敛，而其他学习率可能使模型越过较小的局部最优，从而找到全局最优。总的来说，这种方法有助于提升模型的泛化能力，进而增强模型对未知数据的预测性能。
除此之外，我们还可以通过学习轮次、特征图或模型融合等方式进行集成学习[24]。在深度学习任务中，当模型表现不佳时，我们未必能轻松找到更优秀的神经网络结构，但是集成学习是更直观有效的优化手段。集成学习在各类AI应用竞赛中被普遍使用，这也间接说明其有效性被广泛接受。
3. 结论
本研究通过伪标签的半监督学习方法对页岩孔隙SEM图像分割进行了探索，结果表明，在基于FCN和PSPNet的模型上使用伪标签进行训练，并能够显著提高模型的精度。本次研究的贡献在于，提出了一种新的基于伪标签的数据增强方法，可以提高模型的泛化能力，同时在实验中还证明了该方法的有效性。此外，通过可视化分析，本研究还展示了不同神经网络在图像特征提取上的差异和优缺点。
但是，本研究仍存在一些局限性，如图像数据量较少、训练时间较长等问题，这些问题限制了模型的性能，未来研究可以在数据集的收集和处理、算法优化等方面进行改进。此外，本研究的网络训练的数据是基于SEM图像的，未来还可以通过Nano-CT成像数据进一步补充数据。尽管SEM图像和Nano-CT成像都是纳米级的，但分辨率还是有细微差别。为了增加训练网络的泛化性能，还可以考虑引入迁移学习（transfer learning）进行微调（fine tuning）。
总之，本研究的结果证明了基于伪标签的数据增强方法在页岩孔隙图像分割中的有效性，同时也为相关领域的研究提供了一定的参考和启示。
-
![]()
![]()
图 2 地震台站和数据分布情况
（a）地震台站（三角）以及50 s周期的数据方位分布（玫瑰图）；（b）地震事件（细黑线）和环境噪音（细灰线）波频散观测及其区域平均（粗灰线、虚线）。玫瑰图中扇形半径与每30°方位间隔内的观测数量成正比；扇形半径越长，该方位观测数量越大；玫瑰图越接近于圆形，表示观测数据方位分布越均匀。
Figure 2. Seismic stations and data
![]()
图 3 相似路径（插图）的地震面波（a）和噪音格林函数（b）时频分析实例
Figure 3. Example of group-velocity dispersion analysis for earthquake surface wave (a) and noise Green’s function (b) with similar travelling paths (inset map)
![]()
图 4 三维检测板分辨率测试结果
（a）异常尺寸为1.2°×1.2°×（15～40 km）；（b）异常尺寸为1.8°×1.8°×（20～60 km）；（c）检测板尺寸为2.4°×2.4°×（30～70 km）。注为“深度”和“剖面”的子图分别表示不同深度水平切片和穿过不同剖面的垂直切片。水平切片中白线为相应垂直剖面位置。
Figure 4. Results of 3D checkerboard resolution tests
-
[1] FU W, HOU H S, GAO R, et al. Lithospheric structures of the central Solonker-Xar Moron-Changchun-Yanji suture (Inner Mongolia) revealed by a deep seismic reflection profile[J]. Tectonophysics, 2021, 817: 229043. doi: 10.1016/j.tecto.2021.229043
[2] LIU Y J, LI W M, FENG Z Q, et al. A review of the Paleozoic tectonics in the eastern part of Central Asian Orogenic Belt[J]. Gondwana Research, 2017, 43: 123−148. doi: 10.1016/j.gr.2016.03.013
[3] WILDE S A. Final amalgamation of the Central Asian Orogenic Belt in NE China: Paleo-Asian Ocean closure versus Paleo-Pacific plate subduction: A review of the evidence[J]. Tectonophysics, 2015, 662: 345−362. doi: 10.1016/j.tecto.2015.05.006
[4] 潘桂棠, 肖庆辉, 陆松年, 等. 中国大地构造单元划分[J]. 中国地质, 2009,36(1): 1−28. doi: 10.3969/j.issn.1000-3657.2009.01.001 PAN G T, XIAO Q H, LU S N, et al. Subdivision of tectonic units in China[J]. Geology in China, 2009, 36(1): 1−28. (in Chinese). doi: 10.3969/j.issn.1000-3657.2009.01.001
[5] ZHU R X, XU Y G. The subduction of the West Pacific plate and the destruction of the North China Craton[J]. Science China Earth Sciences, 2019, 62: 1340−1350. doi: 10.1007/s11430-018-9356-y
[6] GUO Z, WANG K, YANG Y J, et al. The origin and mantle dynamics of quaternary intraplate volcanism in Northeast China from joint inversion of surface wave and body wave[J]. Journal of Geophysical Research, 2018, 123(3): 2410−2425. doi: 10.1002/2017JB014948
[7] TANG Y C, OBAYASHI M, NIU F L, et al. Changbaishan volcanism in Northeast China linked to subduction-induced mantle upwelling[J]. Nature Geoscience, 2014, 7(6): 470−475. doi: 10.1038/ngeo2166
[8] LU M W, LEI J S, ZHAO D P, et al. SKS Splitting measurements in NE China: New insights into the Wudalianchi intraplate volcanism and mantle dynamics[J]. Journal of Geophysical Research, 2020, 125(3): e2019JB018575.
[9] FAN X L, CHEN Q F. Seismic constraints on the magmatic system beneath the Changbaishan volcano: Lnsight into its origin and regional tectonics[J]. Journal of Geophysical Research, 2019, 124(2): 2003−2024. doi: 10.1029/2018JB016288
[10] DENG Y F, XU Y G, CHEN Y. Formation mechanism of the North-South gravity lineament in Eastern China[J]. Tectonophysics, 2021, 818: 229074. doi: 10.1016/j.tecto.2021.229074
[11] CHEN L, JIANG M M, YANG J H, et al. Presence of an intralithospheric discontinuity in the central and western North China Craton: Implications for destruction of the craton[J]. Geology, 2014, 42(3): 223−226. doi: 10.1130/G35010.1
[12] CHEN L. Lithospheric structure variations between the eastern and central North China Craton from S- and P-receiver function migration[J]. Physics of The Earth and Planetary Interiors, 2009, 173(3): 216−227.
[13] CHEN L, TAO W, ZHAO L, et al. Distinct lateral variation of lithospheric thickness in the Northeastern North China Craton[J]. Earth and Planetary Science Letters, 2008, 267: 56−68. doi: 10.1016/j.jpgl.2007.11.024
[14] ZHAO L, ZHENG T Y, CHEN L, et al. Shear wave splitting in Eastern and Central China: Implications for upper mantle deformation beneath continental margin[J]. Physics of The Earth and Planetary Interiors, 2007, 162: 73−84. doi: 10.1016/j.pepi.2007.03.004
[15] ZHENG T Y, ZHU R X, ZHAO L, et al. Intralithospheric mantle structures recorded continental subduction[J]. Journal of Geophysical Research, 2012, 117(B3).
[16] ZHENG T Y, HE Y M, YANG J H, et al. Seismological constraints on the crustal structures generated by continental rejuvenation in Northeastern China[J]. Scientific Reports, 2015, 5(1): 14995. doi: 10.1038/srep14995
[17] FENG M, ASSUMPÇÃO MARCELO S, Van der LEE S. Group-velocity tomography and lithospheric S-velocity structure of the South American continent[J]. Physics of The Earth and Planetary Interiors, 2004, 147(4): 315−331. doi: 10.1016/j.pepi.2004.07.008
[18] 中国地震科学台阵. 中国地震科学探测台阵波形数据[DB/OL]. 中国地震局, 2006. DOI: 10.12001/ChinArray.Data. ChinArray. China seismic array waveform data[DB/OL]. China Earthquake Administration, 2006. DOI://10.12001/ChinArray.Data. (in Chinese).
[19] 中国地震局地球物理研究所国家测震台网数据备份中心. 地震波形数据[DB/OL]. 中国地震局. DOI: 10.11998/SeisDmc/SN. [20] TANG Q S, CHEN L. Structure of the crust and uppermost mantle of the Yanshan Belt and adjacent regions at the northeastern boundary of the North China Craton from Rayleigh wave dispersion analysis[J]. Tectonophysics, 2008, 455(1): 43−52.
[21] 危自根, 陈凌, 杨小林. 辽东台隆、燕山带和兴蒙造山带台站下方地壳厚度和平均波速比(Vp/Vs)的横向变化及其构造意义[J]. 地球物理学报, 2011,54(11): 2799−2808. doi: 10.3969/j.issn.0001-5733.2011.11.010 WEI Z G, CHEN L, YANG X L. Transverse variations of crustal thickness and VP/VS ratio under the stations in the Liaodong anteclise-Yanshan belt-Xingmeng orogenic belt and their tectonic implications[J]. Chinese Journal of Geophysics, 2011, 54(11): 2799−2808. (in Chinese). doi: 10.3969/j.issn.0001-5733.2011.11.010
[22] ZHANG R Q, WU Q J, SUN L, et al. Crustal and oblithospheric structure of Northeast China from S-wave receiver functions[J]. Earth and Planetary Science Letters, 2014, 401: 196−205. doi: 10.1016/j.jpgl.2014.06.017
[23] 张广成, 吴庆举, 潘佳铁, 等. 利用H-K叠加方法和CCP叠加方法研究中国东北地区地壳结构与泊松比[J]. 地球物理学报, 2013,56(12): 4084−4094. DOI: 10.6038/cjg20131213. ZHANG G C, WU Q J, PAN J T, et al. Study of crustal structure and Poisson ratio of NE China by H-K stack and CCP stack methods[J]. Chinese Journal of Geophysics, 2013, 56(12): 4084−4094. DOI: 10.6038/cjg20131213. (in Chinese).
[24] TAO K, NIU F L, NING J Y, et al. Crustal structure beneath NE China imaged by NECESSArray receiver function data[J]. Earth and Planetary Science Letters, 2014, 398: 48−57. doi: 10.1016/j.jpgl.2014.04.043
[25] BENSEN G D, RITZWOLLER M H, BARMIN M P, et al. Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements[J]. Geophysical Journal International, 2007, 169(3): 1239−1260. doi: 10.1111/j.1365-246X.2007.03374.x
[26] HERRMANN R B. Computer programs in seismology: An evolving tool for instruction and research[J]. Seismological Research Letters, 2013, 84(6): 1081−1088. doi: 10.1785/0220110096
[27] SHAPIRO N M, RITZWOLLER M H. Monte-Carlo inversion for a global shear-velocity model of the crust and upper mantle[J]. Geophysical Journal International, 2002, 151: 88−105. doi: 10.1046/j.1365-246X.2002.01742.x
[28] 黄忠贤, 李红谊, 胥颐. 南北地震带岩石圈S波速度结构面波层析成像[J]. 地球物理学报, 2013,56(4): 1121−1131. DOI: 10.6038/cjg20130408. HUANG Z X, LI H Y, XU Y. Lithospheric S-wave velocity structure of the North-South seismic belt of China from surface wave tomography[J]. Chinese Journal of Geophysics, 2013, 56(4): 1121−1131. DOI: 10.6038/cjg20130408. (in Chinese).
[29] 苏伟, 彭艳菊, 郑月军, 等. 青藏高原及其邻区地壳上地幔S波速度结构[J]. 地球学报, 2002,23(3): 193−200. doi: 10.3321/j.issn:1006-3021.2002.03.001 SU W, PENG Y J, ZHENG Y J, et al. Crust and upper mantle shear velocity structure beneath the Tibetan Plateau and adjacent areas[J]. Acta Geoscientica Sinica, 2002, 23(3): 193−200. (in Chinese). doi: 10.3321/j.issn:1006-3021.2002.03.001
[30] LEVENBERG K. A method for the solution of certain nonlinear problems in least squares[J]. Quarterly of Applied Mathematics, 1944, 2: 164−168. doi: 10.1090/qam/10666
[31] TIKHONOV A N. On the solution of ill-posed problems and the method of regularization[J]. Doklady Akademii Nauk SSSR, 1963, 151(3): 501−504.
[32] FENG M, AN M J. Lithospheric structure of the Chinese mainland determined from joint inversion of regional and teleseismic Rayleigh-wave group velocities[J]. Journal of Geophysical Research, 2010, 115: B06317.
[33] AN M J, WIENS D A, ZHAO Y, et al. S-velocity model and inferred Moho topography beneath the Antarctic plate from Rayleigh waves[J]. Journal of Geophysical Research, 2015, 120(1): 359−383. doi: 10.1002/2014JB011332
[34] FENG M, AN M J, MECHIE J, et al. Lithospheric structures of and tectonic implications for the central-east Tibetan plateau inferred from joint tomography of receiver functions and surface waves[J]. Geophysical Journal International, 2020, 223(3): 1688−1707. doi: 10.1093/gji/ggaa403
[35] 冯梅, 安美建. 基于面波频散的三维横波速度方位各向异性层析成像方法[J]. CT理论与应用研究, 2020,29(4): 381−397. DOI: 10.15953/j.1004-4140.2020.29.04.01. FENG M, AN M J. Method on 3D tomography of S-wave velocity azimuthal anisotropy by using surface-wave dispersion curves[J]. CT Theory and Applications, 2020, 29(4): 381−397. DOI: 10.15953/j.1004-4140.2020.29.04.01. (in Chinese).
[36] GASS S I, FU M C. Newton’s method[M]. Boston, MA: Encyclopedia of Operations Research and Management Science, Springer US, 2013: 1051-1051.
[37] MOROZOV V A. Methods for solving incorrectly posed problems[M]. New York: Springer-Verlag, 1984: 1-257.
[38] AN M J. Adaptive regularization of the reference model in an inverse problem[J]. Pure and Applied Geophysics, 2020, 177(10): 4943−4956. doi: 10.1007/s00024-020-02530-z
[39] LASKE G, MA Z T, MASTERS G, et al. A new global crustal model at 1×1 degrees[OL]. http://igppweb.ucsd.edu/~gabi/crust1.html, 2012.
[40] KENNETT B L N, ENGDAHL E R. Traveltimes for global earthquake location and phase identification[J]. Geophysical Journal International, 1991, 105: 429−465. doi: 10.1111/j.1365-246X.1991.tb06724.x
[41] 查小惠, 吕坚, 鲍志诚, 等. 接收函数H-k叠加方法研究综述[J]. CT理论与应用研究, 2020,29(3): 369−379. DOI: 10.15953/j.1004-4140.2020.29.03.14. ZHA X H, LV J, BAO Z C, et al. A review of H-k stack method of receiver function[J]. CT Theory and Applications, 2020, 29(3): 369−379. DOI: 10.15953/j.1004-4140.2020.29.03.14. (in Chinese).
[42] 安美建, 冯梅, 赵琳. 地震层析成像中的不确定性[J]. CT理论与应用研究, 2009,18(2): 24−32. AN M J, FENG M, ZHAO L. Uncertainties in seismic tomography[J]. CT Theory and Applications, 2009, 18(2): 24−32. (in Chinese).
[43] 冯梅, 安美建. 反演模型分辨率的估算方法[J]. CT理论与应用研究, 2013,22(4): 587−604. doi: 10.3969/j.issn.1004-4140.2013.04.003 FENG M, AN M J. How to determine spatial resolution for an inverse problem[J]. CT Theory and Applications, 2013, 22(4): 587−604. (in Chinese). doi: 10.3969/j.issn.1004-4140.2013.04.003
[44] LI Y H, GAO M T, WU Q J. Crustal thickness map of the Chinese mainland from teleseismic receiver functions[J]. Tectonophysics, 2014, 611: 51−60. doi: 10.1016/j.tecto.2013.11.019
[45] HE R Z, SHANG X F, YU C Q, et al. A unified map of Moho depth and Vp/Vs ratio of continental China by receiver function analysis[J]. Geophysical Journal International, 2014, 199(3): 1910−1918. doi: 10.1093/gji/ggu365
[46] FENG M, AN M J, DONG S W. Tectonic history of the ordos block and Qinling orogen inferred from crustal thickness[J]. Geophysical Journal International, 2017, 210(1): 303−320. doi: 10.1093/gji/ggx163
[47] FENG M, AN M J, Van der LEE S. Region-related features of crustal and upper-mantle velocity structure of the Chinese mainland detected by surface waveform modeling[J]. Acta Seismologica Sinica, 2008, 21(2): 118−126. doi: 10.1007/s11589-008-0003-0
[48] 中国地质调查局. 中华人民共和国1︰250万数字地质图说明书[M]. 北京: 中国地图出版社, 2004. China Geological Survey. 1︰2 500 000 geological map of China[M]. Beijing: China Cartographic Publishing House, 2004. (in Chinese).
[49] SONG Y, STEPASHKO A, LIU K Y, et al. Post-rift tectonic history of the Songliao basin, NE China: Cooling events and post-rift unconformities driven by orogenic pulses from plate boundaries[J]. Journal of Geophysical Research, 2018, 123(3): 2363−2395. doi: 10.1002/2017JB014741
[50] 冯梅, 安美建. 中国大陆中上地壳剪切波速结构[J]. 地震学报, 2007,20(4): 359−369. doi: 10.3321/j.issn:0253-3782.2007.04.001 FENG M, AN M J. Middle and upper crust shear-wave velocity structure of the Chinese mainland[J]. Acta Seismologica Sinica, 2007, 20(4): 359−369. (in Chinese). doi: 10.3321/j.issn:0253-3782.2007.04.001
[51] 高延光, 李永华. 中国东北-华北地区地壳厚度与泊松比及其地质意义[J]. 地球物理学报, 2014,57(2): 166−176. doi: 10.1002/cjg2.20094 GAO Y G, LI Y H. Crustal thickness and Vp/Vs in the Northeast China-North China region and its geological implication[J]. Chinese Journal of Geophysics, 2014, 57(2): 166−176. (in Chinese). doi: 10.1002/cjg2.20094
[52] 张凯文, 陈棋福, 陈赟. 接收函数揭示的兴蒙造山带西南部的地壳结构特征[J]. 地球物理学报, 2020,63(4): 1−21. doi: 10.6038/cjg2020N0048 ZHANG K W, CHEN Q F, CHEN Y. Crustal structure beneath the southwestern Xing’an-Mongolia orogenic belt revealed by receiver function analysis[J]. Chinese Journal of Geophysics, 2020, 63(4): 1−21. (in Chinese). doi: 10.6038/cjg2020N0048
[53] AN M J, SHI Y L. Lithospheric thickness of the Chinese continent[J]. Physics of The Earth and Planetary Interiors, 2006, 159: 257−266. doi: 10.1016/j.pepi.2006.08.002
[54] HE Y, CHEN Q F, CHEN L, et al. Distinct lithospheric structure in the Xing'an-Mongolian orogenic belt (submitted)[J]. Geophysical Research Letters, 2022.
[55] ENGDAHL E R, Van der HILST R D, BULAND R. Global teleseismic earthquake relocation with improved travel times and procedures for detph determination[J]. Bulletin of the Seismological Society of America, 1998, 88: 722−743.
[56] FREDERIKSEN A W, BOSTOCK M G, CASSIDY J F. S-wave velocity structure of the Canadian upper mantle[J]. Physics of the Earth and Planetary Interiors, 2001, 124: 175−191. doi: 10.1016/S0031-9201(01)00194-7
[57] Van der LEE S. High-resolution estimates of lithosphere thickness from Missouri to Massachusetts, USA[J]. Earth and Planetary Science Letters, 2002, 203: 15−23. doi: 10.1016/S0012-821X(02)00846-4
[58] 朱介寿, 曹家敏, 蔡学林, 等. 东亚及西太平洋边缘海高分辨率面波层析成像[J]. 地球物理学报, 2002,45(5): 646−664. doi: 10.3321/j.issn:0001-5733.2002.05.007 ZHU J S, CAO J M, CAI X L, et al. High resolution surface wave tomography in East Asia and West Pacific marginal seas[J]. Chinese Journal of Geophysics, 2002, 45(5): 646−664. (in Chinese). doi: 10.3321/j.issn:0001-5733.2002.05.007
[59] ZHU J S, CAI X L, CAO J M, et al. Lithospheric structure and geodynamics in China and its adjacent areas[J]. Geology in China, 2006, 33(4): 793−802.
[60] HUANG X A, BI Z W, DEPAOLO D J. Sm-Nd isotope study of early Archean rocks, Qianan, Hebei Province, China[J]. Geochimica et Cosmochimica Acta, 1986, 50(4): 625−631. doi: 10.1016/0016-7037(86)90111-0
[61] ZHAO G C, WILDE S A, CAWOOD P A, et al. Archean blocks and their boundaries in the North China Craton: Lithological, geochemical, structural and P-T path constraints and tectonic evolution[J]. Precambrian Research, 2001, 107(1): 45−73.
下载:
计量
- 文章访问数: 570
- HTML全文浏览量: 194
- PDF下载量: 80
