Fast EPRI Imaging Based on 3MNet Denoising Network
-
摘要: 电子顺磁共振成像（EPRI）是一种先进的氧成像技术。当前EPRI的瓶颈问题是扫描速度过慢，其原因是每个角度下的投影信号需要被重复采集几千次，以压制随机噪声。一种实现快速扫描的方法是减少投影信号的重复采集次数，然而这又使得投影信号信噪比降低，重建出来的图像噪声较大。为有效压制重建图像中的噪声，本文提出一种基于多通道、多尺度、多拼接的（3MNet）图像去噪网络，以实现高精度快速EPRI成像。该网络由3个子网络构成。第1个子网络是基于注意力机制的卷积网络，其输出的特征图像与输入图像拼接以构成后端网络的输入；第2个子网络是3通道卷积网络；第3个子网络是多尺度卷积网络。实验结果表明，本文提出的3MNet网络可以实现EPRI图像的高精度去噪，进而实现快速成像。Abstract: Electron paramagnetic resonance imaging (EPRI) is an advanced technique for oxygen imaging. The current bottleneck in EPRI is the slow scanning speed, due to the fact that the projection signal at each angle needs to be repeated thousands of times to suppress random noise. One way to achieve fast scanning is to reduce the number of repeated projection signal acquisitions; however, this, in turn, reduces the signal-to-noise ratio of the projection signal and results in a noisy reconstructed image. To effectively suppress the noise in the reconstructed image, this study proposes a multi-channel, multi-scale, multi-concatenation, and convolutional network (3MNet) based image denoising network to achieve high accuracy and fast EPRI imaging. The proposed network consists of three sub-networks. The first sub-network is an attention-based convolutional network, whose output feature images are stitched with the input images to form the input of the back-end network. The second sub-network is a three-channel convolutional network. Finally, the third sub-network is a multi-scale convolutional network. The experimental results demonstrate that the proposed 3MNet network can achieve high accuracy in denoising EPRI images and fast imaging.
-
Keywords:
- deep learning /
- convolutional neural network /
- EPRI /
- rapid imaging
-
研究表明，肿瘤内部的氧气浓度是一个重要的放疗参数，如果可以准确地显示出肿瘤内部的氧浓度图像，便可以根据肿瘤内氧浓度的分布来调整放射剂量，以实现精准放疗[1-2]。电子顺磁共振成像（electron paramagnetic resonance imaging，EPRI）是一种高精度高分辨率的肿瘤氧成像模态[3-5]。然而EPRI的主要缺点是扫描时间过长，因为每个角度下的投影信号需被重复采集数千次，以压制随机噪声。一种提高扫描速度的方法是减少在特定角度下采集投影信号的重复次数，然而如此采样导致投影信号的信噪比下降，进而使得用传统的三维滤波反投影（filtered back projection，FBP）算法重建出的EPRI图像噪声过大。因此图像去噪成为EPRI当前最重要的问题之一。
图像重建中的去噪问题大致分为两类：基于优化的重建方法和基于深度学习的图像后处理方法。
在基于优化的图像重建算法中，以总变差（total variation，TV）最小类算法最为典型。2006年至2008年，Sidky等[6-7]提出的TV最小化算法可以实现高精度稀疏重建和含噪投影重建。人们后来又提出若干改进的TV模型来提高重建精度，如自适应加权TV（adaptive-weighted TV，AwTV）模型[8]、高阶TV（high order TV，HOTV）模型[9-10]、非局部TV（non-local TV，NLTV）模型以及TpV（total p-variation）模型[11]等。迭代法重建精度高，但重建速度慢，尤其在三维重建中，重建速度成为影响其应用的主要障碍。
基于深度学习的图像去噪方法，是当前性能最优的去噪方法。2008年，Jain等[12]首次通过训练卷积神经网络，实现端到端去噪映射；2016年，Mao等[13]提出的卷积编解器网络，采用了卷积和反卷积层之间的跳跃连接结构，大大提升模型的去噪性能；2017年，Zhang等[14]提出了一个深层（denoising convolutional neural network，DnCNN）网络模型，在网络中引入残差学习（residual learning）[15]、线性激活单元（rectified linear unit，ReLU）和批归一化（batch nonmalization，BN）[16]来训练网络；同年Chen等[17]将自编码器和残差连接用到了卷积-反卷积神经网络（residual encoder-decoder convolutional neural network，RED-CNN）中，以实现低剂量CT成像。
随着网络的不断加深加宽，人们发现仅改变网络结构不能从本质上提升性能，而且真实环境下的噪声复杂多变，需设计性能更优的网络以实现图像去噪。Zhang等[18]在2018年先后提出了（fast and flexible denoising network，FFDNet）及（convolutional blind denoising network，CBDNet）用于真实图像去噪。FFDNet将不同的噪声水平和噪声图像作为输入，以应对复杂真实环境的噪声，而CBDNet网络通过子网络先实现噪声水平的估计，再通过改进的UNet网络[19]来获取潜在的干净图像，使整个网络获得了盲去噪能力[20]。
为进一步提高网络的盲去噪能力，Tian等[21]在2019年提出了一个双通道网络（batch-renormalization denoising network，BRDNet），将两个不同的互补网络结合BN、残差学习和空洞卷积[22]用于图像去噪，增强了卷积神经网络（convolutional neural network，CNN）对图像细节信息的表征能力。Zhao等[23]在2020年提出（pyramid real image denoising network，PRIDNet）网络，由噪声估计、多尺度特征提取和特征融合模块构成，大大提高了在真实噪声图像中网络的去噪性能，更多地提取了图像的潜在特征。
上述网络中的CBDNet和PRIDNet通过估计噪声水平来提高网络的盲去噪能力，BRDNet是通过增加网络宽度来提取图像细节特征。受此启发，本文拟结合以上3种去噪网络的优势，构建多通道网络提取图像细节信息，多尺度实现特征信息的融合，多拼接实现盲去噪网络的结构完整性，基于此设计多通道、多尺度、多拼接卷积网络（multi-channel，multi-scale，multi-concatenation，convolutional network，3MNet）以实现EPRI图像去噪。
1. 方法
1.1 基于CNN的EPRI快速成像原理
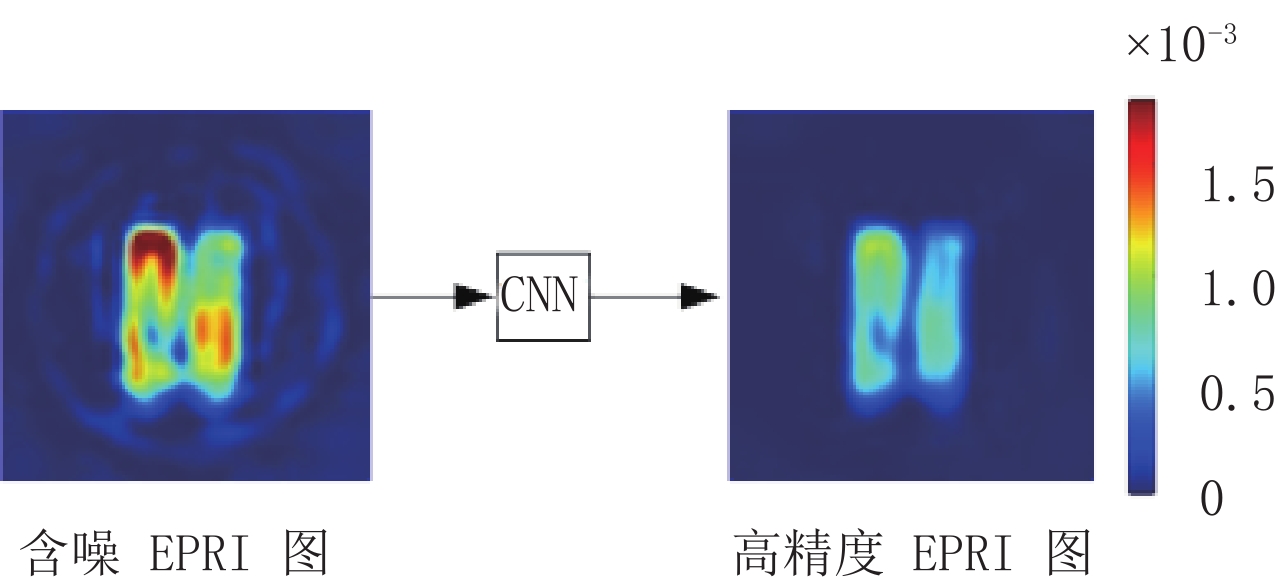
CNN是深度学习的一类经典网络结构，其尤其适用于图像处理，可以学习到输入图像和输出图像之间复杂的、难以被数学建模的非线性映射。为实现EPRI快速成像，首先以快速扫描方式获得低信噪比的投影数据，然后使用FBP算法重建出含噪图像，最后通过CNN大规模训练数据实现图像去噪。CNN去噪的示意图如图1所示。
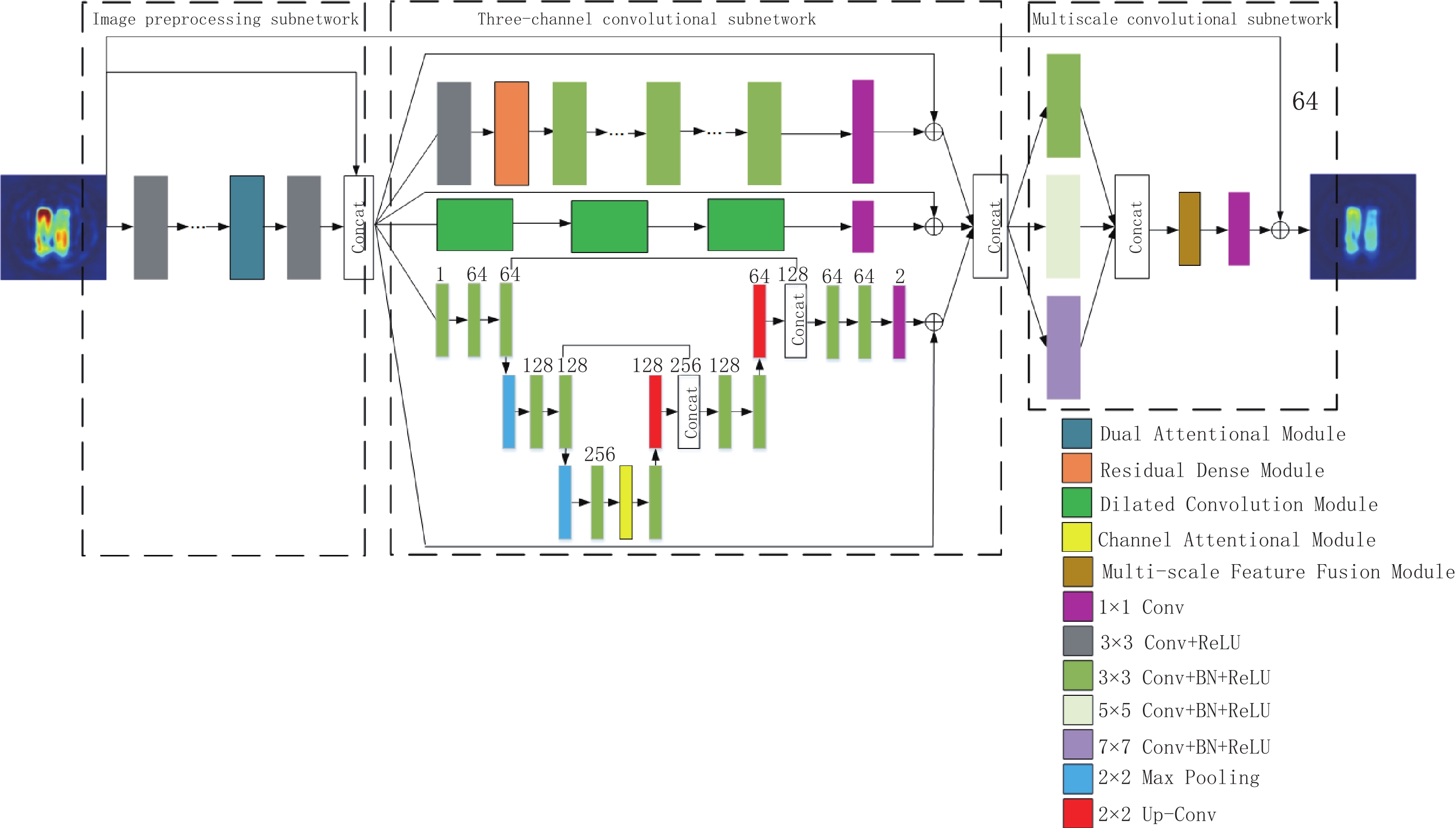
1.2 3MNet网络
3MNet网络结构如图2所示，所提议的网络包括3个子网络：图像预处理子网络、三通道卷积子网络和多尺度卷积子网络，输入的含噪EPRI图像经过3个子网络的处理，输出高精度EPRI图像。
1.2.1 图像预处理子网络
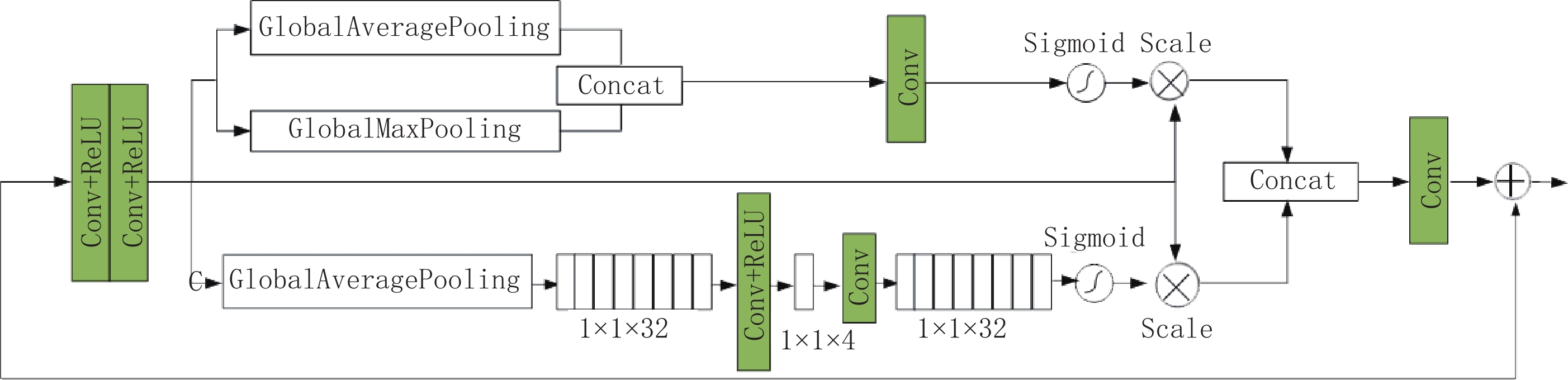
图像预处理子网络是从输入的含噪EPRI图像中提取出特征信息，再将特征图像和高噪图像进行拼接，此拼接图像作为三通道卷积子网络的输入，使整个网络可以学习到更加复杂的未知信息特征[24]。该子网络采用了5层全卷积网络，每个卷积层（convolutional layer，Conv）包含通道数为32的3×3 Conv+ReLU层。在最后一个卷积层之前，引入了一个双重注意力模块，该模块结合通道注意力[25]和空间注意力[26]来充分提取卷积层中的细节信息。
双重注意力模块如图3所示。该模块首先进行两次3×3的Conv+ReLU操作得到特征图；空间注意力机制通过对特征图做全局平均池化（global average pooling，GAP）和全局最大池化（global max pooling，GMP），在拼接操作后通过通道数为1的1×1 Conv；最后sigmoid激活函数将输出的特征权重和输入的特征逐像素相乘保留了更多有用的细节特征。通道注意力机制通过GAP得到大小为1×1×f 的特征图，在1×1 Conv+ReLU操作后通道数变为
${f}/{s}$ ；随后再通过1×1 Conv将通道数转换为f，在sigmoid激活函数后将输出的特征权重和输入的特征相乘；最后两分支输出的特征图进行拼接，通过1×1 Conv后与输入的特征逐像素相加。在本文中参数s=8，f=32。1.2.2 三通道卷积子网络
不断加深网络层数存在性能饱和问题，鉴于不同的网络架构可以提取到互补的特征信息，拟通过增加网络的宽度来提高去噪性能。三通道卷积子网络结合了残差密集块、空洞卷积以及UNet的优点，每个通道上都引入残差学习避免因网络过深而引起的梯度消失和梯度爆炸问题[27-28]。
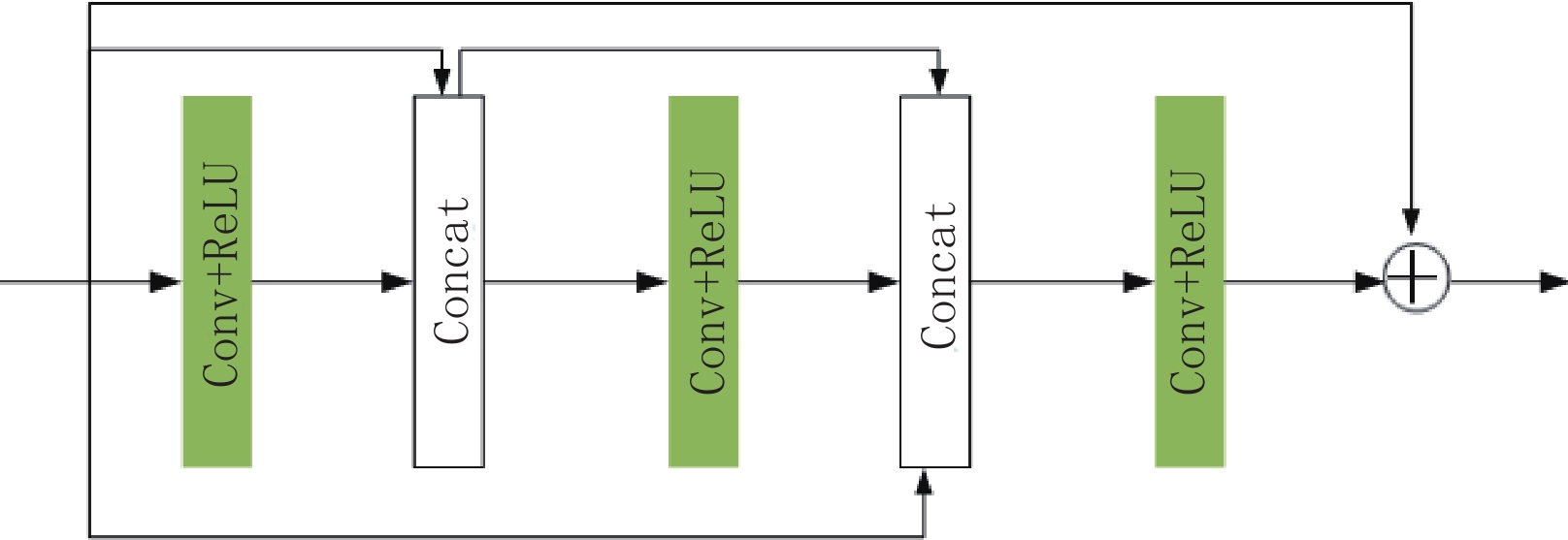
第1层通道：该通道在传统DnCNN网络的第1个卷积层后引入如图4所示的残差密集连接块，该模块由3个Conv+ReLU以及拼接（Concatenate，Concat）操作构成，后1层均与之前层相互连接以增加网络的深度和宽度，使各卷积层之间的特征信息均被充分利用[29]。最后在该模块的输入与输出之间加入了残差学习。
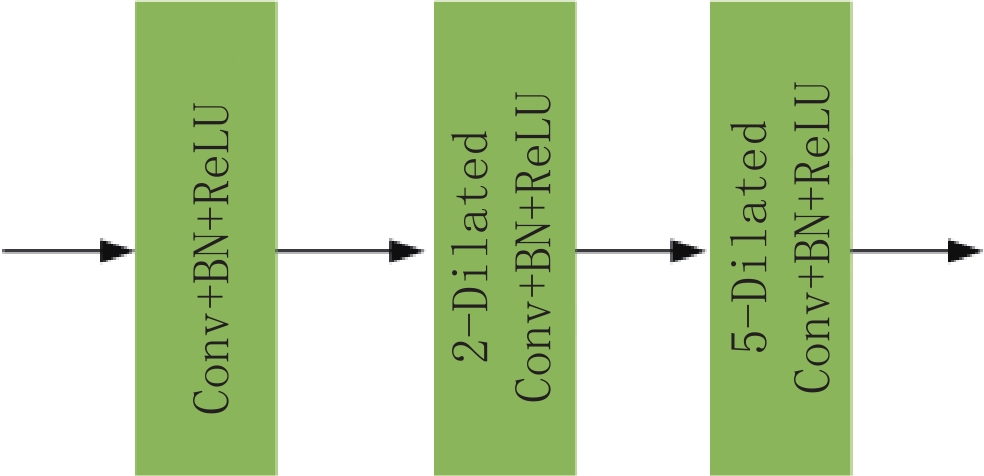
第2层通道：该通道保留传统3×3卷积核的优点，使用扩张因子为1、2、5的空洞卷积提取不同层次的信息[30]，增大了整个网络的感受野，以降低图像去噪的计算成本[31]。空洞卷积模块如图5所示，最后通过卷积操作将通道数变为2，并在输入与输出图像之间进行残差连接。
第3层通道：该通道将传统的UNet网络4层下采样结构减少为2层，减少了参数的计算量。在两次下采样之后加入通道注意力机制以明确特征通道之间的相互依赖性[32]，可以更好的进行特征信息融合，增加网络的非线性映射能力[33]。通道注意力机制如图6所示。最后通过残差学习保证了输入和输出之间信息的完整性。
图6所示的通道注意力机制首先对特征图进行GAP操作，将全局信息压缩到一个通道，得到大小为1×1×256的特征图，再通过两个全连接层（fully connected Layer，FC）+ReLU，中间层的通道数为2，最后在sigmoid激活函数后将输出的特征权重和输入的特征逐像素相乘，以获取到更加丰富的图像细节信息。
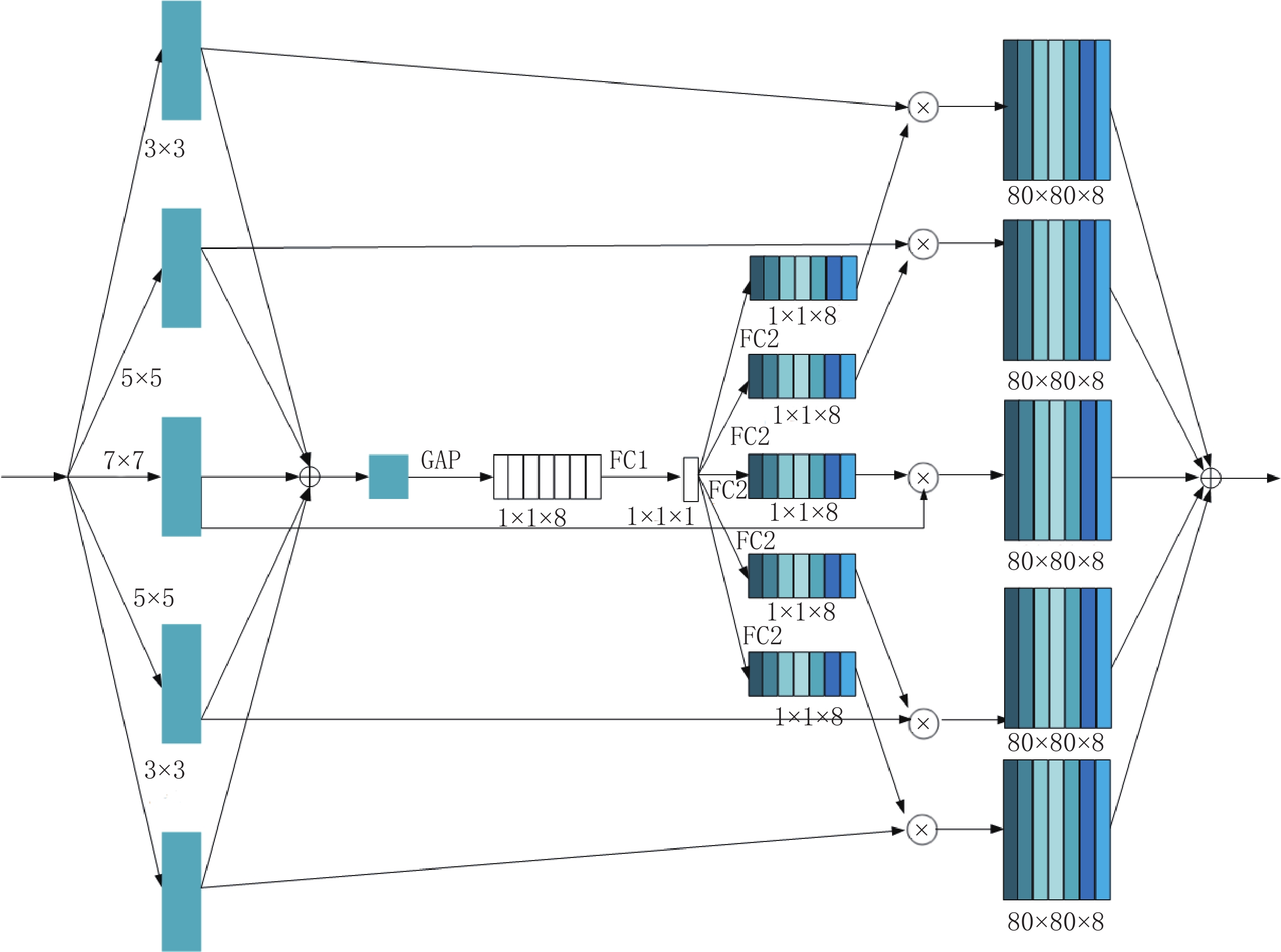
1.2.3 多尺度卷积子网络
该子网络首先使用3×3、5×5和7×7等不同大小的卷积核提取不同尺度的特征信息。3×3 Conv的padding为1，通道数为12。5×5 Conv的padding为2，通道数为32，7×7 Conv的padding为3，通道数为20。通过不同尺度得到的大小相同的特征图进行拼接，通道数为64。之后引入多尺度特征融合模块。
多尺度特征融合模块如图7所示。首先分别通过卷积核大小为3×3、5×5、7×7、5×5和3×3五个Conv操作，然后通过一次GAP和两次FC操作，随后5个分支在相乘操作后进行逐像素相加，最后通过1×1 Conv将通道数变为1，并在该子网络的输入与输出之间进行残差连接，保证了该子网络输入输出之间信息的完整性。
2. 实验设计
2.1 数据集的构建
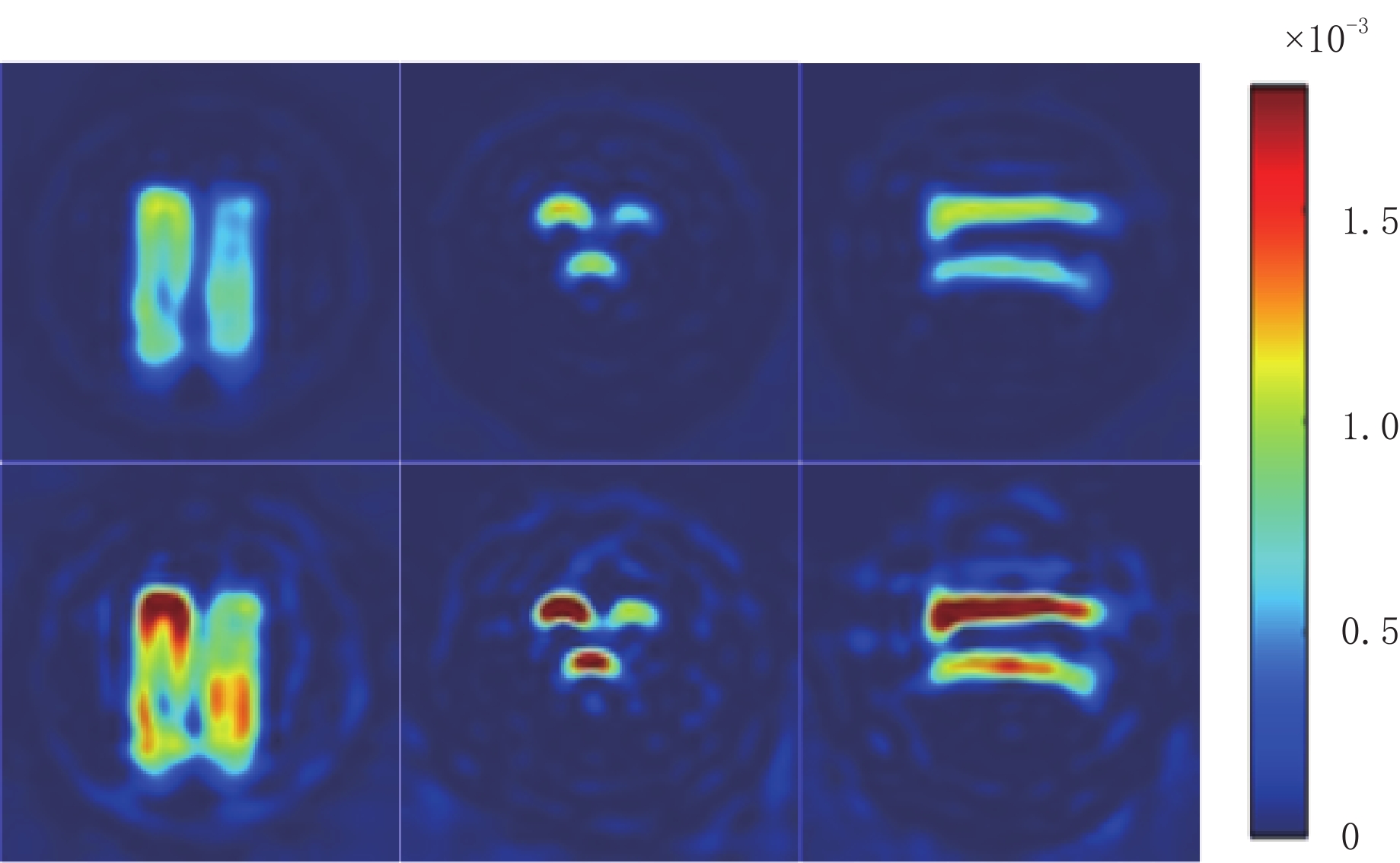
实验数据集均由如图8所示的JIVA-25型小动物EPRI氧成像仪扫描获得。实验模体为5个装有不同浓度三苯甲基溶液的瓶子，通过不同浓度溶液的排列组合共构建了双瓶子和3瓶子模体各10个，共计25个实验模体构成该实验的实验数据，小瓶子示意图如图9 所示。
实验在208个完备投影角度下2000次充分扫描后获得的投影数据作为高精度投影数据，200次不充分扫描后获得的作为含噪投影数据，经过FBP重建后的图像为80×80×80的三维EPRI图像。在X、Y、Z三个方向进行切片处理，可以获得240张二维的80×80 EPRI图像，25个模体共计产生6000 张高精度以及对应的含噪EPRI图像，其中4800张作为训练集来训练网络的性能，600张作为测试集，600张作为验证集。部分EPRI图像如图10所示，第1行表示高精度EPRI图像，第2行表示与之相对应的含噪EPRI图像。在X、Y、Z三个方向上分别选取一张复杂度最高的 EPRI图像，通过比较测试图像的峰值信噪比和结构相似度，以此来评价网络去噪性能的好坏。
2.2 网络训练以及超参数设定
实验使用python 3.7和keras 2.3.1。采用的GPU是NVIDIA Geforce GTX 1080 Ti。采用Adam优化器对损失函数进行优化，迭代次数为12000，初始学习率为0.001，在迭代6000次后，损失函数下降为0.0001，batch_size设置为24。
本文实验中，DnCNN、RED-CNN、UNet迭代12000次大概需运行2 h左右，CBDNet和BRDNet在同样的迭代次数下大概需运行2 h 30 min左右，而公开算法中去噪效果较好的PRIDNet则大约需3 h 40 min左右。本文提议的3MNet网络同样的迭代次数大概需运行2 h 50 min左右，其相较于去噪效果较好的PRIDNet网络有更优的去噪性能，且运行时间更少。虽然3MNet网络的运行时间高于除PRIDNet之外的其他网络，但有更好的去噪结果。
2.3 图像质量评价标准
为了评价网络的去噪性能，本文采用以下两个通用的评价指标：峰值信噪比（peak signal to noise ratio，PSNR）R和均方根误差（root mean square error，RMSE）e。
$$ {{{{R}}}}=20\,{\rm{lg}}\left(\frac{\max{(i)}}{\sqrt{E}}\right)\text{，} $$ (1) $$ {{{e}}} = \sqrt {\frac{1}{{mn}}\sum\limits_{i = 0}^{m - 1} {\sum\limits_{j = 0}^{n - i} {{{\Big( {I(i,j) - K(i,j)} \Big)}^2}} } } \text{，} $$ (2) 其中I表示干净图像；K表示噪声图像；m和n表示图像的高与宽；E表示两张
$m \times n$ 大小的图像之间的均方误差；${\rm{max}}(i)$ 表示图像的最大灰度值；R是一种基于对应像素点之间误差的指标；e是用来衡量两张图像之间的偏差，取值越接近0，说明两张图像越相似。3. 实验结果与分析
本节开展了两个实验，首先是3MNet网络与DnCNN、RED-CNN、UNet、CBDNet、BRDNet及PRIDNet六种经典的去噪网络在相同的EPRI数据集下进行实验对比，然后是3MNet内部子网络的消融实验。
3.1 各种去噪算法的实验比较
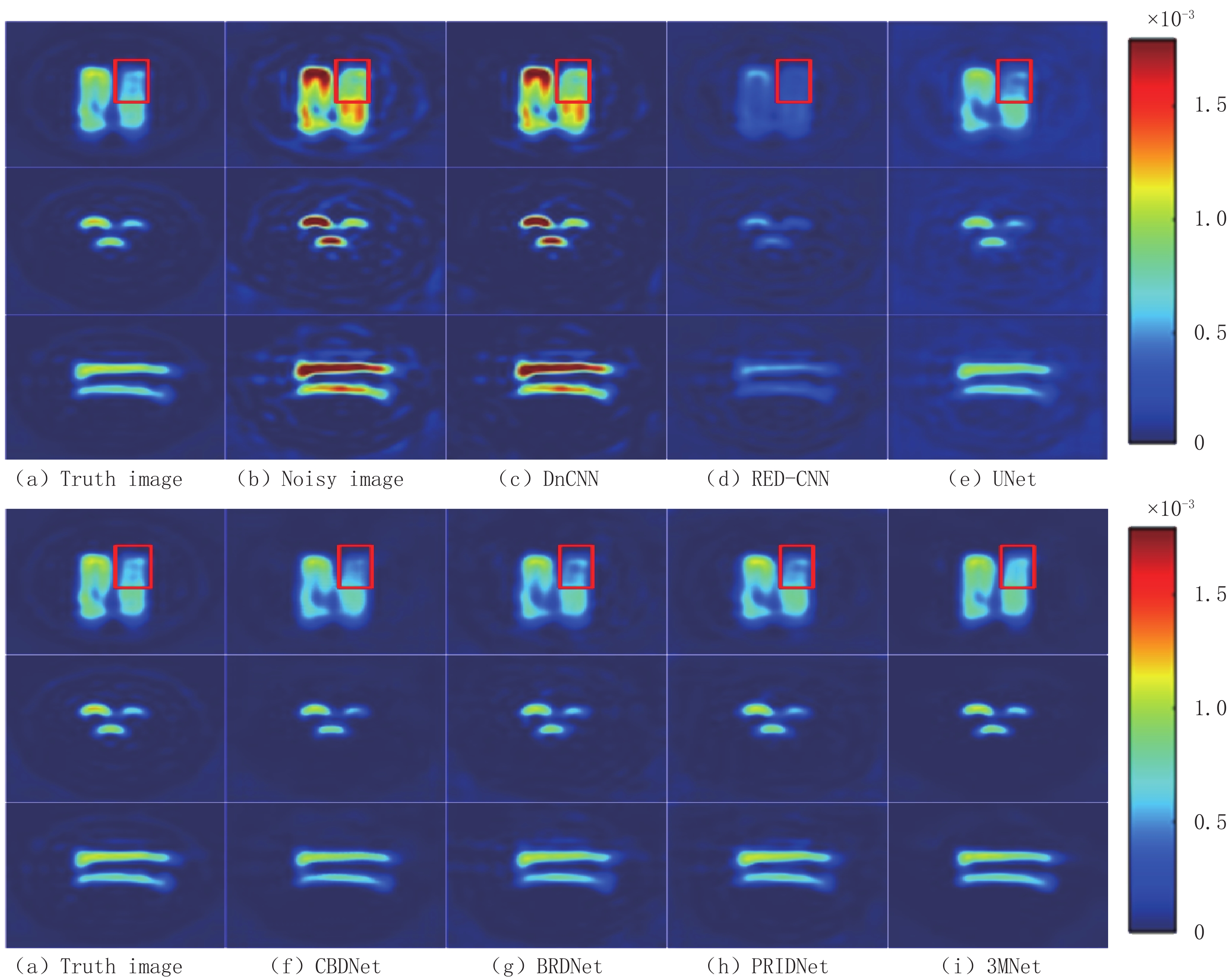
实验将200次不充分扫描后获得的含噪EPRI图像作为网络的输入，将2000次充分扫描后获得的高精度EPRI图像作为标签进行训练。分别在X、Y、Z方向上选取 1张复杂度最高的EPRI图像进行定性分析，测试结果如图11和图12所示。
由图11可见，DnCNN的去噪结果图（c）仍存在明显噪声，组织结构信息模糊，严重干扰重要信息的判断；RED-CNN的去噪结果图（d）中图像重要信息丢失严重且表现过度平滑，未将噪声和重要特征信息分开处理，多数纹理细节被当成噪声去除；尽管UNet的去噪结果图（e）从视觉效果来看有效地压制了噪声，但局部区域的图像细节信息处理效果欠佳；CBDNet的去噪结果图（f）在保留组织边缘信息方面表现较好，肉眼可见的噪声已基本去除，然而图像内部两瓶子交汇之处纹理结构信息恢复不完整，组织边界区分不够清晰，未能处理好复杂的边缘细节部分；BRDNet的去噪结果图（g）周围轮廓处的噪声去除效果不如CBDNet，斑点噪声未完全去除干净，但是一些复杂的细节信息保留比较完整；PRIDNet的去噪结果图（h）相较与其他算法，尽可能地保留了EPRI图像中的细节特征，但图像中心的一些细节纹理结构模糊。
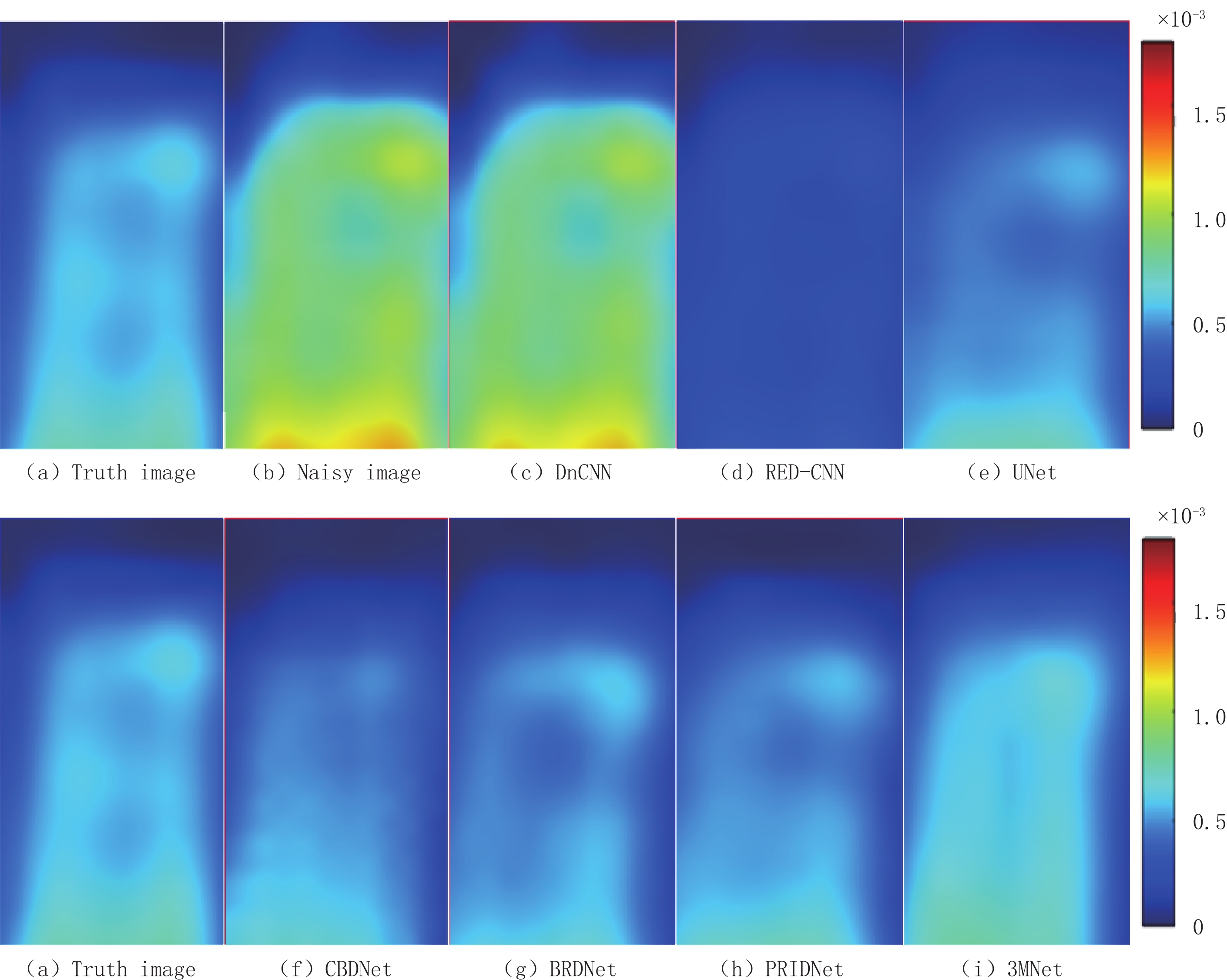
为进一步定性比较本文算法的优越性，选取细节信息较多的X轴方向图像放大同等倍数后截取红色方框部分进行分析比较，由图12明显可见CBDNet、BRDNet、PRIDNet虽然整体上肉眼可见已经恢复大体结构信息，但本文提出的3MNet网络去噪结果图（i）保留了更多的图像细节信息，在局部细节上相似度更高，有效地压制了随机噪声。
为了更加客观地对网络的去噪结果进行评价，表1给出了不同算法去噪实验的定量比较结果。从表1可见，在X、Y、Z三个方向上本文提出的 3MNet网络较传统的去噪网络在PSNR和RMSE上都有较大提高。在X方向上 3MNet比去噪效果较好的PRIDNet网络在PSNR上高出2.823 dB，Y方向上高出 0.973 dB，Z方向上高出 0.744 dB，RMSE也是在X方向上数值变化幅度最大。同样，网络在Y方向上的结果 PSNR数值最高，Z方向上次之，X方向上最低，说明X方向上选取的 EPRI图像最为复杂，这也可以解释X方向上高出的 PSNR值远高于其他两个方向的原因，因为对于简单的图像传统的去噪网络已经可以处理的较好，故数值提高幅度不大，后期网络的改进主要参考在复杂EPRI图像上数值的变化幅度。
表 1 去噪实验对比结果Table 1. Comparison results of denoising experiments方法 X Y Z R/dB e R/dB e R/dB e DnCNN 82.142 1.563e-4 85.175 1.102e-4 82.234 1.547e-4 RED-CNN 83.495 1.338e-4 88.428 7.580e-5 85.440 1.070e-4 UNet 89.157 6.970e-5 89.257 6.890e-5 89.092 7.020e-5 CBDNet 92.837 4.562e-5 95.498 3.358e-5 95.235 3.462e-5 BRDNet 93.519 4.218e-5 96.901 2.858e-5 96.035 3.157e-5 PRIDNet 93.943 4.017e-5 96.284 3.068e-5 95.770 3.255e-5 3MNet 96.766 2.902e-5 97.257 2.743e-5 96.514 2.988e-5 3.2 3MNet内部子网络的性能比较
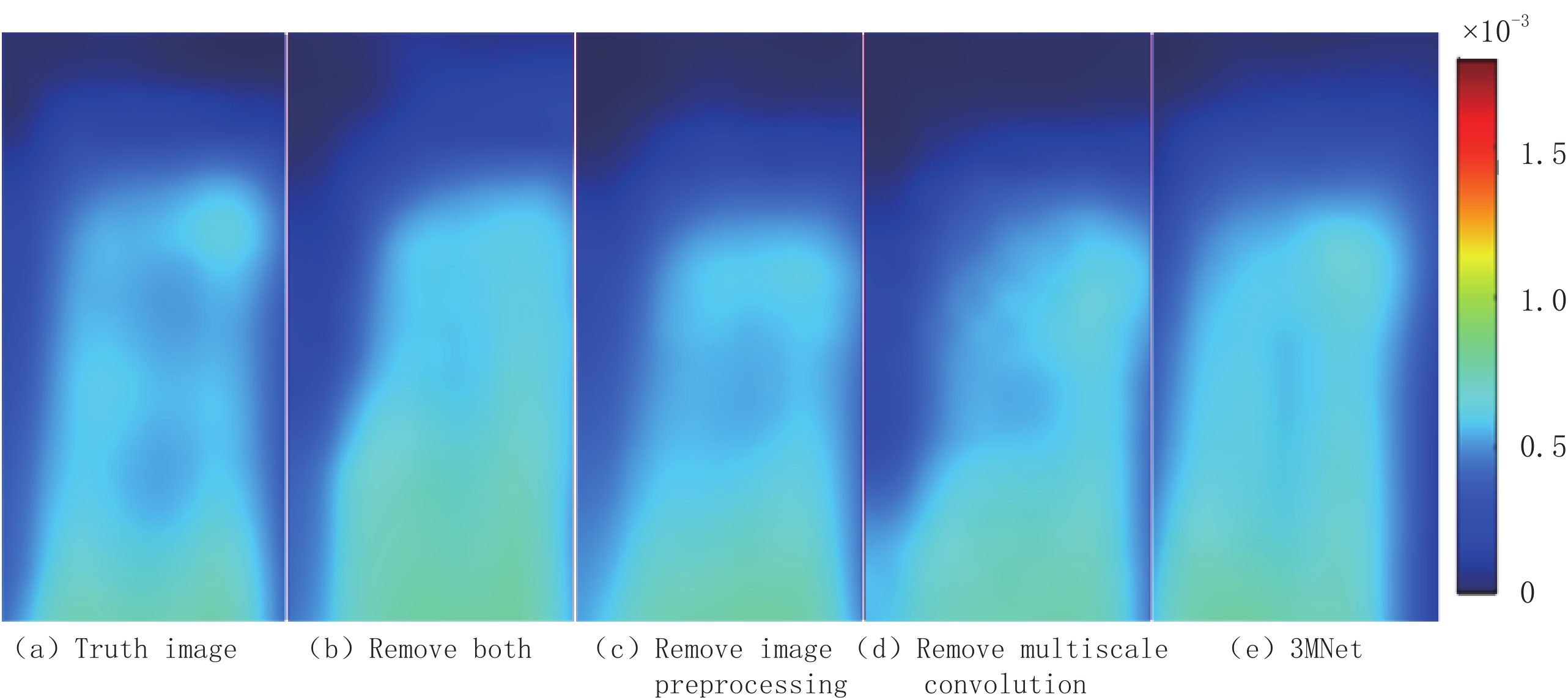
本文提出的3MNet去噪网络共分3个子网络：图像预处理子网络、三通道卷积子网络和多尺度卷积子网络，为探究其他两个子网络对三通道卷积子网络的影响，对3MNet网络去掉图像预处理子网络或多尺度卷积子网络或者两者都去掉进行实验对比分析。本次对比实验选取X方向上的 EPRI图像进行探究，实验结果如图13所示。将红框部分放大至相同倍数后对比分析，由图14可以观察到去掉任一子网络都会影响实验结果，且易发现两个子网络都去掉后细节信息损失较多。
![]()
图 13 3MNet内部子网络实验对比图Figure 13. 3MNet comparison diagram of internal sub-network experiment![]()
图 14 3MNet内部子网络实验局部放大图Figure 14. 3MNet partial enlargement of internal sub-network experiment由表2可见，3MNet网络在去掉多尺度卷积子网络后RSNR降低了1.119 dB，去掉图像预处理子网络后降低了1.444 dB，两者都去掉后降低了3.403 dB。RMSE的变化也符合此规律。定性和定量实验结果表明，两个子网络都去掉后大幅降低了网络的去噪性能，图像预处理比多尺度卷积子网络更能提高3MNet网络压制随机噪声的性能。
表 2 3 MNet内部子网络实验对比结果Table 2. 3 MNet internal sub-network experimental comparison results方法 R/dB e（×10-5） Remove both 93.363 4.294 Remove image preprocessing 95.322 3.427 Remove multiscale convolution 95.647 3.301 3MNet 96.766 2.902 4. 结束语
本文提出的多通道、多尺度、多拼接的3MNet去噪网络，引入双注意力机制，使得网络可以更好的学习到真实环境下复杂的噪声特征；构建三通道卷积子网络，提高了网络对非均匀噪声分布图像的去噪性能；构建多尺度卷积子网络，提高了图像细节信息的学习能力；引入多拼接机制，增强了特征融合。
与现有的其他6种去噪网络对比，本文提出的深度网络在EPRI图像去噪中，表现出更优的性能。基于3MNet的图像去噪技术，实现EPRI扫描过程接近10倍的加速效果。该网络使用的各种有效机制对其他成像模态中的图像处理问题，也有一定的借鉴意义。
未来将在3MNet网络基础上进一步引入迁移学习，探究对EPRI图像细节信息恢复更强的注意力机制，以期实现更高精度的快速EPRI成像。
-
![]()
图 13 3MNet内部子网络实验对比图
Figure 13. 3MNet comparison diagram of internal sub-network experiment
![]()
图 14 3MNet内部子网络实验局部放大图
Figure 14. 3MNet partial enlargement of internal sub-network experiment
表 1 去噪实验对比结果
Table 1 Comparison results of denoising experiments
方法 X Y Z R/dB e R/dB e R/dB e DnCNN 82.142 1.563e-4 85.175 1.102e-4 82.234 1.547e-4 RED-CNN 83.495 1.338e-4 88.428 7.580e-5 85.440 1.070e-4 UNet 89.157 6.970e-5 89.257 6.890e-5 89.092 7.020e-5 CBDNet 92.837 4.562e-5 95.498 3.358e-5 95.235 3.462e-5 BRDNet 93.519 4.218e-5 96.901 2.858e-5 96.035 3.157e-5 PRIDNet 93.943 4.017e-5 96.284 3.068e-5 95.770 3.255e-5 3MNet 96.766 2.902e-5 97.257 2.743e-5 96.514 2.988e-5 
下载: 导出CSV
表 2 3 MNet内部子网络实验对比结果
Table 2 3 MNet internal sub-network experimental comparison results
方法 R/dB e（×10-5） Remove both 93.363 4.294 Remove image preprocessing 95.322 3.427 Remove multiscale convolution 95.647 3.301 3MNet 96.766 2.902
下载: 导出CSV
-
[1] REDLER G, EPEL B, HALPERN H J. Principal component analysis enhances SNR for dynamic electron paramagnetic resonance oxygen imaging of cycling hypoxia in vivo[J]. Magnetic Resonance in Medicine, 2013, 71(1): 440−450.
[2] CHEN J, CHEN Q, LIANG C, et al. Albumin-templated biomineralizing growth of composite nanoparticles as smart nanotheranostics for enhanced radiotherapy of tumors[J]. Nanoscale, 2017, 146(39): 14826−14835.
[3] EPEL B, BOWMAN M K, MAILER C, et al. Absolute oxygen R-1 e imaging in vivo with pulse electron paramagnetic resonance[J]. Magnetic Resonance in Medicine, 2014, 72(2): 362−368. doi: 10.1002/mrm.24926
[4] QIAO Z, REDLER G, EPEL B, et al. Comparison of parabolic filtration methods for 3D filtered back projection in pulsed EPR imaging[J]. Journal of Magnetic Resonance, 2014, 248: 42−53. doi: 10.1016/j.jmr.2014.08.010
[5] EPEL B, SUNDRAMOORTHY S V, BARTH E D, et al. Comparison of 250 MHz electron spin echo and continuous wave oxygen EPR imaging methods for in vivo applications[J]. Medical Physics, 2011, 38(4): 2045−2052. doi: 10.1118/1.3555297
[6] SIDKY E Y, KAO C M, PAN X. Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT[J]. Journal of X-ray Science and Technology, 2006, 14(2): 119−139.
[7] SIDKY E Y, PAN X. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization[J]. Physics in Medicine and Biology, 2008, 53(17): 4777−4807. doi: 10.1088/0031-9155/53/17/021
[8] LIU Y, MA J, FAN Y, et al. Adaptive-weighted total variation minimization for sparse data toward low-dose X-ray computed tomography image reconstruction[J]. Physics in Medicine and Biology, 2012, 57(23): 7923−7956. doi: 10.1088/0031-9155/57/23/7923
[9] ZHANG Y, ZHANG W H, CHEN H, et al. Few-view image reconstruction combining total variation and a high-order norm[J]. International Journal of Imaging Systems and Technology, 2013, 23(3): 249−255. doi: 10.1002/ima.22058
[10] 闫慧文, 乔志伟. 基于ASD-POCS框架的高阶TpV图像重建算法[J]. CT理论与应用研究, 2021,30(3): 279−289. DOI: 10.15953/j.1004-4140.2021.30.03.01. YAN H W, QIAO Z W. High order TpV image reconstruction algorithms based on ASD-POCS framework[J]. CT Theory and Applications, 2021, 30(3): 279−289. DOI: 10.15953/j.1004-4140.2021.30.03.01. (in Chinese).
[11] SIDKY E Y, REISER I, NISHIKAWA R M, et al. Practical iterative image reconstruction in digital breast tomosynthesis by non-convex TpV optimization[J]. Medical Imaging 2008: Physics of Medical Imaging, 2008: 6913. DOI: 10.1117/12.772796.
[12] JAIN V, SEUNG H S. Natural image denoising with convolutional networks[C]//International Conference on Neural Information Processing Systems, 2008: 769-776.
[13] MAO X, SHEN C, YANG Y B. Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections[J]. Advances in Neural Information Processing Systems, 2016, 29: 2802−2810.
[14] ZHANG K, ZUO W, CHEN Y, et al. Beyond a gaussian denoiser: Residual learning of deep CNN for image denoising[C]//IEEE Transactions on Image Processing, 2017, 26(7): 3142-3155.
[15] HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016: 770-778.
[16] IOFFE S, SZEGEDY C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[J]. JMLRorg, 2015, 37: 448−456.
[17] CHEN H, ZHANG Y, KALRA M K, et al. Low-dose CT with a residual encoder-decoder convolutional neural network[J]. IEEE Transactions on Medical Imaging, 2017, 36(12): 2524−2535. doi: 10.1109/TMI.2017.2715284
[18] ZHANG K, ZUO W, ZHANG L. FFDNet: Toward a fast and flexible solution for CNN based image denoising[J]. IEEE Transactions on Image Processing, 2018, 27(9): 4608−4622. doi: 10.1109/TIP.2018.2839891
[19] RONNEBERGER O, FISCHER P, BROX T. U-net: Convolutional networks for biomedical image segmentation[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention, 2015: 234-241.
[20] GUO S, YAN Z, ZHANG K, et al. Toward convolutional blind denoising of real photographs[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018: 1712-1722.
[21] TIAN C, XU Y, ZUO W. Image denoising using deep CNN with batch renormalization[C]//Neural Networks, 2019, 121: 461-473.
[22] YU F, KOLTUN V. Multi-scale context aggregation by dilated convolutions[C]//Intermational Conference on Learning Representations, 2016.
[23] ZHAO Y Y, JIANG Z Q, MEN A, et al. Pyramid real image denoising network[C]//2019 IEEE Visual Communications and Image Processing (VCIP), 2020.
[24] MILDENHALL B, BARRON J T, CHEN J, et al. Burst denoising with kernel prediction networks[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018: 2502-2510.
[25] HU J, SHEN L, SUN G. Squeeze-and-excitation networks[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018: 7132-7141.
[26] WOO S, PARK J, LEE J Y, et al. Cbam: Convolutional block attention module[C]//Proceedings of the European Conference on Computer Vision (ECCV), 2018: 3-19.
[27] SZEGEDY C, IOFFE S, VANHOUCKE V, et al. Inception-v4, inception-resnet and the impact of residual connections on learning[C]//Thirty-First AAAI Conference on Artificial Intelligence. San Francisco: 2017, 31(1): 4278-4284.
[28] WU Z, SHEN C, Van den HENGEL A. Wider or deeper: Revisiting the resnet model for visual recognition[J]. Pattern Recognition, 2019, 90: 119−133. doi: 10.1016/j.patcog.2019.01.006
[29] ZHANG Y, TIAN Y, KONG Y, et al. Residual dense network for image super-resolution[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018: 2472-2481.
[30] LIU C, SHANG Z, QIN A. A multiscale image denoising algorithm based on dilated residual convolution network[C]//Chinese Conference on Image and Graphics Technologies, 2019: 193-203.
[31] WANG T, SUN M, HU K. Dilated deep residual network for image denoising[C]//2017 IEEE 29th International Conference on Tools with Artificial Intelligence (ICTAI), 2017: 1272-1279.
[32] LU Y, JIANG Z, JU G, et al. Recursive multi-stage upscaling network with discriminative fusion for super-resolution[C]//2019 IEEE International Conference on Multimedia and Expo (ICME), 2019: 574-579.
[33] 陈康, 狄贵东, 张佳佳, 等. 基于改进U-net卷积神经网络的储层预测[J]. CT理论与应用研究, 2021,30(4): 403−415. DOI: 10.15953/j.1004-4140.2021.30.04.01. CHEN K, DI G D, ZHANG J J, et al. Reservoir prediction based on improved U-net convolutional Neural network[J]. CT Theory and Applications, 2021, 30(4): 403−415. DOI: 10.15953/j.1004-4140.2021.30.04.01. (in Chinese).
计量
- 文章访问数: 399
- HTML全文浏览量: 175
- PDF下载量: 38
