Research on Image Analysis Method of Spectral CT Based on Principal Component Analysis
-
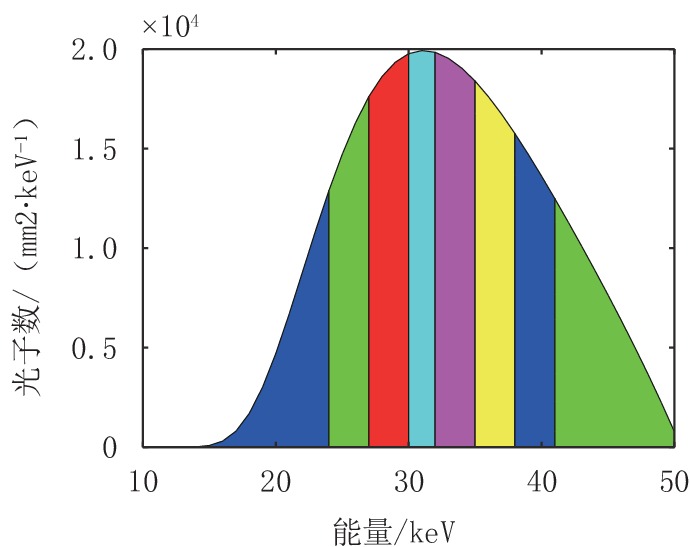
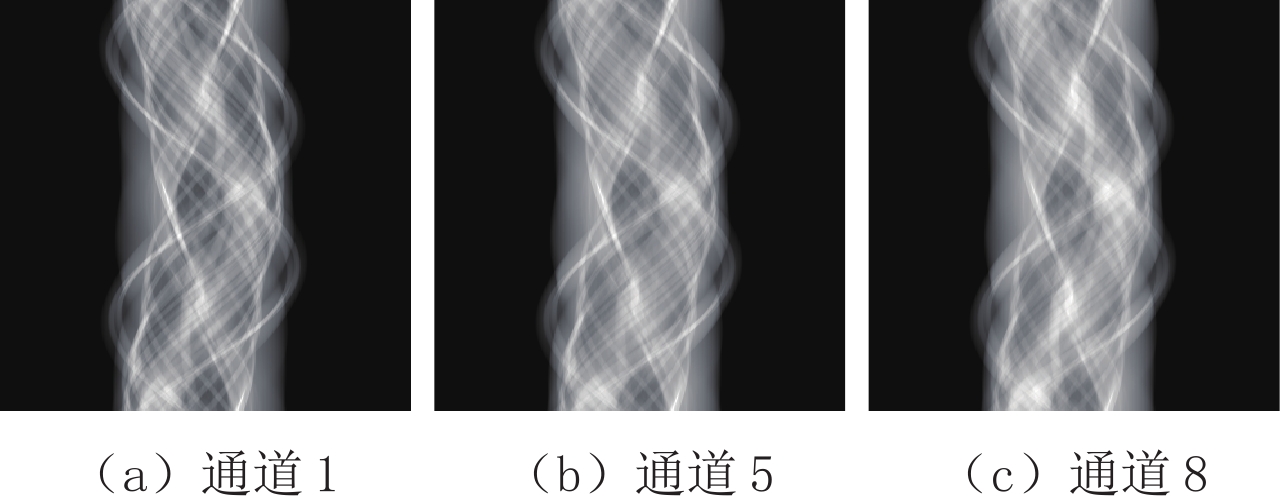
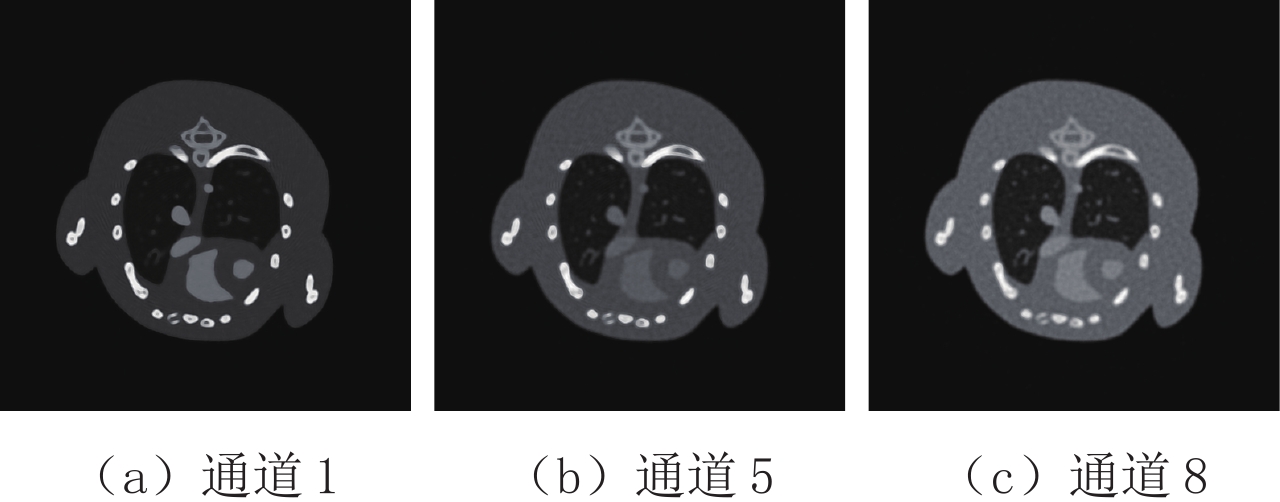
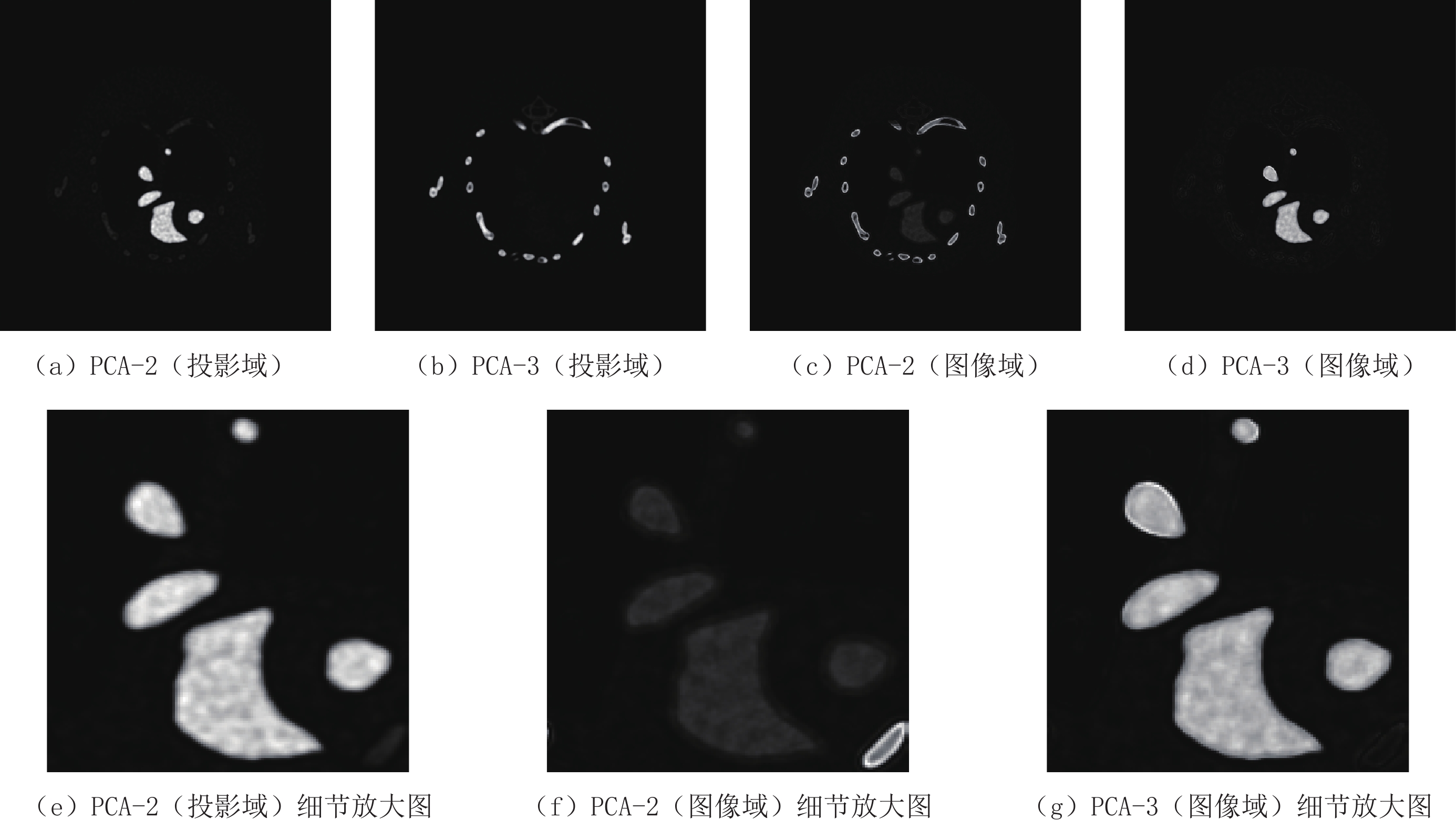
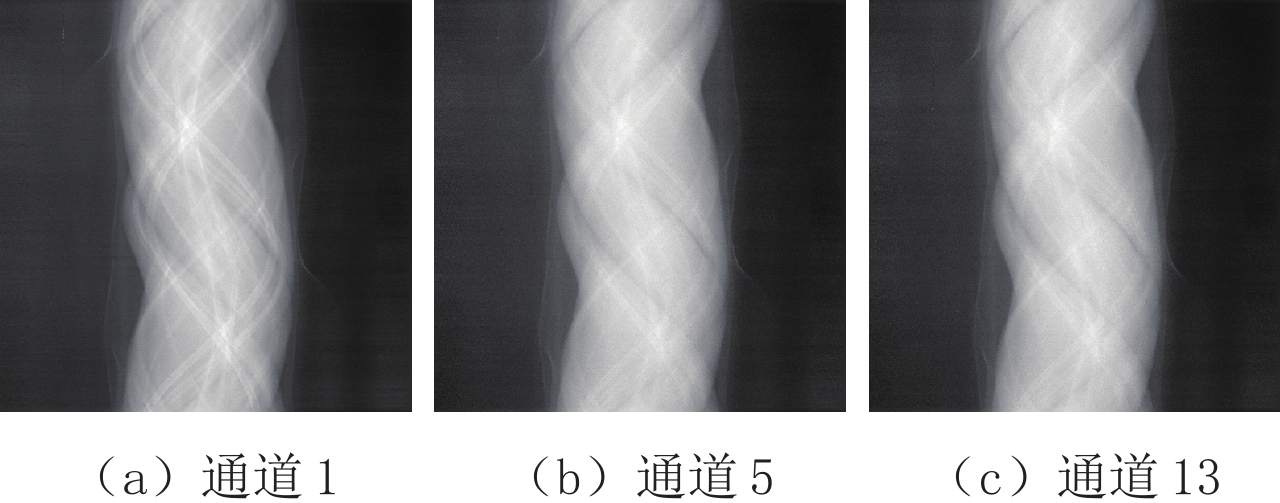
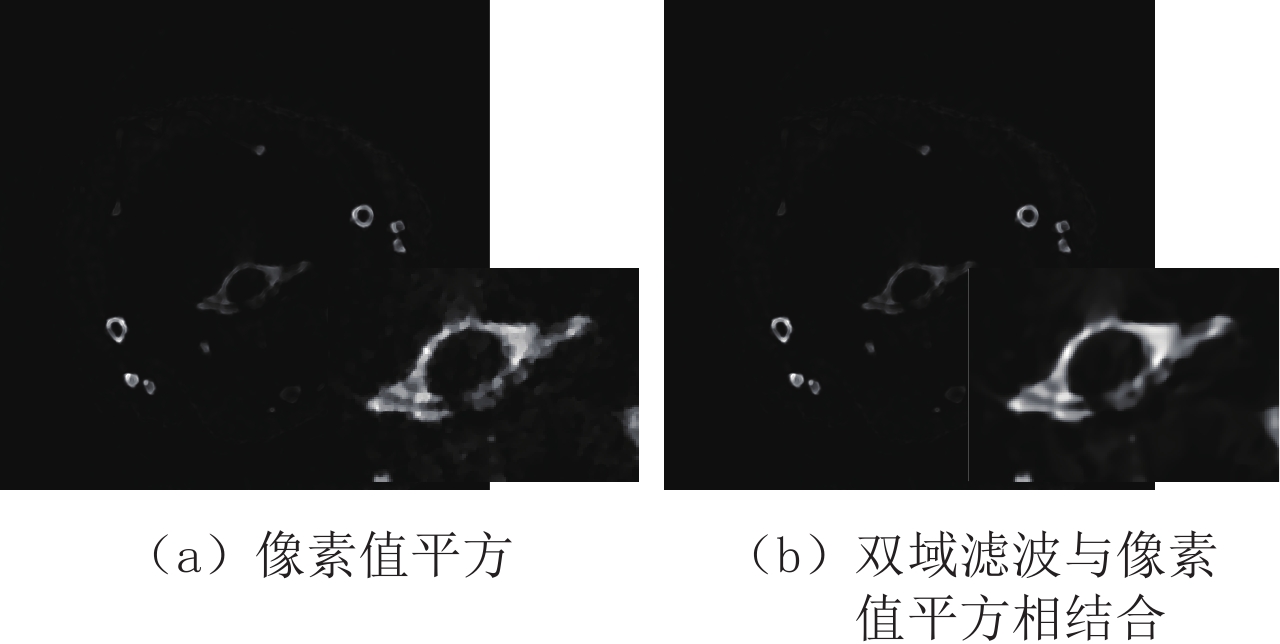
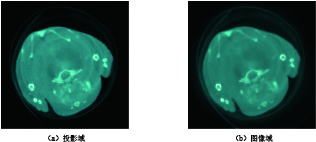
摘要: 基于光子计数探测器的能谱CT，可以同时采集多个能谱通道的投影数据，并获得相应能量范围内物质的吸收特征，可以有效应用于物质识别与材料分解。主成分分析是一种很好的多元数据分析技术，可以用于处理多能谱CT数据。本文分别在投影域和图像域对能谱CT数据进行主成分分析，并对分析结果做出系统比较。为了减少噪声的影响，提高能谱CT图像的彩色表征性能，提出双域滤波与像素值平方相结合的方法，用于含噪声的主成分图像去噪，然后将所选取的主成分图像映射到RGB颜色通道。实验结果表明，无论是在投影域还是图像域进行主成分分析，都可以获取清晰的CT图像，识别出物质的不同成分。相较于在图像域的主成分分析方法，在投影域进行主成分分析能够保留物质的更多细节，获取更清晰的彩色CT图像。Abstract: Spectral computed tomography (CT) based on photon counting detector can simultaneously collect projection data of multiple spectral channels and obtain absorption characteristics of material within corresponding energy ranges, so it can be effectively applied to material identification and material decomposition. Principal component analysis is an excellent multivariate analysis technique, which can be applied to process multi-energy spectral CT data. In this paper, principal component analysis was performed on spectral CT data in projection domain and image domain respectively, and the analysis results were compared systematically. Meanwhile, in order to reduce the influence of noise and improve the color characterization performance of spectral CT images, the method of combining double domain filtering with pixel value square was proposed to denoise the noisy principal component images, and then the selected principal component images were mapped to RGB color channels. The experimental results demonstrate that the principal component analysis can obtain clear CT images and identify the different components of the substance, whether in the projection domain or the image domain. However, compared with the principal component analysis method in the image domain, principal component analysis in the projection domain can retain more details of the substance and acquire clearer color CT images.
-
地震正演模拟是在地下介质结构和物性参数已知的情况下，利用数值计算的方法来研究地震波在地下介质中的传播规律，从而获得理论地震记录。常见的地震波场数值模拟方法包含有限元法[1]、有限差分法[2-3]和伪谱法[4]等。董良国等[5]、裴正林等[6]、井涌泉等[7]、龚明平等[8]先后对地震数值模拟方法进行了改进和完善，为技术发展做出了突出贡献。如今，随着大规模、高密度地震勘探技术的推广和对成像精度要求的提高，地震数值模拟的计算量和花费也在不断增加。因此，如何在有限计算资源下提高计算效率，成为解决大规模地球物理问题的关注焦点。
半精度浮点型数据（half-precision floating-point，FP16）因其数据精度较低，通常不用于地震数值模拟，但它具有比常规浮点数更高的单位时间数据吞吐量，从而在近年得到人们的重视。宋聂平等[9]曾进行了相关测试，证明半精度浮点数在特定情形能提高程序的计算效率；曹克乾等[10]则利用该方法对超越函数设计优化，取得了良好效果；Gabriel[11]将其应用在地震数值模拟，实现过程在保证计算稳定性和精度的前提下，节省计算资源的同时可提高计算效率。
并行计算是将一个计算任务划分为多个子任务，然后让各子任务同时执行来完成计算[12]。有限差分法地震数值模拟具有较高的可并行性，将大规模正演模拟任务按一定标准进行分解，随后分别计算，在保证精度和稳定性的同时，能大幅提高计算效率[13]。OpenMP（Open Multi-Processing）是一种应用程序接口（API），也是较为成熟和应用广泛的编译器指令，为共享内存环境的并行编程提供了支持。因其可移植性好、功能强大、计算效率高等优点，在地球物理研究领域有着普遍的应用[14-16]。Franke等[17]在大地电磁有限元模拟中使用了OpenMP以提高计算效率；张伟等[18]将OpenMP应用于三维有限差分数值模拟，也取得了显著的加速效果。半精度浮点数能优化参与计算的数据类型，而OpenMP则能分割计算区域实现并行计算，若是在大规模地震数值模拟中将这两种方法的优势相结合，即可在提高计算效率的同时大幅减少对计算内存的需求。
为此，本文针对上述两类技术方法的特点，实现基于半精度浮点数优化与OpenMP的三维波动方程地震数值模拟。首先利用半精度浮点数对地震数值模拟常用的浮点型数据（如float32）进行优化；再利用并行应用程序接口OpenMP在多核CPU下，通过划分波场区域的方式将各波场赋予不同的计算核心实现并行；最后的数值试验表明，在保证计算精度和稳定性的条件下，该策略可以有效提高计算效率和计算机CPU的运算能力。
1. 三维波动方程地震数值模拟
1.1 三维波动方程的差分格式
均匀各向同性介质三维声学波动方程可表示为[19]：
$$ \frac{{\text{1}}}{{{v^2}}}\frac{{{\partial ^2}p}}{{\partial {t^2}}} = \frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}} + \frac{{{\partial ^2}u}}{{\partial {z^2}}}\text{，} $$ (1) 式中，x、y、z为空间位置坐标，t为时间，声学波场
$ p = p\left( {x,y,z,t} \right) $ ，速度场$ v = v\left( {x,y,z} \right) $ 。在波动方程离散化过程中，时间导数采用二阶中心差分，空间导数用2N阶精度的差分做近似，则得到差分方程：$$ {p^{n + 1}}\left( {i,j,k} \right) = 2{p^n}\left( {i,j,k} \right) - {p^{n - 1}}\left( {i,j,k} \right) + \Delta {t^2}{v^2}\bigg( {L_x^2\Big( {p\left( {i,j,k} \right)} \Big) + L_y^2\Big( {p\left( {i,j,k} \right)} \Big) + L_z^2\Big( {p\left( {i,j,k} \right)} \Big)} \bigg) \text{，} $$ (2) 其中，Lx、Ly、Lz分别表示波场函数对空间偏导数的差分算子。通过前一时刻波场
$ {p^{n - 1}}\left( {i,j,k} \right) $ 和现在时刻波场$ {p^n}\left( {i,j,k} \right) $ 即可计算后一时刻波场$ {p^{n + 1}}\left( {i,j,k} \right) $ ，依此完成有限差分法的地震波场更新。1.2 稳定性
依据二维地震数值模拟的稳定性分析方法，可以得到三维声学方程2N阶空间差分精度的稳定性条件[20]：
$$ v\Delta t\sqrt {\frac{1}{{\Delta {x^2}}} + \frac{1}{{\Delta {{\text{y}}^2}}} + \frac{1}{{\Delta {z^2}}}} \leq \sqrt {\frac{2}{{\displaystyle \sum {_{n = 1}^NC_n^{(N)}\Big( {1 - \left( { - 1} \right){}^n} \Big)} }}} ，$$ (3) 式中，v是模型中速度的最大值。对于初级的空间2阶差分稳定性条件可简化为：
$$ \frac{{v\Delta t}}{{\Delta x}} \leq \frac{1}{{\sqrt 3 }} 。 $$ (4) 1.3 边界处理
对于模型边界波场反射的问题，本文采用完全匹配层（perfectly matched layer，PML）方法，在波场计算区域的外围加上相应的完全匹配层，并在其层内引入衰减因子，当地震波在匹配层之间传播时其能量将按传播距离指数衰减，从而达到消除虚假反射的目的。
如图1所示，三维波动方程的PML边界处理需在计算区域的边界加上辅助的匹配层，三维波动方程正演模拟的PML区域共包含6个面区、12条棱区和8个棱角区。先将原始地震模型边界按PML层数进行扩充，然后在匹配层内的每一离散结点上添加衰减系数，以此达到边界对波场吸收的效果。
2. 优化策略
针对三维波动方程地震数值模拟计算量大、计算效率低的问题，本文通过半精度浮点数优化与OpenMP技术相结合的方法，达到了提高计算效率的效果。具体措施如下：
①引入半精度浮点数：利用半精度浮点数（FP16）对地震数值模拟常用的浮点型数据类型进行优化，在保证精度的前提下，减少内存占用和加速计算。②OpenMP并行计算：使用OpenMP并行计算框架，将时间循环中的计算区域按照CPU核心数划分成若干子域，然后在每一子域上执行网格点处的波场更新，从而提高计算效率。③数值稳定性：需要选择合适的时间和空间步长，以及边界条件和初始条件。
同时，本文采用放缩震源的方式引入比例标量，对参与数值计算的速度和子波进行重匹配，从而保证计算结果的精度。图2是基于半精度浮点数优化与OpenMP的三维波动方程数值模拟流程图。
![]()
图 2 使用半精度浮点数优化与OpenMP的三维地震数值模拟流程图Figure 2. Flow chart of three-dimensional seismic, numerical simulations using half-precision floating-point number optimization and OpenMP2.1 半精度浮点数优化方法
双精度、单精度浮点型数据因其计算稳定，数据表示范围广的优点被应用于地震数值模拟。若是引入半精度浮点数，将常用浮点型数据通过一定方式转化为半精度浮点型数据，可以达到更高的单位时间数据吞吐量，提高计算效率。
半精度浮点数是一种浮点数表示方法，通常用于节省存储空间和提高计算速度。相对于双精度或单精度浮点数，半精度浮点数仅使用16位（2字节）的存储空间，可以显著减少存储和传输的开销。图3展示了波场数据采用单精度和半精度两种类型的对比。
![]()
图 3 数值模拟中两种精度数据类型的对比Figure 3. Comparison of two data type accuracies in numerical simulations半精度浮点数在地震模拟中的优化可以从几个方面进行：
（1）算法选择：在使用半精度浮点数进行计算时，需要考虑算法的选择。由于半精度浮点数的精度较低，不适用于高精度计算，因此需要选择适合于半精度浮点数的算法，以保证计算精度和效率。传统的单精度浮点型数据可应用于不同行业，但目前半精度浮点型数据却鲜有人使用。这两种类型的浮点数最大的区别在于数据动态范围的不同，单精度浮点型数据拥有1个符号位，8个指数位和23个尾数位，总共占据32个比特，它表示的数值能精确到小数点后6～7位；半精度浮点型数据则拥有1个符号位，5个指数位和10个尾数位，只占据16个比特，所表示的数值只能精确到小数点后3～4位。表1展示了单精度、半精度数据类型的具体对比。
表 1 两种精度数据类型对比Table 1. Comparison of two data precision types精度 符号位 指数位 尾数位 有效位 小数位 总位数 最小值 最大值 单精度 1 8 23 7 6 32 1.17×10-38 3.4×1038 半精度 1 5 10 3 2 16 6.1×10-5 65504 （2）数据类型转换：在进行半精度浮点数计算时，需要将其它的数据类型转换为半精度浮点数。操作人员可以使用硬件指令或软件库来实现半精度浮点数的转换和计算。但在CPU环境下，当前适用于计算机语言的数据类型转换只能通过编程实现。
（3）并行计算：半精度浮点数的计算速度比双/单精度浮点数要快，若想进一步提高计算效率，可以结合多线程或SIMD（single instruction, multiple data）指令来实现半精度浮点数的并行计算，如使用OpenMP进行多线程编程。
（4）数据存储和传输：半精度浮点数可以节省存储空间和传输带宽。但在具体实现时需要考虑相应的一些问题，由于半精度浮点数的精度较低，容易出现计算误差，所以在数据存储和传输过程中应注意数据的精度和有效性。
在CPU平台的Windows系统下，半精度浮点数据类型目前还没有具体的定义，也缺乏相应的计算程序，已有的数值算法大多是在GPU平台开发。为此，我们给出CPU平台下半精度浮点数的自定义方法，以满足实际计算的需求。具体做法是：如图4所示，在地震波场模拟中，假设计算区域的波场值为单精度数据，将其符号位、指数位和尾数位分离，然后保持符号位不变，对指数位向前截取到5位，对尾数位向前截取到10位，达到半精度的位数要求，最后将其组合后输出，完成数据类型的转换。
![]()
图 4 不同精度浮点数的转换Figure 4. Conversion of floating-point numbers with different accuracies上述方法虽能解决CPU情形半精度浮点数的定义，但还需要考虑计算的精度问题。对于地震数值模拟来说，若波场计算中所使用的数据为单精度浮点型，每一离散网格点的波场值至少要精确到小数点后4位，而半精度浮点数只能精确到小数点后 2位。由于半精度数据的范围是6.1×10-5～65504，而单精度数据表示的范围是1.17×10-38～3.4×1038，所以为了保持半精度浮点数的有效精度，我们采用放缩震源的方式，对参与数值计算的地震速度和子波进行重匹配，从而保障计算结果的精度。具体做法为：设震源为雷克子波，给定其振幅初值为1，即波场值的浮动范围整数位不超过1位。在地震数值模拟中单精度浮点数精确到小数点后4位，即有效位是1+4=5位，则半精度浮点数的有效精度也应该是5位。通过将震源初值放大100倍，并使波场值的有效位数与半精度浮点数进行匹配，转换后的数据则可以达到计算精度的要求。
为了保留有效波场信息，程序中需要对放大后的结果进行一定比例的缩小，即引入两个比例因子：
$$ \begin{gathered} {e_v} = - {\log _2}\Big( {\Delta t\max \left( M \right)} \Big) \\ {e_s} = - {\log _2}\Big( {\Delta t\max \left( S \right)} \Big) \\ \end{gathered} \text{，} $$ (5) 式中M为模型最大速度；S为震源信号的最大振幅值。将模型速度参数、震源项进行比例放缩：
$$ \begin{gathered} v' = {2^{{e_v} - {e_s}}}v \\ {{s'}} = {2^{ - {e_s}}}{{s}} \\ \end{gathered} \text{，} $$ (6) 即能最大程度保留有效波场信息。
2.2 OpenMP优化方法
对于地震数值模拟来说，计算量最大、耗时最多的环节是波场更新。波场计算通常采用时间-空间循环的方式，空间循环是更新区域内每一个结点处的波场值，时间循环是更新每一时刻模型内所有的波场值。若是实现过程采用串行，其计算速度缓慢，CPU利用率也较低。OpenMP可以用于波场的更新计算从而实现并行加速。
OpenMP一般是通过编译指令，对空间循环按照CPU核心数进行分区，然后在不同的核心上并行计算。以二维波场外推为例（图5），OpenMP采用区域分割的方法计算t3时刻波场时，需要用到t1时刻和t2时刻的波场，并且各波场由不同的数组存储，相互独立。计算子域边界波场时可以正常进行，不会对计算结果产生影响。因此，在多核情形实现地震波场的并行计算，可以大幅提升计算效率。对于三维地震模拟，可以看作是许多二维模型按一定方向叠加，OpenMP的优化方法对三维波场更新计算同样适用。
3. 数值计算
3.1 试验模型及参数
为了验证文中方法的有效性和加速效果，使用简单和复杂两种介质模型来进行三维地震数值模拟。对于简单模型，设计的是水平层状介质模型（图6（a）），尺寸
$N_x=N_y=N_z=100 $ 。采用30层的PML吸收边界，时间采样间隔是0.5 ms，空间采样间隔是$ \mathrm{\mathit{d}}_x=\mathrm{\mathit{d}}_y=\mathrm{\mathit{d}}_z=5\mathrm{\ m} $ ；两层介质速度分别为2 000 m/s和3 000 m/s。波场快照时间是180 ms，震源采用30 Hz的雷克子波，位置是（$N_x/2 $ ，$N_y/2 $ ，0），检波器均位于$N_z=0 $ 平面。模拟精度使用时间2阶、空间8阶的差分。对于复杂模型，则是采用标准的盐丘模型（图6（b）），尺寸是$N_x=N_y=676 $ 、$N_z=180 $ 。波场快照时间300 ms，模拟精度是空间16阶的差分，其它模拟参数如上所述。计算机硬件参数如下：Intel(R) Core(TM) i5-10400 F CPU @ 2.90 GHz（10核CPU），内存是32 G。本文所用的加速比公式为：
$$ {{\text{S}}_p} = \frac{{{T_1}}}{{{T_p}}} \text{，} $$ (7) 其中，p指所用 CPU核心（处理器）数，T1指顺序执行算法的时间，Tp指用p个核心（处理器）的并行时间。
3.2 计算结果分析
对两模型进行4组试验：传统方法（串行），基于OpenMP的并行方法，基于半精度浮点数（FP16）的优化方法，以及基于OpenMP+FP16优化的并行方法。试验中OpenMP调用CPU共6个核心参与计算。最后统计实际加速比以分析不同方法的加速效果。计算结果如图7和图8所示，加速情况见表2和图9。
![]()
图 7 层状模型数值试验的波场快照切片展示Figure 7. The slices of the numerical result with the layered model![]()
图 8 盐丘模型数值试验的波场快照切片展示Figure 8. The slices of the numerical result with the Salt model表 2 加速试验数据统计Table 2. Speedup experimental data statistics水平层状模型 盐丘模型 理论加速比 时间/s 实际加速比 时间/s 实际加速比 传统方法 384.0 1.00 135118 1.00 1 OpenMP 80.0 4.82 30708 4.41 6 FP16 214.0 1.79 73433 1.84 2 OpenMP+FP16 40.5 8.31 17125 7.89 12 将串行计算方法的加速比定义为1作为参照，在OpenMP情形加速比可以提高到4～5左右，半精度浮点数FP16优化后加速比提高到1.8。在三维盐丘模型测试中最终加速比达到了7.89。由于程序内部存在串行部分及计算机后台进程对CPU资源的占用，会使实际加速比难以达到理论值，但优化方法仍然取得了显著的加速效果。
从数值试验结果来看，利用优化方法得到的波场快照与常规方法基本一致。分析不同方法所得结果的差值，对于水平层状模型，优化后的结果误差仅为0.022％；对于盐丘模型，相应的误差是0.012％。试验结果证明基于半精度浮点数优化与OpenMP方法的地震模拟能保证计算结果的精度，并大幅提高计算效率。
4. 结语
本文提出了适用于三维地震数值模拟的半精度浮点数优化与OpenMP结合的方法，在保证计算精度和稳定性的前提下，提高了计算效率。该方法在有6核CPU的计算机上对三维标准模型进行了正演测试，取得的加速比约为8，并将计算误差控制在10-4以内。通过本文的数值试验可以得出以下认识：
（1）利用半精度浮点数计算速度快和减少计算内存的优势，将其应用于时间域地震数值模拟中，实现了三维有限差分地震数值模拟的高性能计算。通过三维层状模型和盐丘模型的测试，不仅减少了计算内存，还取得了较高的加速比。
（2）该优化方案给出了半精度浮点型数据在地震数值模拟中的定义方式。优化后的地震数值模拟程序有较好的可移植性，能适用于当前通用的CPU。
（3）该方法在实际应用中，会受到数值模拟程序串行部分占比高、计算机后台进程对内存和CPU的占用，半精度浮点数据转换效率以及程序I/O等因素的影响，使地震模拟的实际加速难以达到理论值。但从数值试验结果来看，仍然会取得良好的加速效果，计算资源也得到了高效利用。
-
![]()
图 4 小鼠胸腔投影域的主成分分析图像
Figure 4. PCA images of projection domain of mouse thoracic cavity
![]()
图 5 小鼠胸腔投影域主成分分析重建图像
Figure 5. Reconstructed images of projection domain of mouse thoracic cavity by PCA
![]()
图 6 小鼠胸腔图像域的主成分分析图像
Figure 6. PCA images of the image domain of the mouse thoracic cavity
![]()
图 7 小鼠胸腔的像素值平方去噪的主成分分析图像
Figure 7. PCA image of pixel value square denoising of mouse thoracic cavity
![]()
图 8 小鼠胸腔的双域滤波与像素值平方相结合去噪的主成分分析图像
Figure 8. PCA image denoising combining dual-domain filtering with pixel value square of mouse thoracic cavity
![]()
图 13 临床前小鼠投影域的主成分分析重建图像
Figure 13. Reconstructed images of projection domain preclinical mice by PCA
![]()
图 14 临床前小鼠图像域的主成分分析图像
Figure 14. PCA images of the image domain of the preclinical mice
![]()
图 15 临床前小鼠投影域第2主成分重建图像的去噪图像
Figure 15. Denoised images of the PCA-2 recon-structed images in the projection domain of preclinical mice
![]()
图 16 临床前小鼠图像域第2主成分的去噪图像
Figure 16. Denoised images of PCA-2 in the image domain of preclinical mice
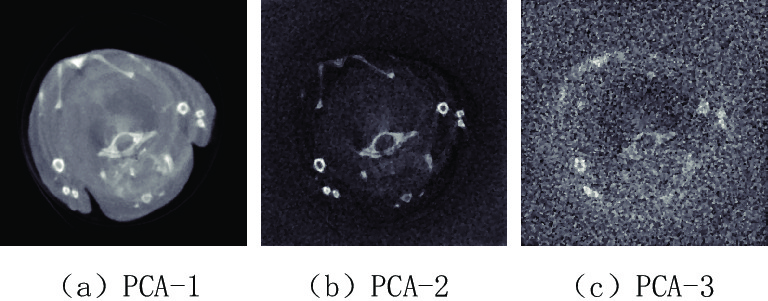
表 1 小鼠胸腔投影域与图像域进行主成分分析的各个主成分的贡献率
Table 1 The contribution rate of each principal component of the projection domain and image domain of the mouse thoracic cavity for PCA
区域 各个主成分的贡献率/％ PCA-1 PCA-2 PCA-3 PCA-4 PCA-5 PCA-6 PCA-7 PCA-8 投影域 99.758 0.146 0.071 0.007 0.005 0.005 0.004 0.004 图像域 98.094 1.234 0.591 0.026 0.020 0.014 0.012 0.009 
下载: 导出CSV
表 2 两种去噪算法在小鼠胸腔投影域与图像域主成分图像上的峰值信噪比
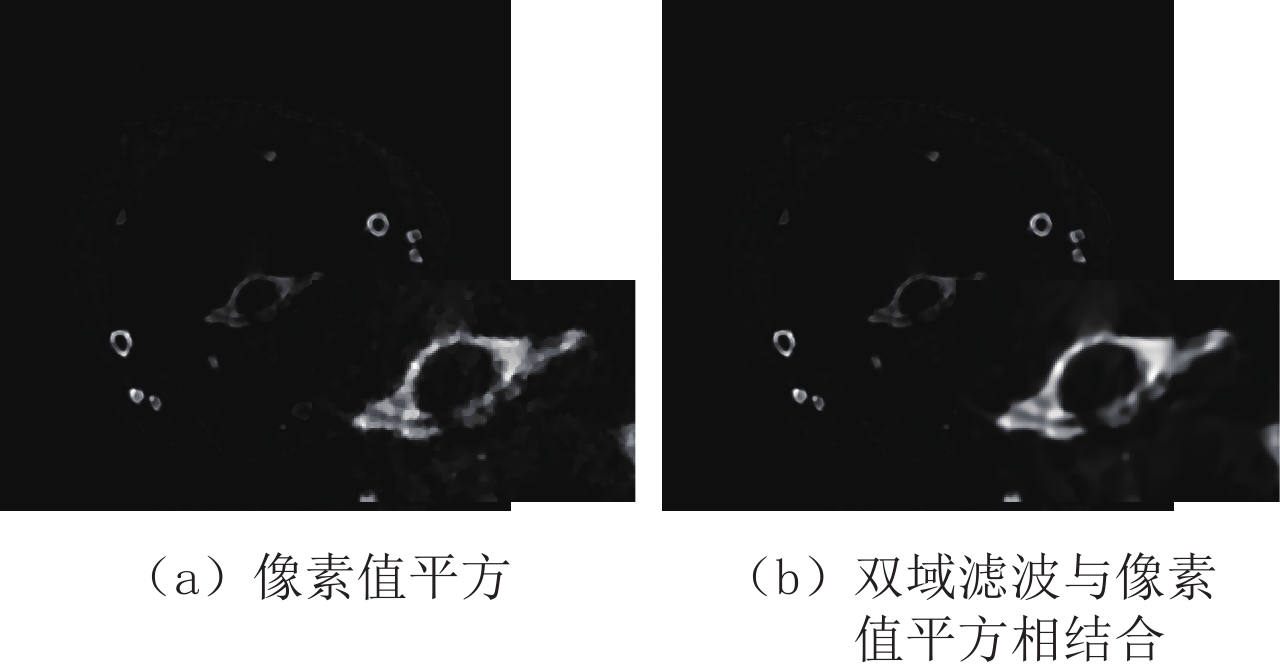
Table 2 Peak signal to noise ratio of the two denoising algorithms for principal component images of mouse thoracic cavity in the projection domain and image domain
方法 投影域 图像域 PCA-2 PCA-3 PCA-2 PCA-3 像素值平方 64.209 49.139 51.590 61.749 双域滤波与像素值平方相结合 64.257 49.139 51.589 61.865
下载: 导出CSV
表 3 临床前小鼠在投影域与图像域进行主成分分析的各个主成分的贡献率
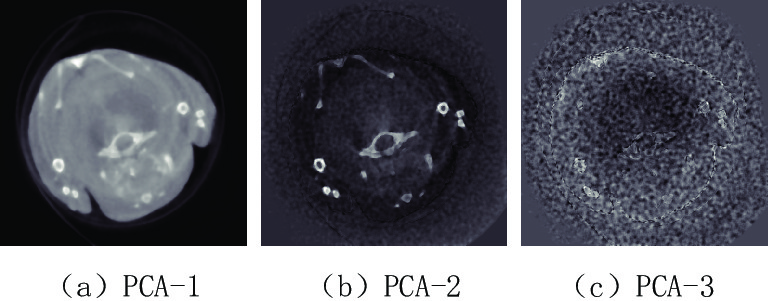
Table 3 The contribution rate of each principal component of the projection domain and image domain of the preclinical mice for PCA
区域 PCA-1 PCA-2 PCA-3 PCA-4 PCA-5 PCA-6 PCA-7 投影域PCA贡献率/％ 99.727 0.060 0.024 0.020 0.020 0.019 0.019 图像域PCA贡献率/％ 99.544 0.222 0.032 0.022 0.021 0.021 0.021 区域 PCA-8 PCA-9 PCA-10 PCA-11 PCA-12 PCA-13 投影域PCA贡献率/％ 0.019 0.019 0.019 0.018 0.018 0.018 图像域PCA贡献率/％ 0.020 0.020 0.020 0.020 0.019 0.018
下载: 导出CSV
-
[1] WU X C, HE P, ZHANG Y, et al. The small animal material discrimination study based on equivalent monochromatic energy projection decomposition method with dual-energy CT system[J]. Journal of X-ray Science and Technology, 2018, 26(6): 919−929. doi: 10.3233/XST-180418
[2] AARON S, SAVVAS N. Spectral computed tomography: Fundamental principles and recent developments[J]. Korean Journal of Radiology, 2021, 22(1): 86−96. doi: 10.3348/kjr.2020.0144
[3] FRÉDÉRIC J, CLARISSE F, MICHEL G, et al. An alternating projection-image domains algorithm for spectral CT[C]//Proceedings. IEEE International Symposium on Biomedical Imaging, United states, 2020: 187-190.
[4] GENG M F, TIAN Z F, JIANG Z, et al. PMS-GAN: Parallel multi-stream generative adversarial network for multi-material decomposition in spectral computed tomography[J]. IEEE Transactions on Medical Imaging, 2021, 40(2): 571−584. doi: 10.1109/TMI.2020.3031617
[5] LIU J L, DING H J, MOLLOI S, et al. TICMR: Total image constrained material reconstruction via nonlocal total variation regularization for spectral CT[J]. IEEE Transactions on Medical Imaging, 2016, 35(12): 2578−2586. doi: 10.1109/TMI.2016.2587661
[6] FENG J, YU H J, WANG S Y, et al. Image-domain based material decomposition by multi-constraint optimization for spectral CT[J]. IEEE Access, 2020, 8: 155450−155458. doi: 10.1109/ACCESS.2020.3016675
[7] WU W W, YU H J, CHEN P J, et al. Dictionary learning based image-domain material decomposition for spectral CT[J]. Physics in Medicine and Biology, 2020, 65(24): 245006. doi: 10.1088/1361-6560/aba7ce
[8] ABASCAL J F P J, DUCROS N, PEYRIN F. Nonlinear material decomposition using a regularized iterative scheme based on the bregman distance[J]. Inverse Problems, 2018, 34(12): 124003. doi: 10.1088/1361-6420/aae1e7
[9] 乔志伟. 总变差约束的数据分离最小图像重建模型及其Chambolle-Pock求解算法[J]. 物理学报, 2018,67(19): 383−396. doi: 10.7498/aps.67.20180839 QIAO Z W. The total variation constrained data divergence minimization model for image reconstruction and its Chambolle-Pock solving algorithm[J]. Acta Physica Sinica, 2018, 67(19): 383−396. (in Chinese). doi: 10.7498/aps.67.20180839
[10] KONG H H, LIU R, YU H Y. Ordered-subset split-bregman algorithm for interior tomography[J]. Journal of X-ray Science and Technology, 2016, 24(2): 221−240. doi: 10.3233/XST-160547
[11] BHAYANA R, PARAKH A, KAMBADAKONE A, et al. Material decomposition with dual- and multi-energy computed tomography[J]. MRS Communications, 2020, 10(4): 558−565. doi: 10.1557/mrc.2020.86
[12] ANTHONY B, JOCHEN B, NANETTE S, et al. Processing of spectral X-ray data with principal components analysis[J]. Nuclear Instruments and Methods in Physics Research, Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2011, 633(S1): S140−S142.
[13] ANDERSON N G, BUTLER A P, SCOTT N J A, et al. Spectroscopic (multi-energy) CT distinguishes iodine and barium contrast material in MICE[J]. European Radiology, 2010, 20(9): 2126−2134. doi: 10.1007/s00330-010-1768-9
[14] HE P, YU H Y, THAYER P, et al. Preliminary experimental results from a MARS micro-CT system[J]. Journal of X-ray Science and Technology, 2012, 20(2): 199−211. doi: 10.3233/XST-2012-0329
[15] KONG H H, LIU R, PAN J X, et al. Evaluation of an analytic reconstruction method as a platform for spectral cone-beam CT[J]. IEEE Access, 2018, 6: 21314−21323. doi: 10.1109/ACCESS.2018.2820500
[16] XIE H Q, REN Y, LONG W T, et al. Principal component analysis in projection and image domains: Another form of spectral imaging in photon-counting CT[J]. IEEE Transactions on Biomedical Engineering, 2021, 68(3): 1074−1083. doi: 10.1109/TBME.2020.3013491
[17] 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016. ZHOU Z H. Machine Learning[M]. Beijing: Tsinghua University Press, 2016.
[18] KNAUS C, ZWICKER M. Dual-domain image denoising[C]//2013 IEEE International Conference on Image Processing, ICIP 2013: Proceedings, Australia, 2013: 440-444.
[19] 孔慧华, 连祥媛, 陈平, 等. 基于能谱CT的材料组分彩色表征研究[J]. 光谱学与光谱分析, 2021,41(11): 3612−3617. KONG H H, LIAN X Y, CHEN P, et al. Research on color characterization of material components based on spectral CT[J]. Spectroscopy and Spectral Analysis, 2021, 41(11): 3612−3617. (in Chinese).
-
期刊类型引用(0)
其他类型引用(1)
计量
- 文章访问数: 701
- HTML全文浏览量: 226
- PDF下载量: 248
- 被引次数: 1
