Nuclear TV Multi-channel Image Reconstruction Algorithm Based on Chambolle-pock Framework
-
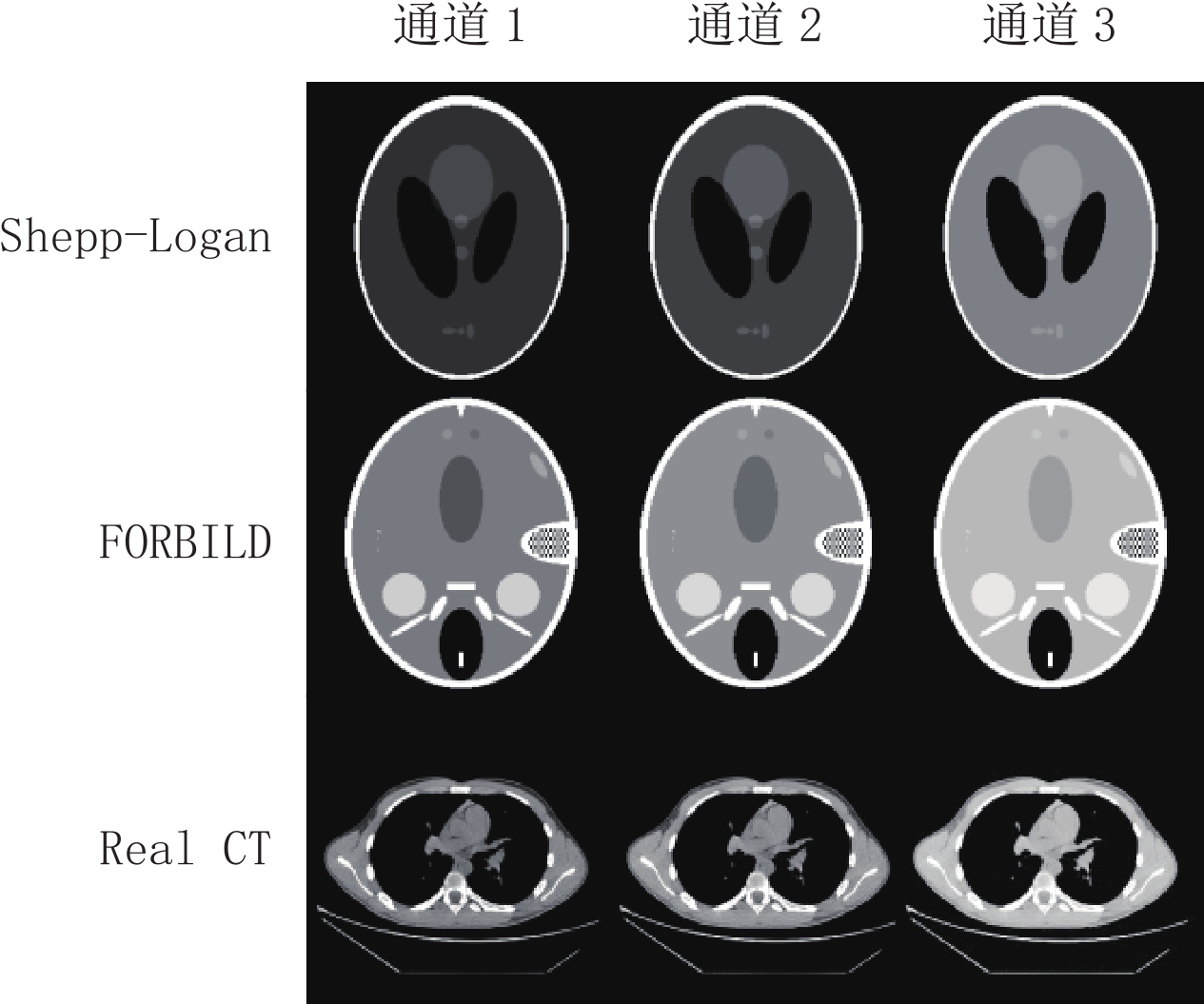
摘要: 总变差最小化算法是一种基于压缩感知理论的图像重建算法，能够从稀疏投影或含噪投影数据中高精度地重建图像，已经被广泛应用于计算机断层成像、磁共振成像、电子顺磁共振成像。能谱CT、T1或T2加权的MRI及EPRI均属于多通道成像。逐通道TV算法可以实现较高精度的图像重建，然而忽略了各通道图像之间的相似性。核TV算法是一种考虑了通道间图像相似性的TV类算法，可以实现高精度图像重建。面向多通道图像重建，以CT重建为研究范例，本文提出一种Chambolle-Pock算法框架下的核TV多通道图像重建算法。通过仿真模体和真实CT图像模体的重建实验，验证算法的正确性，分析算法的收敛性，探索算法参数对收敛速率的影响，评估算法的稀疏重建能力及含噪投影重建能力。结果表明，相对于逐通道TV算法，所提算法可以取得更高的重建精度。核TV算法是一种高精度的多通道图像重建算法，可以应用于各种成像模态的多通道重建场合。Abstract: Total variation (TV) minimum algorithm is an image reconstruction algorithm based on compressed sensing theory, which can realize the reconstruction of images with high accuracy from sparse projection or noisy projection data and has been widely used in computed tomography (CT), magnetic resonance imaging (MRI) and electronic paramagnetic resonance imaging (EPRI). Energy spectrum CT, T1 or T2 weighted MRI and EPRI both belong to multi-channel imaging. The channel-by-channel TV algorithm can achieve high-precision image reconstruction, but it ignores the similarity among the images of each channel while Nuclear TV algorithm is a TV algorithm that considers the image similarity among channels, and can realize high-precision image reconstruction. For multi-channel image reconstruction, taking CT reconstruction as an example, this paper proposes a nuclear TV multi-channel image reconstruction algorithm based on the framework of Chambolle-pock algorithm. Through the reconstruction experiments of simulated phantom and real CT image phantom, the accuracy of the algorithm is verified, the convergence of the algorithm is analyzed, the influence of algorithm parameters on the convergence rate is explored, and the sparse reconstruction ability and noisy projection reconstruction ability of the algorithm are evaluated. The experimental results show that the proposed algorithm can achieve higher reconstruction accuracy than the channel-by-channel TV algorithm. Nuclear TV algorithm is a high-precision multi-channel image reconstruction algorithm, which can be applied to multi-channel reconstruction of various imaging modes.
-
随着我国城市建设的不断发展，地铁工程遇到的地质与环境条件越来越复杂。岩溶是一种典型的不良地质现象，严重影响地铁工程的建设与运营安全[1-3]。在地铁工程勘察阶段，需要查明岩溶发育的位置及规模，为设计、施工提供基础资料。
岩溶勘察中常规的勘探手段主要是钻探。钻探对于点位处垂直方向的地质情况揭露较为准确和直观，然而岩溶的成因、分布、性状具有相当的随机性[4]，通过有限的钻孔难以查清岩溶发育情况。为了克服钻探等勘察手段“以点代面”的局限性，在钻探地质资料的基础上，充分运用物探技术手段，更深入和全面地分析地铁工程施工区域的岩溶分布规律[5-9]。
本文基于南京某地铁项目岩溶勘察的工程实践，探讨以等值反磁通瞬变电磁法、弹性波CT法为主的综合物探方法在岩溶探查中的应用效果。
1. 场地地质概况
南京某地铁工程的部分地段有灰岩分布，场地属于岗地地貌单元，发育坳沟亚地貌。覆盖层主要为第四系的填土、黏性土，厚度变化较大，约3.50～17.00 m。下伏基岩主要是三叠系周冲村组（T2 z）强风化、中风化泥质灰岩，埋深差异较大，整体呈东西高、中间低的趋势。周冲村组（T2 z）强风化、中风化泥质灰岩的方解石含量较高，易被溶解。周冲村组（T2 z）泥质灰岩下方部分地段揭露有燕山期花岗岩（
$ \gamma _5^2 $ ）。根据钻探资料，场地岩溶发育类型有溶洞、溶隙和溶孔等多种形态；土岩结合面处分布大量溶沟、溶槽堆积物。泥质灰岩内部发育的溶洞一般为充填型溶洞，充填物主要为软-可塑状黏土、粉质黏土夹灰岩碎块等。
场地孔隙潜水稳定水位在地下0.50～7.30 m，水位起伏和地形起伏基本一致。水位受季节性变化影响较大，年变化幅度一般在2.0 m左右。
2. 物探工作方法
2.1 物探方法优选及其效果分析
本次物探工作开展的思路是先沿着地铁隧道走向进行物探普查，圈定重点异常区域；然后，对于物探普查发现的重点异常区域及前期勘探揭露的岩溶发育地段，布置横向测线加密测量，并采取分辨率高的物探方法进一步详细探查。
物探普查主要考虑常用的地面工程物探方法，如直流电法中的高密度电阻率法，电磁法中的可控源音频大地电磁法（CSAMT）、EH4、瞬变电磁法、探地雷达法，地震勘探中的折射波法、反射波法、面波法（含天然源面波）等。
从探测深度与分辨率角度分析，本工程最大探测深度约40 m，而CSAMT、EH4等电磁类物探方法主要针对深部勘探，浅层勘探效果和分辨能力相对较差；本工程覆盖层厚度变化较大（约3.50～17.00 m），地下水相对较浅（0.50～7.30 m），探地雷达方法在这种地层条件下电磁信号衰减会比较快，探测深度可能达不到要求。
从物探方法应用效果分析，地震勘探中的折射波、反射波、面波法对地层界面探测效果较好，对岩溶的探测效果受岩溶的赋存状态特征[10]影响较大。高密度电阻率法是进行岩溶等不良地质体探测相对成熟的物探方法，但其需要电极接地向地下供电，对于大面积硬化地面的情况，高密度电阻率法的电极接地实施较为困难。瞬变电磁法是一种不破坏路面的无损探测方法，但其对地上（如车辆、高压线等）、地下（各类管线）的良导体干扰相对较敏感，其测线布置应尽量避开固定干扰源，并采取有效措施减小随机干扰的影响。
详查的物探方法一般采用孔中物探方法，主要包括弹性波CT、电阻率CT、电磁波CT、管波探测等，孔中各类物探方法的区别在于利用介质不同的物理特性差异。本工程主要基岩类型为泥质灰岩，与覆盖层、充填溶洞的物质电阻率差别不大，电磁波在该种类型的基岩中衰减是比较快的。管波探测则主要针对钻孔附近一定范围[4]，无法获得区段范围内的更多信息。
在综合分析工程地质条件、探测目的、探测深度与分辨率、应用效果、实施难度及周围环境干扰等因素的基础上，本文采用等值反磁通瞬变电磁法进行普查，弹性波CT法进行详细探查的综合物探方法，并对两种方法的探测结果进行对比分析。
2.2 等值反磁通瞬变电磁法
等值反磁通瞬变电磁法（以下简称瞬变电磁法）采用上下平行共轴的两个相同线圈通以反向电流作为发射源，在该双线圈源合成的一次场零磁通平面上，测量对地中心耦合的纯二次场。
等值反磁通瞬变电磁法消除了接收线圈一次场的影响，从理论上实现了零至几百米的高精度探测。等值反磁通瞬变电磁法采用上下大小相同的微线圈（直径小于1.0 m），其发射电流相同、方向相反，因此，在上下微线圈的几何中心水平面和无穷远处一次垂直磁场为零，但是其他空间存在一次垂直磁场。断电后，近地表发射线圈的磁场最大，因此，在相同的变化时间的情况下，感应涡流的极大值面集中在近地表；同时，近地表感应涡流的极大值面产生的磁场最强，随着关断间歇的延时，又产生新的涡流极大值面，并逐渐向远离垂直发射线圈的方向扩散，扩散速度和极大值的衰减幅度与大地电阻率有关，大地介质影响涡流扩散速度和衰减幅度的参数主要是大地的电导率和局部良导体的埋深，而均匀大地介质的电导率一般情况视为常数，局部地质体的电导率、规模、埋深、形态等参量的变化是影响涡流极大值面扩散速度和极大值的衰减幅度变化的主要因素[11]。
本文采用湖南五维地质科技有限公司与中南大学联合研制的HPTEM-18瞬变电磁系统，该系统基于等值反磁通理论，消除了瞬变电磁法关断延迟的电磁耦合效应，实现瞬变场早期纯二次场信号测量；采用微线圈、对偶中心耦合装置提高了横向分辨率和信噪比；具备抗干扰能力强、探测精度高、不受场地限制、采集速度快等优势。
HPTEM-18系统由天线、仪器主机和操作PC组成。野外操作时仪器连接如图1所示。
物探野外工作采用定点测量方式，测点间距3.0 m或5.0 m，通过试验选择发送频率为6.25 Hz，叠加次数为200～300次，重复观测两次。
野外获得的等值反磁通瞬变电磁数据采用仪器配套的5 DEM数据处理系统进行处理，数据处理步骤主要包括预处理、定性分析、定量解释和综合解释等步骤，结合已知地质资料得到电性地质断面图[12]。
2.3 弹性波CT方法
弹性波CT方法（即弹性波层析成像技术，简称CT法）是通过扇形测试（图2）获取大量的首波走时数据，然后，求解大型矩阵方程获取两孔之间的速度剖面图像[13-14]。
本次弹性波CT法测试使用的仪器是北京市水电物探研究所研制的SWS-6 A型工程勘探与工程检测仪，配备12道CT测试专用串珠式水听器；电火花震源设备为武汉长大物探科技有限公司研制的CD-2便携式电火花震源，最高电压可达10 kV。弹性波CT测试施工前对仪器及配套辅助设备均进行了检查，确保其各项技术指标满足要求。测试工作开展前首先进行了试验工作，确定了相关工作参数：采样率0.05 ms，采样点数1024，激发炮间距1.0 m，接收点间距1.0 m。
弹性波CT数据处理主要步骤包括建立观测系统、初至拾取、层析成像反演等。地震仪器采集到的波列数据中不仅有直达波，还有折射波、反射波等[15]。初至时间是层析反演中最重要的基础数据，其精度直接影响层析成像的效果，因此，初至拾取是整个数据处理流程中最耗时间甚至有可能要反复多次的工作。
初至拾取之后，利用弹性波CT反演解释软件进行层析成像反演，反演方法一般采用联合迭代重建技术（SIRT）[16]。反演过程中，网格大小一般设置为0.5 m×0.5 m；同时将钻孔的地层作为反演的约束条件，以减少反演解的非唯一性；为了消除局部网格反演的误差，对反演结果一般还需要进行空间平滑。最终根据两钻孔之间的速度剖面图进行地质推断解释，圈定岩溶发育范围。
3. 物探方法资料解释
3.1 测线布设
图3为该地铁工程其中一段物探测线布置示意图。工程实践中先进行瞬变电磁法普查，然后在重点异常区加密瞬变电磁横测线及补充CT法进行详细探查。
3.2 瞬变电磁法资料解释
图4～图6是瞬变电磁法探测反演的电阻率断面图。从图中可以看出，浅部电阻率普遍小于300 Ω·m，推测为覆盖层的电性反映。覆盖层以下，电阻率等值线横向整体变化较大，多处存在低阻凹陷现象，凹陷形态各异；标高10 m～-10 m范围内也存在较多的低阻团块或低阻圈闭现象；随深度加大，尤其是标高 -10 m以下电阻率逐渐增高，呈中、高电阻电性特征。
![]()
图 4 M1测线瞬变电磁法电阻率断面图Figure 4. Transient electromagnetic inversion results of M1 survey line![]()
图 5 M2测线瞬变电磁法电阻率断面图Figure 5. Transient electromagnetic inversion results of M2 survey line![]()
图 6 M3～M5测线瞬变电磁法电阻率断面图Figure 6. Transient electromagnetic inversion results of M3～M5 survey line结合已经知的地质资料，上述低阻凹陷或低阻区域推测为岩溶发育区。根据瞬变电磁法探测结果分析，该工程场地岩溶发育的位置主要集中在土岩结合面并向岩体内部延伸。部分岩体内部发育的岩溶一般也存在通向土岩结合面的低阻“通道”（推测为岩体破碎或裂隙带），如M1测线的M1-5岩溶异常、M4测线的M4-4岩溶异常等；有的尽管在某一条测线上显示为岩体内部发育的岩溶，但是从另外方向的测线上显示是从土岩结合面延伸发育下来的，如M5测线的M5-2岩溶异常对应了M1测线的M1-10岩溶异常，说明岩溶发育具有较明显的方向性。
3.3 弹性波CT资料解释
根据等值反磁通瞬变电磁法反演结果及相关地质资料，在该段工程场地补充了4组弹性波CT测线，图7和图8是弹性波CT测试反演的波速断面图。从波速特征上看，覆盖层地震波速一般在1000～2200 m/s左右；完整性较好的中风化泥质灰岩波速大于3400 m/s，破碎或存在溶蚀现象的泥质灰岩中地震波速则有所减低，降低幅度与岩石破碎程度或溶蚀程度正相关。基岩中分布的溶洞根据充填物的特征和状态，地震波速一般为1500～3000 m/s左右。
根据波速断面图结合钻探资料，场地内覆盖层以下的浅部溶蚀现象较为发育，最大发育深度接近10 m；岩体内部发育的岩溶一般规模不大，部分垂向上呈现“串珠状”发育特征；岩溶异常周围岩体的波速一般呈较明显的降低，表明岩溶周围的岩体较破碎、裂隙较发育或泥质含量相对较高。
3.4 岩溶探测效果综合分析
图9是M2测线附近的钻孔资料投影到瞬变电磁解译成果图上形成的解译对照图。从图9中可以看出，瞬变电磁法探测发现的低阻区域与钻探揭露的溶蚀区域有较好的对应关系，如瞬变电磁法推测的岩溶发育异常区M2-1、M2-4、M2-5、M2-8、M2-9、M2-12等，在相应地段的钻孔中均发现较明显的充填溶洞。但部分钻孔揭露的地质情况与瞬变电磁法推测的岩溶发育边界存在一定差别，这一差别可能受到岩溶异常的体积效应影响。另外岩溶发育存在不确定性，而钻孔位置与瞬变电磁法测线一般也有3～5 m的平面距离。
![]()
图 9 M2测线瞬变电磁法探测成果与地质资料对照图Figure 9. Contrast chart between transient electromagnetic results and geologic information of M2 survey line总体而言，瞬变电磁法探测结果对区域岩溶发育程度判断是基本正确的，因而可以认为等值反磁通瞬变电磁法是一种有效的岩溶探查方法，能够为整个区域的岩溶发育规律的判断提供依据。
从图7和图8中钻探资料与弹性波CT反演结果对比可知，弹性波CT推测的溶洞区域与钻探揭露的结果具有较好的一致性。相对瞬变电磁法圈定的大范围岩溶发育区域，其对成型溶洞的探测结果更为精细、分辨率更高。例如弹性波CT的C4测线大概对应瞬变电磁M2测线85～100 m位置，此处瞬变电磁法反映的是比较大的连续贯通的低阻凹陷异常M2-12；而弹性波CT的C4测线除了显示浅部溶蚀异常的深度和变化趋势外，还分析出测线之间圈闭溶洞R11、R12、R14，靠近G96号钻孔处的R13低速圈闭异常与钻孔揭露的溶洞深度及规模较为接近，R14溶洞异常下部地震波速整体不高，表明岩体破碎或裂隙发育，与此处钻孔揭露的“串珠状溶洞”相对应。
等值反磁通瞬变电磁法与弹性波CT法两种物探方法综合运用，既在宏观上全面了解探测区域的岩溶发育情况，又实现了精细化探查，为设计、施工提供准确的资料。
4. 结论与建议
（1）本文采用等值反磁通瞬变电磁法作为普查方法，弹性波CT作为详查方法，通过与钻探资料的对比分析，基本查清了探测区域的岩溶发育情况，为地铁工程的设计、施工提供了更为详尽的地质资料。
（2）等值反磁通瞬变电磁法具备抗电磁干扰能力强、不受场地限制、采集速度快等优势，能够适应复杂的城市环境，在地铁岩溶物探普查工作中具有良好的应用效果。
（3）弹性波CT法具有较高的分辨率，但要充分运用已有地质资料对反演过程进行约束，避免由于多解性造成对异常的误判。
（4）随着城市地铁勘察遇到的地质条件越来越复杂，需要更多应用物探技术手段解决工程问题。然而，城市物探受到的制约因素较多，如作业环境安全隐患大、噪声及电磁干扰复杂、空间受限等，需要大力发展抗干扰能力强、分辨率高、高效便捷的物探手段，为城市地铁勘察提供助力。
-
![]()
图 2 TnV模型在Shepp-Logan模体的重建结果
Figure 2. Reconstruction results of TnV model in Shepp-Logan phantom
![]()
图 3 TnV模型在FORBILD模体的重建结果
Figure 3. Reconstruction results of TnV model in FORBILD phantom
![]()
图 4 TnV模型重建过程中图像误差趋势图
Figure 4. Trend chart of image error during TnV model reconstruction
![]()
图 5 TnV-CP算法在两种仿真模体的收敛性
Figure 5. Convergence of TnV-CP algorithm in two simulation models
![]()
图 6 不同算法参数对收敛速率的影响
Figure 6. Influence of different algorithm parameters on convergence rate
![]()
图 7 两种算法在Shepp-Logan模体上稀疏重建结果比较
Figure 7. Comparison of sparse reconstruction results between two algorithms on Shepp-Logan phantoms
![]()
图 9 两种算法在FORBILD模体上稀疏重建结果比较
Figure 9. Comparison of sparse reconstruction results between two algorithms on FORBILD phantoms
![]()
图 11 两种算法在真实CT模体上稀疏重建结果比较
Figure 11. Comparison of sparse reconstruction results between two algorithms on real CT phantoms
![]()
图 8 两种算法在10个稀疏角度下重建局部图
Figure 8. Two algorithms for local graph reconstruction under 10 sparse angles
![]()
图 10 20个稀疏角度下重建图像的水平中心线波形图
Figure 10. Horizontal centerline waveform of reconstructed images unader 20 sparse angles
![]()
图 12 两种算法在不同模体上含噪重建结果比较
Figure 12. Comparison of noisy reconstruction results between two algorithms on different phantoms
表 1 TnV-CP算法伪代码
Table 1 The TnV-CP algorithm pseudocode
输入： $ \boldsymbol{g},\boldsymbol{A},\boldsymbol{D},\epsilon ;\mathrm{\nu } $ 1） $L={\parallel \frac{\boldsymbol{A} }{\mathrm{\nu }\boldsymbol{D} }\parallel }_{\mathrm{S}\mathrm{V} },\;\sigma =\frac{1}{L},\;\tau =\frac{1}{L},\;\theta =1,\;n=0$ 2） ${\boldsymbol{u} }_{0}=0,\;{\stackrel{-}{\boldsymbol{u} } }_{0}=0,\;{\boldsymbol{p} }_{0}=0$ 3） $ \mathrm{r}\mathrm{e}\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{t} $ 4） $ {\boldsymbol{p}}_{n+1}=\mathrm{max}(\left|\right|{\boldsymbol{p}}_{n}+\sigma (\boldsymbol{A}\overline{\boldsymbol{u}}-\boldsymbol{g})|{|}_{2}-\sigma \epsilon ,0)\cdot ({\boldsymbol{p}}_{n}+\sigma (\boldsymbol{A}\overline{\boldsymbol{u}}-\boldsymbol{g}\left)\right)/\left|\right|{\boldsymbol{p}}_{n}+\sigma (\boldsymbol{A}\overline{\boldsymbol{u}}-\boldsymbol{g})|{|}_{2} $ 5） $ {\mathbf{z}(\mathrm{i},\mathrm{j})}_{\mathrm{n}+1}=\boldsymbol{U}{\sum }_{\mathrm{P}}{\boldsymbol{V}}^{\mathrm{T}} $ 6） $\theta =\sqrt{\mathrm{\nu }/(\mathrm{\nu }+2\tau )},\;\tau =\theta *\tau ,\;\sigma =\sigma /\theta$ 7） $ {\boldsymbol{u}}_{n+1}={\boldsymbol{u}}_{n}-\tau {\boldsymbol{A}}^{\mathrm{T}}{\boldsymbol{p}}_{n+1}-\tau \mathrm{\upsilon }{\boldsymbol{D}}^{\mathrm{T}}{\boldsymbol{z}}_{n+1} $ 8） $ {\stackrel{-}{\boldsymbol{u}}}_{n+1}={\boldsymbol{u}}_{n+1}+\theta ({\boldsymbol{u}}_{n+1}-{\boldsymbol{u}}_{n}) $ 9） $ n=n+1 $ 10） $\mathrm{u}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{l}\;n\ge N$ 
下载: 导出CSV
表 2 两种算法重建Shepp-Logan模体在不同稀疏角度下评估参数的比较
Table 2 Comparison of evaluation parameters of Shepp-Logan phantom reconstructed by two algorithms under different sparsity angles
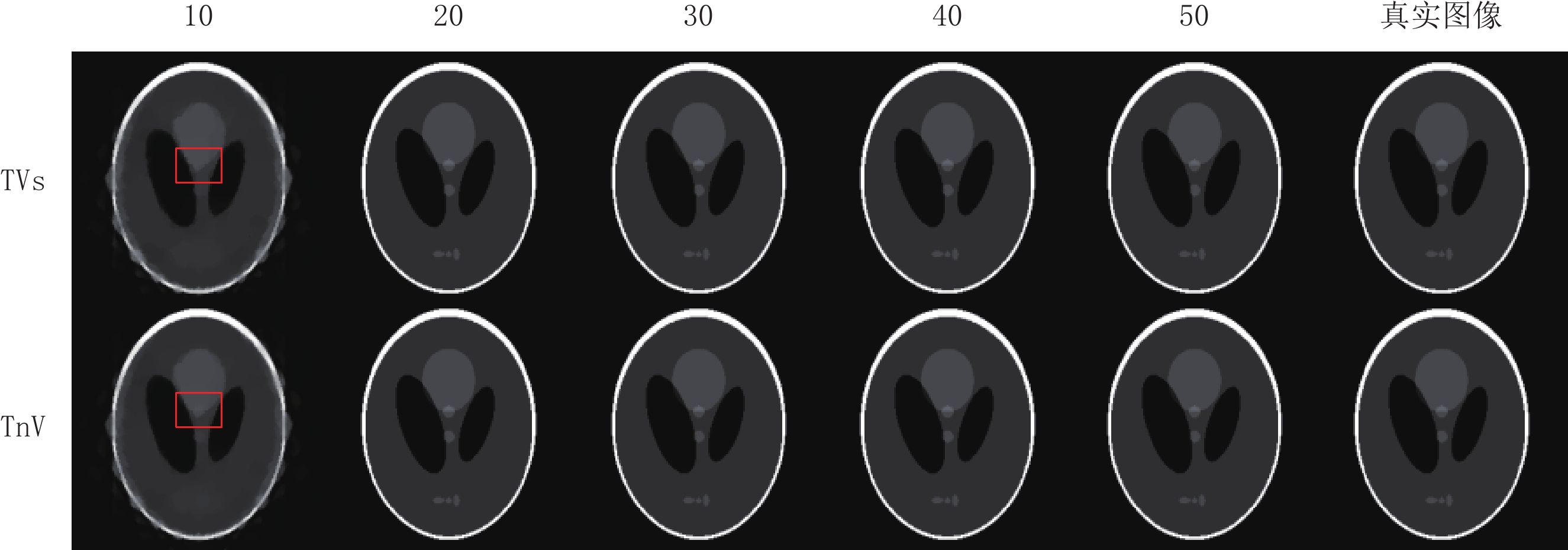
评估参数 算法 投影个数 10 20 30 40 50 RMSE TVs 0.079 0.002 6.626×10-7 4.881×10-7 4.764×10-7 TnV 0.067 1.214×10-6 6.584×10-7 4.651×10-7 4.585×10-7 SSIM TVs 0.798 0.999 1.000 1.000 1.000 TnV 0.831 1.000 1.000 1.000 1.000
下载: 导出CSV
表 3 两种算法重建FORBILD模体在不同稀疏角度下评估参数的比较
Table 3 Comparison of evaluation parameters between two algorithms in reconstructing FORBILD motifs under different sparse angles
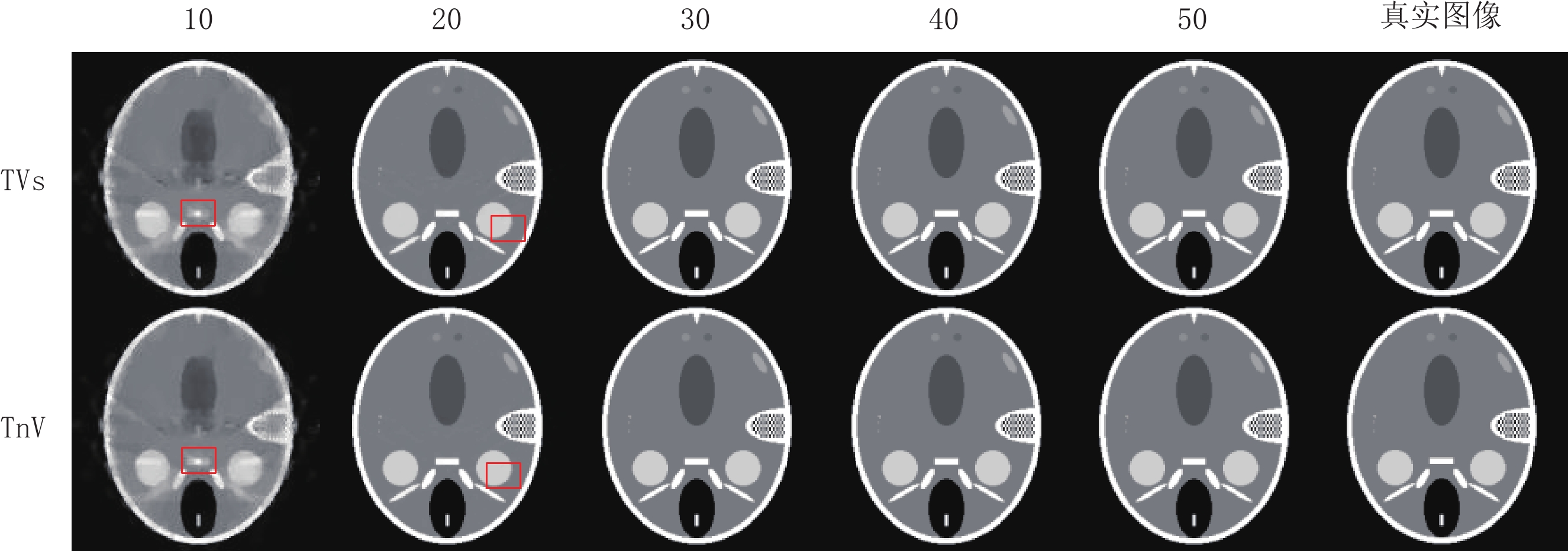
评估参数 算法 投影个数 10 20 30 40 50 RMSE TVs 0.101 0.022 2.022×10-6 1.311×10-6 1.129×10-6 TnV 0.090 0.014 1.484×10-6 1.256×10-6 1.034×10-6 SSIM TVs 0.700 0.981 1.000 1.000 1.000 TnV 0.736 0.992 1.000 1.000 1.000
下载: 导出CSV
表 4 两种算法重建真实CT模体在不同稀疏角度下评估参数的比较
Table 4 Comparison of evaluation parameters between two algorithms in reconstructing real CT phantom under different sparsity angles
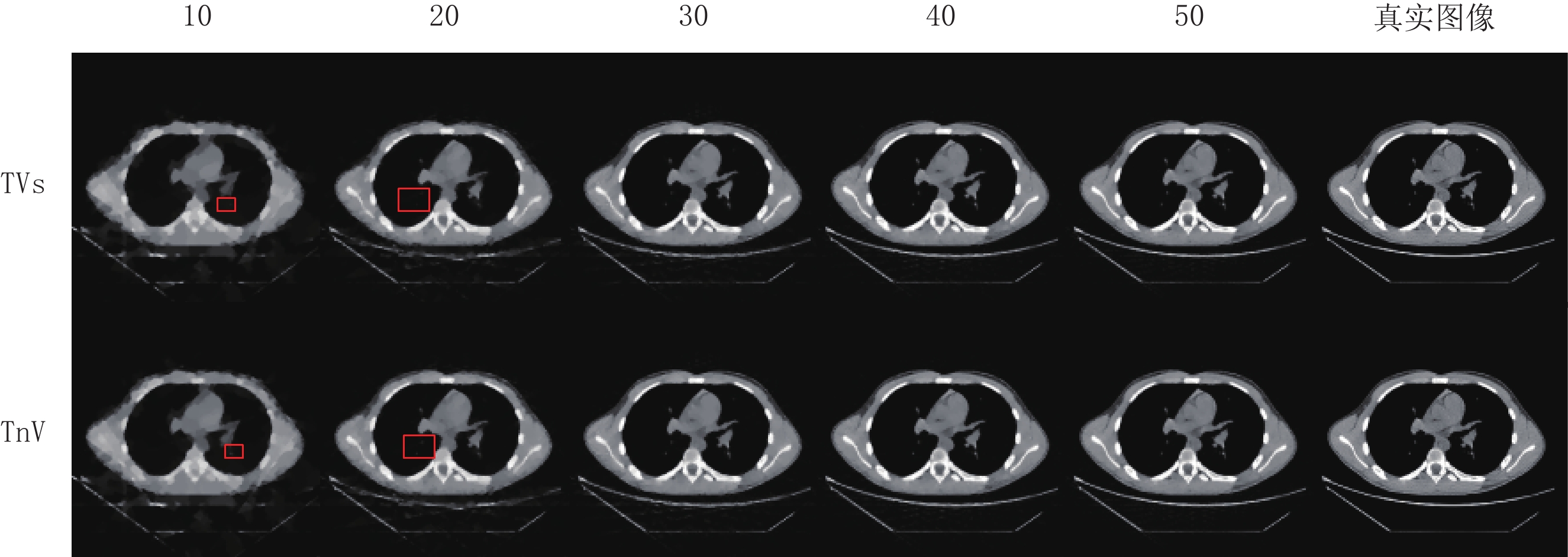
评估参数 算法 投影个数 10 20 30 40 50 RMSE TVs 0.104 0.072 0.054 0.043 0.035 TnV 0.099 0.069 0.052 0.041 0.034 SSIM TVs 0.593 0.748 0.840 0.894 0.923 TnV 0.617 0.764 0.850 0.901 0.927
下载: 导出CSV
表 5 两种算法重建Shepp-Logan模体在不同噪声强度下评估参数的比较
Table 5 Comparison of evaluation parameters of Shepp Logan phantom reconstructed by two algorithms under different noise intensity
评估参数 算法 噪声等级 30 dB 35 dB 40 dB 45 dB 50 dB RMSE TVs 0.035 0.025 0.018 0.012 0.008 TnV 0.032 0.023 0.017 0.011 0.007 SSIM TVs 0.958 0.980 0.989 0.994 0.997 TnV 0.967 0.982 0.990 0.995 0.998 PSNR TVs 29.090 31.910 34.840 38.460 42.270 TnV 29.930 32.590 35.470 39.110 42.920
下载: 导出CSV
表 6 两种算法重建FORBILD模体在不同噪声强度下评估参数的比较
Table 6 Comparison of evaluation parameters between two algorithms in reconstructing FORBILD phantom under different noise intensity
评估参数 算法 噪声等级 30 dB 35 dB 40 dB 45 dB 50 dB RMSE TVs 0.073 0.060 0.043 0.030 0.019 TnV 0.069 0.056 0.038 0.026 0.017 SSIM TVs 0.875 0.913 0.947 0.974 0.988 TnV 0.878 0.916 0.954 0.978 0.990 PSNR TVs 22.700 24.390 27.330 30.570 34.230 TnV 23.260 25.080 28.400 31.610 35.160
下载: 导出CSV
表 7 两种算法重建真实CT模体在不同噪声强度下评估参数的比较
Table 7 Comparison of evaluation parameters between two algorithms in reconstructing real CT phantom under different noise intensity
评估参数 算法 噪声等级 30 dB 35 dB 40 dB 45 dB 50 dB RMSE TVs 0.056 0.046 0.039 0.034 0.031 TnV 0.052 0.044 0.037 0.033 0.030 SSIM TVs 0.842 0.884 0.915 0.935 0.943 TnV 0.854 0.896 0.923 0.938 0.947 PSNR TVs 25.010 26.760 28.280 29.510 30.260 TnV 25.610 27.100 28.630 29.690 30.520
下载: 导出CSV
-
[1] PAN X C, SIDKY E Y, VANNIER M. Why do commercial CT scanners still employ traditional, filtered back-projection for image reconstruction?[J]. Inverse Problems, 2008, 25(12): 1230009.
[2] YU L, YU Z, SIDKY E Y, et al. Region of interest reconstruction from truncated data in circular cone-beam CT[J]. IEEE Transactions on Medical Imaging, 2006, 25(7): 869−881. doi: 10.1109/TMI.2006.872329
[3] CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489−509. doi: 10.1109/TIT.2005.862083
[4] SIDKE E Y, KAO C M, PAN X C. Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT[J]. Journal of X-ray Science & Technology, 2006, 14: 119−139.
[5] PAPAFITSOROS K, SCHOENLIEB C B, SENGUL B. Combined first and second order total variation inpainting using split bregman[J]. Image Processing on Line, 2013, 3: 112−136. doi: 10.5201/ipol.2013.40
[6] XI Y R, QIAO Z W, WANG W J, et al. Study of CT image reconstruction algorithm based on high order total variation - ScienceDirect[J]. Optik, 2020, 204: 163814−163814. doi: 10.1016/j.ijleo.2019.163814
[7] 闫慧文, 乔志伟. 基于ASD-POCS框架的高阶TpV图像重建算法[J]. CT理论与应用研究, 2021,30(3): 279−289. DOI: 10.15953/j.1004-4140.2021.30.03.01. YAN H W, QIAO Z W. High order TPV image reconstruction algorithm based on ASD-POCS framework[J]. CT Theory and Applications, 2021, 30(3): 279−289. DOI: 10.15953/j.1004-4140.2021.30.03.01. (in Chinese).
[8] NING F L, HE B J, WEI J. An algorithm for image reconstruction based on lp norm[J]. Acta Physica Sinica, 2013, 62: 174212−174212. doi: 10.7498/aps.62.174212
[9] 张海娇, 孔慧华, 孙永刚. 基于结构先验的加权NLTV能谱CT重建算法[J]. 光学学报, 2018,38(8): 334−342. ZHANG H J, KONG H H, SUN Y G. Weighted NLTV energy spectrum CT reconstruction algorithm based on structure prior[J]. Acta Optica Sinica, 2018, 38(8): 334−342. (in Chinese).
[10] DURAN J, MOELLER M, SBERT C, et al. Collaborative total variation: A general framework for vectorial TV models[J]. SIAM Journal on Imaging Sciences, 2015, 9(1): 116−151.
[11] RIGIE D S, RIVIèRE P J L. Joint reconstruction of multi-channel, spectral CT data via constrained total nuclear variation minimization[J]. Physics in Medicine & Biology, 2015, 60(5): 1741−1762.
[12] RIGIE D S, SANCHEZ A A, RIVIèRE P J L. Assessment of vectorial total variation penalties on realistic dual-energy CT data[J]. Physics in Medicine & Biology, 2017, 62(8): 3284−3298.
[13] QIAO Z W. A simple and fast ASD-POCS algorithm for image reconstruction[J]. Journal of X-ray Science and Technology, 2021, 29(3): 1−16.
[14] SIDKY E Y, PAN X C. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization[J]. Physics in Medicine & Biology, 2008, 53(17): 4777−4807.
[15] CHAMBOLLE A, POCK T. A first-order primal-dual algorithm for convex problems with applications to imaging[J]. Journal of Mathematical Imaging and Vision, 2011, 40(1): 120−145. doi: 10.1007/s10851-010-0251-1
[16] SIDKY E Y, J∅RGENSEN J H, PAN X C. Convex optimization problem prototyping for image reconstruction in computed tomography with the Chambolle-Pock algorithm[J]. Physics in Medicine & Biology, 2011, 57(10): 3065−3091.
[17] QIAO Z W, REDLER G, EPEL B, et al. A balanced total-variation-Chambolle-Pock algorithm for EPR imaging[J]. Journal of Magnetic Resonance, 2021, 328: 107009. doi: 10.1016/j.jmr.2021.107009
[18] CAI J, CAND E J, SHEN Z. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010.
[19] DUAN Y H, WEN R P, XIAO Y. A singular value thresholding with diagonal-update algorithm for low-rank matrix completion[J]. Mathematical Problems in Engineering, 2020: 2020.
[20] LI W, HU J, CHEN C. On accelerated singular value thresholding algorithm for matrix completion[J]. Applied Mathematics, 2014, 5(21): 3445−3451. doi: 10.4236/am.2014.521322
[21] QIAO Z W, ZHANG Z, PAN X C, et al. Optimization-based image reconstruction from sparsely sampled data in electron paramagnetic resonance imaging[J]. Journal of Magnetic Resonance, 2018, 294: 24−34. doi: 10.1016/j.jmr.2018.06.015
[22] QIAO Z W, ZHU Y N, REDLER G, et al. The integrated acceleration of the Chambolle-Pock algorithm applied to constrained TV minimization in CT image reconstruction[J]. Inverse Problems in Science and Engineering, 2019.
[23] 乔志伟. 总变差约束的数据分离最小图像重建模型及其Chambolle-Pock求解算法[J]. 物理学报, 2018,67(19): 198701. DOI: 10.7498/aps.67.20180839. QIAO Z W. Total variation constrained data separation minimum image reconstruction model and its Chambolle-Pock algorithm[J]. Acta Physica Sinica, 2018, 67(19): 198701. DOI: 10.7498/aps.67.20180839. (in Chinese).
[24] QIAO Z W, REDLER G, GUI Z G, et al. Three novel accurate pixel-driven projection methods for 2D CT and 3D EPR imaging[J]. Journal of X-ray Science and Technology, 2018, 26(1): 83−102. doi: 10.3233/XST-17284
[25] QIAO Z W, REDLER G, EPEL B, et al. A doubly constrained TV algorithm for image reconstruction[J]. Mathematical Problems in Engineering, 2020, (2): 1−15.
[26] QIAO Z W, REDLER G, TANG S J, et al. Comparison of TVcDM and DDcTV algorithms in image reconstruction[J]. Inverse Problems in Science and Engineering, 2020, 28(6): 839−858. doi: 10.1080/17415977.2019.1667343
-
期刊类型引用(0)
其他类型引用(1)
计量
- 文章访问数: 663
- HTML全文浏览量: 209
- PDF下载量: 239
- 被引次数: 1
