Research on Blood Flow Separation Algorithm of Diffuse Light Correlation Spectrum Based on ICA
-
摘要: 血流是人体的一个重要生理参数,实时测量脑部、骨骼肌及乳腺等组织的血流对疾病诊断治疗及手术、重症监护有重要意义。近红外漫射光相关谱(DCS)是新兴的组织血流测量技术,利用DCS技术进行血流测量时,每个距离的光源-探测器(S-D)均含有不同程度的表层组织和深层组织的混合信号,其中表层信号对提取深层组织的血流有较大影响。本文结合N阶线性算法(NL算法)和独立成分分析算法(ICA)对DCS技术获取的近距离和远距离光学信号进行分离处理。计算机仿真表明,本文提出的算法可以较好地分离出表层和深层组织的血流信号,对今后DCS技术在临床的血流测量应用有重要潜力。Abstract: Blood flow is an important physiological parameter of the human body. Real-time measurement of blood flow in the brain, skeletal muscle, and breast tissue is of great significance for disease diagnosis, treatment, surgery, and intensive care. Near-Infrared Diffuse Correlation Spectroscopy (DCS) is a new-type tissue blood flow measurement technology. When using DCS technology for blood flow measurement, the light source-detector (S-D) at each distance contains different degrees of mixed signals of superficial and deep tissues, among which the superficial signals show greater impact on the extraction of blood flow in deep tissues. This paper combines the Nth order linear algorithm (NL algorithm) with the independent component analysis algorithm (Independent Component Analysis, ICA) to separate and process the short-range and long-range optical signals obtained by DCS technology. The computer simulation shows that the algorithm proposed in this paper can better separate the blood flow signals of the superficial and deep tissues, and demonstrates important potential for the application of DCS technology in clinical blood flow measurement in the future.
-
人体组织的血流是一个重要的生理参数,对其进行实时测量有利于很多疾病的诊断和治疗[1-4]。近红外漫射光相关谱(near-infrared diffuse correlation spectroscopy,DCS)是以近红外光(650~900 nm)为测量手段,通过光场时间自相关函数与红细胞运动的物理关系来无创测量微血管血流的一种新兴技术[5],已被应用在脑、骨骼肌和乳腺等多种组织的疾病诊断和治疗监测的临床中[6-8]。在应用DCS技术进行组织血流测量中,其精确性受到解剖结构的影响。具体来看,人体的脑部可分为白质、灰质、脑脊液、颅骨和头皮5层[9],其中头皮、颅骨和脑脊液属于脑部的表层组织,灰质和白质属于深层组织。同样,骨骼肌由外至里为皮肤、脂肪和肌肉;乳腺组织包括皮肤、脂肪和结缔组织[10]。
在利用DCS技术进行血流测量时,通常将一对光源光纤和探测器光纤放置于组织表面,两者距离在3 cm以内。激光器发出的光子由光源光纤进入组织后,需要经过表层组织才可到达深层组织,最后经过吸收和反射后被探测器光纤收集。所以,DCS测得的是表层组织和深层组织的混合血流信号,表层组织会对深层组织的血流测量造成一定程度的影响,并且这种影响与光源-探测器(source-detector,S-D)的距离密切相关。当S-D距离较近时,测到的信号携带的大部分是表层信号,而较远距离S-D测到的信号会携带更多的深层组织信号。因此,从混合信号中分离出深层组织的血流信息具有重要研究意义。
为了解决上述问题,2005年,Li等[11]根据人体头部结构和厚度,提出了3层模型的DCS扩散方程的解析表达式,可以分别提取出头皮和脑皮层的血流指数。在此基础上,2006年,Jaillon等[12]建立了一个分层的人体头部模型,研究了非散射层(脑脊液层)对时间场自相关函数的影响,结果显示,当忽略脑脊液层时,脑皮层的血流指数会被低估约40%;2014年,Baker等[13]提出了修正的比尔-郎伯定律,将血流、散射和吸收等特性的变化与“DCS光密度”的变化联系起来,从中分离出了两层组织的血流成分;2015年,Baker等[14]提出的施加压力的方法来过滤掉浅表组织信号对深层信号的影响;2016年的Sutin等[15]和2017年的Pagliazzi等[16]提出了时域漫射相关光谱(time-domain diffuse correlation spectroscopy,TD-DCS),根据光子在浅层和深层组织内飞行时间(photon time of flight,TOF)的不同,分离出表层和深层组织的血流信息,但是,TD-DCS需要使用长相干的脉冲激光器,极大增加了设备成本。
由以上可知,以往的分离组织血流的算法需要预先知道被测组织(例如:头部、肌肉和乳腺)结构,或者需要使用昂贵的硬件。实际上,人的组织结构和每层厚度存在较大的个体差异性,并且这些信息不易测得,寻求不依赖组织结构信息并简单易行的DCS血流提取算法,对于DCS的临床应用有重要价值。
独立成分分析(independent component analysis,ICA)是一类较为成熟的盲源分离算法,其基本思路是在假设独立成分是非高斯且独立的条件下,从多路混合有独立成分的信号中较好地分离出隐含的独立源信号[17]。本文将我们之前自主开发的N 阶线性算法与ICA结合,构建新的DCS血流算法。计算机仿真表明,新算法可以将输入的两个S-D距离的DCS信号实分解为表层和深层的血流信息,可以有效地获得特定组织的生理信息,具有重要的临床应用价值。
1. 材料与方法
1.1 DCS血流测量的原理
近红外光谱带中具有一个生理观察窗,即波长范围为680~900 nm时,生物组织对近红外光具有高散射低吸收的特点,因此,该波长范围的近红外光可以获得更深层的组织吸收和散射特性[18]。
在利用DCS技术测量组织血流时,在目标组织表面的同一侧放置光源和探测器对(S-D),两者距离为
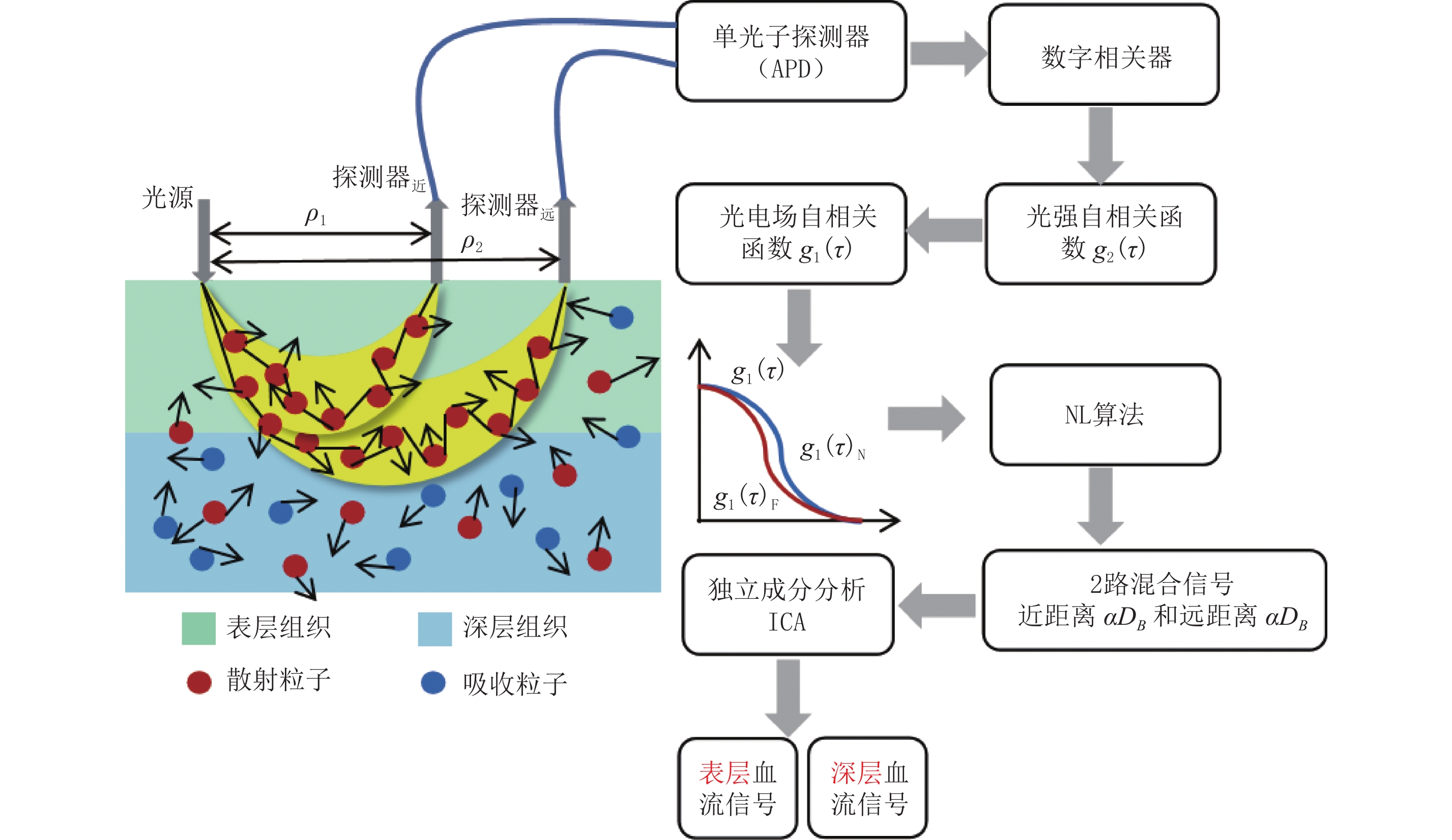
$ \rho $ 。激光器发射出近红外光,通过多模光纤入射到生物组织,光子在组织中进行多次散射和吸收,最终有一部分光子经过多次散射后从组织表面逸出,被放置在组织表面同一侧的单模光纤收集,并传输给单光子探测器(APD),这些光子的散射路径呈“香蕉状”[19-20]。探测深度与S-D距离有关,约为光源和探测器间距离的一半,即$ ~\rho /2 $ 。由APD收集光子经过数字相关器进行时间自相关运算得到光强自相关函数
$ {g}_{2}\left(\tau \right) $ ,利用Siegert关系式$ {g}_{2}\left(\tau \right)=1+\beta \left|{{g}_{1}\left(\tau \right)}^{2}\right| $ 计算出光电场自相关函数$ {g}_{1}\left(\tau \right) $ 。$ {g}_{1}\left(\tau \right) $ 曲线依赖于运动散射体(主要是红细胞)的运动。在特定的S-D距离下,自相关曲线$ {g}_{1}\left(\tau \right) $ 的衰减越大,表示组织血流越高。1.2 N阶线性算法(NL算法)提取血流
N 阶线性(N-order linear,NL)算法将光电场自相关函数
$ {g}_{1}\left(\tau \right) $ 与组织中光子传输的路径信息相结合,用于提取具有任意体积、形状和曲率的非均匀组织的血流值[21],是一种新的提取DCS组织血流指数(blood flow index,BFI)的方法。它是由$ {g}_{1}\left(\tau \right) $ 的积分形式中推导出来的:$$ {g_1}(\tau ) = \frac{{\,\Big\langle {E(0){E^ * }(\tau )} \Big\rangle {\kern 1pt} }}{{\left\langle {{{\left| {E(0)} \right|}^2}} \right\rangle }} = \int\limits_0^{\; \propto } {P(s)\exp \left( { - \frac{1}{{\,3{\kern 1pt} }}k_0^2\left\langle {\Delta {r^2}(\tau )} \right\rangle \frac{s}{{\,{l^*}}}} \right)} \,{\rm{d}}s\text{,} $$ (1) 其中,τ是自相关函数的延迟时间;
$ P\left(s\right) $ 为检测到的光子路径长度s的归一化分布;$ {k}_{0} $ 是介质中光的波矢量大小;$ {l}^{*} $ 为光在组织中的总路径长度,且${l}^{*}=\displaystyle\frac{1}{{\mu }_s'};{\mu }_s'$ 为散射系数;$\left\langle {\Delta {r^2}(\tau )} \right\rangle $ 为运动散射体的均方位移,且$\left\langle {\Delta {r^2}(\tau )} \right\rangle = 6\alpha {D_B}\tau $ ,其中,$ {D}_{B} $ 为有效扩散系数(单位为cm2/s),$ \alpha $ 为运动散射体占总体散射体的比率,$ \alpha {D}_{B} $ 为生物组织的血流值。则公式(1)可写为:$$ {g_1}(\tau ) = \int\limits_0^{\; \propto } {P(s)\exp \left( { - 2k_0^2\alpha {D_B}s\mu _s'\tau } \right)} \,{\rm{d}}s。 $$ (2) 经过
$ {g_1}(\tau ) $ 泰勒公式展开及式(2)求导等数学推导[22],可得一阶和N阶(N>1)线性算法:$$ {g_1}(\tau ) - 1 = ( - H)\bar s\tau ,\quad N = 1 \text{,} $$ (3) $$ {g_1}(\tau ) - 1 - \sum\limits_{i = 2}^N {\left( {\frac{{{{( - H)}^i}\bar {{s^i}} }}{{i!}}} \right)} {\tau ^i} = ( - H)\bar s\tau ,\quad N\ge2 \text{,} $$ (4) 其中,
$\bar{{s}^{i}}=\displaystyle\int _{0}^{\infty }P\left(s\right){s}^{i}\mathrm{d}s$ ,$H=2{k}_{0}^{2}{\mu }_{s}'\alpha {D}_{B}$ ,$\bar{{s}^{i}}$ 为光子在组织内的传输路径信息,可以通过蒙特卡罗仿真获得。令$Z=-2{k}_{0}^{2}{\mu }_s'\bar{s}$ ,式(3)则为:$$ {g_1}(\tau ) - 1 = Z \cdot \alpha {D_B}\tau ,\quad N = 1 。 $$ (5) 从式(5)可以看出,
$ Z\cdot \alpha {D}_{B} $ 是$ {g_1}(\tau ) - 1 $ 的斜率$ Sl $ 。对于一阶线性算法,只要确定了$ {g_1}(\tau ) $ 的斜率就可以求得血流如式(6)。而对于$ N\ge 2 $ 时,等式两边都含有血流$ \alpha {D}_{B} $ ,可将式(4)通过递归的方法得血流如式(7),也即式(8):$$ Z\cdot \alpha {D}_{B}^{\left(1\right)}=Sl \text{,} $$ (6) $$ {g}_{1}\left(\tau \right)-1-\sum _{i=2}^{N}\frac{{\Big(-2{k}_{0}^{2}{\mu }_s'{\alpha {D}_{B}}^{(N-1)}\Big)}^{i}\bar{{s}^{i}}}{i!}{\tau }^{i}=\Big(-2{k}_{0}^{2}{\mu }_s'{\alpha {D}_{B}}^{\left(N\right)}\bar{s}\Big)\tau =Z\cdot {\alpha {D}_{B}}^{\left(N\right)}\tau ,\;\;N\ge 2 \text{,} $$ (7) $$ Z\cdot \alpha {D}_{B}^{\left(N\right)}=S{l}^{\left(N\right)} 。 $$ (8) 1.3 独立成分分析ICA
ICA是一种从混合信号中分离出源信号的信号处理技术,被应用于许多领域,如生物医学信号处理、语音信号处理、特征提取等[23-26]。随机变量
$ {x}_{j} $ (j=1,2,···,m)代表混合信号,$ {s}_{k} $ (k=1,2,···,n)代表相互统计独立且为非高斯变量的源信号,ICA模型可以表示为:$$ {x}_{j}={a}_{j1}{s}_{1}+{a}_{j2}{s}_{2}+\cdots{a}_{jn}{s}_{n} \text{,} $$ (9) 即:
$$ \boldsymbol{x}=\boldsymbol{A}\boldsymbol{s} \text{,} $$ (10) 其中,
$\boldsymbol{x}={\Big({x}_{1}(t),{x}_{2}(t),\cdots ,{x}_{m}(t)\Big)}^{\mathrm{T}}$ 是可以直接被观测到的混合信号,是已知量;A是一个m×n维的列满秩常数矩阵,是未知量;$\boldsymbol{s}={\Big({s}_{1}(t),{s}_{2}(t),\cdots,{s}_{n}(t)\Big)}^{\mathrm{T}}$ 是隐变量,也是未知量。在ICA问题中,只要求出矩阵A,就可以从x中求出独立成分s。但是矩阵A是未知的,考虑到$ {x}_{j} $ 的线性组合,可以用$ {\boldsymbol{y}} = {{\boldsymbol{w}}^{\rm{T}}}{\boldsymbol{x}} = \sum\limits_{j = 1}^m {{w_j}{x_j}} $ 来估计其中的一个独立成分,其中w是矩阵A的逆的一行,称为分离矩阵或解混矩阵[17]。因此,只要确定分离矩阵w,使得$ {\boldsymbol{w}}^{\mathrm{T}}{\boldsymbol{x}} $ 非高斯性最大时,就可以得到源信号的估计。本研究采用峭度度量非高斯性,当预处理后的观测血流信号峭度最大时,就会对应着某个独立成分。非高斯性通常利用峭度的绝对值或平方来度量,采用峭度度量方法的目标函数为[27]:
$$ {J}_{{k}_{4}}\left(\boldsymbol{w}\right)=\left|{k}_{4}\left({\boldsymbol{w}}^{\mathrm{T}}\boldsymbol{z}\right)\right| \;\;或\;\; {J}_{{k}_{4}}\left(\boldsymbol{w}\right)=\Big({k}_{4}\big({\boldsymbol{w}}^{\mathrm{T}}\boldsymbol{z}\big)\Big)^{2} \text{,} $$ (11) 其中,z为观测信号x预处理后得到的零均值白化信号。通过求取目标函数的最大值可以实现源信号的估计,基于峭度的快速不动点迭代算法为[28]:
$$ \left\{\begin{array}{c}w\leftarrow E\left\{z{\left({\boldsymbol{w}}^{\mathrm{T}}\boldsymbol{z}\right)}^{3}\right\}-3w\\ w\leftarrow \displaystyle \frac{\boldsymbol{w}}{\|\boldsymbol{w}\|}\end{array}\right. 。$$ (12) 算法的收敛标准为:
$$ \Big|\left|{\boldsymbol{w}}^{\mathrm{T}}\left(k\right)\boldsymbol{w}(k-1)\right|-1\Big| < \varepsilon ,$$ (13) 其中,ε为很小的正数,本研究取值为10-5。
ICA提取独立分量时,为了保证同一源信号不被重复提取,迭代过程中,在下一个源信号提取之前需进行正交化处理。假设已提取出的p-1个向量
${\boldsymbol{w}}_{1},{\boldsymbol{w}}_{2},\cdots,{\boldsymbol{w}}_{p-1}$ ,构造一个初始化寄存矩阵B,B的每一列就是这p-1个向量,在提取向量$ {\boldsymbol{w}}_{p} $ 之前按照下式进行正交化[27]:$$ {\boldsymbol{w}}_{p}={\boldsymbol{w}}_{p}-\overline{\boldsymbol{B}}\;{\overline{\boldsymbol{B}}}^{{\rm{T}}}{\boldsymbol{w}}_{p} 。 $$ (14) ICA迭代之前需进行去均值和白化预处理。去均值是将混合信号减去它的均值,使其变成零均值向量,此过程不会改变混合矩阵[27]。白化是为了去除信号的相关性[29-30]。对观测信号x预处理可以表示为:
$$ {\boldsymbol{x}}'=\boldsymbol{x}-E\left\{\boldsymbol{x}\right\} \text{,} $$ (15) $$ \boldsymbol{z}=\boldsymbol{V}{\boldsymbol{x}}'\text{,} $$ (16) 式(15)和式(16)中,x为混合的血流信号,
${\boldsymbol{x}}'$ 为去均值后的信号,z为白化后的信号,V为白化矩阵,且:$$ \boldsymbol{V}={\boldsymbol{D}}^{-\frac{1}{2}}{\boldsymbol{E}}^{\mathrm{T}} ,$$ (17) 其中,
$\boldsymbol{D}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({d}_{1},{d}_{2},\cdots,{d}_{n})$ 为${\boldsymbol{x}}'$ 的方差矩阵${\boldsymbol{C}}_x'=\boldsymbol{E}\Big({\boldsymbol{x}}'({{\boldsymbol{x}}'}^{\mathrm{T}})\Big)$ 的特征值构成的对角矩阵,$\boldsymbol{E}=({e}_{1},{e}_{2},\cdots,{e}_{n})$ 为相应的特征向量的正交矩阵[17]。将以上提及的N 阶线性算法(1.2)和ICA(1.3)算法相结合,即
$ \boldsymbol{x}=\alpha {\boldsymbol{D}}_{B} $ ,我们获得了分离浅层和深层组织血流的新算法,其计算流程如图1所示。1.4 血流信号的检验方法
相关系数是用来反映变量之间相关关系密切程度的统计指标,一般用字母r 表示。变量X和Y之间的相关系数公式为:
$$ r=\frac{\sum\limits _{i=1}^{n}\Big({X}_{i}-\bar{X}\Big)\Big({Y}_{i}-\bar{Y}\Big)}{\sqrt{{\sum\limits _{i=1}^{n}\Big({X}_{i}-\bar{X}\Big)}^{2}}\sqrt{{\sum\limits _{i=1}^{n}\Big({Y}_{i}-\bar{Y}\Big)}^{2}}} \text{,} $$ (18) r值的绝对值介于 0~1之间。通常来说,r越接近 1,表示X与Y两个量之间的相关程度越强,反之,r越接近于 0,相关程度越弱。在本研究的ICA分离血流问题中,对于假设的血流信号,用相关系数表示深层和浅层血流值的独立程度,r越接近 0说明假设的表层和深层信号越独立;再者,对于分离后的血流信号,用相关系数来表示恢复的信号与原始假设信号的相似程度,r越接近 1则说明分离效果越好。
2. 实验设计及结果
2.1 仿真实验方案
假设表层和深层组织的血流为相关性很小的信号,且为数据长度是400的周期信号,我们进行3组计算机仿真实验。第1组假设表层信号是周期为200 ms,幅度为2×10-9cm2/s的三角波,深层信号是周期为100 ms,幅度为2×10-9cm2/s的方波,两者的相关关系如图2(a),相关性为3.33×10-15。第2组假设的表层和深层信号是:周期分别为100 ms和40 ms,幅度均为4×10-9cm2/s的正弦波,两者的相关关系如图2(b),相关性为1.54×10-17。第3组预设的表层和深层信号是在第1组的三角和方波基础上加了噪声,模拟实际信号。
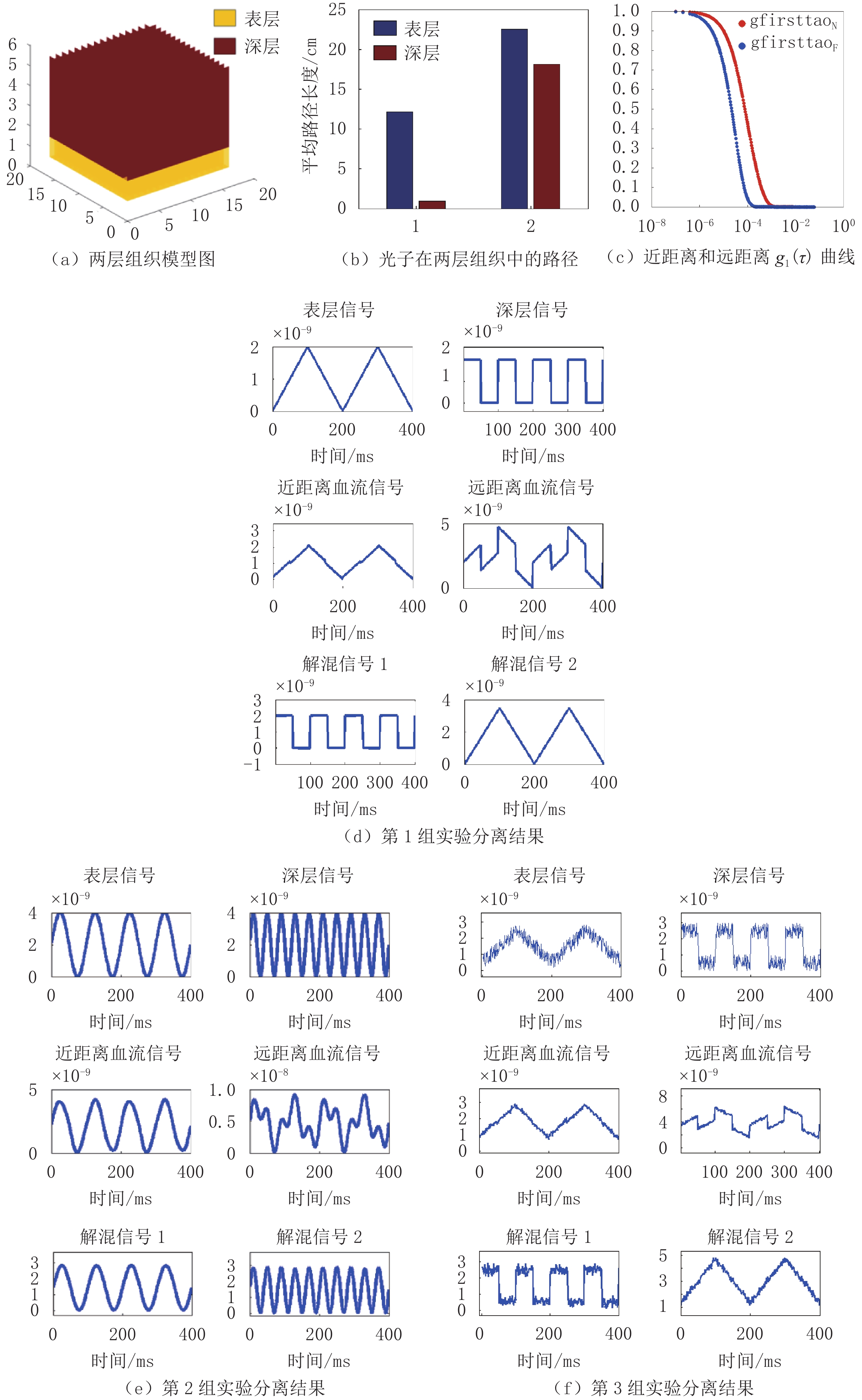
我们建立了一个大小为8 cm×3 cm×8 cm(长×高×宽)的两层结构组织模型,如图3(a),分别设置为头皮颅骨(表层)和脑组织参数(深层)。在组织模型的表面放置一个光源和两个探测器,光源光纤与两个探测器光纤的距离(S-D)分别为1.5 cm和3.0 cm。
蒙特卡罗是一种模拟光在组织内传播的主要方法[31],具有操作简单、灵活可靠、精度高等优点[32]。利用蒙特卡罗仿真软件(MCVM)模拟光子在人体两层组织中的传输情况,将100万个光子发射到组织中以实现较高的信噪比[33]。通过设置输入输出文件名及各组织的光学性质获得光子在每层组织中的传输路径和逸出光子的信息,并带入公式(3)~公式(5),得到近远两个S-D距离下的光电场时间自相关函数
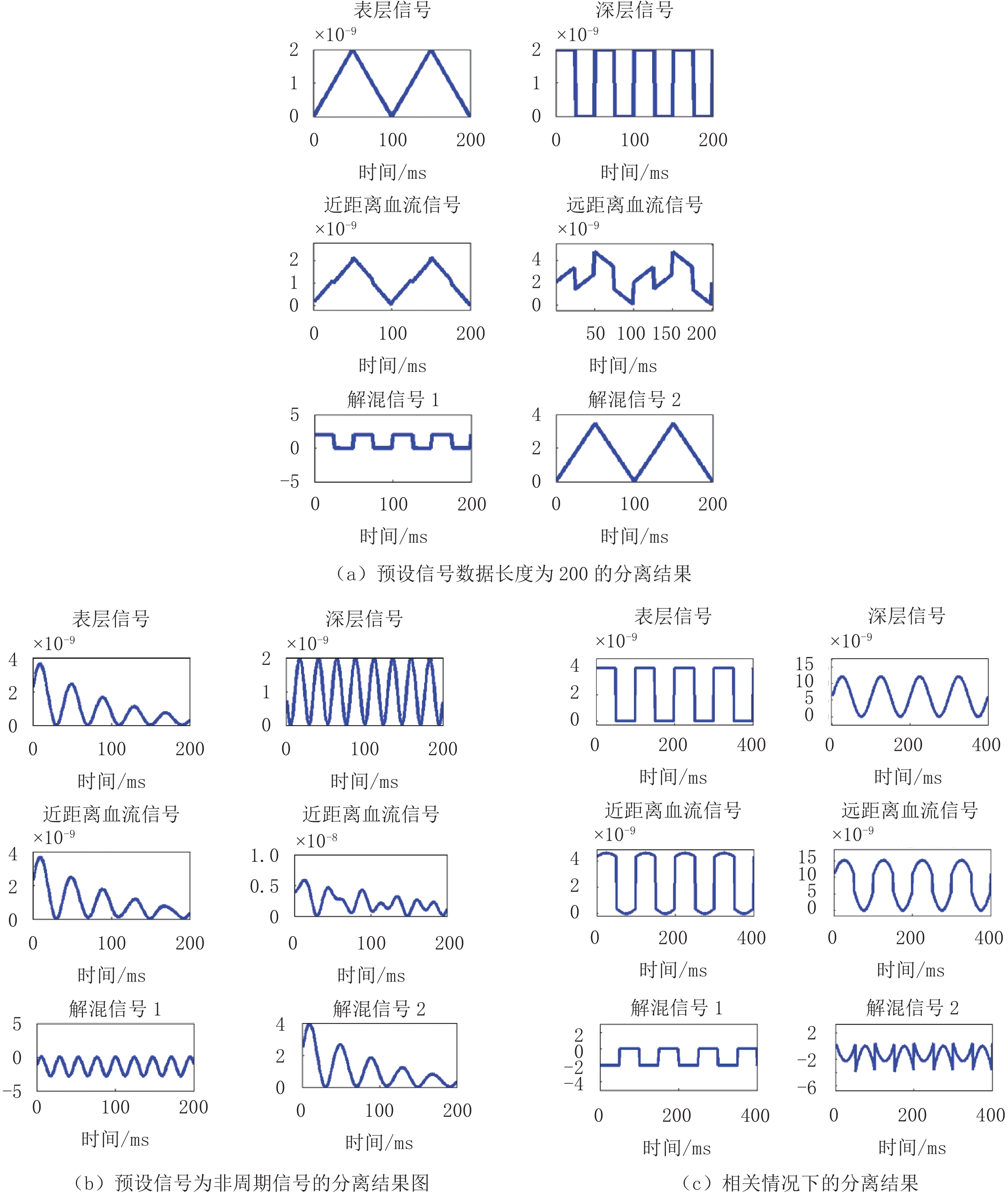
$ {g}_{1}\left(\tau \right) $ 。利用NL算法从$ {g}_{1}\left(\tau \right) $ 中分别得到近远S-D距离的血流信息。将上述得到的信号,经过ICA处理分离出两个血流信号。为了探究信号的数据长度、周期性及相关性质对本文方法提取深层组织血流的准确性的影响,再设计3组对比实验。第1组假设表层信号和深层信号为:数据长度均为200,幅度均为2×10-9cm2/s,周期分别为100 ms和50 ms的三角波和方波。第2组假设的表层信号为非周期信号:按指数逐渐衰减的正弦信号;深层为幅度为2×10-9cm2/s的正弦波。第3组预设的表层和深层信号是相关信号:周期均为100,幅度分别为4×10-9cm2/s和12×10-9cm2/s的方波和正弦波。重复上述实验步骤得到对比实验的分离结果图。
2.2 仿真实验结果
通过上述算法及步骤,蒙特卡罗仿真得到的光子在两层组织模型中的路径如图3(b);S-D对不同距离(近:1.5 cm,远:3 cm)的时间自相关函数如图3(c),其中,gfirsttaoN和gfirsttaoF分别代表近距离和远距离
$ {g}_{1}\left(\tau \right) $ ;第1组实验分离结果如图3(d),第2组实验分离结果如图3(e),第3组实验分离结果如图3(f)。对比实验中:第1组实验分离结果如图4(a),第2组实验分离结果如图4(b),第3组实验分离结果如图4(c)。3. 讨论
压力自动调节是一个器官在血压或灌注压波动的情况下保持稳定血流的内在趋势,是器官灌注压和血流之间的联系[34]。不同器官(如脑血流、肾血流等)之间的自动调节能力是不同的,脑自动调节能力可以用脑血流速度和血压的低频振荡之间的相移来评估[35-36]。脑皮层是重要的大脑功能区,承担着认知、语言,逻辑等任务。脑皮层血流受中枢神经和交感神经的控制,可以对各种生理、病理的情况进行反应,并通过神经-血管耦合机制和血脑屏障保持自身的稳定性,称为“自我控制能力(autoregulation)”。与之不同的是,头皮血流受神经控制较少,更容易受到血压变化的影响。
因此,在很多临床应用情况下(例如:“自我控制能力”评估的倾斜床试验、药物反应、高碳酸反应等),浅层(头皮)和深层(脑皮层)的血流灌注会呈现不同的变化。因此,精确分离脑部血流具有重要的临床价值,在本研究中,假设表层和深层信号是相互独立具有实际意义。
实验结果图3(d)~图3(f)和图4中,第1行为预设的表层和深层血流信号,第2行分别为经过NL算法处理后两个S-D距离分别得到的血流信号(均混合了表层组织和深层组织的血流信息),最后1行为分离出的两个血流信号。从图中可以看出,近距离下测到的血流信号包含大部分的表层信号,远距离下测到的信号包含更多的深层信号,同时会受到表层信号的影响。将图3(d)中的两个解混信号与预设的表层和深层信号做相关验证分离后的信号的准确性,相关系数分别为0.999和0.994,相似度很高,结果表明该算法分离效果较好。
仿真实验结果(图3(d)和图3(e))中,ICA输出的两路独立信号,可能第1路代表深层血流,也可能第2路代表深层血流,也就是说ICA分离信号具有顺序不确定性,分离后的信号与预设信号的顺序可能不一致。因此需要将分离后的信号分别与两个S-D距离的混合血流信号做相关性分析,从而确定解混信号代表的具体组织。如将解混信号分别与远距离S-D(含有更多的深层信号)获得血流信号做相关分析,相关系数大的通道即代表深层血流。由相关系数可知,图3(d)中,解混信号1与近、远S-D距离血流信号的相关性为:0.112、0.783;解混信号2的相关性分别为:0.994、0.622,所以解混信号1代表深层的源信号(0.783>0.112),解混信号2代表表层的源信号(0.994>0.622),结果与预设信号相符。同理,图3(e)中的解混信号1代表表层的源信号,解混信号2代表深层的源信号。
对比实验中,当预设信号的数据长度为200(图4(a))和预设信号是非周期时(图4(b)),ICA均较好的分离出了表层和深层信号。图3(d)与图4(a)对比说明ICA对信号的分离效果不受信号数据长度的影响;图4(b)结果表明:信号的周期性不会影响本文算法提取深层组织血流的准确性。本文算法运用的前提是源信号需是独立的(图3(d)和图3(e))。但是,对于表层和深层组织的信号具有较强相关性时(图4(c)),ICA算法不能很好的进行分离,需要今后继续改进算法。
4. 结论
本文结合N 阶线性算法和ICA算法,从DCS测到的混合血流信号中分离出表层和深层的血流信息,仿真实验结果证实了算法的精确性。本算法局限性表现为分离后的信号在幅度和顺序上具有不确定性,需要利用相关计算来进行判断,并且需假设表层和深层信号是相互独立的。尽管如此,本算法可以不依赖于被测组织的结构信息,较好地分离表层和深层组织的血流信息,在临床应用易于实现,具有重要的实用价值。
-
[1] 张玲. 缺血性卒中急性期中医治疗研究进展[J]. 中国实用医药, 2014,(2): 247−249. doi: 10.14163/j.cnki.11-5547/r.2014.02.203 ZHANG L. Research progress of traditional Chinese medicine treatment in acute ischemic stroke[J]. China Practical Medicine, 2014, (2): 247−249. (in Chinese). doi: 10.14163/j.cnki.11-5547/r.2014.02.203
[2] 刘菊华, 吕江华, 苏小钢, 等. 脑血流监测对缺血性脑卒中血管内治疗术后预后的临床研究[J]. 首都食品与医药, 2021,28(12): 49−50. DOI: 10.3969/j.issn.1005-8257.2021.12.025. LIU J H, LV J H, SU X G, et al. Clinical study of cerebral blood flow monitoring on postoperative prognosis of ischemic stroke after endovascular treatment[J]. Capital Food and Medicine, 2021, 28(12): 49−50. DOI: 10.3969/j.issn.1005-8257.2021.12.025. (in Chinese).
[3] 汪涛, 苏浩波, 顾建平. 评估下肢骨骼肌血流灌注的方法及研究进展[J]. 山西医药杂志, 2019,48(8): 904−907. DOI: 10.3969/j.issn.0253-9926.2019.08.008. WANG T, SU H B, GU J P. Methods and research progress of assessing blood perfusion of lower extremity skeletal muscle[J]. Shanxi Medical Journal, 2019, 48(8): 904−907. DOI: 10.3969/j.issn.0253-9926.2019.08.008. (in Chinese).
[4] 杨扬, 李功杰. 乳腺肿瘤CT灌注成像及其临床应用研究进展[J]. 军事医学科学院院刊, 2007,31(3): 290−293. DOI: 10.3969/j.issn.1674-9960.2007.03.026. YANG Y, LI G J. Research progress of breast tumor CT perfusion imaging and its clinical application[J]. Journal of the Academy of Military Medical Sciences, 2007, 31(3): 290−293. DOI: 10.3969/j.issn.1674-9960.2007.03.026. (in Chinese).
[5] 尚禹, 刘祎, 王冠军, 等. 结合生物体形态学信息实现功能血流成像的近红外漫射光新技术[J]. 中国医学物理学杂志, 2016,33(12): 1212−1216. DOI: 10.3969/j.issn.1005-202X.2016.12.006. SHANG Y, LIU Y, WANG G J, et al. Near-infrared diffuse optical technology for functional blood flow imaging through integrating the morphological information of biological tissues[J]. Chinese Journal of Medical Physics, 2016, 33(12): 1212−1216. DOI: 10.3969/j.issn.1005-202X.2016.12.006. (in Chinese).
[6] DURDURAN T, YODH A G. Diffuse correlation spectroscopy for non-invasive, micro-vascular cerebral blood flow measurement[J]. Neuroimage, 2014, 85: 51−63. doi: 10.1016/j.neuroimage.2013.06.017
[7] SHANG Y, GURLEY K, YU G. Diffuse correlation spectroscopy (DCS) for assessment of tissue blood flow in skeletal muscle: Recent progress[J]. Anatomy & Physiology: Current Research, 2013, 3(2): 128. DOI: 10.4172/2161-0940.1000128.
[8] SHANG Y, LI T, YU G Q. Clinical applications of near-infrared diffuse correlation spectroscopy and tomography for tissue blood flow monitoring and imaging[J]. Physiological Measurement, 2017, 38(4): R1−R26. doi: 10.1088/1361-6579/aa60b7
[9] 乐恺, 罗运晖, 张欣欣. 考虑脑脊液层的局部脑冷却传热分析[J]. 应用基础与工程科学学报, 2010,18(3): 484−492. DOI: 10.3969/j.issn.1005-0930.2010.03013. LE K, LUO Y H, ZHANG X X. Heat transfer analysis of local brain cooling considering cerebrospinal fluid layer[J]. Chinese Journal of Applied Basic and Engineering Sciences, 2010, 18(3): 484−492. DOI: 10.3969/j.issn.1005-0930.2010.03013. (in Chinese).
[10] 李俊来, 赵晓慧. 正常乳腺组织结构与超声表现[J]. 中华医学超声杂志(电子版), 2017,14(8): 561−566. DOI: 10.3877/cma.j.issn.1672-6448.2017.08.001. LI J L, ZHAO X H. Normal breast tissue structure and ultrasound appearance[J]. Chinese Journal of Medical Ultrasound (Electronic Edition), 2017, 14(8): 561−566. DOI: 10.3877/cma.j.issn.1672-6448.2017.08.001. (in Chinese).
[11] LI J, DIETSCHE G, IFTIME D, et al. Noninvasive detection of functional brain activity with near-infrared diffusing-wave spectroscopy[J]. Journal of Biomedical Optics, 2005, 10(4): 044002. doi: 10.1117/1.2007987
[12] JAILLON F, SKIPETROV S E, LI J, et al. Diffusing-wave spectroscopy from head-like tissue phantoms: Influence of a non-scattering layer[J]. Optics Express, 2006, 14(22): 10181−10194. doi: 10.1364/OE.14.010181
[13] BAKER W B, PARTHASARATHY A B, BUSCH D R, et al. Modified Beer-Lambert law for blood flow[J]. Biomedical Optics Express, 2014, 5(11): 4053−4075. doi: 10.1364/BOE.5.004053
[14] BAKER W B, PARTHASARATHY A B, KO T S, et al. Pressure modulation algorithm to separate cerebral hemodynamic signals from extracerebral artifacts[J]. Neurophotonics, 2015, 2(3): 035004. doi: 10.1117/1.NPh.2.3.035004
[15] SUTIN J, ZIMMERMAN B, TYULMANKOV D, et al. Time-domain diffuse correlation spectroscopy[J]. Optica, 2016, 3(9): 1006−1013. doi: 10.1364/OPTICA.3.001006
[16] PAGLIAZZI M, SEKAR S K V, COLOMBO L, et al. Time domain diffuse correlation spectroscopy with a high coherence pulsed source: In vivo and phantom results[J]. Biomedical Optics Express, 2017, 8(11): 5311−5325. doi: 10.1364/BOE.8.005311
[17] HYVARINEN A, OJA E. Independent component analysis: Algorithms and applications[J]. Neural Networks, 2000, 13(4/5): 411−430. doi: 10.1016/S0893-6080(00)00026-5
[18] 梁佳明, 王晶, 梅建生, 等. 基于扩散相关光谱的血流检测方法研究[J]. 光谱学与光谱分析, 2012,32(10): 2749−2752. DOI: 10.3964/j.issn.1000-0593(2012)10-2749-04. LIANG J M, WANG J, MEI J S, et al. Research on blood flow detection method based on diffusion correlation spectroscopy[J]. Spectroscopy and Spectral Analysis, 2012, 32(10): 2749−2752. DOI: 10.3964/j.issn.1000-0593(2012)10-2749-04. (in Chinese).
[19] 刘彩彩, 凌浩, 冯士杰, 等. 诱发生理状态下的脑血流动力学的无创光学评估[J]. 中国医疗设备, 2020,35(2): 36−39. DOI: 10.3969/j.issn.1674-1633.2020.02.009. LIU C C, LING H, FENG S J, et al. Noninvasive optical evaluation of cerebral hemodynamics under induced-physiological status[J]. China Medical Equipment, 2020, 35(2): 36−39. DOI: 10.3969/j.issn.1674-1633.2020.02.009. (in Chinese).
[20] 冯士杰, 桂志国, 张晓娟, 等. 基于3D打印技术的血流成像光纤探头设计[J]. 中国医疗设备, 2022,37(2): 24−28. DOI: 10.3969/j.issn.1674-1633.2022.02.006. FENG S J, GUI Z G, ZHANG X J, et al. Design of optical fiber probe for blood flow imaging based on 3D printing technology[J]. China Medical Equipment, 2022, 37(2): 24−28. DOI: 10.3969/j.issn.1674-1633.2022.02.006. (in Chinese).
[21] SHANG Y, YU G. A Nth-order linear algorithm for extracting diffuse correlation spectroscopy blood flow indices in heterogeneous tissues[J]. Applied Physics Letters, 2014, 105(13): 133702. doi: 10.1063/1.4896992
[22] SHANG Y, LI T, CHEN L, et al. Extraction of diffuse correlation spectroscopy flow index by integration of Nth-order linear model with Monte Carlo simulation[J]. Applied Physics Letters, 2014, 104(19): 193703. doi: 10.1063/1.4876216
[23] HYVARINEN A, Karhunen J, Oja E. 独立成分分析[M]. 周宗潭, 董国华, 徐昕, 等, 译. 北京: 电子工业出版社. 2007. [24] 吴小培. 独立分量分析及其在脑电信号处理中的应用[D]. 合肥: 中国科学技术大学, 2002: 73-102. DOI: 10.7666/d.y480061. WU X P. Independent component analysis and its application in EEG signal processing[D]. Hefei: University of Science and Technology of China, 2002: 73-102. DOI:10.7666/d.y480061. (in Chinese).
[25] 杨竹青, 李勇, 胡德文. 独立成分分析方法综述[J]. 自动化学报, 2002,28(5): 762−772. doi: 10.16383/j.aas.2002.05.012 YANG Z Q, LI Y, HU D W. Review of independent component analysis methods[J]. Chinese Journal of Automation, 2002, 28(5): 762−772. (in Chinese). doi: 10.16383/j.aas.2002.05.012
[26] 杨金成, 张南. 独立成分分析技术综述[J]. 舰船科学技术, 2007,29(2): 83−86. YANG J C, ZHANG N. Review of independent component analysis technology[J]. Ship Science and Technology, 2007, 29(2): 83−86. (in Chinese).
[27] 李云霞. 盲信号分离算法及其应用[D]. 成都: 电子科技大学, 2008: 13-31. DOI: 10.7666/d.Y1450260. LI Y X. Blind signal separation algorithm and its application[D]. Chengdu: University of Electronic Science and Technology of China, 2008: 13-31. DOI:10.7666/d.Y1450260. (in Chinese).
[28] HYVARINEN A, OJA E. A fast fixed-point algorithm for independent component analysis[J]. Neural Computation, 1997, 9(7): 1483−1492. doi: 10.1162/neco.1997.9.7.1483
[29] 田甲略, 朱玉莲, 陈飞玥, 等. 基于局部特征的二维白化重构[J]. 数据采集与处理, 2022,37(2): 308−320. DOI: 10.16337/j.1004-9037.2022.02.005. TIAN J L, ZHU Y L, CHEN F Y, et al. Local-feature-based two-dimensional whitening reconstruction[J]. Journal of Data Acquisition and Processing, 2022, 37(2): 308−320. DOI: 10.16337/j.1004-9037.2022.02.005. (in Chinese).
[30] 江涌, 章林柯, 何琳, 等. 两次去相关用于振动信号盲分离[J]. 振动、测试与诊断, 2011,31(2): 241−245. DOI: 10.3969/j.issn.1004-6801.2011.02.022. JIANG Y, ZHANG L K, HE L, et al. Double decorrelation for blind separation of vibration signals[J]. Vibration, Testing and Diagnosis, 2011, 31(2): 241−245. DOI: 10.3969/j.issn.1004-6801.2011.02.022. (in Chinese).
[31] LI T, GONG H, LUO Q. Visualization of light propagation in visible Chinese human head for functional near-infrared spectroscopy[J]. Journal of Biomedical Optics, 2011, 16(4): 045001. doi: 10.1117/1.3567085
[32] LI T, XUE C, WANG P, et al. Photon penetration depth in human brain for light stimulation and treatment: A realistic Monte Carlo simulation study[J]. Journal of Innovative Optical Health Sciences, 2017, 10(5): 1743002. doi: 10.1142/S1793545817430027
[33] LI T, LIN Y, SHANG Y, et al. Simultaneous measurement of deep tissue blood flow and oxygenation using noncontact diffuse correlation spectroscopy flow-oximeter[J]. Scientific Reports, 2013, 3(1): 1−10.
[34] MENG L, WANG Y, ZHANG L, et al. Heterogeneity and variability in pressure autoregulation of organ blood flow: Lessons learned over 100+ years[J]. Critical Care Medicine, 2019, 47(3): 436−448. doi: 10.1097/CCM.0000000000003569
[35] CHENG R, SHANG Y, HAYES J D, et al. Noninvasive optical evaluation of spontaneous low frequency oscillations in cerebral hemodynamics[J]. Neuroimage, 2012, 62(3): 1445−1454. doi: 10.1016/j.neuroimage.2012.05.069
[36] DIEHL R R, LINDEN D, LUCKE D, et al. Phase relationship between cerebral blood flow velocity and blood pressure: A clinical test of autoregulation[J]. Stroke, 1995, 26(10): 1801−1804. doi: 10.1161/01.STR.26.10.1801
-
期刊类型引用(1)
1. 徐舒宁,桂志国,尚禹. 漫射相关光谱在脑血流自动调节中的研究. 中国医疗设备. 2025(04): 44-49 .  百度学术
百度学术
其他类型引用(1)
































































 下载:
下载: