Removal of Gridline Artifacts in Cone-beam CT Based on Wavelet Transform
-
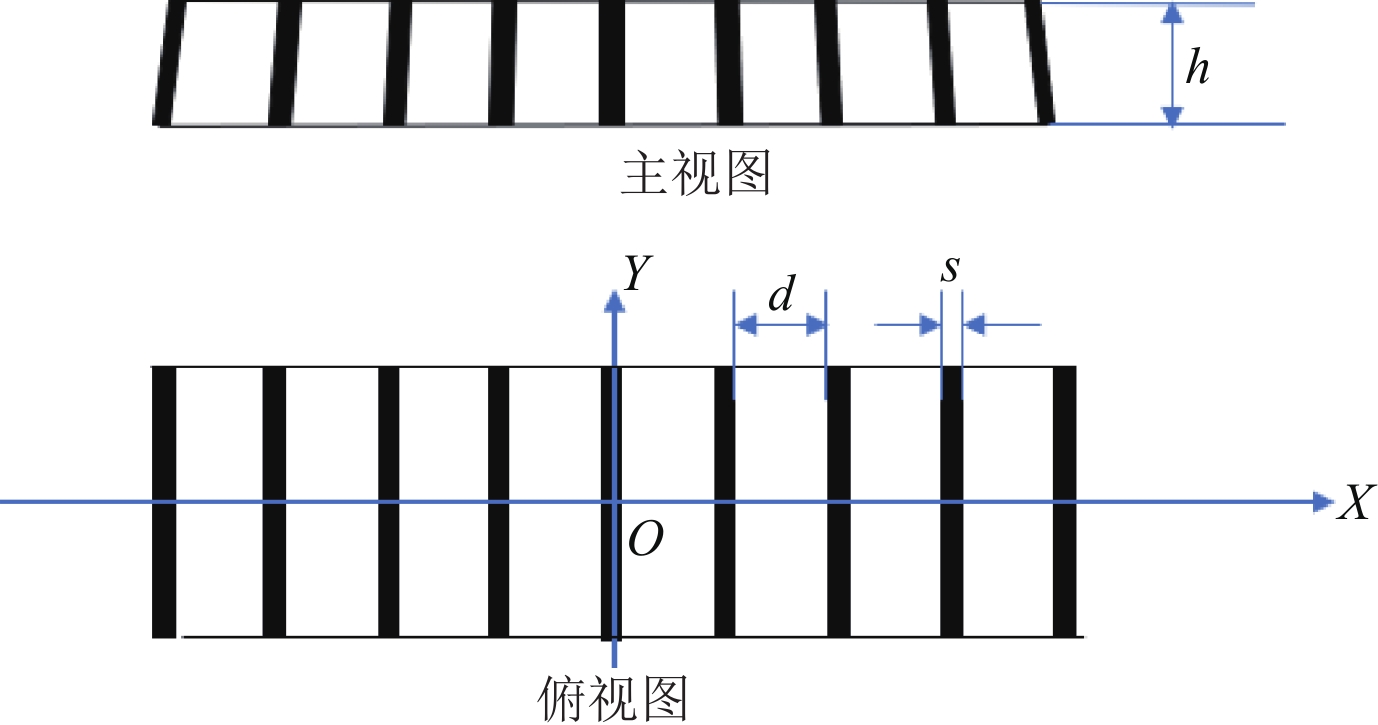
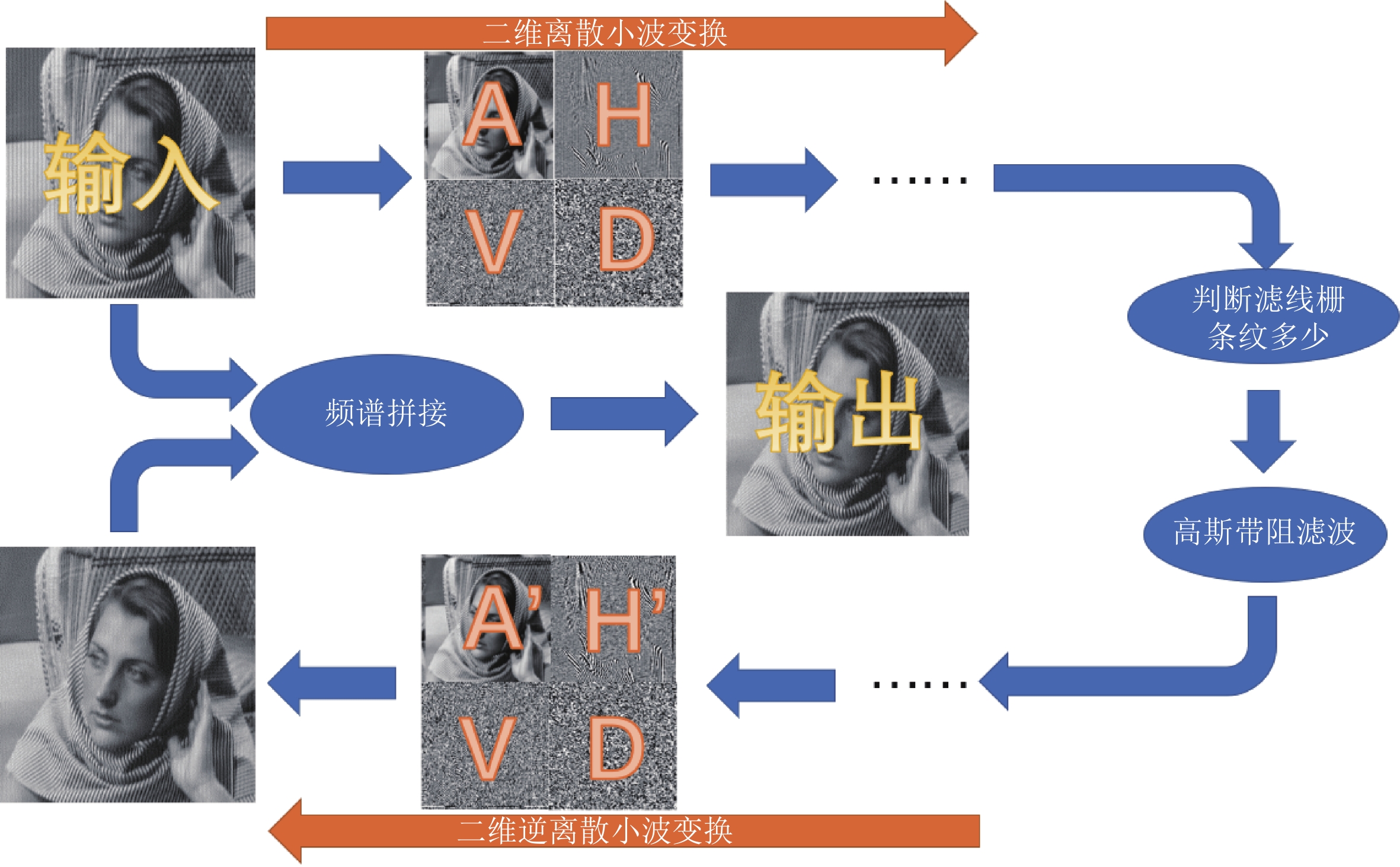
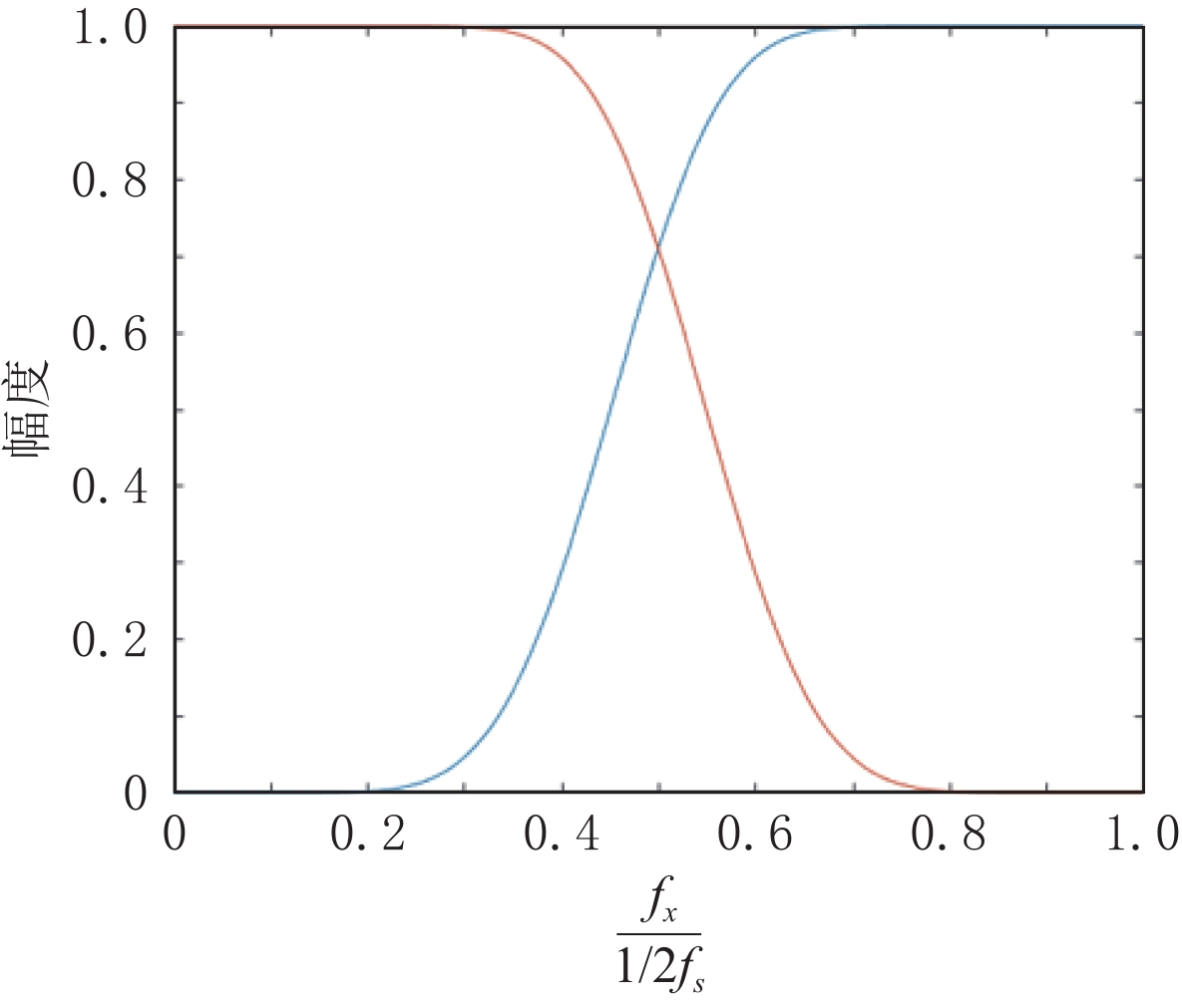
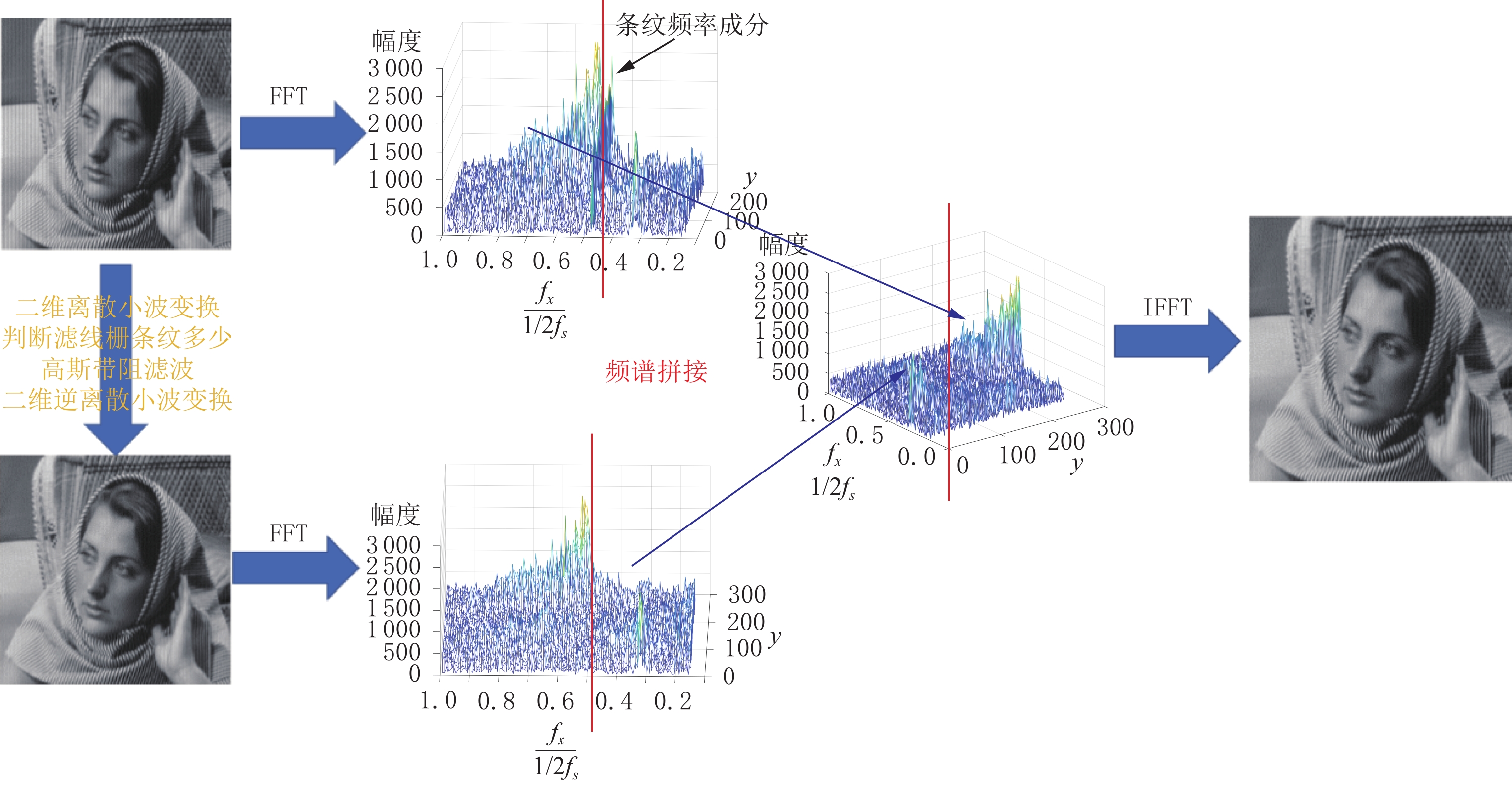
摘要: 采用平板探测器的X射线锥束成像系统中，由于散射会带来图像伪影从而劣化图像质量，通常采用在平板探测器前安装滤线栅来去除散射，但滤线栅会在获取的图像上形成周期性的条状伪影，如何去除条状伪影是X射线锥束成像系统中的一个关键技术问题。本文对已有的滤线栅条纹去除方法进行概述，创新性地提出基于频谱拼接的小波变换方法，既能在损失物体细节信息少的前提下很好地去除滤线栅条纹，又不会引入小波变换谐波。通过实际实验，检验该方法的有效性。Abstract: In cone-beam computed tomography with flat-panel imagers, scattered X-ray photons lead to reduced image quality. Insertion of an anti-scatter grid between the patient or object and the flat-panel imagers is one of the most used techniques for reducing scattered radiation. However, while the scatter is reduced, gridline artifacts can be visible. Suppressing gridline artifacts in cone-beam computed tomography is significant. In this paper, the existing methods of removing gridline artifacts are summarized. Moreover, the wavelet transform method based on spectrum coalescence is innovatively proposed for removing gridline artifacts. Wavelet transform can remove gridline artifacts effectively and without introducing wavelet transform harmonics thus reducing the loss of object details. The effectiveness of this method is verified by experiments.
-
Keywords:
- gridline artifacts /
- wavelet transform /
- spectrum coalescence
-
当储层附近存在泥灰岩、高速砂岩或者煤层等特殊岩性地层时，储层与围岩波阻抗差异较大，在地震剖面上出现强振幅同相轴，使其附近的目标储层的反射信息被掩盖，严重影响了薄储层的精确刻画[1-2]。因此，去除强反射层的屏蔽作用，对于恢复储层的有效信号，提高储层预测精度意义重大。
针对上述问题，已有很多地球物理学者进行了研究和分析，主要分为两种方法。一种是多子波分解重构方法，通过去除重构信号中的强反射频段对应分量实现去强凸弱[3-5]，该方法能快速有效地去除强反射，但同时也可能会去除与强反射频率相近的信号；另一种是基于匹配追踪的强反射分离方法。
1993年，Mallat等[6]首次提出匹配追踪算法；1995年Chakraborty等[7]首次将其应用于地球物理领域；2004年Liu等[8]研究了基于雷克子波原子库的匹配追踪方法，并利用地震信号的三瞬属性作为子波的初始参数；2007年宋维琪等[9]使用瞬时平均频率匹配子波，重建地震剖面并识别薄层砂体；2010年Wang[10-11]在Liu的基础上提出多道匹配追踪算法，同时分解多道地震信号，并应用于煤层强反射的分离，取得了显著效果；2016年张在金等[12]引入沿层信息，实现强反射层的准确提取和分离，并使用广义S变换分析储层低频伴影现象；2019年许璐等[13]使用局部频率代替瞬时频率来匹配和去除强反射同相轴，凸显储层弱反射信息；2019年何峰等[14]从井旁地震道提取子波，并通过动态调整的匹配子波控制参数，匹配煤层强反射再进行去除；2021年杨子鹏等[15]引入残差阈值比作为匹配追踪迭代终止条件，在去除强反射信号的同时保留了更多的有效信号。概括来说，使用匹配追踪算法去除强屏蔽具有运算速度较快、提取强反射精度更高的优点，同时也存在部分情况下横向连续性不佳的问题。
此外，近年来基于压缩感知的强屏蔽去除方法也开始兴起。2019年张云银等[16]应用压缩感知技术反演地震反射系数，并在强反射处开时窗减去其反射系数实现强屏蔽去除。压缩感知方法提取强反射层精度和横向连续性较好，但算法运算耗时较长，且子波及时窗选取不当会导致提取的强反射不完整或去除有效信号的情况发生。
基于上述对多种去强屏蔽方法的讨论分析，本文引入基于横向相关性的自适应加权平均多道算法，通过对强反射层进行局部拉平处理，减弱地层空间构造对提取强反射层的影响。然后引入相邻地震道与中心道之间的相关系数作为多道平均的权值，可以提高断层发育、地层起伏较大资料的匹配精度，改善横向连续性。理论模型测试和实际资料处理结果表明，本文所提出的改进方法具有更好的应用效果。
1. 方法原理
1.1 匹配追踪算法原理
匹配追踪算法是一种常用的信号稀疏分解算法[2]，核心思想是通过在原子库中扫描时移、频率和相位等参数，选取与当前残差信号内积最大的原子，并在残差信号中减去该原子的分量来更新残差，并不断迭代循环这一过程，在一定的迭代次数或残差能量小于阈值时停止迭代[17-18]。对于希尔伯特空间内的原始信号
${\boldsymbol{s}}$ ，其算法第1次迭代可表述为：$$ {{\boldsymbol{R}}^1}({\boldsymbol{s}}) = {\boldsymbol{s}}-\Big\langle {{\boldsymbol{s}}{\text{,}}\;{{\boldsymbol{g}}_{{\gamma _0}}}} \Big\rangle {{\boldsymbol{g}}_{{\gamma_0}}} \text{，} $$ (1) 式中：
${{\boldsymbol{R}}^1}({\boldsymbol{s}})$ 表示经过一次迭代后的残差，$\Big\langle {{\boldsymbol{s}},\;{\boldsymbol{g}}_{\gamma _{0}}} \Big\rangle$ 表示原始信号和第1次迭代时所选取的原子的内积，然后继续以残差作为输入进行循环迭代，优选出最佳匹配原子。图1为匹配追踪原理示意图，使用7个Morlet子波合成输入信号，然后进行匹配追踪迭代分解，每次迭代都优选出与当前输入信号最佳匹配的原子，经过7次迭代后，重构信号能够较好地表示出原始信号，残差基本为随机噪声。
![]()
图 1 匹配追踪分解重构示意图Figure 1. Schematic of matching pursuit decomposition and reconstruction1.2 自适应加权平均多道匹配追踪原理
2010年，Wang[11]提出了多道匹配追踪3步法求取子波。首先，对所选地震道附近L个残差地震道取平均：
$$ {{\boldsymbol{R}}^{n - 1}}({\boldsymbol{y}}) = \frac{1}{{{L}}}\sum\limits_{i = 1}^L {{{\boldsymbol{R}}^{n - 1}}({{\boldsymbol{s}}_i})} \text{，} $$ (2) 式中：
${{\boldsymbol{R}}^{n - 1}}({{\boldsymbol{s}}_i})$ 表示中心道附近第$ i $ 个残差道，${{{{\boldsymbol{R}}}}^{n - 1}}({{{\boldsymbol{y}}}})$ 表示多道平均得到的平均残差道，第1次迭代时初始残差道${{\boldsymbol{R}}^0}({{\boldsymbol{s}}_i}) = {{\boldsymbol{s}}_i}$ ，即${{\boldsymbol{R}}^0}({\boldsymbol{y}}) = \displaystyle\frac{1}{L}\sum\limits_{i = 1}^L {{{\boldsymbol{s}}_i}}$ ，然后对其进行一次Hilbert变换，可以得到信号的瞬时频率$ {\omega _n} $ 、相位$ {\phi _n} $ 以及信号振幅包络中心处的时间延迟$ {u_n} $ ，然后以公式（3）为准则对尺度因子$ {\sigma _n} $ 进行遍历搜索最优值：$$ {{\boldsymbol{g}}_\gamma }_{_n} = \arg \mathop {\max }\limits_{{{\boldsymbol{g}}_\gamma }_{_n} \in {\boldsymbol{D}}} \frac{{\left| {\left\langle {\left. {{{\boldsymbol{R}}^{n - 1}}({\boldsymbol{y}}),\;{{\boldsymbol{g}}_\gamma }_{_n}} \right\rangle } \right.} \right|}}{{\left\| {{{\boldsymbol{g}}_\gamma }_{_n}} \right\|}} \text{，} $$ (3) 式中：D为冗余原子库，
$\left\| {{{\boldsymbol{g}}_\gamma }_{_n}} \right\| = \sqrt {\left\langle {\left. {{{\boldsymbol{g}}_\gamma }_{_n},\;{{\boldsymbol{g}}_\gamma }_{_n}} \right\rangle } \right.}$ 表示对原子进行归一化处理。然后以与相邻L道地震信号内积之和最大为标准，以上一步求得的初始参数为中心设置搜索范围，用公式（4）搜索最优化子波参数组合，迭代循环上述步骤直至信号残差小于预设阈值。$$ {{\boldsymbol{g}}_{{\gamma _n}}} = \arg \mathop {\max }\limits_{{{\boldsymbol{g}}_{{\gamma _n}}} \in {\boldsymbol{D}}} \frac{{\displaystyle\sum\limits_{i = 1}^L {\left| {\left\langle {\left. {{{\boldsymbol{R}}^{n - 1}}({{\boldsymbol{s}}_i}),\;{{\boldsymbol{g}}_\gamma }_{_n}} \right\rangle } \right.} \right|} }}{{\left| {\left| {{{\boldsymbol{g}}_{{\gamma _n}}}} \right|} \right|}} 。 $$ (4) 多道匹配追踪算法可以较好地压制随机噪声，地震道之间的横向连续性也有了很大提升。但在断层等空间变化剧烈处由于相邻地震道之间的差异较大，公式（2）中直接平均后各个地震道的有效信息相互抵消衰减，对其进行时频分析求取的初始参数也会与最优值产生较大偏差。此外，在公式（4）中，由于多个道之间差异较大，匹配得到的子波将不能代表原始信号的特征，而是在多道信号中间进行“折中”来使得子波与多个道的内积之和尽可能地大，增大了算法的不稳定性。
针对多道匹配追踪在地层构造复杂地区匹配效果不佳的问题[19]，本文提出自适应多道匹配追踪改进算法，其思想是首先以中间道为中心，对相邻道在时间维度上进行整体平移实现层拉平处理；然后对中间道和相邻的地震道进行相关运算得到相关系数，并且在处理后作为多道平均的权值。
$$ {r_{ki}} = {{\boldsymbol{s}}_k}(t) \otimes {{\boldsymbol{s}}_{k - i}}(t)\text{，} $$ (5) 式中：
${r_{ki}}$ 代表第k个中间道${{\boldsymbol{s}}_k}(t)$ 与相邻的第i道${{\boldsymbol{s}}_{k - i}}(t)$ 的相关系数。同时，为进一步增大有效信号的能量占比，设置阈值参数λ（0～1之间），将得到的相关系数减去阈值参数后，扩大地震道之间相关性的差异：$$ {w_{ki}} = \frac{{({r_{ki}} - \lambda )}}{{1 - \lambda }}\text{，} $$ (6) 式中：
${w_{ki}}$ 为每个相邻地震道进行加权平均时的权值（当${w_{ki}} < 0$ 时令其等于0），最后得到中间道：$$ {{\boldsymbol{R}}^{n - 1}}({\boldsymbol{y}}) = \frac{\displaystyle\sum\limits_{i = 1}^L {{w_{ki}}{{\boldsymbol{R}}^{n - 1}}({{\boldsymbol{s}}_i})}}{{\displaystyle\sum\limits_{i = 1}^L {{w_{ki}}} }} 。 $$ (7) 图2展示了常规多道匹配追踪平均地震道方法和改进方法的实际效果。从图中可以看到常规方法处理的地震剖面在断层以及倾角较大处信号出现了失真，而使用新方法后，不仅有效压制了随机噪声，而且原始信号的特征信息也得到了很好的保留。
随后对平均道
$ {{\boldsymbol{R}}^{(n-1)}}({\boldsymbol{y}}) $ 进行时频分析求取子波的三瞬信息，并将其作为匹配子波的初始参数。同时，将求解最优参数的公式（4）更新为：$$ {{\boldsymbol{g}}_{{\gamma _n}}}(t) = \arg \mathop {\max }\limits_{{{\boldsymbol{g}}_{{\gamma _n}}} \in {\boldsymbol{D}}} \frac{{\displaystyle\sum\limits_{i = 1}^L {{w_{ki}}\left| {\left\langle {\left. {{{\boldsymbol{R}}^{{\rm{n}} - 1}}({{\boldsymbol{s}}_i}),\;{{\boldsymbol{g}}_{{\gamma _n}}}(t)} \right\rangle } \right.} \right|} }}{{\left| {\left| {{{\boldsymbol{g}}_{{\gamma _n}}}(t)} \right|} \right|}} 。 $$ (8) 由于计算每一道信号与求取子波的内积时约束了前面计算得到的相关系数，地震道的有效信息占有更大的比重，匹配得到的子波也更能体现原信号的特征。
1.3 构造约束强反射层分离方法
地震记录在大多数情况下可视为多个地层界面对地震子波响应的叠加，在一组地层界面中，波阻抗较大的界面的地震响应将占主导作用，并且会压制附近地质界面的反射信息。为去除强反射界面的影响，必须准确地匹配出强反射的波形特征，通常我们选取Morlet子波对信号进行迭代分解，其表达式为：
$$ m(t) = \exp\left( { - \frac{{\ln (2)}}{{{{\text{π}}^2}}}\frac{{{f_m}^2{{(t - {{u}})}^2}}}{{{\sigma ^2}}}} \right) \times \exp\bigg( i\Big({f_m}(t - u) + \phi \Big) \bigg) \text{，} $$ (9) 式中：
${f_m}$ 为子波主频，u为时间延迟，σ为尺度因子，$ \phi $ 为相位。为提高分离精度和运算效率，使用构造约束项，即一方面使用地震解释得到的强反射层位作为初始时间延迟
${u_0}$ ，在保证匹配精度的同时减少搜索参数的个数。另一方面使用强反射的空间构造信息作为约束，使分解得到的强反射具有更好的空间连续性，其核心思想为在进行多道匹配时对选取的L道地震数据以中间道为基点进行局部层拉平处理，以获得波形特征平稳的地震信号：$$ {{\boldsymbol{d}}_i} = {{\boldsymbol{s}}_i}*\delta (t - \Delta {t_i}) \text{，} $$ (10) 式中：
${{\boldsymbol{s}}_i}$ 表示中心道附近所选地震道第i道，${{\boldsymbol{d}}_i}$ 表示经过局部层拉平处理后的第i道，$\delta $ 为冲击函数，$ \Delta {t_i} $ 为第i道层位相对中间道的时间延迟，可通过将${{\boldsymbol{s}}_i}$ 处的强反射层位时间减去中心道的层位时间得到。由于强反射可视为单一界面的地震响应，理论上只需要一次迭代，此时求取子波控制参数公式变为：$$ {{\boldsymbol{g}}_{{\gamma _n}}}(t) = \arg \mathop {\max }\limits_{{{\boldsymbol{g}}_{{\gamma _n}}} \in {\boldsymbol{D}}} \frac{{\displaystyle\sum\limits_{i = 1}^L {{w_{ki}}\Big| {\left\langle {\left. {{{\boldsymbol{d}}_i},{{\boldsymbol{g}}_{{\gamma _n}}}(t)} \right\rangle } \right.} \Big|} }}{{\left| {\left| {{{\boldsymbol{g}}_{{\gamma _n}}}(t)} \right|} \right|}} 。 $$ (11) 最后，将匹配得到的强反射轴从原始地震记录中减去，达到压制强屏蔽、凸显弱储层的目的。
2. 模型测试
为验证本文方法的有效性，参照研究工区某一油藏剖面（图3（a））以及相应的测井数据，建立二维含强反射速度模型（图3（b））。然后对速度模型进行正演模拟，为模拟真实情况下子波随地层变化的特征，设置Morlet子波的主频范围为22～26 Hz，相位范围为 -π/10～π/10，采样间隔为2 ms，每道的子波都按照设置的参数范围随机生成一个子波，采用自激自收方式进行正演，然后加入3％ 的高斯随机噪声后得到如图4（a）所示正演剖面。
![]()
图 4 使用不同方法去强反射层结果Figure 4. Results of using different methods to remove strong reflection layers从合成地震记录中可以看到，强反射信号过于突出，下方靠近低速层的砂体的有效反射信号受强反射同相轴影响识别困难。为了压制强反射突出有效反射，分别使用常规单道匹配追踪、多道匹配追踪以及本文自适应多道匹配追踪算法进行处理，结果如图4所示。
图4中虚线为原始强反射层的层位示意线，从图中可以看出，常规的单道匹配追踪受噪声影响明显，导致在箭头所指等区域匹配精度不够好，在去除强反射后仍有少量强信号残余。使用常规多道匹配追踪进行去强反射后，发现多道匹配的精度相对更高，较好地压制了强反射干扰，同时匹配得到的强反射记录在横向连续性上要明显优于单道匹配追踪。然而在构造变化较大的地方，如图中箭头处，仍存在匹配子波不稳定和匹配精度不高的问题。而本文方法能够完整地匹配出强反射同相轴并将其去除，去除后地剖面中原来下方砂体被压制的弱信号得到有效凸显，并且相较于多道匹配追踪，整体匹配得到的强反射同相轴也具有较好的空间连续性。当然，也需要指出的是，由于需要进行层拉平处理以及使用层位时间作为子波初始时间延迟，本文方法对于解释层位的准确性要求较高。
为进一步讨论本文方法的抗噪能力，对上述速度模型略作修改，设置与前文构建模型相同的子波参数，加入不同比例的高斯随机噪声，分别使用常规匹配追踪方法以及本文方法进行分解重构。从结果（图5）中可以看出：在低噪情况下，常规匹配追踪和本文方法都能较好地重构出原始信号；当噪声能量达到10％ 时，单道匹配追踪容易受噪声的影响匹配出虚假信号，而本文方法能在一定程度上压制随机噪声，减弱噪声对匹配结果的影响；加大噪声，进一步测试方法的抗噪性，当噪声能量达到15％ 时，包括本文方法在内的所有方法均已出现了不可忽视的误差。
![]()
图 5 理论模型分解重构结果对比Figure 5. Comparison of theoretical model decomposition and reconstruction results3. 实际资料处理
江苏油田某地区泰二段湖侵泥灰岩与围岩阻抗差异较大，在地震剖面上形成了明显的强反射同相轴。所选取的B1井标定及综合解释结果如图6所示，泰二段底有一高阻泥灰岩地层形成强反射屏蔽，下方泰一段薄储层的弱反射信号受强屏蔽层的压制较为明显，储层特征难以识别，增大了储层预测难度。
![]()
图 6 B1井标定及综合解释结果Figure 6. B1 well calibration and comprehensive interpretation results为测试本文方法在解决实际问题时的可靠性，选取了一小块工区使用自适应加权多道匹配追踪进行去强屏蔽处理。首先通过对目的层的时频分析，确定主频在22 Hz左右，然后设置相位搜索范围为 -π/10～π/10，尺度参数设置为0.17，使用K2t2正极性解释层位时间作为子波初始时间延迟，分别使用常规方法和本文方法进行强屏蔽分离。
通过分析处理前后的过B7井剖面以及B1井测井解释结果可知：由于泰二段的高阻泥灰岩的强反射屏蔽效应（图7（a）），下部储层的地震特征被掩盖而难以区分，而经过匹配追踪去强屏蔽处理后，泰一段储层的地震响应得到了凸显（图7（c）和图7（e））；同时储层的低SP、GR测井特征（图6）也与地震特征更加对应。此外，从图7（c）中我们也能看到，多道匹配追踪能够较好地去除强反射干扰，但在地层变化剧烈处仍存在匹配子波不稳定、横向连续性变差的现象。而使用层位约束的自适应加权多道匹配追踪进行强反射层的分离和去除后，强反射地震记录得到了有效地压制，并且在全区都具有较好的横向连续性（图7（e））。
图8为应用本文方法以及常规多道匹配追踪处理前后的沿层均方根振幅属性对比，其中，B2井泰一段砂体厚度为0 m，B4井泰一段一砂组和二砂组砂体总厚35 m，不含油，B5井泰一段一砂组砂体厚度56 m且含油；其余井均发育砂体并且大多数含油。从图中我们可以看到，原始地震资料中强反射层在工区大面积分布且能量非常之高，均方根振幅属性难以反映砂体的展布特征。在使用多道匹配追踪处理后，强反射能量得到了较好压制，但局部区域（图8（b）中红色椭圆区域）仍存在强反射残留能量。而本文方法处理后，强反射能量得到了有效去除，井点砂体分布特征与均方根振幅属性具有较好的对应关系，储层信号的能量也得以凸显。
![]()
图 8 沿层均方根振幅属性对比Figure 8. Comparison of root-mean-square amplitude properties along the layer4. 结论和认识
与储层阻抗差异较大的围岩地层会屏蔽储层的弱反射信号，给储层精细描述和预测增添困难。本文针对多道匹配追踪在构造复杂处匹配精度和连续性不佳的问题，提出自适应多道匹配追踪方法。改进方法先对强反射层先进行拉平处理，再使用地震道间的相关系数作为多道匹配的权值，在保证匹配精度的同时提高了匹配结果的空间连续性和稳定性；并且使用解释得到的层位时间作为子波初始时间延迟，提升了运算效率。
通过对二维地震模型的去强屏蔽试验验证了本文方法的可行性，实际资料的应用效果也体现出本方法相较于传统多道匹配在匹配精度和连续性方面有着较为明显的提升，使用本文方法去除强屏蔽后的地震均方根振幅属性更好地指示了砂体的空间分布，井震吻合度有了较大的提高。总体来讲，该方法实际应用效果显著，能为后续储层精细描述提供有力支撑。需要指出的是，使用解释层位作为初始时间可提高运算效率，但在解释层位不准确时匹配结果的可靠性也会受到影响。
-
![]()
图 1 水平放置的防散射滤线栅的主视图和俯视图
Figure 1. Front view and top view of the anti-scattering grid placed horizontally
![]()
图 2 小波变换方法去除滤线栅条纹的整体思路
Figure 2. Schematic representation of the idea to remove gridline artifacts by wavelet transform
![]()
图 3 第10层多贝西小波的低通和高通滤波器响应函数的幅度谱
Figure 3. Amplitude spectrum of low-pass and high-pass filter response functions of layer 10 Daubechies wavelet
![]()
图 8 检验小波变换方法有效性的对照实验
Figure 8. A comparative experiment to test the effectiveness of the wavelet transform method
![]()
图 9 小波变换法处理前后的“水”
Figure 9. “Water” before and after processing by the wavelet transform method
![]()
图 10 小波变换法处理前后的“老鼠”
Figure 10. “Mouse” before and after processing by the wavelet transform method
![]()
图 12 “水”在小波变换法处理前后的差异的一维离散傅里叶变换幅度谱
Figure 12. One dimensional discrete Fourier transform amplitude spectrum of the difference of “water” before and after processing by the wavelet transform method
![]()
图 13 “水”在高斯带阻滤波或小波变换法处理前后的差异的二维离散傅里叶变换幅度谱的局部
Figure 13. The local region of the amplitude spectrum of two-dimensional discrete Fourier transform of the difference in “water” before and after the processing with the Gaussian band stop filter or wavelet transform method
![]()
图 14 经对照组1、实验组1、实验组2处理后的“水”的一维离散傅里叶变换幅度谱
Figure 14. One dimensional discrete Fourier transform amplitude spectrum of “water” treated with control group 1, experimental group 1, and experimental group 2
![]()
图 15 经对照组1、实验组1、实验组2处理的“水”CT重建的中心截面局部图
Figure 15. Local central section of “water” CT reconstruction treated with control group 1, experimental group 1 and experimental group 2
![]()
图 16 经对照组1、实验组1、实验组2处理的“老鼠”CT重建的中心截面局部图
Figure 16. Local central section of “mouse” CT reconstruction treated with control group 1, experimental group 1, and experimental group 2
表 1 频谱拼接的定量效果
Table 1 Quantitative effect of spectrum coalescence
统计参数 加条纹图像 不做频谱拼接图像 做频谱拼接图像 峰值信噪比 29.719 34.475 37.758 结构相似性 0.984 0.995 0.998 与原图差异的标准差 9.122 5.085 3.458 
下载: 导出CSV
-
[1] 庄天戈. CT原理与算法[M]. 1版. 上海: 上海交通大学出版社, 1992. [2] 金慧君, 张蔚, 焦启刚, 等. 应用于口腔医学的锥束CT技术[J]. 口腔材料器械, 2011,20(3): 158−161. JIN H J, ZHANG W, JIAO Q G, et al. Technique of cone-beam computed tomography for oral clinical practice[J]. Oral Material and Equipment, 2011, 20(3): 158−161. (in Chinese).
[3] 吴彦举, 郝冰, 常华峰, 等. 工业锥束CT在直升机承力件检测方面的应用[J]. 新型工业化, 2020,10(5): 67−69. [4] FELDKAMP L A, DAVIS L C, KRESS J W. Practical cone-beam algorithm[J]. Journal of the Optical Society of America A, 1984, 1(6): 612−619. doi: 10.1364/JOSAA.1.000612
[5] RÜHRNSCHOPFA E P, KLINGENBECK K. A general framework and review of scatter correction methods in X-ray cone-beam computerized tomography. Part 1: Scatter compensation approaches[J]. Medical Physics, 2011, 38(7): 4296−4311. doi: 10.1118/1.3599033
[6] RÜHRNSCHOPFA E P, KLINGENBECK K. A general framework and review of scatter correction methods in X-ray cone-beam computerized tomography. Part 2: Scatter estimation approaches[J]. Medical Physics, 2011, 38(9): 5186−5199. doi: 10.1118/1.3589140
[7] KIM D S, LEE S, YOON J K. Grid artifact reduction based on homomorphic filtering in digital radiography imaging[J]. Proc. of SPIE, 2013, 8668: 86682C-1−86682C-9.
[8] LIN C Y, LEE W J, CHEN S J, et al. A study of grid artifacts formation and elimination in computed radiographic images[J]. Journal of Digital Imaging, 2006, 19(4): 351−361. doi: 10.1007/s10278-006-0630-8
[9] TANG H. A new stationary gridline artifact suppression method based on the 2D discrete wavelet transform[J]. Medical Physics, 2015, 42(4): 1721−1729. doi: 10.1118/1.4914861
[10] YU Y. A novel grid regression demodulation method for radiographic grid artifact correction[J]. Medical Physics, 2021, 48(7): 3790−3803. doi: 10.1002/mp.14932
[11] WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment: From error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600−612. DOI: 1109/TIP.2003.819861.
计量
- 文章访问数: 528
- HTML全文浏览量: 236
- PDF下载量: 98
