Seismic Data Reconstruction Based on the POCS Method in the Curvelet Domain with Prior Information
-
摘要:
由于野外采集环境的限制,常常无法采集得到完整规则的野外地震数据,为后续地震处理、解释工作的顺利进行,需要进行地震数据重构。凸集投影(POCS)方法利用地震波形在Curvelet域的稀疏特性,可以重构出高信噪比地震数据,该迭代算法稳定,其收敛速度较快。但在地震数据恢复的时候,由于直达波和炮集上部空白区域的影响,随着迭代的进行,重构数据中噪声干扰越来越严重,导致最终恢复的地震数据信噪比较低。本文在实现POCS迭代阈值算法基础上,引入先验信息约束的思想对算法进行优化。通过先进行坐标映射的方法进行炮集插值,然后将其作为先验信息约束进行插值,可以有效地压制迭代噪音对重构地震波形数据的影响。通过合成地震炮记录与实际炮集进行测试,结果表明本文提出的改进方法可以明显改善重构地震数据的信噪比,并提高地震波场同相轴的连续性。
-
关键词:
- 地震数据重构 /
- 凸集映射(POCS) /
- 曲波变换 /
- 压缩感知
Abstract:Due to limited acquisition conditions in the field, the seismic data is usually incomplete, which affects the following seismic data processing and seismic interpretation. To solve this problem, the seismic data needs reconstruction. The projection onto convex sets (POCS) method utilizes the sparse characteristics of seismic waveforms in the Curvet domain to reconstruct high signal-to-noise ratio seismic data. This iterative algorithm is stable and has a fast convergence speed. However, during the recovery of seismic data, because the influence of direct waves and the blank area in the upper part of the shot gathers as the iteration progresses, the noise interference in the reconstructed data becomes increasingly severe, resulting in a low signal-to-noise ratio of the final recovered seismic data. Based on the implementation of the POCS iterative threshold algorithm, this article introduces the idea of Prior information constraints to optimize the original algorithm. By first performing coordinate mapping for shot gathers interpolation and then using it as a prior information constraint for interpolation, the impact of noise attenuation is dramatic. Finally, the synthesized seismic shot records were tested with actual shot gathers, and the results illustrated that the new method proposed in this paper can significantly improve the signal-to-noise ratio of reconstructed seismic data and enhance the continuity of seismic wave field events.
-
由于采集成本、坏道、噪声、地形等诸多因素的影响,实际的地震数据往往会出现缺失道和野值道[1-2],这些不规则或稀疏的地震数据,给地震数据的处理与解释工作造成了一定的困扰[3-4],因此不完整、不规则数据的数据重构对于地震数据处理具有重要意义[5-6]。常用的地震数据重构方法有基于信号变换重构法[7-8]、基于预测滤波重构法[9-10]、基于波动方程重构法[11-12]等。其中基于信号变换重构方法是将地震数据从时间域转换到变换域,再根据变换域内信号的特征进行重构,计算结果比较稳健,得到了广泛的应用[13-15]。
基于压缩感知理论,在地震数据大量缺失的情况下恢复出地震数据[16-17],可以转化为一个稀疏优化问题,相继出现了基于该理论的多种迭代阈值方法[18-19]。而凸集投影法(project onto convex sets,POCS)由Bregman提出,可以很好地与各种变换域相结合,被应用于地震数据的重构及数据规则化领域[20-23]。Gao等[24-25]基于傅里叶变换及POCS法对不规则缺失地震道进行重构,对线性或拟线性同相轴比较好,但是对弯曲同相轴则需分窗口处理;刘国昌等[26]将POCS法与曲波变换相结合,可以更好地对弯曲同相轴进行恢复;Yang等[27]和Wang等[28]从收缩阈值(iterative shrinking threshold,IST)算法的角度推导出POCS公式,进而比较了两种方法的重构效果的异同,并得出了POCS硬阈值重构效果较好的结论;王本锋等[29]和张华等[30]提出了基于Jitter采样理论的曲波域实现地震数据重构,有效地提高了计算效率;冯飞等[31]、张良等[32]、闫海洋等[33]将Shearlet变换与POCS算法结合起来,在动校正预处理后对地震数据进行重构,增强了地震数据在Shearlet域的稀疏性,有效地解决了假频问题。另一方面阈值函数的选取对于地震数据重构效果产生较大影响,王本锋等[29]、余江奇[34]等、张入化等[35]都对阈值函数进行对比分析,其中指数阈值函数比线性阈值参数效果好。Curvelet域对于曲线同相轴具有较好的重构效果,但是对于线性直达波的恢复方面能力较弱,并且相对其它地震波场(反射波、多次散射波等)直达波的能量较强,使其在迭代重构地震数据的过程中产生较强的干扰噪音。
本文在前人研究的基础上,将直达波及上部空白区域作为约束,对迭代算法进行改进,实现基于先验信息约束的Curvelet域地震数据POCS插值方法(prior project onto convex sets,PPOCS)。该算法可以有效地保留直达波等信息,且可以有效地压制其在迭代后期产生的噪音,保持重构地震波场高信噪比与高精度的特征。最后,通过对简单及复杂速度模型正演地震炮记录的稀疏数据重构测试与实际地震采集炮记录的野值去噪测试,讨论基于先验信息约束的Curvelet域PPOCS方法的优势。
1. 理论方法
1.1 压缩感知理论
压缩感知(compressive sensing,CS)是一种寻找欠定线性系统的稀疏解的技术。对于完整的数据
${\boldsymbol{ D}} $ 可以在$ {\boldsymbol{\varPhi }}$ 域表示:$$ {\boldsymbol{D}}_{{}}^{} = {\boldsymbol{\varPhi}} {\boldsymbol{x}} \text{,} $$ (1) 其中
$ {\boldsymbol{\varPhi}} \in {R^N} $ 为变换域的基函数向量,$ {\boldsymbol{x}} $ 为变换域系数向量,向量$ {\boldsymbol{x}} $ 中非零元素的个数可以表示为$ {\left\| x \right\|_{\text{0}}} = M $ ,若$ M < < N $ ,则数据${\boldsymbol{ D}} $ 可以在${\boldsymbol{ \varPhi }}$ 域稀疏表示。由于采集条件的限制以及后续地震处理中废炮、废道的剔除,致使地震数据不规则或稀疏:
$$ {\boldsymbol{D}}_{{{\text{obs}}}}^{} = {{\boldsymbol{P}}_{}}{\boldsymbol{D}} \text{,} $$ (2) 其中
$ {{\boldsymbol{D}}_{{\text{obs}}}} $ 为观测的不规则或稀疏数据,$ {\boldsymbol{D}} $ 为要恢复的完整数据,$ {{\boldsymbol{P}}_{}} $ 为采样矩阵。将式(2)代入式(1),可以写为:
$$ {\boldsymbol{D}}_{{{\text{obs}}}}^{} = {\boldsymbol{P}}{\boldsymbol{\varPhi}} {\boldsymbol{x}} = {\boldsymbol{Kx}} \text{,} $$ (3) 其中,
$ {\boldsymbol{K}} $ 为$ M \times N $ 的矩阵,称为测量矩阵。地震数据重构就是由不完整数据$ {\boldsymbol{D}}_{{{\text{obs}}}}^{} $ 和采样矩阵$ {\boldsymbol{K }}$ 恢复、重构出完整$ {\boldsymbol{x}} $ 的过程。如果$ {\boldsymbol{x}} $ 可以重构出来,则可以得到完整的地震数据${\boldsymbol{ D}} $ 。由于式(3)的求解是不适定的,考虑到
$ {\boldsymbol{D}} $ 在$ {\boldsymbol{\varPhi }}$ 域的稀疏性,采用稀疏促进策略,构建如下目标泛函:$$ \min \Big(J(x)_{{{\text{obs}}}}^{}\Big) = \frac{1}{2}\big\| {{{\boldsymbol{D}}_{{\text{obs}}}} - {\boldsymbol{Kx}}} \big\|_2^2 + \tau {\big\| {\boldsymbol{x}} \big\|_0} \text{,} $$ (4) 其中
$ \tau $ 为域系数向量的阈值。对于式(4)发展了一系列的迭代求解算法,其中基于阈值收缩法(IST)的凸集投影(POCS)方法在解决地震数据重构的方法中具有较好的效果[27]。1.2 凸集投影
利用阈值收缩求解方程(4)的地震数据重构的公式为:
$$ {\boldsymbol{x}}_{}^{k + 1} = {S_{{\tau _k}}}\bigg( {{x^k} + {{\boldsymbol{K}}^{\mathrm{T}}}\left( {{{\boldsymbol{D}}_{{\text{obs}}}} -{\boldsymbol{ K}}{{\boldsymbol{x}}^k}} \right)} \bigg),\;\;\;\;k = 1,2,\cdots,{{n}} \text{,} $$ (5) 其中,
$ {\boldsymbol{x}}_{}^{k + 1} $ 为${\boldsymbol{k}}+1 $ 次迭代所得到变换域系数向量,$ {{\boldsymbol{K}}^{\mathrm{T}}} $ 为测量矩阵的逆变换,$ {{n}} $ 为迭代的总次数。阈值函数
$ S $ 一般分为硬阈值函数和软阈值函数,Yang等[27]比较了两种阈值函数,认为硬阈值重构效果较好,因此本文采用硬阈值函数:$$ {S_{{\tau _k}}}({x_i}) = \left\{ {\begin{array}{*{20}{c}} {{x_i}{\text{ }}\;\;\left| {{x_i}} \right| \geq {\tau _k}} \\ {0{\text{ }}\;\;\left| {{x_i}} \right| < {\tau _k}} \end{array}} \right. \text{,} $$ (6) 其中,
$ {\tau _k} $ 为第k次的门槛阈值,其随着迭代次数不同而变化。利用式(1)、式(5)可以改写为:$$ \begin{aligned} \;&\quad\qquad{\boldsymbol{{\boldsymbol{D}}}}_{}^{k + 1} = {\boldsymbol{\varPhi}} {{\boldsymbol{x}}^{k + 1}} {\text{ }} = {\boldsymbol{\varPhi}} {S_{{\tau _k}}}\left( {{{\boldsymbol{\varPhi}} ^{\mathrm{T}}}{{\boldsymbol{D}}^k} + {{\Big({\boldsymbol{P}}{\boldsymbol{\varPhi}} \Big)}^{\mathrm{T}}}\Big({{\boldsymbol{D}}_{{\text{obs}}}} - {\boldsymbol{P}}{{\boldsymbol{D}}^k}\Big)} \right)=\\ & {\boldsymbol{\varPhi}} {S_{{\tau _k}}}\bigg( {{{\boldsymbol{\varPhi}} ^{\mathrm{T}}}{{\boldsymbol{D}}^k} + {{\boldsymbol{\varPhi}} ^{\mathrm{T}}}\Big({{\boldsymbol{P}}^{\mathrm{T}}}{{\boldsymbol{D}}_{{\text{obs}}}} - {{\boldsymbol{P}}^{\mathrm{T}}}{\boldsymbol{P}}{{\boldsymbol{D}}^k}\Big)} \bigg) ={\boldsymbol{\varPhi}} {S_{{\tau _k}}}\Bigg( {{{\boldsymbol{\varPhi}} ^{\mathrm{T}}}\bigg( {{{\boldsymbol{D}}^k} + \left( {{{\boldsymbol{D}}_{{\text{obs}}}} - {\boldsymbol{P}}{{\boldsymbol{D}}^k}} \right)} \bigg)} \Bigg){\text{ }} \end{aligned} 。 $$ (7) 通过公式(7)可以得到POCS的迭代公式:
$$ {\boldsymbol{D}}_{}^{k + 1} = {{\boldsymbol{D}}_{{\text{obs}}}} + \left( {{\boldsymbol{I}} - {\boldsymbol{P}}} \right){\boldsymbol{\varPhi}} {S_{{\tau _k}}}\left( {{{\boldsymbol{\varPhi}} ^{{{\mathrm{T}}}}}{{\boldsymbol{D}}^k}} \right) \text{,} $$ (8) 其中,
${\boldsymbol{I }}$ 是单位对角阵。由于式(8)在迭代中考虑了观测炮集的信息,因此其在重构地震数据的过程中,在收敛速度和重构精度方面POCS方法都要高于IST的迭代方法。曲波域对于曲线具有较好的重构效果,但是对于线性直达波的恢复方面能力较弱,并且相对于其它地震波场(反射波、多次散射波等)直达波的能量较强,使其在迭代重构地震数据的过程中产生较强的干扰噪音,影响重构效果。在重构过程中将直达波进行切除处理,再进行数据恢复,然而有些直达波与反射波等波场耦合在一起,并且直达波及早至波在后期处理中,尤其在速度反演中具有重要作用。本文利用先将炮记录直达波区域基本拉平,利用式(8)先进行重构直达波等部分迭代重构地震数据,将变换域的炮记录反变换得到重构的直达波炮集;将其作为约束进行重构,可以有效地压制其在迭代后期产生的噪音,进而保持重构地震波场高信噪比与高精度的特征。本文在式(8)的基础上,通过加入待重构炮集的信息作为约束项,处理得到第k+1次迭代的地震数据公式:
$$ {\boldsymbol{D}}_{{\text{new}}}^{k + 1} = \left( {1 - {\boldsymbol{L}}{m_{k + 1}}} \right)*{{\boldsymbol{D}}^{k + 1}} +{\boldsymbol{ L}}{m_{k + 1}}*{\boldsymbol{D}}_{{\text{pre}}}^{} \text{,} $$ (9) 其中
$ {\boldsymbol{D}}_{{\text{new}}}^{k + 1} $ 为第k+1次迭代的重构地震数据,$ {\boldsymbol{D}}_{{\text{pre}}}^{} $ 为要重构的地震数据中已知的先验信息,例如炮记录上部的空白区域,线性插值得到的直达波信息等,$ {\boldsymbol{L}}{m_{k + 1}} $ 为加权矩阵因子,其值取决于对先验信息的准确性,如果一个区域对先验信息越准确则对应的矩阵元素值越接近于1,${\boldsymbol{ L}}{m_{k + 1}} $ 可以取固定值,也可以随着迭代的次数k改变。由于式(9)加上了对重构数据的先验信息约束,因此可以较好的压制由能量剧烈变化区域(如地震信号的直达波与上部空白区域)随着迭代次数增加而产生的噪音。1.3 曲波变换
由于曲线是稀疏表示地震波场的理想字典,依据反射系数在曲波域更为稀疏的特点,因此可以利用曲波变换实现POCS方法。考虑二维情况下的曲波变换,
$$ {c_m} = \Big\langle {{\boldsymbol{D}},{\phi _m}} \Big\rangle = \sum\limits_{{t_1},{t_2}} {{\boldsymbol{D}}[{t_1},{t_2}]} \overline {{\phi _m}[{t_1},{t_2}]} \text{,} $$ (10) 式中
$ {\phi _m} $ 表示Curvelet基函数,$ m = (j,{k_d},l) $ ,其中$ j,{k_d},l $ 分别为尺度、方向、位置参数,${{\boldsymbol{c}}_m}$ 为曲波域内的系数,$ {t_1},{t_2} $ 为数据D的时间窗,则地震数据可以用曲波系数和基函数表示为:$$ {\boldsymbol{D}} = \sum\limits_m {\Big\langle {{\boldsymbol{D}}{\boldsymbol{}},{\phi _m}} \Big\rangle {\phi _m}} = \sum\limits_m {{{\boldsymbol{c}}_m}{\phi _m}} 。 $$ (11) 将式(1)的
$ \varPhi $ 域选取为Curvelet域,则式(11)与式(1)相对应。即可以推导出Curvelet域地震的数据POCS插值方法的公式,则第k次迭代的地震数据在曲波域的硬阈值约束为:$$ {{\boldsymbol{D}}_k} = \sum\limits_{n \in \left\{ {m:|\left\langle {{\boldsymbol{D}},{\phi _m}} \right\rangle > {\tau _k}} \right\}} {\left\langle {{\boldsymbol{D}},{\phi _n}} \right\rangle {\phi _n}} = \sum\limits_m {{S_{{\tau _k}}}({{\boldsymbol{c}}_m}){\phi _m}} \text{,} $$ (12) 其中,
${S_{{\tau _k}}}({{\boldsymbol{c}}_m})$ 表示对曲波域系数进行硬阈值约束,取大于$ {\tau _k} $ 的部分。本文采用指数衰减的形式阈值函数:
$$ {\tau _k} = {\tau _0} * \exp\left(\frac{1-k}{M}\right),\;\;\;\;k = 1,2,\cdots,{{n}} \text{,} $$ (13) 其中M为控制衰减快慢的系数。给定初始的最大阈值
$ {\tau _0} $ ,系数衰减项M和迭代次数k即可确定对应的阈值。1.4 流程图
本文采用的地震数据重构流程如图1所示:①输入初始的观测地震数据
${\boldsymbol{D}}$ ,并且拾取初至gc;②对炮记录利用坐标映射进行变换得到新的炮集${\boldsymbol{D}}_2 $ ;③对数据${\boldsymbol{D}}_2 $ 做曲波变换得到曲波域内的系数${{\boldsymbol{c}}_m}$ ;④对曲波域的系数利用阈值函数$ {\tau _k} $ 进行滤波;⑤利用 POCS方法进行迭代重构的到新的炮集${\boldsymbol{P}}_2' $ ;⑥反变换得到的炮集$ {\boldsymbol{D}}_{{\text{pre}}}^{} $ ;⑦对$ {{\boldsymbol{D}}^{k + 1}} $ 加上先验约束信息的得到新的重构地震数据$ D_{{\text{new}}}^{k + 1} $ ;⑧满足迭代次数或者信噪比要求,输出最终的重构结果。2. 模型试算
在编程实现方法的基础上,为了测试改进POCS算法的优越性,本节对由4个平层界面构建的速度模型,其中速度从1 500 m/s到3 500 m/s等间隔变化,层的厚度分别为第1层为250 m其余层厚150 m,采用有限差分正演模拟得到的地震炮记录数据,以及Marmousi模型的正演模拟产生的含有复杂波场的地震炮记录数据分别进行抽稀与重构,并对比分析改进方法相对于常规方法的有效性及优点。
2.1 模型 一:简单层状速度模型的炮记录测试
为验证先验信息约束的曲波域POCS方法的有效性及优点,分别对简单层状模型的炮记录(图2(a))进行了随机缺失50% 与70% 的抽稀(图2(b)和图2(c)),并用常规POCS方法与先验信息约束的POCS方法进行重构测试。
重构测试的结果如图3所示,测试中都采用80次迭代,其中图3(a)和图3(b)分别为随机缺失50% 炮记录常规POCS方法、先验信息约束POCS方法重构结果,图3(c)和图3(d)分别为随机缺失70% 的常规POCS方法、先验信息约束POCS方法重构结果。
由图4可知:①当炮记录随机缺失 50% 地震道时,常规POCS与先验信息的POCS方法的重构结果都可以较好的重构反射轴,但是常规POCS方法对于直达波区域存在明显的迭代噪音,而应用先验信息约束后,重构剖面中的直达波区域的噪音得到压制,且剖面重构剖面信噪比更高;②当炮记录随机缺失70%地震道时,常规POCS方法可以较好的恢复深层同相轴,但是由于受到直达波强能量的影响,重构结果中噪音比较强,尤其在靠近直达波的区域,并且由于缺失数据过多,在两侧的边界位置,同相轴恢复出现较强的噪音;③应用先验信息约束的 POCS方法,重构的炮记录剖面的信噪比明显改善,直达波区域可以较好的恢复,并且对反射层可以有一些较好的改善,但是由于缺失数据较多,在中深部没有先验信息,所以重构中边界处依旧存在噪音的影响。
为了对比本文算法与常规POCS的收敛性,图4(a)和图4(b)分别展示整个剖面和直达波以下区域的重建测试信噪比SNR曲线。由图4(a)可以看出:不论是否应用先验信息的约束,迭代重构过程都是稳定的,信噪比都可以提高,但是PPOCS方法的信噪比更高,这是由于直达波的能量较强,PPOCS可以更好的约束直达波的区域,因此信噪比更高,并且两种方法地震数据缺失越少重构的效果更好,信噪比更高。为了比较约束区域以外的信噪比,本文将直达波以下的波场信噪比单独输出,可以看出,曲波域POCS方法对曲线地震同相轴具有较好的重构,信噪比都可以得到很大的提高,但PPOCS也可以对地下的反射波场等具有改善,并且在高精度恢复中(缺失50%)效果更明显。并且当地震缺失70%的时候,POCS方法的重构具有较大误差。
2.2 Marmous模型的炮记录测试
为验证本文方法在复杂波场的适用性,本节对Marmousi模型(图5)进行有限差分正演,得到炮记录如图6(a)所示,对炮记录进行随机抽稀50% 得到抽稀的炮记录如图6(b)所示,并用常规POCS方法与先验信息约束的POCS方法进行重构测试。
采用常规POCS方法与PPOCS方法进行重构测试,结果如图6所示,测试中都采用80次迭代,其中图6(e)~图6(g)分别为随机缺失50% 炮记录直接坐标变换的重构、先验信息约束POCS方法、常规POCS方法重构结果。由图6可知:当炮记录随机缺失50% 地震道时,常规POCS与先验信息的POCS方法的重构结果都可以较好的重构地震反射轴,但是常规POCS方法对于直达波区域存在明显的迭代噪音,而应用先验信息约束后,重构剖面中的直达波区域的噪音得到压制,且剖面重构剖面信噪比更高;而坐标变换域重构方法,直达波区域的噪音得到压制,但是在反射波地震波存在一定的问题,尤其炮点下方存在一定的异常。
为对比本文算法与常规POCS的总信噪比以及对直达波以外恢复的信噪比和恢复效果,图7展示重构测试的信噪比SNR曲线。由图7可以看出,不论是否应用先验信息的约束,迭代重构过程中总的信噪比都随着迭代次数而提高,但是PPOCS方法的信噪比收敛更快并且收敛到更高值,这是由于直达波的能量较强,PPOCS可以更好的约束直达波的区域,信噪比更高。
为了比较约束区域以外的信噪比,本文将直达波以下的波场信噪比单独输出,可以看出,曲波域POCS方法对曲线地震同相轴具有较好的重构,信噪比都可以得到很大的提高,但PPOCS也可以对地下的反射波场等收敛到更高的信噪比值,说明在复杂波场的情况下约束信息对于非约束区域同样具有改善效果。
2.3 实际炮记录测试
本文在模型炮记录试验的基础上对某陆上二维高密度实际地震数据也做了重构测试,该地震资料的接收道距为10 m,479道接收,采样率4 ms,炮记录中含有明显的野值道。对野值道进行抽稀如图8(b),在分别利用常规方法与PPOCS方法进行重构,进行噪音压制,重构结果如图8(c)和图8(d)所示。
通过图8可以看出,原始炮记录中野值道通过两种方法都可以较好的压制,同相轴变的更加连续。但是PPOCS方法可以更好的进行恢复重构炮记录,尤其在近地表区域,为显示比较两种方法重构炮记录的效果,本文对横向1到88道,纵向上1.08 s到1.98 s的区域进行放大(图9)。通过图9还可以看出原始炮记录中野值道比较明显(图9红色箭头的位置),POCS方法可以较好的压制野值道的噪音,实现炮记录同相轴的连续性,相比于常规方法,PPOCS可以更好的重构地震数据,其同相轴连续性可以较好的改善,且重构噪音可以得到更好的压制。
3. 结论与讨论
本文在POCS重构稀疏地震数据的算法基础上通过引入先验信息约束项进行迭代重构稀疏地震数据,发展一种基于先验模型约束的Curvelet域地震数据POCS插值方法。在实现算法的基础上,通过合成地震炮记录与实际炮集进行测试对比,得到了如下认识:
(1)基于先验模型约束的POCS插值方法减弱了常规POCS插值方法对直达波以及上部空白区域对地震数据在迭代重构过程中的噪音干扰,在提高地震数据构建的精度的同时,可以改善剖面的信噪比,并且能保持地震波场同相轴的连续性。
(2)基于先验模型约束的POCS插值方法相对于常规POCS插值方法,对复杂速度模型的地震波场具有更好的适应性。
(3)在理论模型数据重构测试中,基于先验模型约束的POCS插值方法比常规POCS插值方法更快地收敛(SNR),且信噪比最终会收敛到一个较高值。
本文提出的基于先验模型约束的POCS插值方法能够提高重构地震波场的精度,改善常规POCS重构方法的信噪比和对直达波场的适应性。
-
-
[1] 李振春, 张军华. 地震数据处理方法[M]. 东营: 石油大学出版社, 2004. LI Z C, ZHANG J H. Seismic data processing method[M]. Dongying: Petroleum University Press, 2004. (in Chinese).
[2] 周亚同, 滕琳琳, 李玲玲. 基于高阶扩展快速行进法的缺失地震数据重构[J]. 石油地球物理勘探, 2015, 50(5): 873−880, 803. ZHOU Y T, TENG L L, LI L L. Seismic data reconstruction with the high-order expansion fast marching method[J]. Oil Geophysical Prospecting, 2015, 50(5): 873−880, 803. (in Chinese).
[3] 李振春. 地震偏移成像技术研究现状与发展趋势[J]. 石油地球物理勘探, 2014, 49(1): 1−21. DOI: 10.13810/j.cnki.issn.1000-7210.2014.01.001. LI Z C. Research status and development trends for seismic migration technology[J]. Oil Geophysical Prospecting, 2014, 49(1): 1−21. DOI: 10.13810/j.cnki.issn.1000-7210.2014.01.001. (in Chinese).
[4] LI C, HUANG J P, LI Z C, et al. Regularized least-squares migration of simultaneous-source seismic data with adaptive singular spectrum analysis[J]. Petroleum Science, 2017, 14(1): 61−74. DOI:10.1007/ s12182-016-0134-1.
[5] 唐刚. 基于压缩感知和稀疏表示的地震数据重构与去噪[D]. 北京: 清华大学, 2010. TANG G. Seismic data reconstruction and denoising based on compressive sensing and sparse representation[D]. Beijing: Tsinghua University, 2010. (in Chinese).
[6] 李思翰, 刘洪林. 基于组合形态分量分析算法的含噪地震数据重构[J]. 地球物理学进展, 2021, 36(4): 1547−1553. DOI: 10.6038/pg2021DD0364. LI S H, LIU H L. Reconstruction of noisy seismic data based on combined morphological component analysis algorithm[J]. Progress in Geophysics, 2021, 36(4): 1547−1553. DOI: 10.6038/pg2021DD0364. (in Chinese).
[7] SPITZ S. Seismic trace interpolation in the FX domain[J]. Geophysics, 1991, 56(6): 785−794. DOI: 10.1190/1.1443096.
[8] GÜLÜNAY N. Seismic trace interpolation in the Fourier transform domain[J]. Geophysics, 2003, 68(1): 355−369. DOI: 10.1190/1.1543221.
[9] ZWARTJES P, GISOLF A. Fourier reconstruction with sparse inversion[J]. Geophysical Prospecting, 2007, 55(2): 199−221. DOI: 10.1111/j.1365-2478.2006.00580.x.
[10] KABIR M M, VERSCHUUR D J. Restoration of missing offsets by parabolic Radon transform[J]. Geophysical Prospecting, 1995, 43(3): 347−368. DOI: 10.1111/j.1365-2478.1995.tb00257.x.
[11] STOLT R H. Seismic data mapping and reconstruction[J]. Geophysics, 2002, 67(3): 890−908. DOI:10.1190/ 1.1484532.
[12] RONEN J. Wave-equation trace interpolation[J]. Geophysics, 1987, 52(7): 973−984. DOI: 10.1190/1.1442366.
[13] 白兰淑, 刘伊克, 卢回忆, 等. 基于压缩感知的Curvelet域联合迭代地震数据重构[J]. 地球物理学报, 2014, 57(9): 2937−2945. DOI: 10.6038/cjg20140919. BAI L S, LIU Y K, LU H Y, et al. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing[J]. Chinese Journal of Geophysics, 2014, 57(9): 2937−2945. DOI:10.6038/cjg2014 0919. (in Chinese).
[14] 霍志周, 熊登, 张剑锋. 地震数据重构方法综述[J]. 地球物理学进展, 2013, 28(4): 1749−1756. DOI:10.6038/ pg20130415. ZHAI Z Z, XIONG D, ZHANG J F. The overview of seismic data reconstruction methods[J]. Progress in Geophysics, 2013, 28(4): 1749−1756. DOI: 10.6038/pg20130415. (in Chinese).
[15] 王姣, 李振春, 王德营. 基于CEEMD的地震数据小波阈值去噪方法研究[J]. 石油物探, 2014, 53(2): 164−172. DOI: 10.3969/j.issn.1000-1441.2014.02.006. WANG J, LI Z C, WANG D Y. A method for wavelet threshold denoising of seismic data based on CEEMD[J]. Geophysical Prospecting for Petroleum, 2014, 53(2): 164−172. DOI: 10.3969/j.issn.1000-1441.2014.02.006. (in Chinese).
[16] CANDÈS E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21−30. DOI: 10.1109/MSP.2007.914731.
[17] 刘伟, 曹思远, 崔震. 基于压缩感知和TV准则约束的地震资料去噪[J]. 石油物探, 2015, 54(2): 180−187. DOI: 10.3969/j.issn.1000-1441.2015.02.009. LIU W, CAO S Y, CUI Z. Seismic data reconstruction based on sparse constraint in the shearlet domain[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 180−187. DOI: 10.3969/j.issn.1000-1441.2015.02.009. (in Chinese).
[18] 曹静杰, 王彦飞, 杨长春. 地震数据压缩重构的正则化与零范数稀疏最优化方法[J]. 地球物理学报, 2012, 55(2): 596-607. DOI: 10.6038/j.issn.0001-5733.2012.02.001. CAO J J, WANG Y F, YANG C C. Seismic data Restoration based on compressive sensing using regularization and zero-norm sparse optimization[J]. Chinese Journal of Geophysics, 2012, 55(2): 239−251. DOI: 10.6038/j.issn.0001-5733.2012.02.001. (in Chinese).
[19] 周亚同, 王丽莉, 蒲青山. 压缩感知框架下基于K-奇异值分解字典学习的地震数据重构[J]. 石油地球物理勘探, 2014, 49(4): 652−660. ZHOU Y T, WANG L L, PU Q S. Seismic data reconstruction based on K-SVD dictionary learning under compressive sensing framework[J]. Oil Geophysical Prospecting, 2014, 49(4): 652−660. (in Chinese).
[20] BRÈGMAN L M. The method of successive projection for finding a common point of convex sets[J]. Doklady Akademii Nauk Sssr, 1965, 6(3): 487−490.
[21] ABMA R, KABIR N. 3D interpolation of irregular data with a POCS algorithm[J]. Geophysics, 2006, 71(6): E91−E97. DOI: 10.1190/1.2356088.
[22] 赵虎, 赵子涵, 陈伟, 等. 基于Bregman迭代的不同阈值模型地震数据重构方法分析[J]. 地球物理学进展, 2023, 38(1): 409−418. DOI: 10.6038/pg2023FF0310. ZHAO H, ZHAO Z H, CHEN W, et al. Analysis of seismic data reconstruction methods for different threshold models based on Bregman iteration[J]. Progress in Geophysics, 2023, 38(1): 409−418. DOI: 10.6038/pg2023FF0310. (in Chinese).
[23] 郭萌, 张会星, 刘明珠. 基于双重Bregman迭代的地震数据重构与去噪[J]. 石油物探, 2020, 59(5): 804-814. GUO M, ZHANG H X, LIU M Z. Seismic data reconstruction and denoising based on dual Bregman iteration[J]. Geophysical Prospecting for Petroleum. 2020, 59(5): 804-814. (in Chinese).
[24] GAO J J, CHEN X H, LI J Y, et al. Irregular seismic data reconstruction based on exponential threshold model of POCS method[J]. Applied Geophysics, 2010, 7(3): 229−238. DOI: 10.1007/s11770-010-0246-5.
[25] GAO J, STANTON A, NAGHIZADEH M, et al. Convergence improvement and noise attenuation considerations for beyond alias projection onto convex sets reconstruction[J]. Geophysical Prospecting, 2013, 61(S1): 138−151.
[26] 刘国昌, 陈小宏, 郭志峰, 等. 基于Curvelet变换的缺失地震数据插值方法[J]. 石油地球物理勘探, 2011, 46(2): 237−246. DOI: 10.13810/j.cnki.issn.1000-7210.2011.02.014. LIU G C, CHEN X H, GUO Z F, et al. Missing seismic data rebuilding by interpolation based on curvelet transform[J]. Oil Geophysical Prospecting, 2011, 46(2): 237−246. DOI: 10.13810/j.cnki.issn.1000-7210.2011.02.014. (in Chinese).
[27] YANG P, GAO J, CHEN W. Curvelet-based POCS interpolation of nonuniformly sampled seismic records[J]. Journal of Applied Geophysics, 2012, 79: 90−99. DOI: 10.1016/j.jappgeo.2011.12.004.
[28] WANG B, WU R S, CHEN X, et al. Simultaneous seismic data interpolation and denoising with a new adaptive method based on dreamlet transform[J]. Geophysical Journal International, 2015, 201(2): 1182−1194. DOI: 10.1093/gji/ggv072.
[29] 王本锋, 陈小宏, 李景叶, 等. POCS联合改进的Jitter采样理论曲波域地震数据重构[J]. 石油地球物理勘探, 2015, 50(1): 20−28. WANG B F, Chen X H, Li J Y, et al. Seismic data reconstruction based on POCS and improved Jittered sampling in the curvelet domain[J]. Oil Geophysical Prospecting, 2015, 50(1): 20−28. (in Chinese).
[30] 张华, 陈小宏. 基于Jitter采样和曲波变换的三维地震数据重构[J]. 地球物理学报, 2013, 56(5): 1637−1649. DOI: 10.6038/cjg20130521. ZHANG H, CHEN X H. Seismic data reconstruction based on Jittered sampling and curvelet transform[J]. Chinese Journal of Geophysics, 2013, 56(5): 1637−1649. DOI: 10.6038/cjg20130521. (in Chinese).
[31] 冯飞, 王征, 刘成明, 等. 基于Shearlet变换稀疏约束地震数据重构[J]. 石油物探, 2016, 55(5): 682−691. DOI: 10.3969/j.issn.1000-1441.2016.05.007. FENG F, WANG Z, LIU C M, et al. Seismic data reconstruction based on sparse constraint in the Shearlet domain[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 682−691. DOI: 10.3969/j.issn.1000-1441.2016.05.007. (in Chinese).
[32] 张良, 韩立国, 许德鑫, 等. 基于压缩感知技术的Shearlet变换重构地震数据[J]. 石油地球物理勘探, 2017, 52(2): 220−225. ZHANG L, HAN L G, XU D X, et al. Seismic data reconstruction with Shearlet transform based on compressed sensing technology[J]. Oil Geophysical Prospecting, 2017, 52(2): 220−225. (in Chinese).
[33] 闫海洋, 周辉, 刘海波, 等. FK和Shearlet域联合压缩感知数据重构技术[J]. 石油地球物理勘探, 2022, 57(3): 557-569. YAN H Y, ZHOU H, LIU H B, et al. Compressed sensing data reconstruction technology in joint FK and Shearlet domain[J]. Oil Geophysical Prospecting, 2022, 57(3): 557-569. (in Chinese).
[34] 余江奇, 曹思远, 陈红灵, 等. 改进阈值的Curvelet变换稀疏反褶积[J]. 石油地球物理勘探, 2017, 52(3): 426−433. DOI: 10.13810/j.cnki.issn.1000-7210.2017.03.003. YU J Q, CAO S Y, CHEN H L, et al. Sparse deconvolution based on Curvelet transform of improved threshold[J]. Oil Geophysical Prospecting, 2017, 52(3): 426−433. DOI: 10.13810/j.cnki.issn.1000-7210.2017.03.003. (in Chinese).
[35] 张入化, 苟其勇, 黄建平, 等. 基于Seislet域改进POCS算法的地震数据重构[J]. 物探化探计算技术, 2022, 44(5): 578-589. ZHANG R H, GOU Q Y, HUANG J P, et al, Improve POCS algorithm based on compressed sensing for seismic data reconstruction in Seislet domain[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2022, 44(5): 578-589. (in Chinese).
-
期刊类型引用(0)
其他类型引用(1)





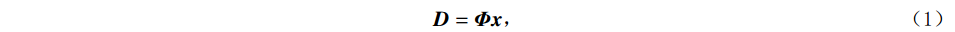

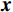



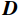
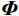

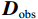
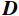


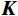
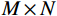
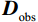
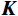
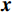
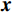
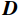
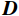
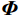

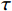

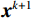

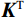
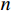
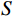

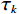




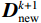
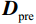
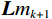
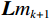


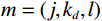
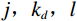
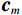
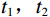

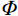

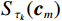
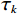

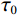



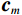
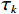

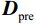
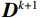
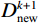

 下载:
下载:










