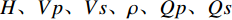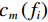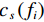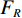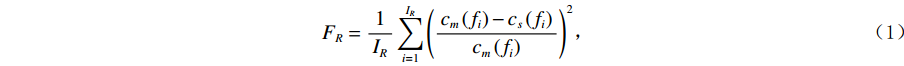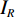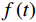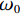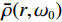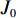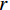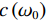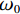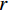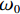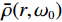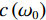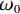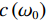Research Advancements in Surface Wave Exploration
-
摘要:
面波勘探通过对提取面波的频散曲线等观测进而反演获得探测目标信息。面波勘探技术始于20世纪60年代，但近几十年来迅猛发展，已经被广泛应用在地震灾害及火山活动预测、深部地质结构、工程施工、矿区采空区、塌陷区探测以及星体近地表结构探测等方面。为了更全面了解面波勘探技术，本文从面波勘探技术的主动震源和被动震源这两种数据类型开始，回顾基于频散曲线和水平垂直振幅谱比观测的面波勘探技术基本理论，简要介绍面波反演方法，并介绍面波勘探技术的应用领域和发展趋势和前景。
Abstract:Surface wave exploration plays a vital role in obtaining target detection information by analyzing and retrieving the dispersion curve of surface waves. Although surface wave exploration technology originated in the 1960s, it has experienced significant advancements in recent decades and has found widespread applications in earthquake disaster and volcanic activity prediction, deep geological structure analysis, engineering construction, mining area and goaf assessment, subsidence area detection, and near-surface structure investigation, including celestial bodies such as stars. This paper aims to provide a comprehensive overview of surface wave exploration technology. It begins by discussing two types of data sources, namely active source and passive source, and proceeds to review the fundamental theory of surface wave exploration based on dispersion curve analysis and observations of horizontal and vertical amplitude ratios. This paper also provides a brief introduction to the surface wave inversion method. Additionally, it highlights the various application domains of surface wave exploration, outlines the current development trend, and presents future prospects for this technology.
-
Keywords:
- surface wave exploration technology /
- dispersion curve /
- Rayleigh wave /
- HVSR
-
浅地表与人类生存和发展息息相关，研究浅层地质结构是重要的研究课题，通过地震波在不同岩石中传播的特征以探测浅部地质构造和测定岩石物理学参数，从而解决建筑物基础的稳定性、探测地下洞穴、地裂缝、滑坡体等以及勘测海底工程问题等。浅层的横波速度在地震学中是一个重要的物性参数，因此建筑工程和地震工程等方面均需要获取横波速度结构。确定横波速度的技术主要包括侵入性技术和非侵入性技术，侵入性技术需要利用钻井，其成本高和收集信息具有局限性；相反，非侵入性技术不需要钻井，从而高效、可靠且能够保护现场完整性，面波勘探技术属于非侵入性技术的一种。20世纪初以来，面波勘探技术的发展更加快速。
早期已有学者利用地震面波数据对层厚、剪切速度和密度等浅地表结构进行了研究[1]。地震面波主要包括瑞利波和勒夫波等，瑞利波是由P波和SV波在自由界面处相互干涉叠加而形成的地震波，沿自由界面传播并且在垂直自由界面方向迅速衰减。这种地震波由Rayleigh于1887年首次在数学上证明其存在，在自由界面附近沿面波传播方向的垂直平面内，瑞利波质点运动的轨迹是椭圆。勒夫波是一种由SH波相互干涉产生的地震波，由Love于1911年提出的。瑞利波和勒夫波的传播特征主要由横波速度决定，因此基于这两种面波均可以从浅层地震中确定横波速度结构，由于勒夫波的激发与存在条件较为严格，其观测难度要远远高于瑞利波。虽然瑞利波的振幅随垂直自由界面方向指数下降，但在浅地表层区域能量高且易于研究，因此将瑞利波作为面波勘探技术主要的研究信号。
Chang和Ballard等利用瑞利波来研究浅部地质问题，引起勘探地球物理学者们的注意，开始了对瑞利波勘探理论及方法的深入研究[1]。1983年，Nazarian等[2]基于人工源面波频散特征提出了面波谱分析法（spectral analysis surface waves，SASW），该方法的提出让面波勘探在工程中得到了广泛关注和应用。多道面波分析技术[3]（multichannel analysis of surface waves，MASW）的研究成果对瑞利波勘探方法的推广应用具有深远影响。
与主动源面波勘探不同，被动源方法在工程应用方面起步较晚，但发展速度较快，被动源面波勘探过程不需要震源，对低频信息的获取更好，降低了时间上和金钱上的投入，可获得高分辨率的近地表、地壳、地幔等地质结构。面波勘探技术通常采用数据的垂直分量，当考虑水平分量时，Nakamura[4]提出了一种不局限于面波频散性质的水平垂直振幅谱比方法，即HVSR方法，该方法在城市尤其适用于传统物探方法很难开展工作的区域中开展地质研究，例如低地震活动区和中等地震活动区，具有不生噪、施工形式灵活、高效、成本低、不会对城市交通、居民生活产生较大的影响的优点，是一项绿色环保的新型探测技术。该方法的提出使得面波勘探方法更加完善，极大地推动了浅层地震勘探的发展。目前，面波勘探技术广泛应用于不同领域，例如，浅层海洋声学、地震学、勘探地球物理、建筑物监测等[5-7]。
为更好了解面波勘探技术过程，本文从数据类型获取、基于频散曲线提取的面波勘探技术、基于水平与垂直谱比的面波勘探技术、面波反演方法和面波勘探应用5个方面进行系统介绍，其中重点介绍了主动震源和被动震源的采集、以及相应的面波勘探技术、HVSR。最后介绍面波勘探技术中存在的问题以及对策。
1. 数据类型
根据震源激发方式不同，面波勘探技术的数据类型包括主动震源和被动震源。主动震源包括人工震源和天然地震，人工震源指用人工敲击或炸药震源激发的面波信号；天然地震是指利用天然地震激发产生的面波信号，与人工震源相比，天然地震对场地要求较低、探测深度深、价格成本较低，但是需要等待天然地震，时间成本高，因此通常使用人工震源来探测。
以背景噪声为主的被动震源克服了对地震活动的依赖性，能够可以在任何时间、任何地点进行记录[8]。背景噪声是一种地球表面持续发生的微弱的地面震动，一直以来作为干扰波将其压制，最早Longuet-Higgins[9]于1950年发现背景噪声在表层土壤坚硬的地方表现出明显的频散异常，得到复杂震源信息、传输路径信息和观测站地下结构信息，逐渐被当作有效波广泛应用在断裂带。
1.1 主动震源
在诸多的震源类型之中，主动源数据采集最常用的是大锤震源。一般认为，在目标层深度小于10 m的土层勘探中10 kg的重锤震源便可获得较好的震源频谱特性，而大于（或小于）10 kg的重锤则用以满足主要目标深度大于（或小于）10 m的地质勘探，面波勘探中使用固有频率低的检波器也是相当重要的，常用的是4.5 Hz检波器，勘探采集过程中3个主要采集参数包括最小炮检距、道间距、检波器排列长度（如图1）。
当最小炮检距过小时，体波部分与面波部分堆叠，面波低频部分数据缺失，因此检波器距离地震源最近的偏移距离应与主要探测深度基本一致[10]；道间距影响面波成像的分辨率，如根据f-k变换法计算原理，大道间距会导致坐标轴附近成分发育不完整，道间距决定采样数据中的最小波长、模型中的地层厚度、反演得到的横波速度模型的分辨率，因此，道间距应同地层模型中最薄的地层的厚度基本一致；不同模式频散能量团更易分离，尤其对于高阶模式下的频散能量，在排列长度较短时，面波的基阶模式与高阶模式混叠而无法识别，随着排列长度增加，逐渐可以观察到高阶模式，同时基阶模式能量谱的宽度变窄，有利于频散曲线的提取[11]。
1.2 被动震源
面波勘探的被动震源来自背景噪声。频率小于1 Hz的背景噪声主要由自然力（如大气和海洋活动）激发，频率大于1 Hz的背景噪声主要由人工活动激发。自然噪声源包括地震、风浪、降雨、生物声波产生和海水热搅动等过程。人为噪声是由各种活动产生的，包括商业航运、石油和天然气勘探、开发和生产（如气枪、船舶、石油钻井）、海军作战（如军事声纳、通信和爆炸）、捕鱼（如商用声纳、声学威慑和骚扰装置）、研究活动（如气枪、声纳、遥测、通信和导航）以及其他活动，如建筑、破冰和休闲划船等[12]。
不同于主动源数据采集用的重锤、炸药和地震等震源，被动源数据采集背景噪声信号，从中处理得到有效数据。基于频散曲线提取的被动震源探测是基于台阵背景噪声数据采集，常用的观测方式有直线型、L型、多重圆观测台阵，如图2所示。多重圆观测台阵是背景噪声单点探测最常用的布设方式，Okada[13]通过将SPAC方法的3、4、5和9个台站阵列相比较，得到3个台站圆阵列是背景噪声的最有效和最有利的因素；但SPAC方法为满足方位角平均的条件，受台站排列的限制。Cho等[14]发展了SPAC方法，提出了仅在圆周上放置台站的无中心圆形台阵法（centerless circular array，CCA）。随着进一步面波勘探技术的研究与探讨，王建楠[15]的VWTM方法可以任意布设台阵，但该方法需要较大规模的台站数和台阵，因此会降低数据采集工作效率。基于椭圆率的HVSR方法采用单台观测获得单台3分量数据，即东西分量（E）、南北分量（N）和垂直分量（Z）。由于该方法仅需要一台3分量检波器，比台阵背景噪声观测法可以解决微动台阵观测中遇到的场地限制等优点，具有较好的应用前景。
![]()
图 2 常用面波单点观测台阵示意图Figure 2. Schematic representations of common surface wave single-point observation arrays1.3 主被动源的差异性
由于主动源和被动源数据采集信号来源完全不同，因此勘探过程存在差异。主要有以下几个方面：
（1）被动源和主动源频带差异较大。主动源面波勘探对浅部地层有较好的分辨能力，在相对较高的频率范围（例如20～50 Hz）内提取频散曲线，但探测深度有限，相同尺度相同排列条件下。被动源面波勘探能够提取到较低频率的面波（例如5～20 Hz），探测深度较大，但对浅层结构的分辨效果不理想[16]。
（2）与其他地球物理勘探采集过程相比较而言，主动源数据采集过程的震源主要利用落重震源或者锤击震源等，容易激发，更加便捷；但在城市进行地表研究时，主动源数据采集过程中会对地表路面有损害。被动源成像技术采集的数据利用背景噪声，地表损害较小；但基于数据随机性质需要大间距的台站和长时间采集。
（3）不同于被动源面波是全方位的，主动源数据采集的震源与排列方向一致，不需要测定现场面波的传播方向。
（4）主动源数据采集过程需要预实验，因为周围环境和操作员熟练程度的不同，采集得到的结果有时会不理想，所以通过预实验来确定各个参数。
（5）被动源数据采集不需要考虑干扰问题。相比较主动源数据采集过程中，当受到外界干扰强时如施工等，得到的数据信噪比低、处理过程复杂。而利用被动源数据采集该问题不严重。
2. 频散曲线提取
瑞利波相速度或群速度之间的频散特性与地层介质弹性参数有关，因此可用来反演不同区域地壳和上地幔的内部结构。面波勘探技术包括主动源面波勘探技术和被动源面波勘探技术。1983年，Nazarian等[2]提出了面波谱分析法（SASW），SASW是一种无损评估地层系统模量和厚度的方法，但是在使用该方法时，有效波难以从干扰波中分离而且精度低。随着面波勘探技术方法的不断改进和优化，开发了多道面波分析技术[3]（MASW）、倾斜叠加法[17]和高分辨率线性拉东变换方法。MASW主要包括f-k变换法、τ-p变换法和相移法等[18]，但该方法必须在大量位置移动和重复激活大型震源，因此成本较为高昂。为解决以上方法对高阶信息不敏感，提出了矢量波数变换方法[15]（VWTM）。
在被动源面波勘探技术研究方面，最早Aki[19]于1957年基于背景噪声的频散特性提出了一种提取频散曲线方法，即空间自相关方法（SPAC），但无法提取高阶面波，并且需满足方位角平均的条件，台站排列是限制的。后来提出F-K法虽然能分辨高阶模态的面波，但分辨率低，且需大量接收点同时采集。此外，被动源面波勘探技术还包括地震干涉法（SI）和折射微动方法（REMI）等[20]。虽然前述方法均可以得到含有高阶的频散曲线，但是在背景噪音中的应用中很难清晰准确的提取出理想的频散曲线。在噪声成像中陈晓非课题组[21]将VWTM也称为频率‒贝塞尔变换法（F-J），使其能够从背景噪音信号中提取到高阶面波频散曲线。
2.1 主动源面波勘探技术
2.1.1 面波谱分析法（SASW）
SASW的原理是通过对地层或土壤沉积物表面施加瞬态冲击，一组具有不同频率分量的波被传输到介质中，通过分析两个接收器之间各频率的瑞利波相速度，据此确定剪切波速，最终确定地层中各层的弹性模量和厚度。
通过调整土壤参数（
$ H、Vp、Vs、\rho 、Qp、Qs $ ）来进行土壤表征，使各频率$ {f}_{i} $ 下观测到的频散曲线$ {c}_{m}\left({f}_{i}\right) $ 和理论频散曲线$ {c}_{s}\left({f}_{i}\right) $ 拟合误差最小，即最小化如下目标函数$ {F}_{R} $ ：$$ {F}_{R}=\frac{1}{{I}_{R}}\sum _{i=1}^{{I}_{R}}{\left(\frac{{c}_{m}\left({f}_{i}\right)-{c}_{s}\left({f}_{i}\right)}{{c}_{m}\left({f}_{i}\right)}\right)}^{2} \text{，} $$ (1) 其中
$ {I}_{R} $ 是观测到的微震垂直运动相速度的数量[22]。该方法具有快速经济、无损检测、完全自动化的特点。但因为在人类活动频繁的城市，巨大的噪声往往掩盖了人工源，因而SASW利用相位差计算频散曲线时，易受到直达波、反射波、折射波和高阶频散曲线的影响，并且无法在频率域中分离出瑞利波相速度。Boore等[23]发现SASW模型在南加州6个钻孔横波速度剖面的位置始终低于预测的浅层速度，从而高估了10％ 至50％ 的地面运动。
2.1.2 多道面波分析方法（MASW）
线性拉东变换方法1999年就被引入工程地质和地球物理学领域之中。离散线性拉东变换的本质是将原来的函数做了一个空间转换，面波频散能量分析需要将时间-空间域的地震二维波场变换到频率-相速度域，因而任何一种提取面波频散能量的方法都需要经过至少两个步骤：①从时间域转换至频率域；②从空间域转换至速度域。前者是时间意义上的，后者是空间意义上的。
MASW属于离散线性拉东变换法，MASW包括f-k变换法、τ -p变换法和相移法等。在石油勘探中利用多道记录及其处理观念的方法早在几十年前就已经得到了广泛采用。于涵等[24]通过对τ -p变换法、相移法、f -k变换法得到的频谱能量谱对比分析了这些方法的优缺点。如图3可见，（a）为合成瑞利波地震记录，（b）～（d）分别为τ -p变换法、相移法、f -k变换法得到的频谱能量谱。τ -p变换法优点为失真小、易于实现、压制端点效应好，对成像多阶模态面波频散效果较好，但对基阶模态低频面波频散信息的成像效果较差，可能出现波场能量延伸和假频现象，从而易导致反变换后的波场相互叠加干涉；相移法抗噪性强、计算量小、分辨率较高，对提取基阶模态的面波频散信息效果较好，降低面波勘探方法对道间距的要求，使用较少道集即可直接产生分辨率较高的面波频散能量成像，但缺点是对高阶模态面波频散信息分辨率不高；f -k变换法具有计算量小，速度快，但要求采集时间、空间间隔相等，采集数据质量要求严格，容易发生空间假频现象，频散能量集中在一个很窄的频带范围。
![]()
图 3 三层速度递增水平层状介质模型地震记录及合成面波频散能量谱[24]（a）合成Rayleigh波地震记录。频散能量谱：（b）$\tau-p $变换法（c）相移法（d）$f-k $变换法Figure 3. Seismic record and synthetic surface wave dispersion energy spectrum of a three-layer horizontal layered media model with increasing velocity2.1.3 倾斜叠加法
f -k变换法、τ -p变换法和相移法这3种方法对高阶频散曲线提取的分辨率也较不理想[25]，为提高成像质量，Xia等[17]于2007年提出的一种离散线性拉东变换法——倾斜叠加法，该方法首先利用１个频率扫描函数与炮集记录（t -x域）进行卷积运算将频率分解，把时间变换为频率；接着利用类似于τ -p变换中倾斜叠加的方式得到每个速度的叠加能量值。由这两步即得到了f -v域的频散能量分布图，频率扫描函数
$ s\left(t\right) $ 公式为：$$ s\left(t\right)=\mathrm{I}\mathrm{m}\Bigg(\mathrm{e}\mathrm{x}\mathrm{p}\left(i2\text{π}\int _{0}^{t}f\left(t\right)\mathrm{d}t\right)\Bigg) 。 $$ (2) $ f\left(t\right) $ 表示与时间相关的线性函数，利用频率线性扫描将频谱细分可以提高频率域上的分辨率。能够更精细地将面波各频率成分分离，再将各频率的准确相速度搜索出来。倾斜叠加的方式和τ -p变换类似，但由于频率的分解，使得叠加过程单一，因而不受其他波形（例如体波等）的影响。另外，更适合分析高阶模式面波能量[17]。2.1.4 高分辨率线性拉东变换方法
使用标准离散线性拉东变换生成高分辨率频散曲线是困难的，Lou等[26]提出了高分辨率线性拉东变换方法，与常用的倾斜叠加算法相比，高分辨率线性拉东变换方法可以将色散图像的整体分辨率提高50％ 以上。此外，更高阶的频散能量扩展到更大的频率范围，从而增加其成像深度，提高分辨率。
2.1.5 矢量波数变换方法（VWTM）
随着对地层分层精度要求的不断提高，高阶面波在地层结构反演分析中起着关键作用，而上述MASW等方法都对高阶面波反应不灵敏，无法准确而清晰的从信号中提取出高阶面波频散曲线，矢量波数变换方法（vector wavenumber transformation method，VWTM）法有效解决了这个问题，清晰准确得到高阶面波频散曲线。该方法通过Fourier-Bessel变换，将多道地震记录变换到F-K域，再进一步变换到F-C域，获得频散能量图，在此基础上提取多阶频散曲线[27]。
苏悦等[28]对比VWTM、相移法和高分辨率线性拉东变换法3种方法的成像效果。从图4中可以看到，VWTM的成像质量明显优于其他两种方法，尤其高阶模式的成像优势明显，分辨率高；相移法的整体分辨率都很低，小于10 Hz低频区域的边界效应严重，高阶面波成像不理想；高分辨率线性拉东变换法保持很高的分辨率，但低频区域的效果明显很差，有较大的误差，且难以分辨不同模式的高阶面波。总之，VWTM在高阶模式的成像质量和基阶模式的成像精度方面具有巨大的优势。
![]()
图 4 实验数据频散能量图[28]Figure 4. Dispersion energy diagrams of Rayleigh wave data from the Changzhou suburb2.2 被动源面波勘探技术
2.2.1 空间自相关（SPAC）法
研究地震波的传统方法是将各震相的走时曲线作为揭示地球内部物质结构和状态的重要线索的方法。但背景噪声是在时间和空间上高度变化、不规则的振动现象，从相位的观点来利用背景噪声并从中推导出任何有用的传播时间曲线几乎是不可能的。因此，1957年，AKI[19]提出了空间自相关方法（SPAC），该方法利用背景噪声信号获得面波频散特征，主要思想是利用噪声信号空间——时间互相关叠加恢复台阵下面波信号。Aki研究说明了二维情况下求取频散曲线的方法，速度随频率变化情况下的二维波由频率为
$ {\omega }_{0} $ 的滤波的方位角平均自相关函数为：$$ \bar{\varnothing }(r)\equiv \varnothing (r,{\omega }_{0})=P\left({\omega }_{0}\right){J}_{0}\left(\frac{{\omega }_{0}}{c\left({\omega }_{0}\right)}r\right) \text{，} $$ (3) 其中，对应的自相关系数
$\bar{\rho }(r,{\omega }_{0})$ 为：$$ \bar{\rho }(r,{\omega }_{0})={J}_{0}\left(\frac{{\omega }_{0}}{c\left({\omega }_{0}\right)}r\right) \text{。} $$ (4) $ {J}_{0} $ 为第1类零阶贝塞尔函数，$ r $ 为两个点之间的距离，$ c\left({\omega }_{0}\right) $ 为频率为$ {\omega }_{0} $ 时的速度，由这个公式可以清楚地看出，第1类零阶贝塞尔函数和空间自相关系数成正比，可以通过空间自相关系数去拟合第1类零阶贝塞尔函数，对于一定的$ r $ 和不同的$ {\omega }_{0} $ ，测量$\bar{\rho }(r,{\omega }_{0})$ 可以得到函数$ c\left({\omega }_{0}\right) $ ，即$ {\omega }_{0} $ 频率范围内的频散曲线。图5为SPAC方法提取频散曲线流程图。由图可见，对于某一特定的频率下，满足公式（4）条件下的相速度
$ c\left({\omega }_{0}\right) $ 存在多个，因此SPAC方法具有多解性。同时在不同距离下的空间自相关系数只能单独计算频散曲线，效率很低，而且SPAC只能提取到基阶面波频散信息。为获得高阶信息，杨振涛[29]对SPAC方法进行了改进，提出了改进的空间自相关（Improved SPAC）算法。优点主要有两个方面：①观测系统可任意布设台站；①可得到不同模态面波在不同频率的相速度以便用于反演。通过频率域分类分析思想对频散曲线进行分类，避免了传统的连接“之”字形频散曲线所带进去的人为误差和平均误差，而且利用了那些成像不好的高阶频散曲线的信息。![]()
图 5 SPAC法提取频散曲线流程图[30]Figure 5. Flow chart outlining the SPAC method for extractingdispersion curve2.2.2 折射微动（REMI）法
REMI研究包括τ -p变换和傅立叶变换两个步骤。第1步，τ -p变换是将空间-时间（x -t）振幅谱转换成特征时间-慢度（τ -p）振幅谱；第2步，经过傅立叶变换是将时间-慢度（τ -p）振幅谱转换至慢度-频率（p -f ）域，由此慢度-频率振幅谱进行频散分析。REMI方法优点是只需要一列直线排列的普通低频检波器，便可快速记录背景噪声，因而具有较好的实用性，而且操作简单，对浅层研究精度高。通过在大量轻型地震仪的线性阵列上记录城市背景噪声，该方法实现了快速简便的野外数据采集[31]。
但是REMI在一定程度上具有局限性。Louie[31]将折射微动法用于研究南加州纽霍尔消防站（图6）时，设置了200米8 Hz地震折射检波器线性阵列。图6（a）为南加州纽霍尔消防站背景噪声记录，并使用折射微动法进行分析。根据箭头指向背景噪声中一个例子的振幅谱，生成的模型速度剖面，由该模型速度剖面匹配ROSRINE钻孔的悬浮测井剪切速度得到结果（图6（b））。由图6（b）可见，该方法对30 m以下的折射纵波速度和110 m以下的横波速度限制得较差。
![]()
图 6 折射微动法用于研究南加州纽霍尔消防站得到的结果图[31]Figure 6. Application of the refraction micromotion method to study the Newhall Fire Station in Southern California2.2.3 地震干涉（SI）法
Claerbout在1968年提出地震干涉法（SI）[20]，地震干涉方法是基于背景噪声信号的相关性和相干性，将背景噪声互相关提取格林函数从而得到面波信息；得到的面波信息反演得到地下介质速度结构以及变化。Yokoi等[32]证明了SI和SPAC法物理本质的一致性。SPAC法的基本公式可以通过基于弹性动力学格林函数恢复来导出，但是得到的频散曲线是台阵下方整个区域的平均效应，而SI法得到的是任意两个台站路径之间的频散曲线。在相同台阵数量上，地震干涉方法可以得到更多台站间的频散信息。
传统的地震干涉法在求解频散曲线时，相干系数拟合使用的是第1个单调递减段贝塞尔函数，计算的有效频散点较少，造成高频段缺失。牟新刚等[33]提出了改进的地震干涉方法，与使用单调递减段拟合的传统方法相比，改进的地震干涉方法使用实测信号的信噪比模型来修正两道信号的相干系数，通过第1类零阶贝塞尔函数的单调性把相干系数划分为不同区间段，分段拟合贝塞尔函数来求解面波相速度拓展了高频段，提高了浅层探测精度，并且相速度剖面较好地反映了测线下方的地下结构面波速度变化情况。
2.2.4 频率-贝塞尔变换（F-J）法
陈晓非课题组提出了一种新的方法频率-贝塞尔变换法（frequency-Bessel transform method，F-J），思路是将野外采集的背景噪音数据两两做互相关，然后对互相关谱做矢量波数变换就可以得到核函数的分布图，从而就得到了频散曲线以及含有高阶models的频散曲线。当基阶面波能量太强，在快速傅里叶变换时掩盖了其他波形能量时，为了解决这个问题，李正波[34]提出了多窗频率贝塞尔变换法（multi-windows F-J method，MWFJ），给定群速度区间计算时间窗，通过时间窗将波形中能量分开来成功地提取出高阶频散曲线。
为证实频率-贝塞尔变换方法在浅地表勘探中的适用性与可行性，黎汉民[35]采集了浙江省宁波市北仑区测量区原始噪声数据，采用矢量波数变换法提取高阶频散曲线，并结合多阶频散曲线的反演得到测点以下的介质速度、密度等结构信息；Ma等[36]采用频率-贝塞尔变换方法推导了Bohemian Massif西北部及邻近地区的一维横波速度模型。虽然该方法能够成功地从噪声数据中提取出高频、高阶频散曲线，但当提取的阶数越多的时候，如何准确的判断阶数成为了一个难题。实际采集工作中需要更多的实验设备，因此如何高效的利用现有资源从实际数据中准确提取更多的面波信息是进一步研究的方向[34]。
2.3 深度学习与频散曲线提取
随着深度学习、更强大的计算和不断增加的数据处理能力的快速发展，最近的研究将深度学习应用于地球物理学。基于深度学习模型构建一个类似人脑的分层架构，可以将输入数据从底层到顶层逐层提取特征，从而建立信号和语义之间的良好映射。
目前有许多学者将深度学习应用于面波频散曲线提取，Zhang等[37]利用神经网络结构U-Net从背景噪声互相关中提取频散曲线；Wang等[38]使用机器学习聚类方法自动提取面波频散曲线；Dai等[39]提出了DCNet，可解决数据量大、工作繁琐的任务，使地球物理数据处理的效率大大提高。
在上述研究中，处理的训练数据集是基于多道地震数据。然而，地震台站是低密度分布，单道被动地震数据的频散曲线提取在背景噪声研究中也很重要。因此，Yang等[40]提出了一种数据驱动的深度学习网络SDCnet用于频散曲线提取。SDCnet是一个改进的U-net，自动和智能地识别不同频率的峰值作为分段任务，在残差块中引入可训练的上下采样策略，以提高提取能力。
3. 基于水平与垂直谱比的面波勘探技术
全球海域地震频发，研究海底台站场地效应可预防海域工程结构在近海和海域地震中遭受的破坏[41]，因此场地效应信息在海域场地工程领域中具有特殊的意义；同时在城市工程领域中，场地效应信息可以用于高铁地震预警、快速震害评估、地震动衰减关系、列车应急处置范围、不同场地条件下高铁地震报警阈值设计以及高铁结构抗震设计等多个领域的科学研究和工程应用；在野外地质工作中，场地效应信息还可以用于岩溶强烈发育区、盆地浅部构造、断层、滑坡等方面的研究[42]。可见，场地效应在地球物理学是十分重要的。
传统求取场地效应的方法（如参考场地方法）需要背景噪声低的条件，当背景噪声高时，传统方法的结果不再可靠。为此，Nakamura[4]提出了一种通过同一场地上的水平与垂直背景噪声傅里叶谱比评估场地效应的面波勘探方法，这种谱比方法被称为HVSR法。利用HVSR方法可以确定场地的共振频率，当与地质信息结合时，可以用于评估场地效应[4]。
由于地脉动中未知源的类型，HVSR曲线会产生未知来源的峰值，而且很难客观地确定测量点的主要频率。此外，建议在凌晨3～4点左右进行测量，以尽量减少人类活动的噪音。当地下为多层硬基岩沉积层时，HVSR曲线会出现一个或多个峰值。Nakamura[4]认为HVSR峰值为垂直入射体波多次反射的结果。Nakamura[43]推广了这个理论，表明面波和体波的贡献都可能影响曲线的形状，但这取决于地下粘弹性特性、距离和地震源的分布。通过对波场和HVSR的本质的联系的研究，发现了HVSR曲线在横波的共振频率。
HVSR法是基于单站地震背景噪声的动力学特征反演横波速度剖面，但背景噪声信息所包含波的主要成分具有争议性。认为其主要成分是基阶瑞利面波，或者高阶瑞利面波，或者勒夫面波，甚至有研究人员认为在某些条件下其主要成分是体波。此外，由于地脉动信息场源所具有的随机性和复杂性，从而使得对地脉动随机波场的正演数值模拟和理论研究不完备，导致HVSR法缺乏系统的应用理论基础的支持。张立等[44]得到瑞利波的水平分量和垂直分量的频谱比物理实质上表征的是瑞利波椭圆率曲线的频散特征，该频散特征与场地的泊松比结构密切相关，为发展基于单点瑞利波的动力学特征的HVSR方法奠定理论基础。
当认为背景噪声中瑞利波的能量占据主导地位时，对水平与垂直背景噪声傅里叶谱比的计算变为瑞利波水平与垂直幅度比，即瑞利波椭圆率。但由于利用单个台站的背景噪声记录，无法定义瑞利波的径向分量，HVSR曲线都不是严格意义上的瑞利波椭圆率。反演中需要考虑不同波型成分计算HVSR曲线，从而与观测的HVSR曲线进行拟合。若以体波的能量为主要成分时，基于谱比计算可获得沉积层横波速度剖面，地下剪切波阻抗变化的信息[45]以及可能的局部场地特征[4,43]。
基于3年内进行的全面和详细的研究工作，欧洲研究项目SESAME中，设计了现场实验设计、数据处理和结果解释的程序，以便使用背景噪声实施HVSR技术[46]。随着处理HVSR曲线程序的发展，处理HVSR曲线的计算方法从基于半空间简单层扩展到多层系统。2008年，Herak[47]发布了一种 Matlab程序ModelHVSR，能够通过HVSR曲线的反演获得地下弹性性质的一维分布。地下调查需要在不同地点进行的多次HVSR测量可构建二维地下图像。
二维HVSR研究的想法是通过“HVSR-profiling”实现。虽然“HVSR-profiling”一定程度上得到有效的结果，但因为它在频率到深度的转换中只使用了一个横波速度值，因此无法给出整个真实的二维地下剖面。另一方面，该软件处理大规模HVSR测量时不能够同时反演多个HVSR曲线。为此，Bignardi等[48]发布了用于同时建模和反演大量HVSR数据集的开源计算机程序“OpenHVSR”。它能够生成二维和三维地下模型。然而，这个工作流通常冗长和耗时；此外，由于绘图是在获得HVSR曲线之后进行的，因此不能验证参数如何影响结果。Bignardi等[49]创建了一个新的计算机程序“OpenHVSR-processing Toolkit”。“OpenHVSR”利用已提供的HVSR曲线进行反演，而新软件“OpenHVSR-processing Toolkit”则直接从原始数据生成HVSR曲线。
常规的HVSR方法是基于被动源信号计算谱比，宓彬彬[50]从主动源信号中计算HVSR证明其是可行的，但前提必须进行面波模式分离。模式分离需要在频散能量图中准确识别各阶能量。当模型中存在强速度差异分界面时，会出现“模式接吻”现象，但不影响HVSR曲线的低谷部分。HVSR的峰值和低谷频率对模型参数非常敏感，用于探测和重建浅地表二维结构的潜力巨大。当地下为多层硬基岩沉积层时，HVSR曲线会出现一个或多个峰值。在多峰HVSR曲线的情况下，为了正确评估峰的统计特性并避免多模态数据分布，通过减小每个峰周围的频率范围来隔离每个峰至关重要[51]。另外，HVSR峰值的地层学解释是一个主观选择过程。与先验信息相关联，Capizzi等[52]使用基于质心的改进算法分析HVSR数据，实现了即使没有先验信息来评估最优分组的选择，也能产生有效的结果。
3.1 体波主导理论
早期主要基于体波占据主导地位解释HVSR曲线，Nakamura[4]认为HVSR曲线的峰值对应SH波基阶共振频率。基于HVSR曲线获得更多的地质信息，主要包括场地放大效应、沉积层厚度、场地的易损因子和平均横波速度。例如，由HVSR方法得到每个点的固有频率可以建立该点与沉积层厚度之间的相关性，从而对阿苏埃拉山谷谷底的地质横截面进行了划定，揭示了以前未定义的构造结构——断层[53]。林国良等[54]将地脉动观测数据采用 HVSR方法获取了龙头山镇高分辨率的卓越频率和放大系数结果，从而得到地震损伤程度。
3.2 瑞利波椭圆率
假设瑞利波占主导地位，背景噪声水平与垂直谱比改进为瑞利波两个方向的分量比，均匀介质中基阶瑞利面波不存在椭圆极化频散现象，而在非均匀介质中基阶瑞利面波存在椭圆极化频散现象，虽然瑞利波椭圆率测量可以追溯到20世纪60年代，但直到最近这个参数才得到了更多的关注。
直接估计椭圆率的技术已经发展，Fäh等[55]提出H/V时频分析（horizontal to vertical time frequency analysis，HVTFA）方法，将HVSR的计算限制在信号中能量最大的瑞利波。另一种单传感器方法是RayDec。近年来的更多研究表明，勒夫波可能对测量的HVSR曲线有显著贡献，并且这种贡献随频率和时间而变化[56]，因此在HVSR计算中去除勒夫波的贡献对瑞利波椭圆率的精确度十分重要。RayDec方法用于突出瑞利波相，削弱地震背景噪声波场中的勒夫波和体波的贡献。此外，最近还提出了另外两种使用地震传感器阵列的方法，第1种技术是由Poggi等[57]提出的高分辨率频率波数技术的改进方法，可以用来估计基阶模式和高阶模式瑞利波椭圆率；第2种技术MUSIQUE结合了采用经典多重信号分类算法和quaternion-MUSIC对勒夫波和瑞利波进行识别，并估计其各自的极化特性。除了椭圆率，这些技术还能得到面波频散曲线。
通过单台数据即可测量瑞利波椭圆率，其只对台站下方的局部结构敏感，因而瑞利波椭圆率适用于稀疏台阵的反演，可获取台站下方的一维速度结构。它不需要像面波速度那样，要求足够的射线路径覆盖，获得交叉台站之间的速度。Ferreira等[58]利用瑞利波椭圆率测量值反演了亚速尔群岛一维横波波速地壳模型。另外，瑞利波椭圆率对浅层速度结构更为敏感，通常将瑞利波椭圆率作为其他数据的补充。但是瑞利波椭圆率一直以来都面临着关键问题，基于瑞利波椭圆率反演获得的地下介质模型具有非唯一性。故基于瑞利波椭圆率信息无法约束地下介质结构，因而常用联合反演用恢复浅层速度构造。杜亚楠[59]提出了基于多阶瑞利波视频散曲线和椭圆率曲线联合反演的微动探测方法。视频散曲线中同时包含基阶波和各高阶瑞利波的信息，基于视频散曲线反演为充分利用多阶瑞利波信息提供了一个新的途径。与仅对视频散曲线进行反演的结果对比，加入椭圆率曲线的联合反演方法可以提高对基岩面以上各岩性层层厚和横波速度的反演精度。
4. 面波反演方法
常见的反演方法主要有观察法、线性化方法以及非线性全局优化算法。观察法是基于半波长理论，是一种简单但十分粗糙的反演方法，受主观性的影响较大。局部线性化方法有很多，如最速下降法、牛顿法、拟牛顿法（Quasi-Newton methods）、高斯牛顿法、共轭梯度法、L-M法（Levenberg-Marquardt）、Occam算法等。线性化方法是基于梯度的计算方法，很大程度上对初始模型有较大的依赖性。非线性全局优化算法方法很多，实际应用中有模拟退火算法（simulated annealing，SA）、遗传算法（genetic algorithm，GA）、蒙特卡洛算法[60]（Monte Carlo method，MC）、多目标演化算法[61]（multiobjective evolutionary algorithm，MOEA）、人工神经网络（artificial neural networks，ANN）、模式搜索算法[62]（pattern search alogrithms）、自然邻域算法[63]（neighborhood algorithm，NA）、混合演化算法[64]（shuffled complex evolution，SCE）、粒子群优化算法[65]（particle swarm optimization，PSO）、差分演化算法[66]（differential evolution algorithm，DE）、种群迁徙智能优化算法[67]（differential search algorithm，DSA）、人工蜂群算法[68]（artificial bee colony，ABC）、灰狼优化算法[69]（grey wolf optimizer，GWO）、热浴模拟退火法[70]、马尔可夫链蒙特卡洛法[71]（Markov-chain Monte Carlo method，MCMC）、正弦余弦算法[72]（Sine Cosine algorithm，SCA）、自适应权重的蜻蜓算法[73]（adaptive weight dragonfly algorithm，AWDA）等。海洋捕食者算法（marine predators algorithm，MPA）是最近用于浅地表勘探新型的反演算法，该算法由Faramarzi等[74]提出的一种新的群体智能优化算法，算法结合Lévy和布朗运动模拟海洋生态系统中食肉动物捕食猎物行为的元启发式优化算法。
常规遗传算法计算耗时较长，粒子群算法容易存在种群多样性趋同，多参数存在串扰现象，易陷入局部极小值。于涵等[75]基于MPA提出了一种改进的海洋捕食者优化算法（ACMPA），针对初始化随机不均匀的现象，引入基于Cubic映射的混沌序列初始化、适应函数因子和精英等级制度。不含噪声数据情况下，用标准MPA方法、粒子群算法（PSO）、遗传算法（GA）、蝴蝶优化算法（BOA）、秃鹫优化算法（BES）、基于螺旋上升机制的鲸鱼优化算法（WOA）、基于4种等级寻优政策的灰狼优化算法（GWO）、基于链状群体模型的樽海鞘优化算法（SSA）、基于振荡反应的黏菌算法（SMA）以及ACMPA算法等多种优化算法分别进行反演，种群数量设为40，分别为迭代次数在50、200次的反演效果见图7。
![]()
图 7 模型不含噪声数据ACMPA与多种优化算法收敛曲线对比[75]Figure 7. Comparison of convergence curves of ACMPA with those of other optimization algorithms; noise-free data from the model are used由图7可见，ACMPA优化算法在反演过程中可以随着迭代次数的增加不断有效寻优，收敛效果更加稳定，迭代次数较少亦可以进行有效寻优。这体现该算法在全局寻优和局部寻优的平衡性，改进的海洋捕食者优化算法可以有效地提取夹低速地层构造的近地表介质信息，精细拾取浅地表地层信息，有效地反演浅地表地层结构。
5. 应用
面波勘探技术广泛应用于地震灾害及火山活动预测、地下地质结构探测、工程施工方面和采空区、塌陷区探测以及行星地质探测等不同领域。
5.1 地震灾害及火山活动预测
利用面波勘探技术对地震灾害或火山活动发生初步原因进行研究，可对其进行预测。通过面波勘探技术得到的地震速度变化为地震预测提供了可靠的依据，推动了地震学勘探的发展。
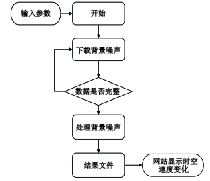
地震灾害方面，HVSR方法可以用来准确估计地震损伤和潜在危险预测[42]，为防灾减灾工作提供基本参考。例如，Matassoni等[76]通过 HVSR方法对252个噪声测量值和29个横波速度模型分析，在受干扰程度最高的土壤内，地震放大对地面运动的峰值加速度超过了国家规定的值（0.175 g），潜在危险更大。在火山内部活动预测方面，定位与潜在喷发相关的地下结构变化是更好地了解火山动力学的关键问题。地震波速变化与先验、共生和后验火山过程有关，对这些地震速度变化的研究能得到岩浆储存分布情况，以及岩浆流体在喷发前几个月侵入并驻留该区域的时间尺度，可预测即将爆发的岩浆活动。Obermann等[77]记录了留尼汪岛富尔奈斯活火山的 19个台站的地震背景噪声，得到背景噪声相关性包含有关活火山爆发过程位置的确定性信息，为即将到来的火山爆发定位提供了依据和可能性；Bennington等[78]利用背景噪声来研究阿拉斯加韦尼亚米诺夫火山过去的7个喷发期。Hutapea等[7]开发了一个连续监测日本列岛地震速度的系统，使用背景噪声数据估计地震速度的变化。该系统包括3个操作：下载背景噪声数据、处理数据和在网站上显示时空速度变化（图8），有效地确定了可能与地震、余震、岩浆活动和环境影响有关的速度变化，但较长的数据周期会产生更稳定的结果，而较短的周期提供更好的时间分辨率。
5.2 地下地质结构探测
采用面波勘探技术可圈定了断层、裂缝和地下结构[79]。但是一些深部断层无法到达地面，很少被发现。Kang等[80]将HVSR方法用于识别韩国浦项盆地兴海地区东部的隐伏断裂区，证实了方法的可行性；Sgattoni等[81]对意大利北部的Bolzano沉积盆地进行地下结构成像，得到HVSR等值线图（图9）。白线表示根据地震反射推断的沉积物-基岩界面的位置，箭头指示单个HVSR曲线的位置。
将二维地质结构研究拓展到三维结构，Manzo等[82]基于HVSR方法获得了第一个伊斯基亚岛（意大利）三维横波速度模型。
5.3 工程施工方面的应用
通过地震波在不同岩石中传播的特征以探测浅部地质构造和测定岩石物理学参数等，因而面波勘探技术广泛应用于城市工程、工程地质和海域场地工程3个方面。在城市工程方面，叶咸等[83]将面波勘探技术应用于公路边坡注浆加固效果检测中，表明面波勘探技术的实用性和适用性。
在野外地质工作中，面波勘探技术广泛应用于岩土工程勘察、第四系分层、堤坝隐患调查、孤石检测、公路软基勘察、滑坡面调查、堤坝渗漏隐患探测、排水项目勘察和隐伏溶洞等[84-85]。吴曲波等[86]使用面波勘探法较好地探测浅层玄武岩的三维空间分布规律特征；周荣亮等[87]使用MASW对两座有效容积为10000 m3的LNG储罐罐体进行地基勘察；李圣林等[88]用面波勘探技术掌握了隐伏溶洞的响应特征。此外，山体滑坡堵江形成的堰塞体物质结构组成不均，局部存在架空现象，对下游沿岸人民生命财产安全造成威胁。熊友亮等[89]基于SPAC研究了堰塞体结构，为堰塞坝险情处置提供了依据。
海域场地工程是岩土地震工程的研究热点。使用MASW来制定沿海环境中的打桩振动标准[90]，通过HVSR方法可以得到场地分类特性，为海域地震动模拟、海洋工程建设等提供参考[41]。
5.4 采空区、塌陷区探测
对于矿产调查应用来说，钻探是昂贵的精确揭示地层的方式，但受场地影响大，存在不连续性。面波勘探具有操作简便、成本低廉，对周围环境影响小等优点，因此面波勘探技术广泛应用于矿产开采领域，包括煤层陷落柱和煤矿踩空区等空洞、塌陷等。
Ivanov等[91]基于面波勘探技术探测堪萨斯州加利纳市与矿山和喀斯特有关的可能具有坍塌潜力的空洞和矿井位置。弃土场也是矿产开采需要考虑的一个部分。煤矿弃土场是由剩余（煤炭）采矿材料建造的人为地形结构，也包括煤和高爆炸性煤尘，因此煤田尖端火灾对环境造成不可逆转的退化。Lewińska等[92]使用MASW找到Bogdanka弃土场尖端体内的潜在空隙，但未检测到明显的空隙或储存材料的显著差异。
5.5 行星地质探测
美国宇航局的洞察号（InSight）直接把地震仪部署在火星表面。参照对地球和月球的研究，基于着陆点浅层地下模型中的背景噪声波场提取高频瑞利波椭圆率，并针对浅层结构进行了反演[93]。Mahvelati等[94]基于HVSR方法从三维角度分析背景噪声记录，以确定固有频率，研究的结果显示在3.2～3.8 Hz的HVSR曲线上产生了局部最大值；利用这些信息估计了观测点的火星风化层厚度为8～10 m，估计的风化层厚度与文献中建议的大对比度界面的深度范围非常吻合。
面波勘探技术也被应用于月震数据的研究。在美国宇航局阿波罗任务期间，地震仪被安装在月球上，从1969年7月到1977年9月向地球传回连续的地震数据。Larose等[95]通过阿波罗17号任务期间放置在月球上的4个传感器记录的地震噪声获得了瑞利波的频散。瑞利波列的“信噪比”依赖于太阳光照，说明了太阳加热是月球上地震噪声的来源。这一结果表明，在未来的行星任务中，即使在没有自然地震的情况下，也可以通过关联地震噪声来提取关于地外物体内部结构的信息。地震干涉测量法可用于研究地表下温度变化对地震速度的影响，从而直接观测月球内部的动态过程[96]。Nishitsuji等[97]提出了深月震地震干涉测量法（deep-moonquake seismic interferometry，DMSI）来应用于深月震，将深部月震的P波或S波尾波的自相关得到反射图像，并用DMSI反演的横波记录来分析了方位各向异性[98]。
6. 存在的问题和对策
面波勘探技术的研究和应用较多。通过对面波勘探技术系统的了解，本文得到以下认识。
（1）传统面波勘探采用等间距垂直分量检波器采集地震数据中的瑞利波，获取关于介质的信息有限；引入径向分量补充地震数据中的瑞利波频散信息，可以得到更加完备、可靠的瑞利波频散曲线[99]。目前面波勘探中多采用多分量探测来反演得到更精细的近地表横波速度结构。
（2）面波勘探技术相比较于探地雷达等地球物理方法探测精度较低。为实现高精度探测，学者们采用联合反演。主要包括瑞利波不同分量联合反演、瑞利波与折射波联合反演、瑞利波与反射波联合反演、瑞利波与勒夫波联合反演以及瑞利波与其他地球物理资料联合反演等。例如，应用HVSR和MASW反演方法的组合来获得横波速度的值有望克服方法的不足[100]；Abdialim等[101]基于HVSR方法同时利用已经存在的钻孔测井数据作为约束得到理想的横波速度剖面；李巧灵等[102]综合利用MASW和SPAC分析斜坡内部结构；刘道涵等[103]通过三维高密度电阻率法、多源面波勘探和地面核磁共振方法等地球物理联合探测隐伏岩溶区地质精细结构；徐吉祥等[104]通过采用主动源面波、主动源和被动源相结合面波勘探和HVSR方法进行城市隐伏活动断裂的研究，对比发现，对断裂探测的特征基本一致，相互印证，提高了解释的可信度。瑞利波椭圆率和相速度或群速度的联合反演也成为研究者关注的课题，并广泛用于弥补单独相速度或群速度反演对浅层结构约束不够的缺点。Perton等[105]对洛杉矶盆地的每个站的瑞利波和勒夫波的水平与垂直谱比和多模频散曲线（相位和群速度）进行了联合反演。
（3）面波多道分析方法大多用于一维和二维地下结构探测，拓展到三维探测。拓展中需考虑浅地表介质的复杂性，不可避免地会涉及面波散射效应，因而需要深入研究面波的散射理论。联合利用瑞利波和勒夫波多道分析方法确定浅地表三维横波速度结构，可以极大地推动高频面波方法理论和应用的发展，对于实现浅地表复杂介质高精度探测具有重要意义[50]。而三维面波多道分析方法仅限于理论研究，利用面波勘探获取地下三维地质结构的实例较少，多波多分量地震勘探是当前研究的热点。另外，为得到更精细地下三维地质结构需要大量数据，大规模地震台阵的出现也为瑞利波椭圆率提供了海量高质量的三分量数据，在面波勘探利用深度学习构建模型为大量地震数据处理提供新的方向。
（4）HVSR采集与解释工作主要集中在陆地上，对海洋采集研究很少。到目前为止，所开发的算法只适用于陆地环境，没有考虑海洋环境[106]，在海洋环境中进行相应HVSR的研究是未来研究的方向之一。
面波勘探技术不可避免存在局限性，但面波勘探技术具有不可替代性和必要性，其研究过程仍是一个长期并且艰苦的过程。
7. 总结
面波勘探是一种浅层地震勘探方法，面波的频散特征使人们利用面波更好地了解地下的可能。如今频散曲线的提取实现了从基阶到高阶的转变，从而获得更精细浅地下结构。另外，水平与垂直地脉动傅里叶谱比拓宽了面波研究的范围。经过数年的创新和发展，面波勘探技术越来越具有可靠性，面波勘探技术已广泛应用于各种地质工作中去，如岩土工程、建筑工程、地震工程和海洋工程建设等，为地震灾害预防、采空区勘探、隐藏断层和裂缝识别提供了依据。此外，面波勘探技术还应用在火星风化层结构和月球内部探测。
目前，面波勘探技术是比较热门的地球物理方法，越来越多的地球物理学者投入到面波勘探技术的研究工作中。
-
![]()
图 2 常用面波单点观测台阵示意图
Figure 2. Schematic representations of common surface wave single-point observation arrays
![]()
图 3 三层速度递增水平层状介质模型地震记录及合成面波频散能量谱[24]
（a）合成Rayleigh波地震记录。频散能量谱：（b）$\tau-p $变换法（c）相移法（d）$f-k $变换法
Figure 3. Seismic record and synthetic surface wave dispersion energy spectrum of a three-layer horizontal layered media model with increasing velocity
![]()
图 4 实验数据频散能量图[28]
Figure 4. Dispersion energy diagrams of Rayleigh wave data from the Changzhou suburb
![]()
图 5 SPAC法提取频散曲线流程图[30]
Figure 5. Flow chart outlining the SPAC method for extractingdispersion curve
![]()
图 6 折射微动法用于研究南加州纽霍尔消防站得到的结果图[31]
Figure 6. Application of the refraction micromotion method to study the Newhall Fire Station in Southern California
![]()
图 7 模型不含噪声数据ACMPA与多种优化算法收敛曲线对比[75]
Figure 7. Comparison of convergence curves of ACMPA with those of other optimization algorithms; noise-free data from the model are used
-
[1] 陈宏林, 丰继林. 工程地质勘察方法[M]. 北京: 地震出版社, 1998: 139-171. CHEN H L, FENG J L. Engineering geological investigation method[M]. Beijing: Seismological Press, 1998: 139-171.
[2] NAZARIAN S, STOKOE K H. Evaluation of moduli and thicknesses of pavement systems by spectral-analysis-of-surface-waves method[R]. Centre for Transportation Research, 1983.
[3] PARK C B. Multi-channel analysis of surface waves using vibroseis (MASWV)[C]//1996 SEG Annual Meeting, 1996.
[4] NAKAMURA Y. Method for dynamic characteristics estimation of subsurface using microtremor on the ground surface[J]. Railway Technical Research Institute, 1989, 30(1): 25−33.
[5] DERODE A, LAROSE E, TANTER M, et al. Recovering the Green's function from field-field correlations in an open scattering medium[J]. The Journal of the Acoustical Society of America, 2003, 113(6): 2973−2976. doi: 10.1121/1.1570436
[6] CAMPILLO M, PAUL A. Long-range correlations in the diffuse seismic coda[J]. Sciences, 2003, 299(5606): 547−549.
[7] HUTAPEA F L, TSUJI T, IKEDA T. Real-time crustal monitoring system of Japanese Islands based on spatio-temporal seismic velocity variation[J]. Earth Planets Space, 2020, 72(1): 1−16. doi: 10.1186/s40623-019-1127-2
[8] YANG Y J, RITZWOLLER M H. Characteristics of ambient seismic noise as a source for surface wave tomography[J]. G-Cubed: Geochemistry, Geophysics, Geosystems, 2008, 9(2): Q02008.
[9] LONGUET-HIGGINS M S. A theory of the origin of microseisms[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1950, 243(243): 1−35.
[10] XIA J, MILLER R D, PARK C B, et al. Utilization of high-frequency Rayleigh waves in near-surface geophysics[J]. Leading Edge (Tulsa, OK), 2004, 23(8): 753−759. doi: 10.1190/1.1786895
[11] 李欣欣. 面波成像技术[M]. 北京: 中国石化出版社出版社, 2019. LI X X. Surface wave imaging technology[M]. Beijing: China Petrochemical Press, 2019.
[12] HILDEBRAND J A. Anthropogenic and natural sources of ambient noise in the ocean[J]. Marine Ecology Progress, 2009, 395: 5−20. DOI: 10.3354/meps08353.
[13] OKADA H. Theory of efficient array observations of microtremors with special reference to the SPAC method[J]. Exploration Geophysics, 2006, 37(1): 73−85. doi: 10.1071/EG06073
[14] CHO I, TADA T, SHINOZAKI Y. A new method to determine phase velocities of Rayleigh waves from microseisms[J]. Geophysics, 2004, 69(6): 1535−1551. doi: 10.1190/1.1836827
[15] 王建楠. 背景噪音提取高阶频散曲线的矢量波数变换方法[D]. 合肥: 中国科学技术大学, 2019. WANG J N. A vector wavenumber transforms method for background noise extraction of high-order dispersion curves[D]. Hefei: University of Science and Technology of China, 2019. (in Chinese).
[16] PARK C B, MILLER R D, RYDEN N, et al. Combined use of active and passive surface waves[J]. Journal of Environmental and Engineering Geophysics, 2005, 10(3): 323−334. doi: 10.2113/JEEG10.3.323
[17] XIA J H, XU Y X, MILLER R D. Generating an image of dispersive energy by frequency decomposition and slant stacking[J]. Pure and Applied Geophysics, 2007, 164(5): 941−956. doi: 10.1007/s00024-007-0204-9
[18] CAPON J, M. I. T. LINCOLN LABORATORY L, MASS. High-resolution frequency-wavenumber spectrum analysis[J]. Proceedings of the IEEE, 1969, 57(8): 1408−1418. doi: 10.1109/PROC.1969.7278
[19] AKI K. Space and time spectra of stationary stochastic waves, with special reference to microtremors[J]. Bulletin, Earthquake Research Institute, 1957, 35: 415−456.
[20] CLAERBOUT J F. Synthesis of a layered medium from its acoustic transmission response[J]. Geophysics, 1968, 33(2): 264. doi: 10.1190/1.1439927
[21] WANG J N, WU G X, CHEN X F. Frequency-bessel transform method for effective imaging of higher-mode rayleigh dispersion curves from ambient seismic noise data[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(4): 3708−3723. doi: 10.1029/2018JB016595
[22] YOUNG C N. Automation in ambient vibration analysis for soil characterisation[D]. Sydney: University of Western Sydney, 2014.
[23] BOORE D M, BROWN L T. Comparing shear-wave velocity profiles from inversion of surface-wave phase velocities with downhole measurements: Systematic differences between the CXW method and downhole measurements at six USC strong-motion sites[J]. Seismological Research Letters, 1998, 69(3): 222−229. doi: 10.1785/gssrl.69.3.222
[24] 于涵, 刘财, 王典, 等. 面波频散能量谱计算方法[J]. 吉林大学学报(地球科学版), 2022,52(2): 602−612. YU H, LIU C, WANG D, et al. Calculation method of surface wave dispersion energy spectrum[J]. Journal of Jilin University (Earth Science Edition), 2022, 52(2): 602−612. (in Chinese).
[25] Dal MORO G, PIPAN M, FORTE E, et al. Determination of Rayleigh wave dispersion curves for near surface applications in unconsolidated sediments[C]//The 2003 SEG Annual Meeting, Seg Technical Program Expanded Abstracts, Dallas, Texas, 2003: 1247-1250.
[26] LUO Y, XIA J, MILLER R D, et al. Rayleigh-wave mode separation by high-resolution linear Radon transform[J]. Geophysical Journal International, 2009, 179(1): 254−264. doi: 10.1111/j.1365-246X.2009.04277.x
[27] 杨振涛, 陈晓非, 潘磊, 等. 基于矢量波数变换法(VWTM)的多道Rayleigh波分析方法[J]. 地球物理学报, 2019,62(1): 298−301, 303-305. YANG Z T, CHEN X F, PAN L, et al. Multichannel Rayleigh wave analysis method based on vector wave-number transformation method[J]. Journal of Geophysics, 2019, 62(1): 298−301, 303-305. (in Chinese).
[28] 苏悦, 杨振涛, 杨博, 等. 基于矢量波数变换法的主动源瑞雷波多模式提取方法在近地表地层结构探测中的应用研究[J]. 北京大学学报(自然科学版), 2020,56(3): 427−435. SU Y, YANG Z T, YANG B, et al. Application of active source rayleigh wave multi-mode extraction method based on vector wavenumber transform in near-surface formation structure detection[J]. Journal of Peking University (Natural Science), 2020, 56(3): 427−435. (in Chinese).
[29] 杨振涛. 被动源面波勘探高阶频散曲线的提取和应用[D]. 合肥: 中国科学技术大学, 2017. YANG Z T. Extraction and application of high order dispersion curve in passive surface wave exploration[D]. Hefei: University of Science and Technology of China, 2017. (in Chinese).
[30] LING S. Research on the estimation of phase velocities of surface waves in microtremors[D]. Hokkaido: Hokkaido University, 1994.
[31] LOUIE J N. Faster, better: Shear-wave velocity to 100 meters depth from refraction microtremor arrays[J]. Bulletin of the Seismological Society of America, 2001, 91(2): 347−364. doi: 10.1785/0120000098
[32] YOKOI T, MARGARYAN S. Consistency of the spatial autocorrelation method with seismic interferometry and its consequence[J]. Geophysical Prospecting, 2008, 56(3): 435−451. doi: 10.1111/j.1365-2478.2008.00709.x
[33] 牟新刚, 周奇, 周晓, 等. 一种高频拓展的改进地震干涉算法研究[J]. 仪器仪表学报, 2021,42(4): 59−66. MOU X G, ZHOU Q, ZHOU X, et al. Research on an improved seismic interference algorithm based on high frequency expansion[J]. Chinese Journal of Instrument, 2021, 42(4): 59−66. (in Chinese).
[34] 李正波. 频率贝塞尔变换法提取地震记录中的频散信息[D]. 合肥: 中国科学技术大学, 2020. LI Z B. Extraction of dispersion information from seismic records using frequency bessel transform[D]. Hefei: University of Science and Technology of China, 2020. (in Chinese).
[35] 黎汉民. 矢量波数变换法在浅层勘探中的应用[D]. 合肥: 中国科学技术大学, 2018. LI H M. Application of vector wavnumber transformation method in shallow exploration[D]. Hefei: University of Science and Technology of China, 2018. (in Chinese).
[36] MA Q, PAN L, CHEN X. Utilizing vector wavenumber transform method to extract multi-mode dispersion curves of Rayleigh waves from ambient seismic noise and the application to structure inversion in Bohemian Massif[J]. Geophysical Research Abstracts, 2019, 21: 1.
[37] ZHANG X T, JIA Z, ROSS Z E, et al. Extracting dispersion curves from ambient noise correlations using deep learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(12): 8932−8939. doi: 10.1109/TGRS.2020.2992043
[38] WANG Z N, SUN C Y, WU D S. Automatic picking of multi-mode surface-wave dispersion curves based on machine learning clustering methods[J]. Computational Geosciences, 2021, 153: 104809.
[39] DAI T Y, XIA J H, NING L, et al. Deep learning for extracting dispersion curves[J]. Surveys in Geophysics, 2021, 42(1): 69−95. doi: 10.1007/s10712-020-09615-3
[40] YANG T W, XU Y, CAO D P, et al. SDCnet: An Unet with residual blocks for extracting dispersion curves from seismic data[J]. Computational Geosciences, 2022, 166: 105183. doi: 10.1016/j.cageo.2022.105183
[41] 周旭彤, 胡进军, 谭景阳, 等. 基于HVSR的DONET1海底地震动场地效应研究[J]. 震灾防御技术, 2021,16(1): 105−115. ZHOU X T, HU J J, TAN J Y, et al. Study on-site effect of DONET1 seabed ground motion based on HVSR[J]. Earthquake Prevention Technology, 2021, 16(1): 105−115. (in Chinese).
[42] 阮明明, 王帅军, 田晓峰, 等. 利用HVSR法探测渭河盆地浅部构造[J]. 大地测量与地球动力学, 2022,42(6): 584−587, 621. RUAN M M, WANG S J, TIAN X F, et al. Exploration of shallow structures in Weihe Basin by HVSR method[J]. Geodesy and Geodynamics, 2022, 42(6): 584−587, 621. (in Chinese).
[43] NAKAMURA Y. Clear identification of fundamental idea of Nakamura's technique and its applications[C]//12th World Conference on Earthquake Engineering (12 WCEE 2000) v.5: Engineering Seismology, 2001.
[44] 张立, 刘争平. 水平层状介质中基阶瑞利面波椭圆极化特征数值分析与研究[J]. 地球物理学报, 2013,(5): 1686−1695. ZHANG L, LIU Z P. Numerical analysis and study on elliptic polarization characteristics of fundamental Rayleigh surface waves in horizontal layered media[J]. Journal of Geophysics, 2013, (5): 1686−1695. (in Chinese).
[45] OUBAICHE E, CHATELAIN J L, BOUGUERN A, et al. Experimental relationship between ambient vibration H/V peak amplitude and shear-wave velocity contrast[J]. Seismological Research Letters, 2012, 83(6): 1038−1046. doi: 10.1785/0220120004
[46] PICOZZI M, ALBARELLO D. Guidelines for the implementation of the H/V spectral ratio technique on ambient vibrations measurements, processing and interpretation[J]. Geophysical Journal International, 2004, 169(1): 189−200.
[47] HERAK M. ModelHVSR—A Matlab® tool to model horizontal-to-vertical spectral ratio of ambient noise[J]. Computational Geosciences, 2008, 34(11): 1514−1526. doi: 10.1016/j.cageo.2007.07.009
[48] BIGNARDI S, MANTOVANI A, ZEID N A. OpenHVSR: Imaging the subsurface 2D/3D elastic properties through multiple HVSR modeling and inversion[J]. Computational Geosciences, 2016, 93(1): 103−113.
[49] BIGNARDI S, YEZZI A J, FIUSSELLO S, et al. OpenHVSR-processing toolkit: Enhanced HVSR processing of distributed microtremor measurements and spatial variation of their informative content[J]. Computational Geosciences, 2018, 120: 10−20. doi: 10.1016/j.cageo.2018.07.006
[50] 宓彬彬. 复杂浅地表弹性介质面波分析方法研究[D]. 武汉: 中国地质大学, 2018. MI B B. Study on surface wave analysis method of complex shallow surface elastic medium[D]. Wuhan: China University of Geosciences, 2018. (in Chinese).
[51] DAL MORO G, PANZA G F. Multiple-peak HVSR curves: Management and statistical assessment[J]. Engineering Geology, 2022, 297: 106500. doi: 10.1016/j.enggeo.2021.106500
[52] CAPIZZI P, MARTORANA R. Analysis of HVSR data using a modified centroid-based algorithm for near-surface geological reconstruction[J]. Geosciences, 2022, 12(4): 147. doi: 10.3390/geosciences12040147
[53] ALONSO-PANDAVENES O, TORRES G, TORRIJO F J, et al. Basement tectonic structure and sediment thickness of a valley defined using HVSR geophysical investigation, Azuela valley, Ecuador[J]. Bulletin of Engineering Geology and the Environment, 2022, 81(5): 1−14.
[54] 林国良, 张潜, 崔建文, 等. 利用地脉动HVSR研究2014年鲁甸6.5级地震场地效应[J]. 地震研究, 2019,42(4): 531−537, 650. LIN G L, ZHANG Q, CUI J W, et al. Study on the side effect of the 2014 Ludian M6.5 earthquake using ground pulsation HVSR[J]. Seismological Research, 2019, 42(4): 531−537, 650. (in Chinese).
[55] FAH D, WATHELET M, KRISTEKOVA M, et al. Using ellipticity information for site characterization[M]. NERIES JRA4 "Geotechnical Site Characterisation", 2009.
[56] ENDRUN B. Love wave contribution to the ambient vibration H/V amplitude peak observed with array measurements[J]. Journal of Seismology, 2011, 15(3): 443−472. doi: 10.1007/s10950-010-9191-x
[57] POGGI V, FAH D. Estimating Rayleigh wave particle motion from three-component array analysis of ambient vibrations[J]. Geophysical Journal International, 2010, 180(1): 251−267. doi: 10.1111/j.1365-246X.2009.04402.x
[58] FERREIRA A M G, MARIGNIER A, ATTANAYAKE J, et al. Crustal structure of the Azores Archipelago from Rayleigh wave ellipticity data[J]. Geophysical Journal International, 2020, 221(2): 1232−1247. doi: 10.1093/gji/ggaa076
[59] 杜亚楠. 基于多阶瑞雷波视频散曲线和椭圆率曲线联合反演的微动探测方法研究[D]. 北京: 中国科学院大学, 2019. DU Y N. Research on fretting detection method based on multi-order Rayleigh wave video dispersion curve and ellipticity curve inversion[D]. Beijing: University of Chinese Academy of Sciences, 2019. (in Chinese).
[60] SOCCO L V, BOIERO D. Improved Monte Carlo inversion of surface wave data[J]. Geophysical Prospecting, 2008, 56(3): 357−371. doi: 10.1111/j.1365-2478.2007.00678.x
[61] DAL MORO G, PIPAN M. Joint inversion of surface wave dispersion curves and reflection travel times via multi-objective evolutionary algorithms[J]. Journal of Applied Geophysics, 2007, 61(1): 56−81. doi: 10.1016/j.jappgeo.2006.04.001
[62] SONG X H, GU H M, ZHANG X Q, et al. Pattern search algorithms for nonlinear inversion of high-frequency Rayleigh-wave dispersion curves[J]. Computational Geosciences, 2008, 34(6): 611−624. doi: 10.1016/j.cageo.2007.05.019
[63] SAMBRIDGE M. Geophysical inversion with a neighbourhood algorithm-I. Searching a parameter space[J]. Geophysical Journal International, 1999, 138(2): 479−494. doi: 10.1046/j.1365-246X.1999.00876.x
[64] SONG X H, TANG L, LV X C, et al. Shuffled complex evolution approach for effective and efficient surface wave analysis[J]. Computational Geosciences, 2012, 42: 7−17.
[65] SONG X H, TANG L, LV X C, et al. Application of particle swarm optimization to interpret Rayleigh wave dispersion curves[J]. Journal of Applied Geophysics, 2012, (84): 1−13.
[66] SONG X H, LI L, ZHANG X Q, et al. An implementation of differential search algorithm (DSA) for inversion of surface wave data[J]. Journal of Applied Geophysics, 2014, 111: 334−345. doi: 10.1016/j.jappgeo.2014.10.017
[67] SONG X H, LI L, ZHANG X Q, et al. Differential evolution algorithm for nonlinear inversion of high-frequency Rayleigh wave dispersion curves[J]. Journal of Applied Geophysics, 2014, 109: 47−61. doi: 10.1016/j.jappgeo.2014.07.014
[68] SONG X H, GU H M, TANG L, et al. Application of artificial bee colony algorithm on surface wave data[J]. Computational Geosciences, 2015, 83: 219−230.
[69] SONG X H, TANG L, ZHAO S T, et al. Grey wolf optimizer for parameter estimation in surface waves[J]. Soil Dynamics and Earthquake Engineering, 2015, 75: 147−157.
[70] LU Y X, PENG S P, DU W F, et al. Rayleigh wave inversion using heat-bath simulated annealing algorithm[J]. Journal of Applied Geophysics, 2016, 134: 267−280. doi: 10.1016/j.jappgeo.2016.09.008
[71] SAIFUDDIN, YAMANAKA H, CHIMOTO K. Variability of shallow soil amplification from surface-wave inversion using the Markov-chain Monte Carlo method[J]. Soil Dynamics and Earthquake Engineering, 2018, 107: 141−151.
[72] MIRJALILI S. SCA: A sine cosine algorithm for solving optimization problems[J]. Knowledge-Based Systems, 2016, 96(0): 120−133.
[73] 高旭, 于静, 李学良, 等. 自适应权重蜻蜓算法及其在瑞雷波频散曲线反演中的应用[J]. 石油地球物理勘探, 2021,56(4): 745−757, 671-672. GAO X, YU J, LI X L, et al. Adaptive weighted Dragonfly algorithm and its application in Rayleigh wave dispersion curve inversion[J]. Petroleum geophysical exploration, 2021, 56(4): 745−757, 671-672. (in Chinese).
[74] FARAMARZI A, HEIDARINEJAD M, MIRJALILI S, et al. Marine Predators Algorithm: A nature-inspired metaheuristic[J]. Expert Systems with Applications, 2020, 152: 113377. doi: 10.1016/j.eswa.2020.113377
[75] 于涵, 刘财, 王典, 等. 基于改进海洋捕食者优化算法和瑞雷波频散曲线的近地表地层参数反演[J]. 地球物理学报, 2023,66(2): 796−809. YU H, LIU C, WANG D, et al. Inversion of near-surface formation parameters based on improved marine predator optimization algorithm and Rayleigh wave dispersion curve[J]. Chinese Journal of Geophysics, 2023, 66(2): 796−809. (in Chinese).
[76] MATASSONI L, FIASCHI A. Assessment of seismic ground motion amplification and liquefaction at a volcanic area characterized by residual soils[J]. Journal of Mountain Science, 2020, 17(3): 740−752. doi: 10.1007/s11629-019-5753-8
[77] OBERMANN A, PLANES T, LAROSE E, et al. Imaging preeruptive and coeruptive structural and mechanical changes of a volcano with ambient seismic noise[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(12): 6285−6294. doi: 10.1002/2013JB010399
[78] BENNINGTON N, HANEY M, THURBER C, et al. Inferring magma dynamics at Veniaminof Volcano via application of ambient noise[J]. Geophysical Research Letters, 2018, 45(21): 11.
[79] MELE M, BERSEZIO R, BINI A, et al. Subsurface profiling of buried valleys in central alps (northern Italy) using HVSR single-station passive seismic[J]. Journal of Applied Geophysics, 2021, 193: 104407. doi: 10.1016/j.jappgeo.2021.104407
[80] KANG S Y, KIM K H. Bedrock depth variations and their applications to identify Blind faults in the Pohang area using the horizontal-to-vertical spectral ratio (HVSR)[J]. Journal of the Korean earth science society, 2022, 43(1): 188−198. doi: 10.5467/JKESS.2022.43.1.188
[81] SGATTONI G, CASTELLARO S. Detecting 1-D and 2-D ground resonances with a single-station approach[J]. Geophysical Journal International, 2020, 223(1): 471−487. doi: 10.1093/gji/ggaa325
[82] MANZO R, NARDONE L, GAUDIOSI G, et al. A first 3-D shear wave velocity model of the Ischia Island (Italy) by HVSR inversion[J]. Geophysical Journal International, 2022, 230(3): 2056−2072. doi: 10.1093/gji/ggac157
[83] 叶咸, 余相贵, 李果, 等. 瞬态瑞雷面波勘探技术在公路边坡注浆加固效果检测中的应用[J]. 公路交通科技(应用技术版), 2016,(2): 89−91, 94. YE X, YU X G, LI G, et al. Application of transient Rayleigh surface wave exploration technology in Detection of reinforcement effect of highway slope grouting[J]. Highway Traffic Technology (Applied Technology Edition), 2016, (2): 89−91, 94. (in Chinese).
[84] 徐佩芬, 李传金, 凌甦群, 等. 利用微动勘察方法探测煤矿陷落柱[J]. 地球物理学报, 2009,52(7): 1923−1930. doi: 10.3969/j.issn.0001-5733.2009.07.028 XU P F, LI C J, LING S Q, et al. Detection of collapse column in coal mine by microdynamic prospecting method[J]. Chinese Journal of Geophysics, 2009, 52(7): 1923−1930. (in Chinese). doi: 10.3969/j.issn.0001-5733.2009.07.028
[85] 刘艳秋, 徐洪苗, 王小勇, 等. 面波勘探在工程勘察中的应用[J]. 安徽地质, 2019,29(1): 40−44. doi: 10.3969/j.issn.1005-6157.2019.01.008 LIU Y Q, XU H M, WANG X Y, et al. Application of surface wave exploration in engineering investigation[J]. Anhui Geology, 2019, 29(1): 40−44. (in Chinese). doi: 10.3969/j.issn.1005-6157.2019.01.008
[86] 吴曲波, 潘自强, 陈金勇, 等. 利用瞬态瑞雷面波法探测浅层玄武岩三维分布−以沙特Sabkhah Ad Dumathah地区为例[J]. 地球物理学进展, 2019,34(5): 1938−1944. doi: 10.6038/pg2019CC0401 WU Q B, PAN Z Q, CHEN J Y, et al. Detection of three-dimensional distribution of shallow basalts by transient Rayleigh surface wave method: A case study of Sabkhah Ad Dumathah area, Saudi Arabia[J]. Progress in Geophysics, 2019, 34(5): 1938−1944. (in Chinese). doi: 10.6038/pg2019CC0401
[87] 周荣亮, 刘彦华, 徐睿知. 多道瞬态面波在LNG罐区地基勘察中的应用[J]. 工程地球物理学报, 2022,19(2): 162−167. doi: 10.3969/j.issn.1672-7940.2022.02.005 ZHOU R L, LIU Y H, XU R Z. Application of multi-channel transient surface waves in the ground investigation of LNG tank area[J]. Chinese Journal of Engineering Geophysics, 2022, 19(2): 162−167. (in Chinese). doi: 10.3969/j.issn.1672-7940.2022.02.005
[88] 李圣林, 胡泽安, 吴海波. 瞬态瑞雷面波勘探中隐伏溶洞的响应特征研究[J]. 物探化探计算技术, 2019,41(4): 541−546. doi: 10.3969/j.issn.1001-1749.2019.04.15 LI S L, HU Z A, WU H B. Study on response characteristics of a hidden cave in transient Rayleigh surface wave exploration[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2019, 41(4): 541−546. (in Chinese). doi: 10.3969/j.issn.1001-1749.2019.04.15
[89] 熊友亮, 高建华, 彭军. 天然源面波法在堰塞体上的研究及应用[J]. 工程地球物理学报, 2022,19(2): 149−154. XIONG Y L, GAO J H, PENG J. Research and application of natural source surface wave method on barrier body[J]. Chinese Journal of Engineering Geophysics, 2022, 19(2): 149−154. (in Chinese).
[90] RUDENKO D, SHARIF M, JUBRAN R, et al. Use of surface wave testing to develop pile driving vibration criteria in a coastal environment[C]//GSP 334·Geo-Congress 2022, 2022.
[91] IVANOV J, LEITNER B, SHEFCHIK W, et al. Evaluating hazards at salt cavern sites using multichannel analysis of surface waves[J]. The Leading Edge, 2013, 32(3): 298−305. doi: 10.1190/tle32030298.1
[92] LEWIŃSKA P, MATUŁA R, DYCZKO A. Integration of thermal digital 3D model and a MASW (Multichannel Analysis of Surface Wave) as a means of improving monitoring of spoil tip stability[J]. Seminary on Geomatics, Civil and Environmental Engineering (2017BGC) E3S Web of Conferences, 2018, 26: 8.
[93] KNAPMEYER-ENDRUN B, GOLOMBEK M P, OHRNBERGER M. Rayleigh wave ellipticity modeling and inversion for shallow structure at the proposed insight landing site in elysium planitia, Mars[J]. Space Science Reviews, 2017, 211(1/4): 339−382. doi: 10.1007/s11214-016-0300-1
[94] MAHVELATI S, COE J T. Horizontal-to-vertical spectral ratio (HVSR) analysis of the Martian Passive seismic data from the Insight mission[J]. Earth and Space 2021: Space Exploration, Utilization, Engineering, and Construction in Extreme Environments, 2021: 108-115.
[95] LAROSE E, KHAN A, NAKAMURA Y, et al. Lunar subsurface investigated from correlation of seismic noise[J]. Geophys Res Lett, 2005, 32(16).
[96] LAROSE C S-S N E. Lunar noise correlation, imaging and monitoring[J]. Earthquake Science, 2010, 23(5): 519−530. doi: 10.1007/s11589-010-0750-6
[97] NISHITSUJI Y, ROWE C A, WAPENAAR K, et al. Reflection imaging of the Moon's interior using deep-moonquake seismic interferometry[J]. Journal of Geophysical Research E:Planets, 2016, 121(4): 695−713. doi: 10.1002/2015JE004975
[98] NISHITSUJI Y, RUIGROK E, DRAGANOV D. Azimuthal anisotropy of the megaregolith at the apollo 14 Landing Site[J]. Journal of Geophysical Research-Planets Section, 2020, 125(5): e2019JE006126.
[99] IKEDA T, MATSUOKA T, TSUJI T, et al. Characteristics of the horizontal component of Rayleigh waves in multimode analysis of surface waves[J]. Geophysics, 2015, 80(1): En1−En11.
[100] BUDI A P, GINTING R A, SUNARDI B, et al. Combination of passive seismic (HVSR) and active seismic (MASW) methods to obtain shear wave velocity model of subsurface in Majalengka[J]. Journal of Physics: Conference Series, 2021, 1805(1): 012002. doi: 10.1088/1742-6596/1805/1/012002
[101] ABDIALIM S, HAKIMOV F, KIM J, et al. Seismic site classification from HVSR data using the Rayleigh wave ellipticity inversion: A case study in Singapore[J]. Earthquakes and Structures, 2021, 21(3): 231−238.
[102] 李巧灵, 张辉, 雷晓东, 等. 综合利用多道瞬态面波和微动探测分析斜坡内部结构[J]. 物探与化探, 2022,46(1): 258−267. LI Q L, ZHANG H, LEI X D, et al. Analysis of slope internal structure by multi-channel transient surface wave and fretting detection[J]. Geophysical and Geochemical Exploration, 2022, 46(1): 258−267. (in Chinese).
[103] 刘道涵, 徐俊杰, 刘磊, 等. 地球物理联合探测在识别岩溶地面塌陷精细结构中的应用−以武汉市为例[J]. 地质与勘探, 2022,58(4): 865−874. LIU D H, XU J J, LIU L, et al. Application of geophysical joint detection in identifying fine structure of Karst ground collapse: A case study of Wuhan city[J]. Geology and exploration, 2022, 58(4): 865−874. (in Chinese).
[104] 徐吉祥, 张晓亮, 李潇, 等. 地表浅部地震勘探方法在城市隐伏活动断裂调查中的应用[J]. 城市地质, 2022,17(1): 79−84. doi: 10.3969/j.issn.1007-1903.2022.01.012 XU J X, ZHANG X L, LI X, et al. Application of shallow surface seismic exploration method in urban hidden active fault investigation[J]. Urban Geology, 2022, 17(1): 79−84. (in Chinese). doi: 10.3969/j.issn.1007-1903.2022.01.012
[105] PERTON M, SPICA Z J, CLAYTON R W, et al. Shear wave structure of a transect of the Los Angeles basin from multimode surface waves and H/V spectral ratio analysis[J]. Geophysical Journal International, 2020, 220(1): 415−427. doi: 10.1093/gji/ggz458
[106] LONTSI A M, GARCIA-JEREZ A, MOLINA-VILLEGAS J C, et al. A generalized theory for full microtremor horizontal-to-vertical
$[H/V(z,f)] $ spectral ratio interpretation in offshore and onshore environments[J]. Geophysical Journal International, 2019, 218(2): 1276−1297. doi: 10.1093/gji/ggz223 -
期刊类型引用(2)
1. 刘丽丛，赵超，汪精华，陈浩辉，马晗宇，肖志伟，王卫星，张俊彬，崔凯鹏. 高密度电法和微动探测技术在某垃圾填埋场渗漏探测中的应用. 工程地球物理学报. 2024(06): 983-995 . 
百度学术
2. 琚铭善，郑鑫，解恒燕，汪金磊. VD-CMA算法反演瑞利波频散曲线的适用性研究. 黑龙江工业学院学报(综合版). 2024(11): 117-122 . 百度学术
其他类型引用(3)
下载:
计量
- 文章访问数: 552
- HTML全文浏览量: 260
- PDF下载量: 152
- 被引次数: 5
