Study on Forward Numerical Simulation and Instantaneous Seismic Attributes of Natural Gas Hydrate in Permafrost Area
-
摘要:
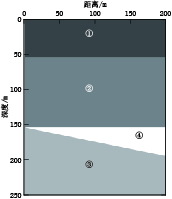
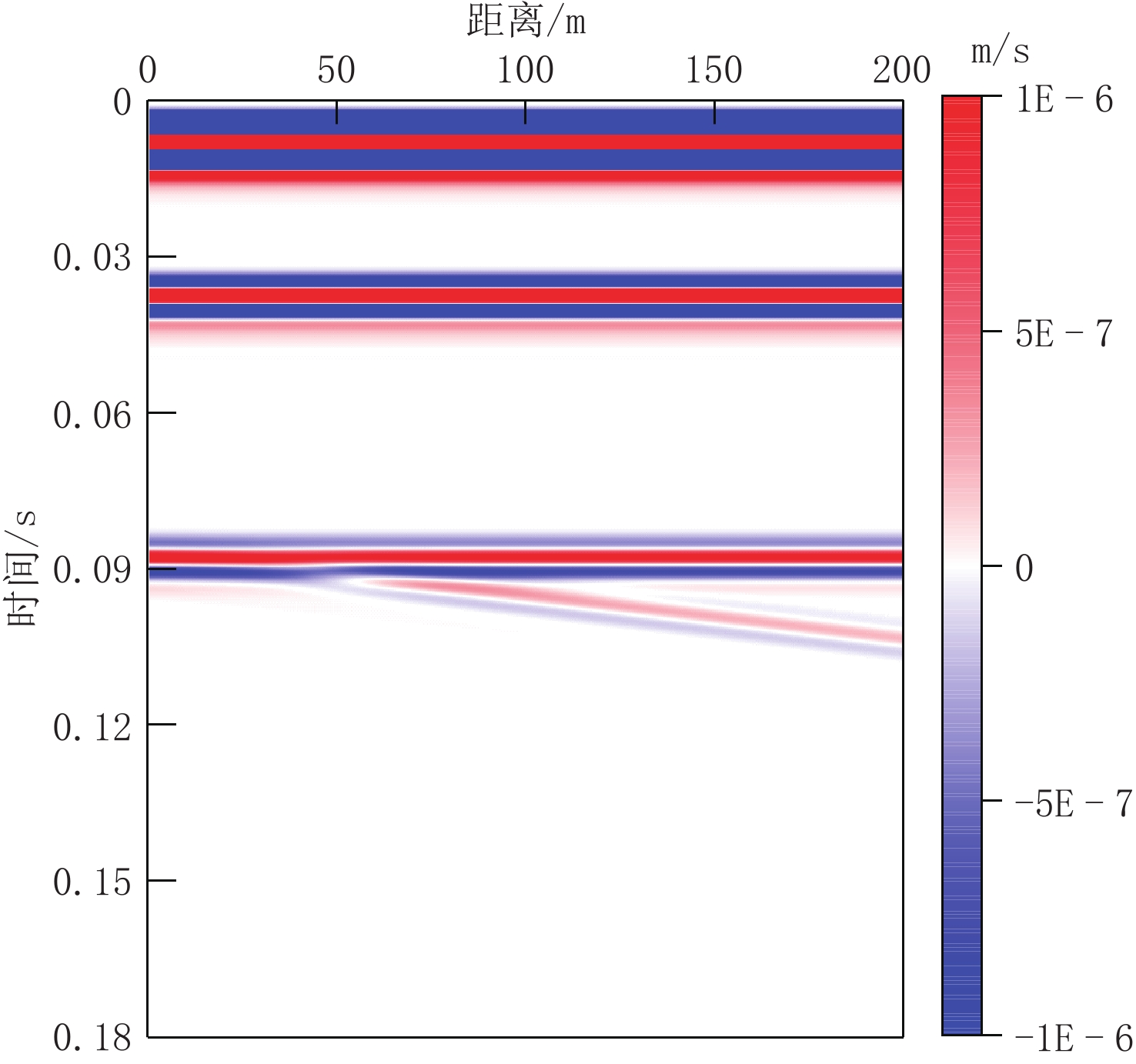
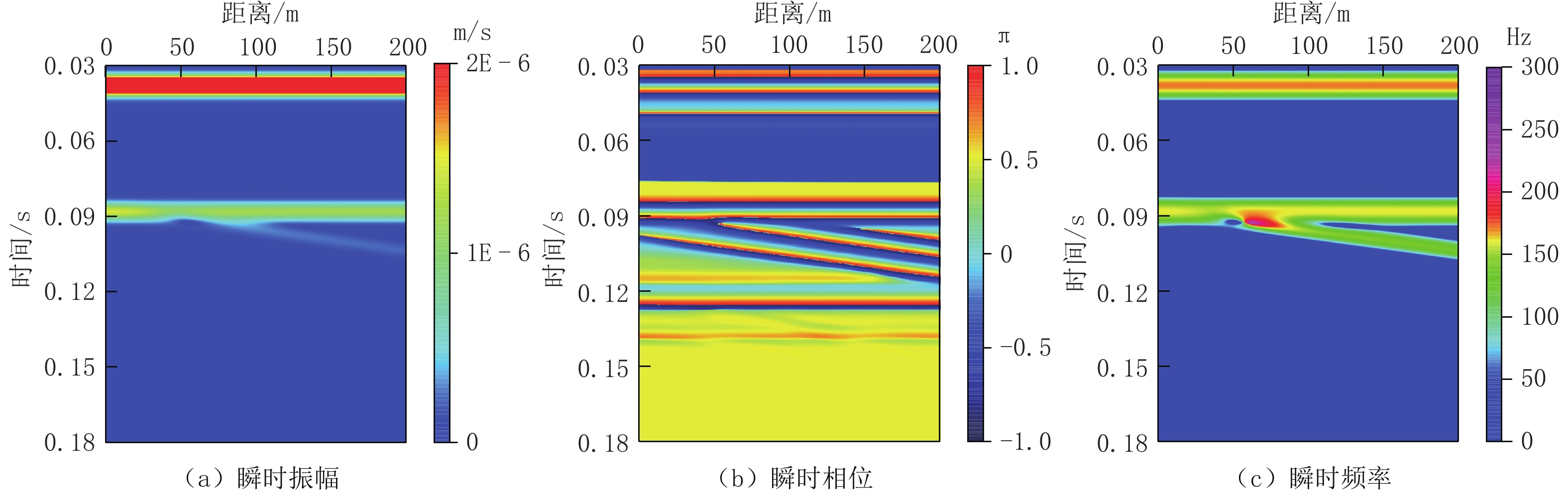
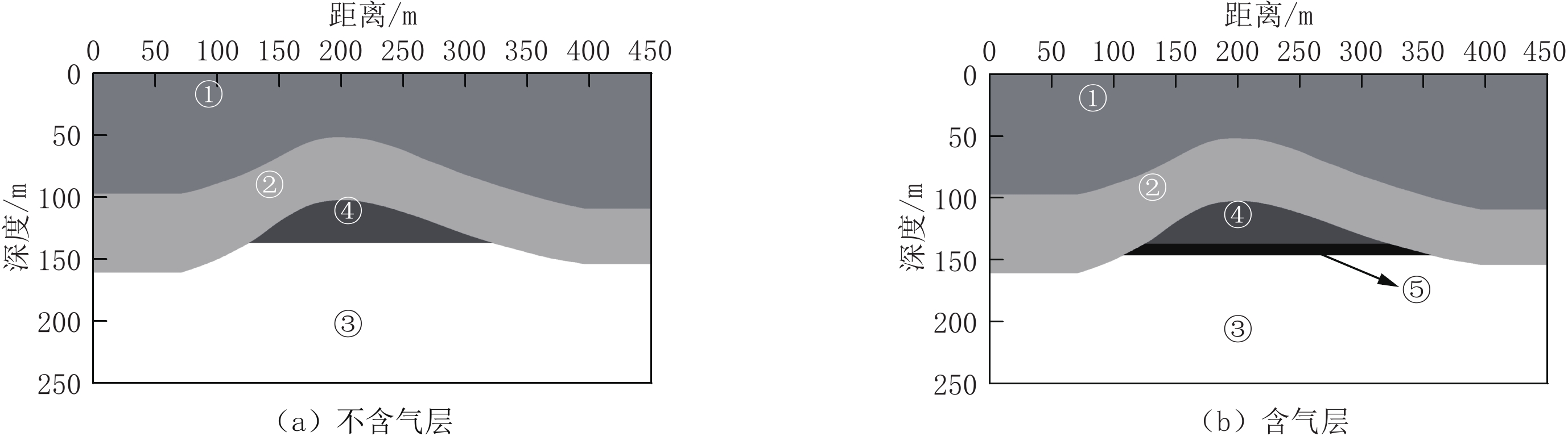
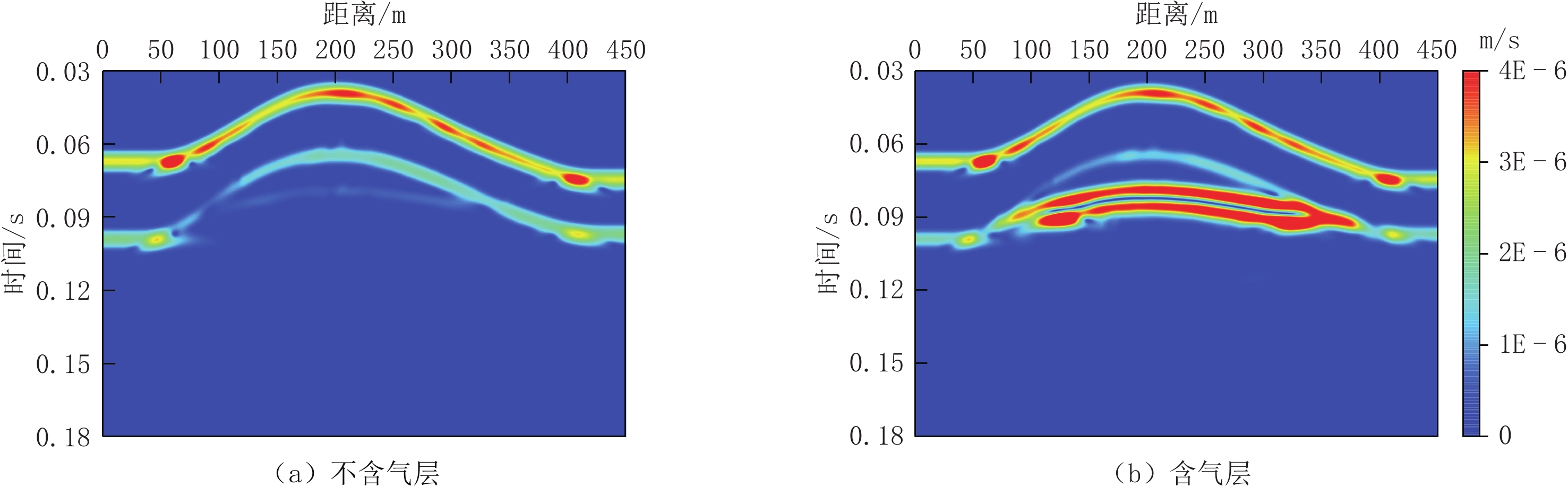
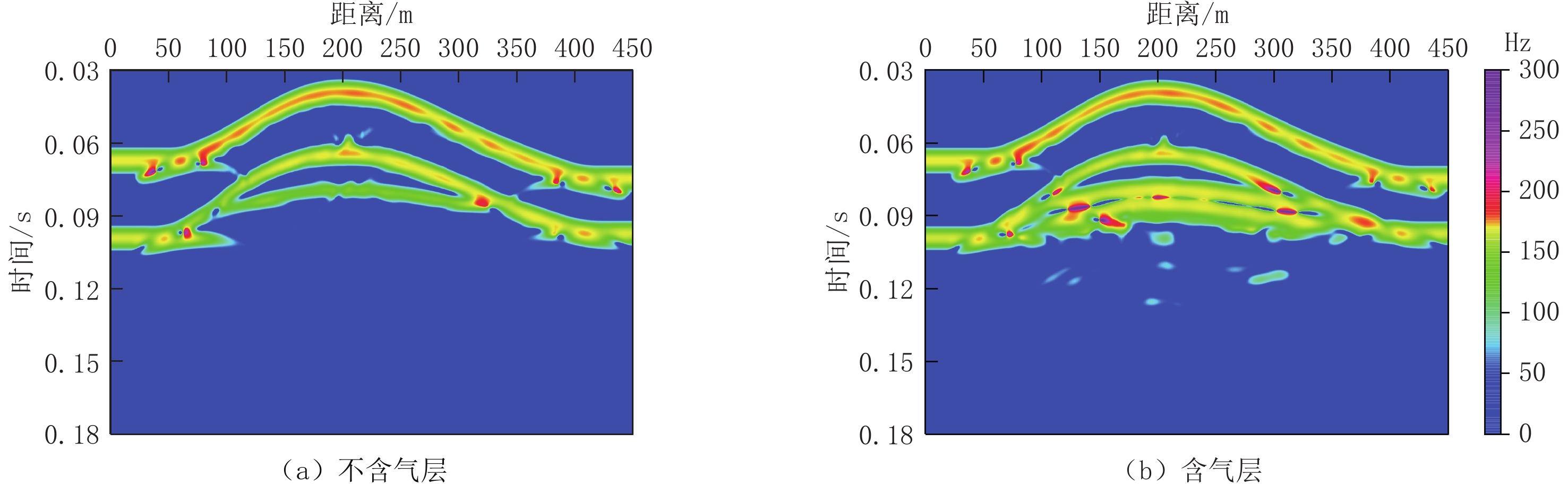
天然气水合物是一种具有巨大潜能的新型能源,研究冻土区天然气水合物的地震响应特征,对我国陆域天然气水合物的勘探和开发具有重要意义。本文运用Kelvin粘弹性介质模型,基于祁连山冻土区的实际地质地层条件,建立理论地质-地球物理模型;采用交错网格有限差分法进行正演数值模拟,并对自激自收地震记录进行波场特征分析和提取瞬时地震属性。研究结果表明:地震波通过天然气水合物地层时,反射振幅能量较弱;在瞬时频率属性剖面可分辨层厚的范围内,瞬时频率随着层厚增加,频率在小幅度衰减;地震波通过含天然气地层时,反射波表现为强反射特征,瞬时频率能量明显增大;瞬时地震属性对波阻抗界面有更好的分辨能力,特别是瞬时相位属性剖面,作用明显。因此,综合分析波场特征与瞬时属性特征可以为陆域天然气水合物的识别、预测提供依据。
Abstract:Natural gas hydrate is a new energy source with great potential. Studying the seismic response characteristics of natural gas hydrate in permafrost area is crucial to the exploration and development of natural gas hydrate in China's land area. Based on the Kelvin viscoelastic media model, our work establishes a theoretical geological-geophysical model based on the actual geological and stratigraphic conditions of the Qilian Mountain permafrost, uses the staggered-grid finite difference method to perform forward numerical simulation, and performs wave field characteristic analysis and instantaneous seismic attribute extraction of self-excitation and self-receiving seismic records. The results show that the reflected amplitude energy is weaker when the seismic wave passes through the gas hydrate formation. In the range where the instantaneous frequency attribute profile can distinguish the layer thickness, the instantaneous frequency decreases marginally with the increase of the layer thickness. When seismic waves pass through natural gas-bearing formations, the reflected waves show strong reflection characteristics, and the instantaneous frequency energy increases. The instantaneous seismic attribute has better resolution for the wave-impedance interface, especially the instantaneous phase attribute profile. Therefore, the comprehensive analysis of the instantaneous attribute characteristics can provide a basis for the identification and prediction of terrestrial gas hydrates.
-
如何在满足诊断需求的情况下减小辐射剂量是CT技术发展的永恒主题。重建迭代(iterative reconstruction,IR)算法与传统的滤波反投影(filtered back-projection,FBP)算法的封闭式解决方案不同,通过匹配预设重建模型辅以渐进式迭代的方式,可以在相同剂量水平下减小图像噪声,改善图像质量,进而为剂量的进一步降低提供可能[1]。不同临床研究表明,IR算法的确有助于减小辐射剂量[2-6]。然而,IR算法有原理上的缺陷,首先,预设重建模型需要同时考虑到物理、统计、图像特性、工程特性以及患者等因素往往较为复杂,优化过程高度依赖专家经验;其次,非线形及非静止性的算法特性使得重建后的图像空间分辨率依靠于对比度和噪声;再者,IR算法会造成噪声纹理的改变,这就使得IR的图像看起来过于平滑或呈“塑料样”改变,造成视觉上的不自然[7-10]。
以深度学习为代表的人工智能目前广泛应用在医学图像领域。最近,在FBP算法的基础上开发的TrueFidelity™(TFI)深度学习重建算法被用来区分信号和噪声,以期可以解决常规IR算法的痛点。TFI算法使用卷积神经网络并行运算,在FBP的基础上,通过不断反馈优化匹配原始图像;这样,TFI在不改变图像纹理的基础上,实现低剂量、低噪声的重建图像[11]。
目前,比较IR算法和该深度学习算法对图像质量影响的研究较少,且都集中在低剂量领域[11-12]。本研究拟在体模的基础上,比较高剂量下混合IR算法——自适应统计迭代重建算法V(the adaptive statistical iterative reconstruction-V,ASIR-V,以下简称AV)与TFI算法对于图像质量的差异。
1. 资料与方法
1.1 体模
采用美国放射学会(American College of Radiology,ACR)质量控制(quality assurance,QA)体模Gammex 464作为扫描对象(图1)。该模直径20 cm,长16 cm,共包括4个模块(module)。
Module 1可以用来检测定位、机器校准、CT值准确性和层厚,嵌入5种物质,包括固态水(0 HU),聚乙烯(Polyethylene,-95 HU),骨(Bone,950 HU),空气(Air,-1000)和丙烯酸(Acrylic,120 HU)。Module 2主要用来检测机器的低对比度分辨率,分布有不同直径(2、3、4、5、6及25 mm),密度为6 HU(0.6% 对比浓度)的圆柱体。Module 3 用来检测CT值均匀性。Module 4用来测量机器的高对比度(即空间)分辨率,其包括4、5、6、7、8、9、10和12共8组线对(line pair)每厘米(lp/cm)。
1.2 扫描方法
通过GE Revolution Apex对ACR Gammex 464体模进行扫描。扫描参数:管电压120 kVp,管电流215 mA,扫描剂量20 mGy,重建层厚0.625 mm,旋转时间0.7 s,准直0.625×40 mm,螺距0.516,矩阵512×512,FOV 30 cm,采用标准重建KernelSTANDARD。
重建AV 30%,60%,90%(分别为A~C组)和深度学习重建算法TFI下low、medium和high(DL,DM,DH,分别为D-F组)3种图像优化算法。
1.3 图像分析
在GE Advantage Workstation工作站(version 4.4)上测量Gammex 464体模module 1~4的5种物质CT值准确性、低对比度分辨率、CT值均匀性和高对比度分辨率。CT值准确性的测量在module中心3个连续层面进行,选取面积为100 mm2的圆形ROI,记录各物质各层面下的平均CT值。低对比度分辨率的测量在module 2上进行,即记录0.6% 对比度下的最小孔径。均匀性的测量是在module 3的中心及3、6、9、12点方向分别放置面积为288 mm2的正方形ROI,记录各ROI下的SD值,与中心层面SD相差最大的边缘SD的差值即为该组图像的均匀性。
调整各组图像module 4的窗宽窗位,记录0.6% 浓度下可分辨的最小一组线对。高/低对比度分辨率的测量有两名在放射诊断领域5年(A)和7年(B)的医生完成,如两人有异议则由另一名高年资放射诊断医生(C,工作10年)作最终评判。CT值准确性和均匀性的测量由A独自完成。
1.4 统计方法
两名放射科医生对于高/低对比度分辨率的一致性采用Kappa检验。各物质CT值准确性的组间和组内比较采用单因素方差分析;组内的P值采用 FDR校正,设P<0.05差异具有统计学意义。
2. 结果
2.1 高/低对比度分辨率
各组图像的高/低对比度分辨率皆一致(高对比度分辨率:10 lp/cm;低对比度分辨率:6 mm)。两名放射科医生高/低对比度分辨率的Kappa一致性良好,分别为1和0.89,差异均具有统计学意义。
2.2 CT值准确性
对于聚乙烯,B组和D组均值(即AV 60% 和TFI DL)与理论值(95 HU)一致;但各组间差异不具有统计学意义,AV组(A~C组)及TFI组(D~F组)组内之间也无显著差异。各组图像对骨组织的测量相近(881.7~881.9),偏向于低估其CT值,与真实CT值误差为7.2%,各组图像组间及两种算法组内均无显著差异。
各组图像对空气和丙烯酸的测量亦比较接近(空气:-994.1~-994.4;丙烯酸:121.1~121.6),与真实值的0.6%与0.9%~1.3%左右;各组图像对两种物质的测量无显著差异;两种物质的各组图像之间均无显著差异。TFI相较AV对固态水的测量更准确,两者偏向于低估CT值(TFI:-1.7~-1.9;AV:-2.1~-2.2),各组图像之间及两种算法组内的测量差异不具有统计学意义(表1)。
表 1 各组图像5种物质CT值与图像均匀性测量结果Table 1. The measurment results of CT values of the five materials and image uniformnity物质/指标 A组(AV 30%) B组(AV 60%) C组(AV 90%) D组(TFI DL) E组(TFI DM) F组(TFI DH) P 聚乙烯 -94.9±0.3 -95.0±0.3 -94.9±0.3 -95.0±0.4 -94.9±0.3 -94.9±0.3 0.994 骨 881.8±0.7 881.8±0.6 881.7±0.6 881.9±0.7 881.9±0.7 881.8±0.8 0.999 空气 -994.1±0.8 -994.3±0.7 -994.3±0.6 -994.3±0.7 -994.3±0.6 -994.4±0.5 0.996 丙烯酸 121.5±0.8 121.6±0.4 121.6±0.4 121.1±0.7 121.1±0.5 121.1±0.4 0.640 固态水 -2.1±1.0 -2.0±1.0 -2.2±1.2 -1.9±0.7 -1.7±0.6 -1.7±0.7 0.979 均匀性 4.0 3.7 2.9 3.8 3.3 2.7 注:聚乙烯、骨、空气、丙烯酸和固态水的理论值分别为 -95、950、-1000 、120和0 HU,图像均匀性的单位是HU。 2.3 均匀性
同等级条件下,TFI算法相较AV算法的图像均匀性更佳,且随着等级的提升,其图像越均匀;6组图像中,TFI DH的图像最均匀(2.7 HU,表1)。
3. 讨论
FBP算法以其稳定和快速的特点被广泛应用于临床。在理想情况下,FBP可以在原始数据的情况下重建精准“副本”图像;但是,受软硬件及临床复杂情况等的影响,FBP重建的CT图像易被噪声、伪影和低对比度下的检出能力所影响,导致其为了满足诊断需求需要维持在一个较高的剂量水平。而开发的IR算法虽然在一定程度上可以降低噪声、保证图像质量,但其非线性的重建特点导致图像有一定的平滑和不自然,进而影响放射科医生的诊断。在这种情况下,TFI算法依赖于深度学习卷积神经网络强劲的计算能力,以FBP算法为基础,在不影响解剖和病理结构的情况下,还可以抑制图像噪声。
近期研究表明,TFI与IR算法相比,可以在不改变图像噪声纹理的基础上,进一步降低图像噪声,使其成为剂量优化的一种技术进步方案[11]。同时,临床研究也表明,TFI算法可以提高病灶的检出能力[12]。
本研究使用体模对比3种混合IR算法等级与深度学习3种等级下重建图像之间的差异。以往的研究发现,低剂量水平下,TFI的空间分辨率相较AV算法更高[13-15]。本研究证明,在高剂量水平下,两种算法6组图像的高/低对比度分辨率无区别;暗示剂量在图像质量中的显著作用。同时,本研究发现,3种TFI等级的均匀性均高于同水平下IR算法的图像均匀性,暗示其图像噪声更小,这与既往的研究相一致[11,13-17]。因此,在高剂量水平下,TFI算法可以在保持图像空间分辨率的基础上,改善图像噪声。
CT值准确性是衡量图像质量、影响诊断结果的另一个重要参数。在高剂量水平下,两种图像重建算法对于5种物质的CT值测量方面无明显差异。其中,两种算法均对聚乙烯(模拟脂肪组织)、空气以及丙烯酸(模拟增强组织)的CT值均有较准确的测量,且均处于轻度高估状态。对于骨组织和固态水,两种算法有一定的低估倾向,其中TFI算法对固态水的估计较AV算法更接近理论值。在CT值准确性方面,两种算法的表现比较接近。
本研究尚存在的不足:①本研究仅比较单一高剂量下两种图像重建算法的表现,在此过程中剂量因素可能占据主导地位,会进一步弱化两者图像质量之间的区别;②本研究仅是体模研究,其临床实用性尚需进一步验证;③本研究使用的是常规 CT图像,两种算法对于双能CT图像(如虚拟平扫、虚拟单能图像及碘图等)的影响尚需进一步探索。
总之,深度学习重建算法可以在保持图像空间分辨率的情况下,改善图像噪声;两种算法对各物质CT值的准确性方面的表现相当。
-
表 1 祁连山DK-1、DK-3和DK-4三个井孔含水合物和不含水合物层段速度和密度[18]
Table 1 Velocities and densities of the hydrate segments and segments without hydrate in the holes of DK-1, DK-3, and DK-4
井孔 深度h/m 岩性 平均纵波速度VP/(m/s) 平均密度ρ/(g/cm3) 含水合物段 不含水合物段 含水合物 不含水合物 含水合物 不含水合物 DK-1 133.90~134.86 92.05~94.75 细砂岩 4728 4204 2.34 2.53 143.35~144.30 49.20~69.70 细砂岩 4676 4171 2.38 2.57 DK-3 139.05~154.45 195.05~196.95 泥岩 2996 2867 2.32 2.43 DK-4 134.40~131.70 151.50~152.45 泥岩 4071 2822 2.25 2.31 165.75~167.25 112.45~115.35 粉砂岩 3823 3356 2.22 2.36 表 2 楔状地质-地球物理模型参数表
Table 2 The parameters of wedge-shaped geological-geophysical model
模型编号 VP/(m/s) VS/(m/s) ρ/(g/cm3) QP QS 层厚/m 冻土层① 3250 1950 2.31 187.2 139.5 54 稳定沉积物② 4000 2000 2.37 295.6 153.0 100 稳定沉积物③ 4450 2130 2.55 373.7 214.8 - 天然气水合物④ 4750 2330 2.29 431.4 373.7 0~40 -
[1] SLOAN JR E D, KOH C A. Clathrate hydrates of natural gases[M]. CRC press, 2007.
[2] KVENVOLDEN K A. Potential effects of gas hydrate on human welfare[J]. Proceedings of the National Academy of Sciences, 1999, 96(7): 3420−3426. doi: 10.1073/pnas.96.7.3420
[3] MAKOGON Y F. Natural gas hydrates: A promising source of energy[J]. Journal of Natural Gas Science and Engineering, 2010, 2(1): 49−59. doi: 10.1016/j.jngse.2009.12.004
[4] 裴发根, 方慧, 杜炳锐, 等. 陆域冻土区天然气水合物勘探研究进展[J]. 物探化探计算技术, 2022,44(6): 751−763. doi: 10.3969/j.issn.1001-1749.2022.06. PEI F G, FANG H, DU B R, et al. Advances in exploration of natural gas hydrate in terrestrial permafrost areas of China[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2022, 44(6): 751−763. (in Chinese). doi: 10.3969/j.issn.1001-1749.2022.06.
[5] 黄朋, 潘桂棠, 王立全, 等. 青藏高原天然气水合物资源预测[J]. 地质通报, 2002,21(11): 794−798. HUANG P, PAN G T, WANG L Q, et al. Prospect evaluation of natural gas hydrate resources on the Qinghai-Tibeti plateau[J]. Geological Bulletin of China, 2002, 21(11): 794−798. (in Chinese).
[6] 刘怀山, 韩晓丽. 西藏羌塘盆地天然气水合物地球物理特征识别与预测[J]. 西北地质, 2004,37(4): 33−38. LIU H S, HAN X L. Geophysical recognition and prediction of natural gas hydrates in Qiangtang basin of Tibet[J]. Northwestern Geology, 2004, 37(4): 33−38. (in Chinese).
[7] 赵省民, 邓坚, 李锦平, 等. 漠河多年冻土区天然气水合物的形成条件及成藏潜力研究[J]. 地质学报, 2011,85(9): 1536−1550. ZHAO X M, DENG J, LI J P, et al. Gas hydrate formation and its accumulation potential in Mohe, permafrost area, China[J]. Acta Geologica Sinica, 2011, 85(9): 1536−1550. (in Chinese).
[8] 祝有海, 张永勤, 文怀军, 等. 青海祁连山冻土区发现天然气水合物[J]. 地质学报, 2009,83(11): 1762−1771. ZHU Y H, ZHANG Y Q, WEN H J, et al. Gas hydrates in the Qilian mountain permafrost, Qinghai, Northwest China[J]. Acta Geologica Sinica, 2009, 83(11): 1762−1771. (in Chinese).
[9] 方慧, 孙忠军, 徐明才, 等. 冻土区天然气水合物勘查技术研究主要进展与成果[J]. 物探与化探, 2017,41(6): 991−997. FANG H, SUN Z J, XU M C, et al. Main achievements of gas hydrate exploration technology in permafrost regions of China[J]. Geophysical and Geochemical Exploration, 2017, 41(6): 991−997. (in Chinese).
[10] 张旭东. 琼东南海域天然气水合物地震反射特征[J]. 物探与化探, 2014,38(6): 1152−1158. ZHANG X D. The seismic reflection characteristics of gas hydrate in southeast Hainan sea area of the South China Sea[J]. Geophysical and Geochemical Exploration, 2014, 38(6): 1152−1158. (in Chinese).
[11] LEE M W, COLLETT T S. In-situ gas hydrate hydrate saturation estimated from various well logs at the Mount Elbert Gas Hydrate Stratigraphic Test Well, Alaska North Slope[J]. Marine and Petroleum Geology, 2011, 28(2): 439−449. doi: 10.1016/j.marpetgeo.2009.06.007
[12] 韩建光, 于常青, 张晓波, 等. 陆域冻土区天然气水合物多波地震数值模拟研究[J]. 地质学报, 2016,90(9): 2502−2512. HAN J G, YU C Q, ZHANG X B, et al. Multiwave seismic numerical simulation study on terrestrial gas hydrate in permafrost area[J]. Acta Geologica Sinica, 2016, 90(9): 2502−2512. (in Chinese).
[13] 罗登贵, 刘江平, 金聪, 等. 活断层的地震响应特征与瞬时地震属性[J]. 地球科学, 2017,42(3): 462−470. LUO D G, LIU J P, JIN C, et al. Instantaneous seismic attributes and response characteristics of active faults[J]. Earth Science, 2017, 42(3): 462−470. (in Chinese).
[14] HASTINGS F D, SCHNEIDER J B, BROSCHAT S L. Application of the perfectly matched layer (PML) absorbing boundary condition to elastic wave propagation[J]. The Journal of the Acoustical Society of America, 1996, 100(5): 3061−3069. doi: 10.1121/1.417118
[15] 祝有海, 张永勤, 文怀军, 等. 祁连山冻土区天然气水合物及其基本特征[J]. 地球学报, 2010,31(1): 7−16, 130. ZHU Y H, ZHANG Y Q, WEN H J, et al. Gas hydrates in the Qilin mountin permafrost and their basic characteristics[J]. Acta Geoscientica Sinica, 2010, 31(1): 7−16, 130. (in Chinese).
[16] 徐明才, 刘建勋, 柴铭涛, 等. 青海木里地区天然气水合物反射地震试验研究[J]. 地质与勘探, 2012,48(6): 1180−1187. XU M C, LIU J X, CHAI M T, et al. An experimental study of natural gas hydrates in the muli region, Qinghai Province by the seismic reflection method[J]. Geology and Exploration, 2012, 48(6): 1180−1187. (in Chinese).
[17] 吕丽新, 陈永进, 张硕, 等. 冻土区天然气水合物基本特征及国内研究现状[J]. 资源与产业, 2012,14(5): 69−75. doi: 10.3969/j.issn.1673-2464.2012.05.013 LV L X, CHEN Y J, ZHANG S, et al. Characteristics and research advances of natural gas hydrate in permafrosts[J]. Resources and Industries, 2012, 14(5): 69−75. (in Chinese). doi: 10.3969/j.issn.1673-2464.2012.05.013
[18] 刘杰, 刘江平, 程飞, 等. 青藏高原冻土区天然气水合物地层的岩石物理分析[J]. 地球物理学进展, 2017,32(3): 1008−1018. LIU J, LIU J P, CHENG F, et al. Rock physics analysis of the hydrate bearing sediments in the permafrost region of Qinghai-Tibet plateau[J]. Progress in Geophysics, 2017, 32(3): 1008−1018. (in Chinese).
[19] ALTERMAN Z, KARAL JR F C. Propagation of elastic waves in layered media by finned difference methods[J]. Bulletin of Seismological Society of America, 1968, 58(1): 367−398.
[20] 奚先, 姚姚. 二维粘弹性随机介质中的波场特征分析[J]. 地球物理学进展, 2004,19(3): 608−615. XI X, YAO Y. The analysis of the wave field characteristics in 2D viscoelastic random medium[J]. Progress in Geophysics, 2004, 19(3): 608−615. (in Chinese).
[21] 李庆忠, 魏继东. 高密度地震采集中组合效应对高频截止频率的影响[J]. 石油地球物理勘探, 2007,42(4): 363−369. doi: 10.3321/j.issn:1000-7210.2007.04.002 LI Q Z, WEI J D. Influence of array effect on cutoff frequency of high frequency in high-density seismic acquisition[J]. Oil Geophysical Prospecting, 2007, 42(4): 363−369. (in Chinese). doi: 10.3321/j.issn:1000-7210.2007.04.002
[22] 狄帮让, 裴正林, 夏吉庄, 等. 薄互层油藏模型黏弹性波方程正演模拟研究[J]. 石油地球物理勘探, 2009,44(5): 622−629,527,650. doi: 10.3321/j.issn:1000-7210.2009.05.020 DI B R, PEI Z L, XIA J Z, et al. Forward simulation of viscoelastic wave equation in thin-interbedded reservoir model[J]. Oil Geophysical Prospecting, 2009, 44(5): 622−629,527,650. (in Chinese). doi: 10.3321/j.issn:1000-7210.2009.05.020
[23] TANER M T, KOEHLER F, SHERIFF R E. Complex seismic trace analysis[J]. Geophysics, 1979, 44(6): 1041−1063. doi: 10.1190/1.1440994
[24] 程乾生. 希尔伯特变换与信号的包络, 瞬时相位和瞬时频率[J]. 石油地球物理勘探, 1979,14(3): 1−14. [25] MATHENEY M P, NOWACK R L. Seismic attenuation values obtained from instantaneous-frequency matching and spectral ratios[J]. Geophysical Journal International, 1995, 123(1): 1−15. doi: 10.1111/j.1365-246X.1995.tb06658.x
-
期刊类型引用(2)
1. 綦维维,程瑾,陈楚韩,安备,刘晓怡,付玲,王屹. 低管电压联合深度学习图像重建算法在降低胸腹部联合增强CT辐射剂量的价值. CT理论与应用研究(中英文). 2025(03): 359-368 .  百度学术
百度学术
2. 叶雄鑫,刘元芬,汤博荣,陈依林,郑莞怡,薛莉薇,张孝勇. 深度学习图像重建和能谱成像在低对比剂流速胸主动脉CTA中的价值. CT理论与应用研究. 2024(06): 683-691 .  本站查看
本站查看
其他类型引用(0)




 下载:
下载: