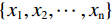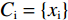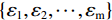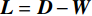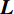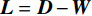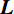Seismic Facies Analysis Based on Spectral Clustering with Waveform Characteristic Vector
-
摘要:
本文提出一种基于地震沉积学原理沿层提取地震波形特征向量，并以谱聚类（spectral clustering）分析进行地震相划分的方法。谱聚类能够处理非线性的数据结构和高维数据的聚类问题，但其相似度矩阵的构建和谱分解的计算较为复杂，需要较高的计算资源和时间成本。为提高谱聚类算法的效率和可扩展性，本文提出将Mini-batch K-means算法与谱聚类算法结合起来的MKSC算法，在提高谱聚类算法精度的同时大大降低谱聚类空间的复杂度。经过对数值模拟、地球物理模型数据和实际地震资料的处理分析，证明该方法在沉积相划分、沉积相特征识别方面的效果明显，是一种具有良好应用前景的新型沉积特征分析工具。
Abstract:Based on the principle of seismic sedimentology, the feature vectors of seismic waveforms are extracted along stratum slices, and spectral clustering analysis is introduced to classify seismic facies. Spectral clustering is an unsupervised machine learning algorithm. Its essence is to simplify the expression of high-dimensional seismic data in the form of feature vectors, which belongs to the process of dimensionality reduction. Considering the traces with specific time windows in the seismic work area as nodes of the graph and the similarity between traces as the weight of the edges, a graph model can be constructed. Spectral clustering must determine the best segmentation method to complete the segmentation of the graph, so that different types of sedimentary characteristics can be distinguished. Physical model and actual data processing and analysis demonstrate that this method is capable of dividing sedimentary facies characteristics and is a new kind of facies analysis tool for reservoir classification, which has good application prospects.
-
地震沉积学是研究地震波在地下沉积物中传播和反射的规律，以及地震波记录中的地质信息的学科，是地震勘探中的一个重要分支，通过地震波在地下沉积物中的传播和反射特征，揭示地下沉积物的物性和结构，描述沉积速率随平面位置的变化，为油气勘探和开发提供重要的地质信息支持。Zeng等[1-4]开展了地震沉积学在油气勘探和开发中的应用研究，探讨了地震沉积学在预测油气藏分布和评价储层性质等方面的应用价值。
地震相划分是地震沉积学领域的一个重要研究方向，旨在通过对地震数据的分析和解释，划分出不同的地震相，从而揭示地层沉积环境和沉积体系演化的信息。随着地震勘探技术的不断发展和完善，地震相划分方法也不断更新和改进[5]。
近年来，随着机器学习技术的不断发展和应用，基于无监督机器学习的地震相划分方法逐渐成为研究热点。这些方法能够综合考虑地震波形的振幅、频率和相位信息，从而提高地震相划分的准确度和分辨能力。这些方法中，聚类分析是一种无监督学习的方法，它的目标是将一组数据分成若干个类别，使得同一类别内的数据相似度较高，不同类别之间的相似度较低。
聚类分析可以用于数据挖掘、图像分析、模式识别等领域。在聚类分析中，通常使用距离或相似度作为衡量数据间相似性的指标，常见的聚类算法包括K-means、层次聚类、DBSCAN等。在油气田勘探开发中，聚类分析是一种常用的方法，可以利用波形特征对储层进行预测和识别。刘爱群、白博、李辉和徐海等都利用聚类分析方法进行了研究[6-10]。然而，传统的聚类分析方法在实际应用中存在一些问题：①传统的聚类分析方法需要预先设定聚类的类别数目，这对于数据的分析和解释可能存在一定的主观性和不确定性；②对于噪声和异常值比较敏感，可能会导致聚类结果的不稳定性和不准确性；③无法处理非线性的数据结构和高维数据的聚类问题，这在实际应用中限制了其应用范围和效果。与传统聚类算法相比，谱聚类方法[11-12]具有聚类精度高、稳定性好的优势，应用非常广泛，却较少应用在地震信号处理中。
本文提出一种新的地震相划分方法，是基于无监督机器学习的波形特征向量谱聚类分析来划分地震相，主要思想是利用拉普拉斯矩阵的特征向量构成的方阵进行聚类，通过设计三维模型进行数据模拟验证该方法的有效性。文中展示谱聚类的工作流程，并使用scikit-learn工具箱作为地震相波形聚类的算法工具。该方法利用地震波形的特征向量进行谱聚类分析，将不同的波形分为不同的类别。与传统的地震相划分方法相比，该方法综合利用地震属性的振幅、相位和频率特征，因此能够更准确、更合理地描述地震相的空间分布。
1. 基本原理
1.1 谱聚类分析
谱聚类是一种基于图论的聚类算法，它通过将数据点之间的相似度计算出来，构建相似度矩阵，再对数据的相似度矩阵进行谱分解，将数据点分成若干个类别。谱聚类能够处理非线性的数据结构和高维数据的聚类问题，不需要预先设定聚类的类别数目，能够有效地处理噪声和异常值的影响，但是相似度矩阵的构建和谱分解的计算较为复杂，需要较高的计算资源和时间成本。聚类结果可能受到相似度矩阵的选择和参数的影响，对于数据分布不均匀或聚类数目较多的情况，谱聚类的效果可能不如其他聚类算法。
谱聚类的关键方法是将数据点通过相似度矩阵构建成一个无向图，然后通过对图的拉普拉斯矩阵进行谱分解，得到特征向量，并将其用于聚类分析。图由3个基本元素组成：节点、连接节点的边和边权重。如果图的每条边指定了方向，则称为有向图；如果边没有方向，则称为无向图。
如果将三维地震数据中的每一个采样点视为一个节点，两个节点之间有边和边权重，将所有三维地震数据组成的向量视为无向图，定义任意两点
$ {p}_{i},{p}_{j} $ 之间相似度权值为$ {s}_{ij} $ ，对于无向图中所有的节点，就构建起相似度矩阵S。通过MKSC将无向图进行切割，使得切割出的每一部分内相似度最大，各部分间相似度最小。目前，基于比例切图（ratio cuts）、最小化切图（minimum cuts）和归一化切图（normalized cuts）等不同的图划分标准形成了不同的谱聚类算法。由于图划分准则的求解最优解是一个非确定性多项式问题，通常需要将这类问题转换为谱分解问题，通过使用从谱分解中获得的特征向量来表达数据的低维结构来求解相似性矩阵，然后在低维空间中使用经典算法（如K-means）进行聚类[11]。本文中的算法是基于比例切图提出的，在比例分割切图中，需要最小化不同组之间的权重，同时最大限度地增加每组中的采样点数量。输入n个数据点的数据集
$ \boldsymbol{X}=\{{x}_{1}{,x}_{2},\cdots ,{x}_{n}\} $ ，建立其中两点相似度矩阵$ \boldsymbol{S}\in {R}_{n\times n} $ ，其高斯相似度定义如下：$$ {s}_{ij}=\left\{\begin{aligned} &\mathrm{exp}\left(-\frac{{\|{x}_{i}-{x}_{j}\|}^{2}}{2{\sigma }^{2}}\right),&i\ne j\\ &0, &i=j\end{aligned}\right. \text{，} $$ (1) 其中σ为尺度参数。设D为度矩阵，可使用如下公式计算度矩阵D：
$$ {d}_{i}=\sum _{j=1}^{n}{s}_{ij} 。 $$ (2) 度矩阵为对角矩阵，将S的每行元素相加得到度矩阵
$ n\times n $ 对角矩阵D。若记$ \boldsymbol{L}\in {R}^{n\times n} $ 为拉普拉斯矩阵：则：$$ {\boldsymbol{L}}={\boldsymbol{D}}-{\boldsymbol{S}} \text{，} $$ (3) 其中L是对称半正定矩阵。对拉普拉斯矩阵
${\boldsymbol{L}}$ 进行特征分解，各特征值为实数且非负，最小值为0，因此，可以将特征值按大小排列：$$ {\lambda }_{n}\ge {\lambda }_{n-1}\ge \cdots \ge {\lambda }_{1}\ge 0 。 $$ (4) 选择前k个特征值的特征向量形成n×k维特征向量矩阵，特征向量矩阵中每一行对应于数据集中的1个数据点，每一列对应于1个特征，特征向量中的每1个元素表示该数据点在该特征上的取值。通过K-means算法对特征向量矩阵进行聚类分析，可以将数据点分成k个类别。最后，通过特征向量作为指示向量，可以将每个数据点指派到相应的类别中。
图1中由样本点组成的拉普拉斯矩阵特征向量的数量为3，这意味着样本点由3个独立的部分组成，图1右侧表格显示：1、2、3、4、5属于一个部分，6、7、8属于一个部分，9、10、11、12、13属于另一部分。
![]()
图 1 无向图及其邻接矩阵特征向量Figure 1. Feature vectors of the undirected graph and its adjacency matrix1.2 小批量K均值-谱聚类
谱聚类能够处理非线性的数据结构和高维数据的聚类问题，但是相似度矩阵的构建和谱分解的计算较为复杂，需要较高的计算资源和时间成本。为解决谱聚类计算复杂的问题，本文提出Mini-batch K-means的谱聚类方法（MKSC），MKSC是一种随机梯度下降算法，它通过随机抽取小批量数据进行聚类计算，从而减少计算量和内存占用。MKSC方法可以先对数据进行Mini-batch K-means聚类，将其聚成很多类，从而得到相应类别数的聚类中心，再对其进行谱聚类处理，以该聚类中心作为相应类别的代表。将MKSC与谱聚类算法结合起来，可以在不影响聚类精度的同时大大降低谱聚类空间的复杂度[14]，提高谱聚类算法的效率和可扩展性。
如图2所示，图2（a）数据分布图中根据距圆点（0,0）的距离，由远到近分为绿、黑、白3种颜色，首先直接用谱聚类算法对图2（a）中的数据集进行聚类，得到图2（b）的聚类结果结果，其聚类结果和实际数据分布还是有一定差距的。为此，我们把聚类分析分为两步，首先应用MKSC分为30类，得到图2（c）的结果，在此基础上应用谱聚类，得到图2（d）的正确聚类结果。
![]()
图 2 相同数据集不同聚类方式分类结果Figure 2. Classification results of the same dataset by different clustering methods表1是不同聚类分析算法计算效率的比较，从表中可以看出，MKSC将数据集分为30类需要0.17 s，直接用谱聚类对数据集进行聚类需要0.21 s，但是聚类结果和真实数据分布相比存在一定的误差。应用MKSC算法，总体需要（0.17+0.09）s，但是聚类的结果和真实数据分布相比是一致的。由于聚类分析算法本身不是耗费大量机时的算法，因此在牺牲一些计算效率的基础上，获得更高精度的聚类分析结果，还是十分划算的。
表 1 不同聚类分析算法计算效率比较Table 1. Comparison of the computational efficiency of different clustering analysis algorithms算法类型 Mini-batch K-means Spectral clustering MKSC 计算时间/s 0.17 0.21 0.17+0.09 1.3 MKSC聚层次聚类流程
该算法沿地层切片提取地震波形特征向量构成样本集
$\left\{{{x}}_{1},{{x}}_{2},\cdots ,{{x}}_{\mathrm{n}}\right\}$ ，利用机器学习算法包Scikit-learn中的Standard Scalar函数对输入数据进行标准化，使其满足正态分布，采用Mini-batch K-means方法对标准化的地震波形特征向量进行粗聚类，聚成${{C}}_{\mathrm{i}}=\left\{{{x}}_{\mathrm{i}}\right\}$ 类，得到m个聚类中心点，记为$ \left\{{\mathrm{\varepsilon }}_{1},{\mathrm{\varepsilon }}_{2},\cdots {,\mathrm{\varepsilon }}_{\mathrm{m}}\right\} $ ，根据聚类中心点的相似度构建相似度矩阵W，大小为m×m，基于相似度矩阵W求度矩阵D，求取拉普拉斯矩阵${\boldsymbol{L}}={\boldsymbol{D}}-{\boldsymbol{W }}$ ，通过求解拉普拉斯矩阵${\boldsymbol{L}}$ 的特征值对应的特征向量，进行最终分类（K-means），求取拉普拉斯矩阵${\boldsymbol{L}}={\boldsymbol{D}}-{\boldsymbol{W}} $ ，通过求解拉普拉斯矩阵${\boldsymbol{L}}$ 的特征值对应的特征向量，进行最终分类（K-means），根据分类结果将MKSC得到的每个聚类中心对应的原始数据进行类别标记，形成地震相图。通过先粗聚类，再通过谱聚类方法进行细分的方法，可以有效地解决谱聚类算法在处理大型数据集合时计算时间和内存容量的问题，同时能够更准确地描述地震相的空间分布。
2. 实例应用
2.1 三维物理模型和地震相分析
三维地震物理模拟是研究地震反射特征问题的有效方法图3。为了建立一个与实际地质特征相符的三维地层模型，需要考虑地质上的合理性和真实沉积层序的地层复杂性。在假设地层界面和阻抗边界的情况下，可以生成一个理想化的三维模型并分析地层界面与地震反射特征之间的关系。本文中的物理模型的空间尺度为1︰10000，模拟的实际地质体体积为8000 m×6400 m×2200 m。在模型中，有5个细砂层，每层厚度约为5～15 m，各层砂体空间分布不同。图4展示了物理模型中砂体的空间分布情况。
![]()
图 3 物理模型的采集尺寸及参数示意图Figure 3. Schematic of the acquisition size and parameters of the physical model图5展示了通过地震正演技术和地震资料处理后得到的三维克希霍夫积分地震偏移数据体。由于物理模型中的砂体较薄且形状各异，因此需要通过地震切片技术研究各层砂体展布特征，这需要选择和拾取等时格架下的反射界面。图5中展示了4个地震同相轴的追踪结果，分别为T（红色）、T2（青色）、T3（粉色）和T4（绿色）。在追踪的两个参考层之间进行等比例划分小层，这些小层代表了地质层面或沉积单元，控制地震的反射特征。
图6是其中一条剖面，根据图5所示的4个参考层划分的地震沉积学单元层位及内幕小层。这些结果为研究地震数据的地质学特征提供了重要的参考。
![]()
图 6 物理模型偏移剖面及基于地震沉积学原理解释的层位Figure 6. Migration section of the physical model and horizon interpretation based on the seismic sedimentology principle传统的均方根振幅属性切片缺少频率和相位信息且易受噪声影响。相比之下，本文提出的无监督机器学习地震波MKSC聚类方法可以克服这一缺点，提高相位划分的准确性。图7为截取长度31 ms的200条波形曲线，这些曲线作为波形维度为31的样本进入聚类过程。
模型中各层的砂泥岩空间形态如图8所示，沿各层提取地层切片的均方根振幅属性如图9所示，图10为MKSC聚类结果。各层中“工字型”、“长条形”、“圆片状”泥岩平面展布清晰，不同形态的砂泥岩边界较清楚。根据图示结果可知，与传统的基于均方根振幅属性地层切片得到的地震相相比，基于MKSC的波形聚类算法在岩性边界描述方面更加清晰，地震相带划分更加准确。这表明，基于地震沉积学原理结合无监督机器学习的波形MKSC聚类方法能够进一步提高地震相划分的准确度和分辨能力。通过综合考虑振幅、频率和相位信息，该方法能够更好地刻画地震相的特征。另外，该方法采用了无监督机器学习算法，不需要事先设定地震相的数量和类型，具有很好的灵活性和自适应性。
![]()
图 8 物理模型第2至第5层砂、泥岩空间展布及形态Figure 8. Spatial distribution and morphology of sand and mudstone in the second to fifth layers of the physical model![]()
图 9 为各层的地层切片均方根振幅地震相Figure 9. Slices of root mean square amplitude seismic phase of stratums![]()
图 10 各层MKSC 聚类地震相分布Figure 10. MKSC clustering seismic facies distribution of stratums2.2 实际资料地震相分析
实际数据来自东海某盆地西湖凹陷西次凹中北部，在目标区域大型反转挤压背景下，圈闭成群成带分布，以背斜、断背斜、断鼻为主，圈闭类型好。研究区域目前已钻探井5口，主要目的层为花港组H3-H6，深度大约在4000～5500 m，双程旅行时为3～4 s，储层厚度大（94～152 m），非均质性强（渗透率0.1～44 mD），具有低孔低渗特征，已钻井显示低渗背景的储层内部发育物性好的“甜点”储层，如何精细刻画“甜点”储层展布特征、优选有利勘探区，是经济有效地开发好低孔渗油气田的关键。
研究过程中，首先利用解释的特征反射格架层，根据地震沉积学原理，以H3层为标志层细划分地层切片（图11）。图12是H3层顶界面时间域构造图，图13是A井H3层取心段解释图，图14是分流河道中心部位A井处不同水动力条件下的相变示意图，从图中可知，强水动力条件在稳定或低摆动条件下，分流河道中心部位（粗粒相带）控制优质储层的发育，其中，最下部稳定强水动力滞留沉积粗粒厚层砂岩储层（反+正旋回），中下部摆动弱水动力分流河道边部细砂岩局部含砾（正旋回），中上部稳定强水动力心滩核部中细砂岩局部含砾（反旋回），上部摆动-弱水动力-心滩边部细砂岩（反旋回））。图15是E～A～D井连井剖面，可明显的看出A井处强水动力-稳定-低摆动条件下的分流河道中心部位（粗粒相带）控制渗透率大于1 m的优质储层发育。
![]()
图 11 目标区基于地震沉积学原理解释的层位Figure 11. Horizon interpretation based on seismic sedimentological principles in the target area![]()
图 14 分流河道中心部位不同水动力条件下的相变示意图Figure 14. Schematic diagram of phase transition in the central part of distributary channel under different hydrodynamic conditions图16（a）是基于三角洲发育模式、利用地震沿层切片，得到的H3c层段MKSC聚类属性平面图，H3层的早期H3c层段受两条北西-南东向主河道控制，河道发育位置粗粒相带相对发育，A井位于河道的主体位置。和综合研究得到的图16（b）沉积相平面图相比较，MKSC聚类属性对河道的变化具有较好的预测性，表征了相对稳定河道演化。图17（a）是H3b层段MKSC聚类属性平面图，H3层的中期H3b层段，北西-南东向主河道方向不变，河道摆动，其中，E井和A井位于河道的主体位置。和综合研究得到的图17（b）沉积相平面图相比较，MKSC聚类属性对河道的变化具有较好的预测性，表征了相对稳定河道演化。
![]()
图 16 H3c段MKSC聚类属性平面图和沉积相平面图Figure 16. MKSC clustering attribute plan and sedimentary facies plan of H3c![]()
图 17 H3b段MKSC聚类属性平面图和沉积相平面图Figure 17. MKSC clustering attribute plan and sedimentary facies plan of H3b3. 结论
物理模型的聚类分析试验表明，基于地震沉积学原理选择合理的参考层和划分等时面的前提下，结合本文引入的波形特征向量MKSC聚类分析技术，显著地提高了地层切片的横向分辨率。在实际资料处理中，通过精细的井震标定和连井对比分析，结合MKSC聚类分析提升地震相刻画的精度和分辨能力。但是实际应用中需要注意以下两点：
（1）谱聚类的聚类结果会受到相似度矩阵的选择和参数的影响，因此合理地解释并划分层位会直接影响聚类分析结果的准确性和可靠性，在选择参考层和划分等时面时，需要结合实际地质情况与钻井资料进行合理的解释和划分；
（2）MKSC聚类类别数的设定对最终聚类结果有一定的影响，需要结合实际情况进行调试分析，以获得最佳的聚类结果。
总体来说，本文提出的地震相划分方法具有较强的鲁棒性和较高的准确性和分辨能力，是沉积相研究和储层特征分析的有效辅助工具，通过对地震数据的处理和分析，可以获得更加准确和可靠的地质信息，为油气勘探和开发提供重要的数据支持。
-
![]()
图 1 无向图及其邻接矩阵特征向量
Figure 1. Feature vectors of the undirected graph and its adjacency matrix
![]()
图 2 相同数据集不同聚类方式分类结果
Figure 2. Classification results of the same dataset by different clustering methods
![]()
图 3 物理模型的采集尺寸及参数示意图
Figure 3. Schematic of the acquisition size and parameters of the physical model
![]()
图 6 物理模型偏移剖面及基于地震沉积学原理解释的层位
Figure 6. Migration section of the physical model and horizon interpretation based on the seismic sedimentology principle
![]()
图 8 物理模型第2至第5层砂、泥岩空间展布及形态
Figure 8. Spatial distribution and morphology of sand and mudstone in the second to fifth layers of the physical model
![]()
图 9 为各层的地层切片均方根振幅地震相
Figure 9. Slices of root mean square amplitude seismic phase of stratums
![]()
图 10 各层MKSC 聚类地震相分布
Figure 10. MKSC clustering seismic facies distribution of stratums
![]()
图 11 目标区基于地震沉积学原理解释的层位
Figure 11. Horizon interpretation based on seismic sedimentological principles in the target area
![]()
图 14 分流河道中心部位不同水动力条件下的相变示意图
Figure 14. Schematic diagram of phase transition in the central part of distributary channel under different hydrodynamic conditions
![]()
图 16 H3c段MKSC聚类属性平面图和沉积相平面图
Figure 16. MKSC clustering attribute plan and sedimentary facies plan of H3c
![]()
图 17 H3b段MKSC聚类属性平面图和沉积相平面图
Figure 17. MKSC clustering attribute plan and sedimentary facies plan of H3b
表 1 不同聚类分析算法计算效率比较
Table 1 Comparison of the computational efficiency of different clustering analysis algorithms
算法类型 Mini-batch K-means Spectral clustering MKSC 计算时间/s 0.17 0.21 0.17+0.09 
下载: 导出CSV
-
[1] ZENG H, BACKUS M M, BARROW T K, et al. Stratal slicing, Part I: Realistic 3-D seismic model[J]. Geophysics, 1998, 63(2): 502−513. doi: 10.1190/1.1444351
[2] ZENG H, HENRY C S, RIOLA P J. Strata slicing; Part II, Real 3-D seismic data[J]. Geophysics, 1998, 63(2): 514−521. doi: 10.1190/1.1444352
[3] ZENG H, HENTZ F T, WOOD J L. Stratal slicing of Miocene-Pliocene sediments in vermilion block 50-Tiger Shoal Area, offshore Louisiana[J]. The Leading Edge, 2012, 20(4): 408−418.
[4] ZENG H, AMBROSE A W, VILLALTA E. Seismic sedimentology and regional depositional systems in Mioceno Norte, Lake Maracaibo, Venezuela[J]. The Leading Edge, 2001, 20(11): 260−269.
[5] BHATTACHARYA S, CARR R T, PAL M. Comparison of supervised and unsupervised approaches for mudstone lithofacies classification: Case studies from the Bakken and Mahantango-Marcellus Shale, USA[J]. Journal of Natural Gas Science and Engineering, 2016, 33: 1119−1133. doi: 10.1016/j.jngse.2016.04.055
[6] 刘爱群, 陈殿远, 任科英. 分频与波形聚类分析技术在莺歌海盆地中深层气田区的应用[J]. 地球物理学进展, 2013, 28(1): 338-344. LIU A Q, CHEN D Y, REN K Y, Frequency decomposition and waveform cluster analysis techniques Yinggehai Basin gas field in the deep area of application[J]. Progress in Geophysics, 2013, 28(1): 0338-0344. (in Chinese).
[7] 白博, 舒梦珵, 康洪全, 等. 基于伪阻抗体波形聚类的贝壳灰岩储层预测方法[J]. 物探化探计算技术, 2015, 37(6): 724-727. BAI B, SHU M C, KANG H Q, et al. Coquina reservoir prediction method of seismic pseudo-impedance waveform clustering[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2015, 37(6): 724-727. (in Chinese).
[8] 李辉, 罗波, 何雄涛, 等. 基于地震波形聚类储集砂体边界识别与预测[J]. 工程地球物理学报, 2017, 14(5): 573-577. LI H, LUO B, HE X T, et al. Boundary identification and prediction of sand body based on seismic waveform[J]. Chinese Journal of Engineering Geophysics. 2017, 14(5): 573-577. (in Chinese).
[9] 徐海, 都小芳, 高君, 等. 基于波形聚类的沉积微相定量解释技术研究−以中东地区 X油田为例[J]. 石油物探, 2018,57(5): 744−755. doi: 10.3969/j.issn.1000-1441.2018.05.014 XU H, DU X F, GAO J, et al. Quantitative interpretation of sedimentary microfaacies based on waveform clustering: A case study of X oilfield, Middle East[J]. Geophysical Prospecting for Petroleum, 2018, 57(5): 744−755. (in Chinese). doi: 10.3969/j.issn.1000-1441.2018.05.014
[10] 刘仕友, 宋炜, 应明雄, 等. 基于波形特征向量的凝聚层次聚类地震相分析[J]. 物探与化探, 2020,44(2): 339−349. DOI: 10.11720/wtyht.2020.1153. LIU S Y, SONG W, YING M X, et al. Agglomerative hierarchical clustering seismic facies analysis based on waveform eigenvector[J]. Geophysical and Geochemical Exploration, 2020, 44(2): 339−349. DOI: 10.11720/wtyht.2020.1153. (in Chinese).
[11] 杨随心, 耿修瑞, 杨炜暾, 等. 一种基于谱聚类算法的高光谱遥感图像分类方法[J]. 中国科学院大学学报, 2019,36(2): 267−274. doi: 10.7523/j.issn.2095-6134.2019.02.015 YANG S X, GENG X R, YANG W T, et al. A method of hyperspectral remote sensing image classification based on spectral clustering[J]. Journal of University of Chinese Academy of Sciences, 2019, 36(2): 267−274. (in Chinese). doi: 10.7523/j.issn.2095-6134.2019.02.015
[12] NG A Y, JORDAN M I, WEISS Y. On spectral clustering: Analysis and an algorithm[J]. Advances in Neural Information Processing Systems, 2001, 14: 849−856.
-
期刊类型引用(0)
其他类型引用(3)
计量
- 文章访问数: 225
- HTML全文浏览量: 114
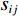
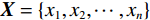
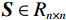
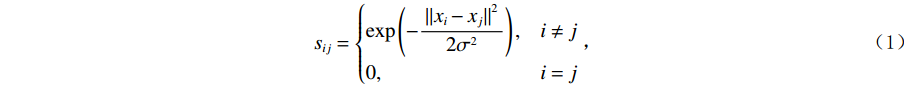
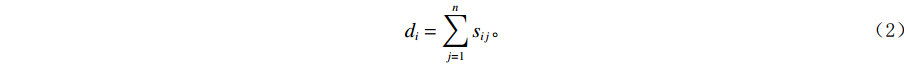
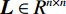
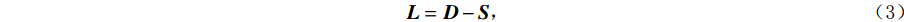
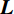
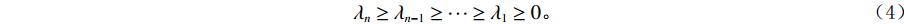
- PDF下载量: 50
- 被引次数: 3
