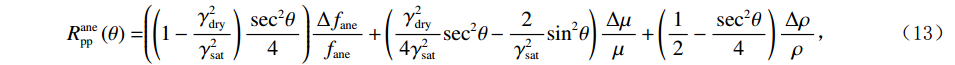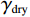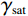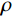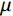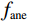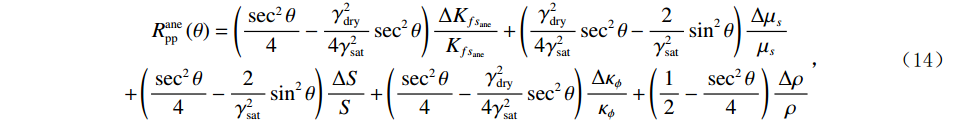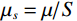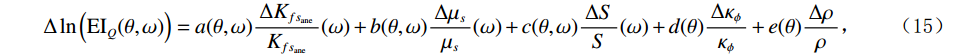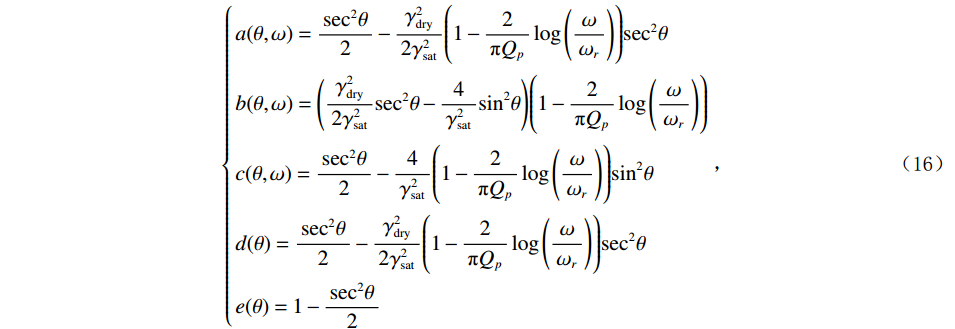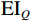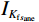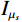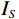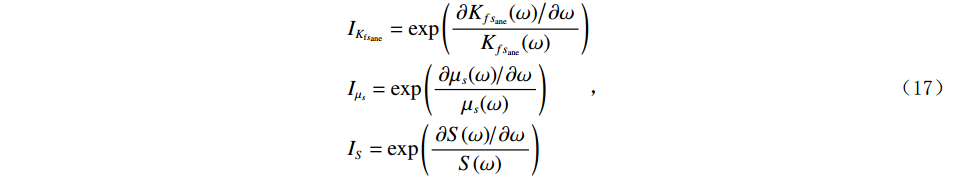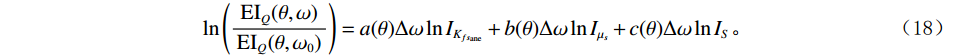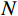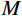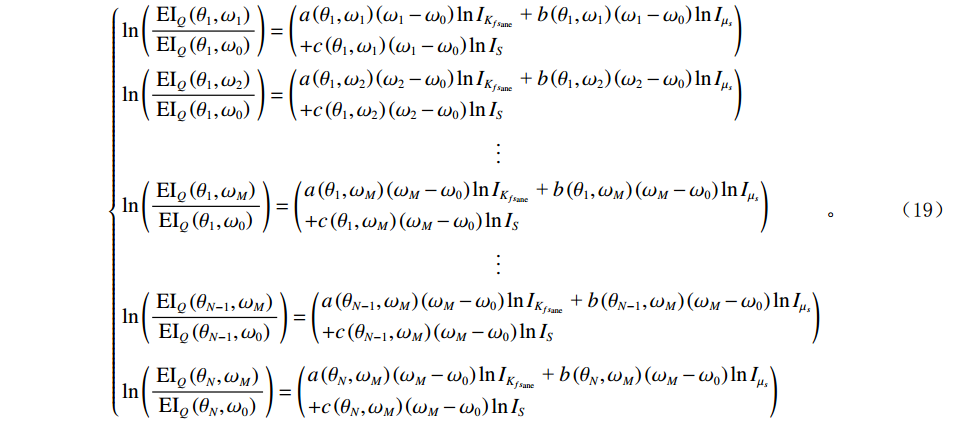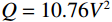A Phantom Experimental Study on Improving the Imaging Quality of Stent CT at a Fast Heart Rate
-
摘要:
目的：本研究探讨不同成像参数对高心率时体模支架成像及支架内狭窄程度判读的影响，在保证图像质量的前提下，降低辐射剂量，为今后临床工作中高心率患者的支架CT成像参数优化提供理论依据。方法：本研究通过设置不同成像参数，获得高心率时体模支架的多组CT图像；共有4支不同内径的冠状动脉支架，每枚支架内设置4种狭窄程度，分批注入2种不同浓度碘对比剂；利用佳能320 CT机分别采用100 kV和120 kV管电压扫描，均以支架重建模式进行图像重建；两位有3年以上冠脉CT诊断经验的放射科医生采用5分制评分法，对支架可视化效果、图像质量、支架内狭窄的评估，进行图像质量主观评分；采用多元回归分析，评估支架内径、支架内狭窄程度、管电压、碘对比剂浓度对图像质量主观评分的统计学影响。结果：在所有参数组合中，4种内径支架的结构均可显示，但支架腔内显示存在差异；支架内径、支架内狭窄程度、碘对比剂浓度对图像质量主观评分影响显著，随着支架内径的增加和支架内狭窄程度的减轻、碘对比剂浓度的减低，评分上升，支架内径对评分的影响最为强烈；管电压对图像质量主观评分影响不显著。结论：高心率条件下，支架内径、支架内狭窄程度和碘对比剂浓度直接影响支架CT成像的图像质量，而管电压对图像质量没有影响。本研究可为优化高心率人群的支架成像方案提供理论基础。
Abstract:Objective: This study aimed to investigate the impact of different imaging parameters on stent imaging and stenosis assessment in a fast heart rate model. The goal was to reduce the radiation dose while ensuring image quality, and to provide a theoretical basis for optimizing computed tomography (CT) imaging parameters for stent imaging in patients with fast heart rates in future clinical practice. Methods: Different imaging parameters were set to obtain multiple sets of CT images of stents in a fast heart rate model. Four coronary artery stents with different internal diameters were used. Each stent was set to four levels of stenosis. Two different concentrations of iodine contrast agents were injected in batches. The Canon 320 CT scanner was used to perform scans at 100 kV and 120 kV tube voltages, and image reconstruction was performed using the stent reconstruction mode. Two radiologists, with more than three years of experience in coronary CT diagnosis, used a 5-point scoring method to subjectively evaluate image quality based on stent visualization, image quality, and stenosis assessment. Multiple regression analysis was conducted to assess the influence of stent diameter, stenosis level, tube voltage, and iodine contrast agent concentration on the subjective image quality scores. Results: The structures of the four stents could be visualized in all parameter combinations, but there were significant differences in the intraluminal display. The stent diameter, stenosis level, and iodine contrast agent concentration had a significant impact on the subjective image quality scores. The scores increased as the stent diameter increased and the stenosis level and iodine contrast agent concentration decreased. Moreover, the stent diameter had the strongest impact on the scores. Tube voltage did not significantly affect the subjective image quality scores. Conclusion: In fast heart rate conditions, the stent diameter, stenosis level, and iodine contrast agent concentration directly affect the image quality of stent CT imaging. Conversely, tube voltage had no impact on image quality. Our findings provided a theoretical basis for optimizing stent imaging protocols in patients with fast heart rates.
-
Keywords:
- computed tomography /
- phantom /
- stent /
- high heart rate
-
随着地震勘探难度的提升，仅依据地震振幅信息难以实现高精度的地震勘探需求，故结合岩石物理信息，利用频散属性和介质的粘弹性等对储层特征进行刻画成为现今研究热点[1]。目前常见的含油气储层大多为裂隙多孔介质，研究发现，当地震波在裂隙多孔介质中传播时，由于受到波致流（宏观Biot流、介观层间流和微观喷射流）的影响，地震波会发生明显的衰减和频散[2-5]，具有粘弹介质传播特性。然而，常规流体检测方法一般基于Biot孔隙弹性理论，没有考虑地震波粘弹介质传播特性，降低了流体识别精度。因此，基于粘弹介质地震岩石物理模型，构建能够更加准确描述流体性质的流体因子，开发相应的地震反演技术，对流体预测描述具有重要意义。
储层流体识别是一项基于流体因子对流体的敏感性进行流体判别的重要技术。因此，构建对流体更为敏感的流体因子是储层流体精准识别的技术关键。流体因子的概念最早是Smith等[6]提出的，特指由纵、横波速度相对变化量的而运算构成的参数。随后，Biot[7]和Gassmann[8]分析了多孔流体饱和岩石的弹性参数构建方法；Russell等[9]利用Biot-Gassmann方程，推导了Gassmann流体项作为流体指示因子；Zong等[10]消除了岩石骨架的影响，构建并反演了固液解耦流体因子作为流体识别指标，然而其缺乏对孔裂隙喷射流引起的衰减的考虑。
由于裂隙的存在会导致岩石在外力作用下产生挤喷流现象，并导致介质呈现粘滞性特征[11-12]。为了更好地描述该现象，Tang等[13-14]分别考虑了硬币型裂隙和钹状裂隙模型中喷流效应的影响，构建了描述孔隙、裂隙并存时的弹性波统一理论，该理论能够更加准确描述弹性波在介质中的传播特征，以此提高流体识别的精度。
地震频变反演是基于粘弹介质理论形成的预测流体的常用方法，而常用的频变反演方法主要有两种，一种是频变AVO反演方法[15-17]，另一种是基于弹性阻抗的频变反演方法[18-20]。频变AVO反演利用的是反射系数近似公式，而基于弹性阻抗的频变反演是通过构建弹性阻抗与弹性参数的弹性阻抗方程，利用弹性阻抗方程进行反演。在弹性阻抗反演方法中，假设弹性阻抗的对数的梯度和反射系数成正比，建立弹性阻抗与反射系数之间的关系，从而将反射系数方程改写为弹性阻抗方程[18,21-22]。
Connolly[23]通过对叠后波阻抗和AVO特点的分析，提出了一种同时考虑波阻抗和AVO特征的弹性阻抗反演方法。Yin等[21]基于Russell提出的多空流体饱和弹性阻抗近似方程，提出了包含Gassmann流体项的弹性阻抗方程，并通过弹性阻抗反演实现流体项反演的方法。Zong等[18]提出了粘弹性介质的弹性阻抗方程，并考虑参数的频变特征，实现粘弹性介质Russell流体因子的频变反演。频变弹性阻抗反演相比于频变AVO反演表现出更强的优势[22]，因此，为了更好的提取与频率相关的新流体因子，本研究开发基于弹性阻抗反演的方法。
在前人的研究基础上，本研究综合利用岩石物理分析，构建粘弹频变固液解耦流体因子，该因子能够保持原有流体因子的基本特征，并且能够提高含对孔隙、裂隙介质中流体的预测能力。同时，探讨基于弹性阻抗的叠前地震频变反演方法，及其在胜利油田胜北地区复杂砂岩储层流体检测中的应用。模型试算和实际资料处理结果表明，基于粘弹频变固液解耦流体因子叠前地震反演的储层含油气性预测方法，能够提取孔裂隙频变粘弹固液解耦流体因子。预测结果能够有效区分储层的流体类型，准确刻画储层流体边界，消除流体识别假象，提高流体识别精度。
1. 基于频变反演的流体识别方法原理
1.1 频变敏感参数构建与分析
地震勘探方法自提出以来，经历了构造解释、储层描述和流体识别3个发展阶段，其中流体识别技术作为勘探开发的前沿技术，需要作为长期研究的课题。而在流体识别方法方面，采用流体指示因子来进行流体判别受到了广泛关注。相比于常规流体因子，频变流体因子由于充分考虑了频率对岩石弹性参数的影响，展示了其在区分烃类流体方面的独特能力[24]。因此，有必要构建敏感程度更高的频变敏感参数。首先，根据Biot-Gassman[8,25]理论，在低频条件下的饱和流体体积模量可以写为：
$$ {K_{{\mathrm{sat}}}} = {K_{\mathrm{d}}} + {\kappa ^2}\chi \text{，} $$ (1) 其中：
$\kappa = 1 - {{{K_{\mathrm{d}}}} / {{K_{\mathrm{s}}}}}$ ，表示Biot系数；$ 1/\chi=(\kappa-\phi)/K_{\mathrm{s}}+\phi/K\mathrm{_f}\mathrm{ } $ ，$ {K_{{\mathrm{sat}}}} $ 、$ {K_{\mathrm{d}}} $ 和$ {K_{\mathrm{s}}} $ 分别为饱和岩石体积模量、干岩石体积模量和岩石基质体积模量；$ {K_{\mathrm{f}}} $ 为饱和流体体积模量，$ \phi $ 为岩石有效孔隙度。考虑到孔裂隙挤喷流体流动，Tang[13]在2011年提出了考虑硬币型裂隙挤喷流效应的饱和岩石体积模量。由于硬币型模型中孔隙与裂隙的流体交换处于硬币的边缘，然而，在力学理论方面，裂隙在硬币边缘处是处于闭合状态的。因此，为了进一步改进模型，Tang等[14]在2012年又提出了钹状裂隙模型，将流体交换位置改变到了硬币模型的中部。该种模型的饱和岩石体积模量可以统一表示为：
$$ {K_{{\mathrm{sat}}}} = {K_{\mathrm{d}}} + \frac{{{\kappa ^2}\chi }}{{1 + S\left( \omega \right)\chi }} \text{，} $$ (2) 其中：
$ S\left( \omega \right) $ 为描述孔裂隙相互作用的挤喷流函数。在本研究中，为了充分考虑孔裂隙挤喷流效应对流体识别的影响，消除流体识别的误差，同时将两种模型耦合到一起，因此，
$ S\left( \omega \right) $ 可以表示为：$$ S(\omega ) = {S_1}(\omega ) + {S_2}(\omega ) \text{，} $$ (3) $$ {S_1}\left( \omega \right) = \frac{8}{3}\text{π} \varepsilon \frac{{\left( {1 - \nu } \right)}}{\mu }f\left( \zeta \right)\frac{\left( {\displaystyle \frac{{{1/ {{K_{\mathrm{d}}} - }}{1 / {{K_{\mathrm{s}}}}}}}{{{1/ {{K_{\mathrm{d}}} - }}{1/ {{K_0}}}}} - f\left( \zeta \right)} \right)}{\left( {1 + \displaystyle \frac{{4\left( {1 - v} \right){K_{\mathrm{f}}}}}{{3\mu \gamma }}\Big( {1 - f\left( \zeta \right)} \Big)} \right)} \text{，} $$ (4) $$ {S_2}\left( \omega \right){\text{ = }}\frac{{8\varepsilon \left( {1 - \nu } \right){{\left( {1 + \lambda } \right)}^3}}}{{3\mu }} \times \frac{{\left( {\displaystyle\dfrac{{{1 / {{K_0}}} - {1 / {{K_{\mathrm{s}}}}}}}{{{1 / {{K_{\mathrm{d}}}}} - {1 / {{K_0}}}}}} \right)M}}{{1 - \displaystyle\dfrac{{3i\omega \eta \left( {1 + 2\lambda } \right)}}{{2{K_{\mathrm{f}}}\lambda {\gamma ^2}}}\left( {1 + \displaystyle\dfrac{{4\left( {1 - \nu } \right){K_{\mathrm{f}}}{{\left( {1 + \lambda } \right)}^3}}}{{3\text{π} \mu \gamma \left( {1 + 2\lambda } \right)}}M} \right)}} \text{，} $$ (5) $$ f\left(\zeta \right)=\frac{2{J}_{1}\left(\zeta \right)}{\zeta {J}_{0}\left(\zeta \right)}\text{，}\zeta =\left({\frac{3i\omega \eta }{{\gamma }^{2}{K}_{{\mathrm{f}}}}} \right)^{\tfrac{1}{2}}\text{，} $$ (6) 其中：
$ {S_1}(\omega ) $ 和$ {S_2}(\omega ) $ 分别为硬币型和钹状裂隙挤喷流函数；$ \lambda = {\left( {\displaystyle\frac{{3\phi }}{{4\text{π} \varepsilon }}} \right)^{\tfrac{1 }{ 3}}} $ ，$ M = 1 + \displaystyle\frac{{4 - 5\nu }}{{2(7 - 5\nu )}}\frac{{{\lambda ^3}}}{{{{(1 + \lambda )}^3}}} + \displaystyle\frac{9}{{2(7 - 5\nu )}}\frac{{{\lambda ^5}}}{{{{(1 + \lambda )}^5}}} $ ，$\omega $ 为圆周角频率，$\lambda $ 为孔裂隙尺度比，$\varepsilon $ 、$\eta $ 和$\gamma $ 分别表示裂隙密度、孔隙流体粘滞系数和裂隙纵横比，$ \nu $ 为干燥介质泊松比；当$S(\omega ) = 0$ 时，岩石体积模量为$ {K_0} $ ；$ {J_0}( * ) $ 和$ {J_1}( * ) $ 分别为第一类零阶和一阶贝塞尔函数；${K_{\mathrm{d}}}$ 和${K_{\mathrm{s}}}$ 分别为干岩石体积模量和岩石基质体积模量，${K_{\mathrm{f}}}$ 为饱和流体体积模量；$\mu $ 为剪切模量，$i$ 为虚数单位。通过将式（2）与Gassmann流体项
$f$ 进行关系构建可得，$$ {K_{{\mathrm{sat}}}} = {K_{\mathrm{d}}} + \frac{f}{{1 + S\left( \omega \right)\chi }} 。 $$ (7) 因此有，
$$ f = S \cdot {\kappa _\phi } \cdot {K_{\mathrm{{fs}}}} \text{，} $$ (8) 其中：
$$ {K_{{\mathrm{fs}}}} = \frac{{{K_{\mathrm{f}}}}}{S} \text{，} $$ (9) $$ S = 1 + S(\omega )\chi \text{，} $$ (10) $$ {\kappa _\phi } = \frac{{{\kappa ^2}}}{\phi } 。 $$ (11) 我们将
$ {K_{{\mathrm{fs}}}} $ 称为孔裂隙固液解耦流体因子，$ S $ 为耦合挤喷流效应项，$ {\kappa _\phi } $ 为与孔隙度相关的Biot系数项。为了流体判别精度的提高，将Futterman[26]近似常 Q模型引入粘弹介质，构建孔裂隙粘弹固液解耦流体因子为：
$$ \begin{aligned}K_{\mathrm{f}\mathrm{\mathit{s}}_{\mathrm{ane}}}=\kappa_{\phi}^{-1}S^{-1}f_{\mathrm{ane}}=\kappa_{\phi}^{-1}S^{-1}\left(\rho V_p^2-\gamma_{\mathrm{dry}}^2\rho V_s^2\right)+\quad\qquad \\ \kappa_{\phi}^{-1}S^{-1}\left(\begin{gathered}\rho V_p^2\left(\frac{2}{\text{π}Q_p}log\left(\frac{\omega}{\omega_{\mathrm{r}}}\right)-\frac{i}{Q_{\mathrm{p}}}\right) \\ -\gamma_{\mathrm{dry}}^2\rho V_s^2\left(\frac{2}{\text{π}Q_{\mathrm{s}}}log\left(\frac{\omega}{\omega_{\mathrm{r}}}\right)-\frac{i}{Q_{\mathrm{s}}}\right)\end{gathered}\right)=K_{\mathrm{f}s_{\mathrm{ela}}}+\Delta K_{\mathrm{f}s_{\mathrm{Q}}}\end{aligned}\text{，} $$ (12) 其中：
$ {Q_{\mathrm{p}}} $ 和$ {Q_{\mathrm{s}}} $ 分别为纵波和横波品质因子，$ \omega $ 和$ {\omega _{\mathrm{r}}} $ 分别为圆周角频率和参考频率，$i$ 为虚数单位。为了验证新提出的孔裂隙粘弹固液解耦流体因子的频率敏感性的优势，分别对纵波速度、横波速度、泊松比、体积模量、杨氏模量、剪切模量、固液解耦流体因子和孔裂隙粘弹固液解耦流体因子进行了分析，模型参数如表1所示，结果如图1所示。
表 1 弹性参数敏感性分析模型数据Table 1. Sensitivity analysis data of elastic parameters岩性 $ V_{\mathrm{P}} $/（m/s） $ V_{\mathrm{s}} $/（m/s） $ \mathrm{\rho} $/（g/cm3） $ {Q}_{{\mathrm{p}}1}$ $ {Q}_{{\mathrm{p}}2} $ $ {Q}_{{\mathrm{s}}} $ 砂岩 2590 1060 2.210 10 20 120 分析结果表明，孔裂隙粘弹固液解耦流体因子对纵波衰减和频率的敏感程度较高，可以作为流体指示因子用来流体检测。
为对比孔裂隙粘弹固液解耦流体因子与其他弹性参数的频散程度，本文优选流体因子，进一步分析不同弹性参数与孔裂隙粘弹固液解耦流体因子的频散程度，分析结果如图2所示。图2的计算过程使用表1中的模型参数。
![]()
图 2 不同弹性参数频散程度分析Figure 2. Analysis of dispersion degree of different elastic parameters计算结果表明，相较于固液解耦流体因子、拉梅参数和体积模量等弹性参数，本文新提出的孔裂隙粘弹固液解耦流体因子的频散程度最高，并且比固液解耦流体因子的频散程度高15％ 左右。因此，我们在胜北断层下降盘A井区储层含油气识别中，将孔裂隙粘弹固液解耦流体因子作为油气指示因子，提高储层流体识别的可靠性。
1.2 基于叠前地震反演的储层含油气性预测方法
借鉴Connolly[23]构建的反射系数与弹性阻抗的关系，Lan等[20]建立了频变弹性阻抗反射系数方程，并发展了基于弹性阻抗的频变反演算法。基于Biot-Gassmann理论，Russel等[9,27]对饱含流体孔隙介质模型进行了分析，推导得到了Gassmann流体项的反射系数近似公式为：
$$ R_{{\mathrm{pp}}}^{{\mathrm{ane}}}\left( \theta \right) =\Biggr( {\left( {1 - \frac{{\gamma _{{\mathrm{dry}}}^2}}{{\gamma _{{\mathrm{sat}}}^2}}} \right)\frac{{{{\sec }^2}\theta }}{4}} \Biggr)\frac{{\Delta {f_{{\mathrm{ane}}}}}}{{{f_{{\mathrm{ane}}}}}} + \left( {\frac{{\gamma _{{\mathrm{dry}}}^2}}{{4\gamma _{{\mathrm{sat}}}^2}}{{\sec }^2}\theta - \frac{2}{{\gamma _{{\mathrm{sat}}}^2}}{{\sin }^2}\theta } \right)\frac{{\Delta \mu }}{\mu } + \left( {\frac{1}{2} - \frac{{{{\sec }^2}\theta }}{4}} \right)\frac{{\Delta \rho }}{\rho } \text{，} $$ (13) 其中：
${\gamma _{{\mathrm{dry}}}}$ 和${\gamma _{{\mathrm{sat}}}}$ 分别为干岩石骨架纵横波速度比和饱和岩石纵横波速度比，$\rho $ 为岩石密度，$\mu $ 表示剪切模量，${f_{{\mathrm{ane}}}}$ 为Gassmann流体项。通过式（8）的关系，将式（13）变换为孔裂隙粘弹固液解耦流体因子的反射系数近似方程为：
$$ \begin{aligned}R_{\mathrm{pp}}^{\mathrm{ane}}\left(\theta\right)=\left(\frac{\sec^2\theta}{4}-\frac{\gamma_{\mathrm{dry}}^2}{4\gamma_{\mathrm{sat}}^2}\sec^2\theta\right)\frac{\Delta K_{fs_{\mathrm{ane}}}}{K_{fs_{\mathrm{ane}}}}+\left(\frac{\gamma_{\mathrm{dry}}^2}{4\gamma_{\mathrm{sat}}^2}\sec^2\theta-\frac{2}{\gamma_{\mathrm{sat}}^2}\sin^2\theta\right)\frac{\Delta\mu_s}{\mu_s}\quad \\ +\left(\frac{\sec^2\theta}{4}-\frac{2}{\gamma_{\mathrm{sat}}^2}\sin^2\theta\right)\frac{\Delta S}{S}+\left(\frac{\sec^2\theta}{4}-\frac{\gamma_{\mathrm{dry}}^2}{4\gamma_{\mathrm{sat}}^2}\sec^2\theta\right)\frac{\Delta\kappa_{\phi}}{\kappa_{\phi}}+\left(\frac{1}{2}-\frac{\sec^2\theta}{4}\right)\frac{\Delta\rho}{\rho}\end{aligned}\text{，} $$ (14) 其中：
${\mu _s} = {\mu \mathord{\left/ {\vphantom {\mu S}} \right. } S}$ 。考虑粘弹介质，并借鉴Connolly[23]构建的反射系数与弹性阻抗的关系，构建得到孔裂隙粘弹固液解耦流体因子弹性阻抗反射系数特征方程为：
$$ {{\Delta }}\ln \Big({{{\mathrm{EI}}}}_{{Q}}(\theta ,\omega )\Big) = a(\theta ,\omega )\frac{{\Delta {K_{f{s_{{\mathrm{ane}}}}}}}}{{{K_{f{s_{{\mathrm{ane}}}}}}}}(\omega ) + b(\theta ,\omega )\frac{{\Delta {\mu _s}}}{{{\mu _s}}}(\omega ) + c(\theta ,\omega )\frac{{\Delta S}}{S}(\omega ) + d(\theta )\frac{{\Delta {\kappa _\phi }}}{{{\kappa _\phi }}} + e(\theta )\frac{{\Delta \rho }}{\rho } \text{，} $$ (15) $$ \left\{\begin{gathered} a(\theta ,\omega ) = \frac{{{{\sec }^2}\theta }}{2} - \frac{{\gamma _{{\mathrm{dry}}}^2}}{{2\gamma _{{\mathrm{sat}}}^2}}\Biggr( {1 - \frac{2}{{\text{π} {Q_p}}}\log \left( {\frac{\omega }{{{\omega _r}}}} \right)} \Biggr){\sec ^2}\theta \\ b(\theta ,\omega ) = \left( {\frac{{\gamma _{{\mathrm{dry}}}^2}}{{2\gamma _{{\mathrm{sat}}}^2}}{{\sec }^2}\theta - \frac{4}{{\gamma _{{\mathrm{sat}}}^2}}{{\sin }^2}\theta } \right)\Biggr( {1 - \frac{2}{{\text{π} {Q_p}}}\log \left( {\frac{\omega }{{{\omega _r}}}} \right)} \Biggr) \\ c(\theta ,\omega ) = \frac{{{{\sec }^2}\theta }}{2} - \frac{4}{{\gamma _{{\mathrm{sat}}}^2}}\Biggr( {1 - \frac{2}{{\text{π} {Q_p}}}\log \left( {\frac{\omega }{{{\omega _r}}}} \right)} \Biggr){\sin ^2}\theta \\ d(\theta ) = \frac{{{{\sec }^2}\theta }}{2} - \frac{{\gamma _{{\mathrm{dry}}}^2}}{{2\gamma _{{\mathrm{sat}}}^2}}\Biggr( {1 - \frac{2}{{\text{π} {Q_p}}}\log \left( {\frac{\omega }{{{\omega _r}}}} \right)} \Biggr){\sec ^2}\theta \\ e(\theta ) = 1 - \frac{{{{\sec }^2}\theta }}{2} \\ \end{gathered} \right.\text{，} $$ (16) 其中
$ \mathrm{EI}_Q $ 为粘弹介质弹性阻抗。最后，式（15）中的弹性参数对频率求偏导，构建孔裂隙频变粘弹固液解耦流体因子
$ I_{K_{\mathrm{f}s_{\mathrm{ane}}}} $ 、孔裂隙频变剪切模量$ {I_{{\mu _s}}} $ 和频变挤喷流模量$ {I_S} $ ，如式（17）所示：$$ \begin{gathered} {I_{{K_{{\mathrm{f}}{s_{{\mathrm{ane}}}}}}}} = \exp \left( {\frac{{{{\partial {K_{f{s_{{\mathrm{ane}}}}}}(\omega )} \mathord{\left/ {\vphantom {{\partial {K_{f{s_{{\mathrm{ane}}}}}}(\omega )} {\partial \omega }}} \right. } {\partial \omega }}}}{{{K_{f{s_{{\mathrm{ane}}}}}}(\omega )}}} \right) \\ {I_{{\mu _s}}} = \exp \left( {\frac{{{{\partial {\mu _s}(\omega )} \mathord{\left/ {\vphantom {{\partial {\mu _s}(\omega )} {\partial \omega }}} \right. } {\partial \omega }}}}{{{\mu _s}(\omega )}}} \right) \\ {I_S} = \exp \left( {\frac{{{{\partial S(\omega )} \mathord{\left/ {\vphantom {{\partial S(\omega )} {\partial \omega }}} \right. } {\partial \omega }}}}{{S(\omega )}}} \right) \\ \end{gathered} \text{，} $$ (17) 根据式（15）和式（17），获得频变反演目标函数为：
$$ \ln\left(\frac{\mathrm{EI}_Q(\theta,\omega)}{\mathrm{EI}_Q(\theta,\omega_0)}\right)=a(\theta)\Delta\omega\ln I_{K_{fs_{\mathrm{ane}}}}+b(\theta)\Delta\omega\ln I_{\mu_s}+c(\theta)\Delta\omega\ln I_S。 $$ (18) 假设有
$N$ 个入射角度，$M$ 个频率信息，式（18）可以展开为：$$ \left\{\begin{gathered}\ln\left(\frac{\mathrm{EI_{\mathit{Q}}}\left(\theta_1,\omega_1\right)}{\mathrm{EI}_Q\left(\theta_1,\omega_0\right)}\right)=\left(\begin{gathered}a\left(\theta_1,\omega_1\right)\left(\omega_1-\omega_{\text{0}}\right)\ln I_{K_{fs_{\mathrm{ane}}}}\text{ + }b\left(\theta_1,\omega_1\right)\left(\omega_1-\omega_{\text{0}}\right)\ln I_{\mu_s} \\ +c\left(\theta_1,\omega_1\right)\left(\omega_1-\omega_{\text{0}}\right)\ln I_S \\ \end{gathered}\right) \\ \ln\left(\frac{\mathrm{EI}_Q\left(\theta_1,\omega_2\right)}{\mathrm{EI}_Q\left(\theta_1,\omega_0\right)}\right)=\left(\begin{gathered}a\left(\theta_1,\omega_2\right)\left(\omega_2-\omega_{\text{0}}\right)\ln I_{K_{fs_{\mathrm{ane}}}}\text{ + }b\left(\theta_1,\omega_2\right)\left(\omega_2-\omega_{\text{0}}\right)\ln I_{\mu_s} \\ +c\left(\theta_1,\omega_2\right)\left(\omega_2-\omega_{\text{0}}\right)\ln I_S \\ \end{gathered}\right) \\ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\vdots \\ \ln\left(\frac{\mathrm{EI}_Q\left(\theta_1,\omega_M\right)}{\mathrm{EI}_Q\left(\theta_1,\omega_0\right)}\right)=\left(\begin{gathered}a\left(\theta_1,\omega_M\right)\left(\omega_M-\omega_{\text{0}}\right)\ln I_{K_{fs_{\mathrm{ane}}}}\text{ + }b\left(\theta_1,\omega_M\right)\left(\omega_M-\omega_{\text{0}}\right)\ln I_{\mu_s} \\ +c\left(\theta_1,\omega_M\right)\left(\omega_M-\omega_{\text{0}}\right)\ln I_S \\ \end{gathered}\right) \\ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\vdots \\ \ln\left(\frac{\mathrm{EI}_Q\left(\theta_{N-1},\omega_M\right)}{\mathrm{EI}_Q\left(\theta_{N-1},\omega_0\right)}\right)=\left(\begin{gathered}a\left(\theta_{N-1},\omega_M\right)\left(\omega_M-\omega_{\text{0}}\right)\ln I_{K_{fs_{\mathrm{ane}}}}\text{ + }b\left(\theta_{N-1},\omega_M\right)\left(\omega_M-\omega_{\text{0}}\right)\ln I_{\mu_s} \\ +c\left(\theta_{N-1},\omega_M\right)\left(\omega_M-\omega_{\text{0}}\right)\ln I_S \\ \end{gathered}\right) \\ \ln\left(\frac{\mathrm{EI}_Q\left(\theta_N,\omega_M\right)}{\mathrm{EI}_Q\left(\theta_N,\omega_0\right)}\right)=\left(\begin{gathered}a\left(\theta_N,\omega_M\right)\left(\omega_M-\omega_{\text{0}}\right)\ln I_{K_{fs_{\mathrm{ane}}}}\text{ + }b\left(\theta_N,\omega_M\right)\left(\omega_M-\omega_{\text{0}}\right)\ln I_{\mu_s} \\ +c\left(\theta_N,\omega_M\right)\left(\omega_M-\omega_{\text{0}}\right)\ln I_S \\ \end{gathered}\right) \\ \end{gathered}\right.。 $$ (19) 通过求解以上方程组，即可获得任意采样点处的孔裂隙频变粘弹固液解耦流体因子，将其应用于实际地震资料，进行储层流体识别。
1.3 模型试算
通过分析胜北断层下降盘A井区的地质构造，本文设计如图3所示的含油砂岩模型，模型参数如表2所示。其中，纵横波品质因子采用Waters[28]经验公式
$Q = 10.76{V^2}$ 计算获得。利用该模型采用褶积方法合成地震记录并添加特定信噪比的高斯随机噪音，采用前边提出的方法技术进行孔裂隙频变粘弹固液解耦流体因子反演试算，结果如图4所示。表 2 含油砂岩模型参数Table 2. Oil-bearing sandstone model parameters储层岩性 $ V_{\mathrm{P}}/ （{\mathrm{m/s}}） $ $ V_{\mathrm{s}}/ （{{\mathrm{m/s}}}） $ $ \mathrm{\rho}/ （{\mathrm{g}}/\mathrm{cm}^3） $ 含油砂岩 4574 2955 2.449 含水砂岩 4803 3056 2.508 泥岩 4102 2508 2.400 ![]()
图 4 含油砂岩模型孔裂隙频变粘弹固液解耦流体因子反演结果Figure 4. Inversion results of frequency-dependent viscoelastic solid-liquid decoupling fluid factor in oil-bearing sandstone model pores and fractures反演结果表明，该方法获取的孔裂隙频变粘弹固液解耦流体因子能够准确识别模型中的含油砂岩储层，区分含油砂岩与含水砂岩。同时，准确刻画了含油砂岩的边界，将两个含油砂岩断开的位置准确识别，验证了该方法的可行性。
2. 实际工区应用
为了验证本文提出的基于孔裂隙频变粘弹固液解耦流体因子叠前地震反演的储层含油气性预测方法在流体识别中的可行性，本文针对我国东营凹陷胜坨地区胜北断层下降盘A井区沙3、沙4段的实际资料进行了处理，本区的研究目标为典型的含油砂岩储层。
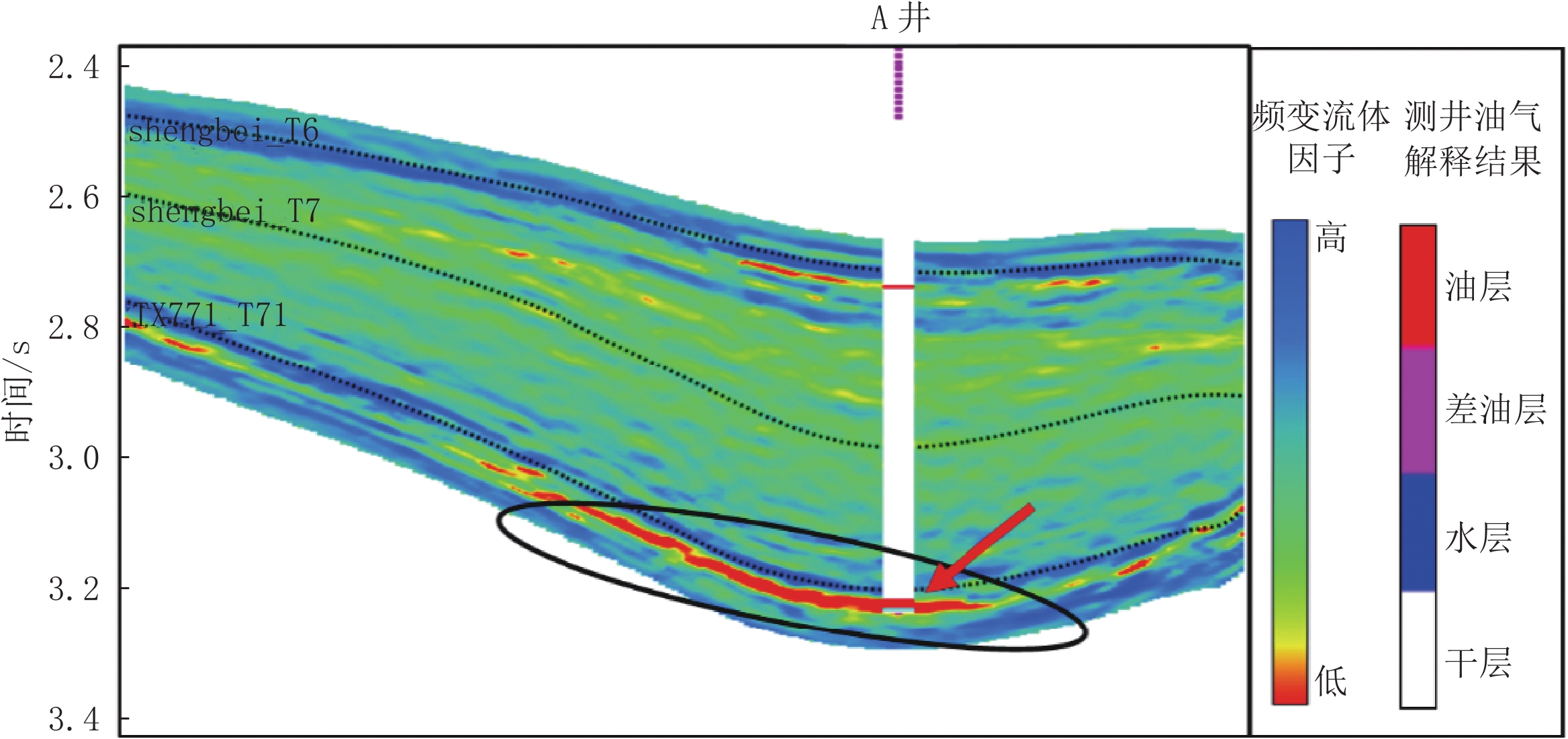
图5为过A井的小角度（11°～19°）、中角度（19°～28°）和大角度（28°～37°）的部分角度叠加地震数据剖面与测井解释结果，图中红色表示油层解释，粉色表示差油层解释，蓝色表示水层，白色为干层，黑色椭圆区域为含油砂岩发育位置。
![]()
图 5 胜北断层下降盘A井区部分角度叠加地震剖面Figure 5. Partial angle stack seismic profiles in the A well area of the Shengbei fault descent plate对该区3个角度地震数据利用连续小波变换进行多尺度频谱分解，获取不同频率地震剖面，之后利用本文提到的基于孔裂隙频变粘弹固液解耦流体因子叠前地震反演的储层含油气性预测方法提取孔裂隙频变粘弹固液解耦流体因子，对该区储层进行流体识别。
图6为孔裂隙频变粘弹固液解耦流体因子反演结果，黑色椭圆圈内位置处发育油藏，红色箭头处反演结果的油层纵向厚度与测井解释结果基本一致。因此，基于孔裂隙频变粘弹固液解耦流体因子叠前地震反演的储层含油气性预测方法具有较高的流体识别精度，基于该技术方法反演的孔裂隙频变粘弹固液解耦流体因子可以作为复杂砂岩储层油气储层的指示因子，为复杂砂岩储层的油气识别提供了新的方法和思路。
![]()
图 6 孔裂隙频变粘弹固液解耦流体因子反演结果剖面与测井解释结果Figure 6. Inversion results of frequency-dependent viscoelastic solid-liquid decoupling fluid factor with pore and fractures and logging interpretation results3. 结论
（1）以考虑挤喷流效应的孔裂隙衰减理论模型为基础，计算得到的弹性参数频散特征结果对优选流体敏感参数具有指导意义，为叠前地震频变反演与储层流体识别提供了具有更高敏感性的频变流体指示因子。
（2）基于孔裂隙频变粘弹固液解耦流体因子构建的弹性阻抗反射系数特征方程，为基于叠前地震反演的储层含油气性预测方法奠定了理论基础。
（3）应用本文提出的基于叠前地震反演的储层含油气性预测方法，可实现基于地震资料的频变敏感特征参数的提取。模型测试和胜北断层下降盘A井区实际资料反演表明，该技术方法能够充分利用地震资料中蕴含的振幅和频率信息，准确识别复杂砂岩储层中的油层分布范围，验证了本文新提出的孔裂隙频变粘弹固液解耦流体因子在储层流体识别中的有效性，为复杂储层流体识别提供了新的思路和方法。
-
![]()
图 1 体模实验中不同内径支架的CT图像
注：模拟心率90次/min时，注入A组碘对比剂后，采用100 kV管电压扫描获得的4种不同内径支架的CT图像，各支架结构均可显示，其中4、3.5和3 mm内径的支架内碘对比剂与梯度狭窄的分界均可显示，2.75 mm内径的支架内部显示不清。
Figure 1. CT images of different internal diameter stents in the phantom experiment
表 1 模型拟合度分析
Table 1 Model fit analysis
模型摘要 R R2 调整后R2 标准误 更改统计 R2 F 自由度1 自由度2 P 1 0.868 0.753 0.736 0.338 0.753 44.981 4 59 0.000 
下载: 导出CSV
表 2 回归模型显著性分析
Table 2 Significance analysis of regression model
模型ANOVA 平方和 自由度 均方 统计检验 F P 回归 20.603 4 5.151 44.981 0.000b 残差 6.756 59 0.115 总计 27.359 63
下载: 导出CSV
表 3 模型参数的显著性检验结果
Table 3 Significance test results of model parameters
模型系数 未标准化系数 标准化系数 统计检验 B的95.0％ 置信区间 相关性 B 标准误 Beta t 显著性 下限 上限 零阶 偏 部分 （常量） 2.584 0.781 3.311 0.002 1.023 4.146 支架内径 1.140 0.088 0.837 12.936 0.000 0.964 1.316 0.837 0.860 0.837 狭窄程度 -0.347 0.161 -0.140 -2.159 0.035 -0.669 -0.025 -0.140 -0.271 -0.140 管电压 -0.005 0.004 -0.072 -1.108 0.272 -0.013 0.004 -0.072 -0.143 -0.072 碘对比剂浓度 -0.004 0.001 -0.167 -2.586 0.012 -0.006 -0.001 -0.167 -0.319 -0.167
下载: 导出CSV
表 4 回归模型预测偏差性分析
Table 4 Regression model prediction bias analysis
残差统计 最小值 最大值 平均值 标准偏差 个案数 预测值 3.382 5.363 4.297 0.572 64 残差 -0.632 0.693 0.000 0.327 64 标准预测值 -1.599 1.864 0.000 1.000 64 标准残差 -1.868 2.049 0.000 0.968 64
下载: 导出CSV
-
[1] TU C C, XIE L, WANG Z J, et al. Association between ceramides and coronary artery stenosis in patients with coronary artery disease[J]. Lipids in Health and Disease, 2020, 19(1): 151. DOI:10.1186/ s12944-020-01329-0.
[2] HAIDEGGER M, KNEIHSL M, NIEDERKORN K, et al. Blood biomarkers of progressive atherosclerosis and restenosis after stenting of symptomatic intracranial artery stenosis[J]. Scientific Reports, 2021, 11(1): 15599. DOI: 10.1038/s41598-021-95135-y.
[3] 中国心血管健康与疾病报告编写组. 中国心血管健康与疾病报告2022概要[J]. 中国循环杂志, 2023, 38(6): 583−612. DOI: 10.3969/j.issn.1000-3614.2023.06.001. [4] BERGSTRÖM G, PERSSON M, ADIELS M, et al. Prevalence of subclinical coronary artery atherosclerosis in the general population[J]. Circulation, 2021, 144(12): 916−929. DOI: 10.1161/CIRCULATIONAHA.121.055340.
[5] AZIZ M U, SINGH S. Computed tomography of coronary artery atherosclerosis: A review[J]. Journal of Medical Imaging and Radiation Sciences, 2021, 52(S3): S19−S39. DOI: 10.1016/j.jmir.2021.08.007.
[6] 李笑石, 耿纪刚, 朱寅虎, 等. 不同迭代算法对冠状动脉CTA人工智能重建与分析的影响[J]. 中国CT和MRI杂志, 2023, 21(5): 63−66. DOI: 10.3969/j.issn.1672-5131.2023.05.022. LI X S, GENG J G, ZHU Y H, et al. Effects of different reconstruction ratios of iterative modes on artificial intelligence reconstruction and analysis of coronary CTA[J]. Chinese Journal of CT and MRI, 2023, 21(5): 63−66. DOI: 10.3969/j.issn.1672-5131.2023.05.022. (in Chinese).
[7] YANG C C, LAW W Y, LU K M, et al. Relationship between heart rate and optimal reconstruction phase in coronary CT angiography performed on a 256-slice multidetector CT[J]. British Journal of Radiology, 2019, 92(1101): 20180945. DOI: 10.1259/bjr.20180945.
[8] LIANG J, WANG H, XU L. et al. Impact of SSF on diagnostic performance of coronary computed tomography angiography within 1 heart beat in patients with high heart rate using a 256-row detector computed tomography[J]. Journal of Computer Assisted Tomography, 2018, 42(1): 54−61. DOI: 10.1097/RCT.0000000000000641.
[9] 吴锟, 陈希奎, 唐贵超, 等. 320排容积CT“Target CTA扫描模式”在低心率患者冠状动脉CT血管成像中的应用探究[J]. 中国医疗设备, 2023, 38(1): 77−82. DOI: 10.3969/j.issn.1674-1633.2023.01.015. WU K, CHEN X K, TANG G C, et al. Application study of “Target CTA Scanning Mode” in 320-row volume CT for coronary angiography in patients with low heart rate[J]. China Medical Devices, 2023, 38(1): 77−82. DOI: 10.3969/j.issn.1674-1633.2023.01.015. (in Chinese).
[10] 康瑞, 王昕, 石峰. 冠状动脉支架术后CTA成像的优化应用及再狭窄危险因素分析[J]. 中国中西医结合影像学杂志, 2020, 18(2): 153-156. DOI: 10.3969/j.issn.1672-0512.2020.02.014. KANG R, WANG X, SHI F. The optimization of CTA imaging and the analysis of risk factors for the patients of coronary artery stent[J]. Chinese Imaging Journal of Integrated Traditional and Western Medicine, 2020, 18(2): 153-156. DOI:10.3969/j.issn.1672-0512.2020.02.014. (in Chinese).
[11] 王莹, 王奇政, 陈永晔, 等. 基于宽体探测器高分辨率扫描模式下的多种不同重建算法对冠状动脉支架可视化评估对比研究[J]. 中国医学计算机成像杂志, 2022, 28(4): 433−438. DOI: 10.3969/j.issn.1006-5741.2022.04.020. WANG Y W, WANG Q Z, CHEN Y Y, et al. Comparison of different reconstruction algorithms for visual evaluation of coronary stents using the whole-organ high-definition CT scanner[J]. Chinese Computed Medical Imaging, 2022, 28(4): 433−438. DOI: 10.3969/j.issn.1006-5741.2022.04.020. (in Chinese).
[12] 阮席武, 蒋佳珅, 邵君, 等. 高心率患者冠状动脉CTA收缩期绝对时相重组的优化[J]. 临床放射学杂志, 2022, 41(5): 866−871. DOI: 10.3969/j.issn.1001-9324.2022.5.lcfsxzz202205014. RUAN X W, JIANG J S, SHAO J, et al. Optimization of absolute phasic systolic acquisition in coronary CT angiography in patients with high heart rate[J]. Journal of Clinical Radiology, 2022, 41(5): 866−871. DOI: 10.3969/j.issn.1001-9324.2022.5.lcfsxzz202205014. (in Chinese).
[13] 陈艳, 卫旭瑛. 探究多层螺旋CTA成像中心率、最佳重建相位窗对其图像质量的影响[J]. 中国CT和MRI杂志, 2022, 20(6): 90−92. DOI: 10.3969/j.issn.1672-5131.2022.06.029. CHEN Y, WEI X Y. Effect of center rate and optimal reconstruction window of multi-slice spiral (MSCT) CTA imaging on its image quality[J]. Chinese Journal of CT and MRI, 2022, 20(6): 90−92. DOI: 10.3969/j.issn.1672-5131.2022.06.029. (in Chinese).
[14] 王晓瑜, 祁荣兴, 黄胜. 低剂量冠状动脉CTA支架成像研究[J]. 放射学实践, 2019, 34(6): 698−702. DOI: 10.13609/j.cnki.1000-0313.2019.06.021. [15] KIYOHARA Y, AIKAWA T, KAYANUMA K, et al. Comparison of clinical outcomes among various percutaneous coronary intervention strategies for small coronary artery disease[J]. The American Journal of Cardiology, 2024, 211: 334−342. DOI: 10.1016/j.amjcard.2023.11.043.
[16] 中华医学会放射学分会心胸学组, 《中华放射学杂志》心脏冠状动脉多排CT临床应用指南写作专家组. 心脏冠状动脉CT血管成像技术规范化应用中国指南[J]. 中华放射学杂志, 2017, 51(10): 732−743. DOI: 10.3760/cma.j.issn.1005-1201.2017.10.004. [17] 张维明, 牟晓静, 张浩, 等. 不同浓度对比剂在冠状动脉CTA检查中的图像质量临床分析[J]. 医学影像学杂志, 2022, 32(9): 1601−1603. ZHANG W M, MOU X J, ZHANG H, et al. Analysis of image quality and safety of different concentrations of contrast agents in coronary CTA[J]. Journal of Medical Imaging, 2022, 32(9): 1601−1603. (in Chinese).
[18] 杨政君, 张昂, 陈勇, 等. 辐射剂量和管电压对CT图像质量的影响: 基于任务的图像质量评价[J]. CT理论与应用研究, 2022, 31(2): 211−217. DOI: 10.15953/j.ctta.2021.060. YANG Z J, ZHANG A, CHEN Y, et al. The effect of radiation dose and tube potential on image quality of CT: A task-based image quality assessment[J]. CT Theory and Applications, 2022, 31(2): 211−217. DOI: 10.15953/j.ctta.2021.060. (in Chinese).
[19] 余燕武, 崔小巍, 王晓慧, 等. 低管电压技术在高心率患者冠状动脉CTA中的临床应用研究[J]. 中国医学创新, 2020, 17(23): 131−134. DOI: 10.3969/j.issn.1674-4985.2020.23.033. YU Y W, CUI X W, WANG X H, et al. Clinical application of low tube voltage technique in coronary artery CTA in patients with high heart rate[J]. Medical Innovation of China, 2020, 17(23): 131−134. DOI: 10.3969/j.issn.1674-4985.2020.23.033. (in Chinese).
[20] LEE J W, KIM C W, LEE H C, et al. High-definition computed tomography for coronary artery stents: Image quality and radiation doses for low voltage (100 kVp) and standard voltage (120 kVp) ECG-triggered scanning[J]. International Journal of Cardiovasc Imaging, 2015, 31(S1): 39−49. DOI: 10.1007/s10554-015-0686-y.
计量
- 文章访问数: 148
- HTML全文浏览量: 28
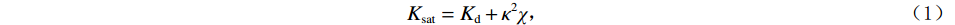
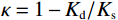
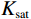
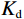
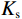
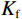
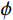
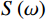
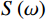
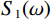
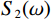
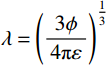
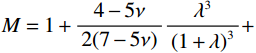
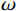
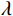
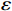
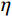
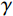
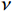
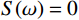
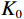
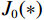
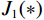
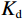
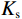
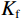
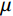
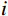
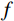
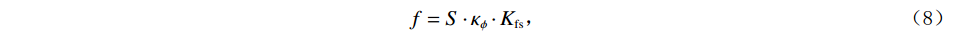
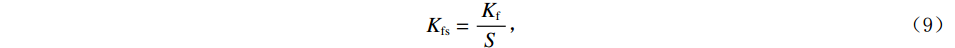
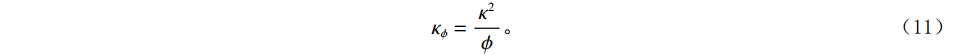
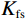
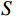
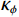
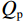
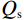
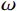
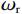
- PDF下载量: 21
