Scattered Wave Simulation Method and Analysis of Influencing Factors
-
摘要:
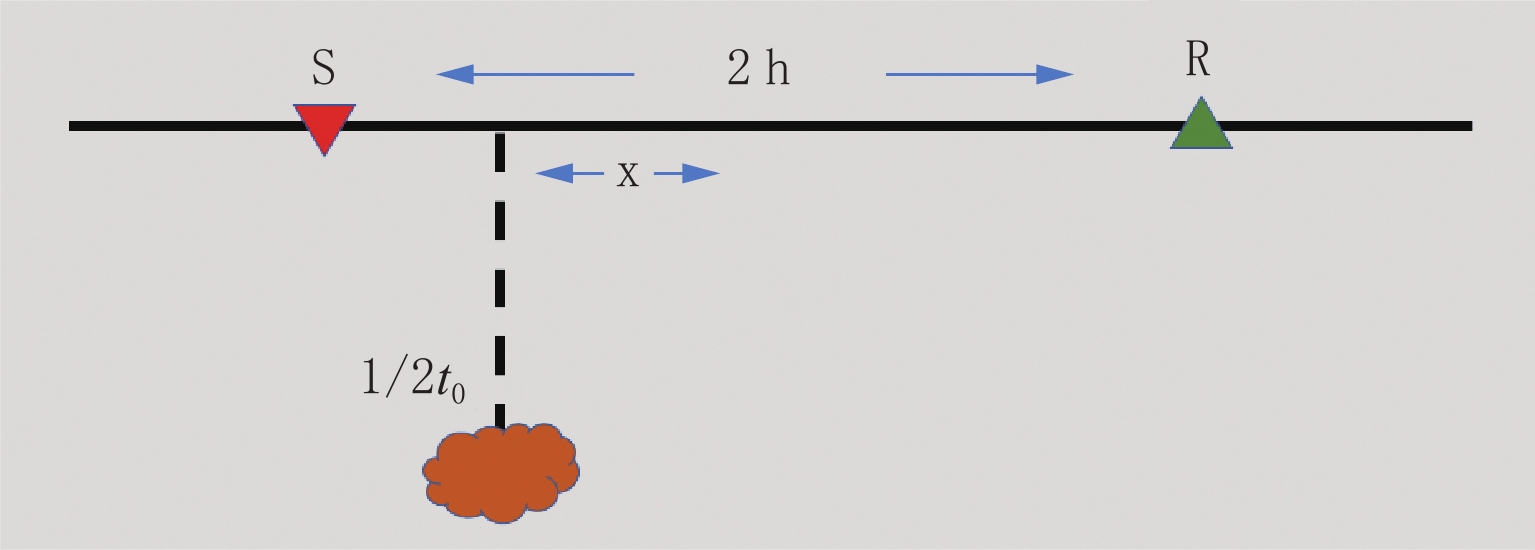
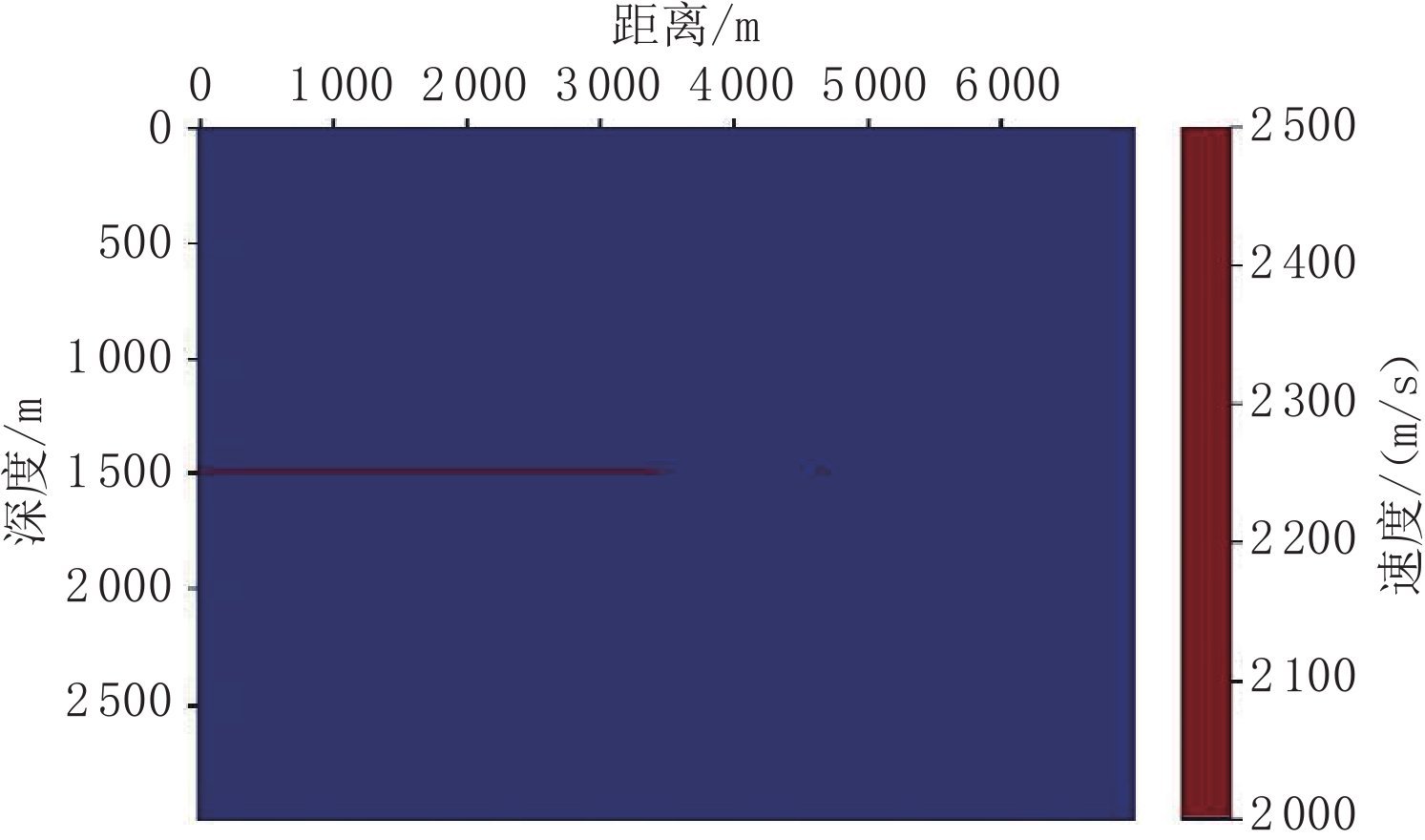
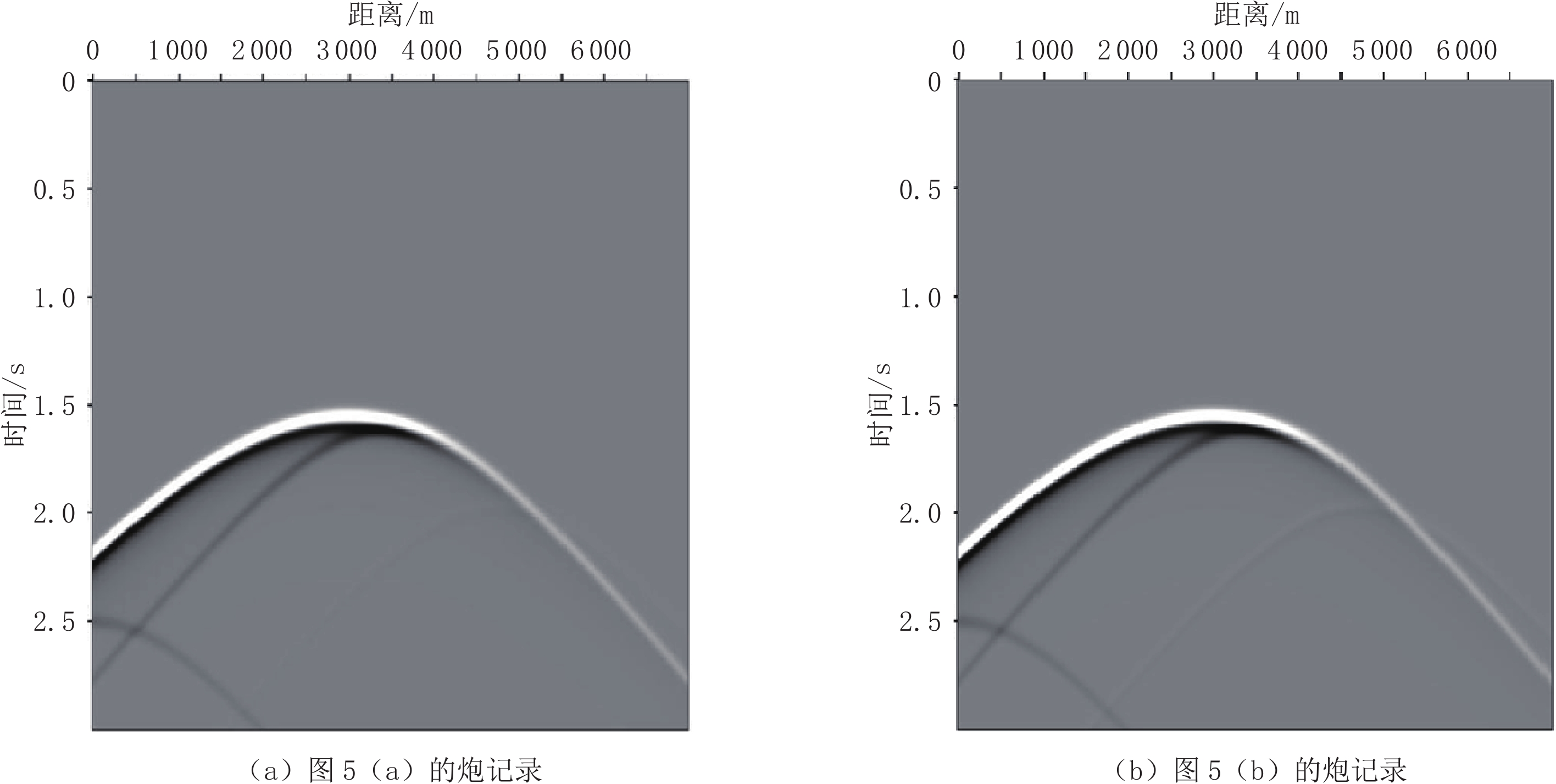
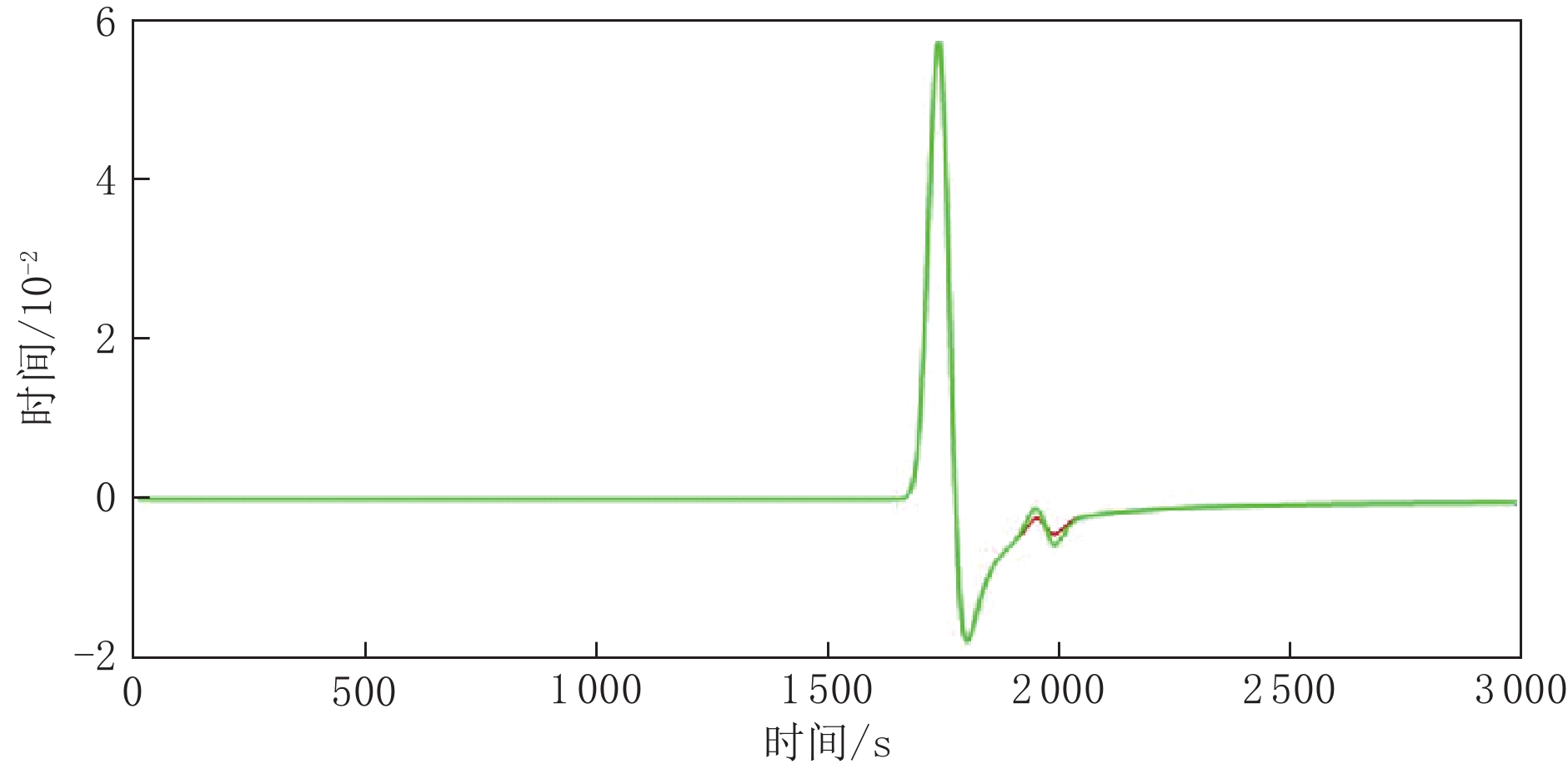
在复杂地质条件下，特别是小断层和裂缝发育的情况下，通常无法利用反射波进行准确探测。将小构造引起的散射波用于地震勘探，有利于提高小尺度离散地质体勘查资料的信噪比和分辨率。本文从理论模拟方法出发，分别推导用于描述散射波传播的时距曲线方程和基于Born近似的波动方程；利用快速步进法对程函方法的求解，通过设计相应的模拟测试，对散射波描述的精度与影响因素进行分析。测试结果表明，传统的时距曲线方程可以给出准确的散射波满足的时距关系，但结合程函方程对其进行成像时并不准确；而基于Born近似的波动方程可以实现对散射波的准确模拟。此外，Born近似中引入的散射体和散射势的假设对最终的模拟结果影响并不大；在保证正演稳定的前提下，子波主频越高，对散射波的描述越准确。
Abstract:In complex geological conditions, especially in the case of small faults and fractures, it is often impossible to use reflected waves for accurate detection. An alternative method is the use of the scattered waves caused by these small structures for seismic exploration. However, with the conventional description and utilization of scattered waves based on time–distance curves, it is difficult to meet the current needs of high-precision exploration. Therefore, starting from the theoretical description method, this study deduces the time–distance curve equation and the wave equation based on Born approximation for describing the propagation of scattered waves. Then, combined with the respective numerical simulation methods, namely, the fast step method to solve the program function method and the finite difference method to simulate the wave equation, the accuracy and influencing factors of the scattered wave description are analyzed. Finally, the corresponding simulation test is designed, and the numerical model is used to further show that the traditional time–distance curve equation can give the accurate time–distance relationship satisfied by the scattered wave, but it is not accurate when combined with the function equation for imaging. The wave equation based on Born approximation can achieve accurate simulation of scattered waves. The resulting assumptions of scatterers and scattering potential have little effect on the final simulation results. Under the premise of ensuring the stability of forward modeling, the higher the dominant frequency of the wavelet, the more accurate is the description of the scattered wave.
-
Keywords:
- scattering wave /
- wave equation /
- ray equation /
- the numerical simulation
-
基底细胞癌（basal cell carcinoma，BCC）与睑板腺癌（sebaceous carcinoma of eyelid，SC）是中老年人最常见的眼睑恶性肿瘤，发病率分别位于第1和第2位，但是因两者恶性程度和侵袭性的不同，患者的治疗方法和预后有很大不同[1-2]。术前对BCC和SC进行定性评估，对手术方法的选择、提高治愈率和降低转移率尤为重要。
本文回顾性分析我院2015年1月至2020年9月经手术病理证实的14例SC及7例BCC的影像学资料，对两种疾病的一般资料与CT、MRI表现做比较和总结，以提高对眼睑部疾病的认识和诊断准确率。
1. 资料和方法
1.1 一般资料
本组SC患者14例，男性1例，女性13例，年龄54～86岁，平均年龄（73.07±10.87）岁。BCC患者7例，男性3例，女性4例，年龄57～84岁，平均年龄（70.71±9.46）岁。临床症状均为发现眼睑部肿物或有异物感，2例既往有眼眶手术史。所有病例最终诊断均由手术病理证实。
1.2 检查方法
14例SC患者术前6例行CT平扫检查，7例行MRI平扫检查，1例行CT与MRI检查。7例BCC患者1例行CT平扫检查，5例行MRI平扫检查，1例行CT与MRI检查。
CT检查采用GE Light speed 16排CT扫描机。扫描参数：120 kV，200 mA，常规扫描层厚3 mm，薄层重建层厚1 mm，螺距1.0；MRI检查采用Philips 3.0 T扫描仪及GE 1.5 T MRI扫描仪，使用眼眶专用线圈，扫描序列包括T1 WI、T2 WI、T2抑脂，DWI，扫描方位包括横断位、冠状位、矢状位，扫描层厚4 mm。
1.3 图像分析
所有患者CT和MRI图像由两位具有5年以上头颈部影像诊断工作经验的放射诊断医师共同阅片，如有意见分歧，两位医师共同协商达成一致意见。分析内容包括病变部位、形态、大小、密度及信号特征、病灶与邻近结构的关系、有无钙化、气体、囊变等。
2. 结果
2.1 睑板腺癌
14例SC患者影像学表现。①发病部位：右眼睑6例，其中4例位于上睑，1例位于下睑，1例病变侵犯眶内；左眼睑8例，3例位于上睑，5例位于下睑。②形态及大小：14例肿瘤长径范围1.1～3.8 cm，平均长径（1.84±0.81）cm；5例肿瘤呈环条状及斑块状附着于眼环前方，可见“弧形征”（图1），8例肿瘤表现为眼睑部软组织结节，其中1例呈“菜花状”向外凸起（图2）；1例肿瘤呈团块状向眼眶内生长；7例病灶边界不清晰，7例边界清晰。③病灶密度及信号特征：7例行CT检查的患者表现为等密度软组织影，病灶较大时密度不均匀，未见囊变坏死区；4例内部见气体密度影，均未见钙化影；8例行MRI检查的患者表现为T1 WI等或低信号，T2 WI呈稍高信号，脂肪抑制序列为高信号，DWI呈高或稍高信号。④病灶与邻近结构的关系：14例中13例局限于眶隔前区，11例表皮受累，2例仅位于皮下未侵及眼睑皮肤（图3），1例肿瘤范围较大，侵犯球内及球后，累及眼外肌、泪腺及视神经。
![]()
图 1 83岁男性，右眼睑板腺癌右眼睑环条状软组织影，边界不清晰，肿瘤累及眼睑皮肤，内见气体密度影，病灶后缘被眼环阻挡呈弧形，即“弧形征”。Figure 1. Male, 83 years old with sebaceous carcinoma in eyelid of the right eye![]()
图 2 81岁女性，左眼睑板腺癌左眼睑软组织结节凸起于眼睑皮肤表面，肿瘤边缘不光整，呈“菜花状”。Figure 2. Female, 81 years old with sebaceous carcinoma in eyelid of the left eye![]()
图 3 56岁女性，右眼睑睑板腺癌（a）T1 WI横断位 （b）T2 WI横断位 右眼睑皮下T1 WI等信号、T2 WI稍高信号结节，边界较清晰，未累及眼睑皮肤。Figure 3. Female, 56 years old with sebaceous carcinoma of eyelid in the right eye2.2 基底细胞癌
7例BCC患者影像学表现。①发病部位：右眼睑4例，左眼睑3例，均位于下睑。②形态及大小：1例呈环条状肿块，3例呈结节状，1例呈扁丘状，边界均较清晰；肿瘤长径范围0.6～4.4 cm，平均长径（1.60±1.58） cm；1例呈边界不清晰的团片状混杂信号影；1例仅见皮肤表面略不光整，未见明显肿块；仅1例见“弧形征”。③病灶密度及信号特征：2例行CT检查的患者表现为密度均匀的软组织影，1例病灶内见点状钙化（图4）；6例行MRI检查的患者表现为T1 WI等或低信号，T2 WI呈稍高或高信号，DWI呈稍高信号。④病灶与邻近结构的关系：7例肿瘤均局限于眶隔前区，2例仅局限在皮肤，未侵犯皮下脂肪组织（图5）。
![]()
图 4 72岁女性，右眼基底细胞癌右眼睑内眦软组织肿块，皮下脂肪间隙存在，病灶内见点状钙化影。Figure 4. Female, 72 years old with basal cell carcinoma in the right eye![]()
图 5 62岁男性，右眼基底细胞癌右眼下睑浅表皮肤扁丘状隆起，T1 WI低信号，T2 WI高信号，边界清楚，未侵犯皮下组织。Figure 5. Male, 62 years old with basal cell carcinoma in the right eye2.3 SC与BCC的鉴别诊断
SC与BCC的一般资料对比（表1）显示，女性患者比例SC（92.9％）高于BCC（57.1％）。
表 1 SC与BCC一般资料对比Table 1. The comparison of general information of SC and BCC肿瘤类型 例数 平均年龄/岁 性别 男 女 SC 14 73.07±10.87 1 13 BCC 7 70.71± 9.46 3 4 SC与BCC发病部位与病灶范围对比（表2）显示，SC上睑发病率高于下睑，BCC则均发生于下睑。SC病例中有1例侵犯眶内，其余病灶均局限于眶隔前区，BCC病例中病灶均局限于眶隔前区。
表 2 SC与BCC发病部位与病灶范围对比Table 2. The comparison of pathogenic sites and lesion range of SC and BCC肿瘤类型 例数 发病部位 病灶范围 上睑 下睑 仅限眶隔前区 向眶内侵犯 SC 14 7 6 13 1 BCC 7 0 7 7 0 SC与BCC影像学特征对比（表3）显示，SC病灶长径大于BCC，形态上28.6％ 的病灶呈环条状，高于BCC（14.3％），SC 14 例病例中有50％ 病灶边界不清晰，高于BCC（14.3％）。病灶出现弧形征、气体征比例SC（35.7％，57.1％）高于BCC（14.3％，0％）。
表 3 SC与BCC影像学特征对比Table 3. The comparison of imaging findings of SC and BCC肿瘤类型 例数 平均长径/cm 形态 边界 弧形征 气体征 环条状 结节状 清晰 不清晰 SC 14 1.84±0.81 4 8 7 7 5 4 BCC 7 1.60±1.58 1 3 6 1 1 0 3. 讨论
3.1 概述
BCC与SC是中老年眼睑常见的两类恶性肿瘤，发病率分别位于第1和第2位，但是因两者恶性程度不同，致使治疗方法和预后有很大不同[1-2]。BCC是最常见的皮肤恶性肿瘤，起源于表皮基底层，男性患者比例稍多于女性，大部分发生在下眼睑[3]，侵袭邻近结构及发生转移概率较低，患者一般预后较好，紫外线照射是其重要的危险因素[4-5]。SC发生于眼睑Meibomian腺或Zeis腺[6]，在我国眼睑恶性肿瘤中，位居第2位，约占31.7％[7]，女性较男性多见，易发生于上睑[8]，而在西方人种中较为罕见[9]。
SC恶性程度较高，可侵犯临近组织结构并发生淋巴结及血行转移，患者预后不良，死亡率可高达50％ 以上，临床上表现为眼睑弥漫性增厚，部分可触及眼睑肿块。目前该疾病主要依靠活检进行组织病理学诊断[10]。
3.2 SC影像学特征
病灶在CT表现为软组织密度影[9]，密度较均匀，囊变及钙化少见，形态多呈环条状、结节状软组织影像。本研究中14例SC中12例呈结节状、环条状，与文献相符[11]。MRI表现为T1 WI等或低信号，T2 WI呈稍高信号，DWI呈高或稍高信号，这可能与SC肿瘤细胞较密集造成扩散受限有关。SC特征性影像学改变为病灶后方被眼环阻挡呈“弧形征”，以及病灶内部因继发坏死感染形成的气体征[11-12]，本研究发生率分别为35.7％（5/14）和57.1％（4/7）。晚期肿瘤可侵犯眶内及球内，并可发生淋巴结转移和远处转移[13]。
3.3 BCC的影像学特征
肿瘤病理学最常见的类型有结节型和浅表型，影像学结节型表现为眼睑部皮肤及皮下软组织结节，浅表型表现为扁丘状及鳞片状软组织斑块[4-5]。本研究中两种病理类型BCC比例分别为42.9％（3/7）和28.6％（2/7）。BCC在MRI中病灶内常有T2 WI高信号区，这与BCC瘤体中含有充满粘液的囊腔有关，此信号特点与本研究病例的MRI特征相符。侵犯皮下组织较少见，本研究7例BCC患者中有2例局限在皮肤，未侵犯皮下，与文献报道[3]稍不符，需要更大样本量加以印证。BCC如果不及时治疗或术后复发也可侵犯至球内及球后，此外CT、MRI检查可评估BCC的淋巴结转移、远处脏器转移及骨骼受累情况[3]。
3.4 SC与BCC的相似点
SC与BCC作为眼睑常见的恶性肿瘤，好发于中老年，均发生于眶隔前区，影像学均表现为眼睑部软组织肿块。CT密度较均匀，病灶内少见囊变、液化坏死，MRI信号相似，均为T1 WI等或低信号，T2 WI呈稍高或高信号，DWI呈稍高信号。
3.5 SC与BCC鉴别诊断要点
结合本组对比研究结果及文献资料，总结SC与BCC鉴别诊断要点如下：
①发病性别和发病部位：SC好发于老年女性，肿瘤多位于上眼睑；BCC患者男女性患者比例相近，肿瘤多位于下眼睑。②病灶起源位置、形态及边界：SC起源于皮下睑板，向表皮层生长，形态多呈环条状和结节状，病灶边界清晰或不清晰；而BCC起源于皮肤，向皮下生长，形态多呈结节状或扁丘状，有时仅见皮肤破损改变，病灶边界较清晰。③影像学特殊征象：弧形征、气体征多见于SC，病灶内钙化可能更多见于BCC，需要更多行CT检查的BCC病例证实。
3.6 本研究的局限性
①本研究为回顾性研究，患者检查设备和扫描方案不完全一致，大部分患者未同时行CT、MRI检查，对分析病灶内部成分造成困难。②入组患者未行增强检查，无法获取肿瘤的血供、强化曲线等信息。③样本量较少，分析结果可能存在一定偏差，需要在今后的工作中进一步收集病例。
综上所述，SC与BCC是中老年眼睑最常见的两种恶性肿瘤，在流行病学、发病部位、影像学特征等方面均有一定的差异，对于老年女性发生于上眼睑的环条状病灶，CT及MRI发现弧形征、气体征的影像学特征，边界不清晰，应首先考虑为SC；如果病灶发生于下眼睑，呈结节状或扁丘状，边界较清晰，病变仅局限于皮肤未侵及皮下，则首先考虑为BCC。掌握以上鉴别要点，可提高眼睑恶性肿瘤术前诊断的准确性，降低误诊率。
-
![]()
图 6 较大尺度和速度散射体对应的炮记录
Figure 6. Shot records corresponding to larger scale and velocity scatterers
![]()
图 7 位于
4500 m处trace对比，绿色代表原始记录，红色代表大散射体记录Figure 7. Comparison of a trace located at
4500 m, where green represents the original record and red represents the large scatter record![]()
图 8 不同主频子波对应的散射波场
Figure 8. Scattered wave fields corresponding to different main frequency wavelets
![]()
图 9 不同差分阶数对应的散射波场
Figure 9. Scattered wave fields corresponding to different differential orders
-
[1] KREY T. The significance of diffraction in the investigation of faults[J]. Geophysics, 1952, 17(4): 843−858. DOI: 10.1190/1.1437815.
[2] KUNZ B F J. Diffraction problems in fault interpretation[J]. Geophysical Prospecting, 1960, 8(3): 381−388. DOI: 10.1111/j.1365-2478.1960.tb01722.x.
[3] HARPER D R. Observed reflection and diffraction wavelet complexes in two-dimensional seismic model studies of simple faults[J]. Geophysics, 1965, 30(1): 72−86. DOI: 10.1190/1.1439546.
[4] GRASMUECK M, MOSER T J, PELISSIER M A, et al. Diffraction signatures of fracture intersections[J]. Interpretation, 2015, 3(1): SF55−SF68. DOI: 10.1190/INT-2014-0086.1.
[5] BASHIR Y, GHOSH D P, SUM C W. Influence of seismic diffraction for high-resolution imaging: Applications in offshore Malaysia[J]. Acta Geophysica, 2018, 66: 305−316. DOI: 10.1007/s11600-018-0149-7.
[6] SCHWARZ B. An introduction to seismic diffraction[M]//Advances in geophysics. Elsevier, 2019, 60: 1-64.
[7] HILTERMAN F J. Three-dimensional seismic modeling[J]. Geophysics, 1970, 35(6): 1020−1037. DOI: 10.1190/1.1440140.
[8] HILTERMAN F. Amplitudes of seismic waves: A quick look[J]. Geophysics, 1975, 40(5): 745−762. DOI: 10.1190/1.1440565.
[9] TROREY A W. Diffractions for arbitrary source-receiver locations[J]. Geophysics, 1977, 42(6): 1177−1182. DOI: 10.1190/1.1440782.
[10] BERRYHILL J R. Diffraction response for nonzero separation of source and receiver[J]. Geophysics, 1977, 42(6): 1158−1176. DOI: 10.1190/1.1440781.
[11] BUCHEN P W, HADDON R A W. Diffraction of a plane pulse by thin arbitrarily shaped obstacles[J]. The Journal of the Acoustical Society of America, 1980, 68(1): 309−313. DOI: 10.1121/1.384597.
[12] MOSER T J, Howard C B. Diffraction imaging in depth[J]. Geophysical Prospecting, 2008, 56(5): 627−641. DOI: 10.1111/j.1365-2478.2007.00718.x.
[13] LANDA E, KEYDAR S, MOSER T J. Multifocusing revisited-inhomogeneous media and curved interfaces[J]. Geophysical Prospecting, 2010, 58(6): 925−938. DOI: 10.1111/j.1365-2478.2010.00865.x.
[14] STURZU I, POPOVICI A M, PELISSIER M A, et al. Diffraction imaging of the Eagle Ford shale[J]. First Break, 2014, 32(11).
[15] 汤聪, 符力耘, 肖富森, 等. 金属矿地震勘探进展与展望[J]. 地球与行星物理论评, 2022, 53(2): 187−203. DOI: 10.19975/j.dqyxx.2021-015. TANG C, FU L Y, XIAO F S, et al. Review of progress in seismic exploration in metallic deposits[J]. Reviews of Geophysics and Planetary Physics, 2022, 53(2): 187−203. DOI: 10.19975/j.dqyxx.2021-015. (in Chinese).
[16] KLEM-MUSATOV K. Theory of seismic diffractions[M]. Society of Exploration Geophysicists, 1994.
[17] RIEBER F. Visual presentation of elastic wave patterns under various structural conditions[J]. Geophysics, 1936, 1(2): 196−218. DOI: 10.1190/1.1437093.
[18] RIEBER F. Geological causes of poor reflection records[J]. American Association of Petroleum Geologists Bulletin, 1936, 20(11): 1520−1520.
[19] RIEBER F. Complex elastic wave patterns in the earth and their directional analysis[J]. The Journal of the Acoustical Society of America, 1937, 9(1): 75−75.
[20] HAGEDOORN J G. A process of seismic reflection interpretation[J]. Geophysical prospecting, 1954, 2(2): 85−127. DOI: 10.1111/j.1365-2478.1954.tb01281.x.
[21] 叶峻林, 李桂花, 丁仁伟, 等. 基于滤波处理的地震散射波分离方法研究综述[J]. CT理论与应用研究(中英文), 2024, 33(1): 105−117. DOI: 10.15953/j.ctta.2023.085. YE J L, LI G H, DING R W, et al. Review of Research on Filtering-based Methods for Seismic Scattered Wave Separation[J]. CT Theory and Applications, 2024, 33(1): 105−117. DOI: 10.15953/j.ctta.2023.085. (in Chinese).
[22] KELLER J B. Geometrical theory of diffraction[J]. Josa, 1962, 52(2): 116−130. DOI: 10.1364/JOSA.52.000116.
[23] TROREY A W. A simple theory for seismic diffractions[J]. Geophysics, 1970, 35(5): 762−784. DOI: 10.1190/1.1440129.
[24] HARLAN W S, CLAERBOUT J F, ROCCA F. Signal/noise separation and velocity estimation[J]. Geophysics, 1984, 49(11): 1869−1880. DOI: 10.1190/1.1441600.
[25] KHAIDUKOV V, LANDA E, MOSER T J. Diffraction imaging by focusing-defocusing: An outlook on seismic superresolution[J]. Geophysics, 2004, 69(6): 1478−1490. DOI: 10.1190/1.1836821.
[26] FOMEL S. Applications of plane-wave destruction filters[J]. Geophysics, 2002, 67(6): 1946−1960. DOI: 10.1190/1.1527095.
[27] FOMEL S, LANDA E, TANER M T. Poststack velocity analysis by separation and imaging of seismic diffractions[J]. Geophysics, 2007, 72(6): U89−U94. DOI: 10.1190/1.2781533.
[28] KLOKOV A, FOMEL S. Separation and imaging of seismic diffractions using migrated dip-angle gathers[J]. Geophysics, 2012, 77(6): S131−S143. DOI: 10.1190/geo2012-0017.1.
[29] FOMEL S, KAZINNIK R. Non-hyperbolic common reflection surface[J]. Geophysical Prospecting, 2013, 61(1): 21−27. DOI: 10.1111/j.1365-2478.2012.01055.x.
[30] TYIASNING S, MERZLIKIN D, COOKE D, et al. A comparison of diffraction imaging to incoherence and curvature[J]. The Leading Edge, 2016, 35(1): 86−89. DOI: 10.1190/tle35010086.1.
[31] BANCROFT J C, XU Y. Equivalent offset migration for vertical receiver arrays[M]//SEG Technical Program Expanded Abstracts 1999. Society of Exploration Geophysicists, 1999: 1279-1282.
[32] MARGRAVE G F, BANCROFT J C, GEIGER H D. Fourier prestack migration by equivalent wavenumber[J]. Geophysics, 1999, 64(1): 197−207. DOI: 10.1190/1.1444516.
[33] 李雪英, 程云, 聂伟东, 等. 基于两步扫描法的Kirchhoff时间最优偏移孔径[J]. 东北石油大学学报, 2019, 43(3): 12-19. LI X Y, CHENG Y, NIE W D, et al. Optimal migration aperture of Kirchhoff time based on two-step scanning method[J]. Journal of Northeast Petroleum University, 2019, 43(3): 12-19. (in Chinese).
[34] HADDON R A W, BUCHEN P W. Use of Kirchhoff's formula for body wave calculations in the earth[J]. Geophysical Journal International, 1981, 67(3): 587−598. DOI: 10.1111/j.1365-246X.1981.tb06939.x.
[35] 孙辉, 岳玉波, 李猛. 基于Born散射理论的二维黏声介质高斯波束正演[J]. 地球物理学报, 2021, 64(2): 637−644. SUN H, YUE Y B, LI M. Gaussian beam orthogonalization in two-dimensional viscous acoustic media based on Born scattering theory[J]. Chinese Journal of Geophysics, 2021, 64(2): 637−644. (in Chinese).
[36] 李武群, 毛伟建, 欧阳威, 等. 二阶Born近似及其在逆散射GRT反演中的应用[J]. 地球物理学进展, 2017, 32(2): 645−656. LI W Q, MAO W J, OUYANG W, et al. Second-order Born approximation and its application to inverse scattering GRT inversion[J]. Progress in Geophysics, 2017, 32(2): 645−656. (in Chinese).
[37] 李天扬, 李桐林, 孟相禹. 基于程函方程快速行进法的地震走时层析成像法[J]. 世界地质, 2021, 40(3): 664−670, 679. LI T Y, LI T L, MENG S Y. Seismic walk-time laminar imaging based on the fast marching method of the eikonal of equations[J]. World Geology, 2021, 40(3): 664−670, 679. (in Chinese).
[38] 任卫波. 基于快速行进法地震层析成像研究[J]. 矿产勘查, 2020, 11(5): 977−987. DOI: 10.3969/j.issn.1674-7801.2020.05.018. REN W B. Research on seismic tomography based on fast marching method[J]. Mineral Exploration, 2020, 11(5): 977−987. DOI: 10.3969/j.issn.1674-7801.2020.05.018. (in Chinese).
[39] 张剑锋. 一种高精度有限元弹性波场正演方法[J]. 石油地球物理勘探, 1994(1): 29−36, 126. ZHANG J F. A high-precision finite element elastic wavefield orthorectification method[J]. Oil geophysical Prospecting, 1994(1): 29−36, 126. (in Chinese).
[40] 石颖, 陆加敏, 柯璇, 等. 基于GPU并行加速的叠前逆时偏移方法[J]. 东北石油大学学报, 2012, 36(4): 111−115, 11. SHI Y, LU J M, KE X, et al. Prestack reverse time migration based on GPU parallel acceleration algorithm[J]. Journal of Northeast Petroleum University, 2012, 36(4): 111−115, 11. (in Chinese).
[41] 赵越, 李貅, 王祎鹏, 等. 三维起伏地形条件下航空瞬变电磁响应特征研究[J]. 地球物理学报, 2017, 60(1): 383-402. ZHAO Y, LI C, WANG Y P, et al. Characterization of aerial transient electromagnetic response under three-dimensional undulating terrain conditions[J]. ChineseJournal of Geophysics, 2017, 60(1): 383-402. (in Chinese).
-
期刊类型引用(1)
1. 贾红敏，卫宏江，赵瑾璐，杨正汉. CT增强长时间延迟扫描在腹膜假黏液瘤PCI评分中的价值研究. CT理论与应用研究(中英文). 2025(02): 311-318 . 
百度学术
其他类型引用(0)
下载:
计量
- 文章访问数: 176
- HTML全文浏览量: 46
- PDF下载量: 36
- 被引次数: 1
