Image Quality Inprovement for Small Vessel in Diabetic Foot Arteriography Using Dual-energy Computed Tomography
-
摘要:
目的:探究能谱CT在糖尿病患者足部动脉造影中小血管成像的应用价值。材料和方法:前瞻性收集2022年1月至2023年1月于我院放射科行下肢血管CTA检查的30例糖尿病患者。在患者行下肢CT血管造影(传统CTA组)后,立即采集足部血管的能谱图像,获得最佳虚拟单能图像(能谱CTA组),将两组的足部图像进行比较,以观察足部动脉小血管的显示并且计算对比噪声比(CNR)和信噪比(SNR)。使用5分法对动脉走向和小血管显示进行评分。结果:能谱CTA组中的CNR和SNR显著优于传统CTA组。能谱CTA组的胫后动脉和足背动脉的主观评分也显著高于传统CTA组(均 > 3分)。结论:与传统CTA成像相比,能谱成像能够提供更好的图像质量,提高足动脉造影的诊断性能,增加医生对疾病诊断的信心。
Abstract:Objective: To investigate the feasibility of dual-energy computed tomography (DECT) in foot arteriography for small vessel image quality in patients with diabetes . Methods: A total of 30 patients with diabetes were enrolled prospectively between January and November 2022 in the radiology department of our hospital, where DECT was acquired immediately after the CT angiography (routine CTA group) of the lower extremity.The optimal virtual monochromatic images (DECT group) were derived from the DECT data. Image quality was assessed by measuring the CT values and noise in foot arteries, and signal-tonoise ratio (SNR) and contrast-to-noise ratio (CNR) were calculated. The arterial course and small vessel display were scored using a 5-point scale (1, poor; 5, excellent). Results: The CNR and SNR were significantly better in the DECT group than in the routine CTA group. The DECT group received higher subjective scores on the posterior tibial artery and the foot arteries (all > 3) than did the routine CTA group. Conclusion: Compared to the routine CTA imaging, DECT offers superior image quality for foot arteriography, thereby enhancing the diagnostic accuracy of foot arteriography and bolstering physicians’ confidence in disease diagnosis.
-
Keywords:
- dual-energy CT /
- foot angiography /
- virtual monoenergetic images /
- image quality /
- diabetes
-
地球物理勘探转战复杂环境区域,使得勘探数据资料的质量要求也随之提高。由于地震勘探采集到的数据往往不仅包括目标体的信息,同时含有各种各样的噪声干扰,因而需要进行有效的数据去噪处理[1]。地震数据去噪处理主要包括原始采集数据加工、消除噪声影响,提高目标资料的信噪比,为后续处理和资料解释奠定基础。噪声的存在,严重影响资料的准确度和保真性,因而高效的去噪方法研究很有必要[2-3]。
传统的傅里叶变换、小波变换、曲波变换和F-X域反褶积滤波等方法广泛应用于地震勘探数据去噪领域[4]。但传统方法稀疏表示能力差,不能有效反映地震数据的特征。字典学习(dictionary learning,DL)是跨学科研究领域的新代表,集合了稀疏表示、机器学习、图像应用和压缩感知等的理论思想,主要用于解决稀疏表示模型的字典设计问题。贺月等[5]将其用于数据去噪、图像识别、数据重构等领域,得到了出色的效果。字典学习包含固定基函数解析型字典和自适应学习型字典。后者可以不断学习训练更新字典,提高字典的表达能力,得到更稀疏的信号表示,因此自适应学习型字典应用更为广泛。
基于非正交基理论,分解信号数据的同时会得到稀疏系数矩阵,提出了超完备字典方法作为字典学习理论基础。练秋生等[6]将匹配追踪方法作为稀疏表示方法延续技术,取得了不错的进展;随后Chen[7]提出了解决稀疏优化问题的基追踪方法,Olshausen等[8]提出了自适应学习型完备字典。自适应训练并更新字典,使得大多系数等于零或者无限接近为零,达到以更少的信息来反映样本特征的目的。为了更高效地训练得到自适应学习型字典,Aharonm[9]提出了奇异值分解(K-singular value decomposition,K-SVD)算法。该方法基于奇异值分解方法对字典中的元素依次代替刷新,最终获得所需的过完备字典,且随着整体迭代的进行,会同时更新系数矩阵与字典原子。压制噪声的原理为字典与稀疏表示系数重组结合,因而自适应字典学习方法可以达到训练并不断更新字典和有效去噪同步进行的效果。
Tang等[10]率先将学习型完备字典应用到地震勘探数据去噪中,在对输入信号的不断学习训练后,更新字典的同时得到稀疏表示系数,并实现了优于传统方法的去噪效果,但地震勘探数据的复杂性使得迭代次数要求更多,以至于运算时间更长。Simon等[11]提出一个基于变分稀疏表示模型的学习算法,最优方向法(method of optimal directions,MOD)算法更新字典,取得了一定去噪结果。周艳辉等[12]将基于K-SVD的范数稀疏字典学习方法与多震源混合地震记录分离方法结合,证明了方法的可行性,但相比固定基字典计算效率需要进一步加强。许德鑫[13]提出将K-SVD算法中的MOD算法换成StOMP(stagewise orthogonal matching pursuit)算法,既克服正交匹配追踪(orthogonal matching pursuit,OMP)算法导致的过匹配现象,又进一步使收敛速度明显提高。张成[14]提出了一种基于K均值序贯泛化算法字典的地震勘探数据去噪思路,基于控制干扰的Controlled-SGK方法,通过判定信噪比值是否大于设定的阈值来判断是否更新下一个原子,以此来控制噪声干扰,去噪质量得到大的提高。在压制随机噪声方面,屈光中[15]提出了基于固定基字典的双稀疏学习型字典,并首次成功应用于地震信号随机噪声的压制中,该字典通过训练得到的稀疏表示系数结合固定基字典构成,结构性与稀疏性比较高,字典表达能力和去噪效果相比传统固定基字典学习均更有优势。张岩等[16]利用多道相似组稀疏表示方法压制随机噪声;王惠迎等[17]提出自适应学习字典分类得压制方法;王量等[18]提出在线字典学习算法进行地震数据去噪。
然而,学习完整尺寸的数据字典原子是不容易计算的,因为它需要大量的训练样本,每个维度的原子都被学习。经过训练的字典集也太大,无法在实践中使用,因为超过的完整字典包含的原子比它们的维度还要多。分块理论的引入,一定程度上可解决上述问题维度过大的问题。分块理论的应用较为成熟的领域为块匹配三维协同滤波,该方法将数据域与频率域有效结合,通过对观测数据进行分块,采用块匹配和分组进行数据聚集,可较好保留图像或数据的细节信息,取得较好的去噪结果。然而,块理论与字典学习的研究在地震数据处理领域应用较少,因而开展分块字典学习算法地震勘探数据去噪研究具有重要的现实意义。
综上所述,基于字典学习的跨学科去噪方法研究是当前研究热点,新的稀疏编码方法和字典更新方法不断涌现,适应范围也在扩大至三维地震数据去噪、重构和全波形反演、电法和电磁法数据去噪等方向。随着字典学习算法的研究,将在地球物理勘探数据处理中发挥更大的作用。
1. 方法理论
假设Y为输入的时间域地震信号数据,将时间域地震数据通过分块模块函数R进行分块,因此,基于分块理论,字典学习地震勘探数据去噪问题可以分解为单个块数据的字典学习问题:
$$ ({\boldsymbol{X}},{\boldsymbol{D}})\in \underset{x,d}{{\rm{arg\;min}}}\sum\limits_{i,j}\Bigg(\frac{1}{2}{\Big\|{R}_{i,j}\left(Y\right)-d\cdot {x}_{i,j}\Big\|}^{2}+\lambda {\Big\|{x}_{i,j}\Big\|}_{1}\Bigg) \text{,} $$ (1) 其中,X和D为稀疏表示系数矩阵和计算的字典矩阵,x和d为各个块稀疏表示稀疏及字典原子,(i,j)的稀疏表示稀疏及字典的位置,λ为控制因子,由试验确定取值。字典学习算法中更新稀疏表示的稀疏矩阵采用OMP方法,更新字典则使用MOD方法。
1.1 正交匹配追踪(OMP)算法
OMP算法的核心要求是找到输入信号与字典原子内积最大的原子,定义其为匹配检索项,从而除去与之相关的数据,剩余部分再次与其他原子求内积值,寻找结构上有一定相关性的原子,直至剩余信号满足停止条件,就结束迭代。内积表示其实就是反映输入信号和字典原子的相关性,相关性越大,则说明两者的内积越大,结构越相似,进一步表明两者一定程度上可以近似相等。以一维信号为例,对于输入信号
$ y\in {R}^{m\times 1} $ ,建立字典${\boldsymbol{D}}= ({d}_{1},\;{d}_{2},\cdots ,\;{d}_{n})$ ,且满足$\|d_i\|^2 $ =1,D中的n个原子不需要正交。遍历字典中的每一个原子,使其分别与信号做内积,并选出最大内积对应原子d1:$$ (y,{d}_{1}) > (y,{d}_{i})\;{d}_{i}\in {\boldsymbol{D}}(i\ne 1) 。 $$ (2) 通过从信号y中减去其在d1所张成空间上的正交投影得到残差e1[14]:
$$ {e}_{1}=y-{d}_{1}(y,{d}_{1}) 。 $$ (3) 对残差重复继续以上两式,当残差大小或着迭代次数满足条件时,停止迭代。
其正交化所有当前选中原子,继承了原子处理步骤的规则,从而迭代的最优性得到保留。同样以一维信号为例,信号经k步分解后,当前选择出的原子用
${\hat{d}}_{1}(l=\mathrm{1,\;2},\cdots ,\;k)$ 表示,信号y可以表示为:$$ y=\sum _{l=1}^{k}{x}_{l}^{k}{\hat{d}}_{l}+{e}_{k} \text{,} \left({e}_{k},\;{\hat{d}}_{l}\right)=0\left(l=\mathrm{1,2},\cdots ,k-1\right) 。 $$ (4) 在进行k+1步迭代时,从剩余原子中选择出与ek内积最大的原子dk+1,将dk+1与之前选出的k个原子做正交化处理:
$$ {\hat{d}}_{k+1}={d}_{k+1}-\sum _{i=1}^{k}\frac{\left({d}_{k+1},{\hat{d}}_{i}\right)}{\left({\hat{d}}_{i},{\hat{d}}_{i}\right)}{\hat{d}}_{i} 。 $$ (5) 残差
$ {e}_{k} $ 投影到正交化后的$ {\hat{d}}_{k+1} $ 上,可得:$$ {e}_{k+1}={e}_{k}-\frac{\left({e}_{k},{\hat{d}}_{k+1}\right)}{\left({\hat{d}}_{k+1},{\hat{d}}_{k+1}\right)}{\hat{d}}_{k+1} 。 $$ (6) 在k次迭代后,信号表示可约为:
$$ y=\sum_{i=1}^{k}\frac{\left({e}_{i},\;{\hat{d}}_{i}\right)}{\left({\hat{d}}_{i},\;{\hat{d}}_{i}\right)}{\hat{d}}_{i} 。 $$ (7) 1.2 最优方向(MOD)算法
最优方向(MOD)算法把字典学习问题作为嵌套的最小化问题:内层看成给定字典的情况下关于非零项稀疏表示系数Xj个数的最小化问题,外层是定义在字典D之上的最小化问题。这种交替最小化的思路将第k−1步得到的字典D(k-1)来求解第k 步的稀疏系数,可以得到矩阵X(k),最后用最小二乘求解D(k)[19],即
$$ {{\boldsymbol{D}}}_{\left(k\right)}=\mathit{{\rm{arg}}}\underset{D}{{\rm{min}}}\Big\|{{\boldsymbol{Y}}-{\boldsymbol{D}}}{{{\boldsymbol{X}}}}_{\left(k\right)}\Big\|_{2}^{2}={\boldsymbol{Y}}{{\boldsymbol{X}}}_{\left(k\right)}^{\rm{T}}\Big({{\boldsymbol{X}}}_{\left(k\right)}{{\boldsymbol{X}}}_{\left(k\right)}^{\rm{T}}\Big)^{-1}={\boldsymbol{Y}}{{\boldsymbol{X}}}_{\left(k\right)}^+ 。 $$ (8) MOD算法的详细描述如下所示:
Input:给出用于训练的数据,稀疏度L
Output:重构数据字典D
1).初始化:令k=0,用M个随机选择的样本来构造字典
${{\boldsymbol{A}}}_{\left(0\right)}\in {R}^{n\times M}$ ,同时各列归一化处理;2).迭代:k每次加1,并按照一下步骤执行;
3).稀疏编码:用追踪算法近似求解
${\hat{x}}_{j}=\underset{x}{\mathrm{{\rm{arg}}}{\rm{min}}}{\big\|{y}_{j}-{{\boldsymbol{D}}}_{(k-1)}x\big\|}_{2}^{2}\;\;\text{s.t.}\;\;\| x\|_{0}\le L$ ,得出稀疏系数$ {\hat{x}}_{j} $ ,组构成矩阵${{\boldsymbol{X}}}_{\left(k\right)}$ ;4).字典更新:用公式(8)更新字典;
5).达标停止迭代:如果
${‖{\boldsymbol{Y-A{{\boldsymbol{X}}}}}_{\left(k\right)}‖}_{2}^{2}$ 的变化量足够的小则停止迭代,输出结果为${{\boldsymbol{A}}}_{\left(k\right)}$ ;否则继续转到步骤2。对于给定的信号集,MOD算法既能得到冗余字典,又能得到稀疏表示矩阵,且表示误差最小,但其优化结果是一个高度非凸的组合问题,能得到局部最优解。一般来说,MOD算法只需要少量的迭代就可以实现收敛,算法非常高效。结合OMP算法与MOD算法,本文求解字典学习问题流程如下:
(1)归一化原始数据M0,加高斯随机噪声后得含噪数据M;
(2)用OMP思想对原始数据M0编码得稀疏系数X,用MOD思想更新字典D1,重构计算信噪比;
(3)用OMP思想对含噪数据M编码得稀疏系数X,结合上一步的字典D1重构得到去噪后的数据M;
(4)重复第(2)和第(3)两步,即完成两次字典学习。
2. 算例分析
2.1 数值模拟算例
数值模拟算例为合成地震勘探数据,主要包含水平及倾斜地震波同相轴,同时包含复杂的同相轴相交的情况,如图1(a)所示(Data 1)。图1(b)所示为按照5×5矩阵进行分块示意图,可见,分块对原始数据各个不同特征分布均有所涵盖。下文算例中均采用相同分块模式,更新迭代100次,不再图示及概述。对合成模拟数据加入20%(噪声幅值与信号幅值的比值)随机噪声,如图1(b)所示,噪声遍布数据整个范围,地震波同相轴被噪声淹没。去噪结果表明(图1(c)),字典学习数据去噪的效果是可行的,背景噪声滤除较为干净,有效成分被较好保留。图2为上述图1(a)所示相同地震波同相轴成分,但不同分布情况(Data 2)。对Data 2数据加入相同的20% 随机噪声,去噪结果可见,不同类型的同相轴均有效保留,噪声消除效果较好,显示了本文算法的可行性及有效性。
图3是Data 3合成数据字典学习去噪结果,与前述两个合成算例不同,Data 3 数据为单独水平同相轴和相交同相轴地震波形。结合前述图1和图2所示结果分析,Data 3数据分布较为规则(图3(a)),但交叉型地震波同相轴位于数据集中部,其两侧交叉位置同相轴较为复杂。含噪数据则使得上述交叉部分的同相轴更为复杂(图3(b))。从图3(c)去噪结果可见,去噪后同相轴分布与Data 3原始数据同相轴分布一致,复杂同相轴蕴含更多信息被有效保留。当交叉型地震波不对称时,字典学习过程分块对不对称交叉型同相轴的选取亦会不一样,其去噪的难度增加,如图4(a)所示。当加入20%随机噪声,如图4(b)所示,含噪数据在左侧不对称交叉型同相轴更加复杂化。图4(c)去噪结果可见,字典学习有效恢复了不对称交叉型同相轴分布,去噪效果良好,再次显示了该算法的可行性及有效性。
表1所示为上述Data 1-Data 4合成地震数据及其对应去噪结果按照标准信噪比(单位dB)与运行时间对比。由表格结果可见,加入20% 随机噪声地震数据信噪比较低,均小于4 dB;去噪后,4个合成数据算例信噪比得到大大提高,最高算例提高约15 dB。运行时间方面,针对上述4个算例按5×5分块策略及64×64数据集,在普通电脑(RAM 8 G,i7-CPU,2.6 GHz)上需要耗时小于35 s。可见,基于分块理论字典学习算法计算效率是可行的。
表 1 不同模拟数据去噪前后信噪比与运行时间Table 1. SNR and running time of different analog data before and after denoising类型 去噪前信噪比/dB 去噪后信噪比/dB 运行时间/s Data 1 3.539 17.436 30.2 Data 2 2.909 18.553 26.1 Data 3 3.089 18.326 28.2 Data 4 2.883 16.618 32.9 2.2 实测数据算例
实测数据算例1如图5(a)所示,地震波同相轴主要以水平状为主,从采集时间早期到晚期,地震波同相轴由强幅值变化为弱幅值。由于强幅值同相轴与弱幅值同相轴在字典学习过程获得的原子各异,常规字典学习算法在处理此类地震数据过程中存在误处理问题。通过对原始数据进行5×5分块,选取了强弱不同幅值的同相轴均匀分布,保证了不同幅值同相轴在学习过程中出现的概率,因而可一定程度上改善上述误处理问题。如图5(b)所示,加入20% 随机噪声作为干扰成分,可见,噪声的存在使得实测数据更为复杂。图5(c)所示为本文方法去噪结果,采集时间早期和晚期对应不同幅值同相轴得到有效恢复和凸显,噪声消除较为干净,验证了本文算法对不同幅值同相轴同时存在的地震数据去噪领域的可行性及有效性。
图6所示为实测数据算例2字典学习去噪结果。图6(a)为原始数据,可见,算例2中地震波同相轴多以倾斜类型为主,部分区域掺杂了其他微弱杂波。加入20% 随时噪声后,如图6(b)所示,仅可模糊分辨部分较强幅值同相轴,其他同相轴均被随机噪声覆盖,使得原始数据分布更为复杂。图6(c)为字典去噪结果,相对较原始数据分布,去噪结果较好的恢复了倾斜的地震波同相轴分布,其中,绝大部分噪声能得到压制,对于弱幅值地震波同相轴保护较好,波形同相轴质量得到有效保障。
图7所示为实测数据算例3字典学习与其他方法去噪结果对比图。图7(a)为原始实测地震数据,可见,原始数据包含了水平、倾斜及弯曲类型地震波同相轴,同时不同采集时间段内出现了同相轴断缺、强弱幅值同相轴现象,是较为复杂的地震数据。通过采用本文5×5分块策略,得到了分块字典学习示意图(图7(b)),分块图中囊括了原始数据大部分特征区域,为后续分块字典学习去噪奠定了基础。同样,对原始数据加入20% 随机噪声,如图7(c)所示,噪声的存在使得原始地震波形的分布更为复杂,若不进行有效去噪,无法对有效波形进行正确识别。为了进行有效性对比,本文引入小波变换及曲波变换去噪算法进行对比分析,其中,小波变换采用Sym8小波基函数,分解层数为3层;曲波变换采用L2标准差作为阈值函数。图7(d)和图7(e)分别为小波变换和曲波变换算法去噪结果,可见,总体上随机噪声基本得到清除。但由于小波变换采用矩形单元窗口,导致倾斜特征地震波同相轴出现断续波形现象;而曲波变换由于计算的标准差阈值不能完全适用强弱幅值波形同相轴,出现了曲波变换倾斜矩形单元窗口拉长同相轴现象。图7(f)为本文字典学习算法去噪结果,相比之下,由于分块策略选择了各种不同特征波形同相轴,因而去噪结果可有效保留不同强弱幅值、不同类型的地震波同相轴。整体上,字典学习算法去噪效果由于小波变换或曲波变换算法的去噪效果,验证了本文算法可用于复杂地震波数据的去噪领域。
整体上,字典学习算法去噪效果由于小波变换或曲波变换算法的去噪效果,验证了本文算法可用于复杂地震波数据的去噪领域。
3. 结论
针对含随机噪声地震数据处理问题,本文采用基于分块理论的字典学习算法开展了数值模拟算例及实测地震数据算例去噪研究。首先详细介绍了基于分块理论字典学习地震数据去噪算法的基本原理及实现流程。通过对水平及倾斜地震波同相轴、交叉型地震波同相轴合成数据算例加入随机噪声,采用本文去噪方法进行数据恢复,获得较好的去噪效果,各算例的信噪比得到大幅度提升,验证了本文算法的可行性。最后,将本文方法用于加入随机噪声的实测数据算例去噪处理,同时将去噪结果与小波变换、曲波变换算法去噪结果对比,验证了本文算法用于实测数据的有效性。
-
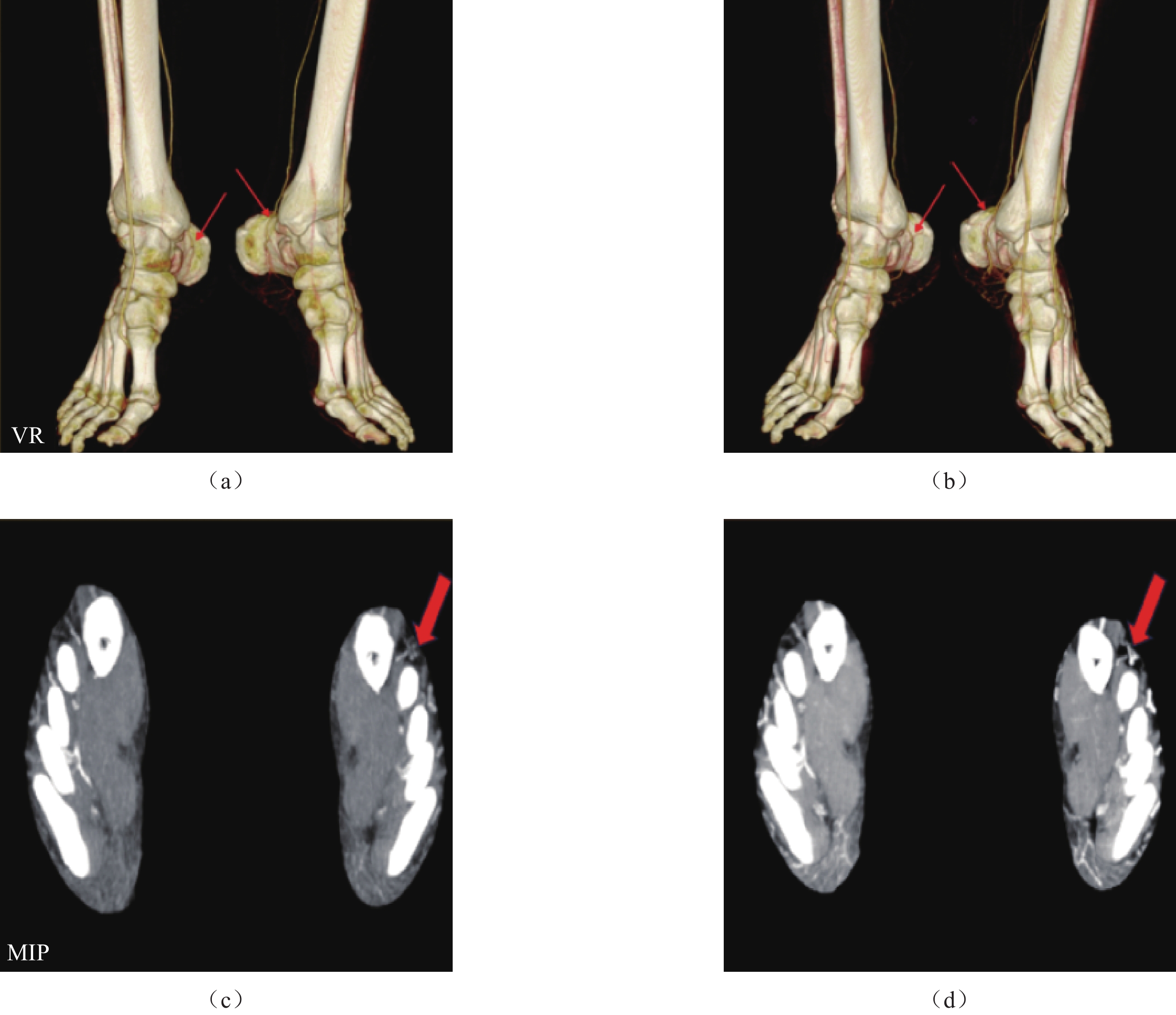
表 1 两组CTA图像质量客观评估
Table 1 Comparison of objective image quality scores between the two CTA groups
组别 项目 传统CTA 双能CTA 统计检验 Z P SNR 胫后动脉 6.66±3.00 10.05±6.40 −3.279 0.001 足背动脉 4.57±2.99 7.37±3.12 −3.748 < 0.001 足底动脉 6.20±3.25 8.60±4.51 −3.416 0.001 CNR 胫后动脉 16.63±4.72 23.72±9.53 −4.008 < 0.001 足背动脉 12.67±6.45 20.50±7.89 −4.012 < 0.001 足底动脉 13.73±4.78 22.75±9.13 −4.349 < 0.001 表 2 主观图像评分
Table 2 Comparison of subjective image quality scores between the two groups
血管走形与对比剂显示 传统CTA 能谱CTA P Score(mean±SD) Kappa value Score(mean±SD) Kappa value 胫后动脉 3.45±0.72 0.80 4.00±0.84 0.88 0.001 足背动脉 2.14±0.89 0.88 3.23±1.05 0.86 0.001 足底动脉 2.33±0.85 0.88 3.23±1.20 0.87 0.001 -
[1] MISHRA S C, CHHATBAR K C, KASHIKAR A, et al. Diabetic foot[J]. British Medical Journal, 2017, 359(S1): 1-7.
[2] 纪东华, 刘暴. 膝下动脉血运重建的临床实践中国专家共识[J]. 中国循环杂志, 2024, 39(2): 116-122. DOI: 10.3969/j.issn.1000-3614.2024.02.002. JI D H, LIU B. Chinese expert consensus on the standards of practice on below-the-knee arteries revascularisation[J]. Chinese Circulation Journal, 2024, 39(2): 116-122. DOI: 10.3969/j.issn.1000-3614.2024.02.002. (in Chinese).
[3] 孙旭, 王东军, 朱朝军, 等. 中医外治视域下糖尿病足研究关键问题及思考[J]. 时珍国医国药, 2023, 34(12): 2984-2986. [4] COLE J B, FLOREZ J C. Genetics of diabetes mellitus and diabetes complications[J]. Nature Review Nephrology, 2020, 16(7): 377-390. DOI: 10.1038/s41581-020-0278-5.
[5] FORBES J M, COOPER M E. Mechanisms of diabetic complications[J]. Physiological Review, 2013, 93(1): 137-188. DOI: 10.1152/physrev.00045.2011.
[6] CORRIERE M, ROOPARINESINGH N, KALYANI R R. Epidemiology of diabetes and diabetes complications in the elderly: An emerging public health burden[J]. Current Diabetes Report, 2013, 13(6): 805-813. DOI: 10.1007/s11892-013-0425-5.
[7] SHARMA S, SCHAPER N, RAYMAN G. Microangiopathy: Is it relevant to wound healing in diabetic foot disease?[J]. Diabetes/Metabolism Reserch and Review, 2020, 36(S1): e3244. DOI: 10.1002/dmrr.3244.
[8] 郭晓曦, 林禹, 吕绍茂, 等. 下肢动脉双能量CT成像不同能量融合图像与单能量图像的对比研究[J]. 临床放射学杂志, 2021, 40(2): 363-368. GUO X X, LIN Y, LV S M, et al. A comparative study of different fusion image and monoenergetic image in dual-energy CT of lower extremity artery[J]. Journal of Clinical Radiology, 2021, 40(2): 363-368. (in Chinese).
[9] 刘衡, 冉启胜, 夏传江, 等. 下肢动脉血管造影技术对糖尿病足患者末梢动脉准确显示的应用研究[J]. 重庆医科大学学报, 2019, 44(10): 1351-1354. LIU H, RAN Q S, XIA C J, et al. Application of CT-angiography in accurate display of peripheral arteries in patients with diabetic foot[J]. Journal of Chongqing Medical University, 2019, 44(10): 1351-1354. (in Chinese).
[10] HSIEH J, FLOHR T. Computed tomography recent history and future perspectives[J]. Journal of Medical Imaging, 2021, 8(5): 52109.
[11] MCCOLLOUGH C H, LENG S, YU L, et al. Dual-and multi-energy CT: Principles, technical approaches, and clinical applications[J]. Radiology, 2015, 276(3): 637-653. DOI: 10.1148/radiol.2015142631.
[12] JACOBSEN M C, THROWER S L, GER R B, et al. Multi-energy computed tomography and material quantification: Current barriers and opportunities for advancement[J]. Journal of Medical Physics, 2020, 47(8): 3752-3771. DOI: 10.1002/mp.14241.
[13] 王文杰, 陈平, 潘晋孝, 等. 基于参考组分的双能CT成像方法[J]. CT理论与应用研究, 2021, 30(1): 61-69. DOI: 10.15953/j.1004-4140.2021.30.01.06. WANG W J, CHEN P, PAN J X, et al. Dual-energy CT imaging method based on reference components[J]. CT Theory and Applications, 2021, 30(1): 61-69. DOI:10.15953/j.1004-4140.2021.30.01.06. (in Chinese).
[14] 梁洪伟, 周旸, 张志伟, 等. 双能CT虚拟单能级成像显示胰周血管: 与线性融合图像对照研究[J]. 中国医学计算机成像杂志, 2022, 28(1): 56-62. DOI: 10.3969/j.issn.1006-5741.2022.01.012. LIANG H W, ZHOU Y, ZHANG Z W, et al. Dual-energy CT with virtual monoenergetic images in demonstration of peripancreatic vessels: Comparison with polyenergetic images[J]. Chinese Computed Medical Imaging, 2022, 28(1): 56-62. DOI: 10.3969/j.issn.1006-5741.2022.01.012. (in Chinese).
[15] 侯凯, 吕鹏, 顾君英, 等. 实时阈值手动触发技术在下肢动脉CT血管成像中的临床应用价值[J]. 中国临床医学, 2016, 23(1): 81-85. HOU K, LV P, GU J Y, et al. The clinical application value of real time threshold manual trigering technique in the lower extremity arterial CT angiography[J]. Chinese Journal of Clinical Medicine, 2016, 23(1): 81-85. (in Chinese).
[16] WICHMANN J L, GILLOTT M R, de CECCO C N, et al. Dual-energy computed tomography angiography of the lower extremity runoff: Impact of noiseoptimized virtual monochromatic imaging on image quality and diagnostic accuracy[J]. Investigative Radiology, 2016, 51(2): 139-146. DOI: 10.1097/RLI.0000000000000216.
[17] JIA X, LI X, LI J, et al. Improving diagnostic accuracy for arteries of lower extremities with dual-energy spectral CT imaging[J]. European Journal of Radiology, 2020, 128: 109061. DOI: 10.1016/j.ejrad.2020.109061.
[18] WANG G, ZHAO D, LING Z, et al. Evaluation of the best single-energy scanning in energy spectrum CT in lower extremity arteriography[J]. Experimental and Therapeutic Medicine, 2019, 18(2): 1433-1439.
[19] SUN H, SAEEDI P, KARURANGA S, et al. IDF diabetes atlas: Global, regional and country-level diabetes prevalence estimates for 2021 and projections for 2045[J/OL]. Diabetes Research and Clinical Practice, 2022, 183: 109-119.
[20] JUDE E B, OYIBO S O, CHALMERS N, et al. Peripheral arterial disease in diabetic and nondiabetic patients: A comparison of severity and outcome[J]. Diabetes Care, 2001, 24(8): 1433-1437. DOI: 10.2337/diacare.24.8.1433.
[21] GOLLEDGE J. Update on the pathophysiology and medical treatment of peripheral artery disease[J]. Nature Reviews Cardiology, 2022, 19(7): 456-474. DOI: 10.1038/s41569-021-00663-9.
[22] LOW WANG C C, BLOMSTER J I, HEIZER G, et al. Cardiovascular and limb outcomes in patients with diabetes and peripheral artery disease: The EUCLID Trial[J]. Journal of the American College of Cardiology, 2018, 72(25): 3274-3284. DOI: 10.1016/j.jacc.2018.09.078.
[23] 任宁, 李启富, 程庆丰. 糖尿病周围动脉疾病的诊疗进展[J]. 重庆医学, 2012, 41(33): 3547-3549. DOI: 10.3969/j.issn.1671-8348.2012.33.037. [24] American Diabetes Association. Microvascular complications and foot care: Standards of medical care in diabetes[J]. Diabetes Care, 2018, 41(S1): S105-S118.
-
期刊类型引用(2)
1. 蒋柏峰. 基于匹配追踪的信号去噪方法性能影响因素分析. 环境技术. 2024(06): 114-119 .  百度学术
百度学术
2. 魏天罡,张珩,李福强,王波. 多尺度曲率在渤海K油田断裂解释中的应用. CT理论与应用研究. 2024(06): 773-780 .  本站查看
本站查看
其他类型引用(2)
























 下载:
下载: