Q-factor Estimation Method Based on Time-varying Wavelet
-
摘要:
谱比法是估计Q值的常用方法,根据不同时刻地震子波对数谱比值与Q值之间的线性关系估算品质因子Q。时频域谱比法的基本思想是用时频谱分析提取不同时刻的频谱,代表对应时刻的地震子波频谱,忽略反射系数对地震子波的影响。由于受到局部反射系数的影响,时频谱比法求取Q时地震子波对数谱比往往具有复杂的多峰形态,偏离了对数谱比随频率线性变化的关系,线性拟合求取的Q值误差较大,不满足地层岩性解释和孔隙流体预测的要求。针对以上问题,将复赛谱分析与广义S变换相结合,提出一种消除反射系数影响的时变子波频谱提取方法,提高Q值估计的精度。利用广义S变换将地震记录变换到时频域,对地震记录的时频谱取对数,得到不同时刻地震记录的复赛谱。在复赛谱域子波位于低频段,反射系数位于中高频段。因此利用最小二乘法对低频段复赛谱进行平滑拟合,得到子波的复赛谱,再取复赛谱的指数,得到时变子波的频谱,通过相邻时刻子波的对数频谱比与Q值的线性关系计算Q值。模型测试结果验证时变子波提取的准确性以及估计Q值的可行性和抗噪性,东部某油田实际地震数据的应用结果验证该方法的有效性。
Abstract:The spectral ratio method is a technique commonly used for estimating Q values. It calculates the quality factor Q based on the linear relationship between the logarithmic spectral ratio of seismic wavelets at different times and the Q value. The core idea of the time-frequency domain spectral ratio method is to extract the spectral distribution at different moments via time-frequency spectrum analysis, representing the frequency spectrum of seismic wavelets at those moments while ignoring the influence of reflection coefficients. However, because of the impact of local reflection coefficients, the logarithmic spectral ratios of seismic wavelets obtained via the time-frequency spectral ratio method often exhibit complex multi-peak patterns, deviating from the linear relationship between logarithmic spectral ratios and frequency. This leads to significant errors in Q values derived from linear fitting, which fail to meet the requirements for lithological interpretation and pore fluid prediction. To address the issues, the present study combines cepstral analysis with the Generalized S-transform to propose a time-varying wavelet spectrum extraction method that eliminates the influence of reflection coefficients, thereby improving the Q estimation accuracy. First, the Generalized S-transform is applied to convert seismic records into the time-frequency domain. The logarithmic time-frequency spectrum of the seismic records is then computed to obtain their cepstra at different times. In the cepstral domain, the wavelet components reside in the low-frequency band, whereas reflection coefficients occupy the mid-to-high-frequency bands. By applying least-squares smoothing to the low-frequency cepstral components, the wavelet cepstrum is derived. Taking the exponential of the cepstrum reconstructs the spectrum of the time-varying wavelet. Finally, Q values are calculated using the linear relationship between the logarithmic spectral ratios of adjacent wavelets and the Q value. Model tests validate the accuracy of time-varying wavelet extraction, as well as the feasibility and noise resistance of Q estimation. Application to real seismic data from an oilfield in eastern China further confirms the effectiveness of the method.
-
近几十年来,冠状动脉支架植入术越来越多地用于阻塞性冠状动脉疾病(coronary artery disease,CAD)的非手术治疗。与球囊血管成形术相比,该方法大大降低了冠状动脉支架内再狭窄(in-stent restenosis,ISR)的发生率[1-2]。然而,在裸金属支架(bare-metal stents,BMS)患者中ISR的发生率仍可达20%~35%,约18%的ISR患者会出现急性冠脉综合征和ST段抬高型心肌梗死[3]。选择性冠状动脉造影(invasive coronary angiography,ICA)可直接观察冠状动脉血管腔,因此仍被认为是检测ISR的金标准。但ICA是一种侵入性手术,具有明显的创伤性。
近年来,冠状动脉计算机断层扫描(coronary computed tomography angiography,CCTA)因其较高的阴性预测值,在冠心病的诊疗中发挥着重要作用[4-6]。然而,CCTA的一个主要局限性是难以准确评估冠状动脉严重钙化或冠状动脉支架患者的管腔[7-8]。为解决在这一问题,Yoshioka等[9]提出了一种冠脉减影的方法(subtraction-CCTA,sub-CCTA),以消除硬化伪影的影响。多项研究表明,sub-CCTA提高了钙化节段的诊断准确性,增强了读片者的诊断信心[9-14],但针对支架节段的研究相对较少。Amanuma等[15]验证了在单次屏气扫描模式下,sub-CCTA可显著提高ISR的诊断准确性,但该方法要求患者要连续屏气25 s,而且额外的减影序列增加了患者的辐射剂量。
本研究旨在探究双屏气模式下,sub-CCTA评估支架内再狭窄的临床价值。
1. 资料与方法
1.1 患者一般资料
本研究经过本院伦理委员会的批准,所有患者签署知情同意书。
2022年10月至2023年5月期间,对来我科进行冠状动脉CTA检查的患者进行前瞻性登记。
纳入标准:①年龄≥18岁;②静息时或用药控制后心率小于等于70 bpm;③有经皮冠状动脉介入治疗(percutaneous coronary intervention,PCI)手术史,至少植入一枚支架;④无心律失常或心力衰竭;⑤若有ICA结果,与CCTA间隔小于一个月。排除标准:①运动伪影严重,减影配对失败;②不耐受β-受体阻滞剂(美托洛尔25~150 mg);③CCTA和ICA之间的间隔大于一个月。
最终入组83名患者,161个支架节段,分析减影冠状动脉技术对支架节段的诊断价值,其中22名患者54个支架节段在随后的一个月内在本院心内科接受ICA检查,这一部分患者纳入诊断准确性研究。
1.2 扫描方法
患者使用320排探测器CT扫描仪器(Aqunlion One Genesis Edition,佳能医疗公司)。探测器宽度160 mm,层厚0.5 mm,管球转速275 ms,采用自适应迭代低剂量技术(AIDR3D)。
根据临床要求,需要扫描钙化积分序列,故采用两次屏气法,以钙化积分平扫作为减影的“蒙片”,再进行增强扫描。所有扫描均采用前瞻性心电门控扫描。根据患者体重指数(body mass index,BMI)值大小选择使用100 kV或120 kV的管电压,管电流由自动曝光控制系统(sure Exposure)确定。目标图像噪声标准差(standard deviation,SD)为26 Hounsfield增强造影剂为碘帕醇(370 mg/mL),保持10 s注射时间,以体重(kg)×0.07 mL/s的速度在10 s(固定时间)内注射,随后注入50 mL盐水冲洗。
1.3 Sub-CCTA处理方法
使用Sure Subtraction Coronary软件进行冠脉减影。
如之前所报道:首先,以70%~80%相位,1%间隔重建平扫和增强的图像,从中挑出最佳质量的相位序列,用于减影配准。减影配准分两步进行:第1步进行全局非刚性配准;第2步对支架节段进行局部刚性配准,保证两次扫描支架位置的一致。最后生成减影后去除支架的图像,导出减影图用于分析报道[8]。测量减影前后的主动脉根部的CT值,以评估减影对CT值的影响。
1.4 图像分析
将常规CCTA图像(conventional CCTA,con-CCTA)和减影图像(sub-CCTA)导入佳能后处理工作站(Vitrea workstation Version 40693),由两位具有10年以上心血管阅片经验的放射科医生采用双盲法进行评估。
对减影前后所有支架节段,管腔内径进行测量、评估,统计医师诊断信心及可评估节段数量。每节段的诊断可信度按5点利克特量表评分估算:5=非常高;4=高;3=中等;2=低;1=非常低。
根据心血管计算机断层扫描学会(Society of Cardiovascular Computed Tomography,SCCT)的18节段模型[16]对所有支架节段进行狭窄度评估,狭窄程度的评估采用目测法。管腔狭窄程度分为以下7类。
1−正常:无斑块,管腔无狭窄;2−轻微狭窄:有斑块,管腔狭窄1%~24%;3−轻度狭窄:管腔狭窄25%~49%;4−中度狭窄;管腔狭窄50%~69%;5−重度狭窄:管腔70%~99%;6−闭塞;7−因硬化伪影而无法判读。狭窄<50%的节段归为ISR阴性(−)组,狭窄百分比≥50的节段归为ISR阳性(+)组,不可评估节段纳入ISR阳性(+)组。
ICA图像由另外两名在ICA解读方面拥有10年以上经验的介入医生进行评估,将所有支架节段按照与CCTA图像相同的等级表及狭窄程度进行评估。对所有符合标准的支架节段进行诊断准确性分析。
1.5 统计分析
采用SPSS 25.0进行统计分析。符合正态分布的连续变量以(均数±标准差)表示,非正态分布变量用中位数(四分位)表示。对正态分布变量采用配对t检验进行评估和比较,对不符合正态分布的变量采用Wilcoxon检验。可判读率分析采用McNemar检验。
以ICA结果为金标准,计算con-CCTA和sub-CCTA的敏感性,特异性、阳性预测值、阴性预测值。用MedCalc绘制两种技术对比的受试者操作特征曲线(receiver operator characteristic curve,ROC),通过ROC曲线下面积(area under the cure,AUC)对诊断准确性进行总体比较。
P<0.05表示差异有统计学意义。
2. 结果
2.1 基本信息
最终入组83名患者。男性63(75.9%)例,女性20(24.1%)例,平均年龄(64.5±10.9)岁,平均心率(56.5±7.1)bpm,体重指数(25.9±3.5)kg/m2(表1)。CCTA总有效剂量为(4.9±2.8)mSV,平均钙化积分(不包括支架节段)为500.6。
表 1 入组患者的基本信息Table 1. Baseline patient characteristics名称 结果 年龄/(岁,平均值±SD) 64.5±10.9 男性/(人数,百分比) 63(75.9%) 心率/bpm 56.5±7.1 BMI/(kg/m2) 25.9±3.5 冠状动脉风险因素(个数,百分比) 高血压(n,%) 61(70.9%) 高血脂(n,%) 60(72.3%) 吸烟(n,%) 46(55.4%) 糖尿病(n,%) 40(48.2%) 总有效辐射剂量/(mSv,中位数,IQR) 4.9±2.8 平均钙化积分(中位数,IQR) 500.6(150.3~ 1500.4 )减影后主动脉根部平均CT值从521.5 HU降到488.8 HU,仍符合诊断标准[17]。支架内的CT值变化由于误差较大,并未纳入统计。
支架节段(共161个)所在位置:右冠状动脉近段11个(6.8%);右冠状动脉中段14个(8.7%);右冠状动脉远段9个(5.6%);左主干2(1.2%);左前降支近段50(31.1%);左前降支中段32(19.8%);左前降支远段5(3.1%);回旋支近段18(11.2%);回旋支远段9(5.6%);后降支1(0.6%);后侧支2(1.2%);后侧支1(0.6%);第1对角支5(3.1%);第1钝圆支2(1.2%)。
减影前医师对支架节段(共161个)的狭窄程度评估分别为:1−正常无斑块101个(62.7%),2−轻微狭窄6个(3.7%),3−轻度狭窄4个(2.5%),4−中度狭窄2个(1.2%),5−重度狭窄1个(3.1%),6−闭塞0个;7−无法判读47个(29.2%)。减影后医师对狭窄度的评估依次为:96个(59.6%),25个(15.5%),8个(4.9%),10个(6.2%),9个(5.6%),0个,13个(8.1%)。
2.2 图像质量评价和医师诊断信心
统计医师诊断信心评分及可判读率。每节段的诊断可信度按5点利克特量表评分估算:5=非常高;4=高;3=中等;2=低;1=非常低。在con-CCTA图像中,医师诊断确信度平均值为(2.55±1.1),相比之下,sub-CCTA图像诊断可信度上升到(3.86±0.7)(表2)。161个支架节段中无法评估节段从47(29.2%)降到13(8.1%)个,差异有统计学意义(表2和图1)。由于错误配准、心脏搏动等原因,仍有8.1%节段无法判读。
表 2 主观评价和可判读率Table 2. Subjective assessment and diagnosable percentage项目 主观评价 con-CCTA sub-CCTA P 诊断可信度 得分(均值±SD) 2.55±1.1 3.86±0.7 <0.01 可判读率 可判读节段数n,(%) 114(70.8) 148(91.9) <0.01 不可判读节段数n,(%) 47(29.2) 13(8.1) 注:con-CCTA为常规冠状动脉计算机扫描,sub-CCTA为减影CCTA,SD为标准差。 ![]() 图 1 一名60岁男性病例注:60岁男性患者,con-CCTA血管树VR图(a),右冠状动脉CPR(b);sub-CCTA右冠状动脉CPR图(c)。在传统CCTA上显示:RCA近段3.5 mm支架(蓝色箭头)有钙化斑块,疑似支架内狭窄度>50%(有ISR),医师诊断信心度低(2分);右冠远段2.5 mm支架(橙色箭头)由于部分容积效应医师无法评估,诊断信心极低(1分)。在sub-CCTA上显示: RCA近段3.5 mm支架(蓝色箭头)轻度狭窄,狭窄度<50%(无ISR),医师诊断信心较高(5分);右冠远段2.5 mm支架(橙色箭头)内官腔通畅,无狭窄,诊断信心高(4分)。Figure 1. Representative images from a 60-year-old male patient
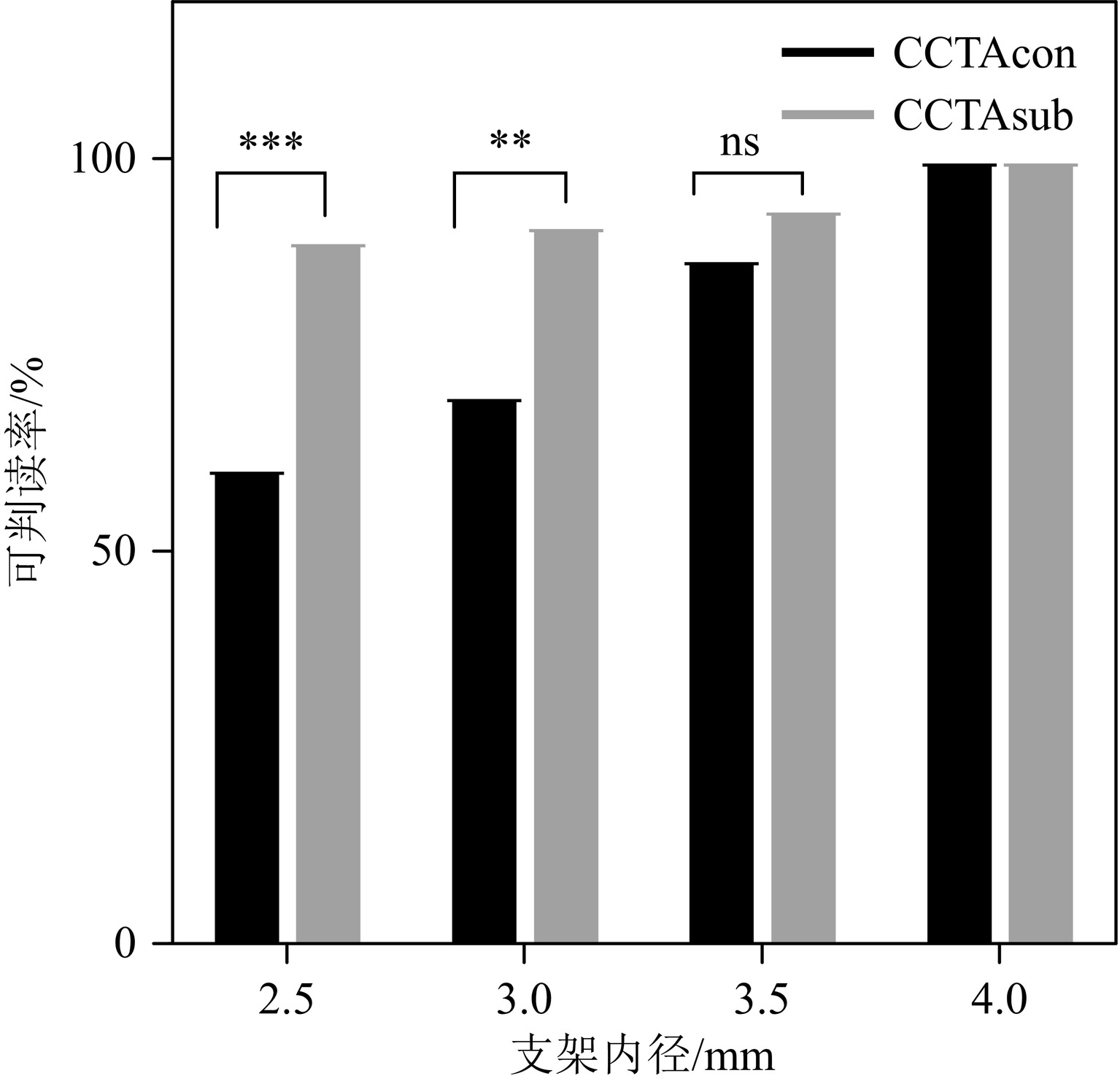
图 1 一名60岁男性病例注:60岁男性患者,con-CCTA血管树VR图(a),右冠状动脉CPR(b);sub-CCTA右冠状动脉CPR图(c)。在传统CCTA上显示:RCA近段3.5 mm支架(蓝色箭头)有钙化斑块,疑似支架内狭窄度>50%(有ISR),医师诊断信心度低(2分);右冠远段2.5 mm支架(橙色箭头)由于部分容积效应医师无法评估,诊断信心极低(1分)。在sub-CCTA上显示: RCA近段3.5 mm支架(蓝色箭头)轻度狭窄,狭窄度<50%(无ISR),医师诊断信心较高(5分);右冠远段2.5 mm支架(橙色箭头)内官腔通畅,无狭窄,诊断信心高(4分)。Figure 1. Representative images from a 60-year-old male patient支架内径为测量值,每次选取3个不同位置得出数据最后取平均值。161个节段中:2.5 mm 69个,3.0 mm 60个,3.5 mm 16个,4.0 mm 16个。在Con-CCTA中,各内径可判读节段数(率)分别为:42(60.8%)、42(70.0%)、14(87.5%)、16(100%);结合减影图像后,可判读节段数(率)分别为62(89.8%)、55(91.7%)、15(93.8%)、16(100%)。
分析结果显示,减影冠状动脉CT成像可大幅提高2.5 mm和3.0 mm支架的可判读性(图1和图2),而在3.5 mm和4.0 mm支架之间没有明显差异。
2.3 诊断准确性评估
对于支架内狭窄(ISR)的评估。以ICA结果作为金标准,患者减影前后的图像由两名具有10年以上诊断经验的放射科医生采用双盲法进行评估,以狭窄率50%为界,≤50%为狭窄阴性(−)组,≥50%为狭窄阳性(+)组,不可评估节段被视为重度狭窄纳入阳性组,意见不一致时,协商决定。
如表3及图3所示,sub-CCTA的假阳性率5.8%较con-CCTA 35.2%有显著下降,特异性从64.7%提升到94.1%;此外,sub-CCTA的阳性预测值和阴性预测值均高于con-CCTA。用ROC曲线下面积AUC来评估两种方法的诊断准确性,AUC分别为0.626(0.496~0.574)和0.817(0.474~0.873),差异有统计学意义(图4)。
表 3 con-CCTA、sub-CCTA对诊断支架节段的准确性指标(节段数=54)Table 3. Diagnostic accuracy of con-CCTA and sub-CCTA in severely calcified segments (n=54)诊断方法 敏感度/% 特异度/% PPV/% NPV/% FP/% 95% CI con-CCTA 60 67.7 50.0 73.3 35.2 0.478~0.749 sub-CCTA 70 94.1 87.5 84.2 5.8 0.707~0.921 注:PPV为阳性预测值,NPV为阴性预测值,FP为假阳性率。 3. 讨论
本研究主要有两个结论:①双屏气法sub-CCTA可大幅提高冠脉支架节段可判读率,提高医生的诊断信心;②sub-CCTA与传统冠脉CT成像结合,可以显著提高对冠状动脉支架内再狭窄的诊断准确性。
近年来随着高端螺旋CT的快速发展,CCTA已经成为冠状动脉粥样硬化心脏病患者评估管腔狭窄的情况最主要的无创方法,然而CCTA的主要局限性之一是在钙化和支架等高吸收材料存在情况下,硬化伪影会增加观察管腔内狭窄的难度[18]。在冠状动脉严重钙化节段或支架节段,由于部分容积效应或线束硬化伪影,通常很难对管腔狭窄情况准确评估。
之前有文献报道,在严重钙化节段,约有38.7%~50%的节段被判定为无诊断意义[10],通过对造影前后获得的数据进行相减,消除造影剂增强以外的高密度区域以及相关伪影,将会使评估管腔变的容易。Amanuma等[15]研究表明当加入sub-CCTA提供的信息后,不可评估节段的数量从74个减少到18个,我们的研究中不可评估节段占比从47个(29.2%)下降到13个(8.1%)。Santis等[19]使用5点利克特量表对诊断信心进行评分,他们的研究表明钙减法算法提高了诊断信心,平均得分从3.1~4.0。本研究医师诊断信心从2.55~3.86,较其他研究者低的原因可能是医师受减影图像质量的影响。
在sub-CCTA中,有两种获得减影图像的方法。一种是单次屏气法,另一种是两次屏气法,两种方法有利有弊。Amanuma等[15]做了在单次屏气模式下减影技术对支架患者的意义,但该研究只针对心率≤61 bpm,且能憋气20~25 s的患者,大部分患者需要在吸氧的情况下才能配合扫描,这在实际工作中很难实现。
针对这种情况,我们采用了Yoshioka等[14]描述的两次屏气法,把钙化积分序列作为减影蒙片,无需改变扫描方案,不额外增加患者扫描剂量:本研究患者平均辐射剂量((4.9±2.8) mSV)较其他研究者的单次屏气法有效剂量((5.6±3.6) mSV)少[11,20],同时可满足大多数老年患者的扫描需求。减影后,诊断准确率、阳性预测率和阴性预测值都得到了显著提高,尤其是相较于传统CCTA,假阳性率显著降低(35.2%~5.2%)。
本研究也存在一些局限性。首先,本研究为单中心研究,可能存在选择偏倚;其次样本量不够大,有ICA对比的仅有54个节段,有ISR的节段更少,这可能会导致诊断准确性上的偏差,以后进一步扩大样本量,寻求多中心联合继续研究;另一方面,减影后的图像会产生独特的减影伪影。由于两次屏气时,患者很难做到心率和位置完全一致,这可能会导致配准错误。由于轻度狭窄很容易受到此类伪影的影响,因此这种技术主要应用于疑似狭窄≥50%的节段评估中。实际应用中,首先应在扫描前反复对患者进行屏气训练,尽量避免“蒙片”和增强图像的不一致;其次,在阅片中应把常规CCTA与sub-CCTA结合起来评估,互相弥补不足,不可忽略con-CCTA直接评估减影后的图像,这可能会导致错误的诊断。
有研究表明,患者平均心率、心脏左横径及心脏支架位置为sub-CCTA图像质量的影响因素[21-23],本研究并未对支架的类型、位置及影响减影图像质量的影响因素进行全面的分析,这可能使统计结果不够全面。
4. 结论
双屏气模式下,减影冠状动脉成像技术可以提高支架节段的可判读性,提高ISR的诊断准确性,降低假阳性率。为支架患者术后随访提供了更多的选择,降低了进一步的有创检查。
-
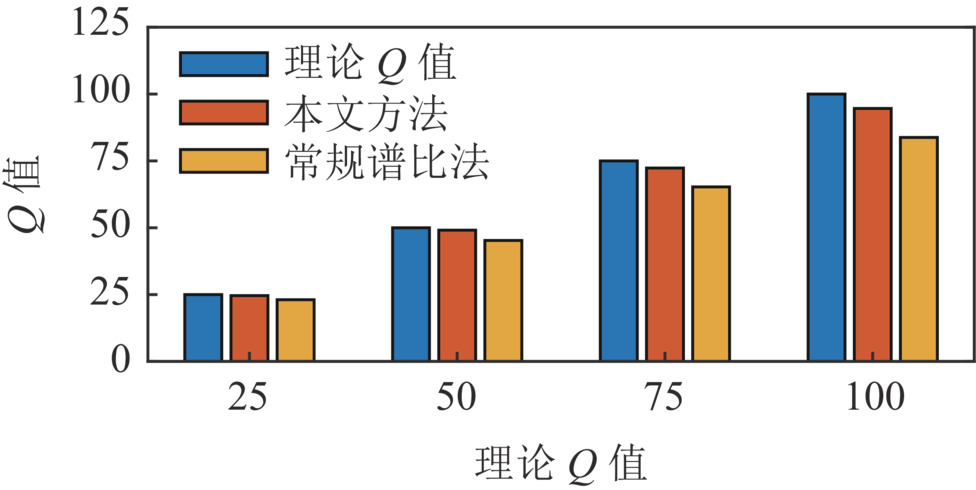
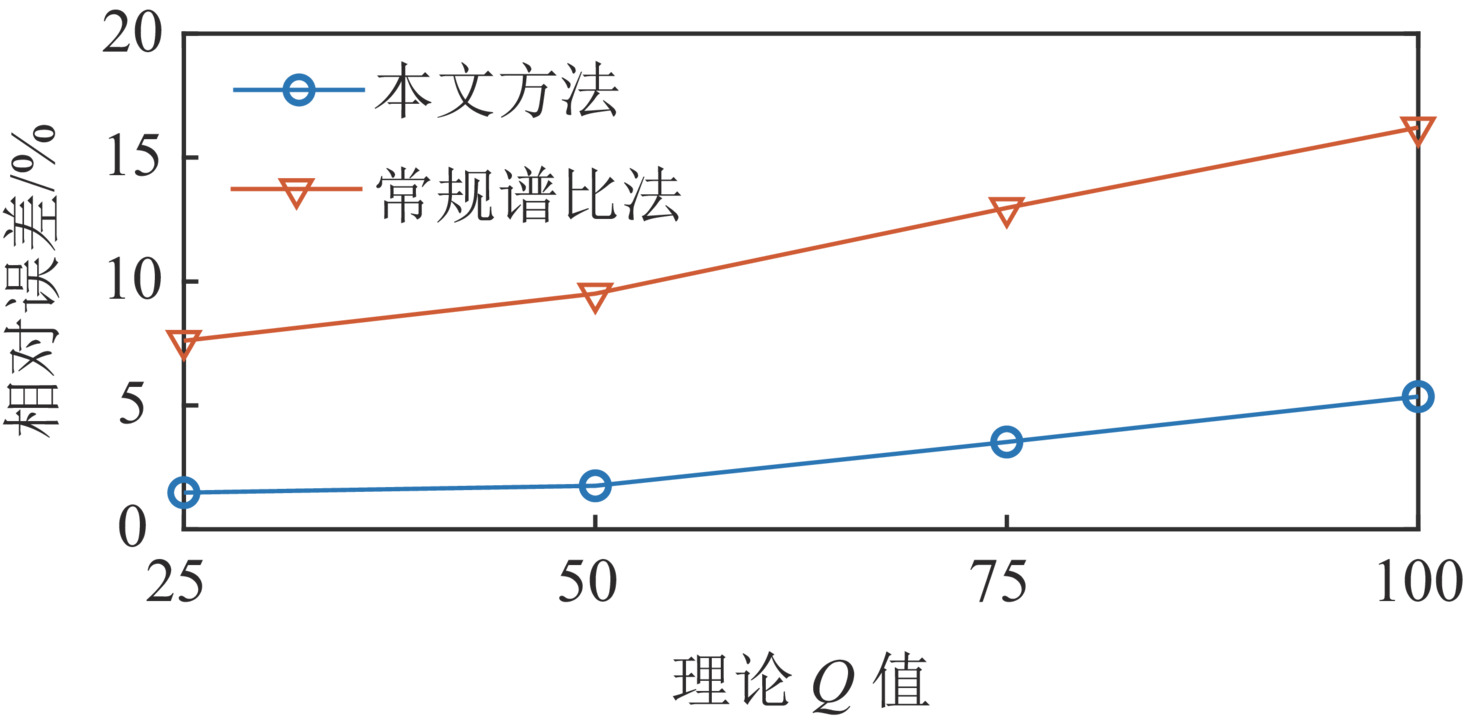
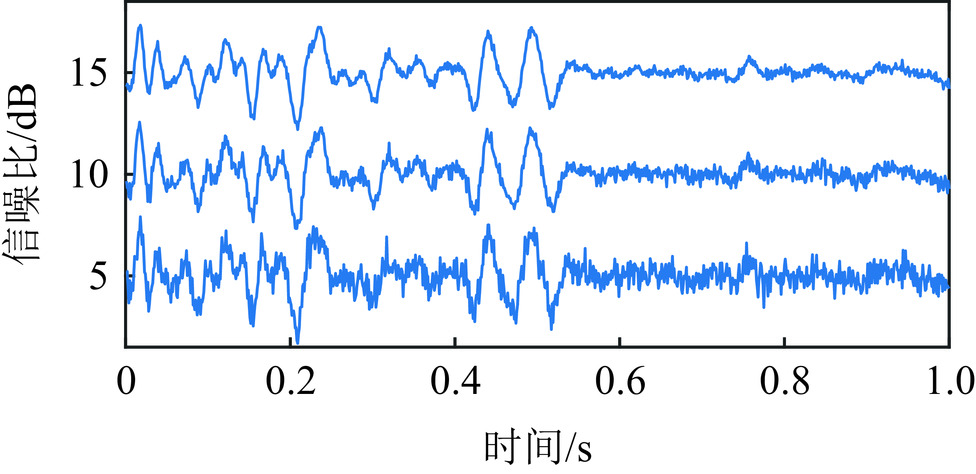
表 1 不同信噪比模型Q值估计统计结果
Table 1 Statistical results of Q estimation for different signal-to-noise ratio models
模型信噪比 5 dB 10 dB 15 dB 本文方法 均值 27.30 25.65 25.28 标准差 6.35 4.03 3.04 常规谱比法 均值 35.20 32.36 27.87 标准差 11.20 10.34 6.81 -
[1] FUTTERMAN W I. Dispersive body waves[J]. Journal of Geophysical Research, 1962, 7(13): 5279-5291.
[2] 李振春, 王清振. 地震波衰减机理及能量补偿研究综述[J]. 地球物理学进展, 2007, 22(4): 1147-1152. DOI: 10.3969/j.issn.1004-2903.2007.04.021. LI Z C, WANG Q Z. A review of research on mechanism of seismic attenuation and energy compensation[J]. Progress in Geophysics, 2007, 22(4): 1147-1152. DOI: 10.3969/j.issn.1004-2903.2007.04.021. (in Chinese).
[3] BATH M. Spectral analysis in geophysics[M]. New York: Elsevier Science Publication Limited Company, 1974: 1-50.
[4] REINE C, VAN D B M, CLARK R. The robustness of seismic attenuation measurements using fixed- and variable-window time-frequency transforms[J]. Geophysics: Journal of the Society of Exploration Geophysicists, 2009, 74(2): WA123-WA135.
[5] 朱耀旭, 包乾宗. 应用遗传算法估计非稳态地震数据的混合相位子波及Q值[J]. 石油地球物理勘探, 2024, 59(4): 763-770. ZHU Y X, BAO Q Z. Estimation of mixed-phase wavelet and Q value of nonstationary seismic data using genetic algorithm[J]. Oil Geophysical Prospecting, 2024, 59(4): 763-770. (in Chinese).
[6] 陈文爽, 管路平, 李振春, 等. 基于广义S变换的叠前Q值反演方法研究[J]. 石油物探, 2014, 53(6): 706-712. DOI: 10.3969/j.issn.1000-1441.2014.06.011. CHEN W S, GUAN L P, LI Z C, et al. Prestack Q-inversion based on generalized S transform[J]. Geophysical Prospecting for Petroleum, 2014, 53(6): 706-712. DOI: 10.3969/j.issn.1000-1441.2014.06.011. (in Chinese).
[7] 杨登锋, 刘军, 吴静, 等. 加权谱比法Q值估计[J]. 石油地球物理勘探, 2022, 57(3): 593-601. YANG D F, LIU J, WU J, et al. Q factor estimation by weighted spectral ratio me-thod[J]. Oil Geophysical Prospecting, 2022, 57(3): 593-601. (in Chinese).
[8] 魏文, 王小杰, 李红梅. 基于叠前道集小波域Q值求取方法研究[J]. 石油物探, 2011, 50(4): 355-360. DOI: 10.3969/j.issn.1000-1441.2011.04.007. WE W, WANG X J, LI H M. Study on extraction method for Q based on pre-stack gather in wavelet domain[J]. Geophysical Prospecting for Petroleum, 2011, 50(4): 355-360. DOI: 10.3969/j.issn.1000-1441.2011.04.007. (in Chinese).
[9] 王小杰, 印兴耀, 吴国忱. 基于S变换的吸收衰减技术在含气储层预测中的应用研究[J]. 石油物探, 2012, 51(1): 37-42. WANG X J, YIN X Y, WU G C. The application of an S transform based absorption and attenuation technique for prediction of gas-bearing reservoir[J]. Geophysical Prospecting for Petroleum, 2021, 51(1): 37-42. (in Chinese).
[10] 王小杰, 栾锡武. 基于小波分频技术的地层Q值提取方法研究[J]. 石油物探, 2015, 54(3): 260-266. DOI: 10.3969/j.issn.1000-1441.2015.03.003. WANG X J, LUAN X W. Q value extraction method based on wavelet frequency division technology[J]. Geophysical Prospecting for Petroleum, 2015, 54(3): 260-266. DOI: 10.3969/j.issn.1000-1441.2015.03.003. (in Chinese).
[11] 李波, 文晓涛, 张懿疆, 等. 基于Lucy-Richardson算法和广义S变换的Q值提取[J]. 石油物探, 2019, 58(5): 689-699. DOI: 10.3969/j.issn.1000-1441.2019.05.007. LI B, WEN X T, ZHANG Y J, et al. Combined generalized S transform and Lucy-Richardson algorithm for Q-value extraction[J]. Geophysical Prospecting for Petroleum, 2019, 58(5): 689-699. DOI: 10.3969/j.issn.1000-1441.2019.05.007. (in Chinese).
[12] LI B, WEN X T, NIE W L, et al. Pre-stack Q estimation based on inverse spectral decomposition[J]. Journal of Petroleum Science and Engineering, 2021, 205: 108775. DOI: 10.1016/j.petrol.2021.108775.
[13] 周东红, 段新意. 浅水环境下气云发育区高孔低胶结地层地震资料成像策略研究——以渤海莱北地区A油田为例[J]. 石油物探, 2023, 62(1): 105-118. DOI: 10.3969/j.issn.1000-1441.2023.01.009. ZHOU D H, DUAN X Y. Seismic data imaging strategy of high-porosity and low-cementation strata in the gas cloud development area of a shallow water environment: Case study of an oilfield in the Bohai Laibei area[J]. Geophysical Prospecting fortroleum, 2023, 62(1): 105-118. DOI: 10.3969/j.issn.1000-1441.2023.01.009. (in Chinese).
[14] 张繁昌, 张汛汛, 张立强, 等. 基于自适应子波分解的品质因子Q提取方法[J]. 石油物探, 2016, 55(1): 41-48. DOI: 10.3969/j.issn.1000-1441.2016.01.006. ZHANG F C, ZHANG X X, ZHANG L Q, et al. Extraction method of Q estimation based on adaptive wavelet decompensation[J]. Geophysical Prospecting for Petroleum, 2016, 55(1): 41-48. DOI: 10.3969/j.issn.1000-1441.2016.01.006. (in Chinese).
[15] 张瑾, 王彦国, 兰慧田, 等. 基于不同阶次泰勒级数展开的含非本征衰减频域振幅比平均的Q值估计方法[J]. 石油地球物理勘探, 2023, 58(6): 1423-1435. ZHANG J, WANG Y G, LAN H T, et al. Amplitude ratio average method in frequency domain for Q estimation of extrinsic attenuation based on Taylor series expansion with different orders[J]. Oil Geophysical Prospecting, 2023, 58(6): 1423-1435. (in Chinese).
[16] 许李囡, 高静怀, 杨阳, 等. 基于S变换和变分法的品质因子Q估计方法[J]. 石油地球物理勘探, 2022, 57(1): 82-90. XU L N, GAO J H, YANG Y, et al. Quality factor Q estimation based on S transform and variational method[J]. Oil Geophysical Prospecting, 2022, 57(1): 82-90. (in Chinese).
[17] 周晨. 基于深度学习的Q值估计和地震衰减补偿[D]. 北京: 中国石油大学(北京), 2023. [18] WANG J, LU W, LI Y. A multitask learning-based dynamic wavelet amplitude spectra extraction method and its application in Q estimation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 1-10.
[19] LI F, YU Z, MA J. An effective Q extraction method via deep learning[J]. Journal of Geophysics and Engineering, 2024, 21(2): 483-495. DOI: 10.1093/jge/gxae011.
[20] AKI K, RICHARDS P G. Quantitative Seismology: Theory and Methods[M]. San Francisco, CA: W. H. Freeman & Co. 1980.
[21] MARCRAVE G F, LAMOUREUX M P, HENLEY D C, et al. Gabor deconvolution: Estimating reflectivity by non-stationary deconvolution of seismic data[J]. Geophysics, 2011, 76(3): W15-W30. DOI: 10.1190/1.3560167.
[22] 刘俊杰, 陈学华, 吴昊杰, 等. 稀疏广义S变换及其在储层地震低频异常检测中的应用[J]. 石油地球物理勘探, 2023, 58(3): 690-699. LIU J J, CHENG X H, WU H J, et al. Sparse generalized S-Transform and its application to detection of low-frequency seismic anomalies in reservoirs[J]. Oil Geophysical Prospecting, 2023, 58(3): 690-699. (in Chinese).
[23] 刘春成, 周慰, 牛聪, 等. 基于改进广义S变换的复赛谱时频域反褶积方法[J]. 中国石油大学学报(自然科学版) 2018, 42(5): 57-64. LUD C C, ZHOU W, NU C, et al. Cepstral time-frequency domain deconvolution based on improved generalized S-transform[J]. Journal of China University of Petroleum (Edition of natural science), 2018, 42(5): 57-64. (in Chinese).
[24] 贾承造, 王祖纲, 姜林, 等. 中国页岩油勘探开发研究进展与科学技术问题[J]. 世界石油工业, 2024, 31(4): 1-11. DOI: 10.20114/j.issn.1006-0030.20240530001. JIA C Z, WANG Z G, JIANG L, et al. Progress and key scientific and technological problems of shale oil exploration and development in China[J]. World Petroleum Industry, 2024, 31(4): 1-11. DOI: 10.20114/j.issn.1006-0030.20240530001. (in Chinese).



 下载:
下载: