Diffusion Models in Medical Imaging: A Comprehensive Survey
-
摘要:
以扩散模型为代表的生成式人工智能近年来在医学成像领域取得了迅猛的进展。为了帮助更多学者全面的了解扩散模型这一先进技术，本文旨在提供扩散模型在医学成像领域的详细概述。首先以扩散模型的起源演变为主线介绍扩散建模框架的基础理论和基本概念；其次根据扩散模型的特点提供其在医学成像领域的系统分类，并涵盖不同成像模态如磁共振成像、计算机断层扫描、正电子发射计算机断层显像和光声成像等的广泛应用；最后讨论目前扩散模型的局限性并展望未来研究的潜在发展方向，为研究者后续的探索提供了一个直观的起始点。部分代码开源在网址：https://github.com/yqx7150/Diffusion-Models-for-Medical-Imaging。
Abstract:Generative artificial intelligence represented by diffusion models has significantly contributed to medical imaging reconstruction. To help researchers comprehensively understand the rich content of diffusion models, this review provides a detailed overview of diffusion models used in medical imaging reconstruction. The theoretical foundation and fundamental concepts underlying the diffusion modeling framework were first introduced, describing their origin and evolution. Second, a systematic characteristic-based taxonomy of diffusion models used in medical imaging reconstruction is provided, broadly covering their application to imaging modalities, including magnetic resonance imaging (MRI), computed tomography (CT), positron emission computed tomography (PET), and photoacoustic imaging (PAI). Finally, we discuss the limitations of current diffusion models and anticipate potential directions of future research, providing an intuitive starting point for subsequent exploratory research. Related codes are available at GitHub: https://github.com/yqx7150/Diffusion-Models-for-Medical-Imaging.
-
-
![]()
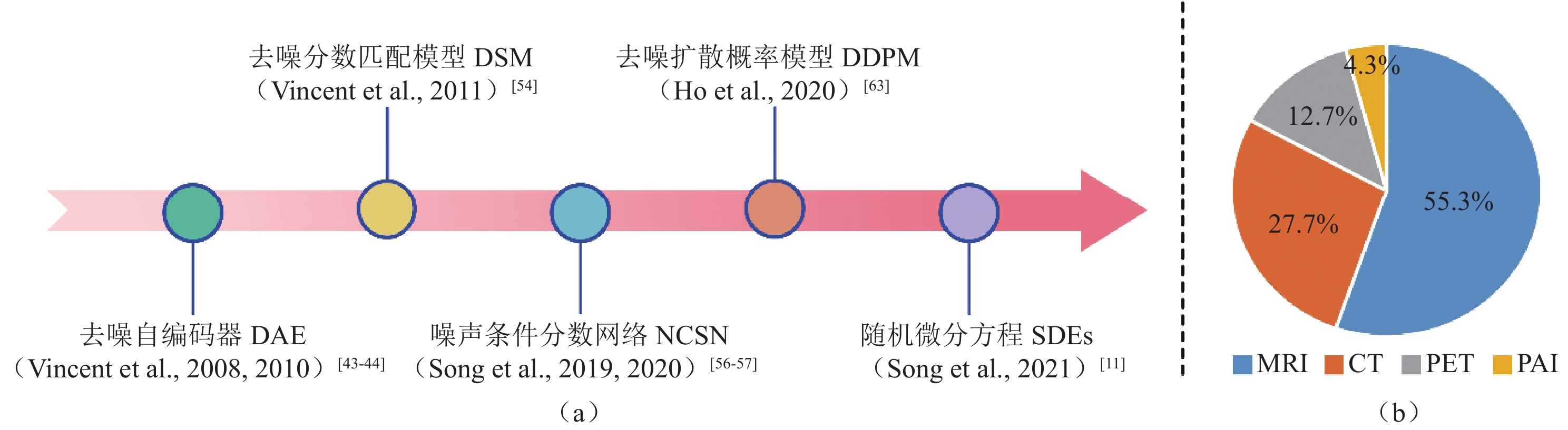
图 1 （a）扩散模型起源演变的时间轴；（b）按照关键词（diffusion model | medical imaging）、（score-based model | medical imaging）、（diffusion | medical | probabilistic model）在Google Scholar和Arxiv Sanity Preserver进行近5年相关论文检索，筛选并删除相同的结果最终统计扩散模型应用于不同成像模态分类的论文比例
Figure 1. (a) Timeline of the origin and evolution of the diffusion model; (b) Relevant papers published within the last five years found via Google Scholar and Arxiv Sanity Preserver searches using the keywords (diffusion model | medical imaging), (score-based model | medical imaging), and (diffusion | medical | probabilistic model). Duplicate results were identified and deleted before calculating the proportion of papers applying a diffusion model to different imaging modality classifications
![]()
图 2 扩散模型应用于不同成像模态的论文分类
Figure 2. Classification of papers describing the application of diffusion models to different imaging modalities
![]()
图 3 扩散模型分别在图像域和K空间域的基本框架。其中前向过程从初始数据开始逐步添加噪声，使其最终接近纯噪声分布；逆向过程通过学习逐步去噪，从随机噪声中还原为高质量的目标数据
Figure 3. Basic framework of the diffusion model in the image and K-space domain. The forward process gradually adds noise from the initial data to approach a pure noise distribution; the reverse process gradually removes noise through learning and recovers high-quality target data from random noise
![]()
图 4 单线圈脑部数据集在伪径向采样模式下欠采样倍数为5时不同方法的重建结果比较。绿色框和红色框分别表示感兴趣区域及其残差图
Figure 4. Comparison of reconstruction results using different methods on a single-coil brain dataset at pseudo-radial under-sampling of 5-fold. The green and red boxes indicate the region of interest and its residual map, respectively
![]()
图 5 不同方法生成的CT图像的数值比较
Figure 5. Numerical comparison of CT images generated by different methods
![]()
图 6 不同算法在泊松采样模式下欠采样倍数为4的重建结果
Figure 6. Reconstruction results of different methods at Poisson under-sampling of 4-fold
![]()
图 7 随机采样模式下欠采样倍数为5和均匀采样模式下欠采样倍数为4的fastMRI膝关节和SIAT脑部重建结果
Figure 7. Reconstruction results of fastMRI knee data and SIAT brain data at random under-sampling of 5-fold and uniform under-sampling of 4-fold
![]()
图 8 不同算法下人体CT扫描有限角度（60°和90°）重建结果（右下角数值为PSNR值）
Figure 8. Reconstruction results of limited angles (60° and 90°) of human CT scan data using different algorithms (the value in each lower right corner is the PSNR value)
![]()
图 9 5 e3剂量下的重建结果及残差图
Figure 9. Reconstruction results and residual images at a dose of 5 e3
![]()
图 10 稀疏角度为32°时重建血管的过程（数字分别代表PSNR值和SSIM值）
Figure 10. Process of blood vessel reconstruction when the sparse angle is 32° (The numbers represent PSNR and SSIM values, respectively)
表 1 五大生成模型全方位对比
Table 1 Comprehensive comparison of five generative models
特点/模型 VAE GAN EBM Flow Diffusion Model 基本原理 由编码器将数据映射到潜在空间概率分布，再由解码器生成数据 生成器和判别器对抗训练，生成器生成数据，判别器区分真假 定义一个可微的能量函数，将数据点的概率分布与其能量值联系 通过可逆变换将简单分布映射到复杂数据分布。 从噪声分布起，逐步去噪恢复目标数据 优点 1.生成质量高
2.训练稳定
3.潜在空间连续1.生成质量高
2.多样性好
3.应用广泛1.灵活性高
2.隐式生成
3.表示能力强1.高效样本生成和密度估计
2.可解释性强1.生成质量高
2.强大的建模能力
3.广泛的应用场景缺点 1.生成样本模糊
2.计算复杂度高
3.难捕捉复杂分布1.训练困难
2.对数据敏感
3.计算资源消耗大1.配分函数难计算
2.训练不稳定
3.采样效率低1.设计合适的变换
2.模块具有挑战性
3.计算资源需求高1.训练过程复杂
2.对噪声模型依赖性
3.生成速度较慢训练稳定性 稳定 不稳定 稳定 稳定 稳定 生成质量 较高 高 较高 高 高 计算资源需求 中等 高 中等 高 高 模型复杂度 中等 高 中等 高 高 可解释性 较好 较差 较好 好 较差 灵活性 较低 高 高 高 高 对数据分布假设 较强 较弱 较强 较强 较弱 数据质量敏感性 较低 高 较低 较低 较低 生成速度 中等 中等 中等 中等 较慢 
下载: 导出CSV
表 2 不同重建算法结果定量比较
Table 2 Quantitative comparison between the results of different reconstruction algorithms
ESPIRiT LINDBERG EBMRec SAKE WKGM SVD-WKGM T1 GE brain 2D random R=4 39.08/0.933 38.98/0.961 40.17/0.968 41.54/0.952 40.67/0.969 43.85/0.970 2D random R=6 36.01/0.921 35.16/0.958 36.55/0.952 38.09/0.932 37.14/0.957 39.94/0.960 T2 transverse brain 2D Poisson R=4 31.74/0.819 32.87/0.901 33.19/0.915 33.91/0.896 33.35/0.907 34.58/0.917 2D Poisson R=10 28.95/0.798 26.17/0.822 29.59/0.839 29.75/0.823 29.17/0.823 31.69/0.841
下载: 导出CSV
-
[1] BAO J M, CHEN D, WEN F, et al. CVAE-GAN: Fine-grained image generation through asymmetric training[C]//Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 2017: 2745-2754. DOI: 10.1109/iccv.2017.299.
[2] RAZAVI A, Van den OORD A, VINYALS O. Generating diverse high-fidelity images with VQ-VAE-2[J]. Advances in Neural Information Processing Systems, 2019, 32. DOI: 10.48550/arXiv.1906.00446.
[3] KONG Z F, PING W, HUANG J J, et al. Diffwave: A versatile diffusion model for audio synthesis[J]. arXiv Preprint arXiv: 2009.09761, 2020.
[4] OORD A, DIELEMAN S, ZEN H, et al. Wavenet: A generative model for raw audio[J]. arXiv Preprint arXiv: 1609.03499, 2016.
[5] LI X, THICKSTUN J, GULRAJANI I, et al. Diffusion-lm improves controllable text generation[J]. Advances in Neural Information Processing Systems, 2022, 35: 4328-4343. DOI: 10.48550/arXiv.2205.14217.
[6] YANG G D, HUANG X, HAO Z K, et al. Pointflow: 3D point cloud generation with continuous normalizing flows[C]//Proceedings of the IEEE/CVF international conference on computer vision, Seoul, Korea (South), 2019: 4541-4550. DOI: 10.48550/arXiv.1906.12320.
[7] BOND-TAYLOR S, LEACH A, LONG Y, et al. Deep generative modelling: A comparative review of VAEs, GANs, normalizing flows, energy-based and autoregressive models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021. DOI: 10.48550/arXiv.2103.04922.
[8] GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[J]. Advances in Neural Information Processing Systems, 2014, 27. DOI: 10.48550/arXiv.1406.2661.
[9] JIMENEZ REZENDE D, MOHAMED S, WIERSTRA D. Stochastic backpropagation and approximate inference in deep generative models[J]. arXiv Preprint arXiv: 1401.4082, 2014.
[10] DINH L, SOHL-DICKSTEIN J, BENGIO S. Density estimation using real nvp[J]. arXiv Preprint arXiv: 1605.08803, 2016.
[11] SONG Y, SOHL-DICKSTEIN J, KINGMA D P, et al. Score-based generative modeling through stochastic differential equations[J]. arXiv Preprint arXiv: 2011.13456, 2020.
[12] KARRAS T, AITTALA M, AILA T, et al. Elucidating the design space of diffusion-based generative models[J]. Advances in Neural Information Processing Systems, 2022, 35: 26565-26577. DOI: 10.48550/arXiv.2206.00364.
[13] SOHL-DICKSTEIN J, WEISS E, MAHESWARANATHAN N, et al. Deep unsupervised learning using nonequilibrium thermodynamics[C]//International Conference on Machine Learning, Lille, France, 2015: 2256-2265. DOI: 10.48550/arXiv.1503.03585.
[14] SONG Y, DURKAN C, MURRAY I, et al. Maximum likelihood training of score-based diffusion models[J]. Advances in Neural Information Processing Systems, 2021, 34: 1415-1428. DOI: 10.48550/arXiv.2101.09258.
[15] SINHA A, SONG J M, MENG C L, et al. D2c: Diffusion-decoding models for few-shot conditional generation[J]. Advances in Neural Information Processing Systems, 2021, 34: 12533-12548. DOI: 10.48550/arXiv.2106.06819.
[16] VAHDAT A, KREIS K, KAUTZ J. Score-based generative modeling in latent space[J]. Advances in Neural Information Processing Systems, 2021, 34: 11287-11302. DOI: 10.48550/arXiv.2106.05931.
[17] SAHARIA C, HO J, CHAN W, et al. Image super-resolution via iterative refinement[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 45(4): 4713-4726. DOI: 10.48550/arXiv.2104.07636.
[18] PANDEY K, MUKHERJEE A, RAI P, et al. Diffusevae: Efficient, controllable and high-fidelity generation from low-dimensional latents[J]. arXiv Preprint arXiv: 2201.00308, 2022.
[19] BAO F, LI C X, ZHU J, et al. Analytic-dpm: An analytic estimate of the optimal reverse variance in diffusion probabilistic models[J]. arXiv Preprint arXiv: 2201.06503, 2022.
[20] DOCKHORN T, VAHDAT A, KREIS K. Score-based generative modeling with critically-damped Langevin diffusion[J]. arXiv Preprint arXiv: 2112.07068, 2021.
[21] LIU N, LI S, DU Y L, et al. Compositional visual generation with composable diffusion models[C]//European Conference on Computer Vision, Tel-Aviv, Israel, 2022: 423-439. DOI: 10.48550/arXiv.2206.01714.
[22] JIANG Y M, YANG S, QIU H N, et al. Text2human: Text-driven controllable human image generation[J]. ACM Transactions on Graphics (TOG), 2022, 41(4): 1-11. DOI: 10.48550/arXiv.2205.15996.
[23] BATZOLIS G, STANCZUK J, SCHONLIEB C B, et al. Conditional image generation with score-based diffusion models[J]. arXiv Preprint arXiv: 2111.13606, 2021.
[24] DANIELS M, MAUNU T, HAND P. Score-based generative neural networks for large-scale optimal transport[J]. Advances in Neural Information Processing Systems, 2021, 34: 12955-12965. DOI: 10.48550/arXiv.2110.03237.
[25] CHUNG H, SIM B, YE J C. Come-closer-diffuse-faster: Accelerating conditional diffusion models for inverse problems through stochastic contraction[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, USA, 2022: 12413-12422. DOI: 10.48550/arXiv.2112.05146.
[26] KAWAR B, ELAD M, ERMON S, et al. Denoising diffusion restoration models[J]. Advances in Neural Information Processing Systems, 2022, 35: 23593-23606. DOI: 10.48550/arXiv.2201.11793.
[27] ESSER P, ROMBACH R, BLATTMANN A, et al. Imagebart: Bidirectional context with multinomial diffusion for autoregressive image synthesis[J]. Advances in Neural Information Processing Systems, 2021, 34: 3518-3532. DOI: 10.48550/arXiv.2108.08827.
[28] LUGMAYR A, DANELLJAN M, ROMERO A, et al. Repaint: Inpainting using denoising diffusion probabilistic models[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, USA, 2022: 11461-11471. DOI: 10.48550/arXiv.2201.09865.
[29] JING B, CORSO G, BERLINGHIERI R, et al. Subspace diffusion generative models[C]//European Conference on Computer Vision, Tel-Aviv, Israel, 2022: 274-289. DOI: 10.1007/978-3-031-20050-2_17.
[30] BARANCHUK D, RUBACHEV I, VOYNOV A, et al. Label-efficient semantic segmentation with diffusion models[J]. arXiv preprint arXiv: 2112.03126, 2021.
[31] GRAIKOS A, MALKIN N, JOJIC N, et al. Diffusion models as plug-and-play priors[J]. Advances in Neural Information Processing Systems, 2022, 35: 14715-14728. DOI: 10.48550/arXiv.2206.09012.
[32] WOLLEB J, SANDKÜHLER R, BIEDER F, et al. Diffusion models for implicit image segmentation ensembles[C]//International Conference on Medical Imaging with Deep Learning, New Orleans, USA, 2022: 1336-1348. DOI: 10.48550/arXiv.2112.03145.
[33] AMIT T, SHAHARBANY T, NACHMANI E, et al. Segdiff: Image segmentation with diffusion probabilistic models[J]. arXiv Preprint arXiv: 2112.00390, 2021.
[34] ZIMMERMANN R S, SCHOTT L, SONG Y, et al. Score-based generative classifiers[J]. arXiv Preprint arXiv: 2110.00473, 2021.
[35] PINAYA W H L, GRAHAM M S, GRAY R, et al. Fast unsupervised brain anomaly detection and segmentation with diffusion models[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention, New Orleans, USA, 2022: 705-714. DOI: 10.48550/arXiv.2206.03461.
[36] WOLLEB J, BIEDER F, SANDKUHLER R, et al. Diffusion models for medical anomaly detection[C]//International Conference on Medical image computing and computer-assisted intervention, New Orleans, USA, 2022: 35-45. DOI: 10.48550/arXiv.2203.04306.
[37] WYATT J, LEACH A, SCHMON S M, et al. Anoddpm: Anomaly detection with denoising diffusion probabilistic models using simplex noise[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, USA, 2022: 650-656. DOI: 10.1109/CVPRW56347.2022.00080.
[38] JALAL A, ARVINTE M, DARAS G, et al. Robust compressed sensing MRI with deep generative priors[J]. Advances in Neural Information Processing Systems, 2021, 34: 14938-14954. DOI: 10.48550/arXiv.2108.01368.
[39] CHUNG H, YE J C. Score-based diffusion models for accelerated MRI[J]. Medical Image Analysis, 2022, 80: 102479. DOI: 10.48550/arXiv.2110.05243.
[40] CAO H Q, TAN C, GAO Z Y, et al. A survey on generative diffusion model[J]. arXiv Preprint arXiv: 2209.02646, 2022.
[41] YANG L, ZHANG Z L, SONG Y, et al. Diffusion models: A comprehensive survey of methods and applications[J]. ACM Computing Surveys, 2023, 56(4): 1-39. DOI: 10.48550/arXiv.2209.00796.
[42] KAZEROUNI A, AGHDAM E K, HEIDARI M, et al. Diffusion models in medical imaging: A comprehensive survey[J]. Medical Image Analysis, 2023: 102846. DOI: 10.1016/jmedia.2023.102846.
[43] VINCENT P, LAROCHELLE H, BENGIO Y, et al. Extracting and composing robust features with denoising autoencoders[C]//Proceedings of the 25th international conference on Machine learning, Helsinki, Finland, 2008: 1096-1103. DOI: 10.1145/1390156.1390294.
[44] VINCENT P, LAROCHELLE H, LAJOIE I, et al. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion[J]. Journal of Machine Learning Research, 2010, 11(12). DOI: 10.5555/1756006.1953039.
[45] VINCENT P. A connection between score matching and denoising autoencoders[J]. Neural computation, 2011, 23(7): 1661-1674. DOI: 10.1162/NECO_a_00142.
[46] SONG Y, ERMON S. Generative modeling by estimating gradients of the data distribution[J]. Advances in Neural Information Processing Systems, 2019, 32. DOI: 10.48550/arXiv.1907.05600.
[47] SONG Y, GARG S, SHI J, et al. Sliced score matching: A scalable approach to density and score estimation[C]//Proceedings of The 35th Uncertainty in Artificial Intelligence Conference, Tel Aviv, Israel, 2020: 574-584. DOI: 10.48550/arXiv.1905.07088.
[48] HO J, JAIN A, ABBEEL P. Denoising diffusion probabilistic models[J]. Advances in Neural Information Processing Systems, 2020, 33: 6840-6851. DOI: 10.48550/arXiv.2006.11239.
[49] ERHAN D, COURVILLE A, BENGIO Y, et al. Why does unsupervised pre-training help deep learning?[C]//Proceedings of the 13th International Conference on Artificial Intelligence and Statistics, Pittsburgh, USA, 2010: 201-208.
[50] Le CUN Y, FOGELMAN-SOULIE F. Modeles connexionnistes de l’apprentissage[J]. Intellectica, 1987, 2(1): 114-143. DOI: 10.3406/intel.1987.1804.
[51] GALLINARI P, LECUN Y, THIRIA S, et al. Distributed associative memories: A comparison[M]. La Villette, Paris: Proceedings of Cognitiva 87, 1987.
[52] SEUNG H S. Learning continuous attractors in recurrent networks[J]. Advances in Neural Information Processing Systems, 1997, 10. DOI: 10.5555/3008904.3008997.
[53] TEZCAN K C, BAUMGARTNER C F, LUECHINGER R, et al. MR image reconstruction using deep density priors[J]. IEEE Transactions on Medical Imaging, 2018, 38(7): 1633-1642. DOI: 10.1109/TMI.2018.2887072.
[54] LIU Q G, YANG Q X, CHENG H T, et al. Highly under-sampled magnetic resonance imaging reconstruction using autoencoding priors[J]. Magnetic Resonance in Medicine, 2020, 83(1): 322-336. DOI: 10.1002/mrm.27921.
[55] WANG S Y, LV J J, HE Z N, et al. Denoising auto-encoding priors in undecimated wavelet domain for MR image reconstruction[J]. Neurocomputing, 2021, 437: 325-338. DOI: 10.1016/j.neucom.2020.09.086.
[56] LIU X S, ZHANG M H, LIU Q G, et al. Multi-contrast MR reconstruction with enhanced denoising autoencoder prior learning[C]//2020 IEEE 17th International Symposium on Biomedical Imaging, Iowa City, USA, 2020: 1-5. DOI: 10.1109/ISBI45749.2020.9098334.
[57] ZHANG M H, LI M T, ZHOU J J, et al. High-dimensional embedding network derived prior for compressive sensing MRI reconstruction[J]. Medical Image Analysis, 2020, 64: 101717. DOI: 10.1016/j.media.2020.101717.
[58] BLOCK A, MROUEH Y, RAKHLIN A. Generative modeling with denoising auto-encoders and Langevin sampling[J]. arXiv Preprint arXiv: 2002.00107, 2020.
[59] PARISI G. Correlation functions and computer simulations[J]. Nuclear Physics B, 1981, 180(3): 378-384. DOI: 10.1016/0550-3213(81)90056-0.
[60] GRENANDER U, MILLER M I. Representations of knowledge in complex systems[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1994, 56(4): 549-581. DOI: 10.1111/j.2517-6161.1994.tb02000.x.
[61] QUAN C, ZHOU J J, ZHU Y Z, et al. Homotopic gradients of generative density priors for MR image reconstruction[J]. IEEE Transactions on Medical Imaging, 2021, 40(12): 3265-3278. DOI: 10.48550/arXiv.2008.06284.
[62] ZHU W Q, GUAN B, WANG S S, et al. Universal generative modeling for calibration-free parallel MR imaging[C]//2022 IEEE 19th International Symposium on Biomedical Imaging, Kolkata, India, 2022: 1-5. DOI: 10.1109/ISBI52829.2022.9761446.
[63] HE Z N, ZHANG Y K, GUAN Y, et al. Iterative reconstruction for low-dose CT using deep gradient priors of generative model[J]. IEEE Transactions on Radiation and Plasma Medical Sciences, 2022, 6(7): 741-754. DOI: 10.48550/arXiv.2009.12760.
[64] LYU Q, WANG G. Conversion between CT and MRI images using diffusion and score-matching models[J]. arXiv Preprint arXiv: 2209.12104, 2022.
[65] CHUNG H, LEE E S, YE J C. MR image denoising and super-resolution using regularized reverse diffusion[J]. IEEE Transactions on Medical Imaging, 2022, 42(4): 922-934. DOI: 10.48550/arXiv.2203.12621.
[66] MENG X X, GU Y N, PAN Y S, et al. A novel unified conditional score-based generative framework for multi-modal medical image completion[J]. arXiv Preprint arXiv: 2207.03430, 2022.
[67] LUO G, BLUMENTHAL M, HEIDE M, et al. Bayesian MRI reconstruction with joint uncertainty estimation using diffusion models[J]. Magnetic Resonance in Medicine, 2023, 90(1): 295-311. DOI: 10.1002/mrm.29624.
[68] PENG C, GUO P F, ZHOU S K, et al. Towards performant and reliable undersampled MR reconstruction via diffusion model sampling[C]// International Conference on Medical Image Computing and Computer-Assisted Intervention, Singapore, Singapore, 2022: 623-633. DOI: 10.1007/978-3-031-16446-0_59.
[69] GUNGOR A, DAR S U H, OZTURK S, et al. Adaptive diffusion priors for accelerated MRI reconstruction[J]. Medical Image Analysis, 2023: 102872. DOI: 10.1016/j.media.2023.102872.
[70] XIE Y T, LI Q Z. Measurement-conditioned denoising diffusion probabilistic model for under-sampled medical image reconstruction[J]. arXiv Preprint arXiv: 2203.03623, 2022.
[71] OZTURKLER B, LIU C, ECKART B, et al. SMRD: Sure-based robust MRI reconstruction with diffusion models[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention, Vancouver, Canada, 2023: 199-209. DOI: 10.1007/978-3-031-43898-1_20.
[72] MIRZA M U, DALMAZ O, BEDEL H A, et al. Learning fourier-constrained diffusion bridges for MRI reconstruction[J]. arXiv Preprint arXiv: 2308.01096, 2023.
[73] BIAN W Y, JANG A, LIU F. Diffusion modeling with domain-conditioned prior guidance for accelerated MRI and qMRI reconstruction[J]. arXiv Preprint arXiv: 2309.00783, 2023.
[74] KORKMAZ Y, CUKUR T, PATEL V M. Self-supervised MRI reconstruction with unrolled diffusion models[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention, Vancouver, Canada, 2023: 491-501. DOI: 10.1007/978-3-031-43999-5_47.
[75] CHEN L X, TIAN X Y, WU J J, et al. JSMoCo: Joint coil sensitivity and motion correction in parallel MRI with a self-calibrating score-based diffusion model[J]. arXiv Preprint arXiv: 2310.09625, 2023.
[76] RAVULA S, LEVAC B, JALAL A, et al. Optimizing sampling patterns for compressed sensing MRI with diffusion generative models[J]. arXiv Preprint arXiv: 2306.03284, 2023.
[77] SONG Y, SHEN L Y, XING L, et al. Solving inverse problems in medical imaging with score-based generative models[J]. arXiv Preprint arXiv: 2111.08005, 2021.
[78] CHUNG H, SIM B, RYU D, et al. Improving diffusion models for inverse problems using manifold constraints[J]. arXiv Preprint arXiv: 2206.00941, 2022.
[79] TU Z J, JIANG C, GUAN Y, et al. K-space and image domain collaborative energy-based model for parallel MRI reconstruction[J]. Magnetic Resonance Imaging, 2023, 99: 110-122. DOI: 10.1016/j.mri.2023.02.004.
[80] PENG H, JIANG C, CHENG J, et al. One-shot generative prior in hankel-k-space for parallel imaging reconstruction[J]. IEEE Transactions on Medical Imaging, 2023. DOI: 10.1109/TMI.2023.3288219.
[81] YU C M, GUAN Y, KE Z W, et al. Universal generative modeling in dual domains for dynamic MRI[J]. NMR in Biomedicine, 2023, 36(12): e5011. DOI: 10.1002/nbm.5011.
[82] GUAN Y, YU C M, LU S Y, et al. Correlated and multi-frequency diffusion modeling for highly under-sampled MRI reconstruction[J]. arXiv Preprint arXiv: 2309.00853, 2023.
[83] ZHANG W, XIAO Z W, TAO H, et al. Low-rank tensor assisted K-space generative model for parallel imaging reconstruction[J]. Magnetic Resonance Imaging, 2023, 103: 198-207. DOI: 10.1016/j.mri.2023.07.004.
[84] CUI Z X, CAO CT, LIU S N, et al. Self-score: Self-supervised learning on score-based models for MRI reconstruction[J]. arXiv Preprint arXiv: 2209.00835, 2022.
[85] CUI Z X, LIU C C, FAN X H, et al. Physics-informed deep MRI: K-space interpolation meets heat diffusion[J]. IEEE Transactions on Medical Imaging, 2024, 43(10): 3503-3520. DOI: 10.1109/TMI.2024.3462988.
[86] CAO C T, CUI Z X, LIU S N, et al. High-frequency space diffusion models for accelerated MRI[J]. arXiv Preprint arXiv: 2208.05481, 2022.
[87] GUAN Y, YU C M, CUI Z X, et al. Correlated and multi-frequency diffusion modeling for highly under-sampled MRI reconstruction[J]. IEEE Transactions on Medical Imaging, 2024, 43(10): 3490-3502. DOI: 10.1109/TMI.2024.3381610.
[88] HUANG B, LU S Y, LIU Q G, et al. One-sample diffusion modeling in projection domain for low-dose CT imaging[J]. IEEE Transactions on Radiation and Plasma Medical Sciences, 2024. DOI: 10.1109/TRPMS.2024.3392248.
[89] WU W W, WANG Y Y. Data-iterative optimization score model for stable ultra-sparse-view CT reconstruction[J]. arXiv Preprint arXiv: 2308.14437, 2023.
[90] ZHANG W H, HUANG B, LIU Q G, et al. Low-rank angular prior guided multi-diffusion model for few-shot low-dose CT reconstruction[J]. IEEE Transactions on Radiation and Plasma Medical Sciences, 2024. DOI: 10.1109/TCI.2024.3503366.
[91] LIU J M, ANIRUDH R, THIAGARAJAN J J, et al. DOLCE: A model-based probabilistic diffusion framework for limited-angle CT reconstruction[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2023: 10498-10508. DOI: 10.48550/arXiv.2211.12340.
[92] XIA W J, SHI Y Y, NIU C, et al. Diffusion prior regularized iterative reconstruction for low-dose CT[J]. arXiv Preprint arXiv: 2310.06949, 2023.
[93] XIA W J, CONG W X, WANG G. Patch-based denoising diffusion probabilistic model for sparse-view CT reconstruction[J]. arXiv Preprint arXiv: 2211.10388, 2022.
[94] XIA W J, NIU C, CONG W X, et al. Sub-volume-based denoising diffusion probabilistic model for cone-beam CT reconstruction from incomplete data[J]. arXiv e-Prints, 2023: arXiv: 2303.12861.
[95] GAO Q, LI Z L, ZHANG J P, et al. CoreDiff: Contextual error-modulated generalized diffusion model for low-dose CT denoising and generalization[J]. arXiv Preprint arXiv: 2304.01814, 2023.
[96] WU W W, WANG Y Y, LIU Q G, et al. Wavelet-improved score-based generative model for medical imaging[J]. IEEE Transactions on Medical Imaging, 2023. DOI: 10.1109/TMI.2023.3325824.
[97] XU K, LU S Y, HUANG B, et al. Stage-by-stage wavelet optimization refinement diffusion model for sparse-view CT reconstruction[J]. arXiv Preprint arXiv: 2308.15942, 2023.
[98] ZHANG J J, MAO H Y, WANG X R, et al. Wavelet-inspired multi-channel score-based model for limited-angle CT reconstruction[J]. IEEE Transactions on Medical Imaging, 2024, 43(10): 3436-3448. DOI: 10.1109/TMI.2024.3367167.
[99] GUAN B, YANG C L, ZHANG L, et al. Generative modeling in sinogram domain for sparse-view CT reconstruction[J]. IEEE Transactions on Radiation and Plasma Medical Sciences, 2023. DOI: 10.1109/TRPMS.2023.3309474.
[100] LIU X, XIE Y Q, DIAO S H, et al. Unsupervised CT metal artifact reduction by plugging diffusion priors in dual domains[J]. IEEE Transactions on Medical Imaging, 2024, 43(10): 3533-3545. DOI: 10.1109/TMI.2024.3351201.
[101] WANG Y Y, LI Z R, WU W W. Time-reversion fast-sampling score-based model for limited-angle CT reconstruction[J]. IEEE Transactions on Medical Imaging, 2024, 43(10): 3449-3460. DOI: 10.1109/TMI.2024.3418838.
[102] WU W W, PAN J Y, WANG Y Y, et al. Multi-channel optimization generative model for stable ultra-sparse-view CT reconstruction[J]. IEEE Transactions on Medical Imaging, 2024, 43(10): 3416-3475. DOI: 10.1109/TMI.2024.3376414.
[103] HAN Z Y, WANG Y H, ZHOU L P, et al. Contrastive diffusion model with auxiliary guidance for coarse-to-fine PET reconstruction[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention, Vancouver, Canada, 2023: 239-249. DOI: 10.1007/978-3-031-43999-5_23.
[104] JIANG C W, PAN Y S, LIU M X, et al. PET-diffusion: Unsupervised PET enhancement based on the latent diffusion model[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention, Vancouver, Canada, 2023: 3-12. DOI: 10.1007/978-3-031-43907-0_1.
[105] XIE T F, CAO C T, CUI Z X, et al. Brain pet synthesis from MRI using joint probability distribution of diffusion model at ultrahigh fields[J]. arXiv Preprint arXiv: 2211.08901, 2022.
[106] XIE T F, CAO C R, CUI Z X, et al. Synthesizing PET images from high-field and ultra-high-field MR images using joint diffusion attention model[J]. arXiv Preprint arXiv: 2305.03901, 2023.
[107] XIE T F, CUI Z X, LUO C, et al. Joint diffusion: Mutual consistency-driven diffusion model for PET-MRI co-reconstruction[J]. arXiv Preprint arXiv: 2311.14473, 2023.
[108] PAN S Y, ABOUEI E, PENG J B, et al. Full-dose PET synthesis from low-dose PET using high-efficiency diffusion denoising probabilistic model[J]. arXiv Preprint arXiv: 2308.13072, 2023.
[109] SONG X L, WANG G J, ZHONG W H, et al. Sparse-view reconstruction for photoacoustic tomography com-bining diffusion model with model-based iteration[J]. Photoacoustics, 2023, 33: 100558. DOI: 10.1016/j.pacs.2023.100558.
[110] TONG S Q, LAN H R, NIE L M, et al. Score-based generative models for photoacoustic image reconstruction with rotation consistency constraints[J]. arXiv Preprint arXiv: 2306.13843, 2023.
[111] DOSOVITSKIY A, BEYER L, KOLESNIKOV A, et al. An image is worth 16x16 words: Transformers for image recognition at scale[J]. arXiv Preprint arXiv: 2010.11929, 2020.
[112] WANG Z H, YANG Y Y, CHEN Y Z, et al. Mutual information guided diffusion for zero-shot cross-modality medical image translation[J]. IEEE Transactions on Medical Imaging, 2024, 43(8): 2825-2838. DOI: 10.1109/TMI.2024.3382043.
[113] CHU J Y, DU C H, LIN X Y, et al. Highly accelerated MRI via implicit neural representation guided posterior sampling of diffusion models[J]. Medical Image Analysis, 2025, 100.
计量
- 文章访问数: 1252
- HTML全文浏览量: 130
- PDF下载量: 207
