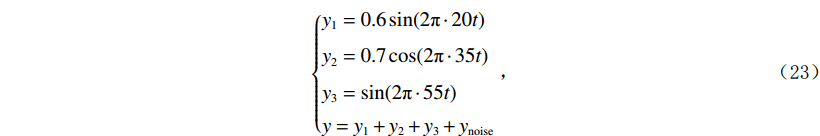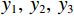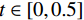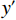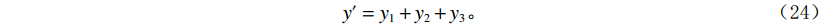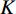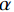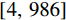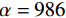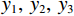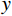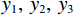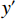Research on High Resolution Seismic Date Processing Method Based on Adaptive VMD
-
摘要: 随着勘探开发的不断深入，常规地震资料受分辨率的限制难以满足精细勘探开发的需求。由于地震信号不同频率成分的衰减程度不同，故可结合分频技术对各频率成分进行差异化补偿，进而提高地震资料分辨率。而常规分频技术普遍分频精度不高，存在模态混叠现象，不能较好地适用于地震资料处理。针对上述问题，本文提出基于自适应变分模态分解（VMD）的地震资料高分辨率处理方法。将多目标蝙蝠算法应用于变分模态分解，利用功率谱熵、能量差、样本熵构建适应度函数，对VMD参数进行优化。模型测试结果表明，优化的VMD方法分频精度较高，避免模态混叠，且具有较强的抗噪能力；将优化VMD方法应用于地震资料高分辨率处理，模型及实际数据测试结果表明，处理后的地震资料分辨率得到有效提高。Abstract: With the deepening of exploration and development, due to the limitation of the resolution of the conventional seismic data, it is difficult to meet the needs of exploration and development. Since the attenuation degree of different frequency components of seismic signals is different, the frequency decomposing technology can be applied to perform differential compensation on each frequency component to improve the resolution of seismic data. However, the conventional frequency division technology generally not only holds low frequency division accuracy but also shows modal aliasing, thus it cannot be well applied to seismic data processing. To solve these problems, this paper proposes a high-resolution processing method for seismic data based on adaptive variational modal decomposition (VMD). The multi-objective bat algorithm is applied to the variational modal decomposition, and the VMD parameters are optimized by the fitness function constructed using power spectrum entropy, energy difference, and sample entropy. The model test results show that the optimized VMD method holds high frequency division accuracy and strong anti-noise ability, and also can avoids modal aliasing, When the optimized VMD method is applied to high-resolution processing of seismic data, the model and actual data test results show that the resolution of processed seismic data is effectively improved.
-
随着油气勘探开发的不断深入，油气藏勘探逐渐以薄层勘探为主，对地震资料分辨率的要求越来越高。由于地下介质的粘弹性性质，地震波在地下介质中传播时会发生振幅能量衰减和波形畸变，使反射波的频带变窄，主频左移，导致地震资料的垂向分辨率降低，难以满足岩性油气藏、非常规油气勘探和开发的需求[1-2]。
近年来，国内外学者提出了多种提高地震数据垂向分辨率的处理方法，如反褶积[3-5]、反Q滤波[6-10]、谱白化[11-12]等。反褶积类方法通过压缩子波来达到提高分辨率的目的，但该方法通常难以提取准确的子波，在提高分辨率的同时，降低了信噪比[3-5]。反Q滤波方法通过对地震记录进行衰减补偿来提高信号分辨率，如何准确估计Q值是该方法的难点[6-10]。谱白化方法操作简单，但保真性较差[11-12]。因上述方法各自的劣势，在实际应用中存在局限性。
随着小波变换[13-15,18-19]、S变换[21-23]等算法的进一步发展，为基于分频处理技术[16-20]的拓频方法奠定了基础。当地震波在地下介质中传播时会产生振幅衰减和频散，其高频分量比低频分量衰减的更快，导致地震数据的时间分辨率较低。因此，对不同频率成分进行差异化补偿有助于提高地震分辨率。杨忠民等[19]将小波变换看成时间和频率的函数，在小波域按不同时间对频率进行补偿，有效提高了分辨率。袁修贵等[20]利用小波变换将叠后地震记录进行分频处理后，对不同频率的地震波采用不同的补偿策略，并应用于实际数据，使薄层的分辨能力得到加强。刘喜武等[21]提出基于广义S变换的吸收衰减补偿方法，利用广义S变换对地震信号进行时频分析，提取各频率的吸收衰减因子对相应的广义S变换系数进行补偿，提高了地震资料的分辨率。孙雷鸣等[22]在利用广义S变换提取吸收衰减因子进行补偿的基础上，采用规范方差模对补偿后的地震数据频谱进行修正，提高了分辨率的同时保持了低频信息、能量相对关系和弱反射层。实践证明，采用不同的补偿策略对不同频率成分进行差异化补偿，可使地震信号因地层滤波损失的高频成分得到一定程度的补偿，从而提高地震数据分辨率。
目前，常规分频方法的分频精度普遍不高。因此，本文引入变分模态分解[24]（variational mode decomposition，VMD）算法对地震信号进行分频处理。变分模态分解是一种新的信号分解方法，具有坚实的数学理论基础，在信号处理及地震资料的处理分析中得到广泛应用[24-28]。变分模态分解通过确定各模态的最佳中心频率和有限带宽，实现本征模态函数（intrinsic mode function，IMF）的有效分离、信号的频域划分，相较于小波变换等算法，VMD能很好的解决相邻模态的频率相近时的混叠问题。该方法中，模态数和带宽控制参数对信号的分频结果有显著影响。传统的VMD方法通常通过经验给定分解参数，难以获得较好的分频结果。
针对上述问题，本文提出基于多目标蝙蝠算法的参数自适应VMD方法，以样本熵、功率谱熵、能量差构建适应度函数，获取全局最优的参数组合对地震信号进行分频处理，并结合最大方差模原理对各IMF分量分别进行差异化补偿。模型测试及实际数据应用表明，优化VMD方法分频精度较高，克服了模态混叠问题，具有较强的抗噪声干扰能力；将该方法应用于地震资料的高分辨率处理，有效避免不同频率成分地震信号的相互影响，并根据优势信噪比频带作信息预测，有效展宽了频带，在保持信噪比的同时，提高了地震资料的垂向分辨率。
1. 方法原理
1.1 变分模态分解算法原理
变分模态分解是一种信号分解技术，其整体框架是一个变分问题，以维纳滤波器、希尔伯特变换、混频原理为基础构建变分模型，通过求解该模型可将信号
$ f $ 分解为一系列集中在中心频率$ {\omega _k} $ 周围具有有限带宽的本征模态分量$ {u_k} $ 。变分模态分解通过估计带宽有效克服模态混叠问题，用信号镜像扩展方法抑制端点效应，分频精度更高，具有更强的频域划分能力。变分模态分解具有坚实的理论基础。变分模型的构建首先采用希尔伯特变换计算每个模态
$ {u_k} $ 的解析信号，获得单边频谱，通过混合中心频率将各模态频谱移至基带，并计算解调信号梯度的L2范数估计各频带的带宽。由此得到如下约束变分问题[24]：$$ \left\{ {\begin{aligned} & {\mathop {\min }\limits_{\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\}} \left\{ {\sum\limits_{k = 1}^K {\left\| {{\partial _t}\Bigg( {\Bigg( {\delta (t) + \frac{j}{{\text{π} t}}} \Bigg) * {u_k}(t)} \Bigg){\exp({ - j{\omega _k}t})}} \right\|_2^2} } \right\}} \\ & {{\rm{s.t}}.{\text{ }}\sum\limits_{k-1}^k {{u_k} = f} } \end{aligned}} \right. \text{，} $$ (1) 其中
$ f $ 为原信号，$ \left\{ {{u_k}} \right\} $ 为经VMD分解得到的本征模态分量，$ k \in [1,K] $ ；$ \left\{ {{\omega _k}} \right\} $ 为各模态中心频率，$ K $ 为模态分量个数，$ t $ 为时间序列，$ j $ 为虚数单位，$ * $ 表示卷积；$ {\partial _t} $ 表示函数关于时间$ t $ 的导数；$ \delta (t) $ 为单位脉冲函数。对于变分模型的求解，通过引入拉格朗日乘子
$ \lambda $ 和二次惩罚项$ \alpha $ 得到增广拉格朗日函数，将约束问题（1）转换为无约束问题（2）进行求解：$$ \begin{aligned} L\Big( {\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\},\lambda } \Big): = \alpha \sum\limits_k {\left\| {{\partial _t}\left( {\Bigg( {\delta (t) + \frac{j}{{\text{π} t}}} \Bigg) * {u_k}(t)} \right){\exp({ - j{\omega _k}t})}} \right\|} _2^2 +\\ \left\| {f(t) - \sum\limits_k {{u_k}(t)} } \right\|_2^2 + \left\langle {\lambda (t),f(t) - \sum\limits_k {{u_k}(t)} } \right\rangle\qquad \qquad \end{aligned} ， $$ (2) 利用交替方向乘子法[24]（ADMM）求解式（2）的鞍点，用分而治之思想，将非约束问题分解为三个子问题分别转换到傅里叶域进行求解，得到迭代更新公式：
$$ \left\{ {\begin{aligned} &{\hat u_k^{n + 1}(\omega ) = \frac{{\hat f(\omega ) - \displaystyle\sum\limits_{i \ne k} {\hat u_i^n(\omega ) + \frac{{\hat \lambda (\omega )}}{2}} }}{{1 + 2\alpha {{\Big(\omega - {\omega _k}\Big)}^2}}}} \\ &{\omega _k^{n + 1} = \frac{{\displaystyle\int_0^\infty {\omega {{\left| {\hat u_k^{n + 1}(\omega )} \right|}^2}{\rm{d}}\omega } }}{{\displaystyle\int_0^\infty {{{\left| {\hat u_k^{n + 1}(\omega )} \right|}^2}{\rm{d}}\omega } }}} \\ & {{{\hat \lambda }^{n + 1}} = {{\hat \lambda }^n}(\omega ) + \tau \Bigg(\hat f(\omega ) - \sum\limits_k {\hat u_k^{n + 1}(\omega )} \Bigg)} \end{aligned}} \right. \text{，} $$ (3) 其中
$ \hat f(\omega ),{\text{ }}{\hat u_k}(\omega ),{\text{ }}\hat \lambda (\omega ) $ 分别为$ f(t),{\text{ }}{u_k}(t),{\text{ }}\lambda (t) $ 的傅里叶变换，$ \tau $ 为对偶变量，$ n $ 表示迭代次数。对于给定误差$ \varepsilon $ ，直至$\displaystyle\sum\limits_k {\frac{{\left\| {\hat u_k^{n + 1} - \hat u_k^n} \right\|_2^2}}{{\left\| {\hat u_k^n} \right\|_2^2}}} < \varepsilon$ ，得到最优解，信号$ f $ 分解为$ K $ 个本征模态分量。原信号$ f $ 在频域可表示为$ K $ 个本征模态分量线性和的形式，经逆傅里叶变换，信号$ f $ 可表示如下：$$ f = {\rm{IFFT}}\left(\sum\limits_{k = 1}^K {{{\hat u}_k}(\omega)} \right) \text{，} $$ (4) 其中IFFT表示逆傅里叶变换。
1.2 多目标蝙蝠算法原理
蝙蝠算法是Yang[29]根据蝙蝠回声定位原理提出的元启发式算法，具有模型简单、参数少、收敛快、鲁棒性强等优势，已成为求解全局优化问题的最常用方法。在实际工程中，目标函数通常不是单一的，因此Yang[30]在原有算法基础上提出多目标蝙蝠算法，继承了原有算法的优势且适用性更强。多目标蝙蝠算法模拟了蝙蝠探寻猎物，躲避障碍的行为，蝙蝠位置代表问题空间中的解，个体的移动过程为解的优化、搜索过程，以适应度函数值来衡量蝙蝠个体所在位置的优劣，在迭代过程中，蝙蝠个体通过更新位置、速度、频率、响度，朝最佳个体移动，最终得到全局最优解。
多目标蝙蝠算法的适应度函数定义如下：
$$ \left\{ {\begin{aligned} &{F = \sum\limits_{i = 1}^M {{\omega _i}{F_i}} } \\ & {\sum\limits_{i = 1}^M {{\omega _i} = 1} } \end{aligned}} \right. \text{，} $$ (5) 其中
$ F $ 为适应度函数值，$ {F_i} $ 表示第$ i $ 个目标函数，$ M $ 为目标函数总个数，$ \omega $ 表示权值。在
$ D $ 维搜索空间中，$ t $ 时刻时，第$ i $ 只蝙蝠的频率$ {q_i} $ 、速度$ v_i^t $ 、位置$ x_i^t $ 更新公式如下：$$ {q_i} = {q_{\min }} + \Big({q_{\max }} - {q_{\min }}\Big)\beta \text{，} $$ (6) $$ v_i^t = v_i^{t - 1} + \Big(x_i^{t - 1} - {x^ * }\Big){q_i} \text{，} $$ (7) $$ x_i^t = x_i^{t - 1} + v_i^t \text{，} $$ (8) $ {q_{\min }} $ 和$ {q_{\max }} $ 分别为频率变化范围的最小值和最大值，$ \beta \in [0,1] $ 为随机向量，$ {x^*} $ 表示当前局部最优位置。生成一个局部解时，以一定概率在该解附近产生一个新解：
$$ {x_{{\rm{new}}}} = {x_{{\rm{old}}}} + \varepsilon {A^t} \text{，} $$ (9) 其中，
$ \varepsilon \in [ - 1,1] $ 为随机数，$ {A^t} $ 为这一代所有蝙蝠的平均响度。随着进一步迭代，响度
$ A_i^t $ 和脉冲率$ r_i^t $ 也进行相应更新：$$ A_i^{t + 1} = \alpha A_i^t \text{，} $$ (10) $$ r_i^{t + 1} = r_i^0\Big(1 - \exp \big( - \gamma t\big)\Big) \text{，} $$ (11) 式中，
$ \alpha 、\gamma $ 为常数。1.3 分频高频补偿
地震波在传播过程中，由于地下传播介质的粘弹性性质，经大地滤波后，地震波能量衰减严重。在相同的传播条件下，高频成分能量衰减速度比低频成分能量衰减速度更快，地震信号的高频成分损失严重，导致地震资料分辨率降低，无法满足精细勘探及细分层精细构造解释的要求。
对于衰减程度不一的各频率段，运用多分辨频率补偿方法[20]分别进行合理补偿，提高地震记录的垂向分辨率。设
$ f(t) $ 是长度为$ L $ 的地震信号，其规范方差模定义为：$$ {V_e} = \frac{{\displaystyle\sum\limits_{t = 1}^L {{Z^2}(t)} }}{{{{\left( {\displaystyle\sum\limits_{t = 1}^L {Z(t)} } \right)}^2}}} \text{，} $$ (12) 其中
$Z(t) = 1 - {\exp\Big({\big( - {f^2}(t)/{a^2}\big)}\Big)}$ ，$ a $ 为一个常数。规范方差模
$ V $ 是对序列$ f(t) $ 能量聚集程度的一种度量，序列的能量越集中，则方差模越大。求修正规范方差模关于频谱$ f(\omega ) $ 的导数：$$ \frac{{\partial {V_e}}}{{\partial f(\omega )}} = 0 。 $$ (13) 由傅里叶变换：
$$ f(\omega ) = \sum\limits_{t = 1}^L {f(t){\exp(-i2\text{π} \omega t}}) \text{，} $$ $$ f(t) = \sum\limits_{k = 1}^L {f(\omega ){\exp({i2\text{π} \omega t}}} )。 $$ 可导出频率补偿公式：
$$ f(\omega ) = \sum\limits_{t = 1}^L {\left( {1 + \frac{{\Big(1 - {Z_t}\Big)}}{{{V_e}\displaystyle\sum\limits_{t = 1}^L {{Z_t}} }}} \right)} {Z_t}f(t)\exp({i2\text{π} \omega t}) 。 $$ (14) 利用变分模态分解算法将信号
$ f $ 分解为$ K $ 个本征模态分量，对各模态分量根据式（15）分别进行频率补偿：$$ {\hat u_k}(\omega ) = \left\{ {\begin{array}{*{20}{c}} {{u_k}(\omega )}&{\omega < {\omega _L}} \\ {\displaystyle\sum\limits_{t = 1}^L {\left( {1 + \displaystyle\frac{{\Big( {1 - {Z_{(k,t)}}} \Big)}}{{{V_{e,k}}\displaystyle\sum\limits_{t = 1}^L {{Z_{(k,t)}}} }}} \right){Z_{(t,k)}}u(t){\exp({i2\omega \text{π} t}}} )}&{\omega \in \left[ {{\omega _L},{\omega _H}} \right]} \end{array}} \right. \text{，} $$ (15) 其中
$ {u}_{k}(\omega )，{\widehat{u}}_{k}(\omega ) $ 分别为补偿前后第$ k $ 个本征模态分量，$ k \in \left[ {1,K} \right] $ ；$ {\omega _L} $ 为截止频率，$ {\omega _H} $ 为最大补偿频率。将补偿后的各分量进行重构，得到最终的补偿结果。2. 基于多目标蝙蝠算法的VMD参数优化
分解数
$ K $ 和惩罚因子$ \alpha $ 对信号的分解结果有显著影响，$ \alpha $ 值确保了信号的重构精度，$ \alpha $ 过小，各模态的带宽较宽，会出现频谱混叠问题；$ \alpha $ 过大，各模态对应的带宽较窄，可能会缺失有用信息。$ K $ 值取值过小时，信号中各频率成分分解不彻底；若$ K $ 值取值过大时会过分解，产生一些虚假的模态分量。通常参数$ K $ 和$ \alpha $ 的值根据经验给定，往往不准确。可利用多目标蝙蝠算法收敛快、全局寻优等优势对VMD参数的选取进行优化，其关键是多个适应度函数的选取。功率谱熵用于衡量功率谱中各频率成分分布的集中程度。在频域信号越稀疏，其功率谱熵越小；反之，功率谱熵越大。对于长度为
$ L $ 的时域信号$ f(t) $ ，其功率谱$ S(\omega ) $ 定义如下：$$ S(\omega ) = \frac{1}{{2\text{π} L}}{\Big| {f(\omega )} \Big|^2} \text{，} $$ (16) 其中
$ f(\omega ) $ 为$ f(t) $ 的傅里叶变换。对功率谱进行归一化，得到功率谱密度的概率密度函数；
$$ {P_i} = \displaystyle\frac{{S(i)}}{{\displaystyle\sum\limits_{j = 1}^L {S(j)} }} ,\;\;\;\; i=1,2,\cdots, L 。 $$ (17) 信号的功率谱熵为
${F_{{\rm{PSE}}}}$ ：$$ {F_{{\rm{PSE}}}} = -\sum\limits_{i = 1}^L {{P_i}\log {P_i}} 。 $$ (18) 信号经VMD最优分解后，各分量的能量之和理论上应等于原信号的能量。当信号过分解时，会产生虚假分量，各分量的能量之和大于原信号的能量。长度为
$ L $ 信号$ f(t) $ 的能量$ E $ 定义如下：$$ E = \sum\limits_{i = 1}^L {{f^2}(i)} 。 $$ (19) 定义各IMF的总能量和原信号能量的差与原信号能量的比值
$ {F_\lambda } $ ：$$ {F_\lambda } = \displaystyle\frac{{\displaystyle\sum\limits_{i = 1}^K {{E_i} - {E_f}} }}{{{E_f}}} \text{，} $$ (20) 其中
$ {E_f} $ 为原信号能量，$ {E_i} $ 为各模态分量能量，$ K $ 为模态分量个数。当信号被最优分解时，$ {F_\lambda } $ 的值最小。样本熵常作为非平稳信号复杂程度的评价指标。若信号的成分单一，具有较强周期性，所含的噪声成分越少，则信号的复杂程度越低，样本熵越低；反之信号越复杂，样本熵越高。同时，根据样本熵的特性，可以区分有效分量和含噪分量。信号的样本熵
$ {F_{{\rm{SE}}}} $ 可表示为：$$ {F_{{\rm{SE}}}} = - \ln \left(\frac{{{B^{m + 1}}(r)}}{{{B^m}(r)}}\right) \text{，} $$ (21) 其中
$ m $ 为重构相空间维数，$ r $ 为相似容限阈值，$ {B^m}(r) $ 表示在$ r $ 下两序列$ m $ 个点的匹配概率。当功率谱熵
${F_{{\rm{PSE}}}}$ 、能量差$ {F_\lambda } $ 、样本熵${F_{{\rm{SE}}}}$ 的值最小时，得到一组全局最优VMD参数组合$ (K,\alpha ) $ ，信号分解彻底，且不存在模态混叠。利用${F_{{\rm{PSE}}}}$ 、$ {F_\lambda } $ 、${F_{{\rm{SE}}}}$ 构建多目标蝙蝠算法的适应度函数：$$ \left\{ {\begin{aligned} & {\mathop {\arg \min {\text{ }}}\limits_{(K,\alpha )}\{ {F_{{\rm{PSE}}}},{F_\lambda },{F_{{\rm{SE}}}}}\} \\ &{{\rm{s.t}}.{\text{ }}K \in [2,{K_{\max }}],\;\;\;\;\alpha \in [200,3000]} \end{aligned}} \right. \text{，} $$ (22) 多目标蝙蝠算法优化VMD参数的具体步骤如下：
步骤1：初步获取参数范围。由于地震数据各道相互独立，单道分析难免会导致VMD参数的不确定性和非唯一性，同时考虑计算效率以及地震数据在空间横向上的连续性，故多道加权平均进行幅频特性分析，以频带高数值
$ {K_{\max }} $ 作为参数$ K $ 的最大值。步骤2：初始化多目标蝙蝠算法参数。初始化种群规模M，迭代次数 N，蝙蝠位置
$ {x_i} $ ，速度$ {v_i} $ ，声波频率$ {q_i} $ ，响度$ {A_i} $ 和脉冲率$ {r_i} $ ，$i = 1,2,\cdots,M$ 。步骤3：计算每只蝙蝠的适应度值，找出最优个体，其位置记为
$ {x_{{\rm{best}}}} $ ，适应度值记为${F_{{\rm{best}}}}$ 。根据式（6）～式（8）更新第$ i $ 只蝙蝠的声波频率、速度和位置。步骤4：生成一个随机数
${\rm{rand}}\; 1 \in [0,1]$ ，若${\rm{rand}}\;1$ 大于最优个体的脉冲率$ {r_i} $ ，则根据式（9）生成一个局部解；否则根据式（8）更新蝙蝠位置。步骤5：重新生成一个随机数
${\rm{rand}}\;2 \in [0,1]$ ,若${\rm{rand}}\;2$ 小于最优个体的响度$ {A_i} $ ，且当前个体新位置的适应度值优于之前的适应度值，则接受个体新位置，并根据式（10）和式（11）更新响度和脉冲率。步骤6：根据适应度值对所有蝙蝠进行排序，找到当前最优解。
步骤7：重复步骤3至步骤6，直至达到最大迭代次数，输出全局最优个体位置
${x_{{\rm{best}}}}$ 。3. 数值实验
3.1 模型测试
为验证本文所述的VMD参数优化算法的有效性，构建一维模拟信号进行测试。根据式（23）构建一组信号，如图1所示：
$$ \begin{split} {}\\\left\{ {\begin{aligned} & {{y_1} = 0.6\sin (2\text{π} \cdot 20t)} \\ & {{y_2} = 0.7\cos (2\text{π} \cdot 35t)} \\ & {{y_3} = \sin (2\text{π} \cdot 55t)} \\ & {y = {y_1} + {y_2} + {y_3} + {y_{{\rm{noise}}}}} \end{aligned}} \right. \text{，} \end{split}$$ (23) 其中简谐信号
${y_1},\;{y_2},\;{y_3}$ 的主频分别为20 Hz、35 Hz、55 Hz,${y_{{\rm{noise}}}}$ 表示随机噪声，$ t \in [0,0.5] $ 。不含噪声信号$ y' $ 表示如下;$$ y' = {y_1} + {y_2} + {y_3} 。 $$ (24) 利用本文提出的VMD参数优化算法对模态数
$ K $ 和惩罚因子$ \alpha $ 进行优化，优化过程中适应度值随迭代次数的变化如图2所示。图2中适应度值为功率谱熵、能量差、样本熵的平均值。功率谱熵越小，表明信号频率成分越单一，越稀疏；能量差越小，表明信号分解越彻底，不存在模态混叠和虚假分量；样本熵越小，表明信号越有规律性、周期性，信号的复杂程度越低，故适应度值最小时对应的参数组合即为最佳VMD参数，此时信号分解彻底且不存在模态混叠。由图2可知，迭代6次后适应度值最小为1.0075，此时对应的参数组合为$ [4,\;986] $ ，即最佳的VMD参数为$ K = 4 $ ，$ \alpha = 986 $ 。使用最优VMD参数对合成信号
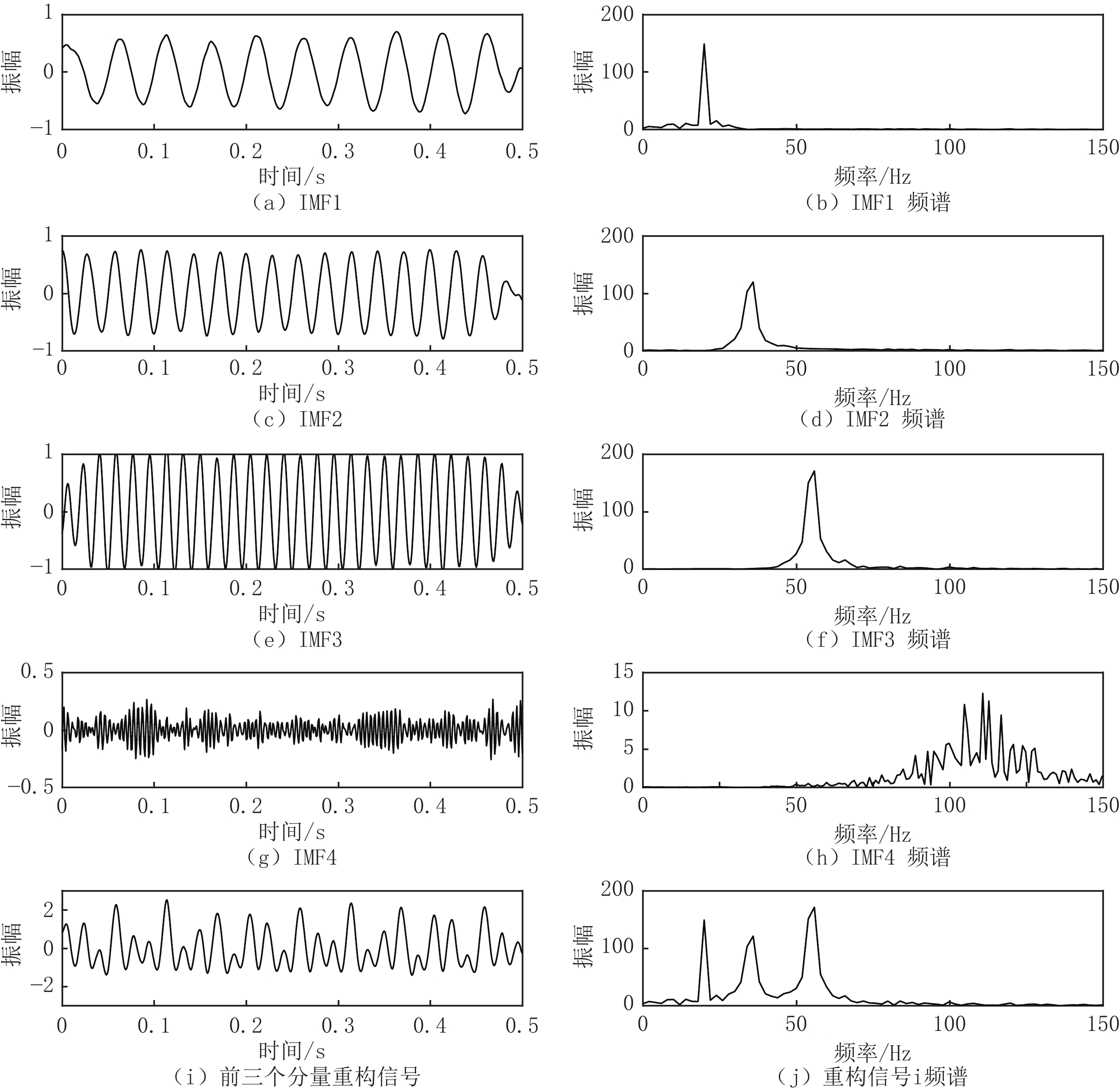
$ y $ 进行分频处理，结果如图3所示。由图3可知，本文提出的参数优化VMD算法在处理合成信号$ y $ 时，分解为4个模态分量，前3个分量（图3（a）、图3（c）、图3（e））分别对应3个简谐信号$ {y_1},\;{y_2},\;{y_3} $ （图1（a）、图1（c）、图1（e）），第4个分量为噪声分量（图3（g））。从图3（b）、图3（d）、图3（f）、图3（h）可知，即使存在噪声干扰的情况下，经优化的VMD算法也能将频率分别为20、35和55 Hz的分量以及高频噪声分量分离开来，且不存在模态混叠。![]()
图 3 信号$ y $ 的VMD分解及重构结果Figure 3. VMD decomposition and reconstruction results of signaly由表1可知，模态分量IMF1、IMF2、IMF3与对应简谐信号
$ {y_1},\;{y_2},\;{y_3} $ 之间的相关性较强，标准误差较小；信号$ y' $ （图1（g））与去除噪声分量的重构信号（图3（i））之间的相关系数较高，标准误差较小，表明本文提出的参数优化VMD方法分解精度较高，具有较强的抗噪声干扰能力。表 1 优化VMD分解精度评价指标Table 1. Optimize the evaluation index of VMD decomposition accuracy对应分量 相关系数 标准误差 IMF1-y1 0.9804 0.1025 IMF2-y2 0.9838 0.0904 IMF3-y3 0.9831 0.1302 Fig.3（i）-Fig.1（g） 0.9951 0.0512 将自适应VMD方法结合最大方差模原理应用于地震资料的高分辨率处理，利用如图4所示的合成地震记录进行测试。该合成地震记录由一组反射系数和主频为20 Hz的雷克子波褶积生成。利用本文1.3节所述的高频补偿方法对图4所示的合成记录进行频率补偿处理，结果如图5所示。对比处理前、后的信号，合成地震记录经参数优化VMD频率补偿处理后原波形被压缩，波形变窄，旁瓣得到压制，分辨率得到有效提高。由图6可知，合成记录进过频率补偿处理后，信号主频显著提升，频率信息得到丰富，拓宽了频带宽度，高频成分得到一定程度的恢复。
![]()
图 5 经VMD高频补偿前后信号对比Figure 5. Signal comparison before and after VMD high frequency compensation![]()
图 6 经VMD高频补偿前后信号振幅谱对比Figure 6. Comparison of signal amplitude spectrum before and after VMD high frequency compensation3.2 实际资料
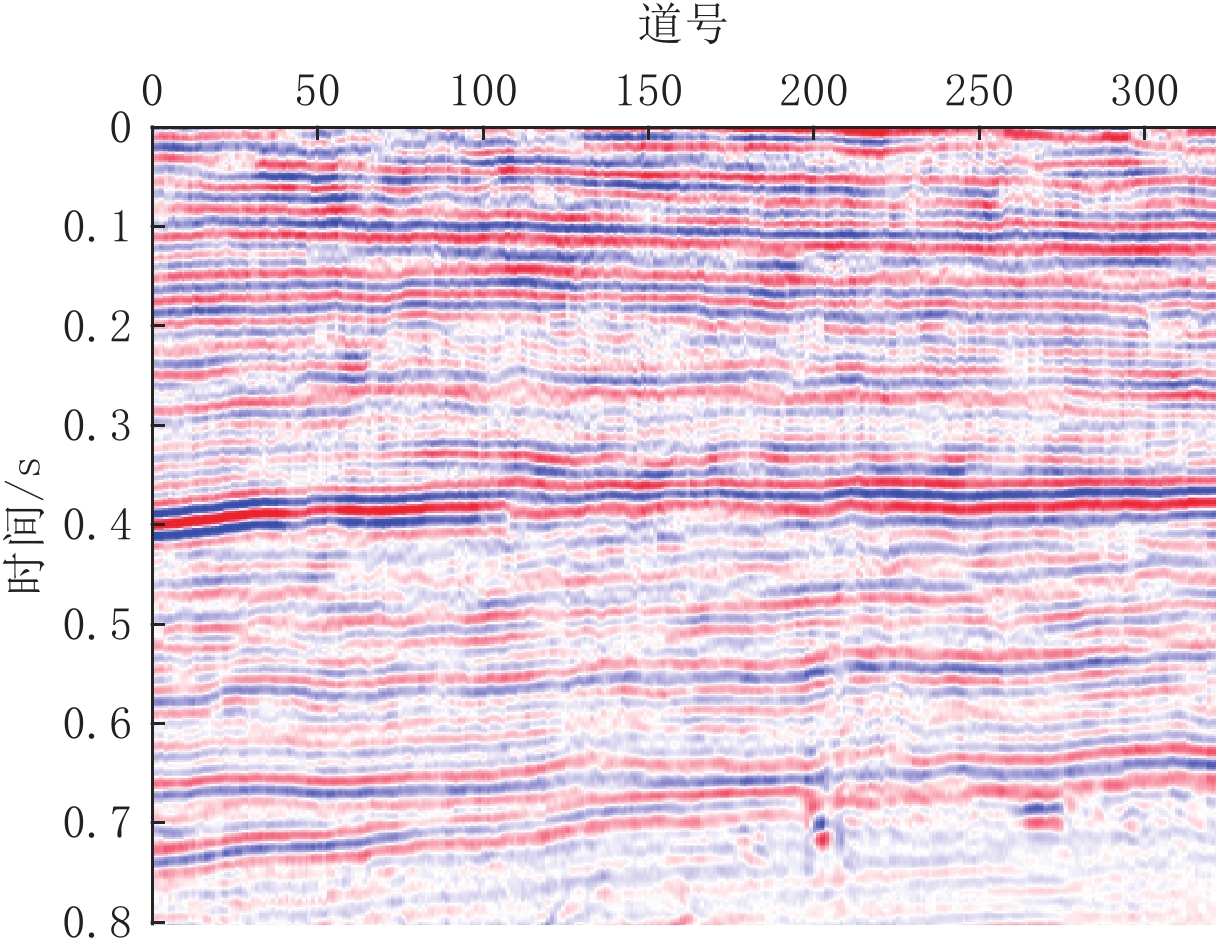
将本文提出的参数优化VMD方法应用于实际地震资料进行高分辨率处理，并与经典的反褶积方法处理结果进行对比。实际资料的原始地震数据（图7）共包含321道，每道数据包含801个采样点，每道采样间隔为1 ms。
图8为使用反褶积方法处理实际资料得到的结果。对比反褶积处理前后的地震剖面可知，反褶积方法使波形得到压缩，可以提高地震数据的垂向分辨率，但是降低了信噪比。利用本文提出的VMD参数优化算法对该实际资料进行高分辨率处理，最优参数为
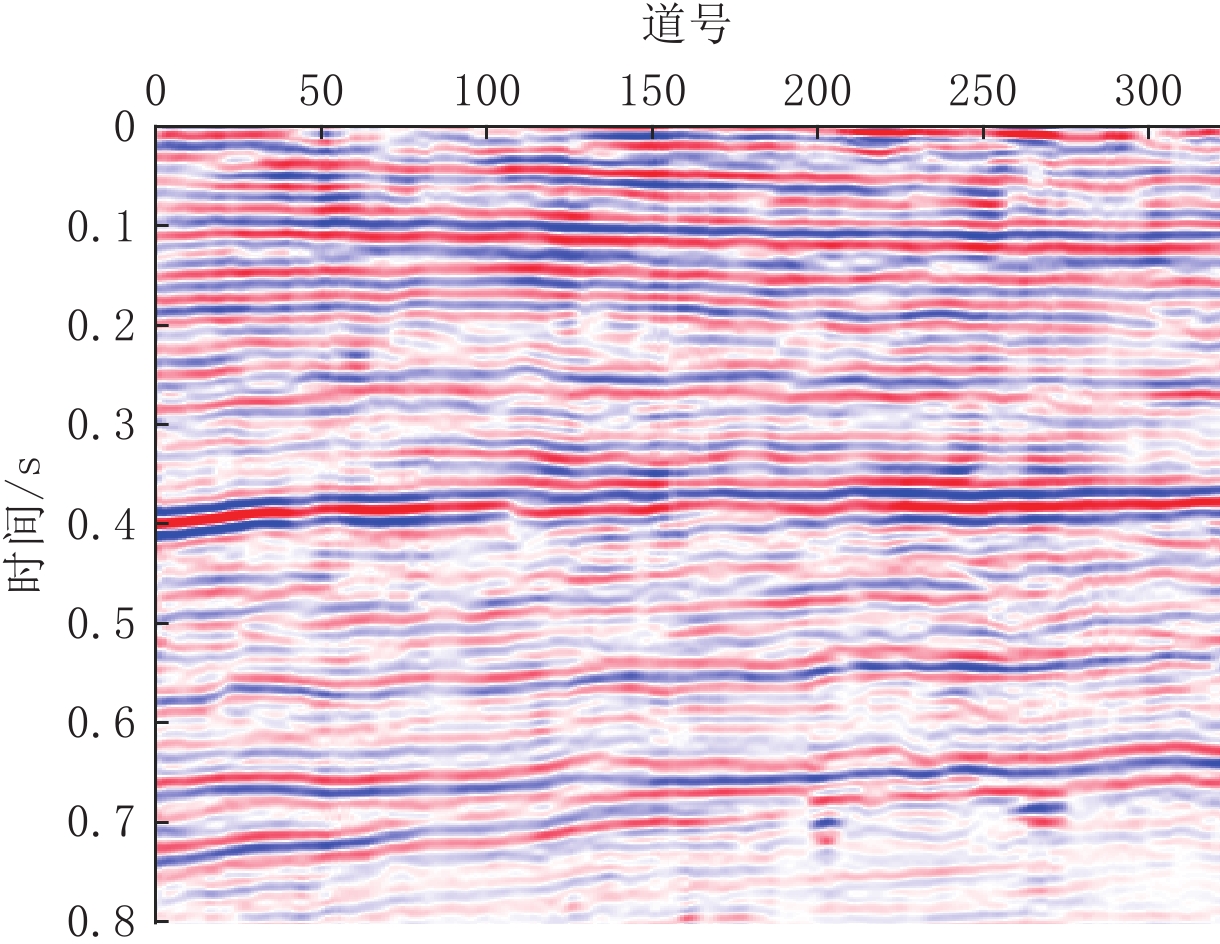
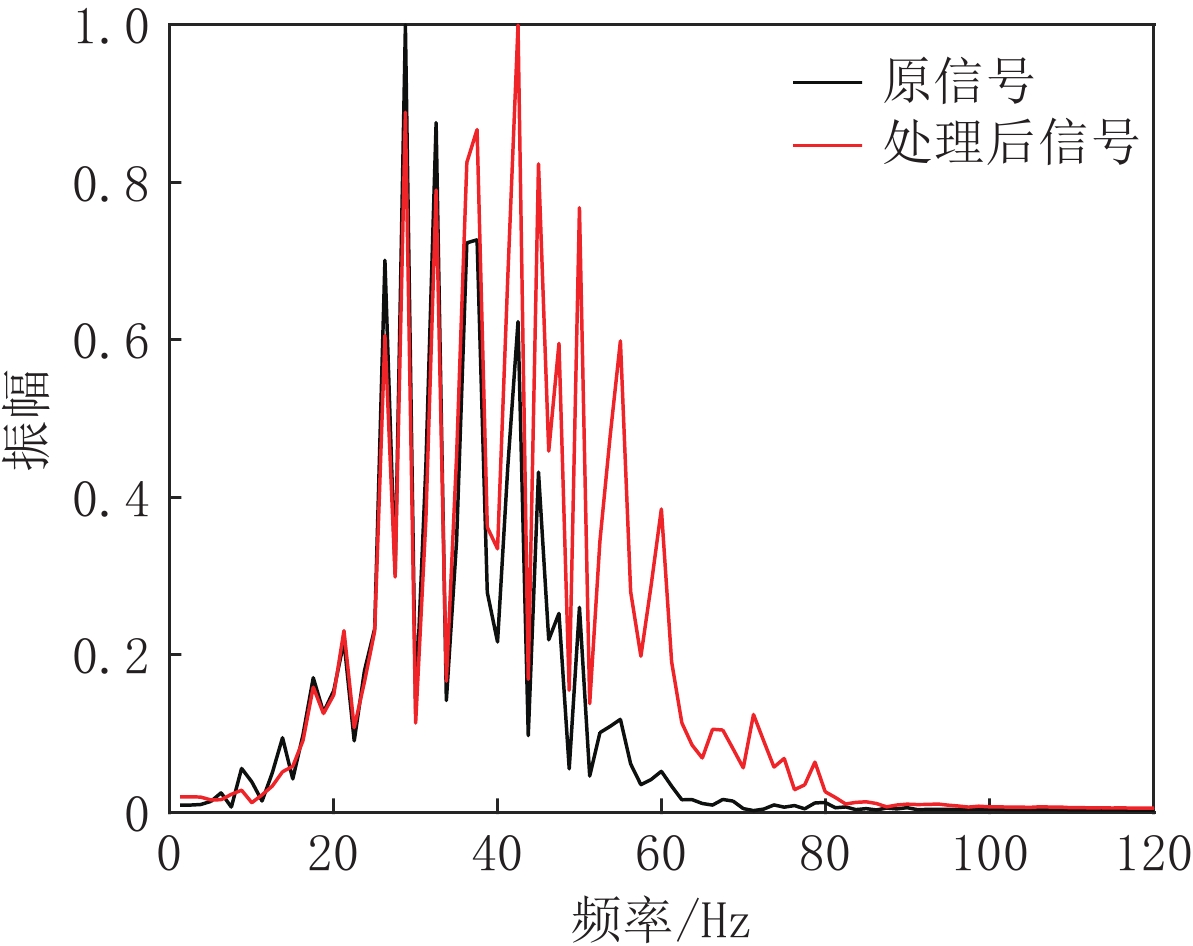
$ K $ =3，$ \alpha$ =1250，此时适应度函数值最小为0.8435。图9为用本文方法处理实际资料得到的结果，与原始地震剖面进行对比可知，经本方法处理后，原始地震数据的波形被压缩，提高了同相轴的精细程度；层间信息更加丰富，可分辨的地层增多，细节刻画更加精细，地震资料的分辨率得到提高。同时相比于反褶积方法，本文方法处理结果同相轴更加连续，地震资料的信噪比更高。图10为实际资料经本文方法处理前后的频谱对比。通过分析可知，处理前实际资料的主频约为30 Hz，经处理后主频提高到约42 Hz，地震资料的频带宽度由处理前的28～39 Hz扩展到28～50 Hz。经本文方法处理后，地震数据的主频得到了提高，有效频宽延展，频率信息得到了丰富。
![]()
图 10 本方法处理前后频谱对比Figure 10. Spectrum comparison before and after processing by this method4. 结论与认识
以提高地震资料分辨率为目的，本文提出了基于自适应VMD的分频高频补偿方法。首先该方法以功率谱熵、能量差、样本熵构建适应度函数，利用多目标蝙蝠算法对VMD参数的选取进行优化，可自适应获取全局最优VMD参数；并且优化后的VMD分频精度较高，克服了模态混叠问题，具有较强的抗噪声干扰能力。
其次利用优化VMD对地震信号各频率成分进行差异化补偿，补偿后的地震资料有效频宽延展，频率信息更加丰富，垂向分辨率得到有效提高，证明了方法的有效性。
但该优化VMD方法的计算效率随迭代次数和种群数量的增加而降低，在保证精度的同时，如何提高计算效率值得进一步研究。
-
![]()
图 3 信号
$ y $ 的VMD分解及重构结果Figure 3. VMD decomposition and reconstruction results of signaly
![]()
图 5 经VMD高频补偿前后信号对比
Figure 5. Signal comparison before and after VMD high frequency compensation
![]()
图 6 经VMD高频补偿前后信号振幅谱对比
Figure 6. Comparison of signal amplitude spectrum before and after VMD high frequency compensation
![]()
图 10 本方法处理前后频谱对比
Figure 10. Spectrum comparison before and after processing by this method
表 1 优化VMD分解精度评价指标
Table 1 Optimize the evaluation index of VMD decomposition accuracy
对应分量 相关系数 标准误差 IMF1-y1 0.9804 0.1025 IMF2-y2 0.9838 0.0904 IMF3-y3 0.9831 0.1302 Fig.3（i）-Fig.1（g） 0.9951 0.0512 
下载: 导出CSV
-
[1] 李振春, 王清振. 地震波衰减机理及能量补偿研究综述[J]. 地球物理学进展, 2007,22(4): 1147−1152. LI Z C, WANG Q Z. A review of research on mechanism of seismic attenuation and energy compensation[J]. Progress in Geophysics, 2007, 22(4): 1147−1152. (in Chinese).
[2] 周发祥, 宁鹏鹏, 刘斌, 等. 吸收衰减对地震分辨率的影响[J]. 石油地球物理勘探, 2008,43(S2): 84−87. ZHOU F X, NING P P, LIU B, et al. Influence of attenuation by absorption on seismic resolution[J]. Oil Geophysical Prospecting, 2008, 43(S2): 84−87. (in Chinese).
[3] 严宁, 程梦英. 地震资料处理中信噪比与反褶积的关系探究[J]. 中国石油和化工标准与质量, 2019,39(3): 122−123. [4] YUAN Y J, LI Y C, ZHOU S C. Multichannel statistical broadband wavelet deconvolution for improving resolution of seismic signals[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 59(2): 1772−1783.
[5] JIANG Y M, CAO S Y, CHEN S Y, et al. A blind nonstationary deconvolution method for multichannel seismic data[J]. Exploration Geophysics, 2021, 52(3): 245−257. doi: 10.1080/08123985.2020.1807319
[6] WANG Y H. Inverse Q-filter for seismic resolution enhancement[J]. Geophysics, 2006, 71(3): V51. doi: 10.1190/1.2192912
[7] LIU G C, LI C, RAO Y, et al. Oriented pre-stack inverse Q filtering for resolution enhancements of seismic data[J]. Geophysical Journal International, 2020, 223(1): 488−501. doi: 10.1093/gji/ggaa329
[8] SANGWAN P, KUMAR D. A robust approach to estimate Q from surface seismic data and inverse Q filtering for resolution enhancement[J]. First Break, 2021, 39(2): 35−43. doi: 10.3997/1365-2397.fb2021009
[9] 余锋. 反Q滤波在提高地震资料分辨率中的研究与应用[J]. 能源技术与管理, 2017,42(1): 153−154. [10] HAO Y J, HUANG H D, GAO J, et al. Inversion-based time-domain inverse Q filtering for seismic resolution enhancement[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(12): 1934−1938. doi: 10.1109/LGRS.2019.2914092
[11] 边国柱, 张立群. 地震数据的谱白化处理[J]. 石油物探, 1986,(2): 26−33. BIAN G Z, ZHANG L Q. Spectral whitening of seismic data[J]. Geophysical Prospecting for Petroleum, 1986, (2): 26−33. (in Chinese).
[12] LI F, LIU R, LOU Y, et al. Revisit seismic attenuation attributes: Influences of the spectral balancing operation on seismic attenuation analysis[J]. Interpretation, 2021, 9(3): 1−50.
[13] 李曙光, 徐天吉, 甘其刚, 等. 频率域小波变换分频处理在川西地震勘探中的应用[J]. 石油物探, 2010,49(5): 500−503. [14] 刘瑞, 何文章, 吴爱弟, 等. 基于多小波变换提高地震数据的分辨率[J]. 数学的实践与认识, 2011,41(20): 43−47. LIU R, HE W Z, WU A D, et al. Improving the Resolution ratio of seismic data by multiwavelets transformation[J]. Mathematics in Practice and Theory, 2011, 41(20): 43−47. (in Chinese).
[15] 路鹏飞, 郭爱华, 赵宝银, 等. 利用小波分析技术提高老爷庙油田地震资料分辨率[J]. 石油地球物理勘探, 2012,47(2): 272−276. LU P F, GUO A H, ZHAO B Y, et al. Seismic data reslution improvement in Laoyemiao by wavelet analysis[J]. Oil Geophysical Prospecting, 2012, 47(2): 272−276. (in Chinese).
[16] 余景奎. 提高分辨率处理的几种途径[J]. 特种油气藏, 2005,(5): 38−41. YU J K. Several ways of improving resolution[J]. Special Oil and Gas Reservoirs, 2005, (5): 38−41. (in Chinese).
[17] 余鹏, 李振春. 分频技术在储层预测中的应用[J]. 勘探地球物理进展, 2006, 29(6): 419-423. YU P, LI Z C. Application of frequency-divided technique in reservoir prediction[J]. Progress in Exploration Geophysics. 2006, 29(6): 419-423. (in Chinese).
[18] 马朋善, 王继强, 刘来祥, 等. Morlet小波分频处理在提高地震资料分辨率中的应用[J]. 石油物探, 2007,(3): 283−287. MA P S, WANG J Q, LIU L X, et al. Application of morlet wavelet frequency-division processing in enhancing the seismic data resolution[J]. Geophysical Prospecting for Petroleum, 2007, (3): 283−287. (in Chinese).
[19] 杨忠民, 黄大云. 小波变换在提高资料的信噪比和分辨率中的应用[J]. 石油地球物理勘探, 1994,29(5): 623−629. YANG Z M, HUANG D Y. Application of wavelet transform in improving both signal/noise ratio resolution of seimic data[J]. Oil Geophysical Prospecting, 1994, 29(5): 623−629. (in Chinese).
[20] 袁修贵, 宋守根, 张建贵, 等. 多分辨迭后地震记录频率振幅补偿方法[J]. 中南工业大学学报(自然科学版), 2001,(3): 224−226. YUAN X G, SONG S G, ZHANG J G, et al. Treatment of stacked seismic data with multiresolution frequency-amplitude compensation[J]. Journal of Central South University (Science and Technology), 2001, (3): 224−226. (in Chinese).
[21] 刘喜武, 年静波, 刘洪. 基于广义S变换的吸收衰减补偿方法[J]. 石油物探, 2006,(1): 9−14. LIU X W, NIAN J B, LIU H. Generalized S-transform based compensation for stratigraphic absorption of seismic attenuation[J]. Geophysical Prospecting for Petroleum, 2006, (1): 9−14. (in Chinese).
[22] 孙雷鸣, 万欢, 陈辉, 等. 基于广义S变换地震高分辨率处理方法的改进及在流花11-1油田的应用[J]. 中国海上油气, 2011,23(4): 234−237. SUN L M, WAN H, CHEN H, et al. An improved method of seismic high-resolution processing based on generalized S transform and its application in LH11-1 oilfield[J]. China Offshore Oil and Gas, 2011, 23(4): 234−237. (in Chinese).
[23] 黄捍东, 冯娜, 王彦超, 等. 广义S变换地震高分辨率处理方法研究[J]. 石油地球物理勘探, 2014,49(1): 82−88. HUAN H D, FENG N, WANG Y C, et al. High-resolution seismic processing based on generalized S transform[J]. Oil Geophysical Prospecting, 2014, 49(1): 82−88. (in Chinese).
[24] DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531−544. doi: 10.1109/TSP.2013.2288675
[25] 何元, 曹思远, 崔震, 等. 变分模态分解及其在地震去噪中的应用[C]//中国地球物理学会, 2014: 1. [26] 徐智, 唐刚, 刘伟, 等. 基于变分模态分解参数优化的地震随机噪声去除方法[J]. 北京化工大学学报(自然科学版), 2019,46(5): 60−68. DOI: 10.13543/j.bhxbzr.2019.05.009. XU Z, CAO S Y, LIU W, et al. Seismic random noise removal based on variational mode decomposition with parameter optimization[J]. Journal of Beijing University of Chemical Technology (Natural Science), 2019, 46(5): 60−68. DOI: 10.13543/j.bhxbzr.2019.05.009. (in Chinese).
[27] 江馀, 张军华, 韩宏伟, 等. 优化变分模态分解方法消除强反射影响−以东营凹陷沙四段滩坝砂目标处理为例[J]. 石油地球物理勘探, 2020,55(1): 147−152, 166. DOI: 10.13810/j.cnki.issn.1000-7210.2020.01.017. JIANG Y, ZHANG J H, HAN H W, et al. Elimination of strong reflection influence based on optimized variational mode decomposition method: A case study of the target processing of beach bar sand of Es4 in Dongying Sag[J]. Oil Geophysical Prospecting, 2020, 55(1): 147−152, 166. DOI: 10.13810/j.cnki.issn.1000-7210.2020.01.017. (in Chinese).
[28] 龙丹, 牛聪, 周怀来, 等. 基于VMD算法在地震数据时频分析中的应用[J]. 地球物理学进展, 2020,35(1): 0166−0173. DOI: 10.10.6038/pg2020CC0462. LONG D, NIU C, ZHOU H L, et al. Application of VMD algorithm in time-frequency analysis of seimic data[J]. Progress in Geophysics, 2020, 35(1): 0166−0173. DOI: 10.10.6038/pg2020CC0462. (in Chinese).
[29] YANG X S. A new metaheuristic bat-inspired algorithm[M]. Nature Inspired Cooperative Strategies for Optimization (NICSO 2010). Springer, Berlin, Heidelberg, 2010: 65-74.
[30] YANG X S. Bat algorithm for multi-objective optimisation[J]. International Journal of Bio-Inspired Computation, 2011, 3(5): 267−274. doi: 10.1504/IJBIC.2011.042259
-
期刊类型引用(1)
1. 张丽平，周小亮. 中国人工智能发展的时空网络结构及驱动因子研究. 福建江夏学院学报. 2024(04): 40-54 . 
百度学术
其他类型引用(1)
计量
- 文章访问数: 509
- HTML全文浏览量: 208
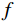
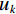
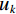
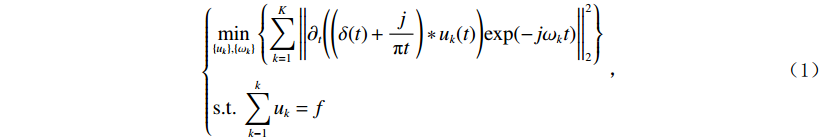
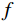
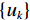
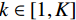
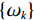
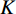
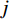
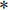
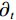
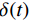
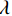
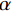
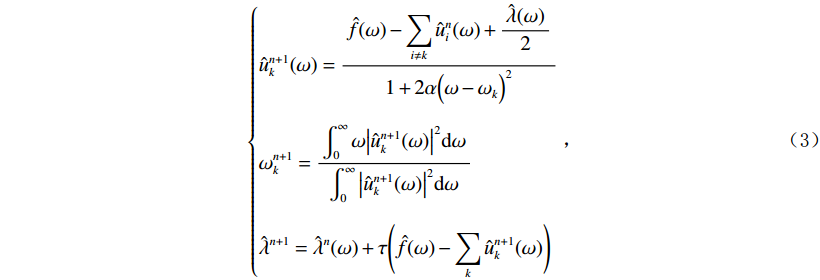
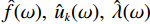
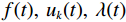
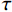
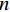
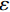
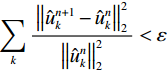
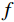
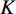
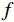
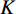
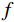
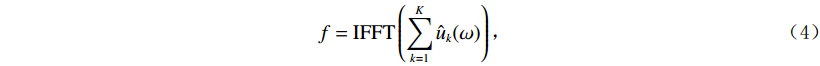
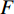
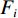
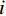
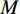
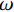
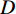
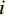
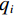
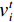
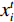
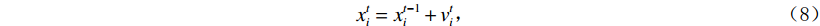
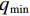
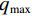
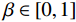
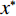
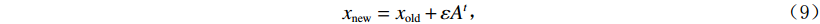
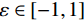
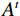
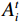
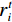
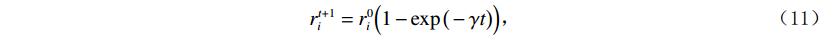
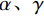
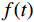
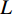
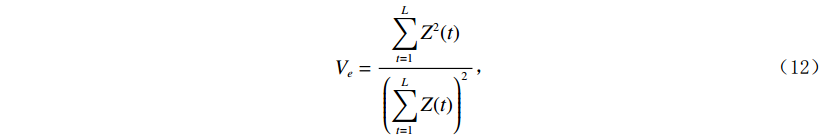
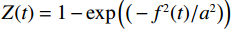
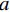
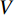
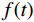
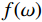
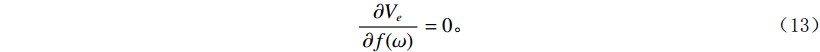
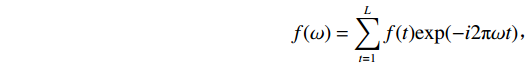
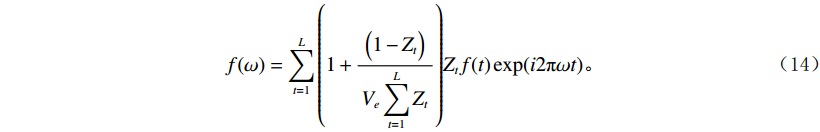
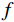
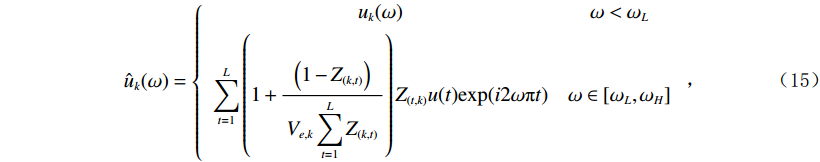
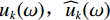
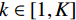
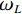
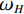
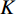
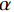
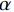
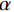
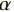
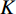
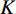
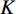
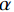
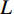
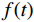
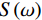
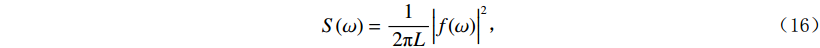
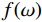
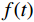
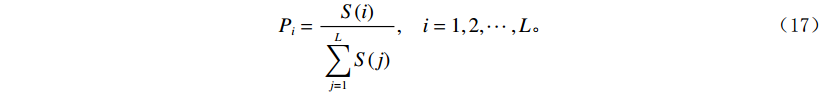
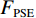
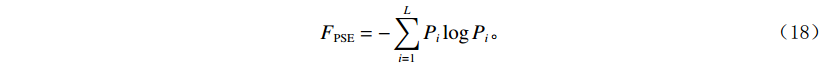
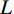
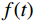
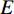
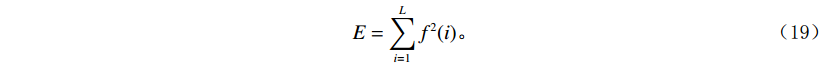
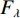
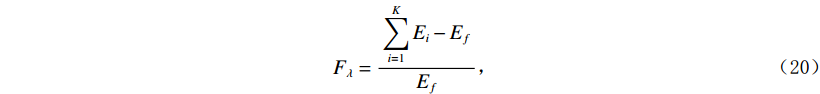
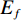
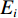
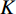
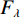
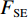
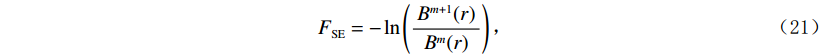
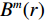
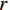
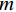
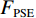
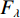
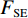
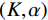
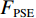
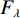
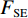
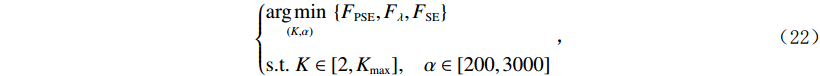
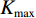
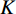
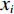
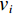
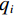
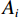
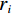
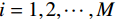
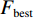
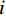
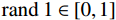
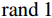
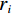
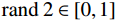
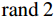
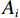
- PDF下载量: 76
- 被引次数: 2
