Research on the Application Value of 18F-FDG PET/CT Combined with Neuronal Antibody Detection in the Diagnosis and Treatment of PNS Patients
-
摘要:
目的:探讨全身<sup<18</sup<F-FDG PET/CT联合神经元抗体检测在神经系统副肿瘤综合征(PNS)患者诊疗中的应用价值。方法:回顾性收集56例临床疑诊PNS患者的临床、神经副肿瘤抗体检测及全身<sup<18</sup<F-FDG PET/CT资料,对照病理及临床随访结果,利用ROC曲线评价PET/CT、神经元抗体及二者联合检测结果的诊断效能。结果:56例疑诊PNS患者中,共有肿瘤患者20例,其中肿瘤伴PNS 19例,肿瘤伴脊髓转移1例。<sup<18</sup<F-FDG PET/CT显像提示肿瘤或可能肿瘤23例,其中20例为真阳性,3例为假阳性(随访结果分别为反流性食管炎、反应性骨改变、颈部炎性病变),其余33例为真阴性;敏感度、特异度、准确度分别为100.0%、91.7%、94.6%。神经元抗体阳性33例,其中PNS伴肿瘤8例(抗Amphiphysin抗体脑炎3例,抗GABAB抗体脑炎2例,抗Yo抗体脑炎1例,抗Hu抗体脑炎2例),PNS不伴肿瘤25例(LGI1抗体脑炎10例,抗Amphiphysin抗体脑炎3例,抗Hu抗体脑炎1例,抗GABAB抗体脑炎3例,抗Yo抗体脑炎3例,抗CASPR2、GAD65、NMDA、PNMA及SOX1抗体脑炎各1例);神经元抗体阴性23例(其中伴肿瘤12例);敏感度、特异度、准确度分别为40.0%、30.6%、33.9%。两种联合检测结果的敏感度、特异度、准确度分别为100.0%、33.3%、57.1%,50.0%、94.4%、78.6%。ROC分析显示AUC分别为0.958(<i<P</i<<0.001;95%CI,0.904~1.000)、0.353(<i<P</i<>0.05;95%CI,0.199~0.506)、0.667(<i<P</i<<0.05;95%CI,0.528~0.806)及0.672(<i<P</i<<0.05;95%CI,0.514~0.830),<sup<18</sup<F-FDG PET/CT及两种联合检测方法具有统计学意义。结论:全身<sup<18</sup<F-FDG PET/CT可作为疑诊PNS患者无创筛查肿瘤的一线检查方法。
Abstract:Objective: To explore the clinical value of whole-body <sup<18</sup<F-FDG PET/CT combined with neuroantibody detection in the diagnosis and treatment of paraneoplastic neurological syndromes (PNS). Methods: Clinical, laboratory, and imaging data of 56 hospitalized patients with suspected PNS who underwent systemic <sup<18</sup<F-FDG PET/CT and neuropathic tumor antibody detection were retrospectively collected and followed-up on. ROC curve analysis was performed to compare the diagnostic efficacy of PET/CT, neuronal antibodies, and their combined detection results. Results: Among the 56 patients with suspected PNS, there were 20 with malignant tumors, including 19 cases complicated with PNS and 1 patient with spinal cord metastasis which also le d to neurological symptoms. <sup<18</sup<F-FDG PET/CT imaging indicated tumors or possible tumors in 23 cases, of which 20 cases were true positive, 3 cases were false positive (the follow-up results were reflux esophagitis, reactive bone changes, or inflammatory lesions in the neck), and the remaining 33 cases were true negative. The sensitivity, specificity, and accuracy of PET/CT were 100%, 91.7%, and 94.6%, respectively. There were 33 cases with positive neuroantibodies, including 8 cases of tumors with PNS (3 cases with anti-amphiphysin antibody encephalitis, 2 cases with anti-GABAb antibody encephalitis, 1 case with anti-Yo antibody encephalitis, and 2 cases with anti-Hu antibody encephalitis). Moreover, there were 25 cases without tumors (10 cases with LGI1 antibody encephalitis, 3 cases with anti-amphiphysin antibody encephalitis, 1 case with anti-Hu antibody encephalitis, 3 cases with anti-GABAb antibody encephalitis, 3 cases with anti-Yo antibody encephalitis, 1 case with Anti-caspr2, 1 case with GAD65, 1 case with NMDA, 1 case with PNMA, and 1 case with SOX1 antibody (1 case each). Of these, 23 cases were negative (12 cases with tumor). The sensitivity, specificity, and accuracy of the neuronal antibody test were 40.0%, 30.6%, and 33.9%, respectively. Furthermore, the sensitivity, specificity, and accuracy of the combined detection were 100.0%, 33.3%, 57.1%, 50%, 94.4%, and 78.6%, respectively. ROC analysis showed that the AUC was 0.958 (<i<P</i<=0.000<0.05; 95% CI 0.904~1.000), 0.353 (<i<P</i<=0.070>0.05; 95% CI 0.199~0.506), 0.667 (<i<P</i<=0.040<0.05; 95% CI 0.528~0.806), and 0.672 (<i<P</i<=0.034<0.05; 95% CI 0.514~0.830). Conclusion: Whole-body 18F-FDG PET/CT has the potential to be the first choice for noninvasive tumor screening in patients with suspected PNS.
-
Keywords:
- FDG /
- PET/CT /
- paraneoplastic syndrome /
- paraneoplastic antibody
-
神经系统副肿瘤综合征(paraneoplastic neurological syndromes,PNS)是与恶性肿瘤相关但非肿瘤转移、感染及神经系统疾病机制引起的一组异质性疾病,发病机制尚未阐明,目前普遍认为由免疫介导引起[1-2]。PNS可于恶性肿瘤发现时或发现前出现,尽早明确PNS诊断、治疗原发疾病具有重要临床意义。
PNS通常病因不明,在寻找恶性肿瘤起源的过程中,影像学检查及实验室检查辅助诊断必不可少。然而,传统影像学方法(B超、CT或MRI等)序贯检查所用时间较长且往往不能确定诊断,实验室检查(如肿瘤标记物、神经元抗体检测等)诊断特异性不高,18F-FDG PET/CT作为一种无创的全身性检查方法,越来越多地被广泛应用于临床。因此,本文旨在探讨全身18F-FDG PET/CT及神经元抗体检测在PNS诊断中的应用价值及前景。
1. 资料和方法
1.1 一般资料
回顾性分析2015年至2021年首都医科大学附属北京天坛医院疑诊PNS住院患者的临床、实验室及影像检查资料,并进行随访。
纳入标准:通过影像系统,回顾性搜索病史中含有关键词“神经系统副肿瘤综合征或PNS”或“副肿瘤症状或综合征”的患者纳入研究。排除标准:新发肿瘤或肿瘤复发病史明确的患者;使用过免疫抑制剂的患者;PET/CT检查图像质量影响评估的患者。
56例住院期间行全身18F-FDG PET/CT及神经元抗体检测的患者纳入研究,其中男33例,女23例;年龄范围28~75岁,平均年龄(55.143±11.725)岁。对患者随访,随访时间为检查日至2022年3月18日,记录非肿瘤患者出现肿瘤或肿瘤患者出现新发肿瘤日期及时间、肿瘤类型,本研究患者的平均随访时间为(49.541±29.266)月。
1.2 检查方法
患者空腹6 h以上,控制血糖低于8.3 mmol/L,按照3.700~5.550 MBq/kg静脉注射18F-FDG平躺休息40~60 min后行PET/CT扫描(GE,Discovery Eilte 690)。扫描范围从颅底至头顶,螺旋CT扫描后3D-TOF模式采集PET图像8 min,有序子集最大期望值迭代法(OSEM)进行图像重建,于AW 4.5工作站图像后处理后传送至MedEx进行图像分析。
由两名高年资医生进行图像分析,在意见不一致的情况下,经过讨论达成统一结果。病灶在PET上为FDG高代谢,诊断为肿瘤或可能肿瘤的情况,定义为PET/CT检查阳性。联合检测分两种情况进行分析,联合检测1为PET或神经元抗体其中一种阳性,即认为联合检测阳性,联合检测2为PET及神经元抗体均为阳性即认为联合检测阳性。经过病理及随访诊断为恶性肿瘤,则定义为病理及随访结果阳性。
1.3 统计学分析
采用SPSS 22.0软件进行数据分析,计数资料采用χ2检验,计量资料用均数±标准差(
$\bar x \pm s $ )表示,分类资料采用例数和百分数表示。采用ROC曲线对比分析各检查的诊断效能。P<0.05认为差异有统计学意义。2. 结果
56例疑诊PNS患者中,共确诊肿瘤20例,包括:肿瘤伴PNS 19例,1例伴脊髓转移。20例肿瘤患者18F-FDG PET/CT显像均为阳性,36例非肿瘤患者显像结果包括33例真阴性结果及3例假阳性(随访结果分别为反流性食管炎、反应性骨改变、颈部炎性病变)。神经元抗体阳性33例,包括:肿瘤伴PNS 8例(抗Amphiphysin抗体脑炎3例,抗GABAB抗体脑炎2例,抗Yo抗体脑炎1例,抗Hu抗体脑炎2例)。不伴肿瘤25例(LGI1抗体脑炎10例,抗Amphiphysin抗体脑炎3例,抗Hu抗体脑炎1例,抗GABAB抗体脑炎3例,抗Yo抗体脑炎3例,抗CASPR2、GAD65、NMDA、PNMA及SOX1抗体脑炎各1例);阴性23例(肿瘤12例)。
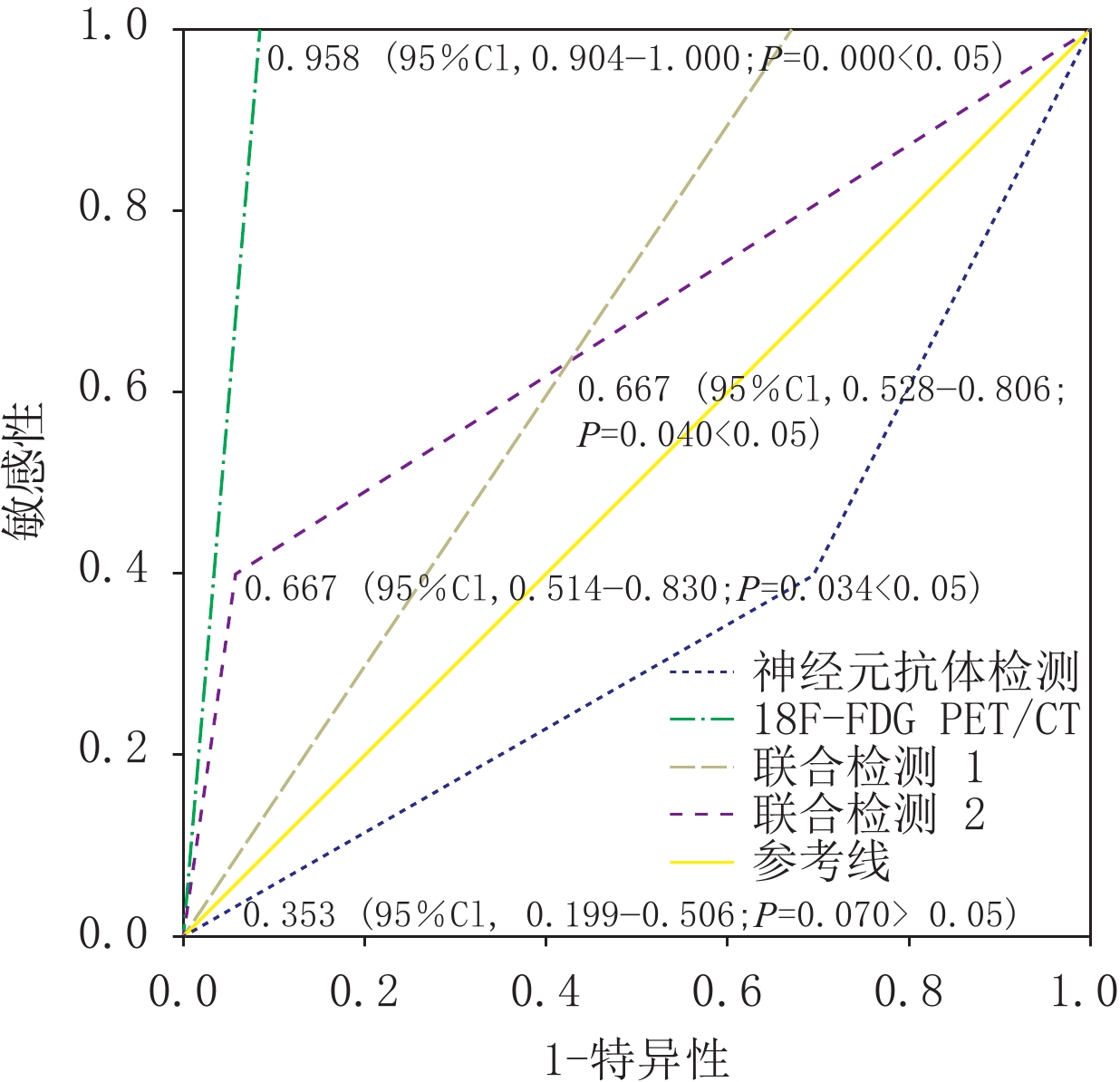
神经元抗体检测结果见表1。对照病理及随访结果,18F-FDG PET/CT检查、神经元抗体检测及两种联合检测的敏感度、特异度、准确度见表2。AUC曲线分析结果见图1。
表 1 疑诊PNS患者神经元抗体检测结果分析Table 1. Analysis of the detection results of the neuronal anstibodies in suspected PNS patients神经元抗体
检测结果合并肿瘤情况 病例数/例 神经元抗体类型/病例数(例) 阳性 肿瘤患者 8 抗Amphiphysin抗体脑炎3例,抗GABAB抗体脑炎2例,抗Yo抗体脑炎1例,抗Hu抗体脑炎2例 非肿瘤患者 25 LGI1抗体脑炎10例,抗Amphiphysin抗体脑炎3例,抗Hu抗体脑炎1例,抗GABAB抗体脑炎3例,抗Yo抗体脑炎3例,抗CASPR2、GAD65、NMDA、PNMA及SOX1抗体脑炎各1例 阴性 肿瘤患者 12 — 非肿瘤患者 11 — 表 2 18F-FDG PET/CT检查、神经元抗体检测及联合检测1、2与病理及随访结果对照Table 2. Comparison of 18F-FDG PET/CT, neuronal antibody detection, and combined detection 1 and 2 with the pathological and follow-up results检查方法 病理及随访 敏感度/% 特异度/% 准确度/% (+) ( − ) 合计 18F-FDG PET/CT检查 100.0 91.7 94.6 (+) 20 3 23 ( − ) 0 33 33 合计 20 36 56 神经元抗体检测 40.0 30.6 33.9 (+) 8 25 33 ( − ) 12 11 23 合计 20 36 56 联合检测1 100.0 33.3 57.1 (+) 20 24 44 ( − ) 0 12 12 合计 20 36 56 联合检测2 50.0 94.4 78.6 (+) 8 2 10 ( − ) 12 34 46 合计 20 36 56 3. 讨论
PNS是非直接由癌症转移或治疗后副作用、感染、营养不良、代谢紊乱或凝血障碍等引起的神经系统疾病,较为罕见,发生率不到肿瘤患者1%[3];可累及神经系统任何部位[4-7];发病机制尚未阐明,目前主要认为潜在肿瘤产生神经系统免疫应答从而引起临床症状[8]。
PNS可累及神经系统任何部分,从大脑皮质到神经肌肉接头和肌肉,主要分为3型:①免疫介导的脑炎包括经典的副肿瘤性脑炎综合征以及“自身免疫性脑炎”[9];②副肿瘤性小脑变性(paraneoplastic cerebellar degeneration,PCD)[10];③累及脊髓(脊髓综合征)、后根神经节(亚急性感觉神经元病)、周围神经、神经肌肉接头(Lambert-Eaton肌无力综合征、重症肌无力)和肌肉(皮肌炎和多发性肌炎等)的副肿瘤综合征[11-12]。
PNS症状复杂,早期、快速诊断并检出原发肿瘤较为困难。正常人很少存在副肿瘤抗体,如果存在抗体,应根据不同抗体提示的筛查方向仔细寻找潜在肿瘤[2]。
本研究中共有56例患者因怀疑PNS而进一步行神经元抗体检测,除外1例肺癌伴脊髓转移的患者,19例肿瘤患者PNS表现主要包括:副肿瘤性和自身免疫性脑炎6例,PCD 4例,累及脊髓、后根神经节、周围神经、神经肌肉接头和肌肉的副肿瘤综合征9例。8例肿瘤(8/20,40.0%)患者存在抗体阳性(8/33,24.2%),包括:6例“特征明确的”副肿瘤性抗体(针对神经元胞内蛋白的抗体)所致PNS,其中4例肺癌(2例抗Amphiphysin抗体脑炎、2例抗Hu抗体脑炎)、1例淋巴瘤(抗Amphiphysin抗体脑炎)、1例卵巢癌(抗Yo抗体脑炎);2例针对神经元细胞表面或突触蛋白的抗体,均为肺癌(抗GABAB抗体脑炎)。不伴肿瘤抗体阳性者25例(25/33,75.8%),包括:8例“特征明确的”副肿瘤性抗体(8/25,32.0%)及17例(17/25,68.0%)针对神经元细胞表面或突触蛋白抗体阳性的患者(表1)。这与以往研究报道一致,即“特征明确的”副肿瘤性抗体常提示存在基础肿瘤,而针对神经元细胞表面或突触蛋白的抗体可能与癌症或肿瘤有关或无关[8]。
神经元抗体对于肿瘤筛查及筛查部位具有一定提示意义,但存在较大局限性:①敏感度、特异度及准确度较低,本研究结果为40.0%、30.6% 及33.9%;②抗体阳性患者仍需要通过系列序贯检查明确原发病变部位、性质等,并且副肿瘤抗体的存在不是进行 18F-FDG PET/CT必不可少的因素[8]。
18F-FDG PET/CT作为无创评估全身的检查手段,在肿瘤筛查中发挥着重要作用,尤其是在检测小的、侵袭性肿瘤方面[3]。本研究中,20例肿瘤患者PET/CT显像均阳性,表现为肿瘤组织FDG摄取增高,包括:14例肺癌、2例前列腺癌、1例淋巴瘤、1例结肠癌、1例卵巢癌、1例输卵管癌复发,PET/CT检查敏感度为100%,阳性预测价值及阴性预测价值分别为87.0% 和100%,这与Marta O等在一项评估PET/CT在PNS中适用性的meta分析结果相一致,PET/CT在疑诊PNS肿瘤诊断中具有较高的敏感度及特异度,分别为0.81及0.88[3]。当然本研究的敏感度高达100%,可能与样本量较小以及来院就诊患者多为脑部肿瘤患者相关。
研究表明在疑诊PNS时,PET/CT在筛查肿瘤方面表现突出,识别了全部肿瘤,与需要检查多次、历时较长的超声、CT/MRI、增强CT/MRI等传统、序贯的影像学检查方法相比,在肿瘤筛查中具有更大优势[8],但PET/CT在FDG代谢增高的良性病变鉴别诊断中存在一定局限性,比如炎性肉芽肿病变、风湿、感染性病变、发热或升白药物等导致的骨反应性FDG代谢增高等,位置也多种多样,如胃肠道、淋巴结、肺、肾上腺、头颈部等[13]。
本研究中,36例非肿瘤患者中有3例为PET/CT显像假阳性,均为FDG代谢增高的良性病变,与恶性肿瘤性病变鉴别困难。另外,神经系统症状可发生在癌症诊断之前或之后,并且肿瘤与PNS或抗体不符时有存在其它肿瘤可能性[14],因此,需要在PET/CT阴性或无法直接取得病理的情况下,仍需进一步通过其他检查手段或随访确诊。本研究平均随访时间为(49.541±29.266)月,至随访结束,未出现新发或者诊断不一致的肿瘤患者。由于随访时间较短,可能存在假阴性的可能。
18F-FDG PET/CT在脑、脊髓等部位评估方面较传统检查方法具有增益价值。在MRI上边缘叶脑炎患者可见颞叶内侧及海马T2 Flair高信号或者异常强化,PCD患者症状出现数月后可见小脑萎缩等[15-16],但大多数患者表现正常,不具有特异性。而PNS患者脑及脊髓的FDG代谢异常较常见,尤其是合并神经元抗体阳性的患者,并且代谢改变程度常和脑炎分期相关。
在本研究中,30例患者出现脑部或脊髓代谢改变,通过全身PET/CT检查,识别出20例肿瘤患者中1例为转移所致,11例(包括6例脑炎抗体阳性)为肿瘤伴PNS所致脑部及脊髓代谢改变,单侧或双侧边缘叶、基底节区核团、脊髓常以代谢增高为主要改变。而脑皮层常表现为代谢不均匀减低,同期CT及近期MRI均未见明显形态学改变,这与Masangkey等[16]在对PNS患者脑 18F-FDG PET特征及与MRI表现相关性分析中所报道的PNS脑代谢改变特征结果相一致。PET/CT相对于传统影像学检查手段,在对患者进行综合评估方面能够提供帮助。
本研究进一步分析PET/CT、神经元抗体检测及两种联合检测结果。ROC分析提示单独PET/CT检测的AUC面积、敏感度及准确度均高于其他3种方法,全身18F-FDG PET/CT可作为疑诊PNS患者的肿瘤筛查及诊断的一线检查方法,但其价格较为昂贵限制了临床应用。神经元抗体检测可以提示某些肿瘤类型,有助于筛选出那些副肿瘤性疾病先于癌症发生的患者进行重点随访[17]。
另外,PNS的存在是否影响肿瘤结局,仍未达成一致观点。多数研究认为,副肿瘤性脑炎综合征(如Hu、Ri、Yo、amphiphysin、CRMP-5等)阳性肿瘤患者,治疗效果不佳,而与肿瘤相关的“自身免疫性脑炎”(如NMDA、GABA-A/B、Caspr2等抗体)阳性患者,治疗后可明显改善或恢复[9],例如,有研究认为合并PNS的小细胞肺癌病变更局限、预后较好[18]。因此,联合检测对于疑诊PNS患者的全面评估具有重要临床意义。
本研究存在一定局限性,样本量不足以对不同种类抗体阳性PNS患者脑部及脊髓的PET/CT表现特点进行归纳总结及亚组分析,需要更大数量样本量入组以进一步分析。
4. 结论
全身18F-FDG PET/CT可作为疑诊PNS患者无创筛查肿瘤的一线检查方法,联合神经元抗体检测能够更好地指导临床制定个体化诊疗策略。
-
表 1 疑诊PNS患者神经元抗体检测结果分析
Table 1 Analysis of the detection results of the neuronal anstibodies in suspected PNS patients
神经元抗体
检测结果合并肿瘤情况 病例数/例 神经元抗体类型/病例数(例) 阳性 肿瘤患者 8 抗Amphiphysin抗体脑炎3例,抗GABAB抗体脑炎2例,抗Yo抗体脑炎1例,抗Hu抗体脑炎2例 非肿瘤患者 25 LGI1抗体脑炎10例,抗Amphiphysin抗体脑炎3例,抗Hu抗体脑炎1例,抗GABAB抗体脑炎3例,抗Yo抗体脑炎3例,抗CASPR2、GAD65、NMDA、PNMA及SOX1抗体脑炎各1例 阴性 肿瘤患者 12 — 非肿瘤患者 11 — 表 2 18F-FDG PET/CT检查、神经元抗体检测及联合检测1、2与病理及随访结果对照
Table 2 Comparison of 18F-FDG PET/CT, neuronal antibody detection, and combined detection 1 and 2 with the pathological and follow-up results
检查方法 病理及随访 敏感度/% 特异度/% 准确度/% (+) ( − ) 合计 18F-FDG PET/CT检查 100.0 91.7 94.6 (+) 20 3 23 ( − ) 0 33 33 合计 20 36 56 神经元抗体检测 40.0 30.6 33.9 (+) 8 25 33 ( − ) 12 11 23 合计 20 36 56 联合检测1 100.0 33.3 57.1 (+) 20 24 44 ( − ) 0 12 12 合计 20 36 56 联合检测2 50.0 94.4 78.6 (+) 8 2 10 ( − ) 12 34 46 合计 20 36 56 -
[1] YAN J, CHEN Z, LIANG Y, et al. Anti-CV2/CRMP5 antibody-positive paraneoplastic neurological syndromes with chronic intestinal pseudo-obstruction in a small-cell lung cancer patient: A case report and literature review[J]. The Journal of International Medical Research, 2020, 48(12): 1220774018.
[2] SUNDERMANN B, SCHRODER J B, WARNECKE T, et al. Imaging workup of suspected classical paraneoplastic neurological syndromes: A systematic review and retrospective analysis of 18F-FDG-PET-CT[J]. Academic Radiology, 2017, 24(10): 1195−1202. doi: 10.1016/j.acra.2017.03.022
[3] SHEIKHBAHAEI S, MARCUS C V, FRAGOMENI R S, et al. Whole-body 18F-FDG PET and 18F-FDG PET/CT in patients with suspected paraneoplastic syndrome: A systematic review and Meta-analysis of diagnostic accuracy[J]. Journal of Nuclear Medicine, 2017, 58(7): 1031−1036. doi: 10.2967/jnumed.116.183905
[4] BINKS S, Uy C, HONNORAT J, et al. Paraneoplastic neurological syndromes: A practical approach to diagnosis and management[J]. Practical Neurology, 2022, 22(1): 19−31. doi: 10.1136/practneurol-2021-003073
[5] LAMBERT N, LUTTERI L, SADZOT B, et al. Paraneoplastic neurological syndromes[J]. Revue Médicale de Liège, 2021, 76(5/6): 413−418.
[6] FU P, HE L, TANG N, et al. A single center retrospective study of paraneoplastic neurological syndromes with positive onconeural antibodies[J]. Journal of Clinical Neuroscience, 2021, 89: 336−342. doi: 10.1016/j.jocn.2021.05.027
[7] 冉艳萍. 儿童中枢神经系统副肿瘤综合征的研究进展[J]. 国际儿科学杂志, 2020,47(8): 552−555. doi: 10.3760/cma.j.issn.1673-4408.2020.08.009 RAN Y P. Research progress of paraneoplastic syndrome of central nervous system in children[J]. International Journal of Pediatrics, 2020, 47(8): 552−555. (in Chinese). doi: 10.3760/cma.j.issn.1673-4408.2020.08.009
[8] OPALINSKA M, SOWA-STASZCZAK A, WEZYK K, et al. Additional value of 18F-FDG PET/CT in detection of suspected malignancy in patients with paraneoplastic neurological syndromes having negative results of conventional radiological imaging[J]. Journal of Clinical Medicine, 2022, 11(6): 1537.
[9] DALMAU J, GEIS C, GRAUS F. Autoantibodies to synaptic receptors and neuronal cell surface proteins in autoimmune diseases of the central nervous system[J]. Physiological Reviews, 2017, 97(2): 839−887. doi: 10.1152/physrev.00010.2016
[10] MASSA F, FILIPPI L, BENEDETTI L, et al. FDG PET Unveils the course of paraneoplastic cerebellar degeneration: A semiquantitative analysis[J]. Clinical Nuclear Medicine, 2021, 46(6): e327-e328.
[11] 刘磊, 杨文秋, 王保平, 等. 貌似运动神经元病的神经系统副肿瘤综合征1例报告及文献分析[J]. 中风与神经疾病杂志, 2021, 38(3): 258-259. LIU L, YANG W Q, WANG B P, et al. A case report and literature analysis of paraneoplastic syndrome of nervous system resembling motor neuron disease[J]. Journal of Stroke & Neuropathy, 2021, 38(3): 258-259. (in Chinese).
[12] 孙江, 王兴臣, 姬琳, 等. 以周围神经病变为首发症状的神经系统副肿瘤综合征1例报道并文献复习[J]. 中华全科医学, 2021, 19(12): 2158-2159. SUN J, WANG X C, JI L, et al. A case report of paraneoplastic syndrome with peripheral neuropathy as the first symptom and literature review[J]. Chinese Journal of General Practice, 2021, 19(12): 2158-2159. (in Chinese).
[13] KRISTENSEN S B, HESS S, PETERSEN H, et al. Clinical value of FDG-PET/CT in suspected paraneoplastic syndromes: A retrospective analysis of 137 patients[J]. European Journal of Nuclear Medicine and Molecular Imaging, 2015, 42(13): 2056−2063. doi: 10.1007/s00259-015-3126-2
[14] 伊骏飞, 郝洪军, 刘琳琳, 等. 神经系统副肿瘤综合征与神经副肿瘤抗体分析[J]. 中国神经免疫学和神经病学杂志, 2020,27(2): 104−108. doi: 10.3969/j.issn.1006-2963.2020.02.005 YI J F, HAO H J, LIU L L, et al. Analysis of paraneoplastic syndrome in nervous system and its antibody[J]. Chinese Journal of Neuroimmunology and Neuropathy, 2020, 27(2): 104−108. (in Chinese). doi: 10.3969/j.issn.1006-2963.2020.02.005
[15] ISHIKAWA H, SHINDO A, NIWA A, et al. Long-term MRI changes in a patient with Kelch like protein 11-associated paraneoplastic neurological syndrome[J]. Journal of the Neurological Sciences, 2021, 28(12): 4261-4266.
[16] MASANGKAY N, BASU S, MOGHBEL M, et al. Brain 18F-FDG-PET characteristics in patients with paraneoplastic neurological syndrome and its correlation with clinical and MRI findings[J]. Nuclear Medicine Communications, 2014, 35(10): 1038-1046.
[17] 康磊, 徐小洁, 马超, 等. FDG PET/CT在诊断神经系统副肿瘤综合征的研究进展[J]. 中国肿瘤临床, 2014,41(10): 667−670. doi: 10.3969/j.issn.1000-8179.20140196 KANG L, XU X J, MA C, et al. Research progress of FDG PET/CT in diagnosis of paraneoplastic syndrome of nervous system[J]. Chinese Journal of Oncology, 2014, 41(10): 667−670. (in Chinese). doi: 10.3969/j.issn.1000-8179.20140196
[18] GRAUS F, DALMOU J, RENE R, et al. Anti-Hu antibodies in patients with small-cell lung cancer: Association with complete response to therapy and improved survival[J]. Journal of Clinical Oncology, 1997, 15(8): 2866−2872. doi: 10.1200/JCO.1997.15.8.2866
-
期刊类型引用(4)
1. 刘德详. 智慧货物安检系统在机场物流的运用探析. 中国航务周刊. 2025(16): 75-77 .  百度学术
百度学术
2. 孙运达,魏云超,张丽. 安检CT图像目标物识别方法研究进展. CT理论与应用研究. 2024(02): 263-271 .  本站查看
本站查看
3. 刘必成,易茜,宗春光,许艳伟,李亮. 基于梯度特征聚类分析的大尺寸物体CT图像环状伪影校正方法. CT理论与应用研究. 2024(06): 781-789 .  本站查看
本站查看
4. 邹伟,朱国平,凌云龙,宗春光,刘必成,易茜,张一鸣,邓艳丽,李君利. 集装箱CT检查系统二维防散射滤线栅作用分析. 强激光与粒子束. 2023(08): 154-159 .  百度学术
百度学术
其他类型引用(1)




 下载:
下载: